Модуль вектора определить: Как найти модуль вектора? Ответ на webmath.ru

7.2.1. Модуль вектора MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MathCAD 12

• Линейная алгебра
• 7.1. Простейшие матричные операции
  • 7.1.1. Транспонирование
  • 7.1.2. Сложение и вычитание
  • 7.1.3. Умножение
• 7.2. Векторная алгебра
  • 7.2.1. Модуль вектора
  • 7.2.2. Скалярное произведение
  • 7.2.3. Векторное произведение
  • 7.2.4. Векторизация массива
• 7.3. Вычисление определителей и обращение квадратных матриц
  • 7.3.1. Определитель квадратной матрицы
  • 7.3.2. Ранг матрицы
  • 7.3.3. Обращение квадратной матрицы
  • 7.3.4. Возведение квадратной матрицы в степень
  • 7.3.5. Матричные нормы
  • 7.3.6. Число обусловленности квадратной матрицы
• 7.4. Вспомогательные матричные функции
  • 7.4.1. Автоматическая генерация матриц
  • 7.4.2. Разбиение и слияние матриц
  • 7. 4.3. Сортировка элементов матриц
  • 7.4.4. Вывод размера матрицы

Модуль вектора (vector magnitude) по определению равен квадратному корню из суммы квадратов его элементов (листинг 7.8).

ВНИМАНИЕ!

Не путайте модуль вектора и определитель матрицы, который обозначается тем же символом (с/м. разд. 7,3.1). Это характерный пример оператора, действующего по-разному на векторы и квадратные матрицы.

Листинг 7.8. Модуль вектора

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9911 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6937 0

Глава 2 Работа с файлами Mathcad 11

12379 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster. ru обязательна. 0.2261 s

Глава 29. Понятие вектора. Проекция вектора

Направленные отрезки принято называто также геометрическими векторами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертовй наверху при условии, что первая из них обозначает начало, вторая — конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца стрелки, изображающей вектор (рис. 1, где изображен вектор

а с началом А и концом В). Начало вектора часто будет называться таже его точкой приложения.

Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.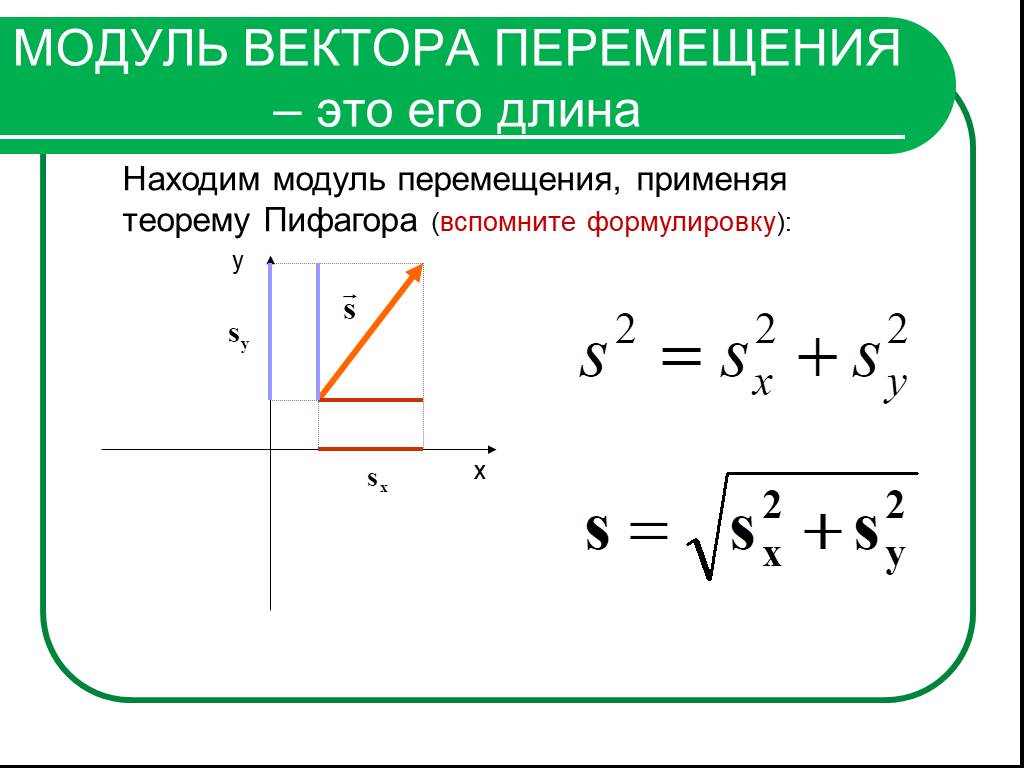

Число, равное длине вктора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом или а. Если , то вектор называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором , называется ортом вектора и обозначается обычно символом .

Проекцией вектора на ось u называется число, равное величине отрезка оси u, где точка является проекцией точки А на ось u, а — проекцией точки В на эту ось.

Проекция вектора на ось u обозначается символом . Если вектор обозначен символом , то его проекцию на ось u принято обозначать: .

Проекция вектора на ось u выражается через его модуль и угол наклона к оси u формулой

.

Проекции произвольного вектора на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, Y, Z.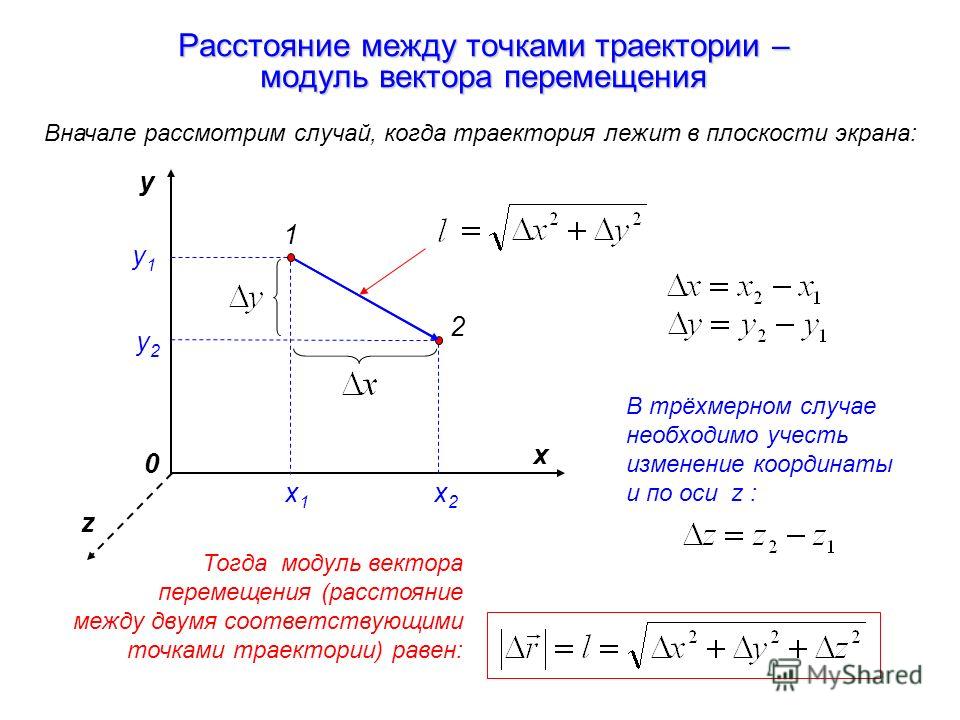 Равенство ={X, Y, Z} означает, что числа X, Y, Z являются проекциями вектора на координатные оси. Вектор, для которого X=Y=Z=0, называется нулевым и обозначается .

Проекции вектора на координатные оси называются также его (декартовыми) координатами. Если даны две точки (, , ) и (, , ), являющиеся соответственно началом и концом вектора , то его координаты X, Y, Z определяются по формулам , , .

Формула

(2)

позволяет по координатам вектора определить его модуль.

Если , , — углы, которые составляет вектор с координатными осями (см. рис. 2), то , , называются направляющими косинусами вектора .

Вследствие формулы (1)

, , .

Отсюда, и из формулы (2) следует, что

.

Последнее равенство позволяет определить один из углов , , , если известны два других.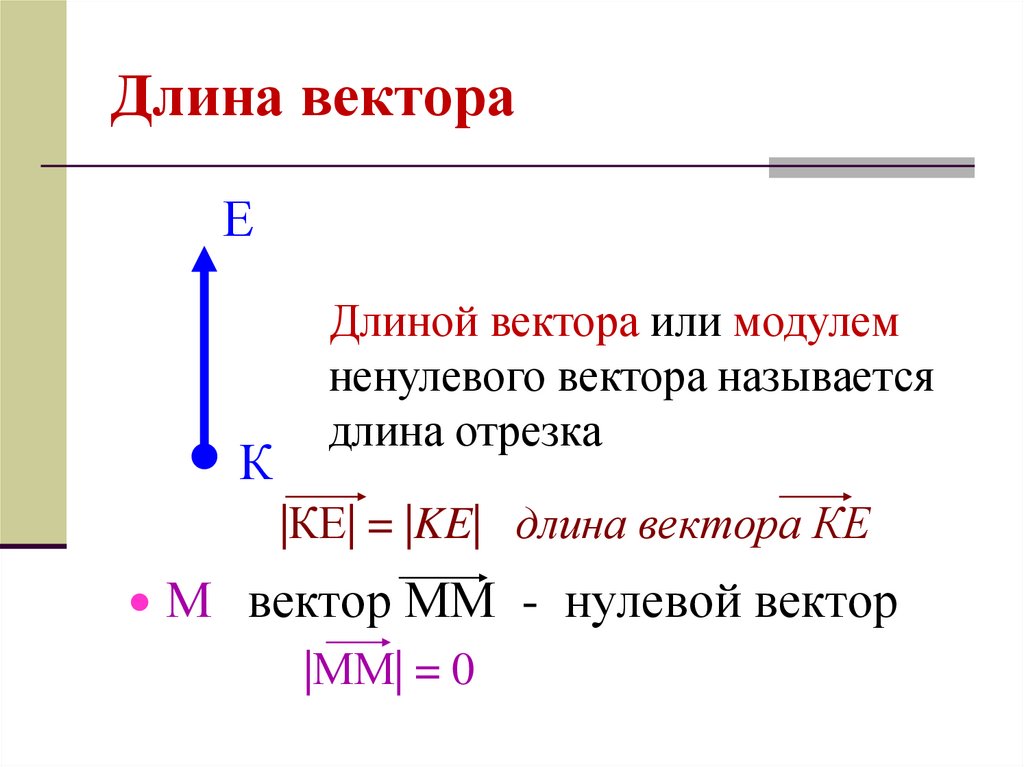

748		Вычислить модуль вектора ={6; 3; -2}.
749		Даны две координаты вектора X=4, Y=-12. Определить его третью координату Z при условии, что =13.
750		Даны точки A(3; -1; 2), B(-1; 2; 1). Найти координаты векторов и .
751		Определить точку N, с которой совпадает конец вектора ={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3).
752		Определить начало вектора ={2; -3; -1}, если его конец совпадает с точкой (1; -1; 2).
753		Дан модуль вектора =2 и углы =450, =600, =1200. Вычислить проекции вектора на координатные оси.
754		Вычислить направляющие косинусы вектора ={12; -15; -16}.
755		Вычислить направляющие косинусы вектора ={3/13; 4/13; 12/13}.
756		Может ли вектор составлять с координатными осями следующие углы:
	756.1	=450, =600, =1200;
	756. 2	=450, =1350, =600;
	756.3	=900, =1500, =600.
757		Может ли вектор составлять с двумя координатными осями следующие углы:
	757.1	=300, =450;
	757.2	=600, =600:
	757.3	=1500, =300.
758		Вектор составляет с осями Ox и Oz углы =1200и =450. Какой угол он составляет с осью Oy?
759		Вектор составляет с координатными осями Ox и Oy углы =600, =1200 . Вычислить его координаты при условии, что =2.
760		Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.

Величина вектора – объяснение и примеры

Мы уже знаем, что две части вектора – это величина вектора и направление вектора. Что мы можем узнать о векторе по его величине?

Величина вектора — это длина или размер вектора.

В этом разделе мы обсудим следующие аспекты величины вектора:

• Что такое величина вектора?
• Величина вектора Формула
• Как найти величину вектора?

 

Какова величина вектора?

В физике и математике величина вектора может быть определена как:

«Длина вектора или расстояние между начальной точкой и конечной точкой вектора».

Величина вектора A записывается как | А |. Если AB — это вектор, который начинается в точке A и заканчивается в точке B, его величина может быть представлена ​​как | АБ |.

Напомним, что векторы также могут быть записаны в виде пары координат, и мы называем это представление вектор-столбцом. Например, вектор A = (x1,y1) является вектор-столбцом. Этот вектор будет смоделирован в декартовой системе координат как отрезок, проходящий от (0,0) до (x1, y1) со стрелкой на конце, как показано ниже. В этом примере величина | A |, вектора A длина отрезка.

 

Величина вектора Формула

В этом разделе мы изучим математические формулы, используемые для определения величины вектора в различных измерениях.

• Величина вектора в двух измерениях
• Величина вектора в трех измерениях
• Величина вектора Формула для n измерений
• Величина вектора с использованием формулы расстояния

Величина вектора Вектор в двух измерениях

Чтобы определить величину двумерного вектора по его координатам, мы возьмем квадратный корень из суммы квадратов каждой из его составляющих. Например, формула для вычисления величины вектора 92

Таким образом, используя эти формулы, мы можем легко определить величину любого вектора в любом измерении.

Величина вектора с использованием формулы расстояния

Поскольку величина вектора MN   представляет собой расстояние между его начальной точкой M и конечной точкой N, его величина обозначается как | МН |. 2

Чтобы использовать приведенную выше формулу, мы сначала берем x-координату конечной точки и вычитаем x-координату начальной точки. Затем возводим полученное значение в квадрат. Точно так же мы вычитаем координату y начальной точки из координаты y конечной точки и возводим полученное значение в квадрат.

Наконец, мы складываем эти квадраты значений вместе и извлекаем квадратный корень. Это даст нам величину вектора.

Как найти величину вектора?

В этом разделе мы будем практиковаться в вычислении величин различных векторов.

Примеры:

Эти примеры включают пошаговые решения для лучшего понимания расчета величины вектора.

Пример 1

Выразите заданный вектор AD , как показано на изображении ниже, в виде вектора-столбца и определите его величину.

Решение

По определению вектор-столбец может быть выражен как упорядоченная пара. На изображении выше видно, что вектор 92

| н. э. | =  √  9+16

| н.э. | = √ 25

| н.э. | = 5

Таким образом, величина или длина вектора AD составляет 5 единиц.

Пример 2

Выразите заданный вектор UV , как показано на изображении ниже, в виде вектора-столбца и определите его величину.

Решение

По определению вектор-столбец может быть выражен как упорядоченная пара. На изображении выше видно, что вектор UV начинается в точке U и заканчивается в точке V. Он смещен на 3 точки вправо по оси x и на 2 точки вниз по оси y.

Таким образом, данный вектор UV может быть выражен как вектор-столбец:

UV = (5, -2)

Примечание: -2 указывает, что вектор смещен вниз по оси y.

Величина данного вектора может быть найдена по формуле величины для двумерных векторов:

92

| УФ | = √ 25 + 4

| УФ | = √   29

Таким образом, модуль или длина вектора UV составляет √   29 единиц.

Пример 3

Определить модуль вектора V = (4,-4,-2).

Решение

Данный вектор является трехмерным вектором, и его величина может быть вычислена по формуле трехмерной величины: 92

| В | = √ 16 + 16 + 4

| В | = √ 36

| В | = 6 единиц

Таким образом, модуль трехмерного вектора V равен 6 единицам.

Пример 4

Определите модуль вектора OW, , начальная точка которого O = (2,5), а конечная точка W = (5,2).

Решение

Мы можем использовать формулу расстояния, чтобы определить величину заданного вектора 92

| ОВ | =    3 √  2 единицы

Таким образом, величина вектора OW составляет приблизительно 4,242 единицы.

Пример 5

Определить модуль вектора PQ, начальная точка которого P = (-4, 2), а конечная точка Q = (3,6).

Решение

Мы можем использовать формулу расстояния для определения величины заданного вектора PQ :

| ПК 92

| ПК | = √ 49 + 16

| ПК | = √ 65 единиц

Таким образом, величина вектора PQ составляет приблизительно 8,062 единицы.

Пример 6

Определить модуль вектора AB, , начальная точка которого A = (3, 2,0), а конечная точка B = (0,5, 3).

Решение

Мы можем использовать формулу расстояния, чтобы определить величину заданного вектора 92

| АБ | = √ 9 + 9 + 9

| АВ | = √ 27

| АВ | = √ 3*9

| АВ | = 3 √ 3 ​​

Таким образом, величина вектора AB составляет примерно 5,196 единицы.

Практические вопросы

Определите величину следующих векторов:

1. x = 20m, север
2. A = (-1, -2/3)
3. F = (4, 10)
4. V = (2, 5, 3)
5. T = (0, 2, -1)
6. CD = (3, 2, 5)
7. Вектор, начальная точка которого

   40 OA

   OA при O = (-1,0, 3) и конечной точке A = (5,2,0)
8. UV, , где U = (1, -2) и V = (-2,2)
9. Выразите данный вектор PQ на изображении ниже как вектор-столбец и определите его величину.
10. Выразите заданный вектор MN , как показано на изображении ниже, в виде вектора-столбца и определите его величину.
11. Вычислите модуль вектора XZ на изображении ниже, где X = (0,1) и Z = (3,6).

Ответы

1. Величина данного вектора | Х | = 2м.
2. Величина заданного вектора A равна | А | =√ 13/9 ед.
3. Величина | Ф | = √ 116 единиц
4. Величина данного вектора равна | В | = √ 38 ед.
5. Величина вектора T | Т | = √ 5 ед.
6. Величина данного вектора | CD | = √ 38 ед.
7. Величина | А |= 7 шт.
8. Величина данного вектора | УФ | = √ 29 ед.
9. Вектор PQ можно выразить в виде вектор-столбца:

PQ = (5,5)

То есть вектор PQ начинается в точке P и заканчивается в точке Q. Он переводится на 5 точек вправо по горизонтальной оси и на 5 пунктов вверх. Модуль вектора PQ | ПК | = √ 50 ед.

10. Вектор MN может быть выражен как вектор-столбец:

MN = (-2, -4)

Это означает, что вектор MN начинается в точке M и заканчивается в точке N. Он переносится на 2 точки влево по горизонтальной оси и на 4 точки вниз по оси y. Величина вектора MN равна | МН | = √ 20 ед.

11. Величина вектора XZ равна | ХЗ | = √ 45 единиц.

Предыдущий урок | Главная страница | Следующий урок

Величина вектора — определение, направление и значение

Вектор – это объект, который содержит как величину, так и направление. Сила и скорость — два примера векторных величин. Понимание величины вектора укажет на силу силы, и точно так же скорость любого объекта связана со скоростью. В следующей статье объясняются величина и направление векторов.

На рисунке ниже показан вектор:

(Изображение будет загружено в ближайшее время)

(Изображение будет загружено в ближайшее время)

Вектор имеет величину (то есть размер) и направление:

Длина приведенной выше линии или стрелки показывает его величину, а острие указывает направление.

Теперь мы можем сложить два вектора, просто соединив их «голова к хвосту». Для лучшего понимания обратитесь к приведенной ниже схеме:

(Изображение будет загружено в ближайшее время) вектора добавлены, мы все равно получаем тот же результат:

(Изображение будет загружено в ближайшее время)

Обозначение

Вектор часто может быть написан жирным шрифтом, как a или b.

Вычитание векторов:

Мы также можем вычесть один вектор из другого, помня о двух точках, указанных ниже:

• Во-первых, нам нужно изменить направление векторов, которые мы хотим вычесть, знак вектора от положительного к отрицательному.

• Во-вторых, нам нужно добавить их, как обычно:

(Изображение будет загружено в ближайшее время)

Какова величина вектора?

Как мы знаем, этот вектор можно определить как объект, который имеет как величину, так и направление. Теперь, если нам нужно найти величину векторной формулы, и нам нужно вычислить длину любого заданного вектора. Такие величины, как скорость, перемещение, сила, импульс и т. д., являются векторными величинами. Но такие величины, как скорость, масса, расстояние, объем, температура и т. д., как известно, являются скалярными величинами. Скалярные величины — это те, которые имеют единственную величину, тогда как векторы обычно имеют и величину, и направление. 9{2}}\]

Формула для величины вектора

Примечание: величина вектора никогда не может быть отрицательной, потому что | | превращает все минусы в плюсы. Таким образом, мы можем сказать, что величина вектора всегда положительна.

Направление вектора А

Направление вектора не что иное, как измерение угла, сделанного с использованием горизонтальной линии. Один из способов найти направление любого заданного вектора AB:

Tan α равен y/x; конечная точка в точке 0.

Где переменная x обозначает изменение горизонтальной линии, а переменная y обозначает изменение вертикальной линии.

Или мы можем написать так: tan\[\alpha\] = \[\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\]

Где переменная Известно, что (x₀, y₀) – это начальная точка, а (x₁, y₁) – конечная точка.

Мы можем знать направление и величину вектора, но нам нужны его длины x и y (или мы можем сказать наоборот):

Величина и направление

(изображение скоро будет загружено)	(изображение будет загружено в ближайшее время) 9	(изображение будет загружено в ближайшее время) 9000	(изображение скоро будет загружено) 9000	4 (изображение будет загружено) 9000	(изображение будет загружено) в декартовых координатах (x,y)	Величина из декартовых координат (x,y) в полярных координатах (r,θ)
x= r × 5 y= 9004 × грех (θ)	r = √x²+y² θ = tan⁻¹ (y/x)

Важные моменты, которые следует помнить, эти пункты, приведенные ниже, помогут решить проблемы:

Величина a вектор всегда определяется как длина вектора.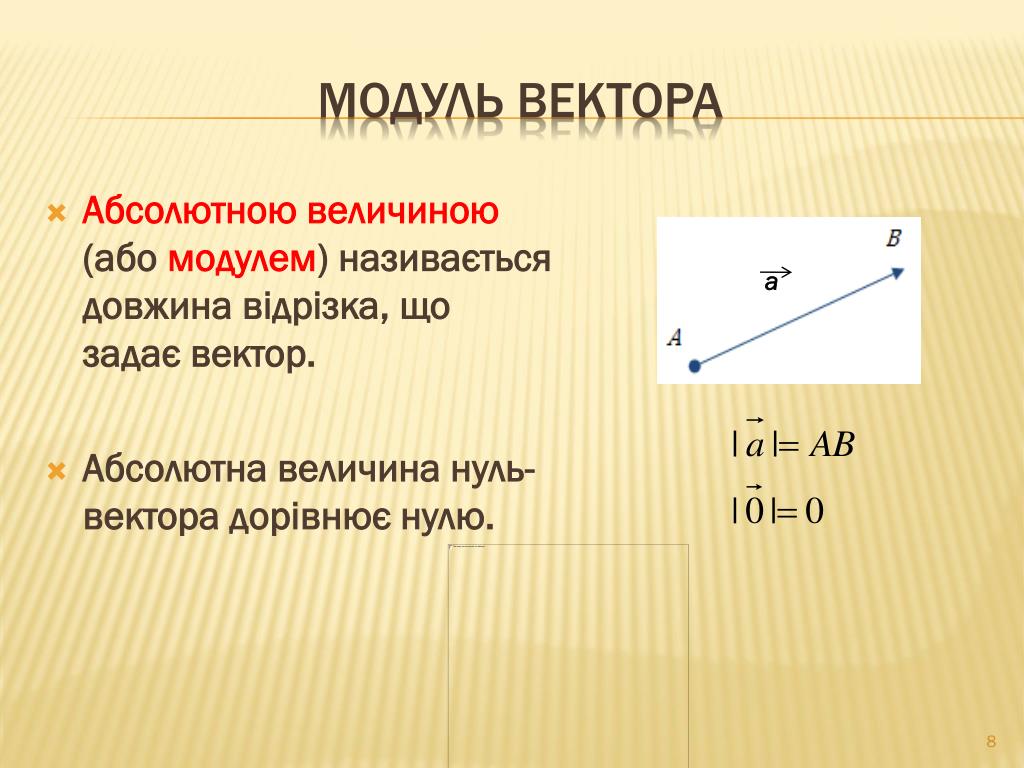 Величина вектора всегда обозначается как ∥a∥.

Для двумерного вектора a, где a = (a₁, a₂ ), ||a|| = √a¹₁+a²₂

Для трехмерного вектора a, где a = (a₁, a₂, a₃), ||a|| = √а²₁+а²₂+а²₃

Формула для величины вектора всегда обобщается для произвольных измерений. Теперь давайте посмотрим, например, если у нас есть четырехмерный вектор, а именно a, где a = a = (a₁, a₂, a₃, a₄) , ||а|| = √a²₁+a²₂+a²₃+a²₄

Решенные вопросы

Q1) Какова величина вектора b = (2, 3) ?

Ответ: Мы знаем величину векторной формулы,

 |b| = (√3²+4²) = √9+16 = √25= 5

Q2) Какова величина вектора a = (6, 8) ?

Ответ: Мы знаем величину векторной формулы,

|a| =  (√6²+8²) = √36+64 = √100 = 10

Q3) Найдите модуль трехмерного вектора 2i + 3j + 4k.

Ответ) Мы знаем, что величина трехмерного вектора xi + yj + zk = √x²+y²+z²

Следовательно, величина трехмерного вектора , то есть 2i + 3j + 4k, равна 

√x² +y²+z² = √(2)²+(3)²+(4)² = 5,38

Следовательно, величина заданного трехмерного вектора 2i + 3j + 4k ≈ 5,38.

Примечание: Символ ≈ обозначает приближение.

Что такое вектор и чем он отличается от скаляра?

Вектор — это любая математическая величина, которая включает в себя как величину, так и направление. Это может быть немного запутанным для понимания, однако это относительно просто, как только вы освоитесь.

Во Вселенной есть определенные величины, выражающие разные вещи. Математики на протяжении многих лет широко классифицировали математические величины на две категории: скалярные и векторные величины.

Скалярные величины — это те, которые имеют только величину. Большинство чисел, с которыми вы имели дело в школе, были бы скалярными величинами.

В то же время векторные величины выражают как величину, так и направление, поэтому они имеют два аспекта. Поскольку их обычно нельзя использовать в тех же математических уравнениях, что и скалярные величины, существует совершенно другая область математики, сосредоточенная на алгебре векторов.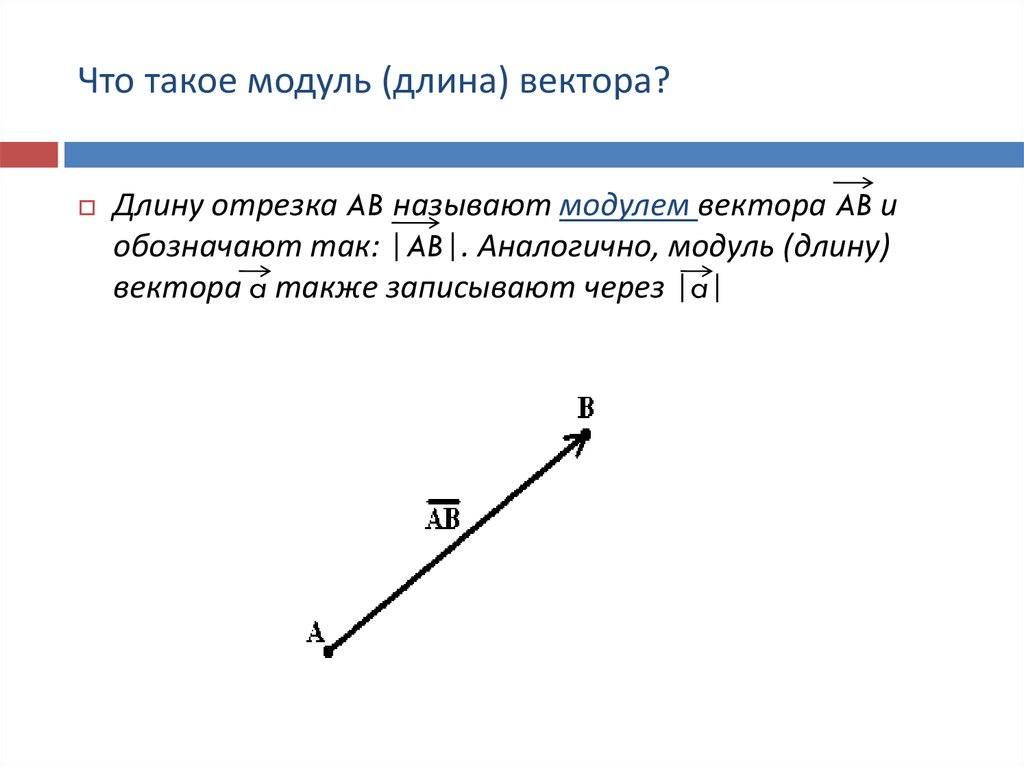

Давайте посмотрим на некоторые распространенные скалярные величины:

• Time

• Mass

• Volume

• Density

• Energy

• Speed ​​

• Temperature

Now let’s look at some common vector quantities:

• Гравитация

• Ускорение

• Сила

• Перемещение

• Тяга

  0014

• Скорость

• Угловой момент

• Линейный момент

Чтобы узнать больше о векторах, нажмите здесь.

No related posts.