Информационный сайт А. М. Белова МАТЕМАТИКА ПРИБЛИЖЕНИЕ ФУНКЦИЙ ИНТЕРПОЛЯЦИЯ АППРОКСИМАЦИЯ КОМПЬЮТЕРНАЯ ГРАФИКА И ЭВОЛЮЦИЯ КАЛЬКУЛЯТОРОВ выполнение вычислений построение графиков решение системы уравнений Mathematics The universal equation Approach (approximation) 0f functions The diagram Figure Artificial intelligence Brain Impossible figures Analytical geometry
Информационный сайт А. М. Белова МАТЕМАТИКА ПРИБЛИЖЕНИЕ ФУНКЦИЙ ИНТЕРПОЛЯЦИЯ АППРОКСИМАЦИЯ КОМПЬЮТЕРНАЯ ГРАФИКА И ЭВОЛЮЦИЯ КАЛЬКУЛЯТОРОВ выполнение вычислений построение графиков решение системы уравнений Mathematics The universal equation Approach (approximation) 0f functions The diagram Figure Artificial intelligence Brain Impossible figures Analytical geometry| О проекте | Главная | Оставить сообщение | Адрес для связи: [email protected] |
МАТЕМАТИКА: ПРИБЛИЖЕНИЕ ФУНКЦИЙ, ИНТЕРПОЛЯЦИЯ, АППРОКСИМАЦИЯ, КОМПЬЮТЕРНАЯ ГРАФИКА И ЭВОЛЮЦИЯ КАЛЬКУЛЯТОРОВ
А.М. Белов
В настоящее
время калькуляторы все еще остаются
наиболее массовыми вычислительными
устройствами. Это объясняется тем, что
калькуляторы просты в использовании и
являясь узко специализированными
вычислительными устройствами, в отличии от
персональных компьютеров не требуют для
своего использования специальной
подготовки людей. Калькуляторы работают в режиме
непосредственного выполнения набираемых
команд, позволяют вычислять значения
выражений, содержащих несколько знаков
операций и функций без записи
промежуточных результатов (т.н. цепочечные
вычисления). При этом при работе с
калькуляторами не требуется составление
программ и ввод в них программного кода.
Это объясняется тем, что
калькуляторы просты в использовании и
являясь узко специализированными
вычислительными устройствами, в отличии от
персональных компьютеров не требуют для
своего использования специальной
подготовки людей. Калькуляторы работают в режиме
непосредственного выполнения набираемых
команд, позволяют вычислять значения
выражений, содержащих несколько знаков
операций и функций без записи
промежуточных результатов (т.н. цепочечные
вычисления). При этом при работе с
калькуляторами не требуется составление
программ и ввод в них программного кода.
В рамках данной статьи
не рассматриваются так называемые
программируемые калькуляторы или
вычислительные устройства требующие для
выполнения всех или части своих функций
ввода программного кода, так как такие
вычислительные устройства уместнее было бы
отнести к микрокомпьютерам.
Программируемые калькуляторы фактически
лишены главного преимущества обычных
калькуляторов —
непосредственного выполнения набираемых
команд.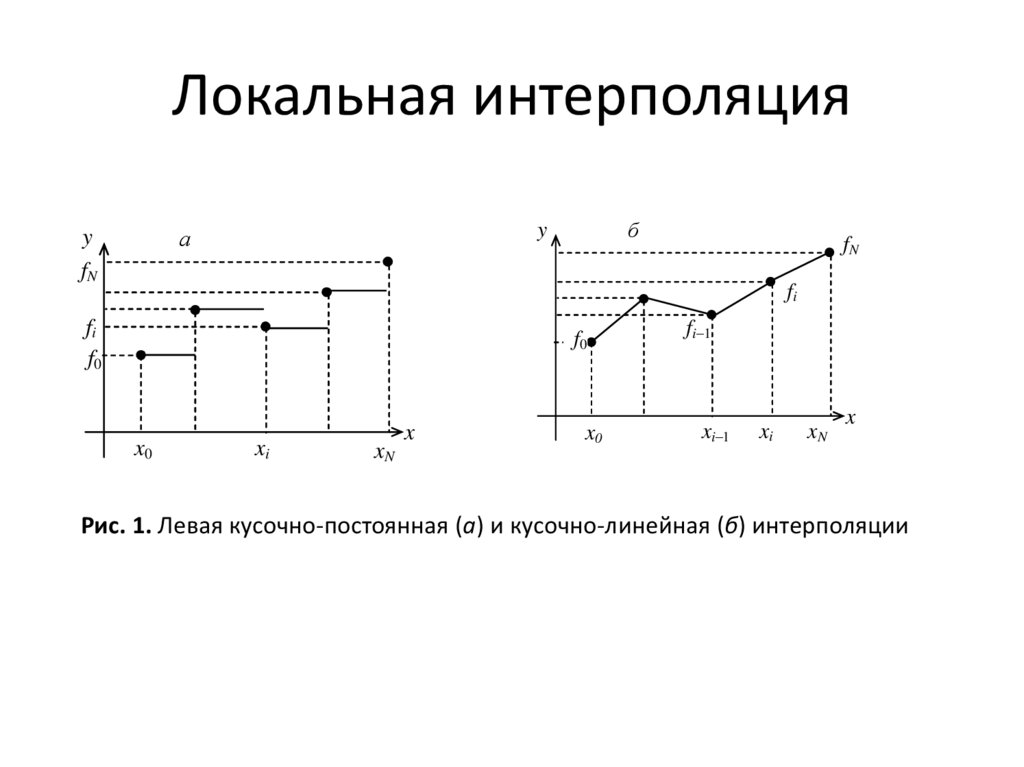
Как следует из приведенной на рис. 1 классификации калькуляторов примерно до середины двадцатого века их эволюция была связана главным образом с изменением принципа действия. Принцип действия калькуляторов изменялся в свою очередь под воздействием изменения элементной базы.
Рис.1 Классификация калькуляторов
Первые вычислительные устройства, которые можно отнести к калькуляторам были механическими и для приведения их в действие использовался ручной привод. Наиболее характерными представителями таких вычислительных устройств являются арифмометры.
С развитием электротехники, появлением малогабаритных и надежных электродвигателей, переключателей были созданы электромеханические счетные машины. Из электромеханических счетных машин большое распространение имела многоклавишная вычислительная машина ВММ-2.
Развитие электроники в свою
очередь вызвало появление электронных
калькуляторов.
В семидесятых годах двадцатого века механические и электромеханические устройства были полностью вытеснены электронными калькуляторами. С этого времени эволюция калькуляторов связана исключительно с совершенствованием и появлением новых типов электронных калькуляторов.
Существующие в настоящее время калькуляторы по своему виду можно подразделить на портативные (карманные и настольные) и виртуальные.
Виртуальные калькуляторы существуют в виде программ для персональных компьютеров, выводятся на экран монитора компьютера и представляют собой имитацию портативных калькуляторов. Сохраняют все основные преимущества портативных калькуляторов. В настоящее время практически все персональные компьютеры в составе своего программного обеспечения имеют программы имитирующие портативные калькуляторы.
Современные
калькуляторы всех видов можно подразделить
на калькуляторы способные совершать
операции только над числами и калькуляторы
способные выполнять операции над функциями.
Калькуляторы выполняющие операции над числами подразделяются на простейшие и инженерные.
Простейшие калькуляторы обычно способны на выполнение четырех арифметических действий, извлечения корня и ряда вспомогательных операций. Например запоминать число, складывать с числом, хранящимся в памяти, или вычитать из него.
Инженерные калькуляторы существуют в разных вариантах и обычно допускают по сравнению с простейшими выполнение дополнительных команд: вычисления значений тригонометрических, логарифмических, показательных, степенных и др. функций.
Пока в массовом
распространении находятся только
простейшие и инженерные калькуляторы
способные выполнять операции
исключительно над числами, но в настоящее
время уже получены все необходимые
компоненты для создания калькуляторов
способных выполнять операции над функциями
целиком в режиме
непосредственного выполнения набираемых
команд без ввода в них программного кода.
Очевидно, что прежде чем с функцией осуществлять какие либо операции ее необходимо задать. Причем задать ее желательно формулой (уравнением), а поскольку с использованием калькулятора может потребоваться совершать операции практически с любой функцией, то используемое для этого уравнение должно обладать исключительной универсальностью.
В качестве такого универсального уравнения можно использовать уравнение (1)
y=[x/x1]·[x1/x]·y1+[x/x2]·[x2/x]·y2+…+[x/xi]·[xi/x]·yi ,
(1)
где []— математический знак обозначающий целую часть числа, xi — значения аргумента.
При бесконечно большом индексе i это уравнение способно точно задать практически любую функцию
включая, как непрерывные, так и разрывные
функции, в т. ч. и функции содержащие целые
интервалы, на которых они не определены.
Поскольку, при выполнении реальных вычислений, значение индекса
y=[(x1+|x1-x|+|x2-x|)/x2]·[x2/(x1+|x1-x|+|x2-x|)]·f(x)+
+[(x2+|x2-x|+|x3-x|)/x3]·[x3/(x2+|x2-x|+|x3-x|)]·f(x)+…
…+[(xi+|xi-x|+|xi+1-x|)/xi+1]·[xi+1/(xi+|xi-x|+|xi+1-x|)]·f(x) ,
(2)
где f(x) — функции приближенно описывающие изменение значений y на интервалах между значениями аргументов xi и xi+1. Функции f(x)
Функции f(x)
Получение универсального уравнения, способного приближенно задать практически любую функцию является хотя и основным, но все же недостаточным условием для создания калькулятора способного выполнять операции над функциями. Вторым необходимым условием для создания такого калькулятора является развитие компьютерной графики достаточное для обеспечения возможности оперативной визуализации функций.
Это, второе условие
прежде всего связано с тем, что человек
способен себе представить функцию целиком
только в виде графика. Никакие формулы или
таблицы не позволяют представить человеку
функцию целиком. По этому изучая функцию,
заданную формулой или таблицей он всегда
стремиться представить себе, как она будет выглядеть
на графике.
Известно, что наиболее простой и доступный способ задания функции по набору экспериментально полученных ее значений это метод построения графика функций по точкам, т.е. выполнение на графике простого соединения известных точек функции плавной кривой.
В настоящее время метод построения графика по точкам, отображение графиков можно легко реализовать за счет применения методов, используемых при создании различных графических редакторов. Эти же методы обеспечивают, параллельно с рисованием графика, формирование информации в цифровой форме, необходимой для составления уравнений, выполнения вычислений с использованием функций и преобразования функций.
На рис. 2 приведен
внешний вид действующего макета
калькулятора способного выполнять операции над функциями
целиком. Этот калькулятор является
виртуальным — существует в виде программы
под наименованием «КАЛЬКУЛЯТОР ФУНКЦИЙ»,
способной имитировать реальный
калькулятор.
Рис. 2 Внешний вид действующего
макета калькулятора способного выполнять операции над функциями
целиком
2 Внешний вид действующего
макета калькулятора способного выполнять операции над функциями
целиком
В приведенном на рис.2 калькуляторе показана функция, загруженная в режиме «для совершения операций». Для примера специально была выбрана такая «угловатая» функция, что бы каждый сам мог оценить сколько времени и сил придется потратить для задания подобной функции традиционными средствами и прийти к выводу, что в конечном итоге задавать ее придется не одним уравнением, как в калькуляторе, а в виде системы уравнений. Сформировать же подобную функцию в калькуляторе можно быстро и без особых усилий.
Программа «КАЛЬКУЛЯТОР ФУНКЦИЙ» позволила подтвердить возможность создания калькулятора способного выполнять операции над функциями в режиме непосредственного выполнения набираемых команд без ввода программного кода.
Калькулятор,
приведенный на рис. 2 имеет в центральной
части рабочий стол для вывода и ввода
графической информации и в правом нижнем
углу окно для вывода информации в цифровом
виде. Продемонстрировал возможность
выполнять практически все арифметические
действия с функциями, включая сложение,
вычитание умножение и т.д. двух
произвольных функций, выполнение операций
взятия функции от функции, которые
приведены на кнопках в левой части
калькулятора на рис. 2, вычислять значения
функций для заданных значений аргумента и
вычислять значения аргумента для заданных
значений функций. Кроме этого калькулятор
может формировать функцию, выражающую
производную созданной (загруженной)
функции, вычислять определенный интеграл,
находить экстремумы функций, решать
системы уравнений, формировать уравнения
функций в виде программного кода для
непосредственного использования их в
других компьютерных программах. Может
использоваться для хранения базы функций и
извлечения из базы отдельных функций для
работы с ними.
Продемонстрировал возможность
выполнять практически все арифметические
действия с функциями, включая сложение,
вычитание умножение и т.д. двух
произвольных функций, выполнение операций
взятия функции от функции, которые
приведены на кнопках в левой части
калькулятора на рис. 2, вычислять значения
функций для заданных значений аргумента и
вычислять значения аргумента для заданных
значений функций. Кроме этого калькулятор
может формировать функцию, выражающую
производную созданной (загруженной)
функции, вычислять определенный интеграл,
находить экстремумы функций, решать
системы уравнений, формировать уравнения
функций в виде программного кода для
непосредственного использования их в
других компьютерных программах. Может
использоваться для хранения базы функций и
извлечения из базы отдельных функций для
работы с ними.
Для ввода графической
информации использовалась мышь. При этом без особых усилий
удавалось задавать функции с отклонением от экспериментально определенных известных значений функции около одного процента. Можно предположить, что более высокую
точность задания функций можно будет
достигнуть если вместо мыши будет
использоваться графический планшет.
Можно предположить, что более высокую
точность задания функций можно будет
достигнуть если вместо мыши будет
использоваться графический планшет.
Созданная программа обеспечивает работу с функциями одной независимой переменной. Нет принципиальных проблем для создания программы, работающей с функциями двух независимых переменных.
При объединении, рассматриваемой программы с обычным инженерным калькулятором можно будет получить калькулятор превосходящий по своим возможностям и удобствам эксплуатации существующие в настоящее время графические программируемые калькуляторы (микрокомпьютеры).
Пример выполнения вычислений с использованием программы
«КАЛЬКУЛЯТОР ФУНКЦИЙ»
Условия задачи :
Необходимо
установить зависимость изменения
предельно допустимого растягивающего
усилия, приложенного к составному стержню
от изменения температуры стержня. Стержень
состоит из прутка чугуна ЧЮ22Ш и прутка
сплава ХН70ВМТЮ. Сечение каждого прутка 1 см2 .
Стержень
состоит из прутка чугуна ЧЮ22Ш и прутка
сплава ХН70ВМТЮ. Сечение каждого прутка 1 см2 .
Экспериментально были определены:
Значения временного сопротивления при растяжении чугуна ЧЮ22Ш в МПа 290, 245, 275, 168, 137, 78 соответственно для температур нагрева чугуна в оС 20, 500, 600, 700, 800, 900.
Значения временного сопротивления при растяжении сплава ХН70ВМТЮ в МПа 1070, 990, 900, 770, 720, 590, 490 соответственно для температур нагрева сплава в оС 20, 600, 700, 750, 800, 850, 900.
Решение задачи :
1.
Последовательно для чугуна и сплава в
калькулятор вводятся экспериментально
определенные значения временного
сопротивления при растяжении. При этом на
рабочем столе калькулятора отображаются,
соответствующие этим значениям точки.
Точки при помощи мыши соединяются плавной
кривой. В результате калькулятор формирует
две функции, приведенные на рис. 3 и 4.
3 и 4.
Рис. 3 График функции выражающей изменение временного сопротивления при растяжении чугуна при увеличении температуры
Рис. 4 График функции выражающей изменение временного сопротивления при растяжении сплава при увеличении температуры
Одновременно калькулятор формирует два файла, в которых хранятся функции, приведенные на рис. 3 и 4 в цифровой форме.
2. На калькуляторе последовательно умножаются каждая из функций приведенные на рис. 3 и 4 на числа 0,0001 и 1000. Затем полученные в результате умножения функции складываются между собой. В результате калькулятор формирует искомую зависимость изменения предельно допустимого растягивающего усилия, приложенного к составному стержню от изменения температуры стержня. График этой зависимости приведен на рис. 5.
Рис. 5 Зависимость изменения
предельно допустимого растягивающего
усилия, приложенного к составному стержню
от изменения температуры стержня
5 Зависимость изменения
предельно допустимого растягивающего
усилия, приложенного к составному стержню
от изменения температуры стержня
Одновременно с графиком искомой зависимости калькулятор формирует уравнение функции этой зависимости в виде программного кода пригодного для непосредственного использования в других программах:
Y=Y/Y1
Уравнение приведено в виде фрагмента, т.к. полное его представление потребует много места. Уравнение разбито на отдельные строки с целью исключения возникновения ситуации с превышением предельно допустимой длины строки.
Можно еще посмотреть информацию на http://zhurnal.lib.ru/editors/b/below_a_m/.
9.2.4.2 Расчёт с использованием интерполяции и экстраполяции
До сих пор мы рассматривали примеры групповых расценок, где для каждой единичной расценки в группе определены постоянные величины A и B, позволяющие учитывать при расчёте стоимости проектируемого объекта его точные характеристики (производительность, протяжённость и т. п.). Наряду с этим в нормативной базе также имеются группы расценок, для которых в таблице приведено только значение постоянной величины А, и вместо диапазонов указаны конкретные значения основного показателя проектируемого объекта.
п.). Наряду с этим в нормативной базе также имеются группы расценок, для которых в таблице приведено только значение постоянной величины А, и вместо диапазонов указаны конкретные значения основного показателя проектируемого объекта.
В качестве наглядного примера рассмотрим в том же сборнике СБЦ11. Объекты водоснабжения и канализации (2008) группу расценок СБЦ11-4-1-65÷СБЦ11-4-1-73 для объектов Сооружения очистки промывной воды производительностью по промывной воде.
При работе с такими группами расценок прямой расчёт возможен только в случаях, когда основной показатель объекта в точности совпадает с каким-либо значением в таблице. А если требуется расчёт стоимости проектирования объекта, основной показатель которого не совпадает с приведёнными в таблице, производится расчёт путём интерполяции или экстраполяции – причём в отличие от предыдущего пункта здесь рассматривается экстраполяция с участием двух граничных значений.
Интерполяция выполняется в ситуации, когда заданный основной показатель проектируемого объекта находится между двумя показателями, приведёнными в таблице. Тогда как экстраполяция выполняется в ситуации, когда заданный основной показатель проектируемого объекта выше или ниже всех показателей, приведённых в таблице – в этом случае производится расчёт с участием нормативных показателей двух граничных единичных расценок из группы: последней и предпоследней или, соответственно, первой и второй.
Таким образом, в каждом из приведённых ниже примеров расчёта стоимости позиции сметы участвуют две единичных расценки из группы; при этом соответствующие строки в таблице стоимостей в окне с дополнительной информацией о позиции выделены синим цветом.
Прежде всего, из нормативной базы в смету копируется произвольная расценка, находящаяся в нужной группе. Далее, для расчёта стоимости по той или иной формуле требуется ввести ненулевое значение в колонке Количество.
- Если в нашем примере ввести в колонке Количество значение, равное 3000, то производится расчёт путём интерполяции с участием расценок СБЦ11-4-1-68 (для объекта производительностью 2000 м3/сут) и СБЦ11-4-1-69 (для объекта производительностью 5000 м3/сут). Формула расчёта:
С = А1 + (А2 — А1)/(Х2 — Х1)*(Хзад — Х1), где
А1 и А2 – постоянная величина A для участвующих расценок;
Х1 и Х2 – основной показатель проектируемого объекта для участвующих расценок;
Хзад – заданный показатель проектируемого объекта.
- Если в нашем примере ввести в колонке Количество значение, равное 100, то производится расчёт путём экстраполяции в сторону уменьшения с участием двух первых расценок в группе: СБЦ11-4-1-65 (для объекта производительностью 160 м3/сут) и СБЦ11-4-1-65 (для объекта производительностью 500 м3/сут).
 Формула расчёта:
Формула расчёта:
С = А1 + (А2 — А1)/(Х2 — Х1)*(Хзад — Х1)*0,6, где
А1 и А2 – постоянная величина A для участвующих расценок;
Х1 и Х2 – основной показатель проектируемого объекта для участвующих расценок;
Хзад – заданный показатель проектируемого объекта.
- Если в нашем примере ввести в колонке Количество значение, равное 90000, то производится расчёт путём экстраполяции в сторону увеличения с участием двух последних расценок в группе: СБЦ11-4-1-72 (для объекта производительностью 40000 м3/сут) и СБЦ11-4-1-73 (для объекта производительностью 80000 м3/сут). Формула расчёта:
С = А2 + (А2 — А1)/(Х2 — Х1)*(Хзад — Х2)*0,6, где
А1 и А2 – постоянная величина A для участвующих расценок;
Х1 и Х2 – основной показатель проектируемого объекта для участвующих расценок;
Хзад – заданный показатель проектируемого объекта.
Замечание: Как и в предыдущем пункте, подчеркнём, что выбор нужной формулы для расчёта стоимости позиции сметы осуществляется в программе автоматически, немедленно при вводе (корректировке) значения в колонке Количество. Также отметим, что в расчёте участвует обязательный для применения коэффициент из технической части Ки1 (на стадию проектирования).
Описанная в данном пункте методика интерполяции и экстраполяции с участием двух табличных значений реализована исключительно для групповых расценок, где приведено только значение постоянной величины А. При этом существует возможность и в таких случаях производить расчёт по базовым формулам, описанным в предыдущем пункте. Переключение между двумя способами расчёта осуществляется при помощи кнопки Интерполировать в окне с дополнительной информацией о позиции на закладке Стоимости.
Newton Interpolating Polynomial Calculator — Online Interpolation
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Интерполирующий многочлен Ньютона
Инструмент для поиска уравнения кривой с помощью алгоритма Ньютона. Алгоритм ньютоновской интерполяции представляет собой полиномиальную интерполяцию/аппроксимацию, позволяющую получить полином Лагранжа как уравнение кривой, зная ее точки.
Результаты
Интерполяционный многочлен Ньютона — dCode
Теги: Функции
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценной помощью в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор ньютоновской интерполяции
Список значений: (x1, y1), (x2, y2) и т. д. (максимум 12) Загрузка. ..
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Экстраполяция
Оцените значение абсиссы x =См. Также: Интерполяционный многочлен Лагранжа — Интерполяционный многочлен Невилла
Ответы на вопросы (FAQ)
Как найти уравнение кривой с помощью алгоритма Ньютона?
dCode позволяет использовать метод Ньютона для полиномиальной интерполяции, чтобы найти уравнение многочлена (идентичное Лагранжу) в ньютоновской форме по уже известным значениям функции.
Из $ n + 1 $ известных точек $ (x_i, y_i) $, ньютоновская форма многочлена равна $$ P(x)= [y_0] + [y_0,y_1] (x-x_0) + \ldots + [y_0,\ldots ,y_n] ( х-х_0) \ldots (х-х_{n-1}) $$ 9k {\ frac {y_j} {\ prod_ {0 \ leq i \ leq k, \, i \ neq j} (x_j-x_i)}} $$ они участвуют в вычислении интерполяции Ньютона.
NB: Если $ k = 0 $, то продукт $ \prod(x_j-x_i) = 1 $ (пустой продукт)
Исходный код
dCode сохраняет право собственности на исходный код «Интерполяционного многочлена Ньютона». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Интерполирующий полином Ньютона», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Интерполяционного полинома Ньютона». Полиномиальные» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Интерполяционного полинома Ньютона» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Интерполирующий полином Ньютона», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Интерполяционного полинома Ньютона». Полиномиальные» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Интерполяционного полинома Ньютона» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Интерполяционный многочлен Ньютона» или любых его результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Интерполяционный многочлен Ньютона на dCode. fr [онлайн-сайт], получено 10 декабря 2022 г., https://www.dcode.fr/newton-interpolating-polynomial
fr [онлайн-сайт], получено 10 декабря 2022 г., https://www.dcode.fr/newton-interpolating-polynomial
Сводка
- Калькулятор ньютоновской интерполяции
- Как найти уравнение кривой с помощью алгоритма Ньютона?
- Что такое разности, разделенные Ньютоном?
Аналогичные страницы
- Невилл. Полиномиальный полином
- .
Поддержка
- Paypal
- Patreon
- Подробнее
Форум/Помощь
Ключевые слова
ньютон,интерполяция,интерполяция,уравнение,полином,лагранж,кривая,точка,значение,функция
Ссылки
▲
Калькулятор билинейной интерполяции с шагом
Калькулятор билинейной интерполяции представляет собой математический калькулятор, запрограммированный для вычисления положения точки, заданной двумя координатами. Этот калькулятор полезен для реальных приложений, где необходимо знать две координаты и точку для заполнения пробела.
Он может находить площадь трапеции, треугольника или любой другой формы, которую могут определить две функции. Если вас интересует больше о поверхности трапеции и ее характеристиках, вы обязательно можете посетить наш калькулятор Калькулятор трапеции .
Билинейная интерполяция – определение?Интерполяция — это процесс нахождения другой функции, близкой к первой. Следовательно, мы можем сказать, что это поиск функции, которая хорошо аппроксимируется и легко вычисляется. Это метод, с помощью которого можно вычислить положение точки на кривой относительно положения двух других точек. Поэтому существует множество видов интерполяций, и это один из них.
Билинейная интерполяция оценивает значения между известными. Другой — двойная интерполяция. Двойная интерполяция описывает ценности, зависящие от двух разных переменных или функций.
Другими словами, вы можете использовать математическую технику для оценки значения точки на кривой в промежуточном положении между двумя известными точками. Этот метод может быть применен к двумерной интерполяции на прямоугольнике.
Этот метод может быть применен к двумерной интерполяции на прямоугольнике.
Например, мы можем взять точки функции (x₁, y₁), (x₁, y₂), (x₂, y₁) и (x₂, y₂), и они будут: (x₁, y₁ ) = Q₁₁; (х₁, у₂) = Q₂₁; (x₂, y₁) = Q₁₂ и (x₂, y₂) равно Q₂₂.
С помощью билинейной интерполяции можно найти любое значение в любой точке (x, y). Пусть в этом случае P неизвестно.
Как и на картинке выше, точки красного цвета — это точки данных. Зеленая точка — это место, где вы хотите интерполировать. Также вы можете использовать данные, представленные в виде таблицы:
| x 1 | x | x 2 | |
| y 1 | Q 11 | Q 21 | |
| y | P | ||
| y 2 | Q 12 | Q 22 | 6162 Q 22 6162 Q 22 6162 Q 22 16161.

 Формула расчёта:
Формула расчёта: 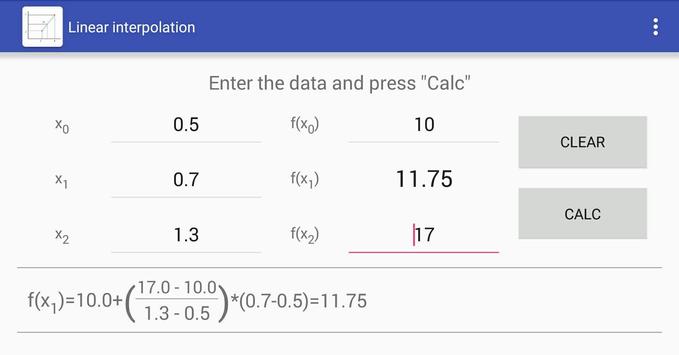
 0129
0129

 Чтобы использовать этот калькулятор, вам нужно ввести координаты двух точек, которые вы хотите интерполировать. После того, как вы введете координаты, вам нужно будет ввести функцию вывода. Это приведет к выходу.
Чтобы использовать этот калькулятор, вам нужно ввести координаты двух точек, которые вы хотите интерполировать. После того, как вы введете координаты, вам нужно будет ввести функцию вывода. Это приведет к выходу.
 Вы можете выполнить билинейную интерполяцию вручную, но это отнимает много времени и подвержено ошибкам.
Вы можете выполнить билинейную интерполяцию вручную, но это отнимает много времени и подвержено ошибкам. Функция имеет решающее значение в конечном числе точек, близких к этой точке. Модуль значительно улучшает алгоритм билинейной интерполяции.
Функция имеет решающее значение в конечном числе точек, близких к этой точке. Модуль значительно улучшает алгоритм билинейной интерполяции.