Модули решение уравнений: Решение уравнений с модулями

Решение уравнения с модулем

12 Задание (2022) (C1)14 Задание (2022) (C3)ВИДЕОУРОКИТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ

Решение уравнений с модулем. В этой статье я покажу алгоритм решения уравнений, которые содержат  несколько выражений под знаком модуля, на примере решения уравнения уровня С1, а затем вы посмотрите ВИДЕОУРОК с подробным разбором тригонометрического уравнения с модулем.

Давайте решим уравнение:

 

Вспомним, что модуль раскрывается по  такому правилу:

Говоря человеческим языком, модуль выражения равен самому выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.

Таким образом, перед нами стоит задача раскрыть все модули в соответствии со знаками подмодульных выражений.

Будем следовать такому алгоритму:

1. Определим, в каких точках каждое подмодульное выражение меняет знак. Для этого приравняем каждое подмодульное выражение к нулю:

, 

, 

Мы получили три точки.

2. Нанесем их на числовую ось:

Эти три числа разбили числовую ось на четыре промежутка:

,   ,   ,  

Обратите внимание, что мы включили крайние точки промежутков в оба промежутка. Ничего страшного не случится, если мы эти точки учтем два раза, главное, о них не забыть.

3. Теперь рассмотрим знаки подмодульных выражений на каждом промежутке:

Выражение меняет знак в точке . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:

Выражение меняет знак в точке . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:

Выражение меняет знак в точке . Слева от этой точки оно отрицательно, а справа положительно. Отметим это в таблице:

Мы получили знаки всех подмодульных выражений на каждом промежутке. Теперь раскроем модули на каждом промежутке с учетом этих знаков.

Наше уравнение «распадается» на четыре уравнения по количеству числовых промежутков.

4. Решим уравнение на каждом промежутке:

1. 

Решение уравнения на первом промежутке 

2.Раскроем модули на втором промежутке:

Мы получили, что второе уравнение системы является тождеством, то есть   второе равенство верно при любом действительном значении . Следовательно, решением системы будут те значения неизвестного, которые удовлетворяют первому неравенству:

.

3. Раскроем модули на третьем промежутке:

Решение уравнения на третьем промежутке: 

4. Раскроем модули на четвертом промежутке:

Решение уравнения на четвертом промежутке: 

Заметим, что решения нашего уравнения на каждом промежутке принадлежали этому промежутку, то есть удовлетворяли неравенству каждой системы. Однако, так бывает не всегда, и если корень уравнения не удовлетворяет неравенству, значит, соответствующая система не имеет решений.

5. Теперь объединим полученные решения, и запишем ответ:

Ответ: -6≤х≤0, х=12

А сейчас я предлагаю вам посмотреть ВИДЕУРОК с подробным решением уравнения уровня С3:

 

И.В. Фельдман, репетитор по математике.

Уравнения с модулем. Решение уравнений с несколькими модулями

Уравнения с несколькими модулями в одной части

Чем больше модулей, тем больше приходиться их раскрывать и тем больше получается различных уравнений. Когда модулей один или два — это не сложно. Сложность возникает когда модулей больше двух. Человек может забыть рассмотреть какой-то из случаев, и получится, что уравнение решено не полностью.

Давайте решим следующее уравнение:

|x − 5| − |x| = 1

У данного уравнения два модуля в левой части. Оно решается путем раскрытия модулей. Не будем комментировать решение, а сразу приведём его:

Такой вид уравнения удобнее решать методом интервалов (или более точно — методом промежутков). Суть этого метода в том, чтобы разбить координатную прямую на несколько промежутков, а затем решить уравнение на каждом из этих промежутков. Модули исходного уравнения на каждом промежутке будут раскрываться по разному.

Решим уравнение |x − 5| − |x| = 1 методом интервалов.

Для начала нарисуем координатную прямую и обозначим её как х

Если координатная прямая содержит все числа, которые существуют в природе, то логично что она содержит и корни нашего уравнения.

Теперь надо разбить координатную прямую на промежутки. Для этого сначала нужно найти на ней те точки, на которых модули нашего уравнения будут менять свой порядок раскрытия. То есть, найти точки перехода для модулей |x − 5| и |x|.

Чтобы найти точки перехода, нужно выяснить при каких значениях x подмодульные выражения равны нулю. Узнать это можно приравняв к нулю подмодульные выражения обоих модулей, и решить обычные линейные уравнения:

Для модуля |x − 5| точкой перехода будет 5. Для модуля |x| точкой перехода будет 0.

Теперь отметим точки перехода на координатной прямой. Мéньшие числа нужно отмечать левее, большие числа правее:

Проведем дуги от точек перехода:

С помощью неравенств подпишем каждый промежуток. Получится три промежутка: от минус бесконечности до нуля, от нуля до пяти, и от пяти до плюс бесконечности. То есть: x x x ≥ 5

Обратите внимание, что в первом промежутке x  значение 0 не включено в данный промежуток. Но зато это значение включено во второй промежуток 0 ≤ x .

Во втором же промежутке 0 ≤ x  значение 5 не включено в данный промежуток, но зато оно включено в третий промежуток x ≥ 5.

Проще говоря, каждый промежуток включает в себя левый конец, и не включает правый. Сделано это специально, чтобы не допустить потерь значений переменной x. Описать с помощью неравенств нужно все значения на координатной прямой, не допуская их потерь.

Включение левого конца в рассматриваемый промежуток и исключение его из правого это лишь общепринятое правило. На самом деле концы рассматриваемого промежутка можно включать в любой из соседствующих промежутков. Например, значение 0 можно было включить в первый промежуток. Тогда он принял бы вид x ≤ 0, а второй промежуток принял бы вид 0 x , потому что ноль уже был включен в первый промежуток.

Но лучше всего исходить из ситуации, потому что в каких-то случаях левый конец промежутка целесообразнее исключить из рассматриваемого промежутка и включить его в правый конец соседнего промежутка. Об этом мы поговорим позже.

Теперь выясним как будут вести себя модули |x − 5| и |x| на каждом из этих промежутков. От этого будет зависеть то, как они будут раскрываться.

Начнем с первого промежутка x 

Если x , то при любом значении x на данном промежутке подмодульное выражение x − 5 станет отрицательным, а значит модуль |x − 5| на промежутке x x| на промежутке x 

В результате после раскрытия модулей на промежутке x x − 5| − |x| = 1 примет вид −(x − 5) + x = 1

Второй модуль |x| на промежутке x x − 5 |− |x| = 1 после выражения |x − 5| тоже располагался минус. В математике два минуса, идущие подряд, дают плюс. Поэтому и получилось выражение −(x − 5) + x = 1.

Решим уравнение −(x − 5) + x = 1, которое получилось после раскрытия модулей на промежутке x 

Это уравнение решений не имеет. Значит на промежутке x  0 исходное уравнение не имеет корней. Проще говоря, корень уравнения не является числом меньшим нуля.

Следующий промежуток, на котором нужно решить уравнение это промежуток 0 ≤ x  5.

Если x больше или равно нулю, но меньше пяти, то подмодульное выражение x − 5, станет отрицательным, а значит модуль |x − 5| на промежутке 0 ≤ x  5 будет раскрываться со знаком минус. Второй модуль |x| на промежутке 0 ≤ x  5 будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке 0 ≤ x  5 уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) − x = 1

Решим это уравнение:

Получили корень 2. Чтобы проверить действительно ли это число является  корнем исходного уравнения, нужно посмотреть принадлежит ли это число рассматриваемому промежутку  0 ≤ x  5. Принадлежит? Да. Значит число 2 является корнем уравнения |x − 5| − |x| = 1. Проверка также показывает это

Следующий промежуток, который нужно рассмотреть это промежуток x ≥ 5.

Если x больше или равно пяти, то модуль |x − 5| на промежутке x ≥ 5 будет раскрываться со знаком плюс. Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке x ≥ 5 уравнение с модулем |x − 5| − |x| = 1 примет вид x − 5 − x = 1.

Решим это уравнение:

Это уравнение не имеет решений. Значит на промежутке x ≥ 5 исходное уравнение корней не имеет.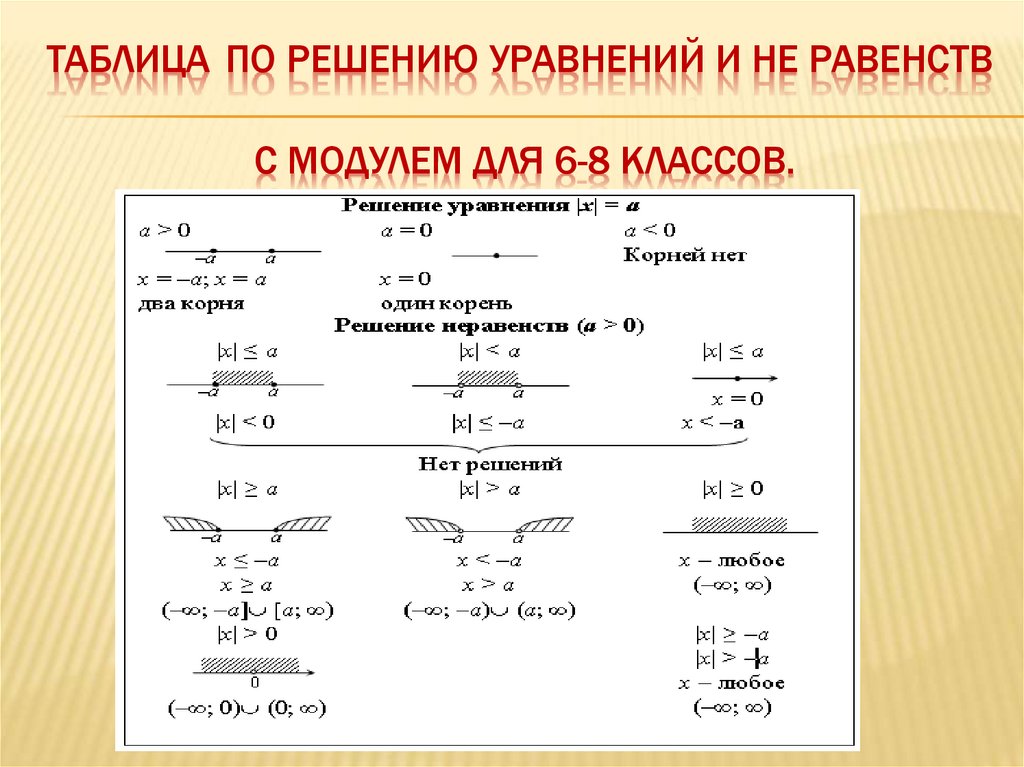 Проще говоря, корень уравнения не является числом, бóльшим либо равным пяти.

В итоге корнем уравнения является число 2, которое мы нашли решив исходное уравнение на промежутке 0 ≤ x  5.

Ответ: 2.

Пример 2. Решить уравнение |x − 3| + |x + 2| = 7

Решение

Шаг 1. Находим точки перехода для модулей |x − 3| и |x + 2|

Шаг 2. Отметим на координатной прямой найденные точки перехода и выделим получившиеся промежутки:

Шаг 3. Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.

На промежутке x  модуль |x − 3| будет раскрываться с минусом. Можно проверить это, подставив в данный модуль любое число из промежутка x . Например, числа −4 или −9

|x − 3| = |−4 − 3| = |−7| = −(−7) = 7

|x − 3| = |−9 − 3| =|−12| = −(−12) = 12

Следующий модуль |x + 2| на промежутке x  тоже будет раскрываться с минусом. Убедимся в этом подставив любые два числа из промежутка x  в подмодульное выражение. Например, числа −6 и −8

|x + 2| = |−6 + 2| = |−4| = −(−4) = 4

|x + 2| = |−8 + 2| = |−6| = −(−6) = 6

Значит после раскрытия модулей на промежутке x  −2 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

−x + 3 − x − 2 = 7

Решим его:

Обязательно нужно проверить входит ли найденный корень −3 в рассматриваемый промежуток x  −2. Для этого нужно подставить в неравенство x  −2 найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3  верно, значит корень −3 входит в промежуток x  −2 и соответственно является корнем исходного уравнения.

На следующем промежутке −2 ≤ x  3 модуль |x − 3| будет раскрываться с минусом, а модуль|x + 2| будет раскрываться с плюсом.

Значит после раскрытия модулей на промежутке −2 ≤ x  3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

−x + 3 + x + 2 = 7

Решим это уравнение:

Это уравнение не имеет решений, значит на промежутке −2 ≤ x 

Наконец рассмотрим промежуток x ≥ 3

На промежутке x ≥ 3 модуль |x − 3| будет раскрываться с плюсом. Модуль|x + 2| так же будет раскрываться с плюсом. Значит на промежутке x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

x − 3 + x + 2 = 7

Решим это уравнение:

Этот корень входит в рассматриваемый промежуток x ≥ 3, значит является корнем исходного уравнения. Проверка также показывает это:

Ответ: −3 и 4.

Пример 3. Решить уравнение |2x − 3| + |2x + 7| = 16

Решение

Найдём точки перехода для модулей |2x − 3| и |2x + 7|

Отметим точки перехода на координатной прямой. Меньшие числа нужно отмечать левее, большие правее:

Решим исходное уравнение |2x − 3| + |2x + 7| = 16 на промежутке  . Оба модуля на этом промежутке будут раскрываться с минусом:

Корень −5 принадлежит промежутку  , значит является корнем исходного уравнения.

Теперь решим исходное уравнение на промежутке  . Модуль |2x − 3| на этом промежутке раскрывается с минусом, а модуль |2x + 7| — с плюсом:

Видим, что на промежутке исходное уравнение не имеет решений (корней).

Теперь решим исходное уравнение на промежутке  . Оба модуля на данном промежутке раскрываются с плюсом:

Корень 3 принадлежит промежутку  , значит является корнем исходного уравнения.

Ответ: −5 и 3.

Пример 4. Решить уравнение |x − 2| + 3x = |x − 5| − 18

Решение

Найдём точки перехода для модулей |x − 2| и |x − 5|

Отметим точки перехода на координатной прямой:

Решим исходное уравнение на промежутке x  2. Модули |x − 2| и |x − 5| на этом промежутке раскрываются с минусом:

Число −5 принадлежит промежутку x  2, значит является корнем исходного уравнения.

Решим исходное уравнение на промежутке 2 ≤ x  5. Модуль |x − 2| на этом промежутке раскрывается с плюсом, а модуль |x − 5| — с минусом:

Число   не принадлежит промежутку 2 ≤ x  5, значит не является корнем исходного уравнения.

Решим исходное уравнение на промежутке x ≥ 5. Модули |x − 2| и |x − 5| на этом промежутке будут раскрываться с плюсом:

Число −7 не принадлежит промежутку x ≥ 5, значит не является корнем исходного уравнения.

Ответ: −5

модулей для дифференциальных уравнений

модулей для дифференциальных уравнений

Учебное пособие по вспомогательному приложению

Численные решения дифференциальных уравнений
Спринты мирового класса
Модель логистического роста
Модели хищник-жертва
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Пружинное движение
Пружинные системы I
Матричные операции
Собственные значения и собственные векторы
Траектории линейных систем
Маятник
Свинец в теле
Коэффициент усиления и фазовый сдвиг
Система Ван дер Поля

Учебное пособие по вспомогательному приложению

Назначение: Чтобы изучить основы Maple V, выпуск 4 или выпуск 5 для использования в модулях дифференциальных уравнений.

Предпосылки: Никто

Доступно для: Клен

Численные решения дифференциальных уравнений

Назначение: Получить опыт работы с численными методами аппроксимации решение начальные задачи первого порядка.

Предпосылки: Проработайте базовый учебник для вашей системы компьютерной алгебры.

Доступно для: Клен

Спринты мирового класса

Назначение: Чтобы изучить применимость линейного дифференциала уравнение как модель для процесс спринта, и чтобы проиллюстрировать важность параметров в моделировании.

Предпосылки: Учебник для вашего вспомогательного приложения и умение решать линейка первого порядка дифференциальное уравнение с постоянными коэффициентами.

Доступно для: Клен

Модель логистического роста

Назначение: Изучить стандартную модель роста населения в стесненная среда.

Предпосылки: Разделение переменных.

Доступно для: Клен

Модели хищник-жертва

Назначение: Разработать и изучить модель Лотки-Вольтерры. для взаимодействия хищник-жертва как прототип первого порядка система дифференциальных уравнений.

Предпосылки: Модуль Численных Решений дифференциальные уравнения.

Доступно для: Клен

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Назначение: Чтобы исследовать качественное поведение решения начальных задач вида

 у" + ау' + у = 0,
                         у(0) = у0,
                        у'(0) = у1.
 

В частности, чтобы определить, как решения зависят от знаки и величины коэффициентов a и b и на первоначальные условия.

Предпосылки: Учебное пособие по вспомогательному приложению и знание символической формы решений дифференциальных уравнения вида

у» + ау’ + бай = 0 .

Доступно для: Клен

Весеннее движение

Назначение: Расследовать математическая модель у» + (к/м)у’ + (К/м)у = 0 для пружинящего движения и изучения эффекта повышенного демпфирования.

Предпосылки: Знание линейных однородных дифференциальные уравнения с константой коэффициенты.

Доступно для: Клен

Системы принудительной пружины I

Назначение: Изучить влияние внешней движущей силы. на простом линейном осцилляторе, демпфированном или незатухающем.

Предпосылки: Модуль и знания Spring Motion символической формы решений дифференциальных уравнения вида у» + ау’ + by = f(t) , где f — функция синуса или косинуса.

Доступно для: Клен

Матричные операции

Назначение: Чтобы поэкспериментировать с матричные операции, особенно умножение, инверсия и детерминанты и изучать приложения к решению систем линейные уравнения. В процессе изучая эти матричные операции, мы научитесь пользоваться помощником приложение для выполнения матрицы вычисления.

Предпосылки: Базовое понимание линейных комбинаций векторов, Знакомство с умножением матриц.

Доступно для: Клен

Собственные значения и собственные векторы

Назначение: Экспериментировать и изучать свойства собственные значения и собственные векторы и их применение к дифференциальные уравнения.

Предпосылки: Модуль операций с матрицами и концепция уменьшенной эшелонированной формы строки.

Доступно для: Клен

Траектории линейных систем

Назначение: Для исследования траекторий на фазовой плоскости 2×2 однородных линейных систем первого порядка дифференциальные уравнения вида X’ = AX.

Предпосылки: Модуль операций с матрицами и понимание смысла собственных значений и собственные векторы матрицы A.

Доступно для: Клен

Маятник

Назначение: Чтобы исследовать фазовую плоскость для второго порядка нелинейное дифференциальное уравнение, в частности стандартное модель для затухающих и незатухающих маятников.

Предпосылки: Модуль Spring Motion.

Доступно для: Клен

Свинец в теле

Назначение: Разработать и изучить модель отсека количества свинца в организме человека и изучить трехмерная управляемая линейная система.

Предпосылки: Модуль по траекториям линейных Уравнения.

Доступно для: Клен

Усиление и фазовый сдвиг

Назначение: Чтобы изучить взаимосвязь между частотой внешней движущей силой и параметрами демпфирующего линейный осциллятор.

Предпосылки: Модуль по принудительному пружинному движению.

Доступно для: Клен

Система Ван дер Поля

Назначение: Чтобы изучить модель Ван дер Поля для нелинейного электрическая цепь — в частности, для изучения предельного цикла явление.

Предпосылки: Модуль по принудительному пружинному движению.

Доступно для: Клен

---

---

| Главная | Ресурсы | Ресурсы для учителей |

модули на math.duke.edu

Решения операторных уравнений на модулях Гильберта C* II

Брейден Х.: Уравнения A ^Т Х ± Х ^T A  =  B . СИАМ Дж. Матричный анал. заявл. 20 , 295–302 (1998)

Статья МАТЕМАТИКА MathSciNet Google ученый

«>

Чой М.Д., Чендлер Д.: Теорема спектрального отображения для совместного аппроксимирующего точечного спектра. Бык. Являюсь. Мат. соц. 80 , 317–321 (1974)

Статья МАТЕМАТИКА Google ученый

Чой М.Д., Холбрук Дж.А., Крибс Д.В., Зычковски К.: Числовые диапазоны высших рангов унитарных и нормальных матриц. Опер. Матрицы 1 , 409–426 (2007)

МАТЕМАТИКА MathSciNet Google ученый

Чой М.Д., Крибс Д.В., Жичковски К.: Коды квантовой коррекции ошибок на основе формализма сжатия. Респ. Матем. физ. 58 , 77–86 (2006)

Статья МАТЕМАТИКА MathSciNet Google ученый

Чой М.Д., Крибс Д.В., Жычковски К.: Диапазоны чисел более высокого ранга и проблемы сжатия. Приложение линейной алгебры. 418 , 828–839 (2006)

Статья МАТЕМАТИКА MathSciNet Google ученый

«>

Чой М.Д., Крибс Д.В.: Метод поиска квантовых бесшумных подсистем. физ. Преподобный Летт. 96 , 050501–050504 (2006)

Артикул Google ученый

Чой М.Д., Ли С.К.: Окончательная оценка верхней границы нормы для суммирования операторов. Дж. Функц. Анальный. 232 , 455–476 (2006)

Статья МАТЕМАТИКА MathSciNet Google ученый

Цветкович-Илич Д.С.: Пересчитать решения матричного уравнения AXB  =  C . Дж. Ост. Мат. соц. 84 , 63–72 (2008)

МАТЕМАТИКА MathSciNet Google ученый

Цветкович-Илич Д.С., Дайич А., Колиха Ю.Я.: Положительные и вещественно-положительные решения уравнения axa * =  c в C *-алгебрах. Линейная полилинейная алгебра 55 , 535–543 (2007)

Статья МАТЕМАТИКА MathSciNet Google ученый

«>

Кросс Р.В.: О возмущении неограниченных линейных операторов с топологически дополняемыми образами. Дж. Функц. Анальный. 92 , 468–473 (1990)

Артикул МАТЕМАТИКА MathSciNet Google ученый

Crouzeix M.: Числовой диапазон и функциональное исчисление в гильбертовом пространстве. Дж. Функц. Анальный. 244 , 668–690 (2007)

Статья МАТЕМАТИКА MathSciNet Google ученый

Дайич А., Колиха Ю.Ю.: Положительные решения уравнений AX  =  C и XB  =  D для операторов гильбертова пространства. Дж. Матем. Анальный. заявл. 333 , 567–576 (2007)

Статья МАТЕМАТИКА MathSciNet Google ученый

Джорджевич Д.С.: Явное решение операторного уравнения A * X  +  X * A  =  B . Дж. Вычисл. заявл. Мат. 200 , 701–704 (2007)

Статья МАТЕМАТИКА MathSciNet Google ученый

Клык X.: Представление топологического группоида. Акта Математика. Грех. 39 , 6–15 (1996)

МАТЕМАТИКА Google ученый

Клык X.: Индуцированное представление C*-группоидной динамической системы. Подбородок. Анна. Мат. (Б) 17 , 103–114 (1996)

МАТЕМАТИКА Google ученый

Фанг Х.: Реализация бимодуля мультипликатора Гильберта на пространстве бидулей и теорема Титце о продолжении. Подбородок. Анна. Матем.(Б) 21 , 375–380 (2000)

Артикул МАТЕМАТИКА Google ученый

Fang X., Yu J., Yao H.: Решения операторных уравнений Гильберта C *-Модули. Приложение линейной алгебры. 431 , 2142–2153 (2009)

Статья МАТЕМАТИКА MathSciNet Google ученый

Groß J.: Явные решения матричной обратной задачи AX  =  Б . Приложение линейной алгебры. 289 , 131–134 (1999)

Статья МАТЕМАТИКА MathSciNet Google ученый

Гирибет Дж.И., Маэстрипьери А., Периа Ф.М.: Замыкающие самосопряженные операторы в гильбертовых пространствах. Приложение линейной алгебры. 428 , 1899–1911 (2008)

МАТЕМАТИКА MathSciNet Google ученый

Хансен А.К.: Об аппроксимации спектров линейных операторов в гильбертовых пространствах. Дж. Функц. Анальный. 254 , 2092–2126 (2008)

Статья МАТЕМАТИКА MathSciNet Google ученый

«>

Дженсен К.К., Томсен К.: Элементы КК-теории. Биркхаузер, Бостон (1991)

МАТЕМАТИКА Google ученый

Караев М.Т.: Символ Березина и обратимость операторов в функциональных гильбертовых пространствах. Дж. Функц. Анальный. 238 , 181–192 (2006)

Статья МАТЕМАТИКА MathSciNet Google ученый

Хатри К.Г., Митра С.К.: Эрмитовы и неотрицательно определенные решения линейных матричных уравнений. СИАМ Дж. Заявл. Мат. 31 , 579–585 (1976)

Статья МАТЕМАТИКА MathSciNet Google ученый

Лэнс Э.К.: Гильберт C *-Модули: набор инструментов для операторов алгебры. Издательство Кембриджского университета, Кембридж (1995)

Книга Google ученый

«>

Лаузон М.М., Трейл С.: Общие дополнения двух подпространств гильбертова пространства. Дж. Функц. Анальный. 212 , 500–512 (2004)

Статья МАТЕМАТИКА MathSciNet Google ученый

Ли С.К., Цинг Н.К.: О к -м числовом диапазоне матрицы. Линейная полилинейная алгебра 28 , 229–239 (1991)

Статья MathSciNet Google ученый

Wegge-Olsen NE: K-теория и C *-Алгебры: дружественный подход. Издательство Оксфордского университета, Оксфорд (1993)

Google ученый

Ван К., Ян К.: Ре-неотрицательно определенные решения матричного уравнения AXB  =  C . Комментарий. Мат. ун-т Каролина 39 , 7–13 (1998)

МАТЕМАТИКА Google ученый

«>

Xu Q.: Общие эрмитовы и положительные решения уравнений присоединяемых операторов AX  =  C , XB  =  D . Приложение линейной алгебры. 429 , 1–11 (2008)

Статья МАТЕМАТИКА MathSciNet Google ученый

Сюй К., Шэн Л., Гу Ю.: Решения некоторых операторных уравнений. Приложение линейной алгебры. 429 , 1997–2024 (2008)

Статья МАТЕМАТИКА MathSciNet Google ученый

Сюй К., Шэн Л.: Положительно полуопределенные матрицы присоединяемых операторов на гильбертовых C *-модулях. Приложение линейной алгебры. 428 , 992–1000 (2008)

Статья МАТЕМАТИКА MathSciNet Google ученый

Юань Ю.: Разрешимость класса матричных уравнений и их приложений. Дж. Нанкин унив.

No related posts.