Круговые функции | это… Что такое Круговые функции?
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку.
Основное соотношение
Функция arcsin
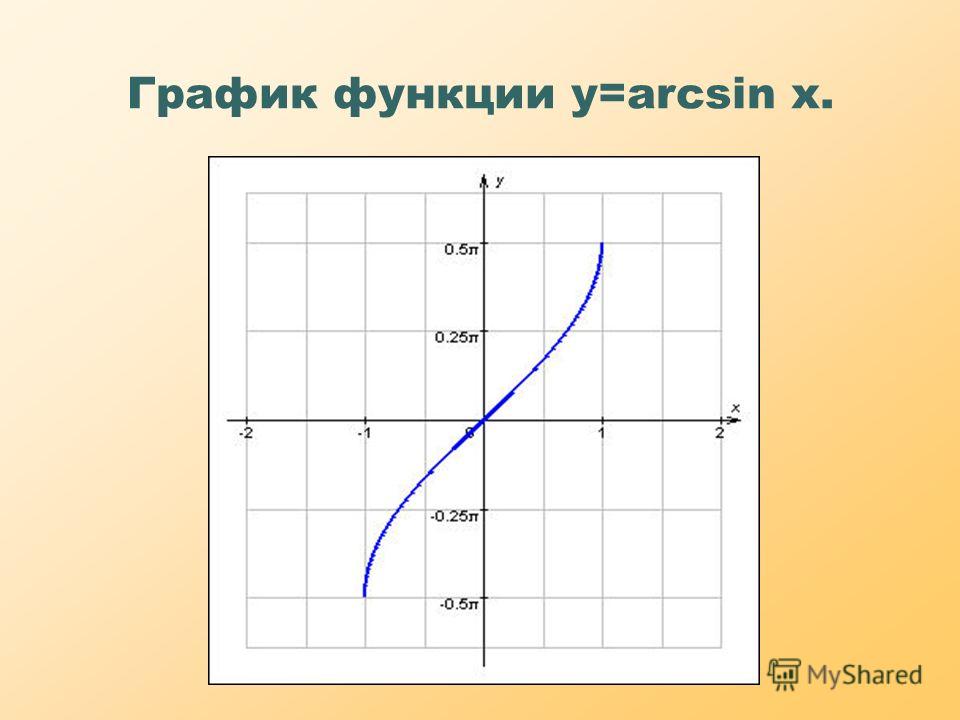
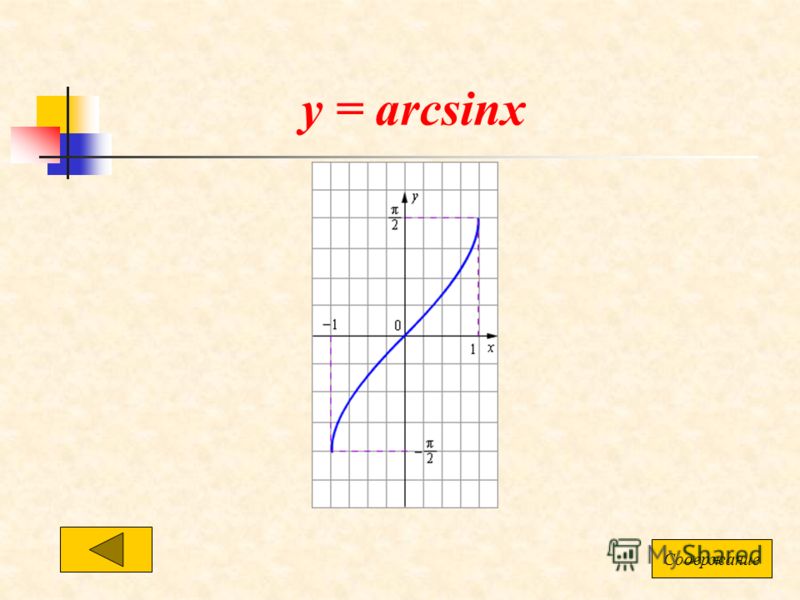
График функции y = arcsinx.
Арксинусом числа m называется такой угол x, для которого
Функция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.
- при
- при
- (область определения),
- (область значений).
Свойства функции arcsin
- (функция является нечётной).
- при
- при x = 0.
- при
Получение функции arcsin
Дана функция y = sinx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsinx функцией не является.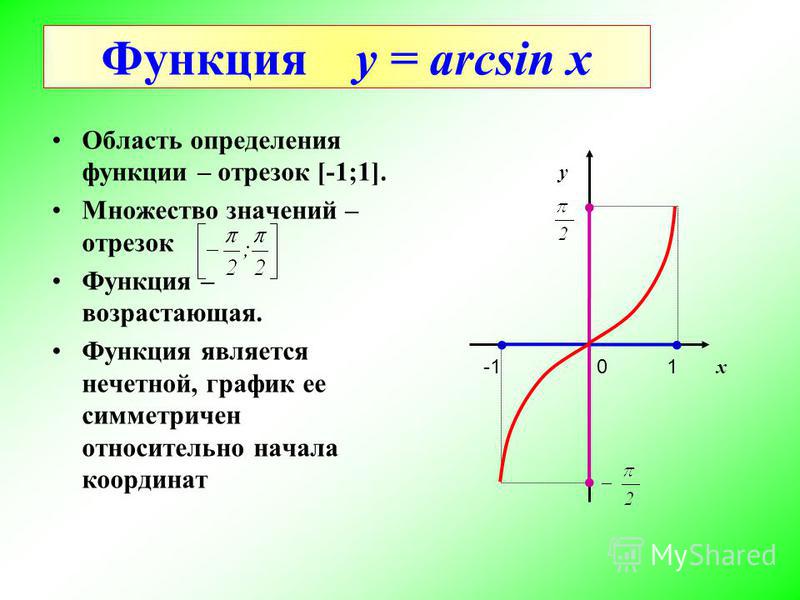
Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции y = sinx на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsinx, график которой симметричен графику функции y = sinx на отрезке относительно прямой y = x.
Функция arccos
График функции y = arccosx.
Арккосинусом числа m называется такой угол x, для которого
Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.
- cos(arccosx) = x при
- arccos(cosy) = y при
- E(arccosx) = [0;π]. (область значений).
Свойства функции arccos
- arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
- arccosx > 0 при
- arccosx = 0 при x = 1.
Получение функции arccos
Дана функция y = cosx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccosx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cosx строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccosx, график которой симметричен графику y = cosx на отрезке [0;π] относительно прямой y = x.
Функция arctg
График функции .
Арктангенсом числа m называется такой угол α, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
- при
- при
Получение функции arctg
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является.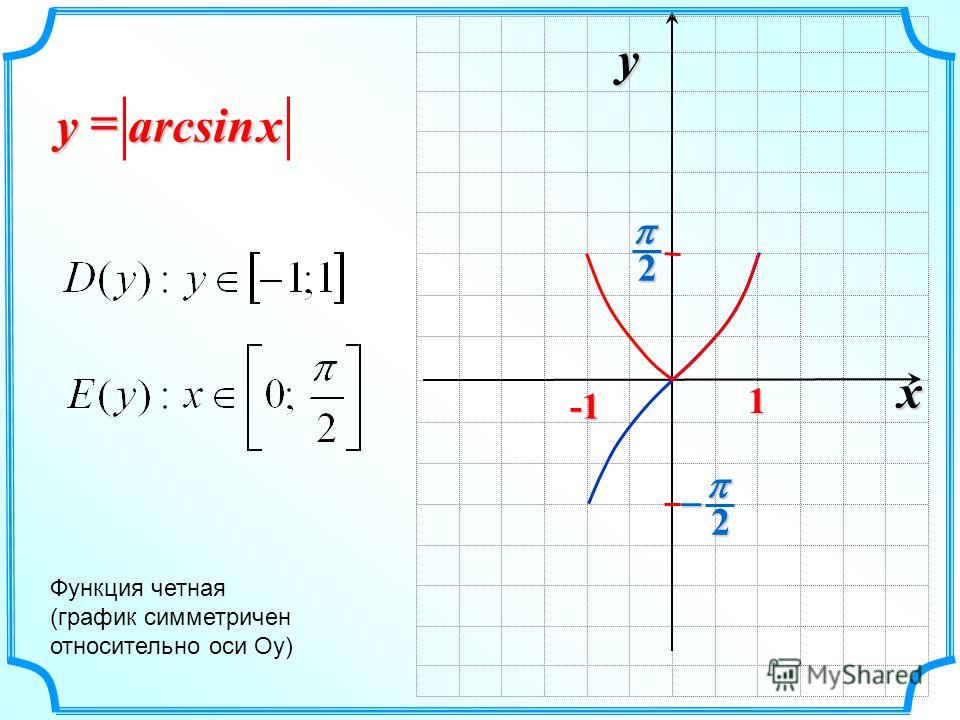
Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой y = x.
Функция arcctg
График функции y=arcctg x
Арккотангенсом числа m называется такой угол x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
- при
- при 0 < y < π,
Свойства функции arcctg
- (график функции центрально-симметричен относительно точки
- при любых x.
Получение функции arcctg
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является.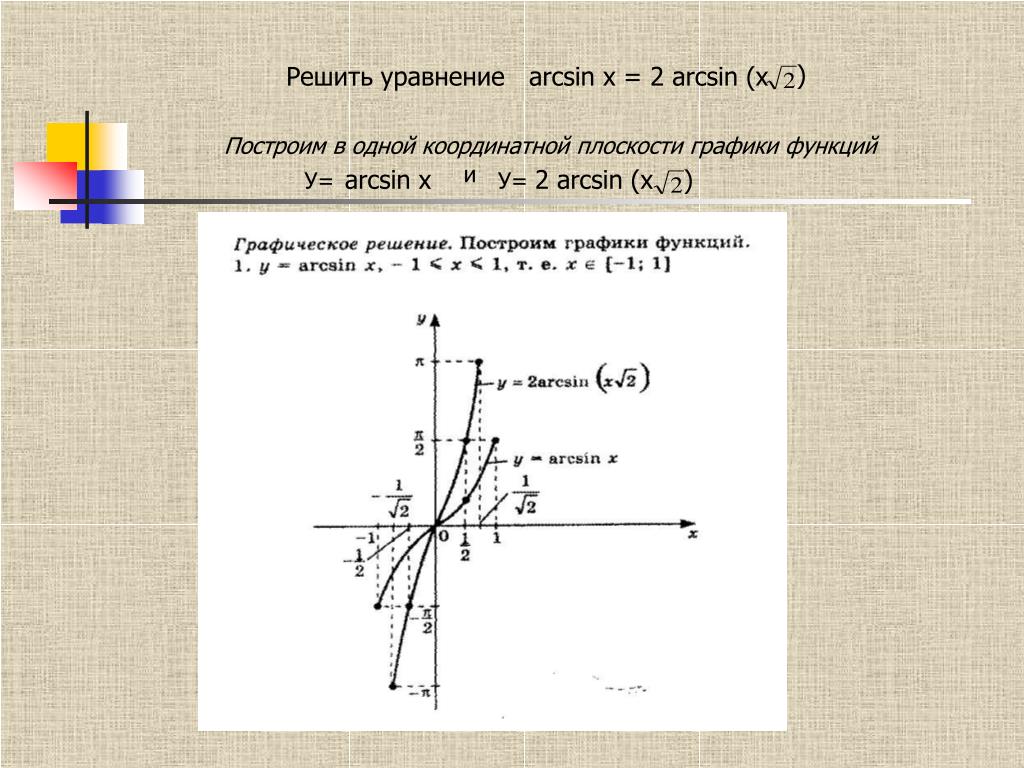
Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция , график которой симметричен графику на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу
Функция arcsec
arcsec(x) = arccos(1/x)
Функция arccosec
arccosec(X) = arcsin(1/x)
Производные от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x≥1:
- См. также Список интегралов от обратных тригонометрических функций
Разложение в бесконечные ряды
Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:
(член в сумме при n= 0 принимается равным 1).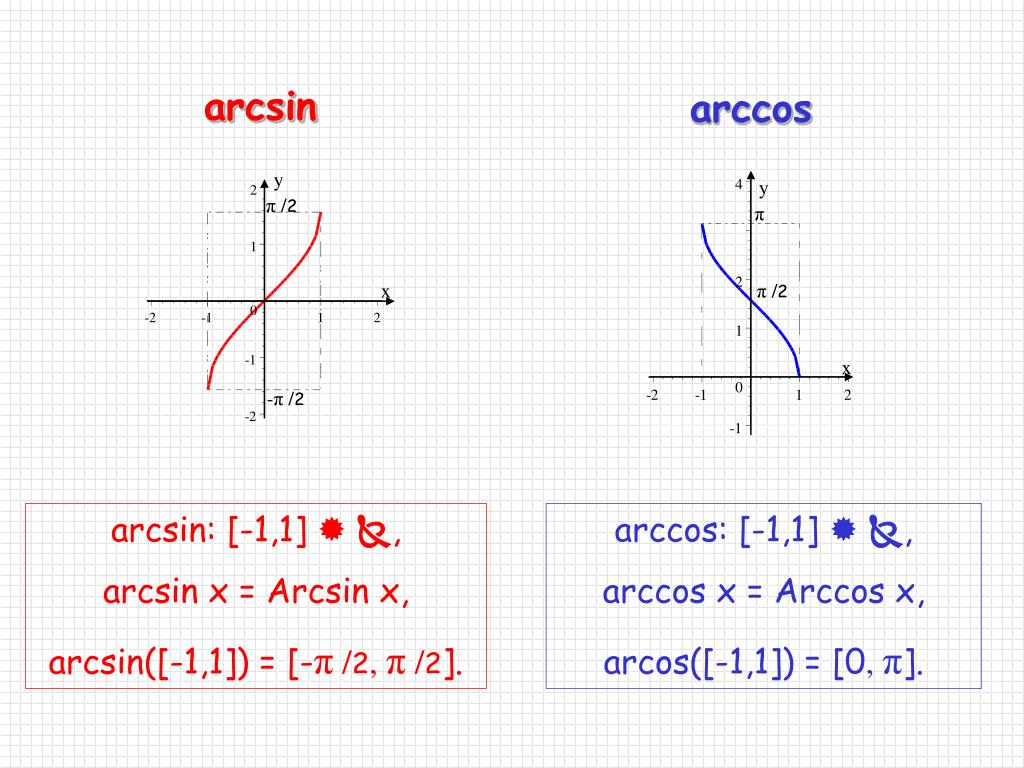
Использование в геометрии
Прямоугольный треугольник ABC
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.
В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:
- α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
См. также
- Тригонометрические функции
- Обратные гиперболические функции
- Теорема Данжуа — Лузина
Ссылки
- Weisstein, Eric W. Обратные тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Обратные тригонометрические функции — статья из Большой советской энциклопедии
- Построение графиков обратных тригонометрических функций онлайн
- Онлайн калькулятор: обратные тригонометрические функции
Обратные тригонометрические функции — презентация онлайн
Похожие презентации:
Обратные тригонометрические функции и их свойства.
(10 класс)
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства. 10 класс
Обратные тригонометрические функции
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции
Обратные тригонометрические функции. Свойства и графики
Обратные тригонометрические функции
10 класс
Обратные тригонометрические функции
и их свойства
Содержание
• Функция y = arcsin x и ее свойства
• Функция y = arccos x и ее свойства
• Функция y = arctg x и ее свойства
• Функция y = arcctg x и ее свойства
Функция y=arcsinx и ее свойства
Если |а| ≤ 1, то arcsin а – это такое число
из отрезка [-π/2; π/2], синус которого
равен а.
Если |а| ≤ 1, то
arcsin а = t
sin t = а,
-π/2 ≤ t ≤ π/2;
sin (arcsin a) = a
Функция y=arcsinx и ее график
у
π/2
y=arcsin x
х
-1
0
-π/2
1
π
Функция y=arcsinx и ее свойства
1.
D(y) = [-1; 1].2. E(y) = [-π/2; π/2].
3. arcsin (-x) = — arcsin x – функция
нечетная.
4. Функция возрастает на [-1; 1].
5. Функция непрерывна.
Функция y=arccosx и ее свойства
Если |а| ≤ 1, то arccos а – это такое число
из отрезка [0; π], косинус которого равен
а.
Если |а| ≤ 1, то
arccos а = t
cos t = а,
0 ≤ t ≤ π;
cos (arccos a) = a
arccos (-a) = π – arccos a, где -1 ≤ а ≤ 1
Функция y=arccosx и ее график
у
y=arccosx
π
π/2
Y=cos x
-1
π
0
1
х
Функция y=arccosx и ее свойства
1. D(y) = [-1; 1].
2. E(y) = [0; π].
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на [-1; 1].
5. Функция непрерывна.
Функция y=arctgx и ее свойства
arctg а – это такое число из интервала (-π/2;
π/2), тангенс которого равен а.
arctg а = t
tg t = а,
-π/2 < t < π/2;
tg (arctg a) = a
Функция y=arctgx и ее график
у
π/2
y=arctg x
π/4
х
-1
0
-π/4
-π/2
y=tg x
1
π
Функция y=arctgx и ее свойства
1.
D(y) = (- ; + ).2. E(y) = (-π/2; π/2).
3. arctg (-x) = — arctg x – функция нечетная.
4. Функция возрастает на (- ; + ).
5. Функция непрерывна.
Функция y=arcctgx и ее свойства
arcсtg а – это такое число из интервала (0;
π), котангенс которого равен а.
arcсtg а = t
сtg t = а,
0 < t < π;
сtg (arcсtg a) = a
arcctg (-a) = π – arcctg a
Функция y=arcctgx и ее график
у
π
y=сtg x
y=arcсtg x
π/2
-π
-π/2
0
π/2
π
х
Функция y=arcctgx и ее свойства
1. D(y) = (- ; + ).
2. E(y) = (0; π).
нечетной.
4. Функция убывает на (- ; + ).
5. Функция непрерывна.
English Русский Правила
Как найти график y=arcsin(x)
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Как найти график y=arcsin(x)» 9-1x` или Asin x
x y = sin x asin y
0 0 0
`pi/4« 1/sqrt2` `pi/4`
` pi/2` 1 `pi/2`
`3pi/4` `1/sqrt2` Таким образом, эта точка не определена для arcsin, поскольку она будет иметь то же значение.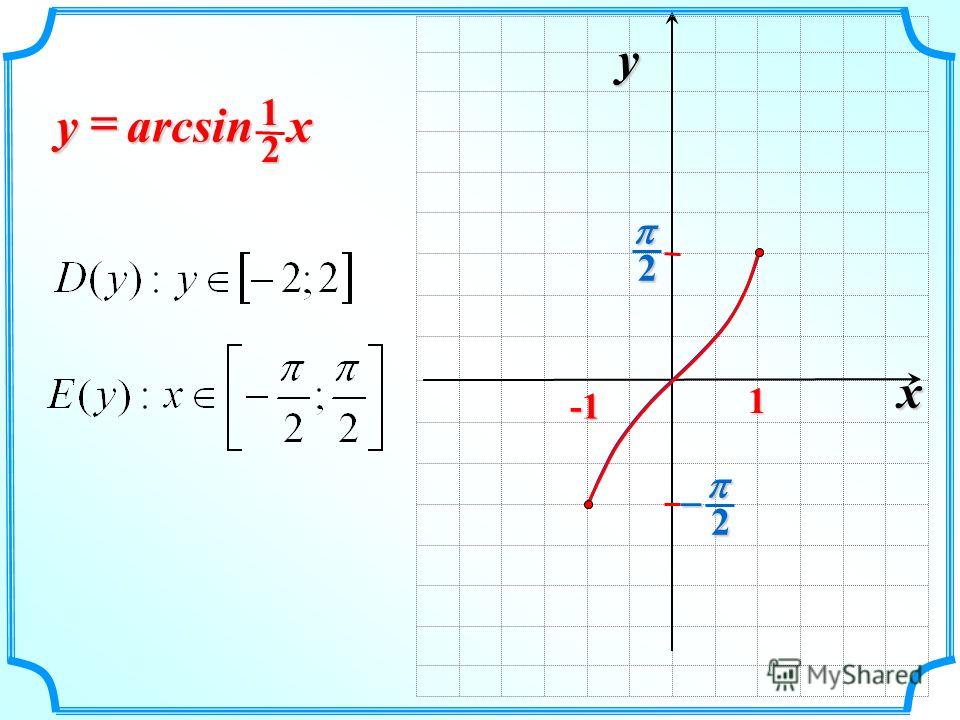
-1(x),null,0,0,,,black,1,none»/>
Утверждено редакцией eNotes
Наука
Последний ответ опубликован 17 июля 2012 г. в 14:55:17.
Каковы три части клеточной теории?
16 Ответы педагога
Наука
Последний ответ опубликован 21 июня 2018 г. в 17:01:30.
Какие десять примеров решений вы можете найти у себя дома?
2 Ответы воспитателя
Наука
Последний ответ опубликован 19 сентября 2015 г. в 21:37:47.
Каковы четыре основные функции компьютерной системы?
2 Ответы воспитателя
Наука
Последний ответ опубликован 06 июля 2009 г. в 21:23:22.
Каковы функции компьютера?
7 Ответы педагога
Наука
Последний ответ опубликован 23 июня 2012 г. в 17:12:04.
В чем сходство и различие фотосинтеза и дыхания? Сравните и сопоставьте основные пути фотосинтеза и дыхания.
3 Ответа воспитателя
Графики и обратные тригонометрические функции
Все ресурсы по предварительному исчислению
12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 Следующая →
Precalculus Help » Графики и обратные тригонометрические функции
Правда или ложь: существует вертикальная асимптота для на
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Утверждение неверно.
Утверждение верно.
Правильный ответ:
Утверждение верно.
Объяснение:
Мы знаем, что родительская функция имеет асимптоты в где – любое целое число. Учитывая , мы можем установить асимптотическое уравнение равным этому и решить для , чтобы увидеть, является ли целым числом. Если является целым числом, то здесь есть вертикальная асимптота.
Итак, когда , то
, значит данное утверждение верно.
Сообщить об ошибке
Укажите домен и диапазон sin(x) и arcsin(x).
Возможные ответы:
sin(x) домен:
sin(x) диапазон:
arcsin(x) домен:
arcsin(x) диапазон:
sin(x003 домен): (x) диапазон:
arcsin(x) домен:
arcsin(x) диапазон:
sin(x) домен:
sin(x) диапазон:
arcsin(x) домен:
arcsin(x) диапазон:
sin(x) домен:
sin(x) диапазон:
arcsin (x) домен:
arcsin(x) диапазон:
Правильный ответ:
sin(x) домен:
sin(x) диапазон:
arcsin(x) домен:
arcsin(x)6 диапазон:
Объяснение:
Два графика помогают представить ситуацию.
Домен — это все возможные значения x, а диапазон — все возможные значения y. Функция арксинуса переворачивает функцию синуса на бок, но для того, чтобы продолжать оставаться функцией (благодаря прохождению теста горизонтальной линии), диапазон функции арксинуса ограничен значением . Это не совпадение, что диапазон функции синуса равен области определения функции арксинуса из-за природы обратных отношений.
y = sin x
y = arcsin x
SIN (x) Домен:
SIN (x) Диапазон:
ARCSIN (x) Домен:
ARCSIN (x) Диапазон: Диапазон: x).
Сообщить об ошибке
Верно или неверно: ни одна из обратных тригонометрических функций не является функцией.
Возможные ответы:
Верно
Неверно
Правильный ответ:
Верно
Объяснение:
Это правда.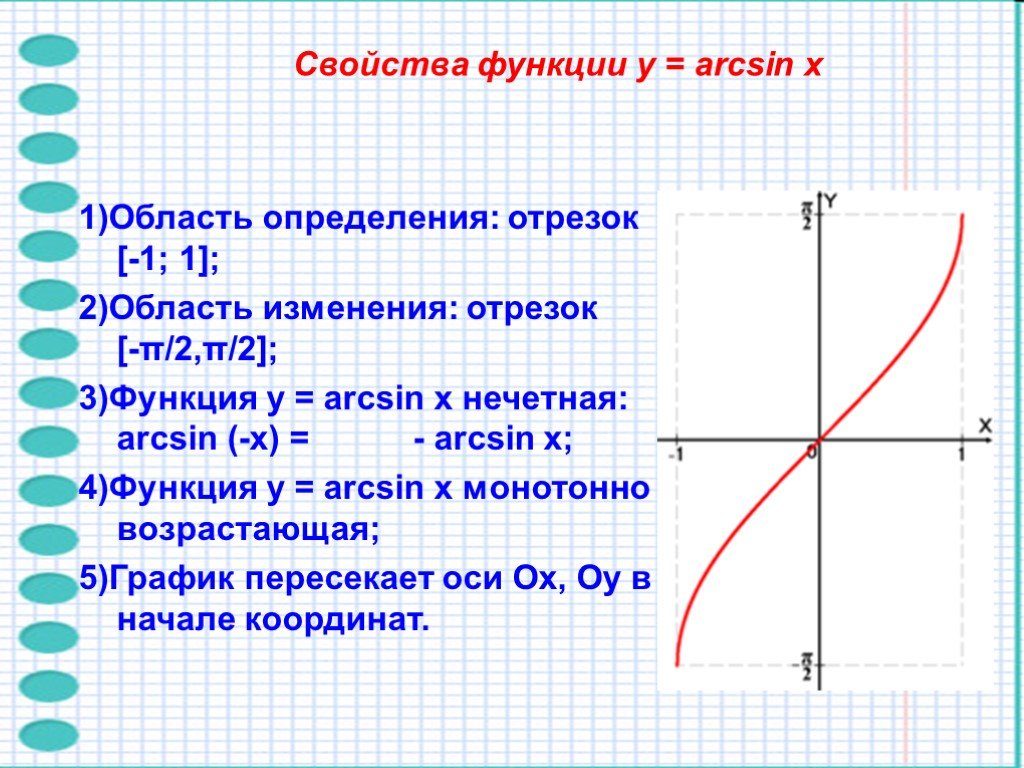
Каждая из обратных триггерных функций не проходит тест вертикальной линии и, следовательно, не является функцией. По этой причине вы также увидите графики обратных триггерных функций, которые ограничивают домен таким образом, что его можно изобразить как функцию.
Сообщить об ошибке
Найти обратную функцию y = sin(x). Затем начертите обе функции.
Возможные ответы:
y = cos(x)
Графики:
y = sin(x)
y = cos (x)
y = sin (x)
Графики:
y = sin (x)
y = sin (x)
y = sin (x)
y = sin (x)
Tan (x)
Графики:
y = sin (x)
y = tan (x)
y = cos -1 (x)
Графики:
y = sin (x)
y = cos -1 (x)
y = sin -1 (x)
Графики:
y = sin (x)
y = sin -1 (x)
Графики:
y = sin (x)
y = sin -1 (x)
Объяснение:
Чтобы найти обратную функцию, поменяйте местами значения x и y, а затем найдите y.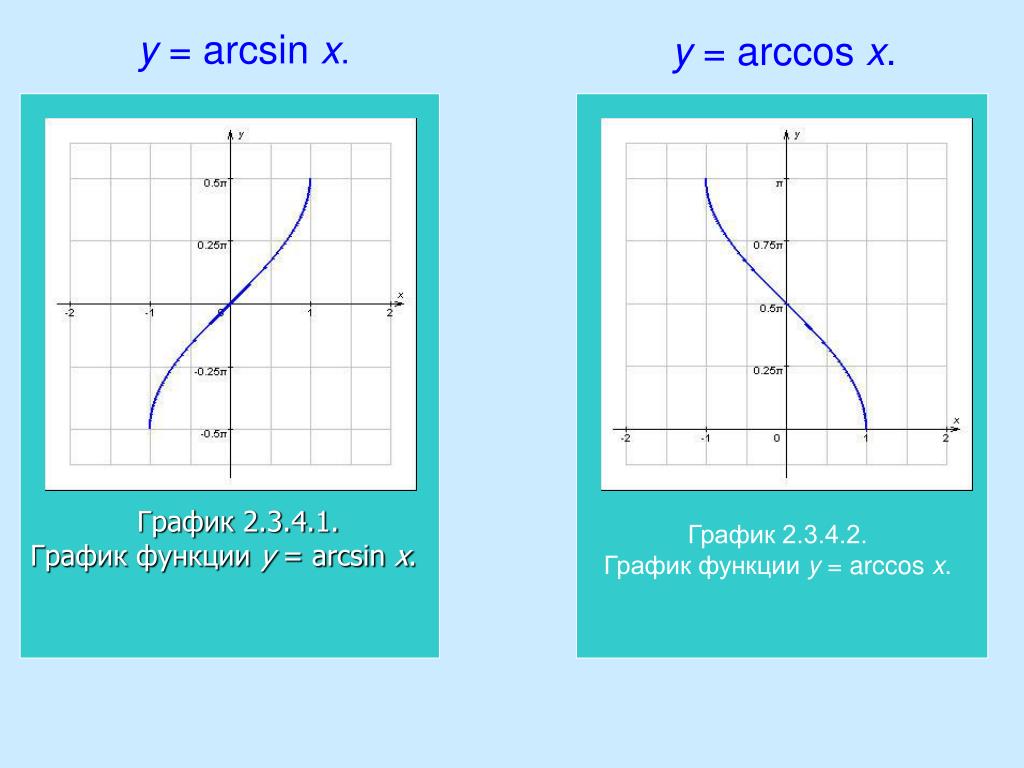
Замените y = sin(x) на x = sin(y). Затем решить для y:
x = sin(y)
sin -1 (x) = sin -1 (sin(y))
sin -1 (x) = y
график каждой функции 900 :
y = sin(x)
y = sin -1 (x)
Если вы посмотрите на верхний график и ограничите домен интервалом [-/2, /2], вы можете более четко увидеть взаимосвязь между двумя графиками.
Чтобы дополнительно проиллюстрировать взаимосвязь между двумя функциями, изучите входные и выходные данные двух функций на интервале [-/2, /2]:
y = sin(x)
y = sin -1 (x)
Сообщить об ошибке
В какой квадрант может попасть arccot (−½)?
Возможные ответы:
I и IV
III и IV
II и III
II и IV
Правильный ответ: 0 0
0 Объяснение:
Функция котангенса отрицательна в квадрантах II и IV, поэтому arccot (−½) может попасть в любой из этих квадрантов.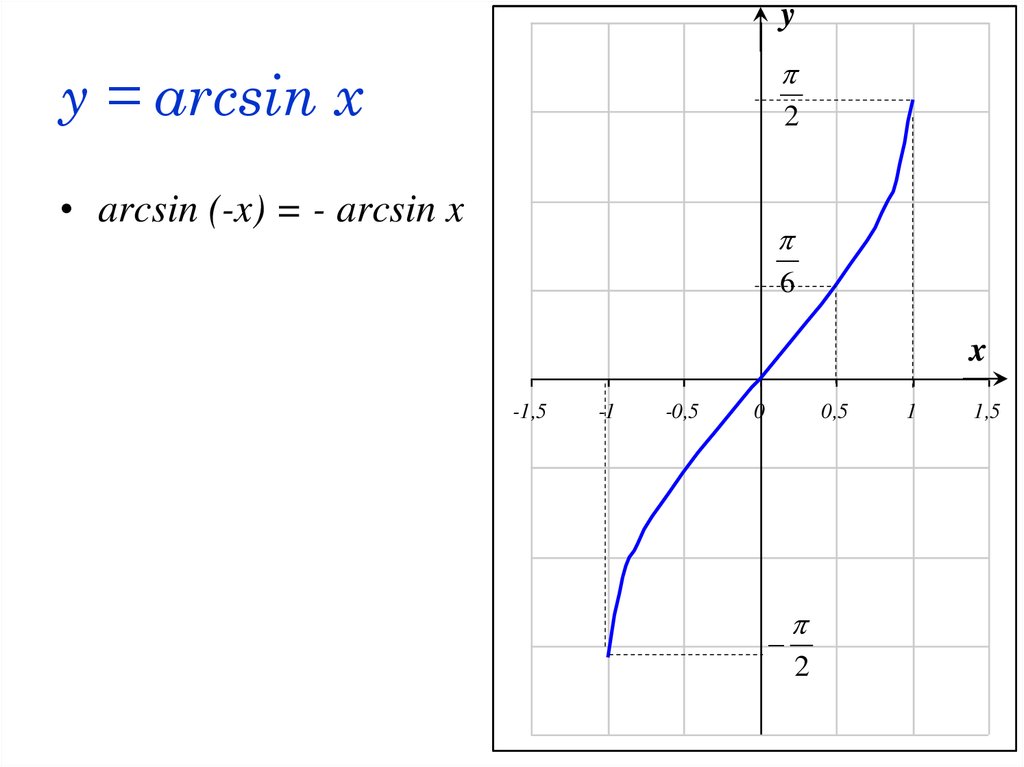
На изображении ниже показано, где каждая функция положительна. Все, что не отмечено, является отрицательным. Поскольку котангенс положителен в квадрантах I и III, он отрицателен в квадрантах II и IV.
Сообщить об ошибке
Какой из следующих функций может быть этот график?
Возможные ответы:
Arctan (x)
Arccos (x)
ARCSEC (x)
ARCSIN (x)
ARCCSC (x)
Правильный ответ:
9
9
6
6
6
6
6
. х)
Объяснение:
Это график угловых секунд (x). Задумайтесь о нескольких точках функции sec(x): (-, -1), (0,1), (, -1). Теперь поменяйте местами значения x и y, чтобы получить: (-1, -), (1, 0), (-1, ). Обратите внимание, что (-1, -) и (1, 0) существуют на этом графике. (-1, ) не существует на этом графике, потому что для того, чтобы сделать это функцией, домен должен был быть ограничен таким образом, чтобы он прошел тест вертикальной линии.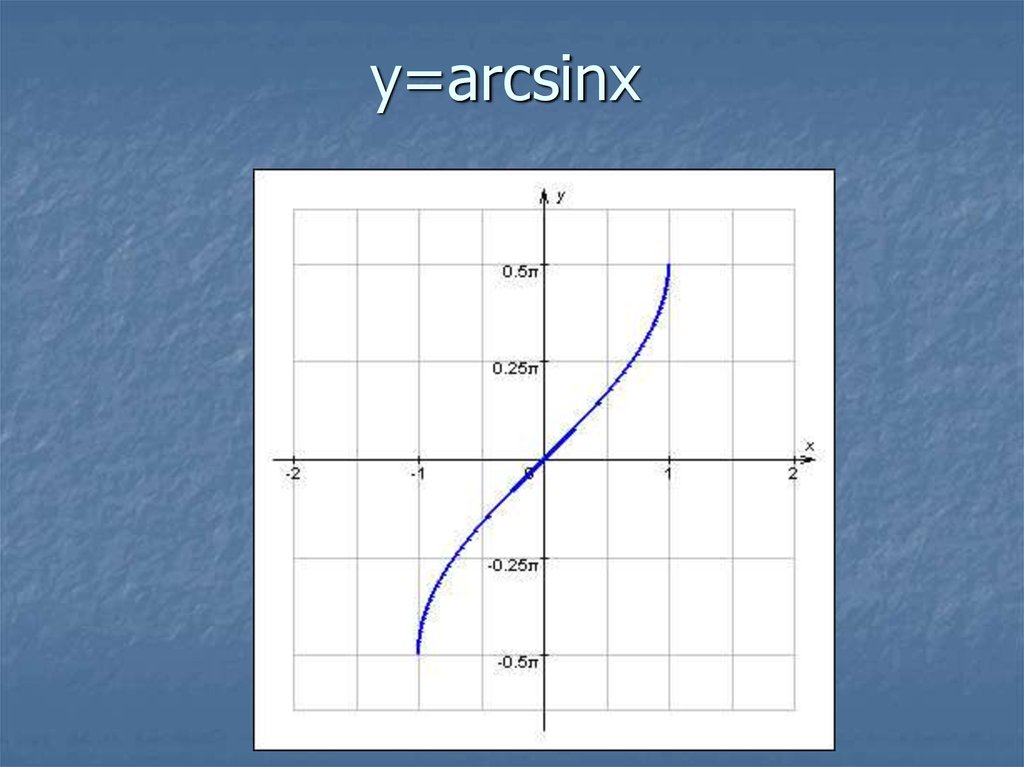
Вы можете увидеть, как график arcsec(x) соотносится с графиком sec(x), сравнив их:
Сообщить об ошибке
В какой квадрант может попасть арксинус (−½)?
Возможные ответы:
I и II
I и III
III и IV
II и III
I и IV
Правильный ответ:
III и IV
Объяснение:
Функция синуса отрицательна в квадрантах III и IV, поэтому арксинус (−½) может попасть в любой из этих квадрантов. На изображении ниже показано, где каждая функция положительна. Все, что не отмечено, является отрицательным. Поскольку синус положителен в квадрантах I и II, он отрицателен в квадрантах III и IV.
Сообщить об ошибке
Этот график может быть графиком какой из следующих функций?
Возможные ответы:
Arctan (x)
ARCCOT (x)
TAN (x)
ARCCSC (x)
COT (x)
Правильный ответ:
Arccot (x) х)
Объяснение:
Это график arccot(x).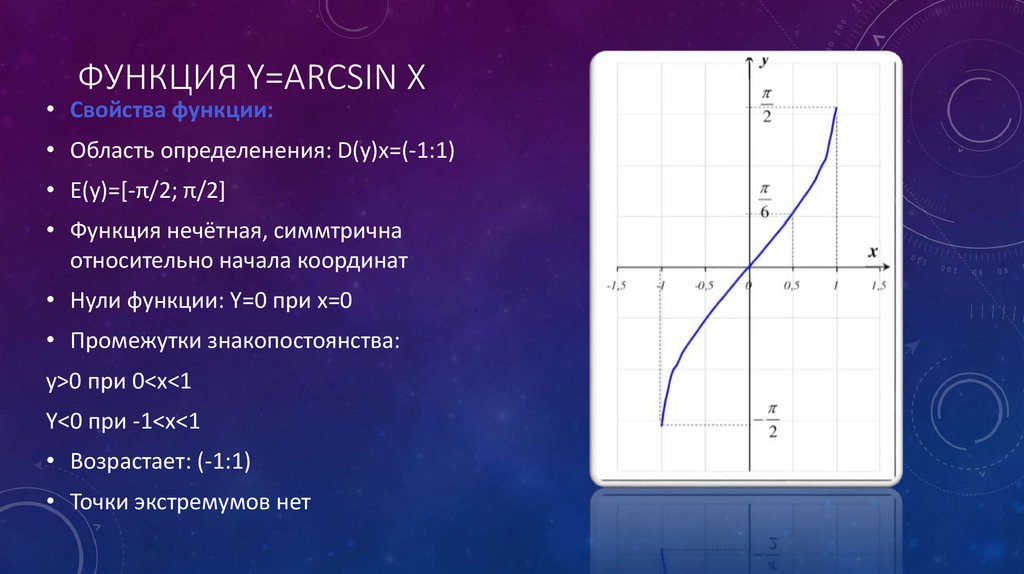
Подумайте о нескольких характеристиках функции cot(x): у нее есть точка в точках (-/2, 0) и вертикальные асимптоты в точках x=-, x=0 и x=. Обратите внимание, что на приведенном выше графике у нас есть точка (0, -/2), которая переворачивает значения x и y точки на cot(x), и мы также можем видеть горизонтальные асимптоты как при y=0, так и при y= . У нас также нет другой горизонтальной асимптоты в y=- , потому что нам нужно было ограничить область определения arccot(x), чтобы она была функцией и прошла тест вертикальной линии. Вы можете посмотреть на график кроватки(х) ниже, сравнить их и увидеть их сходство:
Отчет о ошибке
Оцените следующее выражение, предполагая, что все углы находятся в Квадранте I:
Возможные ответы:
12/13
13/5
5/13
93
13/5
5/13
9
13/5
5/13
5/1212/5
Правильный ответ:
5/12
Объяснение:
Чтобы решить , сначала пусть .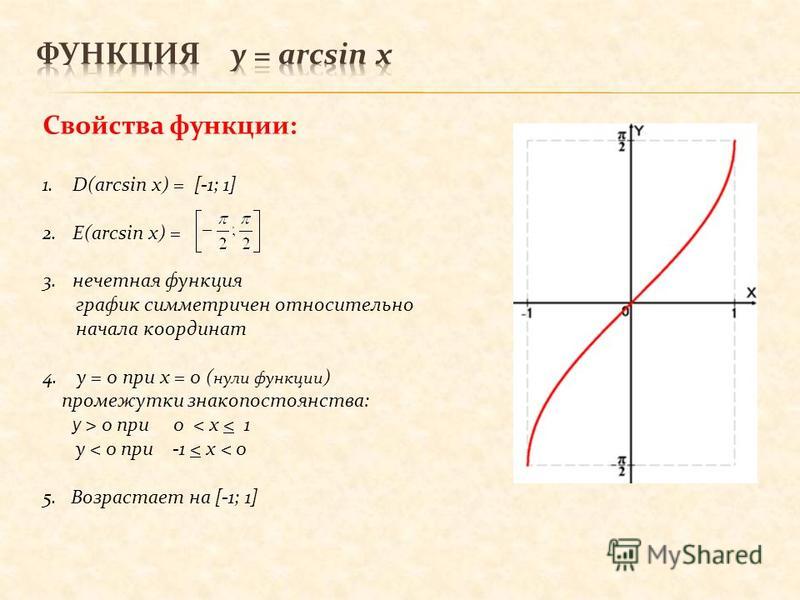
Затем, . Поскольку это значение положительное, мы знаем, что это должно быть в квадранте I или квадранте II, но, учитывая инструкции, мы можем предположить, что A находится в квадранте I.
Далее, вспомните это .
Using the Pythagorean Theorem, you can solve for the following:
x 2 + y 2 = r 2
x 2 + 12 2 = 13 2
x = 5
Следовательно, . Теперь решите:
Следовательно,
Сообщить об ошибке
Оцените следующее выражение, предполагая, что все углы находятся в квадранте I:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить , сначала пусть . Затем, . Поскольку это значение положительное, мы знаем, что это должно быть в квадранте I или квадранте IV, но, учитывая инструкции, мы можем предположить, что A находится в квадранте I.