Онлайн-курс Основы начертательной геометрии — OILEDU
О курсе
Начертательная геометрия, как базовая дисциплина для инженеров, архитекторов и дизайнеров, считается достаточно сложным для восприятия и понимания. Но вместе с тем это очень важная и интересная наука, одна из немногих, при изучении которой развивается пространственное воображение и творческое мышление. Начертательная геометрия – это азбука инженерной графики. Это база для навыка создания чертежей и схем строительных объектов и конструкторских изделий сложной конфигурации. Развивая способности представлять и моделировать в воображении сложные пространственные объекты, вы закладываете «прочный фундамент» своего профессионального будущего.
Курс разработан с применением самых современных средств визуальной коммуникации, яркая и интуитивно понятная анимационная графика поможет разобраться в самых сложных пространственных задачах и сделает процесс обучения приятным и очень увлекательным занятием.
Основоположником этой науки является Гаспар Монж. В 16 лет он проявил большие способности в расчётах военно-инженерных сооружений, а затем создал метод графического решения задач стереометрии на чертежах, который заключается в том, что любой объект изображается в трёх проекциях на плоскость: фронтальной (вид спереди), горизонтальной (вид сверху) и профильной (вид слева). При построении этих проекций необходимо представить себе пучок проецирующих лучей и, если они направлены под прямым углом к плоскости проекций, то проекция называется прямоугольной.
Из курса вы узнаете о методах проецирования, о образовании чертежа геометрических элементов и пространственных объектов, о способах преобразования комплексного чертежа, о способах решения позиционных и метрических задач, связанных с геометрическими элементами и пространственными объектами.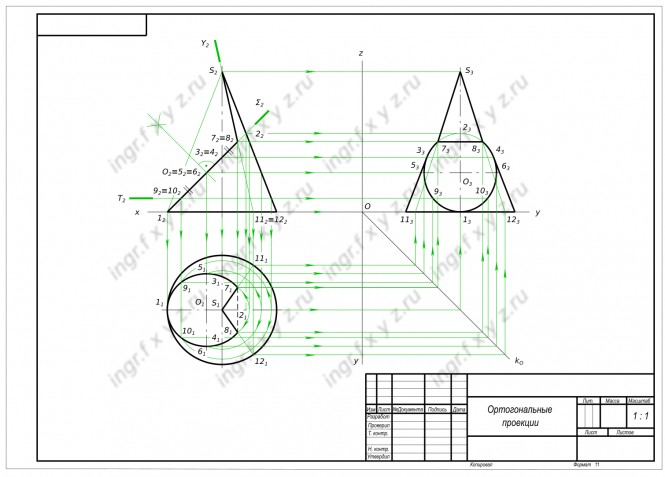
Формат
Курс рассчитан на 6 недель. Недельная нагрузка обучающегося по курсу – 18 академических часов.
Еженедельные занятия включают:
- просмотр видеолекций;
- анализ учебных заданий, иллюстрирующих приложения теории к решению практических задач;
- заполнение рабочей тетради для лекционных занятий;
- тестирование по каждому разделу курса.
Завершается курс итоговым тестированием.
Требования
Для успешного освоения курса «Основы начертательной геометрии» необходимы знания по геометрии (планиметрии, стереометрии и тригонометрии) и черчению.
- Программа
- Результаты обучения
- Направления подготовки
Курс состоит из следующих разделов:
ВВЕДЕНИЕ
- Инструкция к курсу
- История начертательной геометрии
Раздел 1.
МЕТОДЫ ПРОЕЦИРОВАНИЯ
- 1.1 Условные обозначения и знаки
- 1.2 Основные методы проецирования
- 1.2.1 Центральное и параллельное проецирование
- 1.2.2 Свойства параллельного проецирования
- 1.2.3 Ортогональное проецирование
- 1.2.4 Свойства ортогонального проецирования
- 1.3 Образование чертежа точки
- 1.3.1 Двухкартинный комплексный чертеж точки
- 1.3.2 Трехкартинный комплексный чертеж точки
Раздел 2.
КОМПЛЕКСНЫЙ ЧЕРТЕЖ ПРЯМОЙ
- 2.1 Прямые общего положения
- 2.1.1 Следы прямой
- 2.1.2 Восходящие и нисходящие прямые
- 2.2 Натуральная величины отрезка прямой общего положения
- 2.3 Прямые частного положения
- 2.3.1 Конкурирующие точки
- 2.4 Взаимное положение прямых в пространстве
- 2.
 5 Теорема о проецировании прямого угла
5 Теорема о проецировании прямого угла
Раздел 3.
ПЛОСКОСТИ
- 3.1 Плоскость. Определители плоскости
- 3.2 Плоскости общего и частного положения
- 3.2.1 Следы плоскости
- 3.3 Аксиома принадлежности точки и прямой плоскости
- 3.3.1 Теорема о проецировании прямого угла
- 3.3.2 Главные линии плоскости
Раздел 4.
ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ
- 4.1 Основные позиционные задачи
- 4.1.1 Метрические и позиционные задачи
- 4.1.2 Вспомогательные позиционные задачи
- 4.1.3 Первая основная позиционная задача
- 4.1.4 Вторая основная позиционная задача
- 4.2 Взаимное положение прямых и плоскостей
- 4.3 Перпендикулярность прямой и плоскости
Показать все
В результате освоения курса
обучающийся должен знать:
- – принципы построения точки, прямой и плоскости на чертежах;
- – принципы построения, классификацию и образование кривых линий;
- – образование и классификацию криволинейных поверхностей.

обучающийся должен уметь:
- – графическими способами решать позиционные и метрические задачи плоских и пространственных форм на плоскостях проекций, в том числе применяя способы преобразования;
- – воспринимать оптимальное соотношение частей и целого на основе графических моделей, практически реализуемых в виде чертежей конкретных пространственных объектов;
- – использовать для решения инженерных задач методы начертательной геометрии.
обучающийся должен владеть:
- – методами проецирования и изображения пространственных форм на плоскости проекций;
- – основными понятиями, связанными с графическими представлениями информации;
- – возможностями применения полученных знаний в различных областях деятельности.
- 21.05.06 «Нефтегазовые техника и технологии»
- 21.03.01 «Нефтегазовое дело»
- 28.
 03.02 «Наноинженерия»
03.02 «Наноинженерия» - 15.03.02 «Технологические машины и оборудование»
- 13.03.02 «Электроэнергетика и электротехника»
- 13.03.01 «Теплоэнергетика и теплотехника»
- 08.03.01 «Строительство»
- 07.03.01 «Архитектура»
- 54.03.01 «Дизайн»
- 08.05.01 «Строительство уникальных зданий и сооружений»
Авторы курса
ПЕЧЁНКИНА ТАТЬЯНА ВЛАДИМИРОВНА
Кандидат технических наук
Доцент кафедры «Комплексный инжиниринг и компьютерная графика» УГНТУ
ПЕЧЁНКИНА ТАТЬЯНА ВЛАДИМИРОВНА
Кандидат технических наук
Доцент кафедры «Комплексный инжиниринг и компьютерная графика» УГНТУ
Награждена почётными грамотами УГНТУ и Министерства высшего образования РФ.
Ведущий лектор дисциплины «Инженрная компьютерная графика» по направлениям «Строительство», «Архитектура» и «Дизайн».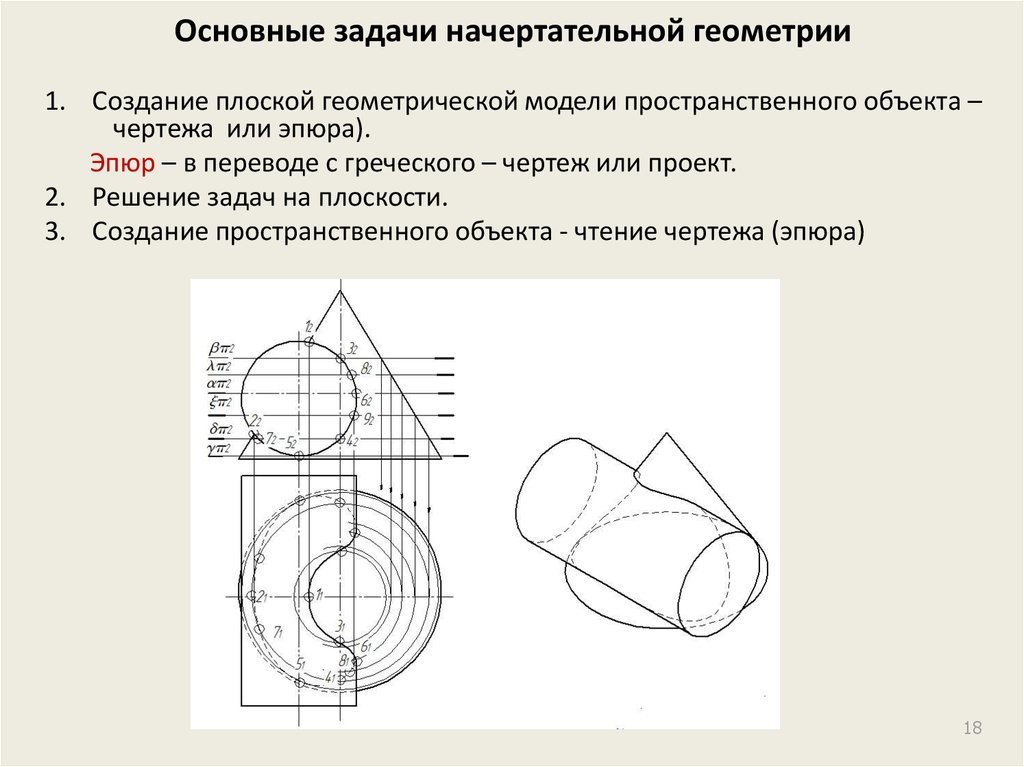
Автор более 80 научных статей, в том числе 10 учебных и учебно-методических пособий в области начертательной геометрии, инженерно-компьютерной графики и информационного моделирования в строительстве.
Основные интересы — дизайн среды и ландшафтный дизайн.
СЕРГИН РОМАН ПЕТРОВИЧ
Преподаватель кафедры «Комплексный инжиниринг и компьютерная графика» УГНТУ.
Заместитель директора по учебно-методической работе и дополнительному образованию Высшей школы информационных и социальных технологий УГНТУ.
Руководитель лаборатории коммуникативного дизайна и автор трех действующих курсов в области Технологий анимационной графики, коммуникативного дизайна и технической эстетики.
СЕРГИН РОМАН ПЕТРОВИЧ
Преподаватель кафедры «Комплексный инжиниринг и компьютерная графика» УГНТУ.
Заместитель директора по учебно-методической работе и дополнительному образованию Высшей школы информационных и социальных технологий УГНТУ.
Руководитель лаборатории коммуникативного дизайна и автор трех действующих курсов в области Технологий анимационной графики, коммуникативного дизайна и технической эстетики.
Автор более 20 научных статей в области технической эстетики и коммуникативных технологий. Более 10 лет практического опыта в руководстве проектами коммуникационных стратегий для промышленных организаций. Основные интересы — эргономика и экология коммуникативной среды, техническая эстетика, motion-дизайн и UX-дизайн.
Другие курсы
Бесплатно Наглядно Доступно
Нефтегазовое образование открытые онлайн-курсыНачертательная геометрия. Краткий курс — презентация онлайн
Похожие презентации:
Основы архитектуры и строительных конструкций. Основы проектирования
Конструктивные схемы многоэтажных зданий
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Маркировка строительных чертежей (лекция №2)
Правила выполнения архитектурно-строительных чертежей
ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)
задачи на построение (геометрия 7 класс)
Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)
Параллельность в пространстве. (Графическая работа 2)
Строительное черчение. Графическое оформление и чтение строительных чертежей
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
1. Начертательная геометрия
Краткий курсАвтор лекций Белокрылова
Ольга Вениаминовна
Кафедра начертательной геометрии и технического
черчения
2. Метод проекций
SЦентральное проецирование
При центральном проецировании
задают плоскость проекций П1 и
центр проекций S.
В
А
Точки А1 и В1 являются
центральными проекциями точек А и
В на заданную плоскость.
В1
П1
А1
Прямые, проходящие через центр
проекций и проецируемые точки,
называют проецирующими
прямыми.
Центральные проекции применяют для изображения предметов в
перспективе. Такие изображения наглядны, но в них не соблюдаются
метрические характеристики.
3. Свойства центрального проецирования
• Точка проецируется в точку• Прямая проецируется в прямую
• Двумерная фигура проецируется в виде
двумерной фигуры
• Трехмерная фигура отображается двумерной
• Центральные проекции фигур сохраняют
взаимную принадлежность, непрерывность и
другие геометрические свойства
4. Параллельные проекции
SА
При параллельном проецировании центр
проецирования удален в бесконечность.
К
В
Проецирующие прямые параллельны
между собой. В зависимости от угла
наклона проецирующей прямой к
плоскости проекций параллельные
проекции разделяются на косоугольные и
прямоугольные или ортогональные.
В1
П1
А1
К1
К уже существующим возникают новые свойства:
— если прямые параллельны, то их проекции тоже
параллельны
-если точка К делит отрезок АВ в некотором
отношении, то проекция К1 делит А1В1 в том же
отношении
-геометрические образы параллельные плоскости
проекций проецируются на неё в натуральную
величину
5.
 Прямоугольное (ортогональное) проецированиеОдна проекция геометрического образа не позволяет воссоздать его
Прямоугольное (ортогональное) проецированиеОдна проекция геометрического образа не позволяет воссоздать егоформу и размеры. Проецирование на две и более плоскости проекций
позволяет сделать чертеж обратимым.
Проецирование на две взаимно перпендикулярные плоскости проекций
Эпюр Монжа
z
П1-горизонтальная плоскость проекций
А2
П2
П2-фронтальная плоскость проекций
А
x
А2-фронтальная проекция точки А
Ах
П1
А1-горизонтальная проекция точки А
А1
x, y, z- взаимно перпендикулярные оси
координат
y
6. Проецирование на две взаимно перпендикулярные плоскости проекций Эпюр Монжа
zz
А2
А2
П2
А
Ах
x
О
О
А1
П1
П1
х
Ах
y
А1
у
А1
Полученный чертеж
называется эпюром Монжа.
y
Две прямоугольные проекции точки вполне определяют ее положение в
пространстве
7. Проецирование на три взаимно перпендикулярные плоскости проекций
zП2
А2
А
x
z
Аz
А2
А3 П3
Az
А3
Ах
П1
А1
Ау
Ах
Ау
х
y
П1-горизонтальная плоскость проекций
П2-фронтальная плоскость проекций
П3 –профильная плоскость проекций
А1-горизонтальная проекция точки А
А2-фронтальная проекция точки А
А3-профильная проекция точки А
А1
Ау
y
Прямая
к проходит под углом 45°
к
8.
 Проецирование отрезка прямой линииz
Проецирование отрезка прямой линииzП2
В2
В
К2
А2
х
А2
к
А
В1
А1
К1
о
В2
К2
х
о
В1
П1
К1
А1
Если какая-либо точка принадлежит
прямой, то ее проекция принадлежит
проекции прямой
y
Длина проекции отрезка прямой
общего положения меньше длины
самого отрезка
9. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций
Вα
А
Метод прямоугольного треугольника
∆Z
В2
К
В1
∆Z
А1
Отрезок АВ является гипотенузой
∆АВК.
α-угол наклона прямой к
горизонтальной плоскости
х
А2
α
А1
В1
∆Z
В
Натуральная величина отрезка
10. Определение натуральной величины отрезка прямой общего положения и углов его наклона к плоскостям проекций
Метод прямоугольного треугольника∆У
В
Натуральная величина
отрезка прямой
В2
β
х
β-угол наклона прямой к
фронтальной плоскости
проекций
А2
В1
∆У
А1
11.
 Прямые частного положенияЭто прямые, расположенные параллельно или перпендикулярно
Прямые частного положенияЭто прямые, расположенные параллельно или перпендикулярноосновным плоскостям проекций.
z
Проецирующие прямые
П2
b2
а2
а
b
c
c3
П3
x
а1
b1
П1
а ┴ П1
Горизонтальнопроецирующая
прямая
b ┴ П2
Фронтальнопроецирующая
прямая
c1
c ┴ П3
Профильнопроецирующая
прямая
y
12. Проецирующие прямые
za2
b2
с2
b1
с1
b -фронтально проецирующая
прямая
с –профильнопроецирующая
прямая
с3
х
a1
а –горизонтальнопроецирующая
прямая
y
13. Линии уровня
Прямые частного положения параллельные какой –либо плоскости проекцийП2
П2
h3
f2
h
f
h2
f1
П1
h3
x
П1
f2
x
h2
Горизонтальная прямаягоризонталь
f1
Фронтальная прямаяфронталь
14. Линии уровня
zП2
z
с2
с3
с
П3
C3
C2
x
с1
х
П1
y
C1
Прямая С расположена параллельно
профильной плоскости проекций
y
С -профильная прямая
English Русский Правила
Технический рисунок с описательной геометрией — ее информационная школа Технологии, Beograd
Программа обучения / учебные программы: Computer Multimedia
Тип и уровень исследований: Прикладные исследования.
Статус: по выбору
Кредиты ECTS: 8
Цель курсаИзучение технического черчения в AutoCAD компании Autodesk, ведущем программном обеспечении для проектирования, черчения, черчения и проектирования. Основными задачами курса являются: развитие способностей пространственного воображения, приобретение навыков разработки и чтения технических чертежей в AutoCAD, а также обучение студентов методам представления трехмерных форм посредством ортогональной проекции, в соответствии с требованиями современных технологий САПР. Теоретические и практические занятия проводятся с использованием интерактивных методов, а лекции сопровождаются упражнениями.
Результат курса Создание и чтение технических чертежей позволяют учащимся грамотно воспринимать трехмерное пространство и объекты, а также понимать конструктивную и структурную компоновку объекта. Кроме того, изучение основных принципов начертательной геометрии способствует развитию логического мышления и расширяет пространственное воображение. В дизайнерской практике это приводит к детальному, точному, креативному и функциональному дизайну продукта. Студенты смогут подготовить проект и представить его с использованием чертежей, выполненных в соответствии со стандартами AutoCAD, в форме, понятной как профессионалам, так и широкому кругу пользователей. Кроме того, курс позволит учащимся развить критический подход к различным типам технических чертежей и методам представления трехмерных объектов и пространства.
В дизайнерской практике это приводит к детальному, точному, креативному и функциональному дизайну продукта. Студенты смогут подготовить проект и представить его с использованием чертежей, выполненных в соответствии со стандартами AutoCAD, в форме, понятной как профессионалам, так и широкому кругу пользователей. Кроме того, курс позволит учащимся развить критический подход к различным типам технических чертежей и методам представления трехмерных объектов и пространства.
Начертательная геометрия
- Введение в начертательную геометрию
- Точка и плоскость
- Линии в космосе
- Самолеты в космосе
- Отношения геометрических элементов в пространстве
- Типы проекций в начертательной геометрии
- Геометрия в космосе
- Сложные геометрические формы
Стандарты технического черчения и работы в AutoCAD
- Введение в технический чертеж
- Технический чертеж (стандартизация, элементы технического чертежа, методы построения элементов)
- Введение в AutoCAD (среда, настройка рабочей поверхности, основы палитры Draw )
- Режимы работы в качестве дополнительных средств рисования
- Чертеж в AutoCAD и модификации нарисованных элементов ( Draw и Modify )
- Изменение свойств элемента на чертеже ( Свойства )
- Ввод текста в чертеж
- Определение размеров – правила и типы
- Простановка размеров в AutoCAD ( Аннотация , настройка стилей)
- Штриховка и градиенты в AutoCAD
- Рисование теней в 2D-перспективе
- Слои
- Важные команды в AutoCAD
- Определение и типы секций
- Блоки
- Сложные чертежи
- Заговор
- Сложные и изогнутые линии (например, Сплайн )
- Рисование и редактирование сложных линий
- Допуск
Геометрические модели — Модели Жюльена для начертательной геометрии
Известный как отец начертательной геометрии, Гаспар Монж (1746-1818) родился в Боне, Бургундия во Франции. Посетив колледж в раннем возрасте, Монж рано проявил математический талант. В восемнадцать лет он нарисовал план своего родного города, что привлекло к нему внимание Королевской школы Жени в Мезьере, где он стал рисовальщиком в 1765 году. В следующем году его попросили нарисовать планы укрепления. Используя свой математический талант, Монж разработал собственный метод представления вертикальных и горизонтальных компонентов архитектурного чертежа.
Посетив колледж в раннем возрасте, Монж рано проявил математический талант. В восемнадцать лет он нарисовал план своего родного города, что привлекло к нему внимание Королевской школы Жени в Мезьере, где он стал рисовальщиком в 1765 году. В следующем году его попросили нарисовать планы укрепления. Используя свой математический талант, Монж разработал собственный метод представления вертикальных и горизонтальных компонентов архитектурного чертежа.
Его новый подход к геометрии стал известен как описательная геометрия. Монж описывает свою новую геометрию как «точное изображение на чертежах, имеющих только два измерения, объектов, имеющих три». В частности, показывая вертикальную и горизонтальную проекции объекта на одном листе бумаги (бумага разделена пополам по горизонтали с вертикальной проекцией вверху и горизонтальной проекцией внизу), можно использовать геометрические свойства для определения различных элементов. изображаемой поверхности, такие как углы пересечения и длины. Все подобные свойства трехмерных объектов необходимы для точного проектирования и строительства различных зданий, а также для решения других проектных задач техники. Термин описательная геометрия до сих пор используется для этого метода представления вертикальной и горизонтальной проекций объекта. Однако современный термин для метода — орфографическая проекция.
Термин описательная геометрия до сих пор используется для этого метода представления вертикальной и горизонтальной проекций объекта. Однако современный термин для метода — орфографическая проекция.
| Этикетка коллекции Жюльена рельефов |
Франция сочла эту новую геометрию настолько важной для проектирования фортификационных сооружений, что в течение нескольких лет она считалась государственной тайной. Примером может служить проектирование звездных фортов. Звездные форты были изобретены в Италии в пятнадцатом веке и стали обычным явлением в Европе и Новом Свете в следующем столетии. С появлением более крупных пушек укрепления должны были быть более продуманно спроектированы, чтобы выдерживать и отражать артиллерийский огонь. Широкие основания и наклонные стены звездных фортов помогали отражать артиллерийский огонь. Прямые наклонные стены позволяли защитникам вести анфиладный или фланговый огонь: стрелять по врагу поперек из точек звезд, чтобы у атакующих не было безопасного места для огня, и удерживали атакующих дальше от стен. Раньше форты часто имели закругленные стены, что позволяло создавать «мертвые зоны», где защитники не могли стрелять по нападавшим. Красивые изображения звездных фортов можно найти в сети.
Раньше форты часто имели закругленные стены, что позволяло создавать «мертвые зоны», где защитники не могли стрелять по нападавшим. Красивые изображения звездных фортов можно найти в сети.
Монж стал учителем в Мезьере, а также членом Академии наук. Он продолжил развивать начертательную геометрию, преподавая ее и издавая учебники. Преподавание начертательной геометрии быстро распространилось по Франции и, в конечном итоге, в Военной академии США в Вест-Пойнте, основанной в 1802 году. Другие практикующие занялись камином и опубликовали тексты по начертательной геометрии. Одним из таких учителей и авторов учебников был французский математик А. Жюльен.
Жюльен, преподавал в лицее Сент-Барти в Париже. Он написал учебник по описательной геометрии, Cours élémentaire de géométrie descriptive . Издание 3 rd , опубликованное в 1881 году, доступно в Интернете через Google Книги. Рельефы или модели в коллекции Смитсоновского института являются учебными пособиями, созданными Жюльеном в дополнение к этому учебнику, точно так же, как современные учебники по математике поставляются с онлайн-приложениями, которые показывают геометрию обсуждаемой математики.

 5 Теорема о проецировании прямого угла
5 Теорема о проецировании прямого угла
 03.02 «Наноинженерия»
03.02 «Наноинженерия»