Примеры решения выражений с корнями: Решение примеров с корнями

Примеры решения задач с корнями с ответами

Алгоритм решения задач с корнями

Теорема

Алгебраические выражения, содержащие неизвестные под знаком корня, относятся к классу выражений с корнями.

При решении задач на вычисление выражений, содержащих корни, используются свойства корней.

Свойства корней

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решений задач с корнями

Пример 1

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

Ответ

Пример 2

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

Ответ

Пример 3

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

Ответ

Пример 4

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

   

   

Ответ

Пример 5

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

   

Ответ

Пример 6

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

   

Ответ

Пример 7

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

Ответ

Пример 8

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

Ответ

Пример 9

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

Ответ

Пример 10

Задача

Упростить выражение:

   

Решение

ОДЗ:

   

   

   

   

Ответ

Средняя оценка 0 / 5. Количество оценок: 0

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

10002

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

8 класс. Алгебра. Свойства квадратных корней. — Вынесение множителя за знак корня.

Комментарии преподавателя

На данном уроке мы познакомимся с одной из важнейших операций при работе с корнями – вынесение множителя из-под знака корня. Кроме того, мы научимся извлекать корень из квадрата положительных и отрицательных чисел. На этом уроке мы сформулируем и докажем свойства квадратных корней, связанных с вынесением множителя из-под знака корня, а также разберём ряд примеров на эти свойства.

 

 

Тема: Функ­ция . Свой­ства квад­рат­но­го корня

Урок: Пре­об­ра­зо­ва­ние вы­ра­же­ний с кор­ня­ми (вы­не­се­ние мно­жи­те­ля из-под знака корня)

На­пом­ним опре­де­ле­ние квад­рат­но­го корня:

квад­рат­ным кор­нем из неот­ри­ца­тель­но­го числа на­зы­ва­ет­ся такое число неот­ри­ца­тель­ное число , квад­рат ко­то­ро­го равен : .

Из опре­де­ле­ния квад­рат­но­го корня сразу сле­ду­ет сле­ду­ю­щее тож­де­ство:

.

Рас­смот­рим несколь­ко при­ме­ров на вы­чис­ле­ние кор­ней: , т. к. ; , т. к. ; , т. к. ; .

На­пом­ним также ос­нов­ные свой­ства квад­рат­но­го корня:

1.  (). Если  и  – неот­ри­ца­тель­ные числа, то ко­рень из их про­из­ве­де­ния равен про­из­ве­де­нию кор­ней.

2.  (). Если  – неот­ри­ца­тель­ное число, а  – по­ло­жи­тель­ное число, то ко­рень из их от­но­ше­ния равен от­но­ше­нию кор­ней.

3.  ().

При­ме­ры:

1. .

2. .

До­ка­жем те­перь ещё одно не менее важ­ное свой­ство квад­рат­но­го корня:

, т. е.: .

До­ка­за­тель­ство:

На­пом­ним вна­ча­ле опре­де­ле­ние мо­ду­ля: . При­ме­ры: , , .

Рас­смот­рим два слу­чая:

1. , т. к.  – можно поль­зо­вать­ся опре­де­ле­ни­ем корня квад­рат­но­го из неот­ри­ца­тель­но­го числа.

2. . В этом слу­чае: . Тогда для числа  можем вос­поль­зо­вать­ся ре­зуль­та­та­ми пер­во­го слу­чая: .

Утвер­жде­ние до­ка­за­но

Есте­ствен­ным обоб­ще­ни­ем дан­но­го свой­ства яв­ля­ет­ся фор­му­ла:

 .

Рас­смот­рим ти­по­вые за­да­чи на при­ме­не­ние ука­зан­но­го свой­ства.

При­ме­ры:

1. 

.

2. 

.

3. 

.

4. 

.

Необ­хо­ди­мо по­ни­мать, что во всех рас­смот­рен­ных при­ме­рах зна­че­ние кор­ней все­гда по­лу­ча­ет­ся неот­ри­ца­тель­ным (несмот­ря на на­ли­чие перед неко­то­ры­ми от­ве­та­ми знака . К при­ме­ру, в при­ме­ре 4 ответ по­ло­жи­тель­ный, так как знак вы­ра­же­ния  , а перед самим вы­ра­же­ни­ем стоит ещё один . Как из­вест­но, минус на минус даёт плюс.

Решим ещё несколь­ко при­ме­ров, в ко­то­рых фи­гу­ри­ру­ют уже несколь­ко пе­ре­мен­ных:

5. 

 ( – по усло­вию,  – все­гда, так как квад­рат все­гда неот­ри­ца­тель­ный).

6. 

 ( – по усло­вию,  – все­гда, так как квад­рат все­гда неот­ри­ца­тель­ный).

7. 

( – по усло­вию,  – так как ).

8. 

 ( – по усло­вию,  – так как ).

Итак, мы рас­смот­ре­ли вы­не­се­ние мно­жи­те­ля из-под знака корня. Мы на­учи­лись вы­но­сить мно­жи­тель из-под корня с учё­том его знака, а также ре­ши­ли несколь­ко при­ме­ров.

На сле­ду­ю­щем уроке мы на­учим­ся вно­сить мно­жи­тель под знак квад­рат­но­го корня.

Источник конспекта: http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/preobrazovanie-vyrazheniy-s-kornyami-vynesenie-mnozhitelya-iz-pod-znaka-kornya?konspekt&chapter_id=920

 

Источник видео: http://www.youtube.com/watch?v=_QowbpPNMR8

Упрощение радикалов Пошаговое решение математических задач

Добро пожаловать в Quickmath Solvers!

• Решить
• Упростить
• Фактор
• Расширить
• График
• ГКФ
• ЛКМ

Новый Пример

Справка Учебник

Упрощение выражения.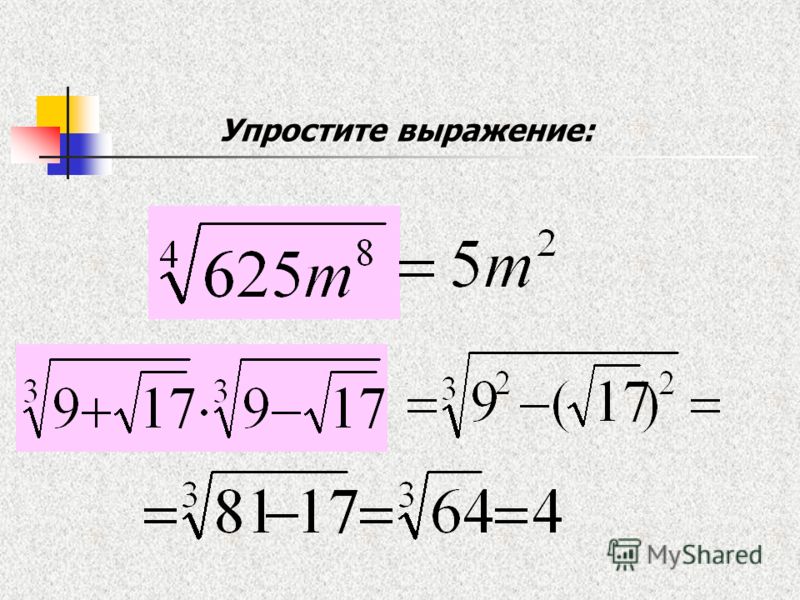 92)/(x-y)

Чтобы увидеть учебник, прокрутите вниз

• Математические статьи
• Упрощение выражений

---

Радикалы были представлены в предыдущем уроке, когда мы обсуждали вещественные числа. Например, корень (25) = 5, а корень (2) = 1,4142135 … (бесконечное неповторяющееся десятичное число). Сейчас мы заинтересованы в разработке методов, которые помогут упростить радикалы и выражения, содержащие радикалы. В этом тексте мы будем иметь дело только с радикалами, являющимися квадратными корнями. Другие радикалы, такие как кубические корни и корни четвертой степени, будут обсуждаться в последующих курсах алгебры.
        Следующие два свойства радикалов являются основными для обсуждения.

Если a и b — положительные действительные числа, то          1. корень(ab)=корень(a)корень(b) и    2. корень(a/b)=корень(a)/корень(b)

Таким образом,

              root(144)=root(36)*root(4)=6*2=12

и         root(9/25)=root(9)/root(25)=3/ 5

Чтобы упростить root(450), мы можем написать

root(450)=root(25*18)=root(25)root(18)=5root(18)

Является ли 5root(18) простейшей формой root(450)? Ответ — нет, потому что root(18) имеет квадратный множитель, 9, и

root(18)=root(9)root(2)=3root(2) .

Мы можем написать

     root(450)=root(25*18)=root(25)*root(9)*root(2)=5*3*root(2)=15root(2)

или корень(450)=корень(225*2)=корень(225)*корень(2)=15корень(2)

          Упрощая радикал, попытайтесь найти наибольший квадратный множитель подкоренного числа.

Считается, что радикал находится в простейшей форме, если подкоренное число не имеет квадратного множителя .

Примеры

Упростите следующие радикалы.

1. root(24)     Разложите на 24 так, чтобы один множитель был квадратным числом.

    корень(24)=корень(4*6)=корень(4)*корень(6)=2корень(6)

2. корень(72)     Перед упрощением найдите наибольший квадратный множитель.

    root(72)=root(36*2)==root(36)*root(2)=6root(2)

Или, если вы не заметили 36 как множитель, вы могли написать

    корень(72)=корень(9*8)=корень(9)*корень(8)=3корень(4*2)=3*корень(4)*корень(2)=3*2*корень(2) )=6root(2)

3.  -root(288)

    -root(288)=-root(144*2)=-root(144)*root(2)=-12root(2)

4 .   root(75/4)

     root(75/4)=root(75)/root(4)=root(25*3)/2=(root(25)*root(3))/2=( 5корень(3))/2

5.  {3+корень(18)}/3

     (3+корень(18))/3=(3+корень(9*2))/3=(3+ корень(9)*корень(2))/3=(3+3корень(2))/3 

                      = 3/3+(3корень(2))/3=1+корень(2)

Решить похожую задачуВведите свою задачу

    

   

← Предыдущая страница

Следующая страница →

Факторинг радикалов — Алгебра II

Все ресурсы по диагностике алгебры II 19012 630 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 Следующая →

Алгебра II Помощь » Математические отношения и основные графики » Радикалы » Упрощение радикалов » Факторинг радикалов

Упростите выражение:

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте свойство умножения радикалов для разделения корней четвертой степени следующим образом:

Упростите новые корни:

Сообщите об ошибке

Упростите выражение.

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте свойство умножения радикалов для разделения идеальных квадратов следующим образом:

Упростить корни,

 

Сообщить об ошибке

Упростить радикал .

Возможные ответы:

Ни один из других ответов

Правильный ответ:

Объяснение:

Чтобы упростить радикалы, нам нужно разложить выражение внутри радикала. Радикал можно упростить только в том случае, если один из множителей имеет квадратный корень, который является целым числом.

Для этой задачи мы сначала найдем все возможные радикалы числа 12: 1 и 12, 2 и 6 и 3 и 4. Затем мы рассмотрим каждый множитель и определим, имеет ли какой-либо из них квадратный корень, равный целое число. Подходящим является только число 4, имеющее квадратный корень из 2. Мы можем переписать радикал как  , что также можно записать как . Извлекая квадратный корень из 4, мы приходим к ответу: .

Сообщить об ошибке

Упростите следующее выражение с радикалами, разложив подкоренные множители:

Возможные ответы:

Правильный ответ:

3

Объяснение:

Чтобы упростить каждый радикал, мы должны найти множители его подкореня, которые имеют целое число как квадратный корень, что позволит нам извлечь квадратный корень этого множителя из радикала. Мы начинаем с разложения каждого подкоренного числа, ища любые множители, которые имеют чистое целое число как квадратный корень:

После факторизации каждого подкоренного числа мы видим, что в каждом из них есть полный квадрат: 25 в первом, 49 во втором и 4 в третьем. Поскольку эти множители являются идеальными квадратами, мы можем легко извлечь их квадратный корень из радикала, который затем умножается на коэффициент, уже стоящий перед радикалом:

После упрощения каждого радикала мы остаемся с тем же значением. в каждом термине, так что теперь мы можем сложить все наши похожие термины вместе, чтобы полностью упростить выражение:

Сообщить об ошибке

Упростить подкоренное выражение.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы решить это уравнение, мы должны увидеть, сколько совершенных кубов мы можем упростить в каждом радикале.

Во-первых, упростим коэффициент под корнем. является идеальным кубом . Следовательно, мы можем убрать из-под корня и вместо этого имеем:

Теперь, чтобы удалить переменные из-под символа квадратного корня, нам нужно удалить переменные по кубу. Поскольку радикалы обладают свойством

, мы можем видеть, что

С выражением в этой форме гораздо легче увидеть, что мы можем удалить один куб из , два куба из , и два куба из , и, следовательно, наши решение:

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Пояснение:

  = =

= 
 = 

Сообщить об ошибке

Упростите радикал.

Возможные ответы:

Дальнейшее упрощение невозможно.

Правильный ответ:

Пояснение:

Найдите множители числа 128, чтобы упростить термин.

Мы можем переписать выражение как квадратные корни этих факторов.

Упрощение.

Сообщить об ошибке

Упростите радикальное.

Возможные ответы:

Правильный ответ:

Объяснение:

Начните с нахождения факторов для радикального члена.

Мы можем переписать радикал, используя эти факторы.

Упростите первый член.

Сообщить об ошибке

Упрощение.

Возможные ответы:

Правильный ответ:

Объяснение:

Всегда работайте над математикой под радикалом перед упрощением. Мы не можем делать никаких математических вычислений, поэтому давайте посмотрим, можно ли это факторизовать. Это тоже не факторизуется, поэтому ответ — это просто поставленная проблема.

 Если не верите, пусть  и 

 

Сообщить об ошибке

Какое из следующих утверждений всегда верно.

I.

II.

III. The smallest integer in a radicand that generates a plausible, real number and smallest value is 0. 

Possible Answers:

I  only

I and  III

I and  II

II и III

III только

Правильный ответ:

9 III только

3 Объяснение:

Разберем каждое утверждение.

I.

Попробуем сложить. Это не факторизуется, поэтому это утверждение обычно ложно, НЕ ВСЕГДА верно.

  Если не верите, пусть и 

Единственный случай, когда это верно, если  или  было  и другая переменная была полным квадратом.

II.

Допустим . Это очень верно ОДНАКО , а что если . . Квадратные корни не генерируют отрицательных значений. Не забудьте сделать математику внутри подкоренной черты перед упрощением. Возможны только положительные значения и ноль, и, поскольку ограничений нет, все предположения основаны на том, что это любое действительное число. Таким образом, мы можем исключить это утверждение, поскольку вопрос задает ВСЕГДА верно.

 

III. Наименьшее целое число в подкоренной дроби, которое дает правдоподобное действительное число и наименьшее значение, равно 0. 

Из рассуждения второго утверждения,  «o возможны только положительные значения и ноль»,  это подтверждает, что это утверждение всегда верно.

No related posts.