Как найти наибольшее и наименьшее значение функции f(x,y) в плоской области D
Найти наибольшее и наименьшее значение функции f(x,y) в плоской области D — еще одна задача на условный экстремум из числа тех, которые изучаются в курсе высшей математики.
Существуют варианты этой задачи: когда область D задана неравенством, системой неравенств, как плоская линия или множество точек на плоскости, возможно, заданных, как точки пересечения нескольких плоских линий (совокупностью или системой уравнений).
Как известно, задачи на условный экстремум в Вольфрам Альфа решаются с помощью запросов minimize, maximize и extrema, к которым дополнительно присоединяются условия, определяющие заданную область. В этом состоит общий подход к решению подобных задач.
Первый, наиболее простой вариант этой задачи — найти наибольшее значение функции двух переменных f(x,y) в плоской области D, заданной одним неравенством, решается в Вольфрам Альфа с помощью запроса
maximize x^2 sin(y) over 4x^2-y-1<=0
Аналогично, с помощью запроса minimize ищется наименьшее значение функции двух переменных f(x,y) в плоской области D, заданной одним неравенством:
minimize x^2 sin(y) over 4x^2-y-1<=0
Запрос extrema, как было сказано, позволяет найти сразу наибольшее и наименьшее значение функции двух переменных в плоской области D, заданной одним неравенством:
extrema x^2 sin(y) over 4x^2-y-1<=0
Второй вариант рассматриваемой задачи: плоская область D, ограничена несколькими линиями,.
2-y-1=0, 2x+y-1=0}
Понятно, что существуют еще и другие варианты задачи «Как найти наибольшее и наименьшее значение функции f(x,y) в плоской области D». Надеюсь, после прочтения данного поста вам захочется рассмотреть самостоятельно.
Наибольшее и наименьшее значение функции на отрезке. Решение задач
Отыскание максимумов и минимумов — одна из самых распространенных задач при исследованиях функций.
Непрерывная на отрезке функция принимает свое наибольшее или наименьшее значение, либо в критических точках (в точках, в которых производная обращается в нуль или не существует), принадлежащих исследуемому промежутке, или на его концах .
На практике нахождения максимумов и минимумов похоже на отыскания локального экстремума, только добавляются края промежутка. Возможны случаи, когда максимумы и минимумы функций находятся в точках локального экстремума, а возможные — на краях отрезка.
Рассмотрим ряд примеров, чтобы ознакомить Вас с методикой исследования.
————————————
Примеры.
Определить наибольшее и наименьшее значение фунции на промежутке.
Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах».
1. (4.55.б)
Функция определена на всем множестве действительных чисел
Найдем производную функции
Приравняем ее к нулю и определим критические точки
Проверим знак производной слева и справа от найденной точки
Производная при переходе через точку меняет знак с положительного на отрицательный , следовательно она является точкой локального максимума.
Найдем значение функции в точке
и на краях отрезка
Таким образом функция достигает максимума в точке локального экстремума и минимума на одном из краев отрезка .
2. (4.55.д)
На заданном промежутке функция определена; вычислим ее производную
Приравнивая нуля найдем критическую точку
Заданная точка принадлежит отрезку.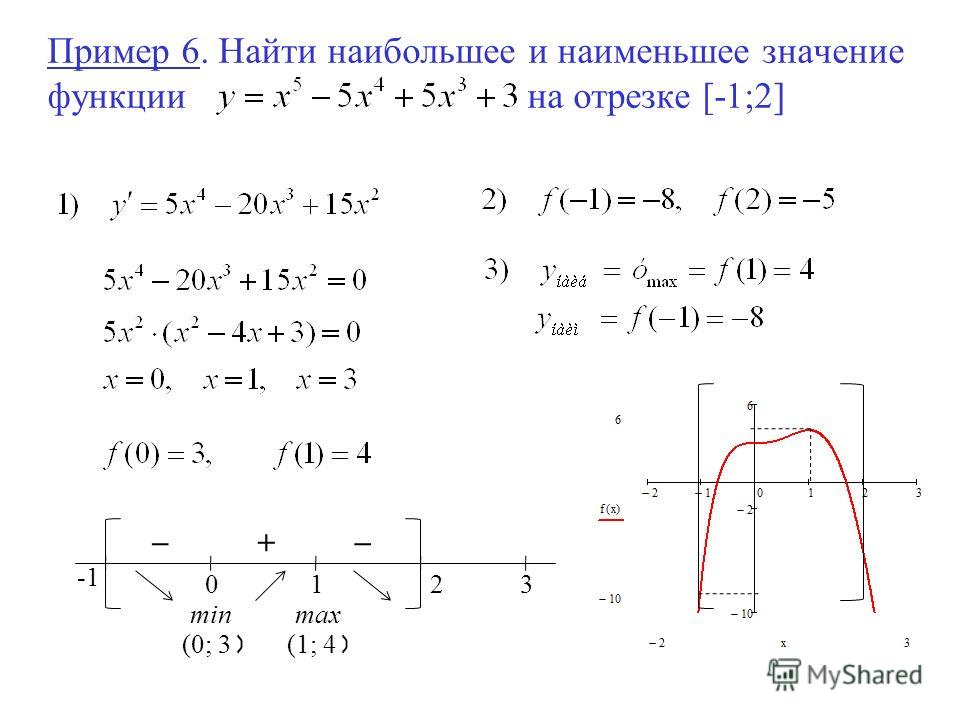
Найдем значения функции во всех точках
Функция приобретает максимум и минимум в точках
3. (4.55.є)
Функция определена для всех значений аргумента .
Найдем производную
Из выражения видно, что производная отлична от нуля на промежутке определения, однако в точке она не существует.
Вычислим значение функции
Наибольшее значение функция принимает в точке , а наименьшее значение в критической точке .
————————————
Приведем решения задач из сборника Дубовика В.П., Юрика И.И. «Высшая математика».
4. (5.770)
Функция определена везде, потому приступим сразу к вычислению производной
Приравняем ее к нулю и находим критические точки
Найдем значения функции во всех подозрительных на экстремум точках
Из полученного набора значений следует, что функция принимает максимум и минимум на краях отрезка
5.
(5.771)
На заданном интервале функция определена, проводим дифференцировку
Приравняв к нулю производную получим
Другую критическую точку найдем из условия, что производная не существует
Одна совпадает с началом отрезка. Вычислим значение функции на краях отрезка и в критических точках
Таким образом функция принимает максимальное значение в критической точке, а минимальное на конце отрезка
Из приведенных решений можно сделать выводы, что главным в исчислении является знание функций и умение дифференцировать. Все остальное сводится к отысканию значений функций в точках и анализа результатов. Изучайте свойства элементарных функций, правила нахождения производных, это Вам пригодится при решении примеров.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Локальный экстремум функции.
Примеры - Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
ПримерыКалькулятор минимума функции
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотр полного списка инструментов dCode
Минимум функции
Инструмент для определения минимального значения функции: минимальное значение, которое может принимать функция. Это глобальный минимум, а не локальный минимум.
Результаты
Минимум функции — dCode
Теги: Функции
Поделиться
dCode и другие
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор минимума
Калькулятор максимума
⮞ Перейти к: Максимум функции
Ответы на вопросы (FAQ)
Что такое минимум функции? (Определение)
Для любой функции $f$, определенной на интервале $I$ и $m$ действительное число, принадлежащее $I$, если $f(x) минимальное значение функции, достигаемое при $x=m$ .
92$ определено над $\mathbb{R}$, его производная равна $f'(x) = 2x$, что равно нулю при $x = 0$, так как $f'(x)=0 \iff 2x = 0 \ тогда и только тогда, когда х=0 $. Производная переходит от отрицательной к положительной в $ x = 0 $, поэтому функция имеет минимум в $ x=0 $, $ f(x=0) = 0 $ и $ f(x) >= 0 $ над $ \mathbb {Р} $.
Как рассчитать локальный минимум на интервале?
Добавьте одно или несколько условий, указывающих интервальные ограничения для каждой переменной.
Пример: Найти минимум $ \sin{x} $ для $ 0
Что такое экстремум?
Экстремум — это экстремальное значение функции, это значение может быть максимальным (максимальное значение функции) или минимальным (минимальное значение функции).
Что такое миноранта функции?
Миноранта — это любое значение, меньшее или равное минимальному значению, достигнутому функцией.
Каков минимум постоянной функции?
Постоянная функция $f(x)=c$ — это линия, которая всегда равна $c$, поэтому ее минимум $c$ достигается при любом значении $x$92 + 4 a c)/(4 a) $ достигается, когда $ x = -\frac{b}{2a} $
— If $ a
Исходный код
dCode сохраняет право собственности на источник «Минимум функции» код.
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Минимум функции», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Минимум функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Минимума функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Минимум функции» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Минимум функции на dCode.
fr [онлайн-сайт], получено 12 декабря 2022 г., https://www.dcode.fr/minimum-function
Сводка
- Калькулятор минимума
- Калькулятор максимума
- Каков минимум функции? (Определение)
- Как найти минимум функции?
- Как рассчитать локальный минимум на интервале?
- Что такое экстремум?
- Что такое миноранта функции?
- Каков минимум постоянной функции?
- Каков минимум аффинной функции?
- Каков минимум полиномиальной функции 2-й степени?
Похожие страницы
- Производная
- Экстремум функции
- Максимум функции
- Stationary Point of a Function
- Definite Integral
- Discriminant of a Polynomial
- Lagrange Interpolating Polynomial
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Ключевые слова
минимум,функция,производная,калькулятор,максимум,экстремум
Ссылки
▲
Минимум функционального калькулятора
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотр полного списка инструментов dCode
Минимум функции
Инструмент для определения минимального значения функции: минимальное значение, которое может принимать функция.
Это глобальный минимум, а не локальный минимум.
Результаты
Минимум функции — dCode
Теги: Функции
Поделиться
dCode и многое другое решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор минимума
Калькулятор максимума
⮞ Перейти к: Максимум функции
Ответы на вопросы (FAQ)
Что такое минимум функции? (Определение)
Для любой функции $f$, определенной на интервале $I$ и $m$ действительное число, принадлежащее $I$, если $f(x) минимальное значение функции, достигаемое при $x=m$ .
Как найти минимум функции? 92$ определено над $\mathbb{R}$, его производная равна $f'(x) = 2x$, что равно нулю при $x = 0$, так как $f'(x)=0 \iff 2x = 0 \ тогда и только тогда, когда х=0 $. Производная переходит от отрицательной к положительной в $ x = 0 $, поэтому функция имеет минимум в $ x=0 $, $ f(x=0) = 0 $ и $ f(x) >= 0 $ над $ \mathbb {Р} $.
Как рассчитать локальный минимум на интервале?
Добавьте одно или несколько условий, указывающих интервальные ограничения для каждой переменной.
Пример: Найти минимум $ \sin{x} $ для $ 0
Что такое экстремум?
Экстремум — это экстремальное значение функции, это значение может быть максимальным (максимальное значение функции) или минимальным (минимальное значение функции).
Что такое миноранта функции?
Миноранта — это любое значение, меньшее или равное минимальному значению, достигнутому функцией.
Каков минимум постоянной функции?
Постоянная функция $f(x)=c$ — это линия, которая всегда равна $c$, поэтому ее минимум $c$ достигается при любом значении $x$92 + 4 a c)/(4 a) $ достигается, когда $ x = -\frac{b}{2a} $
— If $ a
Исходный код
dCode сохраняет право собственности на источник «Минимум функции» код.
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Минимум функции», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Минимум функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Минимума функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Cite dCode
Копирование и вставка страницы «Минимум функции» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Минимум функции на dCode.