Тест по математике Наибольший общий делитель 6 класс
Тест по математике Наибольший общий делитель Наименьшее общее кратное для учащихся 6 класса с ответами. Тест состоит из 2 вариантов, в каждом варианте 11 заданий.
1 вариант
1. Какие числа являются общими делителями чисел 24 и 16?
1) 4, 8
2) 6, 2, 4
3) 2, 4, 8
4) 8, 6
2. Является ли число 9 наибольшим общим делителем чисел 27 и 36?
1) да
2) нет
3. Даны числа 128, 64 и 32. Какое из них является наибольшим общим делителем всех трёх чисел?
1) 128
2) 64
3) 32
4. Имеют ли числа 40, 35, 10, 8 наибольший общий делитель?
1)да
2) нет
5. Являются ли числа 7 и 18 взаимно простыми?
1) да
2) нет
6. Какие числа являются взаимно простыми?
1) 5 и 25
2) 64 и 2
3) 12 и 10
4) 100 и 9
7. Укажите дробь, у которой числитель и знаменатель — взаимно простые числа.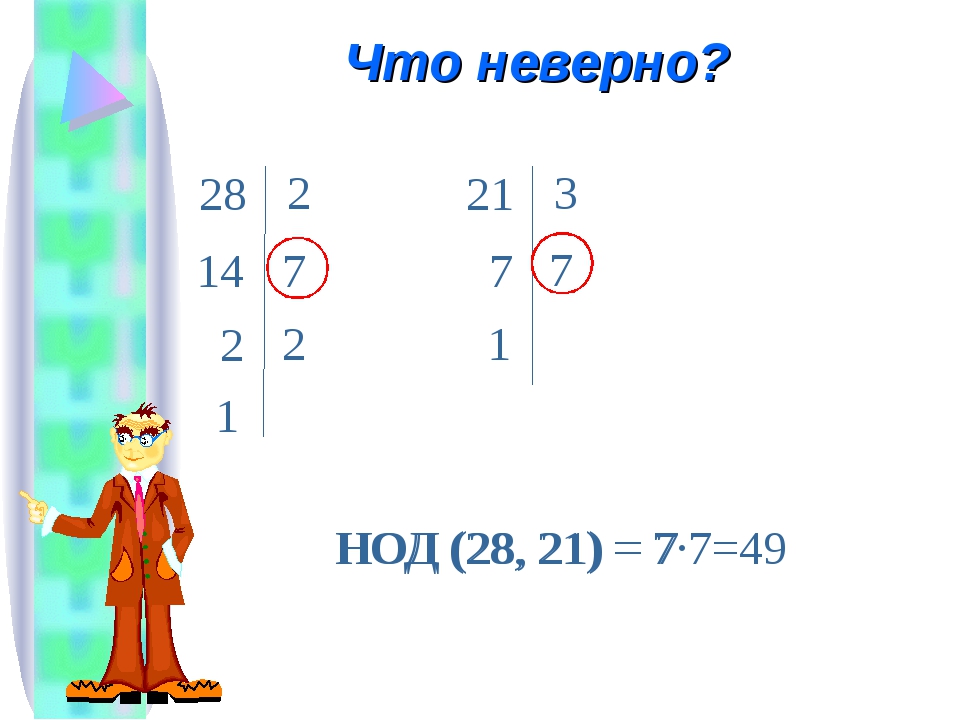
8. Какое число является общим кратным чисел 8, 12, 6?
1) 16
2) 120
3) 96
4) 2
9. Какое число является наименьшим общим кратным чисел 6, 9, 12?
1) 18
2) 36
3) 24
4) 180
10. Число а кратно числу b. Чему равен их наибольший общий делитель?
1) a
2) b
3) a + b
4) ab
11. Даны числа 400, 100, 25, 80. Какое из них является наименьшим общим кратным всех четырёх чисел?
1) 25
2) 400
3) 100
4) 80
2 вариант
1. Какие числа являются общими делителями чисел 18 и 12?
1) 9, 6, 3
2) 2, 3, 4, 6
3) 3, 2
4) 2, 3, 6
2. Является ли число 4 наибольшим общим делителем чисел 16 и 32?
1) да
2) нет
3. Даны числа 300, 150 и 600. Какое из них является наибольшим общим делителем всех трёх чисел?
1) 600
2) 150
3) 300
4.
Имеют ли числа 20, 16, 14, 28 наибольший общий делитель?
1) да
2) нет
5. Являются ли взаимно простыми числа 33 и 44?
1) да
2) нет
6. Какие числа являются взаимно простыми?
1) 9 и 18
2) 105 и 65
3) 44 и 45
4) 6 и 16
7. Укажите дробь, у которой числитель и знаменатель — взаимно простые числа.
8. Какое число является общим кратным чисел 5, 10, 15?
1) 5
2) 100
3) 15
4) 300
9. Какое число является наименьшим общим кратным чисел 4, 8, 10?
1) 40
2) 16
3) 80
4) 32
10. Числа х и у — взаимно простые. Чему равно их наименьшее общее кратное?
1) x
2) у
3) ху
4) х + у
11. Даны числа 5, 130, 65, 260. Какое из них является наименьшим общим кратным всех трёх чисел?
1) 130
2) 65
3) 260
4) 5
Ответы на тест по математике Наибольший общий делитель Наименьшее общее кратное
1 вариант
1-3
2-1
3-3
4-2
5-1
6-4
7-4
8-3
9-2
10-2
11-2
2 вариант
1-4
2-2
3-2
4-1
5-2
6-3
7-4
8-4
9-1
10-3
11-3
Найдите наивеличайший общий делительи наименьшее общее кратное чисел: а)18 и 36
Дано:
Числа 18 и 36;
НОД — ?
НОК — ?
Наибольший общий делитель (НОД) 2-ух данных чисел это величайшее число, на которое оба числа делятся без остатка.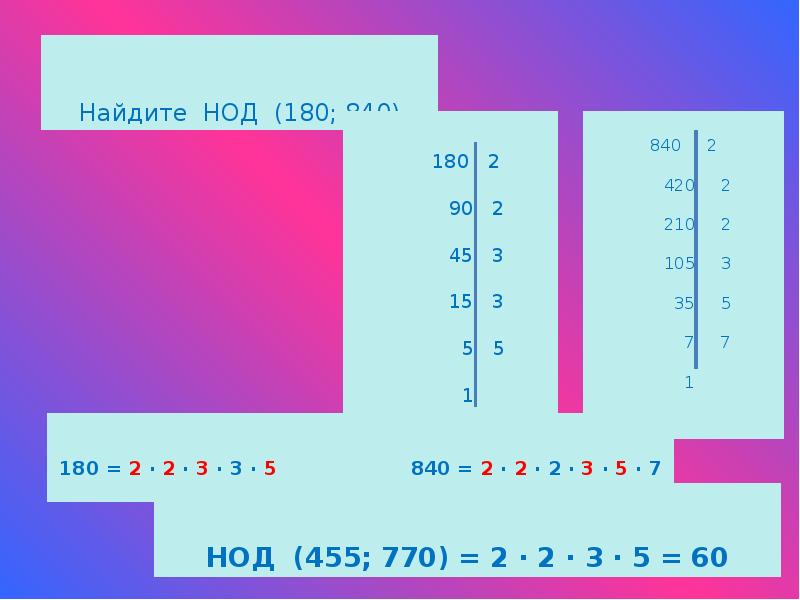
Величайший общее кратное (НОК) данных чисел это наименьшее естественное число, которое без остатка делится нацело на каждое из этих чисел.
362; 183; 62; 33; 1
В обоих числах избираем схожие множители, перемножаем их: 3 * 3 * 2 = 18
Среди всех чисел, которые мы разложили, найдем наименьшее число. Выберем множители, которые не вошли в разложение иных чисел: 2, дальше найдем наивеличайшее число. Добавим наши множители в его разложение и перемножим их: 2 * 1 = 2.
Ответ: НОД (18; 32) = 18. НОК (18; 32) = 2.
Дано:
Числа 33 и 44;
НОД — ?
НОК — ?
Наибольший общий делитель (НОД) двух данных чисел это наибольшее число, на которое оба числа делятся без остатка.
Величайший общее кратное (НОК) данных чисел это меньшее натуральное число, которое без остатка делится нацело на каждое из этих чисел.
333; 1111; 1
442; 222; 1111; 1
В обоих числах избираем одинаковые множители, перемножаем их: 11
Найдем наименьшее число.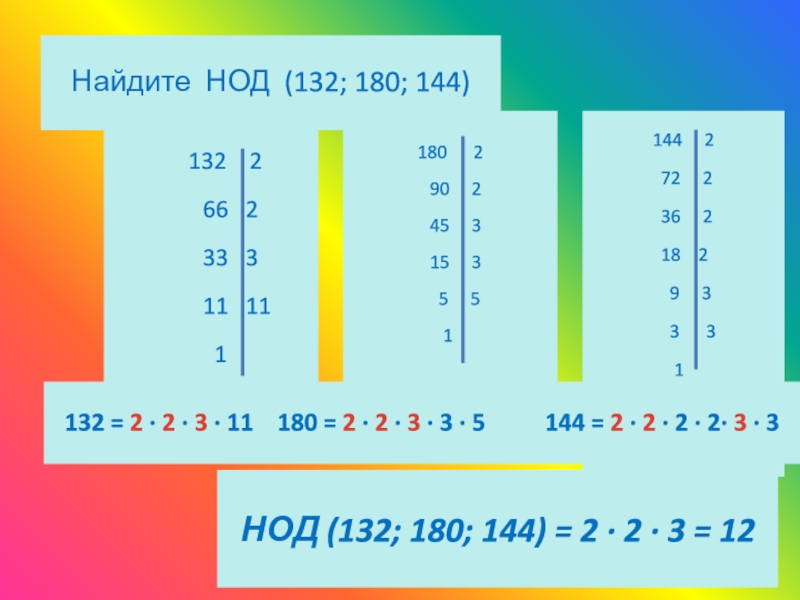
Выберем множители, которые не вошли в разложение иных чисел: 3, далее найдем величайшее число. Добавим наши множители в его разложение и перемножим их: 2 * 2 * 11 * 3 = 132.
Дано:
Числа 378 и 441;
НОД — ?
НОК — ?
Наивеличайший общий делитель (НОД) 2-ух данных чисел это наибольшее число, на которое оба числа делятся без остатка.
Наивеличайший общее кратное (НОК) данных чисел это меньшее естественное число, которое без остатка делится нацело на каждое из этих чисел.
3782; 1893; 633; 213; 77; 1
4412; 1472; 497; 77; 1
В обоих числах избираем схожие множители, перемножаем их: 2 * 7 = 14
Найдем меньшее число. Выберем множители, которые не вошли в разложение иных чисел: 3, дальше найдем величайшее число. Добавим наши множители в его разложение и перемножим их: 2 * 2 * 7 * 7 * 3 * 3 * 3 = 5292.
Ответ: НОД (378; 441) = 14. НОК (378; 441) = 5292.
Дано:
Числа 11340 и 37800;
НОД — ?
Наивеличайший общий делитель (НОД) 2-ух данных чисел это величайшее число, на которое оба числа делятся без остатка.
Величайший общее кратное (НОК) данных чисел это меньшее естественное число, которое без остатка делится нацело на каждое из этих чисел.
113402; 56702; 28353; 9453; 3153; 1053; 355; 77; 1
378002; 189002; 94502; 47255; 9453; 3153; 1053; 355; 77; 1
В обоих числах выбираем однообразные множители, перемножаем их: 3 * 3 *3 * 5 = 135
Найдем наименьшее число. Выберем множители, которые не вошли в разложение иных чисел: 1, далее найдем величайшее число. Добавим наши множители в его разложение и перемножим их: 37800
Ответ: НОД (11340; 37800) = 135. НОК (11340; 37800) = 37800.
Самостоятельная работа по математике Наибольшее общее кратное 6 класс
Самостоятельная работа по математике Наибольшее общее кратное 6 класс с ответами. Самостоятельная работа включает 2 варианта, в каждом по 6 заданий.
Вариант 1
1. Найдите наименьшее общее кратное чисел 8 и 16.
2. Найдите наименьшее общее кратное чисел:
а) 33 и 44
б) 12 и 24
в) 4; 6 и 33
3.
Найдите наименьшее общее кратное и наибольший общий делитель числителя и знаменателя следующих дробей:
а) 14/21
б) 5/132
в) 48/120
4. Какие из следующих утверждений верны:
а) два четных числа всегда взаимно просты
б) два нечетных числа могут быть взаимно просты
в) произведение составных чисел всегда является составным числом
г) наименьшее общее кратное двух нечетных чисел всегда является нечетным числом
5. Между пунктами А и В курсируют два автобуса. Первый тратит на дорогу туда и обратно 35 мин, второй — 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А — в 6 ч 30 мин?
6. Сколько можно составить различных прямоугольников площадью 42 см2 , если длины сторон этих прямоугольников являются натуральными числами (прямоугольники со сторонами, например, 3 см, 4 см и 4 см, 3 см считаются одинаковыми)?
Вариант 2
1.
Найдите наименьшее общее кратное чисел 9 и 18.
2. Найдите наименьшее общее кратное чисел:
а) 21 и 28
б) 18 и 72
в) 3; 5 и 25
3. Найдите наименьшее общее кратное и наибольший общий делитель числителя и знаменателя следующих дробей:
а) 13/26
б) 5/112
в) 36/84
4. Какие из следующих утверждений верны:
а) два нечетных числа всегда взаимно просты
б) два четных числа всегда имеют четное наименьшее общее кратное
в) произведение составных чисел не может быть простым числом
г) составное число не может делиться на простое число
5. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй — 7 суток. Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после первого?
6.
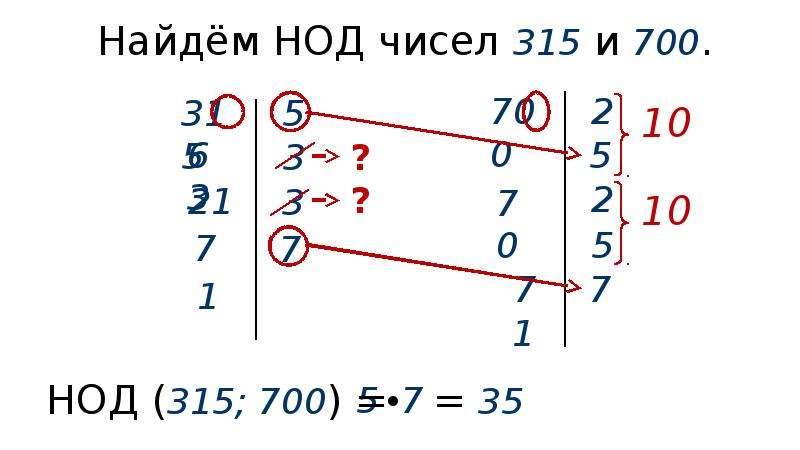Сколько можно составить различных прямоугольников площадью 66 см2, если длины сторон этих прямоугольников являются натуральными числами (прямоугольники со сторонами, например, 3 см, 4 см и 4 см, 3 см считаются одинаковыми)?
Ответы на самостоятельную работу по математике Наибольшее общее кратное 6 класс
Вариант 1
1. 16
2.
а) 132
б) 24
в) 132
3.
а) 42 и 7
б) 660 и 1
в) 240 и 24
4. Верны: б), в), г)
5. В 9 часов 10 минут
6. 4
Вариант 2
1. 18
2.
а) 84
б) 72
в) 75
3.
а) 26 и 13
б) 560 и 1
в) 252 и 12
4. Верны: б), в)
5. Через 36 суток
6. 4
Урок 16. Наименьшее общее кратное | Поурочные планы по математике 6 класс
Урок 16. Наименьшее общее кратное
09.07.2015 10971 0Цели: ввести понятия наименьшего общего кратного; формировать навык нахождения наименьшего общего кратного; отрабатывать навык решения задач алгебраическим способом; повторить среднее арифметическое.
Информация для учителя
Обратить внимание учеников на разный смысл выражений: «общее кратное чисел», «наименьшее общее кратное чисел».
Нахождение наименьшего общего кратного нескольких чисел:
I способ
1. Проверить, не будет ли большее из данных чисел делиться на остальные числа.
2. Если делится, тогда это число будет наименьшим общим кратным всех данных чисел.
3. Если не делится, то проверить, не будет ли делиться на остальные числа удвоенное большее число, утроенное и т.д.
4. Так проверять до тех пор, пока не найдется наименьшее число, которое делится на каждое из остальных чисел.
II способ
1. Разложить все числа на простые множители.
2. Написать разложение одного из чисел (лучше сразу записать наибольшее число).
3. Дополнить данное разложение теми множителями из разложения других чисел, которые не вошли в написанное разложение.
4. Вычислить полученное произведение.
Если числа взаимно простые, то наименьшим общим кратным этих чисел будет являться их произведение.
Ход урока
I. Организационный момент
II. Устный счет
1. Игра «Я самый внимательный».
15, 67, 38, 560, 435, 226, 1000, 539, 3255.
— Хлопните в ладоши, если число кратно 2.
— Запишите, если число кратно 5.
— Топайте ногами, если число кратно 10.
— Почему вы одновременно хлопали, пищали и топали ногами?
2. Назовите все простые числа, удовлетворяющие неравенству 20 < х < 50.
3. Что больше, произведение или сумма этих чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9? (Сумма. Произведение равно 0, а сумма равна 45.)
4. Назовите четырехзначное число, записанное с помощью цифр 1, 7, 5, 8, кратное 2, 5, 3. (1578, 1875, 1515.)
5. У Марины было целое яблоко, две половинки и четыре четвертинки. Сколько у нее было яблок? (3.)
III. Индивидуальная работа
(Дать задание учащимся, допустившим ошибки в самостоятельной работе, разрешив воспользоваться записями в классной тетради.)
1 карточка
1.
Найдите все общие делители чисел и подчеркните их наибольший общий делитель:
а) 20 и 30; б) 8 и 9; в) 24 и 36.
Назовите пару взаимно простых чисел, если есть.
2. Запишите два числа, для которых наибольшим общим делителем будет число: а) 5; б) 8.
3. Найдите наибольший общий делитель данных чисел:
а) 22 и 33; б) 24 и 30; в) 45 и 9; г) 15 и 35.
2 карточка
1. Найдите все общие делители чисел и подчеркните их наибольший общий делитель:
а) 30 и 40; б) 6 и 15; в) 28 и 42.
Назовите пару взаимно простых чисел, если есть.
2. Запишите два числа, для которых наибольшим общим делителем будет число: а) 3; б) 9.
3. Найдите наибольший общий делитель данных чисел:
а) 33 и 44; б) 18 и 24; в) 36 и 9; г) 20 и 25.
IV. Сообщение темы урока
— Сегодня на уроке мы выясним, что такое наименьшее общее кратное чисел и как его находить.
V. Изучение нового материала
(Задача записана на доске.
)
— Прочитайте задачу.
От одной пристани к другой ходят два катера. Начинают работу одновременно в 8 ч утра. Первый катер на рейс туда и обратно тратит 2 ч, а второй — 3 ч.
Через какое наименьшее время оба катера опять окажутся на первой пристани, и сколько рейсов за это время сделает каждый катер?
Сколько раз за сутки эти катера встретятся на первой пристани, и в какое время это будет происходить?
Решение:
— Искомое время должно делиться без остатка и на 2, и на 3, то есть должно быть кратным числам 2 и 3.
— Запишем числа, кратные 2 и 3:
Числа, кратные 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.
Числа, кратные 3: 3, 6, 9, 12, 15, 18, 21, 24.
— Подчеркните общие кратные чисел 2 и 3.
— Назовите наименьшее кратное 2 и 3. (Наименьшее кратное — число 6.)
— Значит, через 6 ч после начала работы два катера одновременно окажутся на первой пристани.
— Сколько рейсов за это время сделает каждый катер? (1 – 3 рейса, 2 — 2 рейса.
)
— Сколько раз за сутки эти катера встретятся на первой пристани? (4 раза.)
— В какое время это будет происходить? (В 14 ч, 20 ч, в 2 ч ночи, в 8 утра.)
Определение. Наименьшее натуральное число, которое делится на каждое изданных натуральных чисел, называется наименьшим общим кратным.
Обозначение: НОК (2; 3) = 6.
— Наименьшее общее кратное чисел можно найти и не выписывая подряд кратные чисел.
Для этого надо:
1. Разложить все числа на простые множители.
2. Написать разложение одного из чисел (лучше наибольшего).
3. Дополнить данное разложение теми множителями из разложения других чисел, которые не вошли в написанное разложение.
4. Вычислить полученное произведение.
— Найдите наименьшее общее кратное чисел:
а) 75 и 60; б) 180, 45 и 60; в) 12 и 35.
— Сначала надо проверить, не делится ли большее число на другие числа.
Если да, то большее число будет наименьшим общим кратным этих чисел.
— Затем определить, не являются ли данные числа взаимно простыми.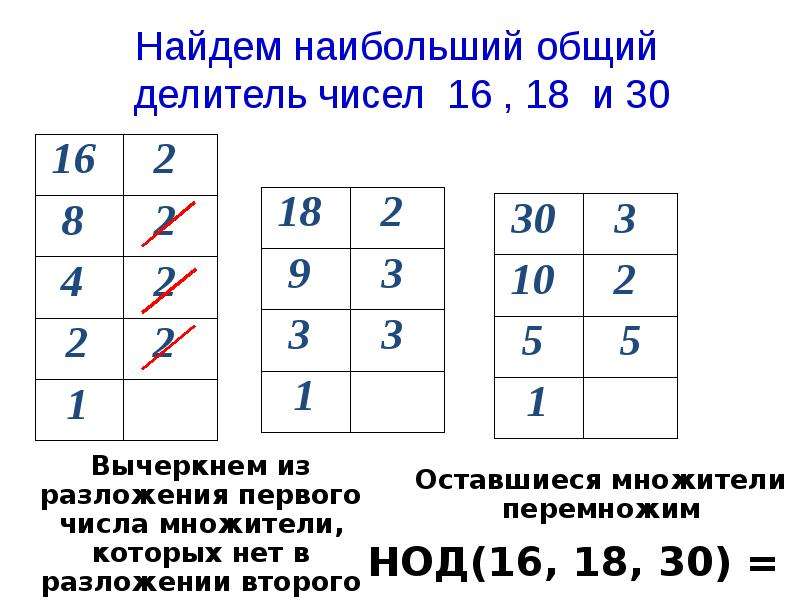
Если да, то наименьшим общим кратным будет произведение этих чисел.
а) 75 не делится на 60, и числа 75 и 60 не взаимно простые, тогда
— Лучше сразу записывать не разложение числа 75, а само это число.
б) Число 180 делится и на 45, и на 60, следовательно,
НОК (180; 45; 60)= 180.
в) Эти числа взаимно простые, значит, НОК (12; 35) = 420.
VI. Физкультминутка
VII. Работа над задачей
1. — Составьте задачу по краткой записи.
(На складе в трех ящиках было 160 кг яблок. В первом ящике на 15 кг меньше, нем во втором, во втором в 2 раза больше, чем в третьем. Сколько кг яблок было в каждом ящике?)
— Решите задачу алгебраическим методом.
(У доски и в тетрадях.)
— Что примем за х? Почему? (Сколько кг яблок в III ящике. За х лучше принимать меньшее число.)
— Тогда, что можно сказать о II ящике? (2х (кг) яблок во II ящике.)
— Сколько будет в I ящике? (2х — 15 (кг) яблок в I ящике.)
— На основании чего можно составить уравнение? (В 3 ящиках всего 160 кг яблок.
)
Решение:
1) Пусть х (кг) — яблок в III ящике,
2х (кг) — яблок во II ящике,
2х — 15 (кг) — яблок в I ящике.
Зная, что в 3 ящиках всего 160 кг яблок, составим уравнение:
х + 2х + 2х — 15 = 160
5х = 160 + 15
Х = 175 : 5
х = 35; 35 кг яблок в III ящике.
2) 35 · 2 = 70 (кг) — яблок во II ящике.
3) 70 — 15 = 55 (кг) — яблок во I ящике.
— Что нужно сделать прежде, чем записать ответ задачи? (Чтобы записать ответ, нужно прочитать вопрос задачи.)
— Назовите вопрос задачи. (Сколько кг яблок было в каждом ящике?)
— Так как мы писали подробное пояснение к действиям, то ответ запишем кратко.
(Ответ: 55 кг, 70 кг, 35 кг.)
2. № 184 стр. 30 (у доски и в тетрадях).
— Прочитайте задачу.
— Что нужно сделать, чтобы ответить на вопрос задачи? (Найти НОК чисел 45 и 60.)
Решение:
45 = 3 · 3 · 5
60 = 2 · 5 · 2 · 3
НОК (45; 60) = 60 · 3 = 180, значит 180 м.
(Ответ: 180 м.)
VIII. Закрепление изученного материала
1. № 179 стр. 30 (у доски и в тетрадях).
— Найдите разложение на простые множители наименьшего общего кратного и наибольшего общего делителя чисел а и b.
а) НОК (а; в) = 3 · 5 · 7
НОД (а; в) = 5.
б) НОК (а; в) = 2 · 2 · 3 · 3 · 5 · 7
НОД (а; в) = 2 · 2 · 3.
2. № 180 (а, б) стр. 30 (с подробным комментированием).
— Расскажите, как удобнее считать.
а) НОК (а; b) = 2 · 3 · 3 · 3 · 5 · 2 · 5 = 2700.
б) Так как b делится на а, то НОК, будет само число b.
НОК (а; b) = 2 · 3 · 3 · 5 · 7 · 7 = 4410.
IX. Повторение изученного материала
1. — Как найти среднее арифметическое нескольких чисел? (Найти сумму этих чисел; полученный результат разделить на количество чисел.)
№ 198 стр. 32 (на доске и в тетрадях).
(3,8 + 4,2 + 3,5 + 4,1) : 4 = 3,9
2. № 195 стр. 32 (самостоятельно).
— Как по-другому можно записать частное двух чисел? (В виде дроби.
)
Решение:
X. Самостоятельная работа
— Записать промежуточные ответы.
Вариант I. № 125 (1—2 строчки) стр. 22, № 222 (а—в) стр. 36, № 186 (а, б) стр. 31.
Вариант II. № 125 (3—4 строчки) стр. 22, № 186 (в, г) стр. 31, № 222 (в—д) стр. 36.
XI. Подведение итогов урока
— Какое число называют общим кратным данных чисел?
— Какое число называют наименьшим общим кратным данных чисел?
— Как найти наименьшее общее кратное данных чисел?
Домашнее задание
№ 202 (а, б, найти НОД и НОК), № 204 стр. 32, № 206 (а) стр. 33, № 145 (а) стр. 24.
Индивидуальное задание: № 201 стр. 32.
Номер (задание) 240 — гдз по математике 6 класс Виленкин, Жохов, Чесноков
Условие / глава 1. / § 2 / тема 8 / 240
240.
Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 18 и 36; б) 33 и 44; в) 378 и 441; г) 11 340 и 37 800.
Решебник №1 / глава 1. / § 2 / тема 8 / 240
Видеорешение / глава 1.
/ § 2 / тема 8 / 240
Решебник №2 / глава 1. / § 2 / тема 8 / 240
Решебник №3 / глава 1.
/ § 2 / тема 8 / 240
Задача №14. Выполнение алгоритма — подготовка к ЕГЭ по Информатике
Автор материалов — Лада Борисовна Есакова.
В этой задаче используется, в основном, описание алгоритмов на псевдокоде (условном алгоритмическом языке, включающем в себя и элементы языка программирования, и элементы обычного естественного языка).
Основные конструкции псевдокода описаны перед текстом задачи.
Исполнитель чертежник
Пример 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n>1):
НАЧАЛО
сместиться на (60, 100)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (33, 44)
КОНЕЦ ПОВТОРИ
сместиться на (13, 200)
сместиться на (-1, 60)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Решение:
В результате выполнения алгоритма Чертежник переместится
по оси х на:
60 + n*a + n*33 + 13 – 1
по оси y на:
100 + n*b + n*44 + 200 + 60
Известно, что в результате перемещения Чертежник вернулся в исходную точку, т.е. перемещение по оси х равно нулю, и перемещение по оси y равно нулю:
60 + n*a + n*33 + 13 – 1 = 0
100 + n*b + n*44 + 200 + 60 = 0
Т.е.
n*(a + 33) = -72
n*(b + 44) = -360
Наибольшее n – это наибольший общий делитель чисел -72 и -360. Это число 72.
Ответ: 72
Исполнитель робот
Пример 2.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
вверх | вниз | влево | вправо |
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.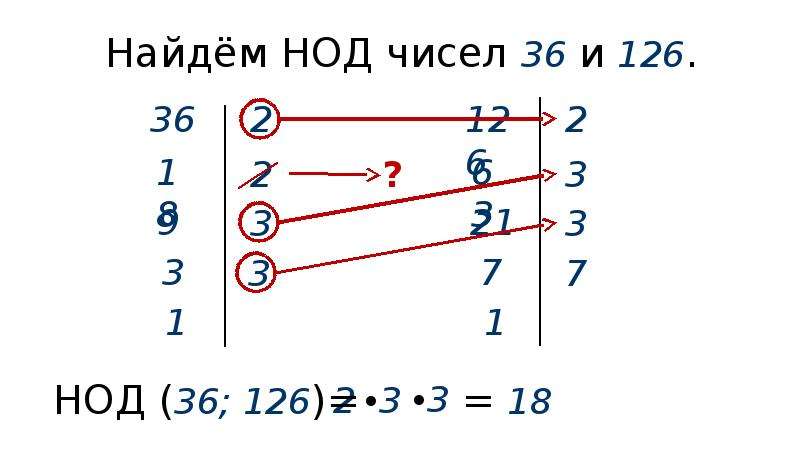
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ (также по отношению к наблюдателю):
сверху | снизу | слева | справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 22
2) 19
3) 15
4) 12
Решение:
В данной программе РОБОТ сначала проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом цикле пока у правой стороны клетки, в которой находится РОБОТ, нет стены, он продолжает двигаться вправо. Как только это условие перестанет выполняться, он переходит ко второму действию внутри цикла. Второе действие, заключается в следующем: РОБОТ передвигается на одну клетку вниз. После чего возвращается к началу внешнего цикла.
Проверив последовательно все клетки по правилу движения РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи равно 15 (вся первая строчка, весь столбец F, клетки D2, E2, D4, D6, E4).
Правильный ответ указан под номером 3.
Ответ: 3
Исполнитель редактор
Пример 3.
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (888)
ЕСЛИ нашлось (222)
ТО заменить (222, 8)
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Решение:
Обозначим строку из 68 восьмерок — 68«8»,
строку из двойки и 65 восьмерок – 1«2»65«8» и т.д.
Отработаем 4 первых цикла программы:
68«8» → 1«2»65«8» → 2«2»62«8» → 3«2»59«8» → 60«8»
В результате количество восьмерок уменьшилось на 8. Не сложно понять, что строка будет уменьшаться на 8 восьмерок каждые 4 итерации. В результате останется строка из 4 восьмерок.
Доработаем программу:
…→ 4«8» → 1«2»1«8» = 28
Ответ: 28
Исполнитель черепашка
Пример 4.
Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед n, где n – целое число, вызывающее передвижение черепашки на n шагов в направлении движения.
Направо m, где m – целое число, вызывающее изменение направления движения на m градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120]
Какая фигура появится на экране?
Решение:
Последовательность действий Вперед 40 Направо 90 рисует отрезок длиной 40 шагов, а затем меняет направление на 90 градусов по часовой стрелке.
Тогда последовательность Повтори 4 [Вперед 40 Направо 90] нарисует квадрат, а направление вернется в исходное.
Затем выполняется команда Направо 120, она изменит направление на 120 градусов от исходного.
Если повторить все рассмотренные действия 5 раз:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120], то будет 5 раз нарисован квадрат. Причем каждый следующий повернут вокруг вершины относительно предыдущего на 120 градусов. Не сложно заметить, что 4-й квадрат будет нарисован поверх первого (120*3 = 360, сделан поворот на целый круг, возврат в исходное положение), а 5-й поверх второго.
Результат изображен под номером 3.
Ответ: 3
Ты нашел то, что искал? Поделись с друзьями!
Самостоятельная работа по теме Наименьшее общее кратное (6 класс)
Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 1.
1. Найдите наименьшее общее кратное чисел:
а) 33 и 44; б) 12 и 24; в) 4, 6 и 33.
2. Между пунктами А и В курсируют два автобуса. Первый тратит на дорогу туда и обратно 35 мин, второй – 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А – в 6 ч 30 мин? Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 2.
1. Найдите наименьшее общее кратное чисел:
а) 21 и 28; б) 18 и 72; в) 3, 5 и 25.
2. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй – 7 суток. Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после второго?
Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 1.
1. Найдите наименьшее общее кратное чисел:
а) 33 и 44; б) 12 и 24; в) 4, 6 и 33.
2. Между пунктами А и В курсируют два автобуса.
Первый тратит на дорогу туда и обратно 35 мин, второй – 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А – в 6 ч 30 мин? Самостоятельная работа №5.Наименьшее общее кратное.
Вариант – 2.
1. Найдите наименьшее общее кратное чисел:
а) 21 и 28; б) 18 и 72; в) 3, 5 и 25.
2. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй – 7 суток. Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после второго?
Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 1.
1. Найдите наименьшее общее кратное чисел:
а) 33 и 44; б) 12 и 24; в) 4, 6 и 33.
2. Между пунктами А и В курсируют два автобуса. Первый тратит на дорогу туда и обратно 35 мин, второй – 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А – в 6 ч 30 мин? Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 2.
1. Найдите наименьшее общее кратное чисел:
а) 21 и 28; б) 18 и 72; в) 3, 5 и 25.
2. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй – 7 суток. Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после второго?
Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 1.
1. Найдите наименьшее общее кратное чисел:
а) 33 и 44; б) 12 и 24; в) 4, 6 и 33.
2. Между пунктами А и В курсируют два автобуса. Первый тратит на дорогу туда и обратно 35 мин, второй – 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А – в 6 ч 30 мин? Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 2.
1. Найдите наименьшее общее кратное чисел:
а) 21 и 28; б) 18 и 72; в) 3, 5 и 25.
2. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй – 7 суток. Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после второго?
Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 1.
1. Найдите наименьшее общее кратное чисел:
а) 33 и 44; б) 12 и 24; в) 4, 6 и 33.
2. Между пунктами А и В курсируют два автобуса. Первый тратит на дорогу туда и обратно 35 мин, второй – 40 мин. В какое время автобусы встретятся в пункте А, если первый автобус отправляется из А в первый рейс в 6 ч 15 мин, а второй тоже из А – в 6 ч 30 мин? Самостоятельная работа №5.
Наименьшее общее кратное.
Вариант – 2.
1. Найдите наименьшее общее кратное чисел:
а) 21 и 28; б) 18 и 72; в) 3, 5 и 25.
2. Между пунктами А и В курсируют два поезда. Первый поезд тратит на путь туда и обратно 6 суток, второй – 7 суток.
Через сколько суток со дня отправления из А первого поезда в пункте А встретятся оба поезда, если второй поезд отправляется из А через сутки после второго?Наибольший общий множитель 33 и 44 (GCF 33, 44)
Вы на охоте за GCF 33 и 44? Поскольку вы находитесь на этой странице, я так и предполагаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий множитель для любых чисел, которые вам нужно проверить. Давайте прыгнем!
Хотите быстро узнать или показать студентам, как найти GCF двух или более чисел? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Во-первых, если вы спешите, вот ответ на вопрос «каков GCF 33 и 44?» :
GCF из 33 и 44 = 11
Каков наибольший общий фактор?
Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т.
е.e целое число, а не десятичное), которое делится на все числа в наборе. Это также широко известно как:
- Наибольший общий знаменатель (НОД)
- Наивысший общий коэффициент (HCF)
- Наибольший общий делитель (НОД)
Существует несколько различных способов вычисления GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.
Для меньших чисел вы можете просто посмотреть множители или кратные для каждого числа и найти их наибольшее общее кратное.
Для 33 и 44 эти коэффициенты выглядят так:
- Факторы для 33: 1, 3, 11 и 33
- Факторы для 44: 1, 2, 4, 11 , 22 и 44
Как вы можете видеть, когда перечисляете факторы каждое число, 11 — это наибольшее число, на которое делятся 33 и 44.
Подводя итоги
По мере того, как числа становятся больше или вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, как перечисление всех факторов может стать слишком большим. Чтобы исправить это, вы можете использовать простые множители.
Перечислите все простые множители для каждого числа:
- Основные множители для 33: 3 и 11
- Основные множители для 44: 2, 2 и 11
Теперь, когда у нас есть список простых множителей, нам нужно найти любые, общие для каждого числа.
В этом случае есть только один общий простой множитель, 11. Поскольку других нет, наибольшим общим делителем является этот простой множитель:
GCF = 11
Найдите GCF с помощью алгоритма Евклида
Последний метод вычисления GCF 33 и 44 — использовать алгоритм Евклида.
Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами GCD.
Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.
Надеюсь, сегодня вы немного научились математике и понимаете, как вычислять НОД чисел. Возьмите карандаш и бумагу и попробуйте сами. (или просто воспользуйтесь нашим калькулятором НОД — никому не скажем!)
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Наибольший общий множитель 33 и 44».
VisualFractions.com . По состоянию на 18 июня 2021 г. https://visualfractions.com/calculator/greatest-common-factor/gcf-of-33-and-44/.«Наибольший общий множитель 33 и 44». VisualFractions.com , https://visualfractions.com/calculator/greatest-common-factor/gcf-of-33-and-44/. По состоянию на 18 июня 2021 г.
Наибольший общий множитель 33 и 44. VisualFractions.com. Получено с https://visualfractions.com/calculator/greatest-common-factor/gcf-of-33-and-44/.
VisualFractions.com . По состоянию на 18 июня 2021 г. https://visualfractions.com/calculator/greatest-common-factor/gcf-of-33-and-44/.GCF из 33 и 44
На этой странице мы определим GCF 33 и 44, научим вас различным способам вычисления GCF 33 и 44, а также покажу вам, для чего можно использовать GCF 33 и 44.
Что такое GCF для 33 и 44?
GCF — это сокращение от Greatest Common Factor. Следовательно, GCF 33 и 44 совпадает с наибольшим общим фактором.
33 и 44. GCF 33 и 44 — это наибольшее положительное целое число, на которое можно разделить 33 и 44.
Кроме того, и 33, и 44 имеют набор факторов, и GCF является наибольшим общим фактором для 33 и 44.
Сравните коэффициенты, чтобы получить GCF 33 и 44
Согласно приведенному выше определению, чтобы найти GCF 33 и 44, вы можете сравнить коэффициент 33 с коэффициентом множитель 44, чтобы увидеть, какой фактор является наибольшим.Когда мы это сделали, мы обнаружили что наибольший общий коэффициент (GCF) 33 и 44 равен 11.
Используйте LCM, чтобы получить GCF 33 и 44
Наименьшее общее кратное (НОК) 33 и 44 равно 132. Вы можете найти НОК 33 и 44, разделив произведение 33 и 44 на НОК 33 и 44. Вот формула и математика:
| = GCF |
| = 11 |
Используйте компьютерную таблицу, чтобы получить GCF 33 и 44
Если у вас есть компьютер, вы также можете использовать электронную таблицу в Excel или Numbers, чтобы вычислить GCF 33 и 44.
Вы хотите ввести
= gcf (33, 44) в ячейку, чтобы получить ответ.gcf (33, 44) = 11
Используйте GCF 33 и 44 для упрощения дроби
GCF 33 и 44 можно использовать для многих вещей. Вы можете, например, упростить дробь, разделив числитель и знаменатель на GCF как это:
| = |
Используйте GCF 33 и 44, чтобы упростить соотношение
Точно так же вы можете использовать GCF 33 и 44, чтобы упростить соотношение, разделив каждую часть отношения на GCF выглядит следующим образом:
= 33: 44
= (33 ÷ 11): (44 ÷ 11)
= 3: 4
Используйте GCF 33 и 44, чтобы найти LCM 33 и 44
Поскольку использование наименьшего общего кратного (НОК) является одним из способов найти НОК 33 и 44, вы можете использовать НОК 33 и 44, чтобы найти НОК 33 и 44.
НОК 33 и 44 можно, например, использовать для сложения и вычитания дробей со знаменателями 33 и 44.
НОК 33 и 44 является произведением 33 и 44, разделенных на НОК 33 и 44. Вот математика:
| = LCM |
| = 132 |
Вот и все! Мы надеемся, что эта страница выполнила свою задачу по определению GCF 33 и 44, показывая вам, как рассчитать GCF, примеры его использования и его отношение к LCM.
Калькулятор GCF
Используйте Калькулятор GCF для решения проблемы, аналогичной описанной на этой странице.
Вот следующий GCF в нашем списке, который мы для вас вычислили и объяснили.
Авторские права | Политика конфиденциальности | Заявление об ограничении ответственности | Контакт Калькулятор наибольшего общего коэффициента
— Дюймовый калькулятор
Найдите наибольший общий множитель, общие множители и все множители для набора чисел, используя калькулятор ниже.
Решение:
Наибольший общий множитель [22, 88, 132]: 22
Найдите множители для каждого числа
Факторы 22 равны [1, 2, 11, 22]
Факторы 88 равны [ 1, 2, 4, 8, 11, 22, 44, 88]
Факторы 132 равны [1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132]
Найдите коэффициенты, общие для всех трех чисел
Общие коэффициенты: [1, 2, 11, 22]
GCF — это наибольший коэффициент, общий для всех трех чисел
GCF — 22
Как найти наибольший общий делитель набора чисел
Наибольший общий множитель (GCF) набора чисел является наибольшим множителем, общим для всех чисел в наборе.
Наибольший общий множитель иногда называют наибольшим общим делителем (HCF) , наибольшим общим знаменателем (GCD) (GCD), наибольшим общим делителем или наибольшим общим делителем .
Коэффициент числа x — это число, которое можно умножить на другое целое число, чтобы получить x.
Есть несколько способов найти наибольший общий фактор. Первый — использовать калькулятор выше, который даже показывает все шаги.Следуйте инструкциям ниже, чтобы узнать о еще трех методах.
Иллюстрация, показывающая множители и общие множители чисел 90 и 165.Метод первый: найти GCF с помощью простого факторизации
Один из способов найти наибольший общий делитель набора чисел — использовать разложение на простые множители. Чтобы использовать разложение на простые множители, найдите простые множители каждого числа.
Чтобы найти простые множители, разделите каждое число в наборе на простой множитель. Затем разделите каждое число на другой простой множитель до тех пор, пока их нельзя будет разделить дальше.
Простые числа, используемые для деления числа, являются простыми множителями.
Чтобы найти наибольший общий делитель 90 и 165 с помощью разложения на простые множители, найдите простые делители каждого числа.
Чтобы найти простые множители, разделите каждое число на другой простой множитель до тех пор, пока их нельзя будет разделить дальше.
Когда у вас есть простые множители для каждого числа в наборе, следующий шаг — найти числа, общие для всех чисел.
Наконец, умножьте все общие простые множители вместе, чтобы найти наибольший общий делитель.
Например, позволяет найти наибольший общий делитель 90 и 165, используя разложение на простые множители.
Чтобы найти простые множители 90, разделите 90 на 2, чтобы получить 45. 2 — простое число, но 45 можно разделить на 5, чтобы получить 9. 5 — простое число, а 9 можно разделить на 3, чтобы получить 3.
Таким образом, простые числа 90 равны [5,3,3,2] .
Повторите этот процесс для 165. 165 разделить на 3 = 55. 3 является простым множителем, но 55 можно разделить на 5, чтобы получить 11.
Простые множители 165 равны [11,5,3] .
Теперь найдите простые множители, общие для обоих чисел. 5 и 3 входят в оба набора простых множителей, которые мы нашли выше.
Чтобы найти наибольший общий множитель, давайте умножим общие простые множители вместе.
5 × 3 = 15
Таким образом, 15 является наибольшим общим делителем 90 и 165.
Совет: используйте наш калькулятор простых множителей, чтобы найти все простые множители числа.
Метод второй: найти GCF по всем факторам
Используя этот метод, можно найти наибольший общий множитель путем нахождения всех множителей для каждого числа в наборе, а затем нахождения множителей, общих для всех чисел в наборе. Наибольший общий фактор для всех чисел — наибольший общий фактор.
Чтобы найти множители числа, разделите их на 2, если результатом является целое число, а не 2, а результат — множители. Повторите этот процесс, разделив на 3, 4 и так далее, пока не дойдете до 1.
Затем найдите факторы, входящие в набор факторов для всех чисел. Это общие множители чисел.
Наконец, найдите наибольшее число в наборе общих факторов. Это самый общий фактор.
Например, давайте найдем наибольший общий делитель 90 и 165, найдя все множители.
Начнем с определения множителей для обоих чисел.
Коэффициенты для 90: [1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90]
Коэффициенты для 165: [1, 3, 5, 11, 15, 33, 55, 165]
Затем найдите факторы, общие для 90 и 165.
Общие множители: [1, 3, 5, 15]
Найдите наибольшее число в наборе общих множителей, чтобы найти наибольший общий множитель.
Наибольшее число в наборе общих множителей 90 и 165 равно 15.
Таким образом, наибольший общий множитель 90 и 165 равен 15 .
Метод третий: найти GCF с помощью алгоритма Евклида
Алгоритм Евклида определяет шаги для эффективного нахождения наибольшего общего делителя двух чисел.Начните с деления большого числа на маленькое, чтобы получить частное и остаток.
Если остаток не равен 0, разделите предыдущий делитель на остаток. Продолжайте делать это до тех пор, пока остаток не равен 0. Как только у вас есть остаток, равный 0, делитель на этом шаге является наибольшим общим множителем.
Например, давайте найдем наибольший общий делитель 90 и 165, используя алгоритм Евклида.
165 ÷ 90 = 1 остаток 75
90 ÷ 75 = 1 остаток 15
75 ÷ 15 = 5 остаток 0
Поскольку 15 является делителем на последнем шаге, когда остаток равен 0, GCF составляет 15 .
Узнайте больше, используя наш калькулятор алгоритма Евклида.
Какой наибольший общий коэффициент используется для
Наибольший общий коэффициент обычно используется для упрощения или сокращения дробей.
Наибольший общий делитель также известен как наибольший общий делитель. Узнайте больше о сокращении фракций с помощью нашего упрощителя дробей.
Калькулятор GCF (наибольший общий коэффициент)
Калькулятор GCF вычисляет наибольший общий коэффициент от двух до шести различных чисел.Прочтите, чтобы найти ответ на вопрос: «Каков наибольший общий фактор данных чисел?», Узнайте о нескольких методах поиска GCF, включая разложение на простые множители или алгоритм Евклида, решите, какой из них вам больше всего нравится, и убедитесь сами наш калькулятор GCF поможет вам сэкономить время при работе с большими числами!
Что такое GCF?
Определение наибольшего общего множителя — наибольший целочисленный множитель, который присутствует между набором чисел . Он также известен как наибольший общий делитель , наибольший общий знаменатель ( GCD ), наибольший общий делитель ( HCF ) или наибольший общий делитель ( HCD ).
Это важно в некоторых приложениях математики, таких как упрощение многочленов, где часто бывает необходимо выделить общие множители. Далее нам нужно знать, как найти GCF.
Как найти наибольший общий множитель
Существуют различные методы, которые помогут вам найти GCF. Некоторые из них — детская игра, другие — более сложные. Стоит знать их все, чтобы вы могли решить, что вам больше нравится:
- Используя список факторов,
- Факторизация чисел на простые множители,
- алгоритм Евклида,
- Бинарный алгоритм (алгоритм Штейна),
- Использование нескольких свойств GCF (включая наименьшее общее кратное, LCM).
Хорошая новость в том, что вы можете оценить НОД с помощью простых математических операций, без корней и логарифмов! В большинстве случаев это просто вычитание, умножение или деление.
GCF finder — список факторов
Основной метод, используемый для оценки наибольшего общего делителя, — это найти все множители данных чисел.
Факторы — это просто числа, умножение которых дает исходное значение. В целом они могут быть как положительными, так и отрицательными, т.е.грамм. 2 * 3 совпадает с (-2) * (-3) , оба равны 6. С практической точки зрения мы рассматриваем только положительные . Причем речь идет только о целых числах. В противном случае вы найдете бесконечную комбинацию различных дробей, являющихся факторами, что в нашем случае бессмысленно. Зная это, давайте оценим наибольший общий знаменатель чисел 72 и 40 .
- Факторы
72:1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72, - Факторы
40:1, 2, 4, 5, 8, 10, 20, 40, - Перечислите все общие множители:
1, 2, 4, 8, - Наибольший общий делитель — 8 , максимальное значение сверху.
Давайте попробуем что-нибудь посложнее. Мы хотим найти ответ на вопрос: «Каков наибольший общий множитель для 33264 и 35640 ?» Все, что нам нужно сделать, это повторить предыдущие шаги:
- Факторы
33264:1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, 21, 22, 24, 27, 28, 33, 36, 42, 44, 48, 54, 56, 63, 66, 72, 77, 84, 88, 99, 108, 112, 126, 132, 144, 154, 168, 176, 189, 198, 216, 231, 252, 264, 297, 308, 336, 378, 396, 432, 462, 504, 528, 594, 616, 693, 756, 792, 924, 1008, 1188, 1232, 1386, 1512, 1584, 1848, 2079, 2376, 2772, 3024, 3696, 4158, 4752, 5544, 8316, 11088, 16632, 33264, - Факторы
35640:1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 15, 18, 20, 22, 24, 27, 30, 33, 36, 40 , 44, 45, 54, 55, 60, 66, 72, 81, 88, 90, 99, 108, 110, 120, 132, 135, 162, 165, 180, 198, 216, 220, 264, 270, 297 , 324, 330, 360, 396, 405, 440, 495, 540, 594, 648, 660, 792, 810, 891, 990, 1080, 1188, 1320, 1485, 1620, 1782, 1980, 2376, 2970, 3240 , 3564, 3960, 4455, 5940, 7128, 8910, 11880, 17820, 35640, - Список всех общих делителей:
1, 2, 3, 4, 6, 8, 9, 11, 12, 18, 22, 24, 27, 33, 36, 44, 54, 66, 72, 88, 99, 108, 132, 198, 216, 264, 297, 396, 594, 792, 1188, 2376, - Окончательный результат: 2376 .
Как видите, чем больше факторов, тем больше времени занимает процедура и легко ошибиться. Стоит знать, как работает этот метод, но вместо этого мы рекомендуем использовать наш калькулятор GCF, просто чтобы убедиться, что результат правильный.
Факторизация на простые множители
Другая широко используемая процедура, которую можно рассматривать как калькулятор наибольшего общего делителя, использует разложение на простые множители. Этот метод в некоторой степени родственен ранее упомянутому.Вместо того, чтобы перечислять все возможные факторы, мы находим только те, которые являются простыми числами. В результате произведение всех общих простых чисел является ответом на нашу проблему, и, что более важно, всегда есть один уникальный способ разложить любое число на простые. Итак, теперь давайте найдем наибольший общий знаменатель 72 и 40 , используя разложение на простые множители:
- Основные множители числа
72равны:2, 2, 2, 3, 3, - Основные множители
40:2, 2, 2, 5, - Другими словами, мы можем написать:
72 = 2 * 2 * 2 * 3 * 3и40 = 2 * 2 * 2 * 5, - Общая часть в обоих случаях равна
2 * 2 * 2 = 8, и это наибольший общий коэффициент.
Мы видим, что для этого простого примера результат согласуется с предыдущим методом. Посмотрим, работает ли он одинаково хорошо для более сложного случая. Что такое GCF для 33264 и 35640 ?
- Основные множители
33264:2, 2, 2, 2, 3, 3, 3, 7, 11, - Основные множители
35640:2, 2, 2, 3, 3, 3, 3, 5, 11, - Мы можем использовать обозначение экспоненты для записи продуктов как:
33264 = 2⁴ * 3³ * 7 * 11,35640 = 2³ * 3⁴ * 5 * 11, - Общее произведение двух чисел:
2³ * 3³ * 11.Мы также можем записать его более компактно и изощренно с учетом факториалов:(3!) ³ * 11. Проверьте, дает ли наш калькулятор GCD такой же результат:2376.
Алгоритм Евклида
Идея, лежащая в основе алгоритма Евклида, гласит, что если число k является наибольшим общим множителем чисел A и B , то k также является GCF для разности этих чисел A - В .
Следуя этой процедуре, мы наконец достигнем 0. В результате наибольший общий делитель будет последним ненулевым числом. Еще раз взглянем на наши примеры — числа 40 и 72 . Каждый раз, когда мы производим вычитание, мы сравниваем два числа, упорядочивая их от наибольшего к наименьшему значению:
- GCF из
72и40: разница72-40равна32, - GCF из
40и32:40-32 = 8, - GCF из
32и8:32-8 = 24, - GCF из
24и8:24-8 = 16, - GCF из
16и8:16-8 = 8, - GCF из
8и8:8-8 = 0СТОП!
На нашем последнем шаге вычитанием мы получаем 0.Это означает, что мы находим наш Наибольший общий делитель и его значение в предпоследней строке вычитаний: 8 .
А как насчет более сложного случая с 33264 и 35640 ? Попробуем решить ее с помощью алгоритма Евклида:
- GCF из
35640и33264:35640 - 33264 = 2376, - GCF из
33264и2376:33264 - 2376 = 30888, - GCF из
30888и2376:30888 - 2376 = 28512, - GCF из
28512и2376:28512 - 2376 = 26136, - GCF из
26136и2376:26136 - 2376 = 23760, - GCF из
23760и2376:23760 - 2376 = 21384, - GCF из
21384и2376:21384 - 2376 = 19008, - GCF из
19008и2376:19008 - 2376 = 16632, - GCF из
16632и2376:16632 - 2376 = 14256, - GCF из
14256и2376:14256 - 2376 = 11880, - GCF из
11880и2376:11880 - 2376 = 9504, - GCF из
9504и2376:9504 - 2376 = 7128, - GCF из
7128и2376:7128 - 2376 = 4752, - GCF из
4752и2376:4752 - 2376 = 2376, - GCF из
2376и2376:2376 - 2376 = 0СТОП!
Как и в предыдущем примере, НОД для 33264 и 35640 является последней отличной от нуля разницей в процедуре, которая составляет 2376 .
Как видите, базовая версия этого искателя GCF очень эффективна и проста, но имеет один существенный недостаток. Чем больше разница между приведенными числами, тем больше шагов необходимо для достижения последнего шага. По модулю — это эффективная математическая операция, которая решает проблему, потому что нас интересует только остаток, меньший обоих чисел. Давайте повторим алгоритм Евклида для наших примеров, используя по модулю вместо обычного вычитания:
- GCF из
72и40:72 мод 40 = 32, - GCF из
40и32:40 мод 32 = 8, - GCF из
32и8:32 mod 8 = 0СТОП!
Наибольший общий знаменатель 8 .А что насчет другого?
- GCF из
35640и33264:35640 мод 33264 = 2376, - GCF из
33264и2376:33264 mod 2376 = 0СТОП!
GCD из 35640 и 33264 — это 2376 , и его можно найти всего за два шага вместо 15.
Неплохо, не так ли?
Алгоритм двоичного наибольшего общего делителя
Если вам нравятся более простые арифметические операции, чем те, которые используются в алгоритме Евклида (например,грамм. по модулю), двоичный алгоритм (или алгоритм Штейна) определенно для вас! Все, что вам нужно использовать, это сравнение, вычитание и деление на 2. При оценке наибольшего общего множителя двух чисел имейте в виду следующие тождества:
-
gcd (A, 0) = A, мы используем тот факт, что каждое число делит ноль, и наблюдение с последнего шага в алгоритме Евклида — одно из чисел упало до нуля, и наш результат был предыдущим, - Если и
A,, иBравны, это означает, чтоgcd (A, B) = 2 * gcd (A / 2, B / 2), поскольку 2 является общим множителем, - Если только одно из чисел четное, скажем,
A, тогдаgcd (A, B) = gcd (A / 2, B).На этот раз 2 не является общим делителем, поэтому мы можем продолжить сокращение, пока оба числа не станут нечетными, - Если и
A, иBнечетные иA> B, тоgcd (A, B) = gcd ((A-B) / 2, B). На этот раз мы объединяем две функции в один шаг. Первый выводится из алгоритма Евклида, определяющего наибольший общий делитель разности обоих чисел и меньшего. Во-вторых, возможно деление на 2, так как разность двух нечетных чисел четная, и согласно шагу 3 мы можем уменьшить четное. - Шаги 2-4 повторяются до достижения шага 1 или
A = B. Результатом будет2ⁿ * A, гдеn— количество факторов 2, найденных на втором этапе.
На этот раз мы объединяем две функции в один шаг. Первый выводится из алгоритма Евклида, определяющего наибольший общий делитель разности обоих чисел и меньшего. Во-вторых, возможно деление на 2, так как разность двух нечетных чисел четная, и согласно шагу 3 мы можем уменьшить четное. Как обычно, давайте попрактикуемся в алгоритме с нашими наборами чисел. Начнем с 40 и 72 :
- Они оба равны
gcf (72, 40) = 2 * gcf (36, 20) = 2² * gcf (18, 10) = 2³ * gcf (9, 5) =…, - Остальные числа нечетные, поэтому
… = 2³ * gcf ((9-5) / 2, 5) = 2³ * gcf (2, 5), - 2 ровно, поэтому мы можем уменьшить его:
… = 2³ * gcf (1, 5), - 1 и 5 нечетны, поэтому:
… = 2³ * gcf ((5-1) / 2, 1) = 2³ * gcf (2, 1), - Удалите 2 из четного числа:
… = 2³ * gcf (1, 1) = 2³ = 8.
На самом деле, мы могли бы остановиться на третьем шаге, так как НОД 1 и любое число равно 1.
Хорошо, а как найти наибольший общий множитель для 33264 и 35640 с помощью двоичного метода?
- Два четных числа:
gcf (35640, 33264) = 2 * gcf (17820, 16632) = 2² * gcf (8910, 8316) = 2³ * gcf (4455, 4158) =…, - Один четный, один нечетный:
… = 2³ * gcf (4455, 2079), - Два нечетных:
… = 2³ * gcf ((4455-2079) / 2, 2079) = 2³ * gcf (1188, 2079), - Один четный, один нечетный:
… = 2³ * gcf (594, 2079) = 2³ * gcf (297, 2079), - Два нечетных:
… = 2³ * gcf ((2079-297) / 2, 297) = 2³ * gcf (891, 297), - Два нечетных:
… = 2³ * gcf ((891-297) / 2, 297) = 2³ * gcf (297, 297) = 2³ * 297 = 2376.
Сопоставимые номера
Мы знаем, что простые числа — это числа, у которых есть только 2 положительных целых делителя: 1 и само себя.
Итак, вопрос в том, что такое взаимно простые числа? Мы можем определить их как чисел, не имеющих общих делителей . Точнее, 1 — их единственный общий делитель, но поскольку мы опускаем 1 при разложении на простые множители, можно сказать, что у них нет общих делителей. Другими словами, мы можем написать, что числа A и B взаимно просты, если gcf (A, B) = 1 .На самом деле это не означает, что любое из них является простым числом, просто список общих факторов пуст. Примеры взаимно простых чисел: 5 и 7 , 35 и 48 , 23156 и 44613 .
Интересный факт: можно вычислить вероятность того, что два случайно выбранных числа взаимно просты. Хотя это довольно сложно, общий результат составляет около 61% . Вы удивлены? Просто проверьте это на себе — представьте два случайных числа (скажем, из пяти цифр), воспользуйтесь нашим калькулятором наибольшего общего коэффициента и выясните, будет ли результат 1 или нет.
Повторите игру несколько раз и оцените, какой процент найденных вами взаимно простых чисел.
Наибольший общий знаменатель более двух чисел
Теперь, когда мы знаем о многочисленных методах нахождения наибольшего общего делителя двух чисел, вы можете спросить: «как найти наибольший общий делитель трех или более чисел?» . Оказывается, это не так сложно, как может показаться на первый взгляд. Что ж, перечисление всех факторов для каждого числа — определенно простой метод, потому что мы можем просто найти самый большой из них.Однако вы быстро поймете, что по мере увеличения числа фигур на это уходит все больше и больше времени.
Метод факторизации простых чисел имеет аналогичный недостаток, но поскольку мы можем сгруппировать все простые числа, например, в порядке возрастания, мы можем представить способ получения результата немного быстрее, чем раньше.
С другой стороны, если вы предпочитаете использовать двоичные или евклидовы алгоритмы для оценки ОКФ нескольких чисел, вы также можете использовать теорему, которая гласит:
gcf (a, b, c) = gcf (gcf (a, b), c) = gcf (gcf (a, c), b) = gcf (gcf (b, c), a) .
Это означает, что мы можем вычислить НОД любых двух чисел, а затем снова запустить алгоритм, используя результат и третье число, и продолжать, пока остаются какие-либо цифры. Неважно, какие два мы выберем в первую очередь.
Наименьшее общее кратное
Еще одно понятие, тесно связанное с НОД, — наименьшее общее кратное. Чтобы найти наименьшее общее кратное, мы используем тот же процесс, который мы использовали для поиска GCF. Как только мы сведем числа к разложению на простые множители, мы ищем наименьших степеней каждого множителя, в отличие от наибольшей степени.Затем мы умножаем наибольшие степени, и в результате получаем наименьшее общее кратное или НОК. Это можно сделать вручную или с помощью калькулятора LCM.
Наибольший общий коэффициент можно оценить с помощью LCM. Допустимо следующее выражение:
gcf (a, b) = | a * b | / см (а, б) .
Может быть удобно сначала найти наименьшее общее кратное из-за сложности и продолжительности.
Естественно, его можно вычислить любым способом, поэтому стоит знать, как найти GCD и LCM.
Свойства GCD
Мы уже представили несколько свойств наибольшего общего знаменателя. В этом разделе мы перечислим самые важные:
Если отношение двух чисел
aиb(a> b) является целым числом, тоgcf (a, b) = b,gcf (a, 0) = a, используется в алгоритме Евклида,gcf (a, 1) = 1,Если
aиbне имеют общих множителей (они взаимно просты), тоgcf (a, b) = 1,Все общие множители
aиbтакже являются делителямиgcf (a, b),Если
b * c / aявляется целым числом иgcf (a, b) = d, тоa * c / dтакже является целым числом,Для любого целого числа
k:gcf (k * a, k * b) = k * gcf (a, b), используется в двоичном алгоритме,Для любого положительного целого числа
k:gcf (a / k, b / k)=gcf (a, b) / k,gcf (a, b) * lcm (a, b) = | a * b |,gcf (a, lcm (b, c)) = lcm (gcf (a, b), gcf (a, c)),пкм (a, gcf (b, c)) = gcf (lcm (a, b), lcm (a, c)).
Калькулятор наибольшего общего коэффициента
Укажите числа, разделенные запятой «,» и нажмите кнопку «Рассчитать», чтобы найти GCF.
Связанный калькулятор LCM | Калькулятор коэффициентов
Какой наибольший общий коэффициент (GCF)?
В математике наибольший общий делитель (GCF), также известный как наибольший общий делитель, двух (или более) ненулевых целых чисел a и b , является наибольшим положительным целым числом, на которое можно разделить оба целых числа. .Обычно его обозначают как GCF (a, b). Например, GCF (32, 256) = 32.
.Метод простой факторизации
Есть несколько способов найти наибольший общий делитель заданных целых чисел. Один из них включает в себя вычисление простых множителей каждого целого числа, определение общих факторов и умножение этих факторов для нахождения НОД. См. Пример ниже.
| Пример: | GCF (16, 88, 104) 16 = 2 × 2 × 2 × 2 88 = 2 × 2 × 2 × 11 104 = 2 × 2 × 2 × 13 ОКФ (16, 88, 104) = 2 × 2 × 2 = 8 |
Факторизация на простые множители эффективна только для меньших целочисленных значений.
Большие значения сделают простое разложение каждого из них и определение общих факторов гораздо более утомительным.
Евклидов алгоритм
Другой метод, используемый для определения GCF, включает использование алгоритма Евклида. Этот метод является гораздо более эффективным, чем использование разложения на простые множители. Алгоритм Евклида использует алгоритм деления в сочетании с наблюдением, что НОД двух целых чисел также может делить их разность. Алгоритм следующий:
| GCF (а, а) = а GCF (a, b) = GCF (a-b, b), когда a> b GCF (a, b) = GCF (a, b-a), когда b> a |
На практике:
- Для двух положительных целых чисел a и b, где a больше, чем b , вычтите меньшее число b из большего числа a , чтобы получить результат c .
- Продолжайте вычитать b из a , пока результат c не станет меньше b .
- Используйте b в качестве нового большого числа и вычтите окончательный результат c , повторяя тот же процесс, что и на шаге 2, пока остаток не станет 0.
- Если остаток равен 0, GCF — это остаток от шага, предшествующего нулевому результату.
| EX: | GCF (268442, 178296) 268442–178296 = |
Из приведенного выше примера видно, что GCF (268442, 178296) = 2.Если бы присутствовало больше целых чисел, тот же процесс был бы выполнен, чтобы найти GCF следующего целого числа и GCF двух предыдущих целых чисел. Ссылаясь на предыдущий пример, если вместо этого желаемое значение было GCF (268442, 178296, 66888), после того, как было обнаружено, что GCF (268442, 178296) равно 2, следующим шагом будет вычисление GCF (66888, 2). В этом конкретном случае ясно, что GCF также будет 2, давая результат GCF (268442, 178296, 66888) = 2.
Simplify 44/33 — Сократите 44/33 до самой простой формы
Упрощение 44/33 объяснено
Каждую дробь можно привести к простейшей форме, в которой числитель и знаменатель должны быть как можно меньше.
Чтобы упростить дробь, вам нужно найти наибольший общий множитель числителя и знаменателя. Общий множитель — это число, на которое можно разделить как числитель, так и знаменатель. Разделив числитель и знаменатель на GCF, ваша дробь приведена к простейшей форме.
Часто GCF можно найти методом проб и ошибок. Но есть также способ найти GCF. Поэтому мы используем простые числа. Простое число — это число, которое делится только на себя и 1:
Список простых чисел бесконечен: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 39, 41, 43, 47, 53 и т. Д.
Чтобы упростить 44/33, мы запишем числитель и знаменатель как произведение только простых чисел (каждое число можно записать как произведение только простых чисел). Этот метод называется простой факторизацией :
| 44 | = | 2 х 2 х 11 | = | 2 х 2 | = | |
| 33 | 3 х 11 | 3 |
GCF — это произведение общих простых чисел (перечеркнутых выше) в числителе и знаменателе:
GCF = 11
Калькулятор упрощенных дробей
Проверьте, есть ли у вас самая простая форма дроби, и посмотрите, есть ли у вас как можно меньшие числитель и знаменатель.
Заполните числитель над линией результата и знаменатель под линией результата и нажмите «Упростить дробь», чтобы произвести расчет. Калькулятор упрощенных дробей показывает дробь в ее простейшей форме и показывает наибольший общий коэффициент (GCF).
Fractioncalculator.com уже произвел
4 486 242
расчетов Множителииз 1452 — из нашего калькулятора коэффициентов
Какие множители у 1452?
Это целые числа, которые можно без остатка разделить на 1452; они могут быть выражены как отдельные факторы или как пары факторов.В данном случае мы представляем их обоими способами. Это математическое разложение определенного числа. Хотя обычно это положительное целое число, обратите внимание на комментарии ниже об отрицательных числах.
Что такое разложение 1452 на простые множители?
Факторизация на простые множители — это результат разложения числа на набор компонентов, каждый член которого является простым числом.
Обычно это записывают, показывая 1452 как произведение его простых множителей.
Для
1452 г., результат будет таким:
(это также известно как разложение на простые множители; наименьшее простое число в этой серии описывается как наименьшее простое множитель)
1452 — составное число?
Да! 1452 — составное число.Это произведение двух положительных чисел, кроме 1 и самого себя.
1452 — квадратное число?
Нет! 1452 — это не квадратное число. Квадратный корень из этого числа (38.11) не является целым числом.
Сколько факторов у 1452?
Это число состоит из 18 факторов: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 121, 132, 242, 363, 484, 726, 1452
Более конкретно, показаны парами. ..
(1 * 1452) (2 * 726) (3 * 484) (4 * 363) (6 * 242) (11 * 132) (12 * 121) (22 * 66) (33 * 44) ( 44 * 33) (66 * 22) (121 * 12) (132 * 11) (242 * 6) (363 * 4) (484 * 3) (726 * 2) (1452 * 1)
Какой наибольший общий делитель числа 1452 и другого числа?
Наибольший общий делитель двух чисел может быть определен путем сравнения факторизации на простые множители (факторизации в некоторых текстах) двух чисел.
и беря наивысший общий простой множитель.Если нет общего множителя, gcf равен 1.
Это также называется наивысшим общим множителем и является частью общих простых множителей двух чисел.
Это самый большой множитель (наибольшее число), которое два числа делят в качестве основного множителя.
Наименьший общий множитель (наименьшее общее число) любой пары целых чисел равен 1.
Как найти наименее распространенное кратное 1452 и другое число?
Здесь у нас есть калькулятор наименьшего общего кратного. Решение — наименьшее общее кратное. из двух номеров.
Что такое дерево факторов
Факторное дерево — это графическое представление возможных факторов числа и их подфакторов.
Он предназначен для упрощения факторизации.
Он создан
нахождение множителей числа, затем нахождение множителей множителей числа. Процесс продолжается рекурсивно
до тех пор, пока вы не получите набор простых множителей, который является факторизацией исходного числа на простые множители.
При построении дерева обязательно запомните второй элемент в факторной паре.
Как найти множители отрицательных чисел? (например, -1452)
Чтобы найти множители -1452, найдите все положительные множители (см. Выше), а затем продублируйте их с помощью добавляя знак минус перед каждым (фактически умножая их на -1). Это устраняет негативные факторы. (обработка отрицательных целых чисел)
1452 — целое число?
Да.
Каковы правила делимости?
Делимость относится к данному целому числу, которое делится на данный делитель.Правило делимости — это сокращение система для определения того, что делится, а что нет. Сюда входят правила о нечетных и четных числовых множителях. Этот пример предназначен для того, чтобы учащийся мог оценить статус данного числа без вычислений.
.