Наименьшее общее кратное чисел 20 и 25: Общий знаменатель чисел 20 и 25

2

Найдите наименьшее общее кратное » задачи

НОД и НОК »

• Найдите наименьшее общее кратное натуральных чисел, представленных в виде произведений простыхмножителей:

  
  1) а=2 в кубе * на 3 * на 5 и b=2*3* 5 в квадрате
  2) с=2 в 4-ой степени умножить на 3 в квадрате и d=2 в квадрате *на 3 в квадрате * 5
  3) е=2 в кубе * на 3 * на 7 и f=2 в квадрате * на 3 в квадрате * на 7
  4) m=2 в квадрате * на 3 в кубе и n=3 в кубе * на 5
  4) p=2 * на 3 в кубе * на 11 и t= 2 в кубе * на 3 * на 11
  5) x=2 в четвертой степени * на 3 * на 5 и y=2 в квадрате * на 3* на 5 в квадрате
  Решение:

  Наименьшим общим кратным (НОК) натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b. Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
  а) разложить их на простые множители;
  б) выписать в строчку множители, входящие в разложение большего из заданных чисел, а под ним — множители, входящие в разложение меньшего из заданных чисел;
  в) отметить в разложении меньшего числа множители, которые не вошли в разложение бóльшего числа и добавить эти множители в разложение бóльшего числа;
  г) найти произведение получившихся множителей, которое и есть НОК. 4×3×5=2×2×2×2×3×5=240;
    НОК (108, 135)=2×2×3×5×5×2×2=1200.

• Найдите наименьшее общее кратное знаменателей дробей 7 / 480, 23 /180 и 31/450 с помощью разложения их на простые множители и приведите эти дроби к наименьшему общему знаменателю.

  
  
  Решение: Разложим знаменатели данных дробей на простые множители: 480=2×2×2×2×2×3×5; 180=2×2×3×3×5; 450=2×3×3×5×5 Найдем НОК(480,180,450), который и будет наименьшим знаменателем этих дробей Найдём совпавшие делители у всех трёх чисел. Это  2,3 и 5. Выпишем у первого числа все делители 2,2,2,2,2,3.5 или само это число 480. У второго числа- не совпавшие делител:2 и3 У третьего числа-не совпавшие делители:3 и 5 Перемножим их:2×2×2×2×2×3×5×2×3×3×5=480×6×15=480×90=43200 То есть НОК(480,180,450)=43200 Приведём дроби к общему знаменателю: Искомые дроби:
  

• Найдите наименьшее общее кратное знаменателей дробей:2)17/24 и 5/16;3)1/6,1/8 и 1/12;4)23/40 и 7/25

  
  Решение: 2)5/16. 3)1/12. 47/25

  2) 17/24 и 5/16 = 34/48 и 15/48

  24 = 2 * 2 * 2 * 3

  16 = 2 * 2 * 2 * 2

  НОК (24 и 16) = 2 * 2 * 2 * 2 * 3 = 48 — наименьшее общее кратное

  3) 1/6 и 1/12 = 2/12 и 1/12

  6 = 2 * 3

  12 = 2 * 2 * 3

  НОК (6 и 12) = 2 * 2 * 3 = 12 — наименьшее общее кратное

  4) 23/40 и 7/25 = 115/200 и 56/200

  40 = 2 * 2 * 2 * 5

  25 = 5 * 5

  НОК (40 и 25) = 2 * 2 * 2 * 5 * 5 = 200 — наименьшее общее кратное

• Найдите наименьшее общее кратное знаменателей дробей

  
  97/100 и 1/125
  Решение: Разложим знаменатели дробей на простые множители
  100=2*2*5*5
  125=5*5*5
  составим произведение из чисел, которые входят в разложение чисел 100 и 125 (берем по наибольшему количеству. Двойка в первом разложении встречается два раза, во втором разложении ни разу (0) Берем две двойки. Пятерка в первом разложении встречается 2 раза, во втором — три раза. Берем три пятерки)
  Получаем 2*2*5*5*5=500
  НОК (100,125)=500

• Найдите наименьшее общее кратное знаменателей дробей 7/198, 5/132 и 25/264 путем разложения их на простые множители и приведите эти дроби к наименьшему общему знаменателю.

  
  Решение: Разложили на множители
  198 = 2*3*3*11
  132 = 2*2*3*11
  264 = 2*2*2*3*11
  НОК(132,198,264) = 792
  ОТВЕТы
  7/198 = 28/792
  5/132 = 30/792
  25/264 =75/792

  .

• Найдите наименьшее общее кратное знаменателей дробей:

  
  1)8\9 и 7\6. 2)11\20 и 24\25
  Решение: НОК(9, 6) = 18
  НОК(20, 25) = 100

  1) 9 = 3 * 3 6 = 2 * 3 
  НОК (9 и 6) = 2 * 3 * 3 = 18 — наименьшее общее кратное
  18 : 9 = 2 — доп. множ. к 8/9 = 16/18 
  18 : 6 = 3 — доп. множ. к 7/6 = 21/18 
  2) 20 = 2 * 2 * 5 25 = 5 * 5
  НОК (20 и 25) = 2 * 2 * 5 * 5 = 100 — наименьшее общее кратное
  100 : 20 = 5 — доп. множ. к 11/20 = 55/100 
  100 : 25 = 4 — доп. множ. к 24/25 = 96/100 

• Найдите наименьшее общее кратное знаменателей дробей 3/16и5/12

  
  18/28и20/63
  Решение: 16 = 2 * 2 * 2 * 2
  12 = 2 * 2 * 3
  НОК (16 и 12) = 2 * 2 * 2 * 2 * 3 = 48 — наименьшее общее кратное
  3/16 = 9/48 и 5/12 = 20/48
  28 = 2 * 2 * 7
  63 = 3 * 3 * 7
  НОК (28 и 63) = 2 * 2 * 3 * 3 * 7 = 252 — наименьшее общее кратное
  18/28 = 162/252 и 20/63 = 80/252

  3\16 и5\12-раскладываем 16=2х2х2х2х 12=2х2х3 нок16 12=2х2х2х2х3=48
  18\28 и 20\63 раскладываем 28=2х2х7 63=3х3х7 нок 28 63=2х2х7х3х3=252
  18\28=162\252 и 20\63=80\252
  3\16=9\48 и 5 \12=20\48

• Найдите наименьшее общее кратное знаменателей дробей :3/16и5/12 13/28и20/63

  
  Решение: Самый простой способ найти НОК — разложить знаменатели на множители (если это возможно) таким образом, чтобы один из множителей был одинаковым. Пример: знаменатели 16 и 12 раскладываем на множители и получаем 4*4 и 4*3. 4 можно вынести за скобку, т. к. этот множитель общий. Получаем 4* (4*3)=48. Это и есть НОК для знаменателей 16 и 12. Кроме того, этот способ позволяет быстро определить на какое число нужно домножить числители дробей. Первый числитель домножаем на 3 (в знаменателе было 4*4, стало 4*4*3) — получаем дробь 9/48, второй числитель домножаем на 4 (в знаменателе было 4*3, стало 4*4*3) — получаем дробь 20/48
  То же самое со вторым примером. Раскладываем знаменатели на множители: 28=7*4, 63=7*9, выносим общий множитель за скобки 7*(4*9) и получаем НОК=252. Теперь домножаем числители. Получили 117/252 и 80/252
  

• 1) приведите дробь к новому знаменателю:

  
  5/8 и 4/5 4/21 и 2/7 9/22 и 14/55 15/54 и 28/48
  2) найдите наименьшее общее кратное знаменателей дробей 7/198, 5/132 и 25/264 с помощью разложения их на простые множители и приведите эти дроби к наименьшему общему знаменателю.
  Решение: 1) 5/8 и 4/5 = 25/40 и 32/40
  4/21 и 2/7 = 4/21 и 6/21
  9/22 и 14/55 = 45/110 и 28/110
  15/54 и 28/48 = 120/432 и 252/432
  2) 198 = 2 * 3 * 3 * 11
  132 = 2 * 2 * 3 * 11
  264 = 2 * 2 * 2 * 3 * 11
  НОК (198; 132 и 264) = 2 * 2 * 2 * 3 * 3 * 11 = 792 — наименьшее общее кратное
  792 : 198 = 4 — доп. множ. к 7/198 = 28/792
  792 : 132 = 6 — доп. множ. к 5/132 = 30/792
  792 : 264 = 3 — доп. множ. к 25/264 = 75/792 

• Найдите наименьшее общее кратное знаменателей дроби:

  
  7/480, 23/180 и 31/450 с помощью разложения на простые множители и приведите эти дроби к наименьшему общему знаменателю.
  Решение: Для чисел:480; 180; 450

  Наименьшее общее кратное:

  7 200

  480 = 2 × 2 × 2 × 2 × 2 × 3 × 5
  180 = 2 × 2 × 3 × 3 × 5
  450 = 2 × 3 × 3 × 5 × 5
  НОК (480, 180, 450) = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 7200
  Найдём дополнительные множители для каждой дроби:
  7200 : 480 = 15
  7200 : 180 = 40
  7200 : 450 = 16
  Теперь умножим числители и знаменатели дробей на дополнительные множители:
  7/480 = (7 × 15) / (480 × 15) = 105/7200
  23/180 = (23 × 40) / (180 × 40) = 920/7200
  31/450 = (31 × 16) / (450 × 16) = 496/7200
  Ответ: 105/7200, 920/7200 и 496/7200
  

1 2 3 > >>

Как найти наименьшее общее кратное 3 чисел.

Как найти НОК (наименьшее общее кратное)

Рассмотрим три способа нахождения наименьшего общего кратного.

Нахождение путём разложения на множители

Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.

Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:

Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:

2 2 · 3 2 · 5 · 7 · 11 = 13 860

Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.

Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.

Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому

НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.

Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.

Нахождение путём подбора

Второй способ заключается в нахождении наименьшего общего кратного путём подбора.

Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:

НОК (60, 30, 10, 6) = 60

В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:

1. Определяем наибольшее число из данных чисел.
2. Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.

Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:

24 · 1 = 24 — делится на 3, но не делится на 18.

24 · 2 = 48 — делится на 3, но не делится на 18.

24 · 3 = 72 — делится на 3 и на 18.

Таким образом, НОК (24, 3, 18) = 72.

Нахождение путём последовательного нахождения НОК

Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.

НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.

Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:

Делим произведение на их НОД:

Таким образом, НОК (12, 8) = 24.

Чтобы найти НОК трёх и более чисел используется следующий порядок действий:

1. Сначала находят НОК каких-нибудь двух из данных чисел.
2. Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
3. Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
4. Таким образом поиск НОК продолжается до тех пор, пока есть числа.

Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа — 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:

Делим произведение на их НОД:

Таким образом, НОК (12, 8, 9) = 72.

Как найти наименьшее общее кратное?

Нужно найти каждый множитель каждого из двух чисел, у которых находим наименьшее общее кратное, а потом перемножить друг на друга множители, которые совпали у первого и второго числа. Результатом произведения будет искомое кратное.

Например у нас есть числа 3 и 5 и нам надо найти НОК(наименьшее общее кратное). Нам надо умножать и тройку и пятрку на все числа начиная с 1 2 3 . .. и т д пока мы не увидим одинаковое число и там и там.

Множим тройку и получаем: 3, 6, 9, 12, 15

Множим пятрку и получаем: 5, 10, 15

Метод разложения на простые множители — самый классический для нахождения наименьшего общего кратного (НОК) для нескольких чисел. Наглядно и просто продемонстрирован этот метод в следующем видеоролике:

Складывать, умножать, делить, приводить к общему знаменателю и другие арифметические действия очень увлекательное занятие, особенно восхищают примеры, занимающие целый лист.

Итак найти общее кратное для двух чисел, которое будет являться самым маленьким числом на которое делятся два числа. Хочу заметить, что не обязательно в дальнейшем прибегать к формулам, чтобы найти искомое, если можешь считать в уме (а это можно натренировать), то цифры сами всплывают в голове и потом дроби щелкаются как орешки.

Для начала усвоим, что можно умножить два числа друг на друга, а потом эту цифру уменьшать и делить поочередно на данные два числа, так мы найдем наименьшее кратное.

Например, два числа 15 и 6. Умножаем и получаем 90. Это явно больше число. Причем 15 делится на 3 и 6 делится на 3, значит 90 тоже делим на 3. Получаем 30. Пробуем 30 разделить 15 равно 2. И 30 делим 6 равно 5. Так как 2 это предел, то получается, что наименьшее кратное для чисел 15 и 6 будет 30.

С цифрами побольше будет немного трудней. но если знать, какие цифры дают нулевой остаток при делении или умножении, то трудностей, в принципе, больших нет.

• Как найти НОК

  Вот видео, в котором вам будет предложено два способа нахождения наименьшего общего кратного (НОК). Поупражнявшись в использовании первого из предложенных способов, вы сможете лучше понять, что такое наименьшее общее кратное.

Представляю ещ один способ нахождения наименьшего общего кратного. Рассмотрим его на наглядном примере.

Необходимо найти НОК сразу трх чисел: 16, 20 и 28.

• Представляем каждое число как произведение его простых множителей:
• Записываем степени всех простых множителей:

16 = 224 = 2^24^1

20 = 225 = 2^25^1

28 = 227 = 2^27^1

• Выбираем все простые делители (множители) с наибольшими степенями, перемножаем их и находим НОК:

НОК = 2^24^15^17^1 = 4457 = 560.

НОК(16, 20, 28) = 560.

Таким образом, в итоге расчета получилось число 560. Оно является наименьшим общим кратным, то есть делится на каждое из трх чисел без остатка.

Наименьшее общее кратное число — это такая цифра, которая разделится на несколько предложенных чисел без остатка. Для того, чтобы такую цифру высчитать, надо взять каждое число и разложить его на простые множители. Те цифры, которые совпадают, убираем. Оставляет всех по одной, перемножаем их между собой по очереди и получаем искомое — наименьшее общее кратное.

НОК, или наименьшее общее кратное , — это наименьшее натуральное число двух и более чисел, которое делится на каждое из данных чисел без остатка.

Вот пример того, как найти наименьшее общее кратное 30 и 42.

• Первым делом нужно разложить данные числа на простые множители.

Для 30 — это 2 х 3 х 5.

Для 42 — это 2 х 3 х 7. Так как 2 и 3 имеются в разложении числа 30, то вычеркиваем их.

• Выписываем множители, которые входят в разложение числа 30. Это 2 х 3 х 5 .
• Теперь нужно домножить их на недостающий множитель, который имеем при разложении 42,а это 7. Получаем 2 х 3 х 5 х 7.
• Находим, чему равно 2 х 3 х 5 х 7 и получаем 210.

В итоге получаем, что НОК чисел 30 и 42 равен 210.

Чтобы найти наименьшее общее кратное , нужно выполнить последовательно несколько простых действий. Рассмотрим это на примере двух чисел: 8 и 12

1. Разлагаем оба числа на простые множители: 8=2*2*2 и 12=3*2*2
2. Сокращаем одинаковые множители у одного из чисел. В нашем случае совпадают 2*2, сократим их для числа 12, тогда у 12 останется один множитель: 3.
3. Находим произведение всех оставшихся множителей: 2*2*2*3=24

Проверяя, убеждаемся, что 24 делится и на 8 и на 12, причем это наименьшее натуральное число, которое делится на каждое из этих чисел. Вот мы и нашли наименьшее общее кратное .

Попробую объяснить на примере цифр 6 и 8. Наименьшее общее кратное — это число, которое можно разделить на эти числа(в нашем случае 6 и 8) и остатка не будет.

Итак, начинаем умножать сначала 6 на 1, 2, 3 и т. д и 8 на 1, 2, 3 и т. д.

Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.

Определение

Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.

НОК — это принятое для обозначения краткое название, собранной из первых букв.

Способы получения числа

Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.

Пример № 1

Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.

Пример № 2

Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:

Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.

Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.

Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:

1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.

2) НОК = 6300.

Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.

Проверка:

6300 / 300 = 21 — верно;

6300 / 1260 = 5 — верно.

Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.

Что значит НОК в математике

Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.

Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:

1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.

2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;

3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;

Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.

Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.

Проверка:

1) 3000 / 250 = 12 — верно;

2) 3000 / 600 = 5 — верно;

3) 3000 / 1500 = 2 — верно.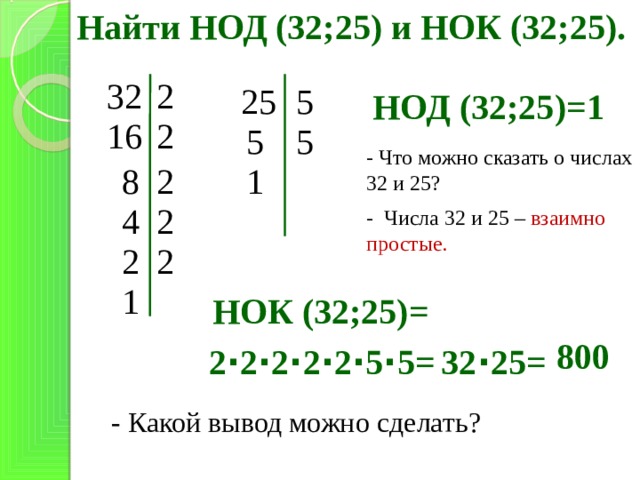

Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.

Еще один способ

В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение. Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.

Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:

1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.

2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.

3) Кратные 42: 84, 126, 168, 210, 252 и т. д.

Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.

Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.

Шаги

Ряд кратных чисел

Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.

• Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.

Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..

• Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.

Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.

• Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.

Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.

• Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.

Разложение на простые множители

1. Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.

   • Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.

2. Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.

   • Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20} и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10} . Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .

3. Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.

   • Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84} , 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42} и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6} . Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .

4. Запишите множители, общие для обоих чисел.

   Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
   • Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times } и зачеркните 2 в обоих выражениях.
   • Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.

5. К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.

   • Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
   • В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} также зачеркнуты обе двойки (2). Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} .

6. Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.

   • Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.

Нахождение общих делителей

1. Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.

   • Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.

2. Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.

   • Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.

3. Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.

   • Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
   • 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.

4. Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.

   • Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.

5. Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.

   • Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
   • 15 ÷ 3 = 5 {\displaystyle 15\div 3=5} , поэтому запишите 5 под 15.

6. Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.

7. Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.

   • Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .

8. Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.

   • Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} . Таким образом, наименьшее общее кратное 18 и 30 равно 90.

Алгоритм Евклида

1. Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.

   • Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2} ост. 3:
     15 – это делимое
     6 – это делитель
     2 – это частное
     3 – это остаток.

Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.

Теорема.

Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК(a, b)=a·b:НОД(a, b) .

Доказательство.

Пусть М – какое-нибудь кратное чисел a и b . То есть, М делится на a , и по определению делимости существует некоторое целое число k такое, что справедливо равенство M=a·k . Но М делится и на b , тогда a·k делится на b .

Обозначим НОД(a, b) как d . Тогда можно записать равенства a=a 1 ·d и b=b 1 ·d , причем a 1 =a:d и b 1 =b:d будут взаимно простыми числами . Следовательно, полученное в предыдущем абзаце условие, что a·k делится на b , можно переформулировать так: a 1 ·d·k делится на b 1 ·d , а это в силу свойств делимости эквивалентно условию, что a 1 ·k делится на b 1 .

Также нужно записать два важных следствия из рассмотренной теоремы.

Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.

Это действительно так, так как любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t .

Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обоснование этого факта достаточно очевидно. Так как a и b взаимно простые, то НОД(a, b)=1 , следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b .

Наименьшее общее кратное трех и большего количества чисел

Нахождение наименьшего общего кратного трех и большего количества чисел можно свести к последовательному нахождению НОК двух чисел. Как это делается, указано в следующей теореме.a 1 , a 2 , …, a k совпадают с общими кратными чисел m k-1 и a k , следовательно, совпадают с кратными числа m k . А так как наименьшим положительным кратным числа m k является само число m k , то наименьшим общим кратным чисел a 1 , a 2 , …, a k является m k .

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Виноградов И.М. Основы теории чисел.
• Михелович Ш.Х. Теория чисел.
• Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.

Наименьшее общее кратное | Методическая разработка по математике (6 класс) по теме:

УРОК 18

21.09.2016г.

«Наименьшее общее кратное»

Цель:

• ввести понятие наименьшего общего кратного;
• формировать навык нахождения наименьшего общего кратного чисел с помощью разложения на простые множители;
• развивать навыки мыслительных операций: анализ синтез, сравнение, обобщение, конкретизации;
• формировать умения высказывать свои мысли, слушать других, вести диалоги, отстаивать свою точку зрения; формировать навыки самооценки.

Тип урока: изучение нового материала и первичное закрепление полученных знаний

Оборудование: компьютер, мультимедийный проектор, доска.

Ход урока

Организационный момент

• Поприветствовать учащихся;
• Проверить санитарно — гигиеническое состояние класса (проветрен ли класс, вымыта доска, наличие мела), если есть не совпадения с санитарно-гигиеническими нормами попросить учеников их исправить вместе с учителем, отметить отсутствующих на уроке.
• Отметить присутствующих на уроке.

Актуализация опорных знаний

1. Даны числа 15, 67, 38, 560, 435, 226, 1000, 3255

— Назовите числа, кратные 2;

— Назовите числа, кратные 5;

— Назовите числа, кратные 10.

2. Назовите все простые числа, удовлетворяющие неравенству 20˂х˂50

3. Что больше, произведение или сумма этих чисел: 0,1,2,3,4,5,6,7,8?

4. Назовите четырехзначное число, записанное с помощью цифр 1,7,5,8, кратное 2, 5, 3

(1578, 1875, 1515.)

5. У Марины было целое яблоко, две половинки и четыре четвертинки. Сколько у нее было яблок?    (3).

– Ребята, а теперь давайте подумаем над такой задачей:

Шаг Коли составляет 45 см, а шаг Вовы 60 см. На каком наименьшем расстоянии они оба сделают по целому числу шагов?

Решение:

Число сантиметров пути должно делиться без остатка и на 45, и на 60, то есть быть кратным 45 и 60.

— Найдем кратные :

45: 45, 90, 135, 180, 225, 270, 315, 360,…

60: 60, 120, 180, 240, 300, 360,…

-Какие кратные общие?

-(ответ) Общие кратные 180, 360.

— Наименьшее кратное 180. Значит, наименьшее расстояние, на котором они сделают целое число шагов 180.

– Так кто же догадался, что мы изучим сегодня на уроке?

Тема: Наименьшее общее кратное

Демонстрация презентации

Определение. (дети записывают в тетрадь)

Наименьшим общим кратным  чисел а и в называется наименьшее натуральное число, которое делится на а и в без остатка.(кратно а и в).

Другой способ нахождения НОКа, без громоздкого перебора кратных чисел:

Разложить числа на простые множители;

Выписать множители, входящие в разложение одного из чисел, добавить к ним недостающие множители из разложений остальных чисел

Найти произведение этих множителей.

60	2
30	2
15	3
5	5
1
45	3
15	3
5	5
1

45=3*3*5

60=2*2*3*5

НОК(45, 60)=3*3*5*2*2=180

— Если из нескольких чисел одно делится на все остальные, то оно и является наименьшим общим кратным. Например: 12, 15, 20 и 60.   НОК=60

Познакомить с алгоритмом нахождения НОК:

1. разложить каждое число на простые множители;
2. выделить множители большего числа;
3. добавить множители меньшего числа, не вошедших в разложение большего числа

Физкультминутка

Отработка навыков

Открываем учебники на стр. 34 № 163, № 165

№ 163

1. НОК (8;12)=24
2. НОК (12;16)=48
3. НОК (6;12)=12
4. НОК (10;21)=210
5. НОК (24;36)=72
6. НОД (6;8;12)=24

№ 165

1. НОД (a;b)=2*3*5=30

НОК (a;b)=2*2*2*3*3*5=360

2. НОД (a;b)=2*2*3=12

НОК(a;b)=2*2*2*2*3*3*3*11*13=61776

Итог урока. Рефлексия.

Домашнее задание п.6 № 164, № 166 стр. 34

№ 164

1. НОК (6;10)=30
2. НОК (9;12)=36
3. НОК (14;28)=28
4. НОК (8;9)=72
5. НОК (32;48)=96
6. НОД (8;9;15)=360

№ 166

1. НОД (a;b)=3*5=15

НОК (a;b)=3*5*5=75

2. НОД (a;b)=2*2*3*3*5*5=900

НОК(a;b)=2*2*2*3*3*3*5*5*5*5=135000

Деление нод и нок онлайн.

Наибольший общий делитель и наименьшее общее кратное. Онлайн калькулятор

Главная > Утепление > Деление нод и нок онлайн. Наибольший общий делитель и наименьшее общее кратное. Онлайн калькулятор

Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.

Определение

Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.

НОК — это принятое для обозначения краткое название, собранной из первых букв.

Способы получения числа

Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.

Пример № 1

Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.

Пример № 2

Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:

Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.

Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.

Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:

1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.

2) НОК = 6300.

Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.

Проверка:

6300 / 300 = 21 — верно;

6300 / 1260 = 5 — верно.

Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.

Что значит НОК в математике

Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.

Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:

1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.

2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;

3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;

Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.

Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.

Проверка:

1) 3000 / 250 = 12 — верно;

2) 3000 / 600 = 5 — верно;

3) 3000 / 1500 = 2 — верно.

Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.

Еще один способ

В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение. Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.

Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:

1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.

2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.

3) Кратные 42: 84, 126, 168, 210, 252 и т. д.

Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Yandex.RTB R-A-339285-1

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Определение 1

Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .

Пример 1

Необходимо найти НОК чисел 126 и 70 .

Решение

Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .

Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .

Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .

Ответ: НОК (126 , 70) = 630 .

Пример 2

Найдите нок чисел 68 и 34 .

Решение

НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .

Ответ: НОК (68 , 34) = 68 .

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Определение 2

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

• составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
• исключаем их полученных произведений все простые множители;
• полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Пример 3

У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .

Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .

Пример 4

Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .

Ответ: НОК (441 , 700) = 44 100 .

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Определение 3

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

• разложим оба числа на простые множители:
• добавим к произведению простых множителей первого числа недостающие множители второго числа;
• получим произведение, которое и будет искомым НОК двух чисел.

Пример 5

Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .

Пример 6

Необходимо вычислить НОК чисел 84 и 648 .

Решение

Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 ​​​​​​ ​.

Ответ: НОК (84 , 648) = 4 536 .

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теорема 1

Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .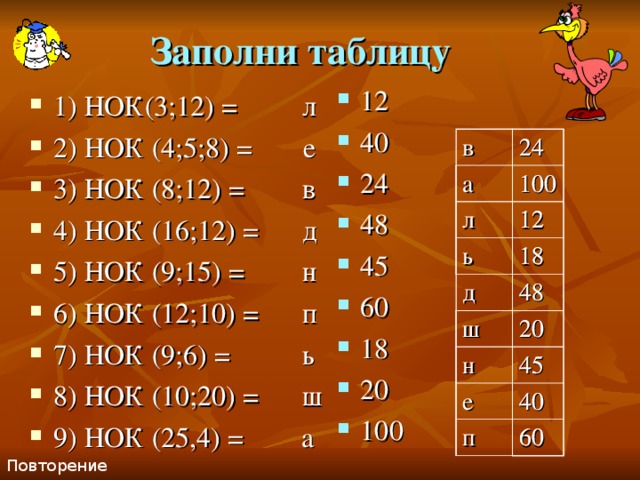

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Пример 7

Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .

Решение

Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .

Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .

Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .

Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .

НОК четырех чисел из условия примера равно 94500 .

Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Определение 4

Предлагаем вам следующий алгоритм действий:

• раскладываем все числа на простые множители;
• к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
• к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
• полученное произведение будет наименьшим общим кратным всех чисел из условия.

Пример 8

Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .

Решение

Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Пример 9

НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .

Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .

Пример 10

Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .

Решение

Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел − 145 и − 45 равно 1 305 .

Ответ: НОК (− 145 , − 45) = 1 305 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Наибольший общий делитель и наименьшее общее кратное — ключевые арифметические понятия, которые позволяют без усилий оперировать обыкновенными дробями. НОК и чаще всего используются для поиска общего знаменателя нескольких дробей.

Основные понятия

Делитель целого числа X — это другое целое число Y, на которое X разделяется без остатка. К примеру, делитель 4 — это 2, а 36 — 4, 6, 9. Кратное целого X — это такое число Y, которое делится на X без остатка. К примеру, 3 кратно 15, а 6 — 12.

Для любой пары чисел мы можем найти их общие делители и кратные. К примеру, для 6 и 9 общим кратным является 18, а общим делителем — 3. Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.

Наименьший делитель не имеет смысла, так как для любого числа это всегда единица. Наибольшее кратное также бессмысленно, так как последовательность кратных устремляется в бесконечность.

Нахождение НОД

Для поиска наибольшего общего делителя существует множество методов, самые известные из которых:

• последовательный перебор делителей, выбор общих для пары и поиск наибольшего из них;
• разложение чисел на неделимые множители;
• алгоритм Евклида;
• бинарный алгоритм.

Сегодня в учебных заведениях наиболее популярными являются методы разложения на простые множители и алгоритм Евклида. Последний в свою очередь используется при решении диофантовых уравнений: поиск НОД требуется для проверки уравнения на возможность разрешения в целых числах.

Нахождение НОК

Наименьшее общее кратное точно также определяется последовательным перебором или разложением на неделимые множители. Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:

НОК (X,Y) = X × Y / НОД(X,Y).

Например, если НОД(15,18) = 3, то НОК(15,18) = 15 × 18 / 3 = 90. Наиболее очевидный пример использования НОК — поиск общего знаменателя, который и является наименьшим общим кратным для заданных дробей.

Взаимно простые числа

Если у пары чисел нет общих делителей, то такая пара называется взаимно простой. НОД для таких пар всегда равен единице, а исходя из связи делителей и кратных, НОК для взаимно простых равен их произведению. К примеру, числа 25 и 28 взаимно просты, ведь у них нет общих делителей, а НОК(25, 28) = 700, что соответствует их произведению. Два любых неделимых числа всегда будут взаимно простыми.

Калькулятор общего делителя и кратного

При помощи нашего калькулятора вы можете вычислить НОД и НОК для произвольного количества чисел на выбор. Задания на вычисление общих делителей и кратных встречаются в арифметике 5, 6 класса, однако НОД и НОК — ключевые понятия математики и используются в теории чисел, планиметрии и коммуникативной алгебре.

Примеры из реальной жизни

Общий знаменатель дробей

Наименьшее общее кратное используется при поиске общего знаменателя нескольких дробей. Пусть в арифметической задаче требуется суммировать 5 дробей:

1/8 + 1/9 + 1/12 + 1/15 + 1/18.

Для сложения дробей выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателей в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь необходимо вычислить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Таким образом, дополнительные множители будут выглядеть как:

• 360/8 = 45
• 360/9 = 40
• 360/12 = 30
• 360/15 = 24
• 360/18 = 20.

После этого умножаем все дроби на соответствующий дополнительный множитель и получаем:

45/360 + 40/360 + 30/360 + 24/360 + 20/360.

Такие дроби мы можем легко суммировать и получить результат в виде 159/360. Сокращаем дробь на 3 и видим окончательный ответ — 53/120.

Решение линейных диофантовых уравнений

Линейные диофантовы уравнения — это выражения вида ax + by = d. Если отношение d / НОД(a, b) есть целое число, то уравнение разрешимо в целых числах. Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.

Проверим уравнение 1320x + 1760y = 10120. Используем калькулятор для нахождения НОД(1320, 1760) = 440. Разделим 10120/440 = 23. В результате получаем целое число, следовательно, диофантово уравнение разрешимо в целых коэффициентах.

Заключение

НОД и НОК играют большую роль в теории чисел, а сами понятия широко используются в самых разных областях математики. Используйте наш калькулятор для расчета наибольших делителей и наименьших кратных любого количества чисел.

Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.

Шаги

Ряд кратных чисел

Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.

• Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.

Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..

• Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.

Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.

• Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.

Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.

• Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.

Разложение на простые множители

1. Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.

   • Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.

2. Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.

   • Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20} и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10} . Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .

3. Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.

   • Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84} , 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42} и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6} . Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .

4. Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).

   • Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times } и зачеркните 2 в обоих выражениях.
   • Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.

5. К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.

   • Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
   • В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} также зачеркнуты обе двойки (2). Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} .

6. Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.

   • Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.

Нахождение общих делителей

1. Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.

   • Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.

2. Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.

   • Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.

3. Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.

   • Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
   • 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.

4. Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.

   • Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.

5. Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.

   • Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
   • 15 ÷ 3 = 5 {\displaystyle 15\div 3=5} , поэтому запишите 5 под 15.

6. Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.

7. Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.

   • Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .

8. Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.

   • Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} . Таким образом, наименьшее общее кратное 18 и 30 равно 90.

Алгоритм Евклида

1. Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.

   • Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2} ост. 3:
     15 – это делимое
     6 – это делитель
     2 – это частное
     3 – это остаток.

НОД и НОК чисел с решением | Наибольший общий делитель и наименьшее общее кратное нескольких чисел

Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.

Калькулятор для нахождения НОД и НОК

Найти НОД и НОК

Найдено НОД и НОК:

Как пользоваться калькулятором

• Введите числа в поле для ввода
• В случае ввода некорректных символов поле для ввода будет подсвечено красным
• нажмите кнопку «Найти НОД и НОК»

Как вводить числа

• Числа вводятся через пробел, точку или запятую
• Длина вводимых чисел не ограничена, так что найти НОД и НОК длинных чисел не составит никакого труда

Что такое НОД и НОК?

Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД.
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК.

Как проверить, что число делится на другое число без остатка?

Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.

Некоторые признаки делимости чисел

1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример: определить, делится ли на 2 число 34938.
Решение: смотрим на последнюю цифру: 8 — значит число делится на два.

2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.

3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример: определить, делится ли число 34938 на 5.
Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.

4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.

Как найти НОД и НОК двух чисел

Как найти НОД двух чисел

Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.

Рассмотрим этот способ на примере нахождения НОД(28, 36):

1. Раскладываем оба числа на множители: 28 = 1·2·2·7, 36 = 1·2·2·3·3
2. Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
3. Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.

Как найти НОК двух чисел

Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.

Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:

1. Находим произведение чисел 28 и 36: 28·36 = 1008
2. НОД(28, 36), как уже известно, равен 4
3. НОК(28, 36) = 1008 / 4 = 252.

Нахождение НОД и НОК для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c).

Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)

Пример: найти НОД и НОК для чисел 12, 32 и 36.

1. Cперва разложим числа на множители: 12 = 1·2·2·3, 32 = 1·2·2·2·2·2, 36 = 1·2·2·3·3.
2. Найдём обшие множители: 1, 2 и 2.
3. Их произведение даст НОД: 1·2·2 = 4
4. Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96.
5. Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3, 36 = 1·2·2·3·3, НОД = 1·2·2·3 = 12.
6. НОК(12, 32, 36) = 96·36 / 12 = 288.

LCM 20, 25 и 60

Калькуляторы Math Learning Resources

1. Главная
2. Math Functions
3. LCM Calculator
4. LCM 20, 25 и 60

LCM 20, 25 и 60 равно 300. Всесторонняя работа дает представление о том, как найти, что больше 300. это lcm 20, 25 и 60 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.

что такое lcm 20, 25 и 60?
lcm (20   25   60) = (?)
20 => 2 x 2 x 5
25 => 5 x 5
60 => 2 x 2 x 3 x 5

= 2 x 2 x 5 x 5 x 3
= 300
lcm (20, 25 и 60) = 300
300 lcm 20, 25 и 60.

где
20 — натуральное число,

19 25 — положительное целое число 300 – это lcm чисел 20, 25 и 60; ,
{5, 3} в {2 x 2 x 5, 5 x 5, 2 x 2 x 3 x 5} — остальные оставшиеся множители 20, 25 и 60.

Использование в математике: НОК 20, 25 и 60
Ниже приведены некоторые математические приложения, где можно использовать МОК 20, 25 и 60:

1. для нахождения наименьшего числа, которое точно делится на 20, 25 и 60.
2. , чтобы найти общие знаменатели для дробей, имеющих 20, 25 и 60 в качестве знаменателей при сложении или вычитании разнородных дробей.

Использование в реальных задачах: 20, 25 и 60 lcm
В контексте задач реального мира lcm, lcm 20, 25 и 60 помогает найти точное время, когда три одинаковых и повторяющихся с разным графиком времени происходят вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуации, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 20 секунд, B звонит через 25 секунд и C повторяется через 60 секунд. Ответ состоит в том, что все колокола A, B и C звонят вместе в 300 секунд в первый раз, в 600 секунд во второй раз, в 9 часов.00 секунд в третий раз и так далее.

Важные примечания: 20, 25 и 60 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 20, 25 и 60:

1. Повторяющиеся и неповторяющиеся простые множители 20, 25 и 60 следует умножить, чтобы найти наименьшее общее кратное 20, 25 и 60, при решении lcm методом простых множителей.
2. Результаты lcm 20, 25 и 60 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.

Для значений, отличных от 20, 25 и 60, используйте этот инструмент ниже:

В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm числа 20, 25 и 60, используя либо метод простых множителей, либо метод специального деления. .

Пример решения с использованием метода простых множителей:
Что такое НОК 20, 25 и 60?

шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 20
B = 25
C = 60

Что нужно найти:
найти lcm числа 20, 25 и 60

шаг 2 Найти простые делители
Простые множители 20 = 2 x 2 x 5
Простые множители 25 = 5 x 5
Простые множители 60 = 2 x 2 x 3 x 5

шаг 3 Определите повторяющиеся и неповторяющиеся простые делители 20, 25 и 60:
{2, 2, 5} — наиболее повторяющиеся множители, а {5, 3} — неповторяющиеся множители 20, 25 и 60.

шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 20, 25 и 60:
= 2 x 2 x 5 x 5 x 3
= 300
lcm(20 и 30) = 300

Следовательно,
lcm 20, 25 и 60 равно 300

Пример решения с использованием специального метода деления:

Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm 20, 25 и 60.

шаг 1 Адресуйте входные параметры, значения и наблюдайте, что нужно найти:
Входные параметры и значения:
Целые числа: 20, 25 и 60

Что нужно найти:
lcm (20, 25, 60) = ?

шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми:
20, 25 и 60

шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (20, 25 и 60), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами. Перенесите целое число на следующую строку, если какое-либо целое число из 20, 25 и 60 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:

2	20	25	60
2	10	25	30
3	5	25	15
5	5	25	5
5	1	5	1
	1	1	1

step 4 Multiply the divisors to find the lcm of 20, 25 и 60:
= 2 x 2 x 3 x 5 x 5
= 300
НОК(20, 25, 60) = 300

Наименьшее общее кратное для трех чисел 20, 25 и 60 равно 300

Калькулятор НОК — наименьшее общее кратное

Калькулятор LCM

Калькулятор LCM из 2 чисел

Работает с целыми числами, дробями, полиномами, вычислениями и т. д.

Номер 1
Номер 2

Подробные пошаговые расчеты

Работает только с натуральными целыми числами

Метод

Вычислить первые кратные каждого числа Использовать разложение на простые множители Найти GDC для вывода НОК

Калькулятор LCM из 3 и более номеров

Работает только с натуральными целыми числами

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

См. также: Кратность числа — Найдите GDC для вывода LCM (наибольшего общего делителя) — Разложение на простые множители

Ответы на вопросы (FAQ)

Что такое LCM? (Определение)

LCM является сокращением от Наименее распространенное кратное из 2 (или более) чисел. Как следует из названия, для двух (отличных от нуля) целых чисел $a$ и $b$ LCM является наименьшим (строго положительным) целым числом, которое одновременно кратно $a$ и кратно $b$.

Как рассчитать LCM? (Алгоритм)

Способ 1: перечислить все кратные и найти наименьшее общее кратное .

Пример: LCM для 10 и 12
10 имеет следующие множители: 0,10,20,30,40,50,60,70 и т. д.
12 имеет следующие множители: 0,12,24,36,48,60,72 и т. д.
Наименьшее общее кратное числа равно 60 .

Метод 2: используйте разложение на простые множители . LCM — это умножение общих множителей на не общие множители

Пример: $ 10 = 2 x 5 $ и $ 12 = 2 x 2 x 3 $
Общие делители: 2 и не общие делители: 2,3,5
LCM(10, 12 ) = $ 2 \times 2 \times 3 \times 5 = 60 $

Метод 3: используйте значение НОД и примените формулу НОД(a, b) = a * b / GCD(a, b)

Пример: НОД(10, 12) = 2
НОД(10, 12) = (10 * 12) / 2 = 60

Как рассчитать НОД с несколькими числами? (LCM из 2 номеров и более)

Способ 1: перечислите все кратные и найдите наименьшее общее кратное .

Пример: LCM для 10, 12 и 15
10 для кратных 0,10,20,30,40,50,60,70 и т.д. 48,60,72 и т. д.
15 имеет для кратных 0,15,30,45,60,75 и т. д.
Наименьшее общее кратное для равно 60. используйте формулу НОК(a,b,c) = НОК( НОК(a,b), c)

Пример: НЦМ(10, 12) = 60
НЦМ(10, 12, 15) = НЦМ ( НЦМ(10, 12) , 15 ) = НЦМ(60,15) = 60

Как вычислить наименьший общий знаменатель дробей?

Чтобы вычислить дроби и/или установить дроби с одинаковым знаменателем, вычислите наименьшее общее кратное знаменателей (дробь под чертой дроби).

Пример: Дроби 7/8 и 15/36, их наименьший общий знаменатель равен НОК(8,36)=72. 9Таким образом, 0019 7/8 можно записать как 63/72, а 15/36 можно записать как 30/72.

Как рассчитать LCM с помощью калькулятора (TI или Casio)?

Калькуляторы обычно имеют функцию для LCM , в противном случае с функцией НОД применяется формула:

$$ \text{L C M}(a, b) = \frac{ a \times b} { \text{G C D} (a, b) } $$

Как рассчитать LCM с нулем 0?

0 не имеет кратного, потому что ни одно число не делится на ноль

Как вычислить НОК с нецелыми числами?

LCM , как это определено математически, не имеет смысла с нецелыми числами. Однако можно использовать и эту формулу: CM(a*c,b*c) = CM(a,b)*c, где CM — общее кратное (не наименьшее) других рациональных чисел.

Пример: CM(1.2,2.4) = CM(12,24)/10 = 2

Что такое НОК для N первых целых чисел?

Следующие числа имеют свойство иметь много делителей, некоторые из них являются очень составными числами.

90(14 LCM ,2,3…7,8)=628006280089739589739504245996706400

LCM(1,2,3)=	6
LCM(1,2,3,4)=	12
LCM(1,2,3,4,5)=	5	5	60
LCM(1,2,3,4,5,6)=	60
LCM(1,2,3…6,7)=	420	840
МОК(1,2,3…8,9)=	2520
МОК(1,2,3…9,10)=	2520
НОКМ(1,2,3…10,11)=	27720
LCM(1,2,3…11,12)=	27720
LCM(1,2,3…12,13)=	360360
LCM(1, 2,3…13,14)=	360360
LCM(1,2,3…14,15)=	360360
LCM(1,2,3…15,164…15,164…15,164…15,164…15,1646 LCM)	720720
LCM (1,2,3… 16,17) =	12252240
LCM (1,2,3… 17,18) =	146146146146146146146146146146146146146146146146146146146146146146146146146146146146146146146146. 2,3…18,19)=	232792560
LCM(1,2,3…19,20)=	232792560
LCM(1,2,3…20,21)=	232792560
LCM (1,2,3…21,22)=	232792560
мл. ) =	5354228880
LCM (1,2,3… 24,25) =	26771144400
LCM (1,2,3 … 3 2665)
(1,2,3… 3 2665)
(1,26145)
(1,26145)
(1,26145
0145
LCM(1,2,3…26,27)=	80313433200
LCM(1,2,3…27,28)=	80313433200
LCM(1,2, 3… 28,29) =	232
LCM (1,2,3… 29,30) =	232
2862800
62800
62800
	62800
	9562800
	9562800.
МОК(1,2,3…31,32)=	144403552893600
МОК(1,2,3…32,33)=	52840330145
LCM (1,2,3… 33,34) =	144403552893600
44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. 3…35,36)=	144403552893600
LCM(1,2,3…36,37)=	5342931457063200
LCM(1,2,3…37,38)=	5342931457063200
МОК(1,2,3…38,39)=	5342931457063200
МОК(1,2,3…39,40)=	5342931457063200
LCM(1,2,3…40,41)=	21
LCM(1,2,3…41,42)=	21
LCM(1,2 ,3…42,43)=	9419588158802421600
LCM(1,2,3…43,44)=	9419588158802421600
LCM(1,2,3…44,45)=	9419588158802421600
LCM(1,2,3…45,46)=	9419588158802421600
LCM(1,2,7)=460145	442720643463713815200
LCM(1,2,3…47,48)=	442720643463713815200
LCM(1,2,3…48,49)=	309

Why the LCM из 2 последовательных чисел кратен 2?

Для любой пары из 2 последовательных чисел одно четное, а другое нечетное, поэтому только одно кратно 2. Согласно методу вычисления НОК путем разложения на простые множители, тогда LCM обязательно кратен 2, что не является общим фактором для 2 чисел.

Почему НОК трех последовательных чисел кратен трем?

Для любой тройки из 3 последовательных чисел только одно из них кратно 3. Согласно методу вычисления НОК посредством разложения на простые множители, тогда МОК обязательно кратно 3, что не является обычным коэффициент для 3 чисел.

В чем разница между LCM и GCD?

LCM является общим кратным 2 чисел, что, следовательно, является большим числом, имеющим в качестве делителя 2 числа.

НОД — это общий делитель двух чисел, который, следовательно, является меньшим числом, кратным двум числам.

LCM и CGD связаны формулой: $$ \text{L C M}(a, b) = \frac{a \times b} { \text{G C D}(a, b) } $$

Зачем рассчитывать LCM?

PPCM — это число, кратное многим, и оно должно быть как можно меньше. Это дает ему большое математическое преимущество и упрощает расчеты.

Пример: Окружность имеет 360°, потому что 360 делится на 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40, 45,60,72,90,120,180,360 что очень практично.

Исходный код

dCode сохраняет за собой право собственности на исходный код «LCM (самый низкий общий множитель)». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «LCM (Lowest Common Multiple)», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или Функции «LCM (Lowest Common Multiple)» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д. ) и все загрузки данных, сценарии или доступ к API для «LCM (самый низкий общий кратный)» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «LCM (самое низкое общее кратное)» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
LCM (самое низкое общее кратное) на dCode.fr [онлайн-сайт], получено 25 сентября 2022 г., https://www.dcode.fr/lcm

Мэтуэй | Популярные проблемы

93-8

1	Фактор
9	Оценить	квадратный корень из 12
10	Оценить	квадратный корень из 20
11	Оценить	квадратный корень из 50	94
18	Оценить	квадратный корень из 45
19	Оценить	квадратный корень из 32
20	Оценить	квадратный корень из 18	92

Произведение GCF и LCM

Когда вы изучали, как найти GCF и LCM двух положительных чисел, вы обнаружили очень интересную связь между двумя величинами?

Я сделал! На самом деле я обнаружил это случайно, когда был молодым студентом, и подумал, что наткнулся на что-то «революционное». Я был так взволнован, что поделился этим со своим учителем. Но, к моему разочарованию, он посмотрел мне в глаза и сказал, что это уже проверенное математическое утверждение. На мгновение я почувствовал себя обескураженным, но вернулся к школьной работе и продолжил.

---

Если вы еще не сталкивались с этим, существует замечательная алгебраическая связь или связь между наибольшим общим делителем (НОК) и наименьшим общим кратным (НОК) двух чисел. В этом уроке нам нужны числа, принадлежащие только множеству положительных целых чисел .

Ниже представлена ​​алгебраическая связь между НОК и НОК двух натуральных чисел.

---

Формула GCF-LCM

ПРЕДУПРЕЖДЕНИЕ. На самом деле не существует такого понятия, как «Формула GCF-LCM». Я просто придумал название для удобства. Вы можете называть его как хотите, пока он служит своей цели.

Проще говоря, наибольший общий делитель чисел a и b при умножении на наименьшее общее кратное чисел a и b равен произведению чисел a и b. То есть a и b — положительные целые числа.

---

Примеры задач

Пример 1: GCF чисел 12 и 16 равен 4 . Что такое LCM 12 и 16 ?

Вы можете определить LCM 12 и 16, используя любой из двух методов, указанных ниже.

• Поиск LCM с использованием метода списка
• Нахождение LCM с использованием метода простой факторизации

Однако есть гораздо более быстрый способ. Вы можете воспользоваться формулой GCF-LCM, потому что знаете два целых числа и их GCF. Просто подставьте значения в формулу, а затем решите LCM.

Я предоставляю вам проверить, что НОК 12 и 16 действительно равен 48.

---

Пример 2: НОК 24 и 40 равен 120 . Что такое GCF 24 и 40 ?

Эта задача полностью противоположна примеру 1, поскольку вам дается значение LCM вместо GCF.

Итак, это информация, которую мы знаем. Разберем их для ясности.

▶︎ НОК(24,40) = 120

▶︎ a=24 и b=40, поэтому ab = \left( {24} \right)\left( {40} \right) = 960

Примечание. на самом деле не имеет значения, какие числа a и b. Это не изменит исход окончательного ответа. Тем не менее рекомендуется стандартизировать решение. Я предлагаю вам позволить a быть меньшим целым числом, а b — большим целым числом.

Давайте подставим известные значения в формулу, а затем найдем НОК 24 и 40.

---

Пример 3: Найдите НГК 20 и 25 , вычислив сначала НОК 20 и 25.

Эта задача будет немного отличаться от примеров №1 и №2. Сначала вам нужно будет вычислить наименьшее общее кратное (НОК) 20 и 25. После этого вы можете найти наибольший общий множитель (НОК) 20 и 25, используя формулу НОК-НОК.

Итак, поехали! Чтобы найти НОК 20 и 25, мы запишем первые несколько кратных 20 и 25. Самое первое общее кратное, которое появится, будет нашим НОК.

Мультипликации 20 : 20, 40, 60, 80, 100 , 120

Множество 25 : 25, 50, 75, 100 , 125, 150

С номером 100 показаны. как первое общее кратное 20 и 25, то мы можем утверждать, что НОК 20 и 25 равно 100.

Теперь у нас есть вся информация для использования формулы. Ниже приведены значения, которые мы собираемся подставить в формулу для решения НОК 20 и 25.

◉ Произведение a и b → ab = \left( {20} \right)\left( {25} \right) = 500

◉ НОК 20 и 25 → НОК\left( {20,25 } \right) = 100

Вот вычисление НОК 20 и 25:

---

Пример 4: Найдите НОК 63 и 84 , вычислив сначала НОК 6 4 84 .

Эта задача очень похожа на пример №3. Единственное отличие состоит в том, что сначала вы будете вычислять GCF, а не LCM, как указано в самой задаче.

Найдем все делители чисел 63 и 84 . Вы можете использовать технику «метода радуги», чтобы разложить заданные целые числа на множители.

Обратите внимание, что наибольший общий множитель между двумя списками равен 21. 3, 4, 6, 7, 12, 14, 21 , 28, 42, 84

Следовательно, наибольший общий делитель чисел 63 и 84 равен 21. Таким образом, GCF\left( {63,84} \right) = 21,

Так как ab = \left( {63} \right)\left( {84} \right) = 5,292 и GCF\left( {63,84} \right) = 21, теперь мы можем подставить эти значения в затем найдите НОК 63 и 84 .

---

Пример 5: Найдите LCM 72 и 90 , используя формулу GCF-LCM.

Как мы уже знаем, мы можем найти НОК двух целых чисел по значению их НОК, используя формулу НОК-НОК.

Перечисление обоих множителей числа 72 и 90 , у нас есть:

Все факторы 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18 , 24, 36, 72

3 Все факторы 9 из 90 : 1, 2, 3, 5, 6, 9, 10, 15, 18 , 30, 45, 90

Сравнивая списки множителей, мы видим, что 18 — это множитель, общий для оба, но имеет наибольшую или наибольшую ценность. Это означает, что GCF 72 и 90 равен 18, то есть GCF\left( {72,90} \right) = 18.

Теперь мы готовы подставить значения ниже в формулу.

❖ ab = \left( {72} \right)\left( {90} \right) = 6,480

❖ GCF\left( {72,90} \right) = 18

Вот вычисление для нахождения LCM, учитывая, что мы уже знаем GCF двух целых чисел и их произведение.

Как найти наименьшее общее кратное

Как найти наименьшее общее кратное — ACT Math

—>

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • MCAT Репетиторство
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский диалект
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочее

  • Бухгалтерский учет
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Мы открыты в субботу и воскресенье!

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Арифметика » Целые числа » Факторы / мультипликаторы » Наименьший общий множитель » Как найти наименьшее общее кратное

Чему равно наименьшее общее кратное чисел 4 и 6?

Возможные ответы:

10

24

16

12

20

Правильный ответ:

12

Объяснение:

12 является наименьшим общим кратным 4 и 6.

Сообщить об ошибке

Каково наименьшее общее кратное 8, 25 и 40?

Возможные ответы:

Правильный ответ:

Пояснение:

Найдите числа, кратные 40, и найдите наименьшее число, которое делится на 8 и 25.

Сообщить об ошибке

Если ab < 96 и b кратно 4, каково максимально возможное значение a ?

Возможные ответы:

23,5

6

12

24

Правильный ответ:

24

Объяснение:

Поскольку мы хотим, чтобы a было как можно больше, мы хотим, чтобы b было как можно меньше. Наименьшее возможное значение b равно 4. Если b равно 4, то мы можем найти a , составив уравнение: Ошибка

Каково наименьшее общее кратное чисел 20, 16 и 32?

Возможные ответы:

320

4

5

160

Правильный ответ: 50 30903 160002 Объяснение:

Наименьшее общее кратное — это наименьшее кратное всех трех чисел. 160 это 32х5, 16х10 и 8х20.

Сообщить об ошибке

Чему равно наименьшее общее кратное  и ?

Возможные ответы:

Не существует наименьшего общего кратного, так как оба числа простые.

Правильный ответ:

Объяснение:

Чтобы найти наименьшее общее кратное двух чисел, если они оба простые, просто перемножьте числа.

Таким образом, мы получаем, что

Мы могли бы также выписать кратные каждого числа и посмотреть, какие числа у них общие. Наименьшим общим кратным будет общее число, которое встречается первым в обоих наборах.

Сообщить об ошибке. Объяснение:

Чтобы найти наименьшее общее умножение, нам нужно найти наименьшее значение, которое является множителем каждого из трех чисел. Мы знаем, что это должно быть даже с коэффициентом два. Если мы посмотрим на значение, наименьшее кратное этого числа равно  Поскольку два других значения также делятся на это число, это наименьшее общее кратное.

Сообщить об ошибке

Нарезанный торт можно поровну разделить между 4, 5 или 6 людьми, при этом каждый получит одинаковое количество кусочков. Какой из следующих ответов представляет возможное количество кусочков, которые могут состоять из торта?

Возможные ответы:

56

24

120

30

116

Правильный ответ:

120

Объяснение:

Если вы разделите варианты ответа на 4, 5 и 6, 120 будет единственным вариантом, который делится без остатка на все три числа.

Сообщить об ошибке.

Уведомление об авторских правах. Гарвардский университет, магистр делового администрирования, бизнес, общие.

Просмотр ACT Репетиторы по математике

Уильям
Сертифицированный репетитор

Салезианский колледж Дона Боско, бакалавр естественных наук. Universidad Rafael Landívar, бакалавр искусств, бизнес-реклама…

View ACT Math Tutors

Александр
Сертифицированный преподаватель

Университет Хьюстона, бакалавр наук, биомедицинская инженерия.

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции

Кратные и обычные кратные — Уроки Wyzant

Кратность — это произведение числа на целое число, или проще говоря, когда вы умножаете
два целых числа вместе. Каждое число имеет бесконечное число кратных. Например, число
кратно 2: 2, 4, 6, 8, 10, 12, 14 и так далее до бесконечности.
вас могут попросить составить список множителей, пока вы не нажмете определенное число (например,
перечислите числа, кратные 2 от 2 до 50), или вас могут попросить указать определенное число кратных
(например, список первые 5 кратных 4). Важная часть
здесь заключается в том, чтобы вы внимательно прочитали инструкции и убедились, что понимаете
что вопрос задает вам, прежде чем вы ответите. Вот несколько примеров:

Назовите первые пять кратных следующих чисел: 3, 6, 9, 10, 7, 12, 50

3: 3, 6, 9, 12, 15

6: 6, 12, 18, 24, 30

9: 9, 18, 27, 36, 45

10: 10, 20, 30, 40, 50

7: 7, 14, 21, 28, 35

12: 12, 24, 36, 48, 60

50: 50, 100, 150, 200, 250

Вы также можете распознать кратность как «считая по» перечисленным выше числам.

Наименее распространенное кратное

Как только вы узнаете, что такое кратные и как их найти, вас часто будут просить
найти «наименьшее общее кратное» между двумя числами. Например, вот как для
вы находите наименьшее общее кратное (НОК) между 4 и 5:

Сначала перечислите кратные каждого числа. Теперь это может продолжаться до бесконечности,
, поэтому мы рекомендуем перечислять только первые 5 кратных каждого числа, а затем продолжать
, если вам нужно.

4: 4, 8, 12, 16, 20

5: 5, 10, 15, 20, 25

Затем подчеркните (или обведите) любые общие для них факторы. Если у них нет
общих делителей, вам нужно продолжать (проверьте следующие пять множителей). Если они
имеют общие кратные, подчеркните их, например:

4: 4, 8, 12, 16, 20

5: 5, 10, 15, 20 , 25

Теперь нужно найти наименьшее общее кратное. В нашем примере у нас есть только одно общее кратное
, так что это наш LCM. Однако, если бы у нас было более одного общего кратного,
, мы бы выбрали наименьшее из них. Следовательно, наш LCM между 4 и 5 равен 20.

Когда бы вы использовали LCM?

Очень редко вас попросят просто найти LCM между двумя числами. Однако
этот процесс особенно полезен для нахождения общих знаменателей. Например,
допустим, у нас была задача 5/8 + 2/5. Сначала нам нужно найти общий знаменатель.
Вот как мы могли бы использовать LCM, чтобы найти общий знаменатель.

Во-первых, нам нужно перечислить кратные каждому из знаменателей в задаче,
8 и 5.

8: 8, 16, 24, 32, 40

5: 5, 10, 15, 20, 25

На данный момент мы не видим общих кратных, поэтому мы перечислим еще 5 для каждых
один:

8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80

5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50

Теперь подчеркнем общие кратные, например:

. 8: 8, 16, 24, 32, 40 , 48, 56, 64, 72, 80

5: 5, 10, 15, 20, 25, 30, 35, 40 , 45, 50

Мы замечаем, что 40 — это наше единственное общее кратное, поэтому для этой задачи это также наш LCM
. Затем вы должны использовать LCM в качестве нового общего знаменателя между
две дроби. Вы бы разложили каждую дробь так, чтобы она имела знаменатель 40
следующим образом:

Затем вы просто сложите две дроби вместе: 25/40 + 16/40 = 41/40. Затем,
, вы должны преобразовать свою дробь в смешанное число (поскольку дробь неправильная)
, и вы получите 1 1/40.

Давайте попробуем еще один пример. На этот раз вы можете попробовать решить ее самостоятельно, а затем
ввести свой ответ в поле ответа, чтобы убедиться, что вы правы!

Вычесть: 7/9 – 5/12

Во-первых, перечислите кратные обоих знаменателей дробей, например:

9: 9, 18, 27, 36, 45

12: 12, 24, 36, 48, 60

Затем подчеркните любые общие кратные:

9: 9, 18, 27, 36 , 45

12: 12, 24, 36 , 48, 60

Мы замечаем, что пока что 36 — это наше единственное общее кратное, поэтому оно также является нашим НОК.

No related posts.