Теория вероятности примеры задач с решением: Математическое Бюро. Страница 404

Теория вероятностей — Основные Формулы и Примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Событие и виды событий

Событие — это базовое понятие теории вероятности. События бывают достоверными, невозможными и случайными.

• Достоверным является событие, которое в результате испытания обязательно произойдет. Например, камень упадет вниз.

• Невозможным является событие, которое заведомо не произойдет в результате испытания. Например, камень при падении улетит вверх.

• Случайным называется событие, которое в результате испытания может произойти, а может не произойти. Например, из колоды карт вытащили туза.

Обычно события обозначают большими латинскими буквами. Например, А — событие, при котором из колоды вытащили туза, D — событие, при котором из колоды вытащили семерку.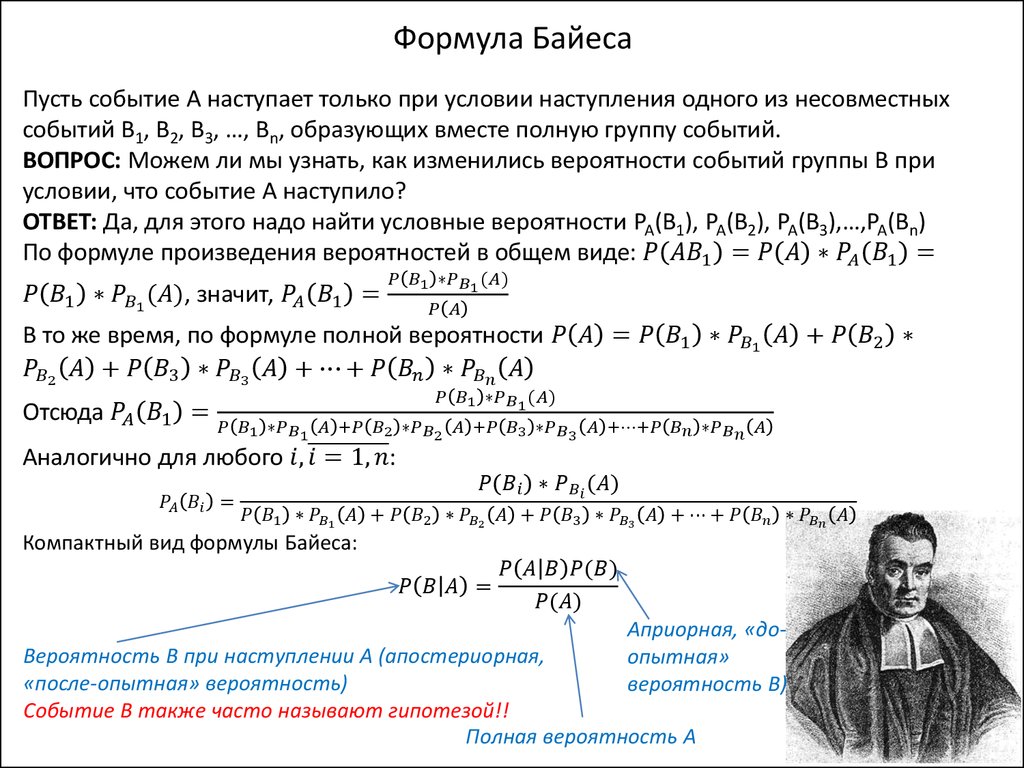

Несовместными называются события, в которых появление одного из событий исключает появление другого (при условии одного и того же испытания). Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с черточкой вверху. Например:

Полная группа событий — это множество несовместных событий, среди которых в результате отдельно взятого испытания обязательно появится одно из этих событий.

Алгебра событий

Операция сложения событий означает логическую связку ИЛИ, а операция умножения событий — логическую связку И.

Сложение событий

Суммой двух событий A и B называется событие A+B, которое состоит в том, что наступит или событие A, или событие B, или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие A, или событие B.

Правило распространяется и на большее количество слагаемых, например, событие A₁ + A₂ + A₃ + A₄ + A₅ состоит в том, что произойдет хотя бы одно из событий A₁, A₂, A₃, A₄, A₅, а если события несовместны — то одно и только одно событие из этой суммы: или событие A₁, или событие A₂, или событие A₃, или событие A₄, или событие A₅.

Примеров масса:

• Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

• Событие B₁,2 = B

  1 + B₂ (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

• Событие B_Ч = B₂ + B₄ + B₆ (будет чётное число очков) состоит в том, что выпадет или 2 , или 4 , или 6 очков.

Умножение событий

Произведением двух событий A И B называют событие AB, которое состоит в совместном появлении этих событий. Иными словами, умножение AB означает, что при некоторых обстоятельствах наступит и событие A, и событие B. Аналогичное утверждение справедливо и для большего количества событий: например, произведение A₁A₂A₃ … A₁₀ подразумевает, что при определенных условиях произойдет

и событие A₁, и событие A₂, и событие A₃,…, и событие A₁₀.

Рассмотрим испытание, в котором подбрасываются две монеты, и следующие события:

• A₁ — на 1-й монете выпадет орел;

• Ā₁ — на 1-й монете выпадет решка;

• A₂ — на 2-й монете выпадет орел;

• Ā₂ — на 2-й монете выпадет решка.

Тогда:

• событие A₁A₁ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орел;

• событие Ā₂Ā₂ состоит в том, что на обеих монетах (на 1-й

  и на 2-й) выпадет решка;

• событие A₁Ā₂ состоит в том, что на 1-й монете выпадет орел и на 2-й монете решка;

• событие Ā₁A₂ состоит в том, что на 1-й монете выпадет решка и на 2-й монете орел.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Классическое определение и формула вероятности

Вероятностью события A в некотором испытании называют отношение:

формулы и примеры решения задач :: SYL.ru

«Случайности не случайны»… Звучит так, словно сказал философ, но на деле изучать случайности удел великой науки математики. В математике случайностями занимается теория вероятности. Формулы и примеры заданий, а также основные определения этой науки будут представлены в статье.

Что такое теория вероятности?

Теория вероятности – это одна из математических дисциплин, которая изучает случайные события.

Чтобы было немного понятнее, приведем небольшой пример: если подкинуть вверх монету, она может упасть «орлом» или «решкой». Пока монета находится в воздухе, обе эти вероятности возможны. То есть вероятность возможных последствий соотносится 1:1. Если из колоды с 36-ю картами вытащить одну, тогда вероятность будет обозначаться как 1:36. Казалось бы, что здесь нечего исследовать и предугадывать, тем более при помощи математических формул. Тем не менее, если повторять определенное действие много раз, то можно выявить некую закономерность и на ее основе спрогнозировать исход событий в других условиях.

Если обобщить все вышесказанное, теория вероятности в классическом понимании изучает возможность возникновения одного из возможных событий в числовом значении.

Со страниц истории

Теория вероятности, формулы и примеры первых заданий появились еще в далеком Средневековье, когда впервые возникли попытки спрогнозировать исход карточных игр.

Изначально теория вероятности не имела ничего общего с математикой. Она обосновывалась эмпирическими фактами или свойствами события, которое можно было воспроизвести на практике. Первые работы в этой сфере как в математической дисциплине появились в XVII веке. Родоначальниками стали Блез Паскаль и Пьер Ферма. Длительное время они изучали азартные игры и увидели определенные закономерности, о которых и решили рассказать обществу.

Такую же методику изобрел Христиан Гюйгенс, хотя он не был знаком с результатами исследований Паскаля и Ферма. Понятие «теория вероятности», формулы и примеры, что считаются первыми в истории дисциплины, были введены именно им.

Немаловажное значение имеют и работы Якоба Бернулли, теоремы Лапласа и Пуассона. Они сделали теорию вероятности больше похожей на математическую дисциплину. Свой теперешний вид теория вероятностей, формулы и примеры основных заданий получили благодаря аксиомам Колмогорова. В результате всех изменений теория вероятности стала одним из математических разделов.

Базовые понятия теории вероятностей. События

Главным понятием этой дисциплины является «событие». События бывают трех видов:

• Достоверные. Те, которые произойдут в любом случае (монета упадет).
• Невозможные. События, что не произойдут ни при каком раскладе (монета останется висеть в воздухе).
• Случайные. Те, что произойдут или не произойдут. На них могут повлиять разные факторы, которые предугадать очень трудно. Если говорить о монете, то случайные факторы, что могут повлиять на результат: физические характеристики монеты, ее форма, исходное положение, сила броска и т. д.

Все события в примерах обозначаются заглавными латинскими буквами, за исключением Р, которой отведена другая роль. Например:

• А = «студенты пришли на лекцию».
• Ā = «студенты не пришли на лекцию».

В практических заданиях события принято записывать словами.

Одна из важнейших характеристик событий — их равновозможность. То есть, если подбросить монету, все варианты исходного падения возможны, пока она не упала. Но также события бывают и не равновозможными. Это происходит, когда кто-то специально воздействует на исход. Например, «меченые» игральные карты или игральные кости, в которых смещен центр тяжести.

Еще события бывают совместимыми и несовместимыми. Совместимые события не исключают появления друг друга. Например:

• А = «студентка пришла на лекцию».
• В = «студент пришел на лекцию».

Эти события независимы друг от друга, и появление одного из них не влияет на появление другого. Несовместимые события определяются тем, что появление одного исключает появление другого. Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.

Действия над событиями

События можно умножать и складывать, соответственно, в дисциплине вводятся логические связки «И» и «ИЛИ».

Сумма определяется тем, что может появиться или событие А, или В, или два одновременно. В случае когда они несовместимы, последний вариант невозможен, выпадет или А, или В.

Умножение событий заключается в появлении А и В одновременно.

Теперь можно привести несколько примеров, чтобы лучше запомнились основы, теория вероятности и формулы. Примеры решения задач далее.

Задание 1: Фирма принимает участие в конкурсе на получение контрактов на три разновидности работы. Возможные события, которые могут произойти:

• А = «фирма получит первый контракт».
• А₁ = «фирма не получит первый контракт».
• В = «фирма получит второй контракт».
• В₁ = «фирма не получит второй контракт»
• С = «фирма получит третий контракт».
• С₁ = «фирма не получит третий контракт».

С помощью действий над событиями попробуем выразить следующие ситуации:

• К = «фирма получит все контракты».

В математическом виде уравнение будет иметь следующий вид: К = АВС.

• М = «фирма не получит ни одного контракта».

М = А₁В₁С₁.

Усложняем задание: H = «фирма получит один контракт». Поскольку не известно, какой именно контракт получит фирма (первый, второй или третий), необходимо записать весь ряд возможных событий:

Н = А₁ВС₁υ АВ₁С₁ υ А₁В₁С.

А₁ВС₁ – это ряд событий, где фирма не получает первый и третий контракт, но получает второй. Соответственным методом записаны и другие возможные события. Символ υ в дисциплине обозначает связку «ИЛИ». Если перевести приведенный пример на человеческий язык, то фирма получит или третий контракт, или второй, или первый. Подобным образом можно записывать и другие условия в дисциплине «Теория вероятности». Формулы и примеры решения задач, представленные выше, помогут сделать это самостоятельно.

Собственно, вероятность

Пожалуй, в этой математической дисциплине вероятность события – это центральное понятие. Существует 3 определения вероятности:

• классическое;
• статистическое;
• геометрическое.

Каждое имеет свое место в изучении вероятностей. Теория вероятности, формулы и примеры (9 класс) в основном используют классическое определение, которое звучит так:

• Вероятность ситуации А равняется отношению числа исходов, что благоприятствуют ее появлению, к числу всех возможных исходов.

Формула выглядит так: Р(А)=m/n.

Р обозначает вероятность события А.

А – собственно, событие. Если появляется случай, противоположный А, его можно записывать как Ā или А₁.

m – количество возможных благоприятных случаев.

n – все события, которые могут произойти.

Например, А = «вытащить карту червовой масти». В стандартной колоде 36 карт, 9 из них червовой масти. Соответственно, формула решения задания будет иметь вид:

Р(А)=9/36=0,25.

В итоге вероятность того, что из колоды вытянут карту червовой масти, составит 0,25.

К высшей математике

Теперь стало немного известно, что такое теория вероятности, формулы и примеры решения заданий, которые попадаются в школьной программе. Однако теория вероятностей встречается и в высшей математике, которая преподается в вузах. Чаще всего там оперируют геометрическими и статистическими определениями теории и сложными формулами.

Очень интересна теория вероятности. Формулы и примеры (высшая математика) лучше начинать изучать с малого — со статистического (или частотного) определения вероятности.

Статистический подход не противоречит классическому, а немного расширяет его. Если в первом случае нужно было определить, с какой долей вероятности произойдет событие, то в этом методе необходимо указать, как часто оно будет происходить. Здесь вводится новое понятие «относительная частота», которую можно обозначить W_n(A). Формула ничем не отличается от классической:

W_n(A)=m/n.

Если классическая формула вычисляется для прогнозирования, то статистическая – согласно результатам эксперимента. Возьмем, к примеру, небольшое задание.

Отдел технологического контроля проверяет изделия на качество. Среди 100 изделий нашли 3 некачественных. Как найти вероятность частоты качественного товара?

А = «появление качественного товара».

W_n(A)=97/100=0,97

Таким образом, частота качественного товара составляет 0,97. Откуда взяли 97? Из 100 товаров, которые проверили, 3 оказались некачественными. От 100 отнимаем 3, получаем 97, это количество качественного товара.

Немного о комбинаторике

Еще один метод теории вероятности называют комбинаторикой. Его основной принцип состоит в том, что если определенный выбор А можно осуществить m разными способами, а выбор В — n разными способами, то выбор А и В можно осуществить путем умножения.

Например, из города А в город В ведет 5 дорог. Из города В в город С ведет 4 пути. Сколькими способами можно доехать из города А в город С?

Все просто: 5х4=20, то есть двадцатью разными способами можно добраться из точки А в точку С.

Усложним задание. Сколько существует способов раскладывания карт в пасьянсе? В колоде 36 карт – это исходная точка. Чтобы узнать количество способов, нужно от исходной точки «отнимать» по одной карте и умножать.

То есть 36х35х34х33х32…х2х1= результат не вмещается на экран калькулятора, поэтому его можно просто обозначить 36!. Знак «!» возле числа указывает на то, что весь ряд чисел перемножается между собой.

В комбинаторике присутствуют такие понятия, как перестановка, размещение и сочетание. Каждое из них имеет свою формулу.

Упорядоченный набор элементов множества называют размещением. Размещения могут быть с повторениями, то есть один элемент можно использовать несколько раз. И без повторений, когда элементы не повторяются. n — это все элементы, m – элементы, которые участвуют в размещении. Формула для размещения без повторений будет иметь вид:

A_n^m=n!/(n-m)!

Соединения из n элементов, которые отличаются только порядком размещения, называют перестановкой. В математике это имеет вид: Р_n = n!

Сочетаниями из n элементов по m называют такие соединения, в которых важно, какие это были элементы и каково их общее количество. Формула будет иметь вид:

A_n^m=n!/m!(n-m)!

Формула Бернулли

В теории вероятности, так же как и в каждой дисциплине, имеются труды выдающихся в своей области исследователей, которые вывели ее на новый уровень. Один из таких трудов — формула Бернулли, что позволяет определять вероятность появления определенного события при независимых условиях. Это говорит о том, что появление А в эксперименте не зависит от появления или не появления того же события в ранее проведенных или последующих испытаниях.

Уравнение Бернулли:

P_n(m)=C_n^m×p^m×q^n-m.

Вероятность (р) появления события (А) неизменна для каждого испытания. Вероятность того, что ситуация произойдет ровно m раз в n количестве экспериментов, будет вычисляться формулой, что представлена выше. Соответственно, возникает вопрос о том, как узнать число q.

q=1-p

Если событие А наступает р количество раз, соответственно, оно может и не наступить. Единица – это число, которым принято обозначать все исходы ситуации в дисциплине. Поэтому q – число, которое обозначает возможность ненаступления события.

Теперь вам известна формула Бернулли (теория вероятности). Примеры решения задач (первый уровень) рассмотрим далее.

Задание 2: Посетитель магазина сделает покупку с вероятностью 0,2. В магазин зашли независимым образом 6 посетителей. Какова вероятность того, что посетитель сделает покупку?

Решение: Поскольку неизвестно, сколько посетителей должны сделать покупку, один или все шесть, необходимо просчитать все возможные вероятности, пользуясь формулой Бернулли.

А = «посетитель совершит покупку».

В этом случае: р = 0,2 (как указано в задании). Соответственно, q=1-0,2 = 0,8.

n = 6 (поскольку в магазине 6 посетителей). Число m будет меняться от 0 (ни один покупатель не совершит покупку) до 6 (все посетители магазина что-то приобретут). В итоге получим решение:

P₆(0)=C₀⁶×p⁰×q⁶=q⁶=(0,8)⁶=0,2621.

Ни один из покупателей не совершит покупку с вероятностью 0,2621.

Как еще используется формула Бернулли (теория вероятности)? Примеры решения задач (второй уровень) далее.

После вышеприведенного примера возникают вопросы о том, куда делись С и р. Относительно р число в степени 0 будет равно единице. Что касается С, то его можно найти формулой:

C_n^m=n!/m!(n-m)!

Поскольку в первом примере m = 0, соответственно, С=1, что в принципе не влияет на результат. Используя новую формулу, попробуем узнать, какова вероятность покупки товаров двумя посетителями.

P₆(2)=C₆²×p²×q⁴ = (6×5×4×3×2×1)/(2×1×4×3×2×1)×(0,2)²×(0,8)⁴=15×0,04×0,4096=0,246.

Не так уж и сложна теория вероятности. Формула Бернулли, примеры которой представлены выше, прямое тому доказательство.

Формула Пуассона

Уравнение Пуассона используется для вычисления маловероятных случайных ситуаций.

Основная формула:

P_n(m)=λ^m/m!×e^(-λ).

При этом λ = n х p. Вот такая несложная формула Пуассона (теория вероятности). Примеры решения задач рассмотрим далее.

Задание 3: На заводе изготовили детали в количестве 100000 штук. Появление бракованной детали = 0,0001. Какова вероятность, что в партии будет 5 бракованных деталей?

Как видим, брак — это маловероятное событие, в связи с чем для вычисления используется формула Пуассона (теория вероятности). Примеры решения задач подобного рода ничем не отличаются от других заданий дисциплины, в приведенную формулу подставляем необходимые данные:

А = «случайно выбранная деталь будет бракованной».

р = 0,0001 (согласно условию задания).

n = 100000 (количество деталей).

m = 5 (бракованные детали). Подставляем данные в формулу и получаем:

Р₁₀₀₀₀₀(5) = 10⁵/5! Х е^-10 = 0,0375.

Так же как и формула Бернулли (теория вероятности), примеры решений с помощью которой написаны выше, уравнение Пуассона имеет неизвестное е. По сути его можно найти формулой:

е^-λ= lim _n->∞(1-λ/n)ⁿ.

Однако есть специальные таблицы, в которых находятся практически все значения е.

Теорема Муавра-Лапласа

Если в схеме Бернулли количество испытаний достаточно велико, а вероятность появления события А во всех схемах одинакова, то вероятность появления события А определенное количество раз в серии испытаний можно найти формулой Лапласа:

Р_n(m)= 1/√npq x ϕ(X_m).

X_m = m-np/√npq.

Чтобы лучше запомнилась формула Лапласа (теория вероятности), примеры задач в помощь ниже.

Задание 4: Рекламный агент раздает 800 листовок. Согласно статистическим исследованиям, каждая третья листовка находит своего потребителя. Какова вероятность того, что сработает ровно 267 рекламных листовок?

n = 800;

m = 267;

p = 1/3;

q = 2/3.

Сначала найдем X_m, подставляем данные (они все указаны выше) в формулу и получим 0,025. При помощи таблиц находим число ϕ(0,025), значение которого 0,3988. Теперь можно подставлять все данные в формулу:

Р₈₀₀(267) = 1/√(800 х 1/3 х 2/3) х 0,3988 = 3/40 х 0,3988 = 0,03.

Таким образом, вероятность того, что рекламная листовка сработает ровно 267 раз, составляет 0,03.

Формула Байеса

Формула Байеса (теория вероятности), примеры решения заданий с помощью которой будут приведены ниже, представляет собой уравнение, которое описывает вероятность события, опираясь на обстоятельства, которые могли быть связаны с ним. Основная формула имеет следующий вид:

Р (А|B) = Р (В|А) х Р (А) / Р (В).

А и В являются определенными событиями.

Р(А|B) – условная вероятность, то есть может произойти событие А при условии, что событие В истинно.

Р (В|А) – условная вероятность события В.

Итак, заключительная часть небольшого курса «Теория вероятности» — формула Байеса, примеры решений задач с которой ниже.

Задание 5: На склад привезли телефоны от трех компаний. При этом часть телефонов, которые изготавливаются на первом заводе, составляет 25%, на втором – 60%, на третьем – 15%. Известно также, что средний процент бракованных изделий у первой фабрики составляет 2%, у второй – 4%, и у третьей – 1%. Необходимо найти вероятность того, что случайно выбранный телефон окажется бракованным.

А = «случайно взятый телефон».

В₁ – телефон, который изготовила первая фабрика. Соответственно, появятся вводные В₂ и В₃ (для второй и третьей фабрик).

В итоге получим:

Р (В₁) = 25%/100% = 0,25; Р(В₂) = 0,6; Р (В₃) = 0,15 – таким образом мы нашли вероятность каждого варианта.

Теперь нужно найти условные вероятности искомого события, то есть вероятность бракованной продукции в фирмах:

Р (А/В₁) = 2%/100% = 0,02;

Р(А/В₂) = 0,04;

Р (А/В₃) = 0,01.

Теперь подставим данные в формулу Байеса и получим:

Р (А) = 0,25 х 0,2 + 0,6 х 0,4 + 0,15 х 0,01= 0,0305.

В статье представлена теория вероятности, формулы и примеры решения задач, но это только вершина айсберга обширной дисциплины. И после всего написанного логично будет задаться вопросом о том, нужна ли теория вероятности в жизни. Простому человеку сложно ответить, лучше спросить об этом у того, кто с ее помощью не единожды срывал джек-пот.

Задачи ОГЭ и ЕГЭ, решаемые по правилам сложения и умножения вероятностей

В открытом банке заданий ОГЭ и ЕГЭ в разделе «Элементы комбинаторики, статистики и теории вероятностей» есть задачи, для решения которых необходимо знать не только классическое определение вероятности, но и правила сложения и умножения вероятностей. Вспомним эти правила и разберем примеры решения задач. Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них (подсказка: по смыслу в тексте задачи такие события можно связать союзом «ИЛИ»). Сумма двух событий обозначается А+В. правило сложения вероятностей несовместных событий А и В (несовместные события не могут произойти одновременно в одном испытании): Р(А+В) = Р(А)+Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В. Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет ( подсказка: по смыслу в тексте задачи такие события можно связать союзом «И»). Произведение двух событий обозначается А*В. правило умножения вероятностей независимых событий А и В (появление одного независимого события не меняет вероятности наступления другого): Р(А*В) = Р(А)*Р(В), где Р(А) – вероятность события А, Р(В) – вероятность события В. Применяем правило сложения вероятностей несовместных событий при решении задач Задача 1. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Окружность», равна 0,21. Вероятность того, что это вопрос по теме «Углы», равна 0,33. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение. События А={школьнику достанется вопрос по теме «Окружность»} и В={школьнику достанется вопрос по теме «Угол»} являются несовместными, то есть не могут произойти одновременно в одном испытании. Событие D={школьнику достанется вопрос по одной из этих двух тем} означает наступление события А или события В, то есть D=А+В. По формуле вероятности суммы двух несовместных событий находим: Р(D)=Р(А+В)=Р(А)+Р(В)= 0,21+0,33=0,54 Задача 2. На тестировании по географии учащийся Петров решает задачи: — вероятность того, что он верно решит больше 10 задач, равна 0,67; — вероятность того, что он верно решит больше 9 задач, равна 0,75. Найдите вероятность того, что Петров верно решит ровно 10 задач. Решение. Рассмотрим события: А={Петров верно решит 10 задач}, Р(А) -? В={Петров верно решит больше 10 задач}, Р(В)=0,67 А и В являются несовместными событиями, тогда наступление события А или события В означает, что {Петров верно решит больше 9 задач}. Это есть сумма событий А+В ={Петров верно решит больше 9 задач}, Р(А+В)=0,75 По формуле вероятности суммы двух несовместных событий: Р(А+В)=Р(А)+Р(В). Отсюда находим Р(А) = Р(А+В) – Р(В) = 0,75-0,67=0,08 Применяем правило умножения вероятностей независимых событий при решении задач Задача 3. Вероятность того, что батарейка бракованная, равна 0,07. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. Решение. Событие А={батарейка исправна} противоположно событию А̄={батарейка бракованная}, Р(А̄)=0,07. Тогда Р(А) = 1-0,07=0,93. Вероятность произведения независимых событий А*А={обе батарейки исправны} (первая батарейка исправна и вторая исправна) находим по правилу: Р(А*А)=Р(А)*Р(А)= 0,93*0,93=0,8649 Задача 4. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых. Решение.Событие А = {Биатлонист попал в мишень} противоположно событию А̄={Биатлонист промахнулся}. Р(А)=0,7, тогда Р(А̄)=1-0,7=0,3. Находим вероятность события В=А*А*А*А̄*А̄, применяя правило умножения вероятностей независимых событий: Р(В)= Р(А)*Р(А)*Р(А)*Р(А̄)*Р(А̄)= 0,7*0,7*0,7*0,3*0,3=0,03087≈0,03. Применяем в одной задаче правила сложения и умножения вероятностей Задача 5. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля. Решение. Событие D={батарейка будет забракована системой контроля} может произойти только в следующих случаях: A = {батарейка неисправна и забракована}, Р(А)=0,02*0,99=0,0198 или В = {батарейка исправна и забракована по ошибке}, Р(В)=(1-0,02)*0,01=0,0098 Поскольку А и В несовместные события, то D=А+В. Тогда: Р(D)=Р(А+В)=Р(А)+Р(В)=0,0198+0,0098=0,0296. Задача 6. Если шахматист А играет белыми фигурами, то он выигрывает у шахматиста Б с вероятностью 0,65. Если А играет черными, то А выигрывает у Б с вероятностью 0,28. Шахматисты играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А выиграет хотя бы одну из партий. Решение. По условию задачи события {А играет белыми и выигрывает} и {А играет черными и выигрывает} являются независимыми. В ситуации, когда шахматисты играют две партии и во второй партии меняют цвет фигур (порядок смены цвета не влияет на результат), возможны следующие исходы: 1. шахматист А выигрывает и белыми, и черными; Р1 = 0,65*0,28=0,182 2. шахматист А выигрывает белыми и проигрывает черными; Р2 = 0,65*(1-0,28)=0,468 3. шахматист А проигрывает белыми и выигрывает черными; Р3 = (1-0,65)*0,28=0,098 4. шахматист А проигрывает белыми и проигрывает черными; Р4 = (1-0,65)*(1-0,28)=0,252 Вероятность события {А выиграет хотя бы одну из партий} находим одним из следующих способов: 1 способ — как вероятность суммы несовместных событий 1, 2, 3: Р = Р1+Р2+Р3=0,182+0,468+0,098=0,748. 2 способ – как вероятность события, противоположного четвертому (заметим, что сумма вероятностей Р1+Р2+Р3+Р4=1): Р = 1-Р4 = 1-0,252=0,748. Другие статьи по данной теме: назад: Операции над событиями. Правила сложения и умножения вероятностей далее: Формула полной вероятности. Формулы Бейеса. Примеры решения задач Список использованных источников Алимов А.Ш., Колягин Ю.М., Ткачева М.В. и др. Алгебра и начала математического анализа. 10-11 классы. Базовый и углубленный уровни / Учебник. — 3-е изд. — М.: Просвещение, 2016; Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004; Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006; Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007; Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008; Яковлев И. В. Комбинаторика-олимпиаднику — MathUs.ru.

Решение простейших задач по теории вероятности

Похожие презентации:

Решение простейших задач по теории вероятности

Решение задач по теории вероятностей. ОГЭ

Статистика и теория вероятностей. Подготовка к решению задач на ОГЭ и ЕГЭ

Решение простейших задач по теории вероятности

Основные понятия теории вероятностей

Теория вероятностей и комбинаторные правила решения задач

Теория вероятностей

Решение простейших задач по теории вероятности

Решение задач по теории вероятности

Простейшие вероятностные задачи

1. Решение простейших задач по теории вероятности

Выполнил студент
группы 1 ИС
Литвинов Даниил

3. Пример задачи по определению вероятности 1. На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет

взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
2. На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает
один пирожок. Найдите вероятность того, что он окажется с вишней.
3. В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность
того, что наугад взятая лампочка из партии будет исправной.
1.Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно
оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас
количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
2.Решение:
3.Решение: Количество исправных лампочек 1000-20=980.
Тогда вероятность того, что взятая наугад лампочка из партии
будет исправной:

5. Теоремы сложения и умножения вероятностей, формулы.

6. Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом

наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям.
Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому
из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных
места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех
вариантов, надо найти произведение, которое обозначается символом 6! и читается «шесть факториал».

7. Примеры решения задач из ЕГЭ по математике на определение вероятности

Задача 1.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67.
Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно
решит ровно 9 задач.
Задача 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов.
Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по
теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Задача 3.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года
равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Пример 1. В корзине 9 красных шаров и 3 синих. Шары различаются только цветом. Наугад (не глядя) достаём один из
них. Какова вероятность того, что выбранный таким образом шар окажется синего цвета?
Решение. Теперь вычислим вероятность выбора синего шара.
Событие А: «выбранный шар оказался синего цвета»
Общее число всех возможных исходов: 9+3=12 (количество всех шаров, которые мы могли бы вытащить)
Число благоприятных для события А исходов: 3 (количество таких исходов, при которых событие А произошло, — то есть,
количество синих шаров)
P(A)=3/12=1/4=0,25
Ответ: 0,25
Пример 2. Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20.
Какова вероятность того, что доклад профессора М. выпадет на третий день, если порядок докладов определяется
жеребьевкой?
Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных
порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора
М. может получить один из 50 номеров. Значит, и элементарных исходов всего 50.
А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть,
последние 20 номеров.
По формуле вероятность P(A)= 20/50=2/5=4/10=0,4
Ответ: 0,4
Пример 3. В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца. Какова вероятность того, что первым
(/вторым/седьмым/последним – не важно) будет выступать француз.
Количество элементарных исходов – количество всех возможных людей, которые могли бы по жеребьевке попасть на
данное место. 5+8+3=16 человек.
Благоприятные исходы – французы. 8 человек.
Искомая вероятность: 8/16=1/2=0,5
Ответ: 0,5
Пример 4. Когда подбрасываем монету, какова вероятность выпадения решки?
Исходов 2 – орел или решка. (считается, что монета никогда не падает на ребро) Благоприятный исход – решка, 1.
Вероятность 1/2=0,5
Ответ: 0,5.
Пример 7. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)
Для одного кубика 6 возможных исходов. Значит, для двух, по вышеупомянутому правилу, 6·6=36.
Какие
исходы
будут
благоприятными
для
того,
чтоб
в
сумме
выпало
10?
10 надо разложить на сумму двух чисел от 1 до 6. Это можно сделать двумя способами: 10=6+4 и 10=5+5. Значит, для
кубиков
возможны
варианты:
(6
на
первом
и
4
на
втором)
(4
на
первом
и
6
на
втором)
(5
на
первом
и
5
на
втором)
Итого,
3
варианта.
Искомая
вероятность:
3/36=1/12=0,08
Ответ: 0,08

English     Русский Правила

Учебные материалы по теории вероятностей для дистанционных занятий со студентами МФТИ



На этой странице нашего сайта размещены электронные версии учебных пособий по теории вероятностей, которые использовались при проведении дистанционных занятий со студентами МФТИ в марте-мае 2020 года во время самоизоляции, вызванной коронавирусной инфекцией.

Для полноты изложения в дополнение к материалам, использованным для проведения дистанционных занятий, мы размещаем на этой странице учебно-методическое пособие «Случайные события и их вероятности. Примеры решения задач», в котором разобраны разделы курса теории вероятностей МФТИ, предшествующие дистанционным занятиям.

Каждое из учебных пособий содержит теоретические сведения и примеры решения типовых задач по изучаемой теме. Практически все разобранные в учебных материалах задачи ранее предлагались для решения студентам МФТИ в заданиях для самостоятельной работы и при приеме зачетов. Необходимая для решения задач теория приводится в справочной форме.

Мы надеемся, что эти учебные материалы будут полезными не только студентам МФТИ, осваивающим теорию вероятностей, но и студентам других ВУЗов.

Учебно-методическое пособие на тему «Случайные события и их вероятности.

Примеры решения задач»

В данном учебно-методическом пособии приведены примеры решения типовых задач, относящихся к материалу, включенному в первое домашнее задание по дисциплинам «Теория вероятностей» и «Основы теории вероятностей».

Разобранные в пособии по каждой теоретической теме задачи расположены в порядке увеличения сложности: от простых задач, призванных наглядно проиллюстрировать теоретический материал, до сложных, выбор которых продиктован желанием представить наиболее широкий спектр методов решения.

Студенты, освоившие методы решения сложных задач, приведенных в пособии, смогут решать и другие сложные задачи по этой тематике, в частности, входящие в их домашние задания.

Содержание

1. Элементы комбинаторики
   • Перестановки
   • Размещения
   • Сочетания
   • Примеры решения задач
2. Понятие вероятностного пространства
   • Множество элементарных исходов
   • Алгебра (сигма-алгебра) событий
   • Вероятность
   • Примеры решения задач
3. Классическое определение вероятности
   • Примеры решения задач
4. Геометрическое определение вероятности
   • Примеры решения задач
5. Теорема сложения вероятностей
6. Формула полной вероятности. Формулы Байеса
   • Условная вероятность
   • Независимость событий
   • Формула полной вероятности. Формулы Байеса
   • Примеры решения задач

Методический материал на тему «Случайные события и их вероятности. Примеры решения задач»

Дистанционное занятие на тему «Случайные величины и их распределения. Примеры решения задач»

Дистанционное занятие посвящено решению задач, связанных с распределениями дискретных и непрерывных случайных величин.

Содержание

1. Понятие случайной величины
2. Борелевские множества
3. Дискретные случайные величины
4. Основные распределения дискретных случайных величин
5. Функция распределения случайной величины
6. Непрерывные случайные величины. Плотность распределения случайной величины
7. Основные распределения непрерывных случайных величин

Методический материал на тему «Случайные величины и их распределения. Примеры решения задач»

Дистанционное занятие на тему «Совместное распределение случайных величин»

Дистанционное занятие посвящено решению задач, связанных с совместными распределениями дискретных и непрерывных случайных величин.

Содержание

1. Совместное распределение нескольких случайных величин
2. Многомерная функция распределения. Многомерная плотность распределения
3. Независимость случайных величин
4. Распределение суммы двух независимых случайных величин

Методический материал на тему «Совместное распределение случайных величин»

Дистанционное занятие на тему «Числовые характеристики случайных величин»

Дистанционное занятие посвящено решению задач, связанных с вычислением математических ожиданий, дисперсий и ковариаций случайных величин.

Содержание

1. Математическое ожидание
2. Дисперсия. Среднее квадратическое отклонение
3. Вычисление числовых характеристик основных распределений
4. Ковариация. Коэффициент корреляции
5. Примеры решения задач

Методический материал на тему «Числовые характеристики случайных величин»

Дистанционное занятие на тему «Неравенство Чебышева. Закон больших чисел. Схема Бернулли»

Дистанционное занятие посвящено решению задач, связанных с применением неравенства Чебышева, закона больших чисел, усиленного закона больших чисел, а также предельных теорем Муавра-Лапласа и Пуассона для схемы Бернулли.

Содержание

1. Неравенство Чебышева
2. Закон больших чисел
3. Схема Бернулли
4. Примеры решения задач
5. Вероятностные таблицы

Методический материал на тему «Неравенство Чебышева. Закон больших чисел. Схема Бернулли»

Дистанционное занятие на тему «Характеристические функции. Центральная предельная теорема»

Дистанционное занятие посвящено решению задач, связанных с вычислением характеристических функций случайных величин и применением аппарата характеристических функций к поиску предельных распределений, а также задач на применение центральной предельной теоремы.

Содержание

1. Характеристическая функция случайной величины
2. Центральная предельная теорема
3. Примеры решения задач

Методический материал на тему «Характеристические функции. Центральная предельная теорема»

Наверх

примеры задач с решением на математические классические формулы комбинаторики Пуассона или Лапласа

События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти.

В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).

Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Основные понятия теории вероятности

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

События А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .

Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.

Вероятность принимает значения на отрезке от 0 до 1, т.е.

Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.

Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные  из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .

Пример задачи из ЕГЭ по математике по определению вероятности

На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?

Решение

Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:

Ответ: 0,4

Независимые, противоположные и произвольные события

Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Теоремы сложения и умножения вероятностей, формулы

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам.

Источник: https://repetitor-mathematics.ru/teoriya-veroyatnosti-formulyi-i-primeryi-resheniya-zadach/

Теория вероятности — формулы нахождения с примерами и решениями

Развитие науки

Изучение вероятности наступления того или иного события берёт своё начало со Средних веков. Первоначально наблюдаемые закономерности не имели математического описания и основывались на различных эмпирических фактах. Ранние работы были непосредственно связаны с азартными играми. Французские учёные Паскаль и Ферма пытались выявить и рассчитать закономерности при бросании костей.

Независимо от них этим вопросом занимался и голландский физик Гюйгенс. В своей работе он оперировал такими понятиями, как величина шанса, математическое ожидание, цена случайности. Он первый, кто попробовал применить теоремы сложения и умножения в описание вероятности.

Фундаментальное значение для развития науки имели труды Бернулли, Байеса, Лапласа и Пуассона. Их стараниями были сформулированы и доказаны предельные теоремы, предложены первые формулы и примеры. В теории вероятности начали использовать анализ ошибочного наблюдения. Но лишь Карл Гаусс детально смог разобраться в нормальном распределении случайной величины.

В XIX веке русские и европейские учёные смогли доказать сделанные ранее предложения. В первую очередь это касалось закона больших чисел и центральной предельной теоремы. Формальная система для описания теории была принята в 1933 году.

Предложил её академик СССР Андрей Колмогоров. Руководствуясь идеями теории множеств, меры и интегрирования, он смог систематизировать аксиомы и с их помощью описать классическую теорию вероятности.

На основании его работ была создана новая теория — случайных процессов.

В его систему входит:

• алгебра событий — состоит из множества подмножеств, называемых событиями и их пространства;
• существование возможности появления событий — каждому случаю приписывается в соответствие вещественная вероятность наступления;
• нормировка — состояние, при котором вещественное число имеет вероятность свершения равное единице;
• аддитивность — если 2 события не пересекаются, их вероятность находится суммированием.

Объекты, удовлетворяющие системе, были названы полем вероятности (вероятностным пространством). Было принято, что аксиомы не могут противоречить друг другу. Аксиоматизация позволила привести все предположения к строгому математическому виду и стала восприниматься как один из разделов математического вычисления.

Предметом изучения науки являются закономерности, появляющиеся в случайных событиях, результат которых нельзя установить заранее. Но не все эксперименты можно изучать с помощью теории, а лишь те, что повторяются при одних и тех же условиях. Существует понятие «статистической устойчивости».

Если существует некоторое событие «А», которое может наступить в результате события или не произойти, то часть экспериментов должна стабилизироваться.

При этом с увеличением числа экспериментов вероятность повторения стремится к определённому числу Р(А). Оно и является характеристикой, определяющей степень возможности наступления события «А».

Объяснить основы теории вероятности для чайников можно с помощью классических понятий:

1. Вероятность, что событие «А» сможет произойти описывается выражением: Р (А) = m/n, где: n — общее количество исходов эксперимента, имеющих равные возможности; m — число исходов, соответствующих событию «А».
2. Для геометрического определения вместо чисел используется мера. В числитель формулы подставляется показатель, выражающий количество благоприятных исходов наступления рассматриваемого события, а в знаменатель — геометрическая мера. Например, ширина, плотность, объём.
3. При расчётах принимается, что полная группа событий образует вероятность равную единице: P (A1) + P (A2) + + P (An) = 1, при этом сумма противоположных событий также будет равна одному.
4. Шанс, что одно из двух несовместимых событий обязательно случится, определяется сложением этих вероятностей. Это формулировка справедлива и к любому количеству ожидаемых исходов: P (C +B +A) = Р(С) + Р (B) +P (A).
5. Исход, что любое из двух событий сбудется, равен вероятности суммы без учёта возможного их совместного появления: P (А+В) = Р (А) + Р (B) — P (АВ).

Основополагающими формулами являются выражения Байеса и Бернулли.

Согласно первому, если существует гипотеза «Вн», а событие уже наступило, вероятность её правдивости определяется как Pа (Вн) = Р (Вн) * Рв (А) / Р (А). Это выражение ещё называют формулой полной вероятности. Равенство же Бернулли помогает оценить вероятность, что конкретное событие «А» случится n количество раз при m вариантах: P = C n * p n * qn — m.

Алгоритм решения

Теория вероятностей используется, когда необходимо сделать прогноз на выпадение того или иного шанса в эксперименте. Случайность является основным понятием предмета.

Она обозначает явление, для которого невозможно точно вычислить периодичность наступления, поэтому в задачах находят именно число возможностей.

По своей сути вероятность — функция, способная принимать 3 значения:

• ноль — ожидание никогда не выполнится;
• единица — событие произойдёт при любых условиях;
• паритет — существует равная возможность выполнения или невыполнения ожидания.

Чтобы высчитать случайность, рекомендуется придерживаться разработанного алгоритма. Следует внимательно изучить задание и определить, вероятность чего необходимо вычислить, а также события, от которых случайность будет изменяться.

Определив схему задачи, подобрать формулу и, подставив в неё все имеющиеся данные, рассчитать шанс.

Чтобы правильно определиться с нужной схемой, необходимо знать о количестве экспериментов, существовании между ними зависимости, возможности применения нескольких гипотез.

Для понятия принципа нахождения случайности часто предлагается к решению следующая задача. В закрытом ящике лежит 6 разноцветных перемешанных между собой шаров. Из них 2 красного цвета, 3 зелёного и 1 белый. Нужно посчитать, насколько шансов достать белый шар меньше, чем цветной.

Случайность доставания цветного шара обозначают как событие «А». Согласно определению вероятность «А» определяется отношением благоприятствующих шансов к общему числу исходов.

Существует 6 различных возможностей вытянуть шар, из них 5 относятся к благоприятным, поэтому эксперимент покажет, что вероятность достать из ящика цветной шар будет составлять P = 5 / 6 = 0,83(3).

Это и есть показатель оценки степени случайности.

Таким способом можно узнать различную вероятность любого исхода, не прибегая к собиранию статистики и её анализу, то есть решить задачу математически, как, например, следующую.

В таксопарке используется 2 синих, 9 красных и 4 чёрных машины. Нужно определить, какая существует возможность приезда по вызову красного автомобиля. Решение простое.

Так как всего имеется 15 машин, вероятность приезда именно красной составит Р = 9/15 или 0,6.

Теорема Муавра — Лапласа

Это предельное определение, предложенное Лапласом в 1812 году. В основе теоремы используется формула Бернулли, но применяется она к довольно большому количеству экспериментов.

Суть её в следующем: если при независимых экспериментах n существует вероятность свершения случайного события N равная нулю или единице, при этом число испытаний равняется m, искомое значение близко к интегральной функции Лапласа.

Стандартные значения, соответствующие нормальному распределению, сведены в статистические таблицы. Взять их можно в решебниках задач по теории. Под приведёнными значениями понимается площадь кривой от нуля до числа x. Например, если придумать какую-либо величину площади между числами 0 и 2,34, согласно таблице она составит 0,49036.

При рассмотрении свершения m событий в n экспериментах существует вероятность, заключённая в определённом отрезке между значениями a и b, поэтому выражение для нахождения можно найти из формулы: Р(m) = (n! * pm * qn-m) / m!(n-m)!.

Уравнение требует сложных и громоздких расчётов, поэтому, чтобы найти вероятность, в математике из формулы используют асимптотическое распределение.

Но возможно это только при условии, что Р(m) неизменное, а число экспериментов будет стремиться к бесконечности.

Реальная формула, описывающая теорему сложна, поэтому используется приближённая:

Р(m) = 1 / ((2p*n*p*q)1/2) exp (-X2m/2).

Использовать её рекомендуют только при значениях событий больше 20, а экспериментов 100. Например, брак выпускаемых изделий составляет 15%. Поступает товар в упаковках по 100 штук. Нужно найти вероятность, что случайно взятая коробка будет укомплектована 13 бракованными изделиями. При этом число товара низкого качества в упаковке не превысит 20.

За испытание необходимо принять изготовление. Вероятность появления события, которое необходимо искать составит p = 0,15. Далее, находится случайность: n * p = 15 и n * p * q = 12,75. Таким образом, примерно 9,5% упаковок от общего количества содержат 13 товаров плохого качества, а в 92% случаях число изделий с браком не превышает 20.

Сочетание взаимных событий

При рассмотрении задач может возникнуть вопрос, как различные события могут зависеть друг от друга. Для характеристики их взаимосвязи вводится понятие условная вероятность. Например, имеются 2 случайных исхода одного эксперимента «А» и «В». Тогда условной вероятностью первого события «А» при условии, что второе произошло, называется отношение P (AB) / P (B).

Необходимо определить, с какой вероятностью в семье с ребёнком-девочкой родится мальчик. За вероятность появления в семье двух мальчиков нужно взять «А», а за ребёнка противоположного пола событие «В».

Существует 4 возможных исхода, поэтому справедливо будет записать: P (AB) = 1/4, P(B) = 3/4. Подставив эти значения в формулу можно рассчитать вероятность: P (A/B) = (1/4) / (3/4) = 0,3.

Первый исход считается независимым от второго, если наступление события «В» не оказывает влияние.

Если же события взаимны, они влияют друг на друга. В этом случае используется их перемножение: P(AB) = P(A) *PB (А). Например, в пачке 26 лотерей, из которых 3 призовых. Нужно определить шанс, что первый билет будет призовой и вероятность, что второй билет также будет с выигрышем, но при условии, что первый билет уже убрали.

Для решения задачи вначале нужно найти шанс, что первый билет будет с выигрышем: P (A) = 3/26 = 0,115. Затем рассчитать вероятность двух выигрышей подряд: P(AB) = P(A) * P(B) = (3/26) * (2/25) = 0,009.

Это довольно простые задачи, но существуют задания, для решения которых понадобится применять несколько формул. Такой расчёт вероятности наступления того или иного события может быть трудным, требующим повышенного внимания.

Источник: https://nauka.club/matematika/algebra/teoriya-veroyatnosti.html

Теорема Байеса Проблемы, определение и примеры

Что такое теорема Байеса?

Посмотрите видео с кратким примером решения задачи по теореме Байеса:

Пример №1 по теореме Байеса

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Теорема Байеса — это способ вычислить условную вероятность. Условная вероятность — это вероятность того, что событие произойдет, при условии, что оно связано с одним или несколькими другими событиями. Например, ваша вероятность получить парковочное место зависит от времени суток, когда вы паркуетесь, где вы паркуетесь и какие соглашения происходят в любое время. Теорема Байеса немного более тонкая. В двух словах, это дает вам фактическую вероятность событие предоставило информацию о тестах .

• «События» Отличаются от «тестов». Например, существует тест на заболевание печени, но он отличается от события фактического наличия заболевания печени.
• Тесты ошибочны : только потому, что у вас положительный тест, не означает, что вы действительно больны. Многие тесты имеют высокий уровень ложноположительных результатов. Редкие события, как правило, имеют более высокий уровень ложноположительных результатов , чем более распространенные события. Мы говорим здесь не только о медицинских тестах. Например, фильтрация спама может иметь высокий уровень ложных срабатываний. Теорема Байеса берет результаты теста и вычисляет ваши реальная вероятность того, что тест идентифицировал событие.

Формула

Теорема Байеса (также известная как правило Байеса) — это обманчиво простая формула, используемая для расчета условной вероятности. Теорема названа в честь английского математика Томаса Байеса (1701-1761). Формальное определение правила:

В большинстве случаев вы не можете просто подставить числа в уравнение; Вы должны выяснить, что ваши «тесты» и «события» в первую очередь. Для двух событий, A и B, теорема Байеса позволяет вычислить p(A|B) (вероятность того, что событие A произошло при условии, что тест B был положительным) из p(B|A) (вероятность того, что тест B произошло, если произошло событие А). Это может быть немного сложно понять, поскольку технически вы работаете в обратном направлении; вам, возможно, придется переключать свои тесты и события, что может привести к путанице. Пример должен пояснить, что я имею в виду под «поменять местами тесты и события».

Теорема Байеса Пример #1

Вам может быть интересно узнать вероятность заболевания печени у пациента, если он алкоголик. «Быть ​​алкоголиком» — это тест (что-то вроде лакмусовой бумажки) на заболевание печени.

• Код может означать событие «У пациента заболевание печени». Прошлые данные говорят вам, что 10% пациентов, поступающих в вашу клинику, имеют заболевание печени. Р(А) = 0,10.
• B может означать лакмусовую бумажку, что «Пациент — алкоголик». Пять процентов пациентов клиники — алкоголики. Р(В) = 0,05.
• Возможно, вы также знаете, что среди пациентов с диагнозом заболевания печени 7% составляют алкоголики. Это ваш B|A: вероятность того, что пациент алкоголик, при условии, что у него заболевание печени, составляет 7%.

Теорема Байеса говорит вам:
P(A|B) = (0,07 * 0,1)/0,05 = 0,14
Другими словами, если пациент алкоголик, его шансы заболеть болезнью печени составляют 0,14 (14%). ). Это большое увеличение по сравнению с 10%, которые предполагались в прошлых данных. Но по-прежнему маловероятно, что у какого-либо конкретного пациента есть заболевание печени.

Дополнительные примеры теоремы Байеса

Пример задач по теореме Байеса № 2

Другой способ взглянуть на теорему — сказать, что одно событие следует за другим. Выше я сказал «испытания» и «события», но также правомерно думать об этом как о «первом событии», которое ведет ко «второму событию». Не существует единственно правильного способа сделать это: используйте терминологию, которая кажется вам наиболее понятной.

В конкретной клинике боли 10% пациентов прописывают наркотические обезболивающие. В целом, пять процентов пациентов клиники пристрастились к наркотикам (включая обезболивающие и запрещенные вещества). Из всех людей, прописавших обезболивающие, 8% являются наркоманами. Если пациент наркоман, какова вероятность того, что ему пропишут обезболивающие?

Шаг 1: Выясните, какое у вас событие «А», из вопроса. Эта информация выделена курсивом в этом конкретном вопросе. Событие, которое происходит первым (А), — это назначение болеутоляющих таблеток. Это указано как 10%.

Шаг 2: Выясните, какое у вас событие «Б», из вопроса. Эта информация также выделена курсивом в этом конкретном вопросе. Событие Б — стать наркоманом. Это указано как 5%.

Шаг 3: Определите, какова вероятность события B (Шаг 2) при заданном событии A (Шаг 1) . Другими словами, найдите, что такое (B|A). Мы хотим знать: «Учитывая, что людям прописывают обезболивающие, какова вероятность того, что они наркоманы?» Это указано в вопросе как 8%, или 0,8.

Шаг 4: Вставьте ответы из шагов 1, 2 и 3 в формулу и решите.
P(A|B) = P(B|A) * P(A) / P(B) = (0,08 * 0,1)/0,05 = 0,16

Вероятность того, что наркоману пропишут обезболивающие, равна 0,16 (16). %).

Пример #3: Медицинский тест

Немного более сложный пример включает медицинский тест (в данном случае генетический тест):

Существует несколько форм теоремы Байеса , и все они эквивалентны (они просто пишутся немного по-разному). В следующем уравнении «X» используется вместо «B». Кроме того, вы увидите некоторые изменения в знаменателе. Доказательство того, почему мы можем перестроить уравнение таким образом, выходит за рамки этой статьи (иначе это было бы 5000 слов вместо 2000!). Однако, если вы столкнетесь с вопросом, связанным с медицинскими тестами, вы, вероятно, будете использовать эту альтернативную формулу, чтобы найти ответ:

Посмотрите видео с примером теоремы Байеса:

Пример теоремы Байеса

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

1% людей имеют определенный генетический дефект.
90% тестов на ген выявляют дефект (истинно положительные результаты).
9,6% тестов ложноположительны.
Если человек получает положительный результат теста, каковы шансы, что у него действительно есть генетический дефект?

Первым шагом в решении задач теоремы Байеса является присвоение событиям букв:

• A = вероятность наличия дефектного гена. В вопросе это было указано как 1%. Это также означает, что вероятность того, что , а не имеют ген (~A), составляет 99%.
• X = положительный результат теста.

Итак:

1. P(A|X) = вероятность того, что ген даст положительный результат теста.
2. P(X|A) = Вероятность положительного результата теста при условии, что у человека действительно есть ген. Это было указано в вопросе как 90%.
3. p(X|~A) = Вероятность положительного результата теста, если человек не имеет гена . Это было указано в вопросе как 9,6%

Теперь у нас есть вся информация, которую нужно ввести в уравнение:
P(A|X) = (0,9 * 0,01) / (0,9 * 0,01 + 0,096 * 0,99) = 0,0865 (8,65 %).

Вероятность наличия дефектного гена в тесте составляет 8,65%.

Задачи по теореме Байеса № 4: тест на рак

В своем посте о неправильном чтении результатов маммографии я писал о том, как сложно врачи считают вероятность и статистику ошибочными. Неудивительно, что врачи ошибаются в своей интерпретации результатов, учитывая, что в игру вступают некоторые хитрые вероятности. Вот второй пример того, как работает теорема Байеса. Я использовал похожие числа, но вопрос сформулирован по-другому, чтобы дать вам еще одну возможность обдумать, как вы решаете, какое событие является событием А, а какое событием X.

В. Учитывая следующие статистические данные, какова вероятность того, что у женщины рак, если у нее положительный результат маммографии?

• У одного процента женщин старше 50 лет рак молочной железы.
• Девяносто процентов женщин с раком молочной железы дают положительный результат на маммограмме.
• У восьми процентов женщин будут ложные срабатывания.

Шаг 1: Назначьте события A или X. Вы хотите знать, какова вероятность того, что женщина заболеет раком, при положительном результате маммографии. Для этой проблемы фактическое наличие рака — это А, а положительный результат теста — Х.
Шаг 2: Перечислите части уравнения (это облегчает работу с фактическим уравнением):
P(A)=0,01
P(~A)=0,99
P(X|A)=0,9
P( X|~A)=0,08
Шаг 3: Вставьте части в уравнение и решите. Обратите внимание, что поскольку это медицинский тест, мы используем форму уравнения из примера № 2:
(0,9 * 0,01) / ((0,9 * 0,01) + (0,08 * 0,99) = 0,10.

Вероятность женщина, больная раком, при положительном результате теста составляет 10%.0016 Вот еще одно уравнение, которое вы можете использовать, чтобы решить вышеупомянутую проблему. Вы получите точно такой же результат:

Основное отличие этой формы уравнения в том, что в нем используются члены вероятности пересечение (∩) и дополнение ( ^c ). Думайте об этом как о сокращении: это одно и то же уравнение, записанное по-другому.

Чтобы найти вероятности в правой части этого уравнения, используйте правило умножения:

P(B ∩ A) = P(B) * P(A|B)

Две части уравнения эквивалентны, и P(B) * P(A|B) — это то, что мы использовали при решении числитель в задаче выше.
P(B) * P(A|B) = 0,01 * 0,9 = 0,009

В знаменателе мы имеем P(B ^c ∩ A) как часть уравнения. Это можно (эквивалентно) переписать как P(B ^c *P(A|B ^c ). Это дает нам:
P(B ^c *P(A|B ^c ) = 0,99 * 0,08 = 0,0792.

Подставляя эти два решения в формулу, получаем:
0,009 / (0,009 + 0,0792) = 10%.

Проблемы теоремы Байеса: другой взгляд на это.

Проблемы теоремы Байеса можно решить без с помощью уравнения (хотя использование уравнения, вероятно, проще). Но если вы не можете понять, почему это уравнение работает (или что оно делает), вот неуравненное решение той же проблемы в № 1 (задача генетического теста) выше.

Шаг 1: Найдите вероятность истинно положительного результата теста. Это равняется количеству людей, у которых действительно есть дефект (1 %), * истинно положительным результатам (9 %).0%) = 0,009.

Шаг 2: Найдите вероятность ложноположительного результата теста. Это равняется людям, у которых нет дефекта (99%) * ложноположительные результаты (9,6%) = 0,09504.

Шаг 3: Рассчитайте вероятность получения положительного результата теста. Это равно вероятности истинного положительного результата (Шаг 1) плюс ложноположительный результат (Шаг 2) = 0,009 + 0,09504 = 0,0,10404.

Шаг 4: Найти вероятность наличия гена при положительном результате. Разделите шанс получения реального положительного результата (шаг 1) на шанс получения какого-либо положительного результата (шаг 3) = 0,009./0,10404 = 0,0865 (8,65%).

Другие формы теоремы Байеса

Теорема Байеса имеет несколько форм. Вы, вероятно, не столкнетесь ни с одной из этих других форм в классе элементарной статистики. Разные формы могут использоваться для разных целей. Например, в одной из версий используется то, что Рудольф Карнап назвал «отношением вероятностей ». Правило отношения вероятностей гласит, что любое событие (например, пациент с заболеванием печени) должно быть умножено на этот коэффициент PR(H,E)=P _E (H)/P(H). Это дает вероятность события, зависящую от E. Правило отношения шансов очень похоже на отношение вероятностей, но отношение правдоподобия делит долю истинно положительных результатов теста на долю его ложноположительных результатов. Формальное определение правила отношения шансов: OR(H,E)=P _H, (E)/P _{~ H} (E).

Байесовская фильтрация спама

Хотя теорема Байеса широко используется в медицинских науках, у нее есть и другие применения. Например, он используется для фильтрации спама. Событие в этом случае означает, что сообщение является спамом. тест на спам заключается в том, что сообщение содержит некоторые помеченные слова (например, «виагра» или «вы выиграли»). Вот составленное уравнение (из Википедии), которое читается как «Вероятность сообщения как спама при условии, что оно содержит определенные помеченные слова»:

Реальные уравнения, используемые для фильтрации спама, немного сложнее; они содержат больше флагов, чем просто содержимое. Например, время отправки сообщения или частота просмотра фильтром одного и того же содержимого — это два других теста на спам.

Следующий : Обратное распределение вероятностей

Ссылки

Dodge, Y. (2008). Краткая энциклопедия статистики. Спрингер.
Эверитт, Б.С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Задачи по теореме Байеса, определение и примеры» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/probability-main-index/bayes-theorem-problems/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Задачи по теории вероятностей, математической статистике и теории случайных функций — Свешников А. А. Свешникова.

Студенты всех уровней изучения теории вероятностей и теории статистики найдут в этой книге широкий и глубокий анализ задач (и их решений), начиная от простейших комбинаторных вероятностных задач на конечных выборочные пространства с помощью теории информации, предельных теорем и использования моментов.
Введение к разделам в каждой главе устанавливает основные формулы и обозначения и дает общий набросок той части теории, которая должна быть охвачена последующими проблемами. Каждой группе задач предшествуют типичные примеры и их решения, выполненные очень подробно. Каждый из них связан с самими проблемами, так что учащийся, ищущий руководства в решении проблемы, может, проверив примеры, обнаружить подходящую технику, необходимую для решения.

Книга была переведена с русского компанией Scripta Technica под редакцией Бернарда Гелбаума и опубликована в 1968 году.

Авторы, загрузившие оригинал.

Вы можете получить книгу здесь.

Следите за нами в Интернет-архиве: https://archive.org/details/@mirtitles

Следуйте за нами в Twitter: https://twitter.com/MirTitles

Пишите нам: [email protected]

Разветвите нас в GitLab: https://gitlab.com/mirtitles/

Добавьте новые записи в подробный каталог книг здесь.

 

I. СЛУЧАЙНОЕ СОБЫТИЕ 1

1. Отношения между случайными событиями l
2. Прямой метод оценки вероятностей 4
3. Геометрические вероятности 6
4. Условная вероятность. Теорема умножения вероятностей 12
5. Теорема сложения вероятностей 16
6. Формула полной вероятности 22
7. Вычисление вероятностей гипотез после испытания (формула Байеса) 26
8. Оценка вероятностей появления событие в повторных независимых испытаниях 30
9. Полиномиальное распределение. Формулы рекурсии. Генерирующие функции 36

II. СЛУЧАЙНЫЕ: ПЕРЕМЕННЫЕ 43

10. Ряд распределения вероятностей, полигон распределения и функция распределения дискретной случайной величины 43
11. Функция распределения и функция плотности вероятности непрерывной случайной величины 48
12. Численные характеристики дискретной случайной величины случайные величины 54
13. Численные характеристики непрерывных случайных величин 62
14. Закон Пуассона 67
15. Нормальный закон распределения 70
16. Характеристические функции 74
17. Вычисление полной вероятности и плотности вероятности через условную вероятность 80

III. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН 84

18. Законы распределения и числовые характеристики систем случайных величин 84
19. Нормальный закон распределения на плоскости и в пространстве. Многомерное нормальное распределение 91

20. Законы распределения подсистем непрерывных случайных величин и условные законы распределения 99

IV. ЧИСЛЕННЫЕ ХАРАКТЕРИСТИКИ И ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН 107

21. Численные характеристики функций случайных величин .107
22. Законы распределения функций случайных величин. 115
23. Характеристические функции систем и функции случайных величин 124
24. Свертка законов распределения 128
25. Линеаризация функций случайных величин 136
26. Свертка двумерных и трехмерных нормальных законов распределения с помощью понятия отклонения 145

V. ЭНТРОПИЯ И ИНФОРМАЦИЯ 157

27. Энтропия случайных событий и величин 157
28. Количество информации 163

VI. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 171

29. Закон больших чисел 171
30. Теоремы де Муавра-Лапласа и Ляпунова 176

 

VII. КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ФУНКЦИЙ 181

31. Общие свойства корреляционных функций и законы распределения случайных функций 181
32. Линейные операции со случайными функциями. 185
33. Задачи на переходы 192
34. Спектральное разложение стационарных случайных функций. 198
35. Расчет вероятностных характеристик случайных функций на выходе динамических систем 205
36: Оптимально-динамические системы 216
37: Метод огибающих 226

VIII.

МАРКОВСКИЕ ПРОЦЕССЫ 231

38. Марковские цепи 231
39. Марковские процессы с дискретным числом состояний 246
40. Непрерывные марковские процессы 256

IX. МЕТОДЫ ОБРАБОТКИ ДАННЫХ 275

41. Определение моментов случайных величин по экспериментальным данным 275
42. Доверительные уровни и доверительные интервалы 286
43; «Тесты согласия 300
44. Обработка данных методом наименьших квадратов 325
45. Статистические методы контроля качества 346
46. Определение вероятностных характеристик случайных функций по экспериментальным данным 368

ОТВЕТЫ: ​​И РЕШЕНИЯ 375
ИСТОЧНИКИ ТАБЛИЦ, ССЫЛАЕМЫЕ В ТЕКСТЕ 471
БИБЛИОГРАФИЯ 475

 

Нравится:

Нравится Загрузка…

Эта запись была размещена в книги, математика, советские, статистика и помечены методы обработки данных, распределения случайных величин, энтропия, информация, предельные теоремы, марковские процессы, математика , теория вероятностей, задачник, задачи и решения, случайные события, случайные функции, случайные величины, совет, статистика. Добавьте постоянную ссылку в закладки.

pr.probability — Каковы большие проблемы в теории вероятностей?

$\begingroup$

В большинстве разделов математики есть большие, сексуальные знаменитые открытые задачи. В теории чисел есть гипотеза Римана и программа Ленглендса, среди многих других. В геометрии долгое время существовала гипотеза Пуанкаре, а в настоящее время имеется классификация 4-многообразий. Теория PDE имеет дело с уравнением Навье-Стокса.

Итак, каковы основные проблемы теории вероятностей и стохастического анализа?

Я аспирант, работающий в этой области, но я не могу назвать какие-либо основные нерешенные гипотезы или открытые проблемы, которые стимулируют исследования. Я слышал, что стохастическая эволюция Лёвнера в наши дни является большой областью изучения, но я не знаю, какие догадки или проблемы связаны с ними.

У кого-нибудь есть предложения?

• пр.вероятность
• большой список
• открытые проблемы

$\endgroup$

3

$\begingroup$

На мой взгляд, одна из самых больших открытых проблем теории вероятностей, в том смысле, что это известное основное утверждение, которое мы не знаем, как решить, состоит в том, чтобы показать, что «в критической точке нет перколяции» (упомянутой в особенно в разделе 4. 1 вклада Гордона Слейда в Princeton Companion to Mathematics). Резюме капсулы: $\mathbb{Z}_{d,p}$ обозначим случайным подграфом $d$-мерной целочисленной решетки ближайших соседей, полученным путем независимого сохранения каждого ребра с вероятностью $p$. Тогда известно, что существует критическая вероятность $p_c(d)$ ( порог перколяции }) такое, что при $p < p_c$ с вероятностью единица $\mathbb{Z}_{d,p}$ не содержит бесконечных компонент, а при $p > p_c$ с вероятностью единица существует единственная бесконечная компонента.

Гипотеза состоит в том, что с вероятностью один $\mathbb{Z}_{d,p_c(d)}$ не содержит бесконечных компонент. Известно, что гипотеза верна, когда $d =2$ или $d \geq 19$.

Между прочим, один из самых эффективных имеющихся у нас способов понимания перколяции — техника, известная как расширение кружева, в значительной степени разработанная Такеши Хара и Гордоном Слейдом — также является одним из ключевых инструментов для изучения самоизбегающих прогулок и множество других моделей случайных решеток.

Эта статья Слэйда на самом деле полна интригующих догадок в области критических явлений, но гипотеза, которую я только что упомянул, вероятно, самая известная из всех.

$\endgroup$

1

$\begingroup$

Возможно, проблема №1 теории вероятностей состоит в том, чтобы сделать строго то, что можно найти практически в любом учебнике по статистической механике. Другими словами, это должно строго обосновать предсказания теории ренормализационных групп Вильсона. Многие из тем, упомянутых в этом посте, являются частными предположениями в этой более широкой программе.

---

Обновление: хороший недавний обзор Гордона Слэйда на эту тему можно найти здесь.

$\endgroup$

$\begingroup$

Понимание самоизбегающих случайных блужданий, см. http://gowers.wordpress.com/2010/08/22/icm2010-smirnov-laudatio/.

$\endgroup$

2

$\begingroup$

Нормальное распределение и множество мест, где оно встречается в математике и его приложениях, являются основным примером универсального явления. Доказательство и понимание других универсальных явлений вероятности имеет большое значение. Один из примеров, который мне нравится, — это понимание распределений, полученных из теории случайных матриц и встречающихся в различных других местах. Одним из таких распределений является распределение наибольшего собственного значения случайной матрицы, обнаруженное Трейси и Видомом.

$\endgroup$

3

$\begingroup$

У Мишеля Талагранда есть несколько открытых задач (с вознаграждением), перечисленных на его веб-сайте. Я не смотрел их все, но, зная его, гарантирую вам, что они очень тяжелые и достаточно важные. Это мотивировано направлениями его исследований, но, в отличие от некоторых областей, в настоящее время в теории вероятностей доминирует не одно направление исследований и не один набор открытых проблем.

$\endgroup$

1

$\begingroup$

Одной из основных проблем является распространение прекрасного понимания плоских стохастических моделей на более высокие измерения. Таким образом, понимание 3,4-мерной перколяции, модели Изинга, самоизбегающих блужданий, случайных блужданий со стиранием петель и пределов их масштабирования является довольно важной проблемой.

$\endgroup$

$\begingroup$

Для определения предельной формы перколяции первого прохода.

В $n$-мерной сетке начните с одной вершины, окрашенной в черный цвет, а все остальные — в белый. Равномерно выберите двухцветное ребро (один черный конец, один белый конец) и закрасьте черным его белый конец. Продолжайте этот процесс вечно.

Черная часть растет, и известно, что если мы масштабируем ее так, чтобы она имела постоянный диаметр, она сходится к выпуклой форме. Чего мы не знаем, так это формы.

$\endgroup$

2

$\begingroup$

Отсутствие так называемой большой проблемы в теории вероятностей, по-видимому, указывает на богатство самого предмета. Одним из самых интересных подполей является определение скорости сходимости марковских цепей с конечным пространством состояний. Многие проблемы сходимости даже на конечных группах исчерпали современные аналитические методы. Например, интуитивные выводы из задачи коллекционера купонов подсказывают, что случайное блуждание по соседним транспозициям демонстрирует отсечение сходимости полной вариации к равномерной мере на симметричной группе, а разрыв верхней и нижней границ составляет всего два раза. Существует множество инструментов, которые можно было бы использовать. использовать для изучения таких задач, как теория представлений и дискретная версия неравенств из теории частных производных, что делает решения очень творческими.

$\endgroup$

7

$\begingroup$

У Дэвида Олдоса есть список открытых проблем на его веб-сайте, хотя они выглядят как личные любимые, а не как «большие» вопросы. Вы можете взглянуть на проблемы, которые Олдос называет «Тип 2: у нас есть точная математическая проблема, но мы не видим правдоподобного плана для потенциального доказательства».

Глава 23 недавно вышедшей монографии «Цепи Маркова и времена смешивания» представляет собой список открытых проблем. Однако опять же, я не могу сказать, какие из них «большие».

$\endgroup$

2

$\begingroup$

Может быть, гипотеза Кантелли 1917 года? Если $f$ — положительная функция действительных чисел, если $X$ и $Z$ — $N(0,1)$ независимые с. nX_j$ асимптотически нормально распределена. 9{2+\delta}$ конечно для некоторого положительного $\delta$ (кажется, Ибрагимова).

$\endgroup$

$\begingroup$

Формирование инструментов для обработки случайных поверхностей и доказательство универсальной центральной предельной теоремы для них при минимальных условиях (вспомните обычную CLT):

а) Гауссово свободное поле (GFF) оказалось ограничивающим универсальным объектом для многих случайных поверхностей ( в KPZ 2+1, случайные мозаики, теория случайных матриц, ансамбли Жинибре (см. работы Бородина и Кеньона)

б) Эволюция Шрамма-Левнера (SLE) оказалась ограничивающим интерфейсом для семейств статистических моделей.

c) Наконец, слияние двух изображений выше, поскольку SLE могут быть связаны с GFF (см. Sheffield).

Другим важным результатом будет демонстрация эквивалентности случайных плоских карт и квантовой гравитации Лиувилля (LQG) (многообещающий подход Миллера и Шеффилда). Это происходит потому, что на этих случайных поверхностях становится легче работать со статистическими моделями (модель Казанова-Изинга, LERW-Дюплантье).

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Теоретическая вероятность — определение, примеры и решенные задачи

Вероятность в буквальном смысле означает вероятность наступления события, т. е. возможность наступления события. С академической точки зрения вы будете изучать вероятность как раздел математики, который имеет дело с возникновением случайного события.

Мы не можем предсказать многие события с полной уверенностью. Поскольку мы можем предсказать только вероятность того, что событие произойдет, то есть насколько вероятно, что оно произойдет. Кроме того, Вероятность может принимать значения от 0 до 1, где 0 означает, что событие невозможно, а 1 указывает на определенное событие. Например: какова вероятность того, что монета достоинством в одну рупию окажется двусторонней, если ее подбросить в воздух? Возможны два исхода: голова и хвост.

В этой конкретной статье мы подробно обсудим следующие концепции —

• Введение

• Теоретическая вероятность — пример

• Экспериментальная вероятность с примером

• Экспериментальная вероятность с примером

  9

• Экспериментальная вероятность

• . Вероятность

• Основные выводы 

• Часто задаваемые вопросы

 

(Изображение будет загружено в ближайшее время)

Определение теоретической вероятности

Математическое определение теоретической вероятности утверждает, что оно связано с теорией, лежащей в основе вероятности. В теоретической вероятности мы используем знание ситуации для расчета вероятности события. Мы не проводим никаких экспериментов; вместо этого мы просто используем знание ситуации. Теоретическая формула вероятности выглядит следующим образом: она утверждает, что вероятность возникновения события равна количеству благоприятных исходов, деленному на общее число возможных исходов.

Математическая формула того, как мы определяем теоретическую вероятность:

P(E)=Количество благоприятных исходов/Общее количество возможных исходов

Количество благоприятных исходовОбщее количество возможных исходов.

Примеры теоретической вероятности

Давайте рассмотрим некоторые теоретические вопросы вероятности:

1. Найдите вероятность того, что при броске правильной кости выпадет 4. 6. 

Количество благоприятных исходов = количество раз, когда на игральном кубике может выпасть 4 за один бросок = 1

Согласно формуле теоретической вероятности, ‘

P(E) = количество благоприятных исходов/общее число возможных исходов

Количество благоприятных исходовОбщее количество возможных исходов.

Итак, P (правильная кость выбрасывает 4 при броске) = 1/6 

2. Брошена честная игральная кость. Найдите вероятность того, что на кубике выпадет нечетное число.

Ответ: Здесь общее количество возможных исходов равно 6. 

Количество благоприятных исходов = количество раз, когда на честной кости может выпасть нечетное число за один бросок.

Сумма исходов честной кости = {1,2,3,4,5,6}

Благоприятные исходы (Нечетные числа) = {1,3,5} =3

Итак, количество благоприятных исходов = 3.

Согласно формуле теоретической вероятности, ‘

P(E)= количество благоприятных исходов/общее количество возможных исходов.

Количество благоприятных исходовОбщее количество возможных исходов.

Итак, P (выпадает нечетное число) = 3/6 = 1/2 .

Что такое экспериментальная вероятность?

Также известна как эмпирическая вероятность. Он рассчитывается на основе проведения реальных экспериментов или испытаний и их результатов. Опыты проводят серийно. Такие эксперименты называются случайными, поскольку результаты этих экспериментов непредсказуемы. Эксперименты проводятся несколько раз для определения результатов.

Математическая формула того, как мы определяем экспериментальную вероятность, выглядит следующим образом: 

P(E) = количество раз, когда событие E происходит/общее количество испытаний эксперимента.

Решенные задачи

Давайте рассмотрим некоторые экспериментальные вероятностные вопросы: —

1. Два друга A и B подбрасывают правильную монету 10 раз подряд. Результаты этого эксперимента следующие:

Монету подбросили:	Number of heads	Number of tails
A	5	5
B	2	8

Найдите экспериментальную вероятность для каждого исхода.

Ответ: Согласно формуле экспериментальной вероятности, 

P(E) = количество раз, когда произошло событие E/общее количество попыток эксперимента

количество раз, когда событие E происходит общее количество попыток эксперимента.

Теперь P (появление орла) = количество раз, когда выпадает орёл/общее количество попыток.

P (Появление решки) = количество раз выпадения решки / общее количество попыток.

Расчет экспериментальной вероятности

Монета, брошенная.0700 Number of Tails	Experimental Probability for Heads	Experimental Probability for Tails
A	5	5	5/10= 0.5	5/10 = 0.5
B	2	8	2/10 = 0.2	8/10 = 0.8

Теоретическая вероятность и экспериментальная вероятность

Сравнивая экспериментальную и теоретическую вероятности, мы должны внимательно изучить их определения, чтобы понять фундаментальное различие между ними. В случае экспериментальной вероятности мы неоднократно проводим эксперименты, чтобы узнать результаты и вычислить вероятность этих серий результатов. Эти эксперименты известны как случайные эксперименты, поскольку результаты этих экспериментов непредсказуемы. Совокупность результатов и составляет событие. Если исходы имеют равные шансы произойти, событие называется равновероятным событием. Каждая повторность проведения эксперимента называется пробой. По определению вероятности мы можем написать эту формулу для расчета вероятности события:

P(E)=Количество благоприятных исходовОбщее количество возможных исходов

Количество благоприятных исходовОбщее количество возможных исходов.

Когда в случае экспериментальной вероятности число испытаний чрезвычайно велико, экспериментальная вероятность начинает приближаться к теоретическим значениям вероятности. Теоретическая вероятность означает, что вероятность рассчитывается с использованием знаний об определенной ситуации, а не путем фактического проведения эксперимента.

В реальной жизни бывают ситуации, когда проведение экспериментов невозможно или слишком дорого. В таких случаях теоретические вероятности рассчитываются, чтобы иметь четкое представление о том, насколько вероятны результаты, и чтобы можно было предпринять необходимые шаги или меры предосторожности, чтобы избежать опасных ситуаций. Например, когда мы запускаем спутник, рассчитанные вероятности являются теоретическими, а не экспериментальными.

Ключевые выводы из главы

• Вероятность бывает двух типов: теоретическая вероятность и экспериментальная вероятность

• Теория теоретической вероятности используется для определения вероятности в экспериментальной вероятности

• Когда число сравниваемых событий больше, используется теоретическая вероятность

• Для получения более точных и надежных результатов используется теоретическая вероятность

• Оба типа имеют свои преимущества и недостатки.

Решенные задачи вероятности 16

В этой статье мы решим несколько примеров, связанных с вероятностью. Итак, давайте начнем.

Пример 1

В классе из 32 учеников 25 изучают математику, 22 — естественные науки и 15 учеников изучают и математику, и естественные науки. Найти вероятность того, что случайно выбранный студент:

a) изучает только математику

b) изучает только естественные науки

c) изучает математику

d) изучает естественные науки

e) изучает математику и естественные науки

f) изучает математику, учитывая, что он уже изучает естественные науки

Решение

Этот вопрос состоит из многих частей. Мы будем решать каждую часть одну за другой, но сначала мы нарисуем диаграмму Венна из информации в вопросе, например:

Часть а

Количество студентов, изучающих только математику = 10

Общее количество учеников в классе = 32

Вероятность того, что случайно выбранный ученик будет изучать только математику = P(A) =

 

Часть b

Количество учеников, изучающих только естественные науки = 7

Общее количество учащихся в классе = 32

Вероятность того, что случайно выбранный учащийся будет заниматься только наукой = P(B) =

 

Часть c

Количество учащихся, изучающих математику  = 10 + 15 = 25

класс = 32

Вероятность того, что случайно выбранный учащийся будет изучать математику = P(C) =

 

Часть d

Количество учащихся, изучающих естественные науки  = 7 + 15 = 22

Общее количество учащихся в классе = 32

Вероятность что случайно выбранный учащийся изучает естественные науки = P(D) =

 

Часть e

Число учащихся, изучающих математику и естественные науки = 15

Общее число учащихся в классе = 32

Вероятность того, что выбрано случайно ученик изучает и математику, и естествознание =

 

Часть f

Количество студентов, изучающих естественные науки = 7 + 15 = 22

Количество студентов, изучающих математику и естественные науки = =  15

Вероятность того, что случайно выбранный учащийся будет изучать математику, при условии, что он уже занимается естественными науками =

 

Лучшие репетиторы по математике

Поехали

Пример 2

Два друга отправляются на охоту. Первый друг убивает в среднем 3 животных каждые 6 выстрелов, а друг убивает двух животных каждые 7 выстрелов. Если они одновременно выстрелили в одно и то же животное, найти вероятность того, что они добьются цели.

Решение

Предположим, что A — событие, когда первый друг совершает убийство. Тогда вероятность убийства первого друга будет представлена ​​как P(A).

Вероятность того, что первый друг совершит убийство = P(A) =

Предположим, что B — событие, при котором второй друг совершает убийство. Тогда вероятность убийства второго друга будет представлена ​​как P(B).

Вероятность убийства второго друга = P(B) =

Вероятность того, что первый и второй друг совершат убийство = =

Вероятность того, что оба друга совершат убийство = =

=

 

Пример 3

Вероятность того, что ежегодное мероприятие состоится в определенный день, равна 0,57. Найти вероятность того, что:

а) событие не состоится в этот день

б) событие произойдет или не состоится в этот день

Решение

Часть а

определенный день = P(E) = 0,57

Вероятность того, что событие не произойдет в определенный день = P(E)’ = 1 — P(E) = 1 — 0,57 = 0,43

Часть b

Вероятность того, что событие произойдет в определенный день = P (E) = 0,57

Вероятность того, что событие не произойдет в определенный день = P(E)’ = 1 — P(E) = 1 — 0,57 = 0,43

Вероятность того, что событие произойдет или не произойдет в определенный день. определенный день = P(E U E’) = 0,57 + 0,43 = 1,00

 

Пример 4

Класс делится на три группы на основе комбинации предметов, которые учащиеся предпочитают. В первой группе 20 учеников, из которых 5 любят математику. Во второй группе 12 учеников, из которых 7 любят математику. В третьей группе 18 учеников, из которых трое любят математику. Найти вероятность случайного выбора учащегося из одной из трех групп, которым нравится математика.

Решение

Общее количество групп = 3

Количество групп, из которых будет выбран ученик, любящий математику = 1

Вероятность = P(B_i) =

Общее количество учеников в первой группе = 20

Количество учеников, которым нравится математика = 5

Вероятность выбора ученика, которому нравится математика, из первой группы =

Общее количество учеников во второй группе = 12

Количество учеников во второй группе, которым нравится математика = 7

Вероятность выбора учащегося, которому нравится математика, из второй группы =

Общее количество учащихся в третьей группе = 18

Количество учащихся, любящих математику, в третьей группе = 3

Вероятность выбора учащегося, которому нравится математика из третьей группы =

Вероятность выбора учащегося, которому нравится математика, из одной из трех групп будет рассчитана по правилу полной вероятности.

П (девушка) =

 

Пример 5

В группе из 50 человек 35 владеют автомобилем, 25 владеют велосипедом и 20 владеют и автомобилем, и велосипедом. У 10 человек нет ни машины, ни велосипеда. Найти вероятность того, что случайно выбранный человек:

 

а) владеет только автомобилем

б) владеет только велосипедом

в) владеет автомобилем

г) владеет велосипедом

д) владеет автомобилем и велосипед

f) не владеет ни автомобилем, ни велосипедом

g) владеет автомобилем, учитывая, что у него уже есть велосипед

Решение

Этот вопрос состоит из многих частей. Мы будем решать каждую часть одну за другой, но сначала мы нарисуем диаграмму Венна из информации в вопросе, например:

Часть a

Количество людей, у которых есть только машина = 15

Общее количество людей = 50

Вероятность того, что случайно выбранный человек владеет только автомобилем = P(A) =

 

Часть b

Количество людей, у которых есть только велосипед = 5

Общее количество людей = 50

Вероятность того, что случайно выбранный человек владеет только велосипедом = P(B) =

 

Часть c

Количество людей, владеющих автомобилем  = 20 + 15 = 35

Общее количество людей = 50

Вероятность что случайно выбранный человек владеет автомобилем = P(C) =

 

Часть d

Количество людей, владеющих велосипедом  = 5 + 20 = 25

Общее количество людей = 50

Вероятность того, что случайно выбранный человек владеет велосипедом = P(D) =

 

Часть e

Количество студентов, которые владеют автомобилем и велосипедом = 20

Общее количество людей = 50

Вероятность того, что случайно выбранный человек владеет автомобилем и велосипедом =

 7

7 Часть f

Количество людей, у которых нет ни автомобиля, ни велосипеда = 10

Общее количество людей = 50

Вероятность того, что случайно выбранный человек не имеет ни автомобиля, ни велосипеда =

 

Часть g

Вероятность того, что случайно выбранный человек владеет автомобилем при условии, что у него уже есть велосипед = P(A|B) =

 

Профессор Колледжа Св.

Олафа

    Это прошлый курс, который уже завершен. Если вы ищете текущий курс, пожалуйста, нажмите здесь.

Добро пожаловать в теорию вероятностей! Информацию о курсе и правилах см. в программе. Чтобы получить оценки, войдите в Moodle. Если вам нужна помощь или у вас есть вопросы, пожалуйста, свяжитесь с профессором Райтом.

Часы работы профессора Райта: Пн. 12:45–14:00 в RNS 160R, Вт. 10–11 утра в Zoom, среда. 3:15–4:15 в RMS 405, чт. 10–11 утра в RMS 405, пт. 12:45–14:00 в RNS 160R, в другое время по предварительной записи

Сеансы помощи: Пн. и четверг. 19:00–20:00 в Томсоне 186

Верхний

Сегодня

Нижний

Среда
9 февраля

Введение; что такое вероятность?

Вводный опрос Домашнее задание 1

• Заполните вводный опрос, если вы еще этого не сделали.
• Прочтите учебный план и выполните викторину по учебному плану (в Moodle).
• Из учебника прочитайте §1. 1 и §1.2, по крайней мере, до страницы 10, и посмотрите сопровождающее видео Примеры пространств, событий и аксиом. Ответьте на три вопроса, встроенных в видео, перед занятием в пятницу.
• Взгляните на Домашнее задание 1, которое нужно сдать в понедельник.

Пятница
11 февраля

Примеры пространств и событий; аксиомы вероятности

решения задач Примеры пространств, событий и аксиом

• Выполнить домашнее задание 1 (сдать в понедельник).
• Прочтите §1.3 учебника и просмотрите прилагаемый видеоролик «Методы подсчета». Ответьте на три вопроса, встроенных в видео, перед занятием в понедельник.

Понедельник
14 февраля

Методы подсчета; перестановки и комбинации

задач решения Способы подсчета Домашнее задание 2

Домашнее задание 1
сдать в 17:00

Бонусное видео: John Urschel-NFL Math Whiz

• Начало домашнего задания 2 (сдать в пятницу).
• Просмотрите видео «Четыре типа проблем с расчетами» и ответьте на вопросы, встроенные в видео, перед занятием в среду.

Среда
16 февраля

Дополнительные методы подсчета

заметки проблемы решения Четыре типа задач подсчета

• Завершить домашнее задание 2 (сдать в пятницу).
• Посмотрите видео «Условная вероятность» и ответьте на вопросы, встроенные в видео, прежде чем прийти на занятие в пятницу. Также прочитайте примеры в §1.4 учебника.

Пятница
18 февраля

Условная вероятность; Теорема Байеса

заметки проблемы решения Условная вероятность Домашнее задание 3

Домашнее задание 2
сдать в 17:00

• Приступить к домашнему заданию 3 (сдать в среду).
• Посмотрите видео «Независимость» и ответьте на вопросы, встроенные в видео, прежде чем прийти на занятия в понедельник. Также прочитайте §1.5 в учебнике.

Понедельник
21 февраля

Индепенденс

отмечает проблемы решения Индепенденс

Бонусное видео: Юджиния Ченг на позднем шоу

• Завершить домашнее задание 3 (к сдаче в среду).
• Посмотрите видео «Моделирование случайных событий» и ответьте на вопросы, встроенные в видео, прежде чем прийти на занятия в среду. Также прочитайте §1.6 в учебнике.
• Если возможно, принесите компьютер с Mathematica или R на занятия в среду.

Среда
23 февраля

Моделирование случайных событий

решения задач Моделирование случайных событий

Домашнее задание 3
к 17:00

• Посмотрите видео Дискретные случайные величины и ответьте на вопросы, записанные в видео Понедельник. Также прочитайте §2.1 и §2.2 в учебнике.
• Приступить к домашнему заданию 4 (сдать в понедельник).

Пятница
25 февраля

Случайные величины; дискретные распределения

примечания проблемы решения дискретные случайные величины

• Посмотрите видео Ожидаемое значение и стандартное отклонение и ответьте на вопросы, содержащиеся в видео, прежде чем прийти на занятия в среду. Также прочитайте §2. 3 в учебнике.
• Завершить домашнее задание 4 (сдать в понедельник).

Понедельник
28 февраля

Ожидаемое значение, дисперсия и стандартное отклонение

отмечает задачи решения Ожидаемое значение и стандартное отклонение

Домашнее задание 4
сдать в 17:00

Бонус: видео Как не ошибиться: сила математического мышления — с Джорданом Элленбергом и статья Джордана Элленберга «Психология статистики»

• Просмотрите решения задач в классе, особенно тех, которые связаны с неравенством Чебышева.
• Посмотрите видео «Биномиальное распределение» и ответьте на вопросы, встроенные в видео, прежде чем прийти на занятие в пятницу. Также прочитайте §2.4 в учебнике.
• Приступить к домашнему заданию 5 (сдать в пятницу).

Среда
2 марта

Биномиальное распределение

заметки проблемы решения Биномиальное распределение

• Посмотрите видео Распределение Пуассона и ответьте на вопросы, содержащиеся в видео, прежде чем прийти на занятия в понедельник. Также прочитайте §2.5 в учебнике.
• Завершить домашнее задание 5 (сдать в пятницу).
• Прочитайте информацию об экзамене 1.

Пятница
4 марта

Распределение Пуассона

Примечания Проблемы Решения Распределение Пуассона

Домашнее задание 5
к 17:00

• Выполнить домашнее задание 6. Это домашнее задание не будет собираться, но оно важно для вашей собственной практики при подготовке к экзамену 1.
• Просмотрите информацию об экзамене 1.

Понедельник
7 марта

День проверки

решения проблем

Домашнее задание 6
(не собрано)

Бонусное видео: Ханна Фрай — Красивые уравнения: как насекомые ходят по воде и формируют галактики Посмотрите видео «Гипергеометрическое распределение» и ответьте на вопросы, встроенные в видео. Также прочитайте §2.6.1 в учебнике.

Пятница
11 марта

Гипергеометрическое распределение

примечания проблемы решения Гипергеометрическое распределение

• Посмотрите видео Отрицательное биномиальное распределение и ответьте на вопросы, встроенные в видео. Также прочитайте §2.6.2 в учебнике.
• Приступить к домашнему заданию 7 (сдать в среду).

Понедельник
14 марта

Отрицательные биномиальные и геометрические распределения

заметки проблемы решения Отрицательное биномиальное распределение

Бонусные видео: Satyan Devadoss — Blue Collar Mathematics and Mage Merlin’s Unsolved Mathematical Mysteries

• Посмотрите видеоролик «Функции создания моментов, часть 1» и ответьте на вопросы в видеоролике. Также прочитайте §2.7 в учебнике.
• Завершить домашнее задание 7 (сдать в среду).

Среда
16 марта

Функции генерации моментов

заметки проблемы решения Функции генерации моментов, часть 1

Домашнее задание 7
к 17:00 . Перечитайте §2.7 в учебнике.

Приступить к домашнему заданию 8 (сдать в понедельник).

Если возможно, принесите компьютер с Mathematica на урок в пятницу.

Пятница
18 марта

Функции, производящие моменты

Решение математических задач Функции, производящие моменты, часть 2

• Посмотрите видео Моделирование дискретных случайных величин и ответьте на вопросы в видео. Также прочитайте §2.8 в учебнике.
• Завершить домашнее задание 8 (сдать в понедельник).
• Принесите компьютер с Mathematica или R на занятия в понедельник.

Понедельник
21 марта

Моделирование дискретных случайных величин

задач Очередь симуляция Очередь симуляция решения Моделирование дискретных случайных величин

Домашнее задание 8
к 17:00 Посмотрите видео Непрерывные случайные величины и ответьте на вопросы в видео. Также прочитайте §3.1 в учебнике.

Приступить к домашнему заданию 9 (сдать в пятницу).

Среда
23 марта

Непрерывные случайные величины; равномерное распределение

заметки проблемы решения непрерывные случайные величины

• Просмотрите проблемы и решения в классе.
• Посмотрите видео Ожидаемые значения непрерывных случайных величин и ответьте на вопросы в видео. Также прочитайте §3.2 в учебнике.
• Завершить домашнее задание 9 (сдать в пятницу).

Пятница
25 марта

Ожидаемые значения непрерывных распределений

отмечает проблемы решения Ожидаемые значения непрерывных случайных величин

Домашнее задание 9
к 17:00

Хороших весенних каникул! Без занятий с 28 марта по 1 апреля.

• Посмотрите видео Нормальное распределение и ответьте на вопросы в видео. Также прочитайте §3.3 в учебнике.

Понедельник
4 апреля

Нормальное распределение

Демонстрационная программа Mathematica отмечает решения проблем Нормальное распределение

Бонусное видео: Фрэнсис Су — Математика для человеческого процветания

• Посмотрите видео Экспоненциальное распределение и ответьте на вопросы в видео. Также прочитайте §3.4.1 в учебнике.
• Выполнить домашнее задание 10 (в среду).

Среда
6 апреля

Экспоненциальное распределение

заметки проблемы решения Экспоненциальное распределение

Домашнее задание 10
к 17:00

• Посмотрите видео Гамма-распределение и ответьте на вопросы в видео. Также прочитайте §3.4.2 в учебнике.
• Приступить к домашнему заданию 11 (сдать в понедельник).

Пятница
8 апреля

Гамма-распределение

Mathematica примеры заметки проблемы решения Гамма-распределение

• Просмотрите информацию об экзамене 2.
• Завершить домашнее задание 11 (сдать в понедельник).

Понедельник
апреля 11

День обзора

Проблемы Решения

Домашнее задание 11
С Должны в 17:00

Бонусные видео -интервью с Карен Уленбек и статья Карен Уленбек, Неоткрытый Геометрия и Анализ. 13

Экзамен 2 : разделы с 2.1 по 3.4 в учебнике

Информация об экзамене

• Посмотрите видео Преобразование случайной величины. Также прочитайте §3.7 в учебнике.

Пятница
15 апреля

Преобразования непрерывных случайных величин

заметки задачи решения Преобразование случайной величины

• Посмотрите видео Моделирование непрерывных случайных величин и ответьте на вопросы в видео перед занятием в среду. Также прочитайте §3.8 в учебнике.
• Приступить к домашнему заданию 12 (сдать в среду).

Понедельник
18 апреля

Моделирование непрерывных случайных величин

Моделирование Mathematica Моделирование R отмечает проблемы решения Моделирование непрерывных случайных величин

Бонусное видео: Yitang Zhang: Невероятная математическая звезда восходит

• Посмотрите видео Совместное распределение и ответьте на вопросы в видео перед занятием в пятницу. Также прочитайте §4.1 в учебнике.
• Завершить домашнее задание 12 (сдать в среду).

Среда
20 апреля

Совместная раздача

Примечания проблемы решения Совместная раздача

Домашнее задание 12
к 17:00

• Посмотрите видео «Ковариация и корреляция» и ответьте на вопросы в видео перед уроком в понедельник. Также прочитайте §4.2 в учебнике.
• Приступить к домашнему заданию 13 (сдать в понедельник).

Пятница
22 апреля

Ожидаемые значения, ковариация и корреляция

Трехмерные графики заметки проблемы решения Ковариация и корреляция

• Посмотрите видео «Линейные комбинации, часть 1» и ответьте на вопросы в видео перед занятием в среду. Также читайте с начала §4.3 до заголовка §4.3.1.
• Завершить домашнее задание 13 (сдать в понедельник).

Понедельник
25 апреля

Линейные комбинации случайных величин

заметки задачи решения Линейные комбинации, часть 1

Домашнее задание 13
к 17:00

Бонусное видео: ЗНАКОМЬТЕСЬ с математиком! — Трачетт Джексон

• Посмотрите видео «Линейные комбинации, часть 2» и ответьте на вопросы в видео перед занятием в пятницу. Также прочитайте остальную часть §4.3 в учебнике.
• Приступить к домашнему заданию 14 (сдать в пятницу).

Среда
27 апреля

Свойства линейных комбинаций

демонстрационные свертки заметки задачи решения Линейные комбинации, часть 2

• Посмотрите видео Условные распределения и ответьте на вопросы в видео перед занятием в понедельник. Также прочитайте §4.4 в учебнике.
• Завершить домашнее задание 14 (сдать в пятницу).

Пятница
29 апреля

Условные распределения и ожидание

заметки проблемы решения Условные распределения

Домашнее задание 14
сдать в 17:00

• Посмотрите видео Центральная предельная теорема и ответьте на вопросы в видео перед уроком в среду. Также прочитайте §4.5 до конца §4.5.3.
• Приступить к домашнему заданию 15 (сдать в среду).

Понедельник
2 мая

Предельные теоремы

Демонстрационные заметки по Mathematica решения задач Центральная предельная теорема

Бонус: Чем полезна математика — Роберт Грист и Applied Dynamical Systems Vol. 1

• Посмотрите видео «Закон больших чисел» и ответьте на вопросы в видео перед занятием в пятницу. Также прочитайте §4.5.4 в учебнике.
• Завершить домашнее задание 15 (сдать в среду).

Среда
4 мая

Предельные теоремы

Демонстрация LLN Решения демо-задач LLN Закон больших чисел

Домашнее задание 15
к 17:00

• Посмотрите видео «Двумерные преобразования, часть 1» и ответьте на вопросы в видео перед занятием в понедельник. Также прочитайте §4.6 в учебнике.
• Приступить к домашнему заданию 16 (сдать в понедельник).

Пятница
6 мая

Преобразования (метод cdf)

отмечает проблемы решения Двумерные преобразования, часть 1

• Посмотрите видео Двумерные преобразования, часть 2 и ответьте на вопросы в видео перед занятием в среду.

  No related posts.