Онлайн калькулятор матрицы вычислить определитель: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Определитель матрицы. Онлайн калькулятор

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Данный калькулятор позволит вам легко найти определитель матрицы, а так же получить подробное решение. Калькулятор вычисляет определитель для матриц размерности от 1 × 1 до 9 × 9

Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.

Элементы матрицы обозначаются как a_ij, где i – номер строки, j – номер столбца.
Определитель квадратной матрицы – это число, ставящееся в соответствие матрице и которое может быть вычислено по ее элементам.

Как найти определитель матрицы

Определитель квадратной матрицы – это число, скалярная величина характеризующее данную матрицу. Также вместо термина определитель, используют слово – детерминант.

Вычислить определитель можно только для квадратной матрицы.

Квадратная матрицы – это матрица у которой число строк совпадает с числом столбцов.

Определитель матрицы A может обозначатся как: det(A), |A| или Δ(A).

---

Как найти определитель матрицы размерности 2 × 2

Для матрицы 2 × 2 определитель вычисляется по формуле:

Приведем пример, вычислим определитель для матрицы A.

A =

1 2 3 4

Исходя из формулы получим:
det A = ad – bc = 1 ⋅ 4 — 3 ⋅ 2 = -2

det A =

1 2 3 4

= -2

---

Как найти определитель матрицы размерности 3 × 3

Для матрицы 3 × 3 определитель вычисляется по формуле:

det A =

a11	a12	a13
a 21	a22	a23
a31	a32	a33

= a₁₁

a22	a23
a32	a33

— a₁₂

a21	a23
a31	a33

+ a₁₃

a21	a22
a31	a32

= a₁₁a₂₂a₃₃ — a₁₁a₂₃a₃₂ — a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ — a₁₃a₂₂a₃₁

Приведем пример, вычислим определитель для матрицы A.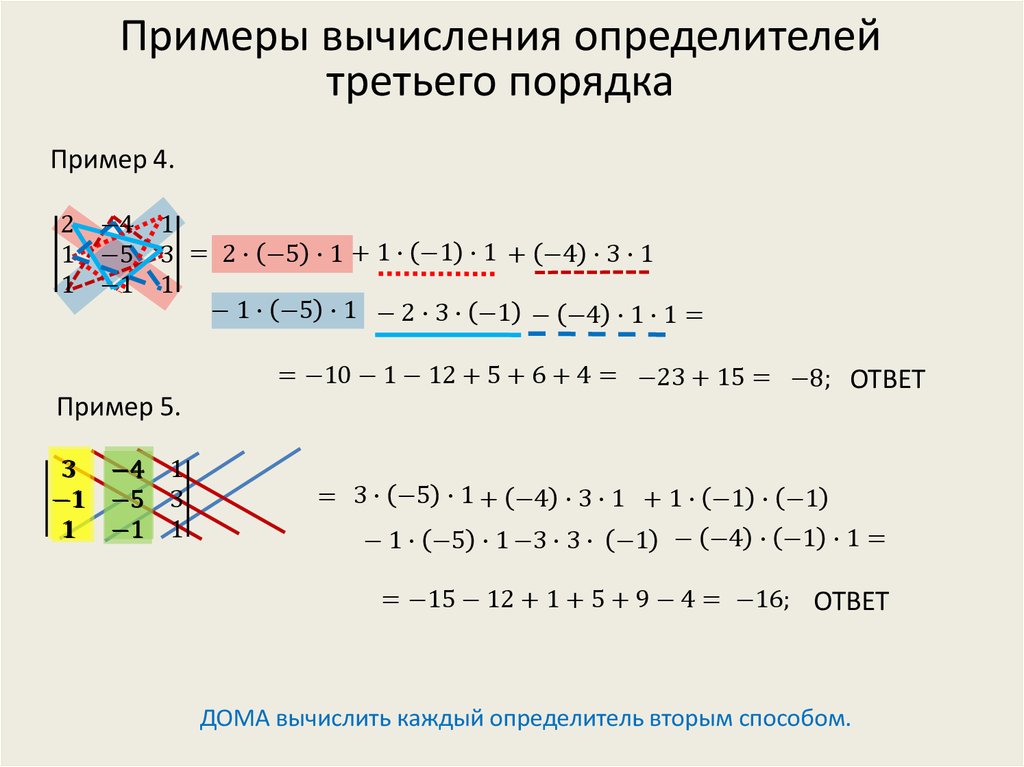

A =	1 2 3 5 7 0 9 0 -3

A =	a11 a12 a13 a21 a22 a23 a31 a32 a33	где,	a11 = 1 a12 = 2 a13 = 3 a21 = 5 a22 = 7 a23 = 0 a31 = 9 a32 = 0 a33 = -3

Исходя из формулы получим:
det A = a₁₁a₂₂a₃₃ — a₁₁a₂₃a₃₂ — a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ — a₁₃a₂₂a₃₁ = (1 ⋅ 7 ⋅ (-3)) — (1 ⋅ 0 ⋅ 0) — (2 ⋅ 5 ⋅ (-3)) + (2 ⋅ 0 ⋅ 9) + (3 ⋅ 5 ⋅ 0) — (3 ⋅ 7 ⋅ 9) = -180

det A =

1 2 3 5 7 0 9 0 -3

= -180

---

Как найти определитель матрицы размерности 4 × 4

Для матрицы 4 × 4, как и для любой матрицы n × n определитель вычисляется по формуле разложения по строке:

Приведем пример, вычислим определитель для матрицы A.

det A =

1 3 7 0 5 -3 0 8 0 4 -3 2 1 2 0 9

A =	a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44	где,	a11 = 1 a12 = 3 a13 = 7 a14 = 0 a21 = 5 a22 = -3 a23 = 0 a24 = 8 a31 = 0 a32 = 4 a33 = -3 a34 = 2 a41 = 1 a42 = 2 a43 = 0 a44 = 9

Для матрицы размерности n × n значение определителя вычисляется по формуле

M_1j — дополнительный минор к элементу a_1j, получаемый из исходной матрицы А путем вычеркивания первой строки и j-го столбца

Значение n = 4, поэтому необходимо найти 4 дополнительных минора путем вычеркивания первой строки и j-го столбца

M₁₁ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

=

-3	0	8
4	-3	2
2	0	9

= 129

M₁₂ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

=

5	0	8
0	-3	2
1	0	9

= -111

M₁₃ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

=

5	-3	8
0	4	2
1	2	9

= 122

M₁₄ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

=

5	-3	0
0	4	-3
1	2	0

= 39

Исходя из приведенной выше формулы, распишем сумму

det A = (-1)¹ ⋅ a₁₁ ⋅ M₁₁ + (-1)² ⋅ a₁₂ ⋅ M₁₂ + (-1)³ ⋅ a

13 ⋅ M₁₃ + (-1)⁴ ⋅ a₁₄ ⋅ M₁₄

det A = (-1)¹ ⋅ 1 ⋅ det

-3	0	8
4	-3	2
2	0	9

+ (-1)² ⋅ 3 ⋅ det

5	0	8
0	-3	2
1	0	9

+ (-1)³ ⋅ 7 ⋅ det

5	-3	8
0	4	2
1	2	9

+ (-1)⁴ ⋅ 0 ⋅ det

5	-3	0
0	4	-3
1	2	0

= (-1)¹ ⋅ 1 ⋅ 129 + (-1)² ⋅ 3 ⋅ (-111) + (-1)³ ⋅ 7 ⋅ 122 + (-1)⁴ ⋅ 0 ⋅ 39 = 1316

det A = (-1)¹ ⋅ 1 ⋅ 129 + (-1)² ⋅ 3 ⋅ (-111) + (-1)³ ⋅ 7 ⋅ 122 + (-1)⁴ ⋅ 0 ⋅ 39 = 1316

det A =

1 3 7 0 5 -3 0 8 0 4 -3 2 1 2 0 9

= 1316

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.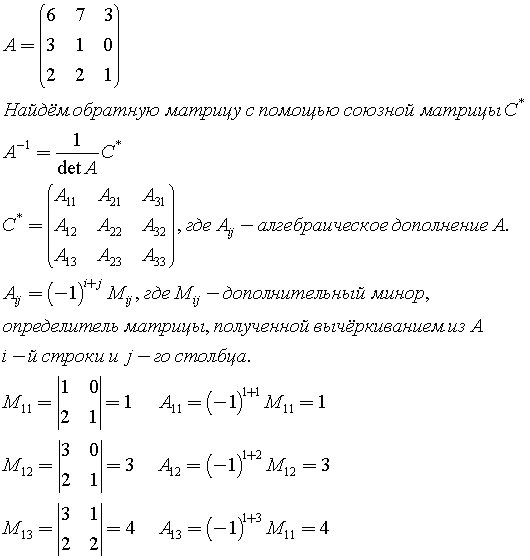 Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Калькулятор определителя матрицы — MathCracker.com

Инструкции: Используйте этот калькулятор определителя матрицы, чтобы вычислить заданный определитель матрицы, показывая все шаги. Сначала нажмите одну из кнопок ниже, чтобы изменить размер матрицы, если это необходимо.

Затем щелкните первую ячейку и введите значение и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы определить ВСЕ значения матрицы.

В линейной алгебре и при использовании матриц понятие определителя матрицы «XYZA» имеет глубочайшее значение.

Это связано с тем, что его использование связано почти со всеми важными операциями, которые вы захотите выполнять с матрицами, такими как проверка обратимости матриц, найти обратную матрицу или же решающие системы .

Итак, куда бы вы ни посмотрели по сторонам при работе с матрицами, вы так или иначе найдете определители. Поэтому очень важно с ними ознакомиться.

Как этот матричный калькулятор может помочь вам

1. Все, что вам нужно сделать, это ввести свою матрицу
2. Это должна быть квадратная матрица, то есть матрица с одинаковым количеством строк и столбцов.
3. Просто нажмите на кнопку и калькулятор покажет вам все шаги и конечное значение определителя
4. Работа над детерминантными вычислениями может быть чрезвычайно трудоемкой и подверженной ошибкам. Этот калькулятор избавит вас от этих проблем

Как вычислить определитель матрицы?

Это может быть длинный ответ, потому что есть много способов вычислить определитель матрицы. Скажем сначала, что определитель вычисляется только для квадратных матриц (это матрицы, которые имеют одинаковое количество строк и столбцов).

Итак, наименьшая матрица, для которой мы можем вычислить определитель, — это матрица 2×2. Давайте рассмотрим общую матрицу 2×2, как показано ниже:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

Какова формула определителя? В этом случае определитель матрицы \(A\) просто вычисляется как \(\det(A) = a d — bc\)

Так, например, если бы у нас было:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

определитель матрицы \(A\) будет \(\det(A) = 1 \cdot 3 — 2 \cdot 1 = 3 — 2 = 1\). Легко, верно?

Как найти определитель матрицы 3×3?

Теперь для матриц большего размера построим вычисление определителя на основе субдетерминанта меньших матриц. Чтобы дать вам представление, давайте рассмотрим один из способов вычисления определителя матрицы 3×3. Рассмотреть возможность

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

В этом случае определитель матрицы 3х3 матрицы \(A\) вычисляется на основе действия нескольких определителей 2х2

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} — b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

В приведенных уравнениях значения \(a\), \(b\), \(c\) играют роль опорных и могут принимать отрицательный знак. 3 = -1\) (отрицательный) и так далее.

Магия заключается в том, чтобы выбрать любую строку или столбец в качестве опорных. Каждая опорная точка будет иметь связанный знак (положительный или отрицательный) и субдетерминант, которые связаны с опорной точкой. матричные кофакторы .

Этот субдетерминант является фактическим определителем исходной матрицы после удаления строки \(i\) и столбца \(j\) для опорной точки, которая находится в строке \(i\) и столбце \(j\).

Наиболее логичное соглашение указывает на выбор строки или столбца с наибольшим количеством нулей для опорных точек, чтобы, по возможности, избежать вычисления некоторых субдетерминантов.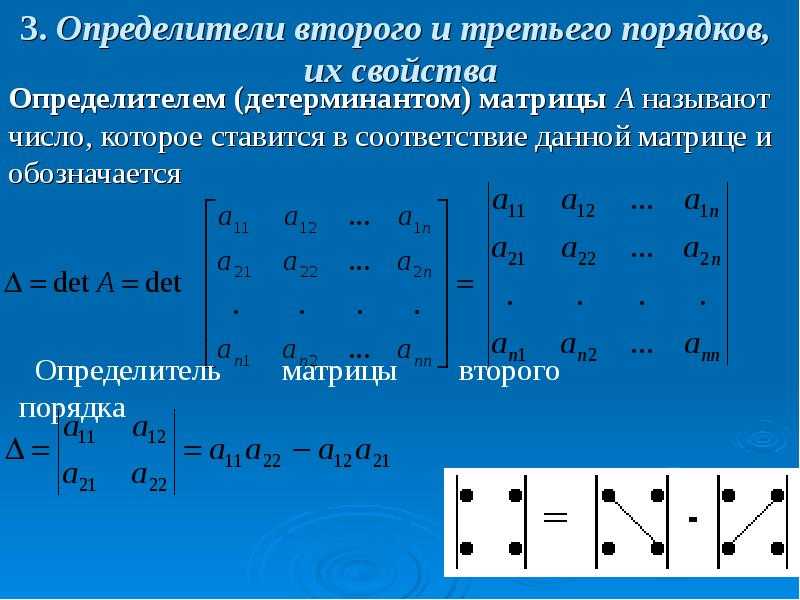

Как найти определитель матрицы 3×4?

Вы не можете сделать это. Матрица 3×4 не является квадратной матрицей, и, следовательно, определитель не может быть вычислен. Чтобы вычислить определитель, матрица должна иметь одинаковое количество строк и столбцов.

Калькулятор определителя 4×4

Для больших матриц методология та же: выберите одну строку или столбец для опорных точек, в идеале ту, в которой больше всего нулей. Найдите знак, соответствующий каждому опорному элементу, и найдите соответствующие субдетерминанты.

Итак, вы сводите вычисление определителя матрицы 4×4 к операции с четырьмя определителями 3×3. И, в свою очередь, каждый из определителей 3х3 находится как действие нескольких определителей 2х2, для которых мы знаем формулу.

Так что запутаться можно очень быстро.

Пример вычисления определителя матрицы

Вопрос: Рассмотрим следующую матрицу:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Вычислите определитель данной матрицы, показав шаги.

Отвечать: Нам нужно вычислить определитель предоставленной матрицы \(3 \times 3\).

По формуле субдетерминанта получаем:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) — 3 \cdot \left(4 \right) \right) — 2 \cdot \left( 3 \cdot \left( 8 \right) — 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) — 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) — 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Вывод : На основании вычислений, показанных выше, установлено, что определитель матрицы равен \(\det A = \displaystyle -15\).

Другие полезные матричные калькуляторы, которые вы можете использовать

Матричные расчеты, выполняемые вручную, трудоемки, поэтому вы можете воспользоваться нашими решателями линейной алгебры.

Во-первых, вы можете использовать этот калькулятор обратной матрицы для вычисления обратной матрицы, показывающей шаги, и вы можете сделать это либо с помощью сопряженный метод , или с помощью снижение RREF .

Зануление строки матрицы онлайн. Понижение порядка определителя

Матрицы применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. При этом количество строк матрицы соответствует числу уравнений, а количество столбцов – количеству неизвестных. Как результат – решение систем линейных уравнений сводится к операциям над матрицами.

Матрица записывается в виде прямоугольной таблицы элементов кольца или поля (к примеру, целых, комплексных или действительных чисел). Является совокупностью строк и столбцов, на пересечении которых находятся ее элементы. Размер матрицы задается количеством строк и столбцов.

Важным значением любой матрицы является её определитель, который вычисляется по определённой формуле. Вручную необходимо проделать ряд операций с матрицей, чтобы вычислить её определитель. Определитель может быть как положительным, так отрицательным, так и равен нулю. Чтобы проверить свои вычисления определителя матрицы, Вы можете воспользоваться нашим онлайн калькулятором. Онлайн калькулятор мгновенно посчитает определитель матрицы и выдаст точное значение.

Определитель матрицы – это своеобразная характеристика матрицы, а точнее с помощью него можно определить имеет ли соответствующая система уравнений решение. Определитель матрицы широко используется в науке, такой как физика, с помощью которого вычисляется физический смысл многих величин.

Решение систем линейных алгебраических уравнений

Также с помощью нашего калькулятора вы сможете решить систему линейных алгебраических уравнений (СЛАУ).

Решение систем линейных алгебраических уравнений входит в число обычных задач линейной алгебры. СЛАУ и методы их решения лежат в основе многих прикладных направлений, в том числе в эконометрике и линейном программировании.

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Определитель матрицы

Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн . Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн !

Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных — возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение.

Задание. Вычислить определитель , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:

Полученный определитель разложим по элементам первого столбца:

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:

Ответ.

12. Слау 3 порядка

1. Правило треугольника

Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т. е.

2. Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

3. Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Задание. Разложив по первой строке, вычислить определитель

Решение.

Ответ.

4.Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду . Рассмотрим разложение определителя по строке или столбцу.

Определитель матрицы равен сумме умноженных элементов строки определителя на их алгебраические дополнения:

Разложение по i -той строке.

Определитель матрицы равен сумме умноженных элементов столбца определителя на их алгебраические дополнения:

Разложение по j -той строке.

Для облегчения разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример

Найдем определитель матрицы четвертого порядка.

Будем раскладывать этот определитель за столбцом №3

Сделаем ноль вместо элемента a 4 3 =9 . Для этого из строки №4 вычтем от соответствующие элементы строки №1 умноженные на 3 .
Результат записываем в строке №4 все остальные строки переписываем без изменений.

Вот мы и сделали нолями все элементы, кроме a 1 3 = 3 в столбце № 3 . Теперь можно преступить и к дальнейшему разложению определителя за этим столбцом.

Видим, что только слагаемое №1 не превращается в ноль, все остальные слагаемые будут нолями, так как они умножаются на ноль.
Значит, далее нам надо разложить, только один определитель:

Будем раскладывать этот определитель за строкой №1 . Сделаем некоторые преобразования, что бы облегчить дальнейшие расчеты.

Видим, что в этой строке есть два одинаковых числа, поэтому вычтем из столбца №3 столбец №2 , и результат запишем в столбце №3 , от этого величина определителя не изменится.

Далее нам надо сделать ноль вместо элемента a 1 2 =4 . Для этого мы элементы столбца №2 умножим на 3 и вычтем от него соответствующие элементы столбца №1 умноженные на 4 . Результат записываем в столбце №2 все остальные столбцы переписываем без изменений.

Но при этом надо не забывать, что если мы умножаем столбец №2 на 3 , то и весь определитель увеличится в 3 . А что бы он не изменился, значит надо его поделить на 3 .

Определитель рассчитывается только для квадратных матриц и является сумой слагаемых n-ого порядка. Подробный алгоритм его вычисления будет описан в готовом решении, которое вы сможете получить сразу после ввода условия в данный онлайн калькулятор. Это доступная и простая возможность получить детальную теорию, поскольку решение будет представлено с подробной расшифровкой каждого шага.

Инструкция пользования данным калькулятором проста. Чтобы найти определитель матрицы онлайн сначала вам нужно определиться с размером матрицы и выбрать количество столбцов и, соответственно, строк в ней. Для этого кликните на иконку «+» или «-». Далее остаётся только ввести нужные числа и нажать «Вычислить». Можно вводить как целые, так и дробные числа. Калькулятор сделает всю требуемую работу и выдаст вам готовый результат.

Чтобы стать экспертом в математике, нужно много и упорно тренироваться. A ещё никогда не помешает дополнительный раз себя перепроверить. Поэтому, когда перед вами поставлена задача вычислить определитель матрицы, целесообразно воспользоваться онлайн калькулятором. Он справится очень быстро, и в течение нескольких секунд на мониторе появится, готовое решение. Это не предполагает, что онлайн калькулятор должен заменять вам традиционные расчёты. Но он является превосходным помощником, если вам интересно понять алгоритм вычисления определителя матрицы. K тому же, это превосходная возможность проверить, правильно ли выполнена контрольная, подстраховаться от неудачной оценки.

our online calculator — Translation into Russian — examples English

Premium History Favourites

Advertising

Download for Windows It’s free

Download our free app

Advertising

Advertising

No ads with Premium

English

Arabic German English Spanish French Hebrew Italian Japanese Dutch Polish Portuguese Romanian Russian Swedish Turkish Ukrainian Chinese

Russian

Synonyms Arabic German English Spanish French Hebrew Italian Japanese Dutch Polish Portuguese Romanian Russian Swedish Turkish Ukrainian Chinese Ukrainian

These examples may contain rude words based on your search.

These examples may contain colloquial words based on your search.

наш онлайн калькулятор

нашим онлайн-калькулятором

For multiple product orders and to get the best deal, use our online calculator.

Используйте наш онлайн калькулятор для получения выгодной сделки и выбора подходящей для вас конфигурации продуктов.

That’s where our online calculator can help.

В этом вам поможет наш онлайн калькулятор.

Then, you need to input your equation F(x, y) into our online calculator and press «Calculate» button.

Затем, вам необходимо ввести свое уравнение F(x, y) в наш онлайн калькулятор.

Our online calculator helps to find the determinant just in a few clicks.

Наш онлайн калькулятор помогает найти определитель матрицы всего в несколько кликов.

Our online calculator helps you to find GCD and LCM of two numbers just in a few minutes and without any special skills.

Наш онлайн калькулятор помогает находить НОД и НОК двух чисел всего за пару минут и без особых навыков.

Our online calculator is based on Wolfram Alpha system.

Наш онлайн калькулятор построен на основе системы Wolfram Alpha.

You can also use our online calculator.

Также вы можете воспользоваться нашим онлайн-калькулятором.

Use the calendar to select dates of your arrival and departure, and our online calculator will instantly calculate the amount to be paid.

С помощью календаря выберите дату заезда и выезда, а онлайн-калькулятор мгновенно посчитает сумму к оплате.

Using our online calculator is easy.

Пользоваться нашим онлайн-калькулятором очень легко!

Possibly inappropriate content

Examples are used only to help you translate the word or expression searched in various contexts. They are not selected or validated by us and can contain inappropriate terms or ideas. Please report examples to be edited or not to be displayed. Rude or colloquial translations are usually marked in red or orange.

No results found for this meaning.

Results: 9. Exact: 9. Elapsed time: 74 ms.

More features with our free app

Voice and photo translation, offline features, synonyms, conjugation, learning games

Калькулятор матриц разложение по столбцу. Вычисление определителя матрицы онлайн. Приведение определителя к треугольному виду

Образование

Матрицы применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. При этом количество строк матрицы соответствует числу уравнений, а количество столбцов – количеству неизвестных. Как результат – решение систем линейных уравнений сводится к операциям над матрицами.

Матрица записывается в виде прямоугольной таблицы элементов кольца или поля (к примеру, целых, комплексных или действительных чисел). Является совокупностью строк и столбцов, на пересечении которых находятся ее элементы. Размер матрицы задается количеством строк и столбцов.

Важным значением любой матрицы является её определитель, который вычисляется по определённой формуле. Вручную необходимо проделать ряд операций с матрицей, чтобы вычислить её определитель. Определитель может быть как положительным, так отрицательным, так и равен нулю. Чтобы проверить свои вычисления определителя матрицы, Вы можете воспользоваться нашим онлайн калькулятором. Онлайн калькулятор мгновенно посчитает определитель матрицы и выдаст точное значение.

Определитель матрицы – это своеобразная характеристика матрицы, а точнее с помощью него можно определить имеет ли соответствующая система уравнений решение. Определитель матрицы широко используется в науке, такой как физика, с помощью которого вычисляется физический смысл многих величин.

Решение систем линейных алгебраических уравнений

Также с помощью нашего калькулятора вы сможете решить систему линейных алгебраических уравнений (СЛАУ).

Решение систем линейных алгебраических уравнений входит в число обычных задач линейной алгебры. СЛАУ и методы их решения лежат в основе многих прикладных направлений, в том числе в эконометрике и линейном программировании.

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Определитель матрицы

Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн . Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн !

Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных — возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение.

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду . Рассмотрим разложение определителя по строке или столбцу.

Определитель матрицы равен сумме умноженных элементов строки определителя на их алгебраические дополнения:

Разложение по i -той строке.

Определитель матрицы равен сумме умноженных элементов столбца определителя на их алгебраические дополнения:

Разложение по j -той строке.

Для облегчения разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример

Найдем определитель матрицы четвертого порядка.

Будем раскладывать этот определитель за столбцом №3

Сделаем ноль вместо элемента a 4 3 =9 . Для этого из строки №4 вычтем от соответствующие элементы строки №1 умноженные на 3 .
Результат записываем в строке №4 все остальные строки переписываем без изменений.

Вот мы и сделали нолями все элементы, кроме a 1 3 = 3 в столбце № 3 . Теперь можно преступить и к дальнейшему разложению определителя за этим столбцом.

Видим, что только слагаемое №1 не превращается в ноль, все остальные слагаемые будут нолями, так как они умножаются на ноль.
Значит, далее нам надо разложить, только один определитель:

Будем раскладывать этот определитель за строкой №1 . Сделаем некоторые преобразования, что бы облегчить дальнейшие расчеты.

Видим, что в этой строке есть два одинаковых числа, поэтому вычтем из столбца №3 столбец №2 , и результат запишем в столбце №3 , от этого величина определителя не изменится.

Далее нам надо сделать ноль вместо элемента a 1 2 =4 . Для этого мы элементы столбца №2 умножим на 3 и вычтем от него соответствующие элементы столбца №1 умноженные на 4 . Результат записываем в столбце №2 все остальные столбцы переписываем без изменений.

Но при этом надо не забывать, что если мы умножаем столбец №2 на 3 , то и весь определитель увеличится в 3 . А что бы он не изменился, значит надо его поделить на 3 .

Дальнейшие свойства связаны с понятиями минора и алгебраического дополнения

Минором элемента называется определитель, составленный из элементов, оставшихся после вычеркивания стоки и столбца, на пересечении которых находится этот элемент. Минор элемента определителя порядка имеет порядок . Будем его обозначать через .

Пример 1. Пусть , тогда .

Этот минор получается из A путём вычёркивания второй строки и третьего столбца.

Алгебраическим дополнением элемента называется соответствующий минор, умноженный на , т.е , где –номер строки и -столбца, на пересечении которых находится данный элемент.

VІІІ. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.

Пример 2. Пусть , тогда

Пример 3. Найдём определитель матрицы , разложив его по элементам первой строки.

Формально эта теорема и другие свойства определителей применимы пока только для определителей матриц не выше третьего порядка, поскольку другие определители мы не рассматривали. Следующее определение позволит распространить эти свойства на определители любого порядка.

Определителемматрицы порядка называется число, вычисленное с помощью последовательного применения теоремы о разложении и других свойств определителей.

Можно проверить, что результат вычислений не зависит от того, в какой последовательности и для каких строк и столбцов применяются вышеуказанные свойства. Определитель с помощью этого определения находится однозначно.

Хотя данное определение и не содержит явной формулы для нахождения определителя, оно позволяет находить его путём сведения к определителям матриц меньшего порядка. Такие определения называют рекуррентными.

Пример 4. Вычислить определитель:

Хотя теорему о разложении можно применять к любой строке или столбцу данной матрицы, меньше вычислений получится при разложении по столбцу, содержащему как можно больше нулей.

Поскольку у матрицы нет нулевых элементов, то получим их с помощью свойства VII . Умножим первую строку последовательно на числа и прибавим её ко строкам и получим:

Разложим получившийся определитель по первому столбцу и получим:

так как определитель содержит два пропорциональных столбца.

Некоторые виды матриц и их определители

Квадратная матрица, у которой ниже или выше главной диагонали стоят нулевые элементы ()называется треугольной.

Их схематичное строение соответственно имеет вид: или

.

1.Теорема разложения:

Всякий определитель равен сумме парных произведений элементов какого-либо ряда на их алгебраические дополнения.

Для i- й строки:

или для j -го столбца:

Пример 7.1. Вычислить определитель разложением по элементам первой строки:

1∙(1+12+12 ) ∙(2+16+18 )+

3∙(4+8+27 ) ∙(8+4+18 )=

Теорема разложения позволяет заменить вычисление одного определителя n- го порядка вычислением n определителей (n- 1)-го порядка.

Однако для упрощения вычислений целесообразно для определителей высоких порядков использовать метод «размножения нулей», основанный на свойстве 6 раздела 5. Его идея:

Сначала «размножить нули» в некотором ряду, т. е. получить ряд, в котором только один элемент не равен нулю, остальные нули;

Затем разложить определитель по элементам этого ряда.

Следовательно, на основании теоремы разложения исходный определитель равен произведению ненулевого элемента на его алгебраическое дополнение.

Пример7.2. Вычислить определитель:

.

«Размножим нули» в первом столбце.

От второй строки вычтем первую, умноженную на 2, от третьей строки вычтем первую, умноженную на 3, а от четвертой строки вычтем первую, умноженную на 4. При таких преобразованиях величина определителя не изменится.

По свойству 4 раздела 5 можем вынести за знак определителя из 1-го столбца, из 2-го столбца и из 3-го столбца.

Следствие: Определитель с нулевым рядом равен нулю.

2. Теорема замещения:

Сумма парных произведений каких-либо чисел на алгебраические дополнения некоторого ряда определителя равна тому определителю, который получается из данного, если в нем заменить элементы этого ряда взятыми числами.

Для -й строки:

1. Теорема аннулирования:

Сумма парных произведений элементов какого-либо ряда на алгебраические дополнения параллельного ряда равна нулю.

Действительно, по теореме замещения получаем определитель, у которого в k -й строке стоят те же элементы, что и в i -й строке

Но по свойству 3 раздела 5 такой определитель равен нулю.

Т.о., теорему разложения и ее следствия можно записать следующим образом:

8. Общие сведения о матрицах. Основные определения.

Определение 8.1 . Матрицей называется следующая прямоугольная таблица:

Применяют также следующие обозначения матрицы: , или , или .

Строки и столбцы матрицы именуются рядами.

Величина называется размером матрицы.

Если в матрице поменять местами строки и столбцы, то получим матрицу, называемую транспонированной . Матрица, транспонированнаяс , обычно обозначается символом .

Например:

Определение 8.2 . Две матрицы A и B называются равными , если

1) обе матрицы одинаковых размеров, т.е. и ;

2) все их соответствующие элементы равны, т.е.

Тогда . (8.2)

Здесь одно матричное равенство (8.2) эквивалентно скалярных равенств (8.1).

9. Разновидности матриц.

1) Матрица, все элементы которой равны нулю, называется ноль-матрицей:

2) Если матрица состоит только из одной строки, то она называется матрицей-строкой, например . Аналогично этому матрица, имеющая только один столбец, именуется матрицей-столб­цом, например .

Транспонирование переводит матрицу-столбец в матрицу-строку и наоборот.

3) Если m = n , то матрица называется квадрат­ной матрицей n-го порядка.

Диагональ членов квадратной матрицы, идущая из левого верхнего угла в ее правый нижний угол, называется главной . Другая же диагональ ее членов, идущая из левого нижнего угла в ее правый верхний угол, именуется побочной .

Для квадратной матрицы может быть вычислен определитель det(A) .

Решение системы линейных уравнений методом гаусса-жордана

метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком, что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

1. На основании системы линейных уравнений составляем расширенную матрицу системы;
2. Приводим матрицу к «треугольному» виду;
3. Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
4. В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

1. Рассматриваем строку i(начиная с первой). Если, элемент a i i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a 1 1 отличен от нуля — переходим к следующему шагу;
2. Для каждой строки j, ниже i-й находим значение коэффициента K j =a j i /a i i ;
3. Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a j k нов. =a j k -K j *a i k ; После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A
4. В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пa i i , которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце. Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк. Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

Размер матрицы: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 X 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

1. Записываем расширенную матрицу.
2. Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
3. Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.

Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?

…да, такое бывает только по любви =)

Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:

Ну, и совсем замечательно, если отработано понижение порядка определителя .

Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .

Не мудрствуя лукаво:

Пример 1

Решить систему методом Гаусса-Жордана

Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .

Идеальный с точки зрения простоты случай:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

Ответ :

Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

Решение : первая часть задания хорошо знакома:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.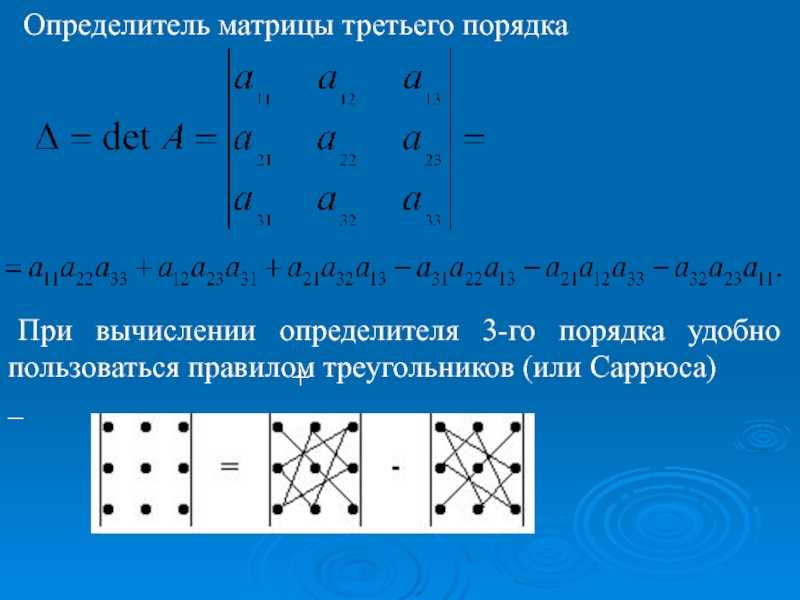 е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

Элементарно выражаем базисные переменные через свободную:

и записываем:

Ответ : общее решение:

В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.

И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .

Для самостоятельного решения:

Пример 3

Найти базисное решение с помощью элементарных преобразований

Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!

Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .

Продолжаем совершенствовать свои навыки на следующей прикладной задаче:

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Демо-пример 4

Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:

(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Ответ :

Сверьтесь с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:

Пример 5

Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :

(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».

(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.

(3) К 3-й строке прибавили 2-ю строку, умноженную на –1

Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.

К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:

(5) К 1-й и 2-й строкам прибавили третью строку.

(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.

(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.

(8) К первой строке прибавили вторую строку.

(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.

(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.

(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ :

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .

Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.

Аналогичное задание для самостоятельного решения:

Пример 6

Найти обратную матрицу методом Гаусса-Жордана.

Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .

Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:

Пример 7

Найти обратную матрицу с помощью элементарных преобразований

Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:


(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :

Ответ : общее решение:

Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:


(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.


(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :

Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.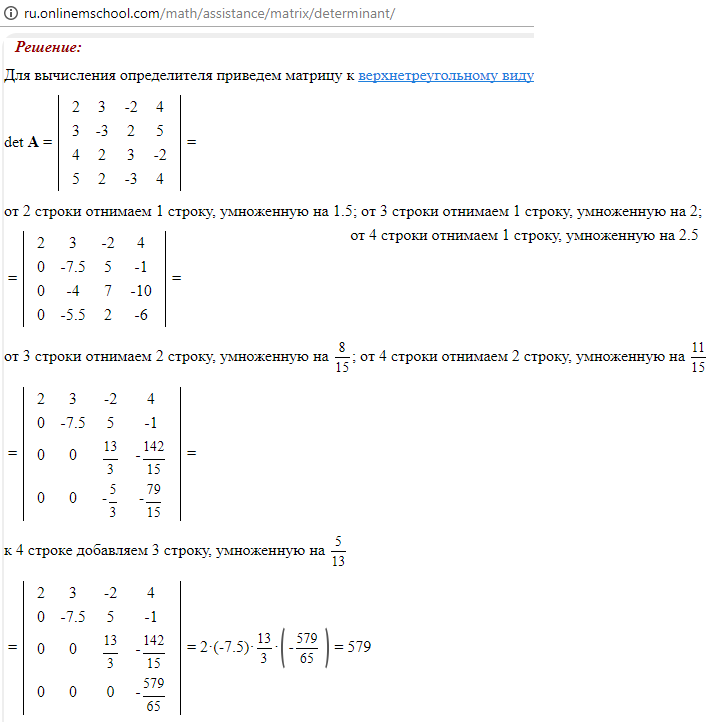
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:


(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :

Березнёва Т. Д.

Тема 7

«СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.»

(Учебная дисциплина “Введение в линейную алгебру и аналитическую геометрию”)

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

МЕТОД ГАУССА – ЖОРДАНА.

Основные понятия

Уравнение с n переменными называется линейным , если все переменные (x 1 , x 2 , … x n ) входят в него в степени 1. Общий вид такого уравнения формально записывается следующим образом:

a 1 x 1 + a 2 x 2 + … a j x j + … a n x n = b , (*)

= b .

Величины a j , j = 1,…, n , и b являются известными (заданными). Величиныa j называются коэффициентами при переменных (при неизвестных), а b — свободным членом .

Решением линейного уравнения (*) ,,…,) значений переменных, который при подстановке в уравнение (т.е. при заменеx j на при всехj от 1до n обращает его в тождество. Подчеркнем, что решение уравнения с n переменными всегда есть набор из n чисел и каждый такой набор из n чисел представляет собой одно решение. Очевидно, что если хотя бы один коэффициент при переменных не равен 0, то уравнение (*) имеет решение. В противном случае решение существует только при b = 0, и это все произвольные наборы из n чисел.

Рассмотрим одновременно m уравнений вида (*), т.е. систему m линейных алгебраических уравнений с n переменными . Пусть каждое i — е уравнение, i = 1,2,…,m, задается коэффициентами при переменных a i 1 , a i 2 , …, a in и свободным членом b i , т.е. имеет вид

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i .

Тогда в общем виде система m линейных алгебраических уравнений с n переменными может быть записана в виде:

a 11 x 1 + a 12 x 2 + … + a 1j x j + … + a 1n x n = b 1

a 21 x 1 + a 22 x 2 + … + a 2j x j + … + a 2n x n = b 2

………………………………………………………………………………

a i1 x 1 + a i2 x 2 + … + a ij x j + … + a in x n = b i (1)

…………………………………………………

a m1 x 1 + a m2 x 2 + … + a mj x j + … + a mn x n = b m

или, что то же самое,

= b i , i = 1,…, m .

Если все свободные члены равны нулю, то система (1) называется однородной , т.е. имеет вид

= 0, i = 1,…, m, (1 0 )

в противном случае — неоднородной . Система (1 0 ) является частным случает общей системы (1) .

Решением системы уравнений (1) называется упорядоченный набор (,,…,) значений пере­менных, который при подстановке в урав­нения системы (1) (т.е. при заменеx j на , j = 1,…,n) все эти уравнения обращает в тождества, т.е.
=b i при всех i = 1,…,m.

Система уравнений (1) называется совместной, если у нее существует хотя бы одно решение. В противном случае система называется несовместной .

Совокупность всех решений системы уравнений (1) мы будем называть множеством ее решений и обозначать X b (X 0 , если система однородная). Если система несовместна, то X b = .

Основная задача теории систем линейных алгебраических уравнений состоит в том, чтобы выяснить, совместна ли система (1), и, если совместна, то описать множество всех её решений. Существуют методы анализа таких систем, которые позволяют описывать множество всех решений в случае совместных систем или убеждаться в несовместности в противном случае. Одним из таких универсальных методов является метод последовательного полного исключения неизвестных, или метод Гаусса — Жордана , который мы будем подробно изучать.

Прежде, чем переходить к описанию метода Гаусса — Жордана, приведем ряд полезных для дальнейшего определений и утверждений.

Две системы уравнений называются эквивалентными , если они имеют одно и то же множество решений. Другими словами, каждое решение одной системы является решением другой, и наоборот. Все несовместные системы считаются эквивалентными между собой.

Из определений эквивалентности и множества решений систем вида (1) сразу же вытекает справедливость следующих утверждений, которые мы сформулируем в виде теоремы.

Теорема 1. Если в системе (1) имеется уравнение с номером k , 1k m , такое, что a kj = 0 j , то

Справедливость утверждений теоремы становится очевидной, если заметить, что k – е уравнение имеет вид

0 x 1 + 0 x 2 + … + 0 x j + … + 0 x n = b k .

Теорема 2. Если к одному уравнению системы (1) прибавить другое уравнение этой же системы, умноженное на любое число, то получится система уравнений, эквивалентная исходной системе.

Доказательство. Умножим, например, второе уравнение системы (1) на некоторое число и прибавим его к первому уравнению. В результате этого преобразования получим систему (1’), в которой все уравнения, начиная со второго, не изменились, а первое имеет следующий вид

= b 1 + b 2 .

Очевидно, если какой-нибудь набор (,,…,) значений переменных обращает в тождества все уравнения системы (1), то он обращает в тождества и все уравнения системы (1’). Наоборот, решение (x’ 1 ,x’ 2 ,…,x’ j , … ,x’ n) системы (1’) является также решением системы (1), так как система (1) получается из системы (1’) с помощью аналогичного преобразования, когда к первому уравнению системы (1’) прибавляется второе уравнение системы (1’), умноженное на число (-).

Точно также доказывается и следующее утверждение.

Теорема 2’ . Умножение произвольного уравнения системы (1) на любое число, отличное от нуля, переводит систему (1) в эквивалентную ей систему уравнений .

Теоремы 2 и 2’ дают два вида преобразований, которым подвергалась система (1), оставаясь эквивалентной:

а) умножение (или деление) произвольного уравнения системы (1) на любое число, отличное от нуля;

б) прибавление (или вычитание) к одному уравнению другого, умноженного на некоторое число.

Такие преобразования а) и б) называются элементарными преобразованиями системы уравнений (1).

Если к системе уравнений (1) несколько раз применить элементарные преобразования, то полученная в результате система, очевидно, также будет эквивалентна первоначальной.

Систему уравнений (1) можно записать в табличной форме:

Прямоугольная таблица чисел, составленная из коэффициентов a ij при неизвестных системы (1), называется матрицей системы (1) и обозначается A (в ней m строк и n столбцов), столбец свободных членов обозначается b. Прямоугольная таблица, составленная из коэффициентов a ij при неизвестных и из столбца свободных членов b системы (1), называется расширенной матрицей системы (1) и обозначается (в нейm строк и (n+1) столбцов), т.е = (A, b). В i – ой строке матрицы содержатся всеизвестные параметры, характеризующие i — ое уравнение системы (1), i = 1,…, m. В j – м столбце матрицы A содержатся все коэффициенты при неизвестном x j , встречающиеся в системе (1).

Числа a ij называются элементами матрицы А. Элемент a ij находится в i — ой строкеи в j — м столбце матрицы А. Принято говорить, что элементa ij находится на пересечении i — ой строки и j — го столбца матрицы А. Если все элементы строки (столбца) матрицы А (кроме одного) равны нулю, а ненулевой элемент равен единице, то такая строка (столбец) называется единичной (единич­ным).

Элементарным преобразованиям системы (1) соответствуют следующие элементарные преобразования таблицы (2):

а) умножение (или деление) всех элементов произвольной строки таблицы (2) на любое число, отличное от нуля ,

б) прибавление (или вычитание) к одной строке (поэлементно) другой строки, умноженной на некоторое число.

В результате любого элементарного преобразования получается новая таблица , в которой вместо той строки, к которой прибавляли (или умножали на любое число, отличное от нуля), пишется новая строка , а осталь­ные строки (в том числе и та, которую прибавляли) пишутся без из­менения . Новая таблица соответствует системе уравнений, эквивалентной исходной системе .

Применяя элементарные преобразования можно таблицу (2) и соответственно систему (1) упростить так, что решить исходную систему становится просто. На этом и основан предлагаемый метод.

Метод последовательного полного исключения неизвестных

(Метод Гаусса — Жордана)

Метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана , является универсальным методом анализа любых (заранее неизвестно, каких — совместных или несовместных) систем линейных алгебраических уравнений. Он позволяет решать совместные системы или убеждаться в несовместности несовместных систем.

Отметим принципиальное отличие предлагаемого метода решения систем линейных алгебраических уравнений от метода решения, ска­жем, стандартного квадратного уравнения. Оно решается с помощью хорошо известных формул, в которых неизвестные выражаются через коэффициенты уравнения. В случае общих систем линейных алгебраических уравнений мы таких формул не имеем и используем для отыскания решения метод итераций , или итеративный метод , или итерационный метод . Такие методы задают не формулы, а последовательность действий.

Метод Гаусса — Жордана представляет собой последовательную реализацию ряда однотипных больших шагов (или итераций ). Это конкретный итерационный метод — один из многих методов итераций, предложенных для решения систем линейных алгебраических уравнений вида (1). Он состоит из начального этапа, основного этапа и заключительного этапа . Основной этап содержит повторяющиеся итерации – наборы однотипных действий.

Пусть задана конкретная система линейных алгебраических уравнений (1). Это значит, что известны n , m , a ij , b i , i = 1,…, m ; j = 1,…, n . Опишем предлагаемый метод решения этой системы.

Начальный этап включает в себя построение таблицы I (0) вида (2) и выбор в ней ведущего элемента – любого ненулевого коэффициента при переменных из таблицы (2). Столбец и строка, на пересечении которых стоит ведущий элемент, называются ведущими . (Пусть выбран элемент a i 0 j 0 . Тогда i 0 – ая строка ведущая, j 0 — й столбец ведущий.) Переходим к основному этапу. Заметим, что часто ведущий элемент называют разрешающим .

Основной этап состоит из повторяющихся однотипных итераций с номерами k = 1, 2,…. Опишем подробно итерации метода Гаусса — Жордана.

К началу каждой итерации известна некоторая таблица I вида (2), в ней выбран ведущий (разрешающий) элемент и, соответственно, ведущий столбец и ведущая строка. Кроме того, имеется информация о том, какие строки и столбцы уже были ведущими. (Так, например, после начального этапа, т.е. на итерации 1 известны I (0) , ведущий (разрешающий) элемент a i 0 j 0 и i 0 – ая строка ведущая, j 0 — ой столбец ведущий.)

Итерация(с номером k ) состоит из следующих действий.

Преобразование ведущего столбца (т.е. столбца, содержащего ведущий элемент) в единичный с 1 на месте ведущего элемента путем последовательного поэлементного вычитания ведущей строки (т.е. строки, содержащей ведущий элемент), умноженной на некоторые числа, из остальных строк таблицы. Сама ведущая строка преобразуется путем поэлементного деления ее на ведущий элемент.

Выписы­вается новая таблица I (k) , (k — номер итерации), в которой все столбцы, которые были когда-либо ведущими, – единичные .

Проверяется, можно ли в таблице I (k) выбрать новый ведущий (разрешающий) элемент . По определению это любой ненулевой элемент, который стоит на пересечении строки и столбца, которые еще не были ведущими .

Если такой выбор возможен, то столбец и строка, на пересечении которых стоит ведущий (разрешающий) элемент, называются ведущими . Затем итерация повторяется с новой таблицей I (k) , т.е. действия 1 – 3 повторяются с новой таблицей I (k) . При этом строится новая таблица I (k +1) .

Если нельзя выбрать новый ведущий элемент, то переходим к заключительному этапу.

Заключительный этап. Пусть проделано r итераций, получена таблица I (r) , состоящая из матрицы коэффициентов при переменных A (r) и столбца свободных членов b (r) , и в ней нельзя выбрать новый ведущий элемент, т. е. метод остановился . Заметим, что метод обязательн о остановится за конечное число шагов , т.к. r не может быть больше min{m,n}.

Каковы варианты остановки метода? Что значит «нельзя выбрать новый ведущий элемент»? Это значит, что после r – ой итерации в матрице A (r) новой системы, эквивалентной системе (1), либо

а) все строки A (r) были ведущими, т.е. в каждой строке стоит одна и ровно одна единица, которая не стоит больше не в какой другой строке,

б) остались строки в A (r) , состоящие только из нулей.

Рассмотрим эти варианты.

а) В этом случае r = m, m n. Переставив строки и перенумеровав переменные (т.е. переставив столбцы), можно таблицу I (r) представить в виде

Подчеркнем, что в таблице (3) каждая переменная с номером i, не превосходящим r, встречается только в одной строке. Таблица (3) соответствует системе линейных уравнений вида

x 1 +
=b (r) 1 ,

x 2 +
=b (r) 2 ,

………………………, (4)

x r +
=b (r) r ,

в которой каждая переменная с номером i, не превосходящим r , однозначно выражается через переменные x r +1 , … ,x n , коэффициенты матрицы a (r) ij , j = r+1,…,n, и свободный член b (r) i , представленные в таблице (3). На переменные x r +1 , … , x n не накладываются никакие ограничения , т.е. они могут принимать любые значения . Отсюда произвольное решение системы, описываемой таблицей (3), или, что то же самое, произвольное решение системы (4), или, что то же самое, произвольное решение системы (1) имеет вид

x i = b (r) i — a (r) ij x j , i = 1,…,r = m; x j – любое при j = (r+1),…,n. (5)

Тогда множество решений системы (1) можно записать как

X b = {x=(x 1 , … ,x n) : x i = b (r) i — a (r) ij x j при i = 1,…, r = m; x j – любое при j =(r+1),…,n.}.

б) В этом случае r r, (предполагаем, что сделана перестановка строк и столбцов такая же, как в пункте а)) такая, что a (r) kj = 0 при всех j. Тогда, если соответствующий свободный член b (r) k не равен 0, то k — е уравнение не имеет решения, и, следовательно, вся система не имеет решения, т.е. система (1) несовместна .

Если же соответствующий b (r) k равен 0, то k — ое уравнение является лишним и его можно отбросить. Отбросив все такие уравнения, получим, что система (1) эквивалентна системе изr уравнений с n переменными, которая через r шагов записывается с помощью таблицы вида (3), в которой все строки были ведущими. Таким образом, мы пришли к рассмотренному выше случаю а) и можем выписать решение вида (5).

Метод Гаусса – Жордана описан полностью. За конечное число итераций система линейных алгебраических уравнений будет решена (если она совместна) или будет очевидно, что она несовместна (если она действительно несовместна).

Переменные, соответствующие ведущим (разрешающим) элементам , или стоящие в ведущих столбцах, принято называть базисными , а ос­тальные переменные —свобод­ными .

Обратим внимание на следующее.

1) Когдамы начинаем решать систему методом Гаусса — Жордана, мы можем не знать, совместна эта система или нет. Метод Гаусса — Жордана за конечное число итераций r даст ответ на этот вопрос. В случае совместной системы на основании последней таблицы выписывается общее решение исход­ной системы. В этом случае число базисных переменных обязательно равно номеру r последней итерации, т.е. числу выполненных итераций. Число r всегда не превосходит min{m,n},гдеm — число уравнений системы,а n — число переменных системы. Если r , то ( n – r) равно числу свободных переменных.

2) При записи общего решения не нужно перенумеровывать переменные, как это делалось для простоты понимания при описании Заключительного этапа. Это сделано для более ясного понимания.

3) При решении системы (1) методом Гаусса — Жордана базисными переменными будут только переменные, соответствующие столбцам, которые на каких-то итерациях выступали в роли ведущих , и наоборот, если на какой-то итерации столбец выступал в качестве ведущего, соответствующая ему переменная обязательно будет в числе базисных.

4) Если общее решение системы (1) содержит хотя бы одну свободную переменную, то эта система имеет бесконечно много част­ных решений, если же свободных переменных нет, то система имеет единственное решение, которое совпадает с общим решением.

5) Ведущие элементы могут быть выбраны на каждой итерации различным способом. Важно только то, что это ненулевые коэффициенты, стоящие на пересечении строки и столбца, которые до этого не были ведущими. Различный выбор ведущих элементов может дать различные записи множества решений. Однако, само множество решений при любой записи одно и то же.

Поясним работу метода на примерах.

Пример I. Решить следующую систему линейных алгебраических уравнений

2 x 1 – 3 x 2 + 3 x 3 + 5 x 4 = -1,

3 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 2, (6)

5 x 1 – 4 x 2 + 6 x 3 + 10 x 4 = 2

методом последовательного полного исключения неизвестных (методом Гаусса — Жордана).

Начальный этап. Сначала выпишем систему уравнений (6) в более удобной форме — в виде таблицы I (0) .

Каждой системе линейных уравнений поставим в соответствие расширенную матрицу , полученную присоединением к матрице А столбца свободных членов:

Метод Жордана–Гаусса применяется для решения системы m линейных уравнений с n неизвестными вида:

Данный метод заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений с матрицей определенного вида.

Над строками расширенной матрицы осуществляем следующие элементарные преобразования:

1. перестановка двух строк ;

2. умножение строки на любое число, отличное от нуля ;

3. прибавление к одной строке другой строки, умноженной на некоторое число ;

4. отбрасывание нулевой строки (столбца) .

Пример 2.11. Решить методом Жордана–Гаусса системы линейных уравнений:

а ) Х 1 + Х 2 + 2Х 3 = -1

2Х 1 — Х 2 + 2Х 3 = -4

4Х 1 + Х 2 + 4Х 3 = -2

Решение: Составим расширенную матрицу:

Итерация 1

В качестве направляющего элемента выбираем элемент . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на (-2) и (-4). Получим матрицу:

На этом первая итерация закончена.

Итерация 2

Выбираем направляющий элемент . Так как , то делим вторую строку на -3. Затем умножаем вторую строку соответственно на (-1) и на 3 и складываем соответственно с первой и третьей строками. Получим матрицу

Итерация 3

Выбираем направляющий элемент . Так как , то делим третью строку на (-2). Преобразуем третий столбец в единичный. Для этого умножаем третью строку соответственно на (-4/3) и на (-2/3) и складываем соответственно с первой и второй строками. Получим матрицу

откуда Х 1 = 1, Х 2 = 2, Х 3 = -2.

Закончив решение, на этапе обучения необходимо выполнять проверку, подставив найденные значения в исходную систему, которая при этом должна обратиться в верные равенства.

б ) Х 1 – Х 2 + Х 3 – Х 4 = 4

Х 1 + Х 2 + 2Х 3 +3Х 4 = 8

2Х 1 +4Х 2 + 5Х 3 +10Х 4 = 20

2Х 1 – 4Х 2 + Х 3 – 6Х 4 = 4

Решение: Расширенная матрица имеет вид:

Применяя элементарные преобразования, получим:

Исходная система эквивалентна следующей системе уравнений:

Х 1 – 3Х 2 – 5Х 4 = 0

2Х 2 + Х 3 + 4Х 4 = 4

Последние две строки матрицы A (2) являются линейно зависимыми.

Определение. Строки матрицы e 1 , e 2 ,…, e m называются линейно зависимыми , если существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

где 0 =(0, 0…0). Строки матрицы являются линейно независимыми , когда комбинация этих строк равна нулю тогда и только тогда, когда все коэффициенты равны нулю.

В линейной алгебре очень важно понятие ранга матрицы , т.к. оно играет очень большое значение при решении систем линейных уравнений.

Теорема 2.3 (о ранге матрицы). Ранг матрицы равен максимальному числу её линейно независимых строк или столбцов, через которые линейно выражаются все остальные её строки (столбцы).

Ранг матрицы A (2) равен 2, т.к. в ней максимальное число линейно независимых строк равно 2 (это первые две строки матрицы).

Теорема 2.4 (Кронекера–Капели). Система линейных уравнений совместна и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы системы меньше числа переменных, т.е. r

В данном случае система имеет 4 переменных, а её ранг равен 2, следовательно, она имеет бесконечное множество решений.

Определение. Пусть r n , r переменных x 1 , x 2 ,…, x r называются базисными , если определитель матрицы из коэффициентов при них (базисный минор ) отличен от нуля. Остальные n – r переменных называются свободными .

Определение. Решение системы, в котором все n – r свободных переменных равны нулю, называется базисным .

Совместная система m линейных уравнений с n переменными (m ) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где .

В нашем случае , т.е. система имеет не более 6 базисных решений.

Общее решение имеет вид:

Х 1 = 3Х 2 +5Х 4

Х 3 = 4 – 2Х 2 – 4Х 4

Найдем базисные решения. Для этого полагаем Х 2 = 0, Х 4 = 0, тогда Х 1 =0, Х 3 = 4. Базисное решение имеет вид: (0, 0, 4, 0).

Получим другое базисное решение. Для этого в качестве свободных неизвестных примем Х 3 и Х 4 . Выразим неизвестные Х 1 и Х 2 через неизвестные Х 3 и Х 4:

Х 1 = 6 – 3/2Х 2 – Х 4

Х 2 = 2 – 1/2Х 3 – 2Х 4 .

Тогда базисное решение имеет вид: (6, 2, 0, 0).

Пример 2.12. Решить систему:

X 1 + 2X 2 – X 3 = 7

2X 1 – 3X 2 + X 3 = 3

4X 1 + X 2 – X 3 = 16

Решение.Преобразуем расширенную матрицу системы

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = –1, следовательно, данная система несовместна. Данный вывод можно также получить, если заметить, что ранг матрицы системы равен 2, тогда как ранг расширенной матрицы системы равен 3.

Найдите определитель матрицы

Скоро Эти математические инструменты уже в пути

Функции построения графиков

Рисовать графики математических функций.

Рисование формулы LaTeX

Создание изображения из выражения LaTeX.

Найти n-ю цифру

Вычислить n-ю цифру числа Эйлера.

Найти n-ю цифру золотого сечения

Вычислить n-ю цифру золотого сечения.

Найти n-ю цифру числа пи

Вычислите n-ю цифру константы Пи.

Вычислить сумму e цифр

Найти сумму e цифр.

Вычислить сумму цифр золотого сечения

Найти сумму цифр золотого сечения.

Вычислить сумму пи цифр

Найти сумму пи цифр.

Генерировать цифры Чамперноуна

Генерировать цифры константы Чамперноуна.

Найти n-ю цифру Чамперноуна

Вычислить n-ю цифру константы Чамперноуна.

Декодировать последовательность «посмотри и скажи»

Выполни обратную операцию над последовательностью «посмотри и скажи».

Создание P-адических расширений

Вычисление p-адических расширений произвольных чисел.

Создать последовательность панцифровых чисел

Создать список панцифровых чисел.

Создать последовательность номеров Стэнли

Создать список номеров Стэнли.

Создать последовательность номеров звонков

Создать список номеров звонков.

Создать последовательность чисел Кармайкла

Создать список чисел Шармишеля.

Создать последовательность каталонских номеров

Создать список каталонских номеров.

Создать последовательность треугольных чисел

Создать список треугольных чисел.

Создать последовательность составных чисел

Создать список составных чисел.

Создать последовательность секущих чисел

Создать список секущих чисел.

Создать последовательность чисел Голомба

Создать список чисел Голомба-Сильвермана.

Создать последовательность чисел Эйлера Тотиент

Создать список фи-чисел Эйлера.

Создать последовательность номеров жонглеров

Создать список номеров жонглеров.

Создать последовательность счастливых номеров

Создать список счастливых номеров.

Создать последовательность номеров Моцкина

Создать список номеров Моцкина.

Создать последовательность номеров Padovan

Создать список номеров Padovan.

Генерация псевдосовершенной числовой последовательности

Создать список полусовершенных чисел.

Создать последовательность номеров Ulam

Создать список номеров Ulam.

Создать последовательность странных чисел

Создать список странных чисел.

Создать последовательность суперсовершенных чисел

Создать список суперсовершенных чисел.

Продолжить числовую последовательность

Найти закономерность в числовой последовательности и расширить ее.

Разбить число

Найти все разбиения данного целого числа.

Создать последовательность номеров разделов

Создать список функциональных номеров разделов.

Создание арифметической прогрессии

Создание арифметической последовательности чисел.

Создание геометрической прогрессии

Создание геометрической последовательности чисел.

Создание полиномиальной прогрессии

Создание полиномиальной последовательности чисел.

Создать последовательность натуральных чисел

Создать список натуральных чисел.

Генерировать степени двойки

Создать список чисел степеней двойки.

Создание степеней десяти

Создание списка чисел в степени десятка.

Создание плотной матрицы

Создание матрицы с очень небольшим количеством нулевых элементов.

Создать разреженную матрицу

Создать матрицу с очень небольшим количеством ненулевых элементов.

Умножение матрицы на скаляр

Умножение всех элементов матрицы на число.

Проверить, является ли матрица единственной

Определить, является ли матрица вырожденной.

Найти матрицу кофакторов

Для заданной матрицы найти ее матрицу кофакторов.

Найдите вспомогательную матрицу

По заданной матрице найдите ее дополнение.

LU Factor a Matrix

Разложить матрицу на LU-факторы.

Найти собственные значения матрицы

Найти собственные значения матрицы.

Украсьте матрицу

Украсьте матрицу, аккуратно выровняв все ее столбцы.

Переформатировать матрицу

Преобразование матрицы одного формата в другой формат.

Рисование архимедовой спирали

Создание архимедовой спирали.

Рисование спирали Эйлера

Создание кривой спирали Корню (полиномиальной спирали).

Рисование спирали Фибоначчи

Создание кривой спирали Фибоначчи.

Рисование спирали Теодора

Создание спирали квадратного корня.

Нарисуйте спираль Ферма

Создайте кривую в виде параболической спирали.

Рисование прямоугольников Фибоначчи

Создание рисунка прямоугольников Фибоначчи.

Нарисуйте головку семени Фибоначчи

Создайте головку цветка Фибоначчи.

Нарисовать фрактал Падована

Создать фрактал равнобуквенных треугольников Падована.

Нарисуйте аполлонову прокладку

Создайте фрактал аполлоновой прокладки.

Нарисовать фрактал Мандельброта

Создать фрактал Мандельброта.

Нарисовать фрактал Юлии

Создать фрактал Джулии.

Нарисовать фрактал Рози

Создать фрактал Рози.

Нарисовать кривую фрактала Бланманже

Создать фрактал Бланманже.

Рисование функции Вейерштрасса

Создание фрактала Вейерштрасса.

Нарисовать кривую Минковского в виде вопросительного знака

Создать фрактал Минковского в виде вопросительного знака.

Нарисуйте функцию Тома

Создайте функцию Тома (также известную как функция попкорна или капли дождя).

Нарисуйте функцию Дирихле

Создать функцию Дирихле.

Нарисуйте рог Гавриила

Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.

Преобразование слов в числа

Преобразование чисел из английского текста в реальные цифры.

Преобразование чисел в слова

Преобразование чисел в письменный текст на английском языке.

Преобразование десятичной записи в экспоненциальную запись

Преобразование чисел, записанных в десятичной форме, в экспоненциальную форму.

Преобразование научного представления в десятичное представление

Преобразование чисел, записанных в научной форме, в десятичную форму.

Округление чисел вверх

Применение операции ceil к числам.

Округление чисел в меньшую сторону

Применить операцию пола к числам.

Анализ чисел

Подсчитайте, сколько раз встречается каждое число.

Преобразование числа в виде суммы

Создайте сумму, которая в сумме равна заданному числу.

Создать таблицу умножения

Нарисовать таблицу умножения n×m.

Нарисовать круговую диаграмму

Нарисовать круговую диаграмму и показать относительные размеры данных.

Визуализация процентов

Нарисуйте диаграмму, показывающую проценты.

Подбрось монетку

Подбрось монетку и выпадет орел или решка.

Бросьте кубик

Бросьте кубик и получите число на его стороне.

Калькулятор определителя матрицы

Допустим, вы хотите вычислить определитель следующей матрицы :

A

=

⌈ 2 5 1 3 ⌉ | 4 1 7 9 ｜ | 6 8 3 2 ｜ ⌊ 7 8 1 4 ⌋

Определитель матрицы 4×4 , да? Мы видели формулу определителя единицы в разделе «Определитель матрицы 2×2, 3×3 и 4×4», так что мы знаем, что это не будет очень занимательно, не так ли? Но с тех пор мы узнали некоторые свойства определителей, так почему бы нам не заставить их работать на нас ?

Прежде чем мы это сделаем, давайте воспользуемся калькулятором определителя матрицы , чтобы посмотреть, как наш инструмент упрощает такие задачи. Прежде всего, мы имеем дело с матрицей 4×4, поэтому нам нужно сообщить об этом калькулятору , выбрав соответствующую опцию в разделе « Размер матрицы ».

Это покажет нам пример такой матрицы с символическим обозначением ее элементов . Как видим, a₁ , b₁ , c₁ и d₁ обозначают числа в первой строке, поэтому давайте прокрутим туда, где мы вводим данные, и загрузим калькулятор определителя матрицы тем, что у нас есть в нашем упражнении:

a₁ = 2 , б₁ = 5 , с₁ = 1 , d₁ = 3 .

Аналогично, для других рядов мы имеем:

A₂ = 4 , B₂ = 1 , C₂ = 7 , D₂ = 9 ,

a₃ = 6 ,

A₃ = 6 ,

A₃ = 6 ,

A₃ = 6 ,

A₃ = 6 9042,

A₃ = 6 ,

A₃ = 6 ,

A₃ = 6 ,

A₃ = 6 ,

. 0421 B₃ = 8 , C₃ = 3 , D₃ = 2 ,

A₄ = 7 , B₄ = 8 , C₄ = 1 , D₄ = 4 .

В тот момент, когда мы запишем последнее число, калькулятор определителя матрицы сделает свое волшебство и выдаст ответ :

|A| = 630 .

Хорошо, теперь, когда у нас есть этот спойлер ответа, давайте посмотрим, как мы можем получить этот ответ вручную . Очевидно, что один из способов — просто использовать формулу определителя с 24 членами, но мы хотели бы получить дополнительные баллы за творческий подход и использовать свойства определителей .

Мы воспользуемся разложением Лапласа, но по-умному. Мы выбираем произвольную строку или столбец, скажем, первую строку матрицы, и пытаемся сделать расширение немного проще. Ведь если мы воспользуемся формулой сразу, то получим сумму четырех определителей 3х3. Не ужасно, но и не здорово. Однако мы можем кое-что сделать сначала - использовать элементарные операции со столбцами .

В предыдущем разделе мы видели, что если мы добавим любое ненулевое число, кратное столбцу, к другому столбцу, определитель останется прежним. Так почему бы нам не добавить (-2) -кратное третьего столбца к первому ?

|А|

=

| 2+(-2)*1 5 1 3 ｜ | 4+(-2)*7 1 7 9 ｜ | 6+(-2)*3 8 3 2 ｜ | 7+(-2)*1 8 1 4 ｜

что дает

|A|

=

| 0 5 1 3 ｜ | -10 1 7 9 ｜ | 0 8 3 2 ｜ | 5 8 1 4 ｜

И зачем мы это сделали? Вспомним, что в разложении Лапласа слагаемые были такими: (-1) в некоторой степени, умноженное на элемент выбранной строки или столбца, умноженный на меньший определитель. Поэтому, если мы теперь разложим |А| по отношению к первой строке, слагаемое, соответствующее первой ячейке в первой строке, будет равно (-1) в некоторой степени, умноженной на 0 , умноженной на некоторый определитель. И это ноль , потому что все, что умножается на ноль, равно нулю.

Отлично, мы уменьшили количество слагаемых на единицу! Так как насчет того, чтобы повторить процедуру и получить еще меньше ? Для этого мы хотим, чтобы в первой строке было больше нулей, поэтому давайте сделаем 5 и 3 в 0 -с. Как и раньше, мы добавляем к этим столбцам правое число, кратное третьему столбцу (тому, что 1 ):

|A|

=

| 0 5+(-5)*1 1 3+(-3)*1 ｜ | -10 1+(-5)*7 7 9+(-3)*7 ｜ | 0 8+(-5)*3 3 2+(-3)*3 ｜ | 5 8+(-5)*1 1 4+(-3)*1 ｜

что дает

|A|

=

| 0 0 1 0 ｜ | -10 -34 7 -12 ｜ | 0 -7 3 -7 ｜ | 5 3 1 1 ｜

Вот это больше похоже! В этой форме, если мы применим разложение Лапласа к первой строке, мы получим только одно слагаемое, потому что три других будут равны 0 умножить на что-то, что равно 0 . Точнее, мы получаем

|A|

=

(-1) 1+3 *1*

| -10 -34 -12 ｜ | 0 -7 -7 ｜ | 5 3 1 ｜

И мы прекрасно знаем, как найти определитель матрицы 3x3, не так ли? Но помните, что если вы хотите повеселиться , вы можете снова использовать разложение Лапласа, чтобы получить определитель матрицы 2x2. В противном случае мы можем просто использовать формулу определителя и на основе вышеизложенного получить:

|А| = (-1)⁴ * (-10*(-7)*1 + (-34)*(-7)*5 + (-12)*0*5 - (-12)*(-7)*5 - (-10)*(-7)*3 - (-34)*0*1) = 630 .

Ура, это согласуется с тем, что у нас было выше! Посмотрите, сколько времени может сэкономить калькулятор определителя матрицы? Вы знаете, сколько страниц нашей любимой книги мы могли прочитать за это время?

Вычисление определителя матрицы — онлайн-инструменты для работы с числами

Скоро в продаже Эти числовые инструменты уже в пути

Генерация номеров Numberwang 9б форма.

Преобразование научной записи в число

Преобразование числа в научной записи в обычное число.

Создать символьную нумерацию

Создать список буквенных чисел (a, b, c, …, z, aa, ab, …).

Создать римскую нумерацию

Создать список римских цифр (i, ii, iii, iv, v…).

Создать нумерацию Брайля

Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …).

Генерация случайных двоичных чисел

Создать список случайных двоичных чисел.

Создание случайных восьмеричных чисел

Создание списка случайных восьмеричных чисел.

Создание случайных десятичных чисел

Создание списка случайных десятичных чисел.

Создание случайных шестнадцатеричных чисел

Создание списка случайных шестнадцатеричных чисел.

Вычислить текущую сумму

Вычислить кумулятивную сумму списка чисел.

Вычисление текущего произведения

Вычисление кумулятивного произведения списка чисел.

Вычислить факториал

Найти факториал числа.

Создание числовых анаграмм

Создание одной или нескольких числовых анаграмм.

Создание числовых биграмм

Создание списка цифровых биграмм из числа.

Создание числовых триграмм

Создание списка цифровых триграмм из числа.

Генерация числовых N-грамм

Создание списка цифровых nграмм из числа.

Создание полиномиальной последовательности

Создать список чисел полиномиальной прогрессии.

Создание префиксов SI

Создание списка префиксов метрик.

Анализ числа

Сообщить, сколько цифр встречается сколько раз.

Преобразование числа в порядковое

Преобразование количественного числительного в порядковое.

Преобразование порядкового числа в число

Преобразование порядкового числа в количественное.

Преобразование числа в римское число

Преобразование арабских цифр в римские.

Преобразование римских чисел в обычные числа

Преобразование римских цифр в арабские.

Создание чисел Негафибоначчи

Вычисление серии расширенных чисел Фибоначчи.

Генерация простых чисел Фибоначчи

Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами.

Проверка числа Фибоначчи

Проверка, является ли число числом Фибоначчи.

Проверка простых чисел Фибоначчи

Проверяет, является ли число одновременно числом Фибоначчи и простым числом.

Построить слова Фибоначчи

Создать последовательность слов Фибоначчи.

Создать слова Трибоначчи

Создать последовательность слов Трибоначчи.

Генерировать числа Негалука

Вычислить серию расширенных чисел Лукаса.

Генерировать простые числа Лукаса

Вычислить серию расширенных чисел Лукаса.

Lucas Prime Test

Проверить, является ли число одновременно числом Лукаса и простым числом.

Вычисление следа матрицы

Найдите сумму элементов главной диагонали матрицы.

Вычислить собственные значения матрицы

Найти собственные значения матрицы.

Умножение матриц

Вычисление произведения двух матриц.

Добавить матрицы

Вычислить сумму двух матриц.

Вычитание матриц

Вычисление разности двух матриц.

Генерация чисел Мозера де Брюйна

Вычисление последовательности чисел Мозера-Брейна.

Сгенерировать числа Колакоски

Вычислить последовательность чисел Ольденбургера-Колакоски.

Сгенерировать числа Стэнли

Вычислить последовательность чисел Стэнли.

Генерировать числа Гийсвейта

Вычислить последовательность самоописывающих чисел Гийсвейта.

Сгенерировать числа Рудина-Шапиро

Вычислить последовательность чисел Русина-Шапиро.

Генерация чисел Баума-Свита

Вычисление последовательности чисел Баума-Свита.

Генерация последовательности Туэ-Морса

Вычисление членов ряда чисел Туэ-Морса.

Создание идеальных чисел

Создание списка совершенных чисел.

Создание почти идеальных чисел

Создание списка почти идеальных чисел.

Создать последовательность избыточных чисел

Вычислить последовательность избыточных чисел.

Создать последовательность неполных чисел

Вычислить последовательность неполных чисел.

Расчет чисел кривой дракона

Создать список порядковых номеров для складывания бумаги.

Создание составных чисел

Создание списка чисел, которые не являются простыми.

Нарисовать таблицу чисел

Создать таблицу чисел.

Проверить, является ли число совершенным

Проверить, является ли заданное число совершенным числом.

Проверить, является ли число обильным

Проверить, является ли данное число обильным числом.

Проверить, является ли число недостаточным

Проверить, является ли данное число недостаточным.

Вычислить модуль

Найти модуль числа.

Группировка цифр числа

Группировка цифр числа.

Разделить число на цифры

Создать список цифр из числа.

Printf Numbers

Применение функций sprintf или printf к числам.

Создайте номера Zalgo

Позвольте Zalgo уничтожить ваши номера.

Повторить номер

Повторить номер несколько раз.

Зеркальное число

Создать зеркальную копию номера.

Дополнение числа нулями

Добавление нулей к числу.

Обратный порядок цифр

Обратный порядок цифр в числе.

Поворот числа

Циклический поворот цифр числа влево или вправо.

Увеличить число

Добавить единицу к заданному числу.

Увеличить все цифры в числе

Добавить единицу к каждой цифре в числе.

Уменьшить число

Вычесть единицу из заданного числа.

Уменьшить все цифры в числе

Вычесть единицу из каждой цифры в числе.

Находить закономерности в числах

Находить закономерности в последовательностях чисел.

Подсчет числа вхождений

Узнайте, как часто появляются числовые значения.

Вычисление процентов

Найти x% числа.

Создание больших чисел

Создание списка больших чисел.

Генерация малых чисел

Создать список маленьких чисел.

Создание натуральных чисел

Создание списка натуральных чисел.

Создание рациональных чисел

Создание списка рациональных чисел.

Создать последовательность констант

Создать серию чисел, в которой все термины одинаковы.

Создание действительных чисел

Создание последовательности действительных чисел.

Создание комплексных чисел

Создание списка комплексных чисел.

Создать двоичные числа

Создать последовательность двоичных чисел.

Создание пар чисел

Создание последовательности пар чисел.

Создание троек чисел

Создание последовательности троек чисел.

Создание кортежей чисел

Создание последовательности n-кортежей чисел.

Переплетение чисел

Переплетение двух или более чисел поразрядно.

Найти десятичное представление числа

Переписать число в десятичной форме.

Преобразование дроби в десятичную

Преобразование дроби в десятичное число.

Преобразование десятичного числа в дробь

Преобразование десятичного числа в дробь.

Преобразование двоичного числа в восьмеричное

Преобразование числа с основанием два в число с основанием восемь.

Преобразование двоичного числа в десятичное число

Преобразование числа с основанием два в число с основанием десять.

Преобразование двоичного числа в шестнадцатеричное

Преобразование числа с основанием два в число с основанием шестнадцать.

Преобразование восьмеричного числа в двоичное

Преобразование числа с основанием восемь в число с основанием два.

Преобразование восьмеричного числа в десятичное

Преобразование числа с основанием восемь в число с основанием десять.

Преобразование восьмеричного числа в шестнадцатеричное

Преобразование числа с основанием восемь в число с основанием шестнадцать.

Преобразование десятичного числа в двоичное

Преобразование числа с основанием десять в число с основанием два.

Преобразование десятичного числа в восьмеричное число

Преобразование десятичного числа в восьмеричное.

Преобразование десятичного числа в шестнадцатеричное

Преобразование числа с основанием десять в число с основанием шестнадцать.

Преобразование шестнадцатеричного числа в двоичное число

Преобразование числа с основанием шестнадцать в число с основанием два.

Преобразование шестнадцатеричного числа в восьмеричное

Преобразование числа с основанием шестнадцать в число с основанием восемь.

Преобразование шестнадцатеричного числа в десятичное число

Преобразование числа с основанием шестнадцать в число с основанием десять.

Преобразование любого числа в любое основание

Преобразование любого числа в любом основании в любое другое основание.

Изменение мантиссы числа

Изменение значения числа.

Изменить показатель степени числа

Изменить степень числа.

Замена цифр буквами

Замена цифр в числе буквами алфавита.

Создание спирали чисел

Создание спирали из цифр числа.

Удалить десятичную точку

Удалить десятичный разделитель из десятичного числа.

Проверка числа Numberwang

Проверка, является ли данный номер числом numberwang.

Калькулятор определителя - Примеры, Калькулятор определителя онлайн

Калькулятор определителя — это онлайн-инструмент, который помогает найти определитель квадратной матрицы 3 x 3, используя формулу определителя. Найти определитель можно только квадратных матриц.

Что такое определительный калькулятор?

Калькулятор определителя помогает вычислить определитель квадратной матрицы 3 x 3. Когда мы находим сумму произведений элементов квадратной матрицы по какому-то заданному правилу, полученная таким образом величина называется определителем. Чтобы использовать калькулятор определителя введите значения в поля ввода.

Калькулятор определителя

ПРИМЕЧАНИЕ: Вводите значения только до 3 цифр.

Как пользоваться калькулятором определителя?

Выполните следующие действия, чтобы найти определитель матрицы 3 x 3 с помощью онлайн-калькулятора определителя.

• Шаг 1: Перейдите к онлайн-калькулятору определителя Cuemath.
• Шаг 2: Введите элементы матрицы в указанные поля ввода.
• Шаг 3: Нажмите кнопку "Вычислить" , чтобы найти определитель.
• Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.

Как работает калькулятор определителя?

Определитель можно рассматривать как функцию, которая принимает элементы квадратной матрицы в качестве входных данных и выводит единственное значение. Детерминанты являются скалярными величинами. Определитель квадратной матрицы используется для нахождения обратной этой матрицы. Кроме того, нам потребуются определители, если мы решаем линейные уравнения, используя метод обращения матриц. Шаги для нахождения определителей матриц приведены ниже:

1. Матрица 2 x 2

Пусть \(A_{2\times 2}\) = \(\begin{bmatrix} a & b\\ c & d \end{bmatrix}\)

Формула для вычислить определитель следующим образом:

\(\begin{vmatrix}A_{2\times 2} \end{vmatrix}\) = (a x d) - (b x c)

2. 3 x 3 Матрица

Пусть \ (A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix}\)

Шаг 1: Умножаем номера привязок с соответствующей квадратной подматрицей.

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a . \(\begin{vmatrix} e & f\\ h & i \end{vmatrix}\) - b . \(\begin{vmatrix} d & f\\ g & i \end{vmatrix}\) + c . \(\begin{vmatrix} d & e\\ g & h \end{vmatrix}\)

Шаг 2: Используя формулу определителя матрицы 2 x 2, мы решаем выражение на шаге 1, как указано ниже.

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei - fh) - b(di - fg) + c(dh - eg).

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Решенные примеры на определители

Пример 1: Найдите определитель следующей матрицы \(\begin{bmatrix} 3 & 4 & 5\\ 1& 2& 3\\ 2& 0 & 9 \ end{bmatrix}\) и проверьте его с помощью онлайн-калькулятора определителей.

Решение:

Дано: \(A_{3\times 3}\) = \(\begin{bmatrix} 3 & 4 & 5\\ 1& 2& 3\\ 2& 0 & 9 \end{bmatrix}\ )

По формуле

\(A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix} \)

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei - fh) - b(di - fg) + c(dh - eg)

Подставляя эти значений получаем

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = 3 (2 x 9- 0 x 3) - 4 (1 x 9 - 0 x 3) + 5 (1 x 0 - 2 x 2)

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = 22

Пример 2: Найдите определитель следующей матрицы \(\begin{bmatrix} -1 & 2 & -4\\ 7.2& 6& 2.3\\ -5& 1.3 & 3 \end{bmatrix}\) и проверьте это с помощью онлайн-калькулятора определителя.

Решение:

Дано: \(A_{3\times 3}\) = \(\begin{bmatrix} -1 & 2 & -4\\ 7.2& 6& 2.3\\ -5& 1.3 & 3 \ конец{bmatrix}\)

По формуле

\(A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix}\ )

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei - fh) - b(di - fg) + c(dh - eg)

Подстановка этих значений получаем

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = -1 (6 x 3 - 2,3 x 1,3) - 2 (7,2 x 3 - 2,3 x (-5) ) - 4(7,2 x 1,3 - 6 x (-5))

\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = -238,65

Точно так же вы можете попробовать калькулятор определителей, чтобы найти определители для следующего:

• \(\begin{bmatrix} 3. 2 & -2 & 3\\ 1& 0& 4\\ -1& -7 & 4.7 \end{ бматрица}\)
• \(\begin{bmatrix} 8.2 & -3 & 5\\ 1.9& 2.8& -3\\ 9& 1 & 1 \end{bmatrix}\)

☛ Математические калькуляторы:

Калькулятор определителя матрицы nxn

• логин
• Регистр
• Дом
• Математика
• Финансы
• Инженерия

Рассчитайте

Отчет об этом AD

Расчет

14. Это онлайн-инструмент, запрограммированный для вычисления значения определителя заданных входных элементов матрицы. Калькулятор предназначен для вычисления значения определителя матрицы $2\times 2$, $3\times3$ и $4\times 4$. Выберите подходящий калькулятор из списка трех.

Необходимо выполнить следующие шаги:

1. Ввести элементы матрицы в поле. Элементы матриц должны быть действительными числами.
2. Нажмите кнопку " GENERATE WORK ", чтобы выполнить расчет;
3. Калькулятор определителя матрицы nxn выдаст действительное значение, представляющее полезную информацию о матрице.

Ввод: Матрица с действительными элементами;
Вывод: Действительное число.

$2\times 2$ Формула умножения матриц:


Определитель матрицы $A=(a_{ij})_{2\times 2}$ определяется по следующей формуле $$det(A)=|A|=\left| \begin{массив}{cc} а &б\\ CD \\ \конец{массив} \right|=ad-cb$$

$3\times 3$ Формула умножения матриц:

Определитель матрицы $A=(a_{ij})_{3\times 3}$ определяется формулой следующая формула $$\begin{align} det(A)=|A|&=\left| \begin{массив}{ccc} а и б и в \\ д&е&ф \\ г & ч & я \\ \конец{массив} \право| \\&=а\влево| \begin{массив}{cc} е&ф \\ Здравствуй \\ \конец{массив} \право|-b\лево| \begin{массив}{cc} д&ф \\ г & я \\ \конец{массив} \право|+с\лево| \begin{массив}{cc} д & д \\ г & ч \\ \конец{массив} \right|\\& =a(ei-fh)-b(di-fg)+c(dh-eg) \\& =aei+bfg+cdh-ceg-afh-bdi\end{align}$$

$4\times 4$ Формула умножения матриц:

Определитель матрицы $A=(a_{ij})_{4\times 4}$ определяется по следующей формуле $$\begin{align} det(A)=|A|&=\left| \begin{массив}{cccc} а&б&в&г \\ е & ж & г & ч \\ я&й&к&л\\ м&н&о&р\ \конец{массив} \право| \\&=а\влево| \begin{массив}{ccc} ж&г&ч \\ й&к&л \\ н&о&п\ \конец{массив} \право|-b\лево| \begin{массив}{ccc} е & г & ч \\ я&к&л\\ м&о&р\\ \конец{массив} \право|+с\лево| \begin{массив}{ccc} е & ж & ч \\ я & j & л \\ м&н&п\ \конец{массив} \право|-d\лево| \begin{массив}{ccc} е & ж & г \\ я & j & k \\ м&н&о \\ \конец{массив} \право| \end{выравнивание}$$

Понятие определителя матрицы появилось в Германии и Японии практически в одно и то же время. Секи впервые написал об этом в 1683 г. его метод решения скрытых проблем. Секи разработал шаблон для определителей для $2 \times 2$, $3 \times 3$, Матрицы $4\times 4$ и $5\times 5$ и использовали их для решения уравнений. В том же году Г. Лейбниц написал о методе решения система уравнений. Этот метод известен как правило Крамерса. Определитель квадратной матрицы $A$ — это уникальное вещественное число, являющееся атрибутом матрицы $A$. Определитель матрицы $A$ обозначается через $det(A)$ или $|A|$.

Как найти определитель матрицы?

Рассмотрим матрицу $A=\left[ \begin{массив}{cc} а &б\\ CD \\ \конец{массив} \right]$ размера $2\times2$. Настоящее число $$\left|\begin{массив}{cc} а &б\\ CD \\ \конец{массив} \right|=ad-cb$$ является определителем матрицы $A$. Точнее, чтобы найти определитель матрицы $2\times 2$, нам нужно выполнить следующие шаги:

• Умножить элемент в первой строке и первом столбце на элементы во второй строке и втором столбце;
• Умножить элемент в первой строке и втором столбце на элемент во второй строке и первом столбце;
• Определитель матрицы $2\times 2$ равен разнице между вторым произведением и первым произведением.

Минор элемента любого $n\times n$ матричного определителя есть $(n-1)\times (n-1)$ матричный определитель. Если мы удалим строку и столбец, содержащие элемент, то получим соответствующий минор. Например, минор элемента $a$, элемента первой строки и первого столбца определителя

Чтобы вычислить определитель $n\times n$ матрицы, нужно разложить определитель по минорам. Во-первых, мы выбираем строку в матрице. В каждой позиции в строке мы умножаем количество элементов на его младший умножить на знак положения и добавить все суммы для всей строки. Знаки положения в матрице плюс или минус в зависимости от положения элемента. Например, знаки положения в матрице $3\times 3$ равны $$\слева[ \begin{массив}{ccc} + & - & + \\ -& + & - \\ + & - & + \\ \конец{массив} \право]$$ Это означает, что $$\begin{align} det(A)=|A|&=\left| \begin{массив}{ccc} а и б и в \\ д&е&ф \\ г & ч & я \\ \конец{массив} \право| \\&=а\влево| \begin{массив}{cc} е&ф \\ Здравствуй \\ \конец{массив} \право|-b\лево| \begin{массив}{cc} д&ф \\ г & я \\ \конец{массив} \право|+с\лево| \begin{массив}{cc} д & д \\ г & ч \\ \конец{массив} \right|\end{выравнивание}$$ Если мы применим этот метод для вычисления определителя $4\times 4$, мы получим $$\begin{align} det(A)=|A|&=\left| \begin{массив}{cccc} а&б&в&г \\ е & ж & г & ч \\ я&й&к&л\\ м&н&о&р\ \конец{массив} \право| \\&=а\влево| \begin{массив}{ccc} ж&г&ч \\ й&к&л \\ н&о&п\ \конец{массив} \право|-b\лево| \begin{массив}{ccc} е & г & ч \\ я&к&л\\ м&о&р\\ \конец{массив} \право|+с\лево| \begin{массив}{ccc} е & ж & ч \\ я & j & л \\ м&н&п\ \конец{массив} \право|-d\лево| \begin{массив}{ccc} е & ж & г \\ я & j & k \\ м&н&о \\ \конец{массив} \право| \end{выравнивание}$$ Для каждого элемента исходной матрицы его минор является определителем $3\times 3$.

Существует еще один способ вычисления определителя $3\times 3$, хорошо известный как правило Сарруса или схема Сарруса.

• Расширьте определитель, переписав первые два столбца чисел:
• Сложите произведения красных диагоналей и вычтите произведения синих диагоналей, т.е. $$det(A)=aei+bfg+cdh-ceg-afh-bdi$$ Это правило можно запомнить, вспомнив о диагоналях расширенного определителя прочитанные диагонали означают плюс $(aei+bfg+cdh)$, а синие диагонали означают минус $(-ceg-afh-bdi)$.

Правило Сарруса неприменимо для вычисления определителя $4\times 4$, оно требует некоторых модификаций. Например, найдем определитель матрицы $3\times 3$ $$\left|\begin{массив}{ccc} 10 и 20 и 10\ 4 и 5 и 6 \\ 2 и 3 и 5 \\ \конец{массив} \right|$$ Используя правило Сарруса, получаем $$\left|\begin{массив}{ccc|cc} 10 и 20 и 10 и 10 и 20 \\ 4 и 5 и 6 и 4 и 5 \\ 2 & 3 & 5 & 2 & 3 \\ \конец{массив} \right.=10\cdot5\cdot5+20\cdot6\cdot2+10\cdot4\cdot 3-10\cdot5\cdot2-10\cdot6\cdot3-20\cdot4\cdot5=-70$$ Работа определителя матрицы $n\times n$ с шагами показывает полный пошаговый расчет для нахождение определителя $3\times 3$ матрицы $A$ по формуле определителя. За любые другие матрицы, просто укажите действительные числа в качестве элементов матрицы и нажмите кнопку GENERATE WORK. Учащиеся начальной школы и люди, изучающие математику, используют этот калькулятор определителя матрицы nxn для создания работать, проверять результаты вычисления определителя матрицы, полученные вручную, или эффективно выполнять домашние задания. Учащиеся начальной школы также могут использовать этот калькулятор для решения системы линейных уравнений.

Реальные задачи с использованием определителя матрицы

В геометрической прогрессии определитель представляет объем $n$-мерного параллелепипеда, натянутого на вектор-столбец или вектор-строку матрицы. Векторное произведение и скалярное произведение — это два способа умножения векторов, применимые практически во всех областях науки. Если векторы выразить через единичные векторы $\vec i, \vec j,$ и $\vec k$ в направлениях $x, y,$ и $z$, то векторное произведение двух векторов $\vec a=(x_a,y_a,z_a)$ и $\vec b=(x_b,y_b,z_b)$ $$\left|\begin{массив}{ccc} \vec i & \vec j &\vec k \\ х_а& х_б & х_с \\ y_a & y_b & y_c \\ \конец{массив} \право|$$ Определитель можно использовать для вычисления площадей параллелограммных песчаных треугольников на координатной плоскости. Например, площадь треугольника $\Delta ABC$ с $A(x_A,y_A)$, $B(x_B,y_B)$ и $C(x_C,y_C)$ определяется по формуле $$A(\Delta ABC)=\frac12|\left|\begin{массив}{ccc} х_А и у_А &1 \\ х_В& у_В&1 \\ х_С &у_С&1 \\ \конец{массив} \право| |$$ Еще одним важным применением определителя матрицы является решение систем линейных уравнений, так называемое правило Крамера. Определитель сообщает нам, имеет ли система единственное решение. Определитель также может быть полезен при нахождении обратной невырожденной матрицы и т. д.

Определяющая матрица Практические задачи

Практическая задача 1 :
Найдите векторное произведение векторов $\vec a=(1,-3,0)$ и $\vec b=(3,5,7). $

Практическая задача 2 :
Дан треугольник $\Delta ABC$ с $A(0,0)$, $B(3,4)$ и $C(-2,5)$. С помощью определителя найдите площадь треугольника $\Delta ABC$.

Калькулятор определителя матрицы nxn, формула, пример расчета (работа с шагами), задачи из реальной жизни и практические задачи будут очень полезны учащимся начальной школы (образование K-12) для понимания концепции определителя матрицы. Эта концепция используется практически во всех областях науки, поэтому она будет полезна при решении более сложных задач.

• Transpose Matrix Calculator
• nxn Inverse Matrix Calculator
• 4x4 Matrix Addition & Subtraction Calculator
• 3x3 Matrix Addition Calculator
• 3x3 Matrix Subtraction Calculator
• 2x2 Matrix Addition & Subtraction Calculator

• 4x4 Matrix Multiplication Calculator
• Калькулятор умножения матриц 3x3
• Калькулятор умножения матриц 2x2
• Калькулятор квадратной матрицы
• Калькулятор исключения Гаусса

Калькулятор определителя онлайн - Solumaths

Определитель, расчет онлайн

Резюме:

Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.

определитель онлайн

---

Описание :

Калькулятор определителей позволяет найти определители онлайн. Калькулятор может рассчитать определитель двух векторов , определитель трех векторов или определитель матрицы .

Определитель двух векторов

В ортонормированной системе координат (O,`vec(i)`,`vec(j)`) вектор `vec(u)` имеет координаты (x,y) (`vec(i)`,`vec(j)`), вектор `vec(v)` имеет координаты (x',y'). Определитель vec(u) и vec(v) равен число хх'-уу'.

Калькулятор может вычислять определители давать точные результаты: вычислять определитель (3,`1/2`) и (`4/5`,2), введите определитель(`[[3;1/2];[4/5;2]]`), после расчета возвращается результат.

Калькулятор позволяет производить символьные расчеты, можно использовать буквы: к вычислить определитель двух векторов следующим образом: (a,b) и (3a,2), введите определитель(`[[a;b];[3a;2]]`), после расчета возвращается результат.

Примечание. Когда определитель двух векторов равен нулю, эти два вектора коллинеарны.

Определитель трех векторов

В ортонормированной системе координат (O,`vec(i)`,`vec(j)`,`vec(k)`) вектор `vec(u)` имеет координаты ( х, у, г) , вектор `vec(v)` имеет координаты (x',y',z'), вектор `vec(k)` имеет координаты (x'',y'',z''). Определитель vec(u)`, `vec(v)`, `vec(k)` равен числу xy'z''+x'y''z+x''yz'-xy'' z'-x'yz''-x''y'z.

Чтобы вычислить определитель трех векторов , используйте следующий синтаксис: определитель(`[[3;1;0];[3;2;1];[4;0;7]]`).

Определитель матрицы

Калькулятор определителя можно использовать с квадратными матрицами порядка n, он также может выполнять символьные вычисления. Чтобы вычислить определитель матрицы , используйте следующий синтаксис: определитель(`[[3;1;0];[3;2;1];[4;1;2]]`).

Синтаксис:

определитель(матрица)

---

Примеры:

определитель(`[[3;1;0];[3;2;1];[4;1;7]]`), возвращает 22

Рассчитать онлайн с определителем (калькулятор определителя)

См. также

Список связанных калькуляторов:

• Векторный калькулятор : vector_calculator. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
• Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
• Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
• Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
• Вычисление нормы вектора : vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
• Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
• Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

  No related posts.