Методы вычисления площади фигуры, ограниченной линиями » Kupuk.net
Существует тип задач из области высшей математики, в которых нужно вычислить площадь фигуры, ограниченной линиями. В этом случае необходимо использовать интегралы. Однако в интернете слишком много неправильных методов решения. Это может существенно замедлить обучение, поэтому следует запомнить алгоритм нахождения площади.
Общие сведения
Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.
Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.
Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.
Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.
Информация об интегралах
С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.
Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.
Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.
Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.
Для нахождения первообразной используется специальная таблица интегралов:
Рисунок 1. Таблица интегралов и их первообразные.
В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Криволинейные фигуры
Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.
Рисунок 2. Фигуры с криволинейными сторонами.
Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.
Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).
Способы вычисления и рекомендации
Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.
Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.
Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.
Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:
Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.
Основной алгоритм
При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:

Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.
Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
Во всех остальных случаях изображается декартовая система координат.
Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.
Следующим шагом является правильное изображение прямых
. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой. После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции.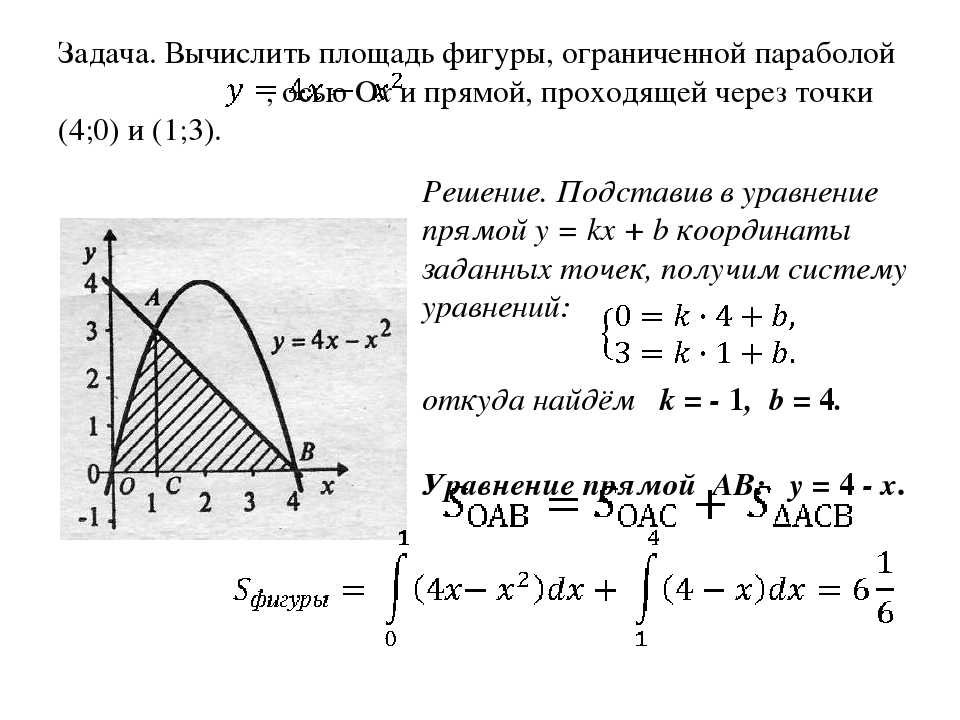 2
2
Вычислить площадь фигуры ПРИМЕРЫ
Вычислить площадь фигуры, ограниченной линиями .
Решение.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
или .
Находим: x1 = -2, x2 = 4.
Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
По формуле Ньютона-Лейбница находим:
Найти площадь области, ограниченной эллипсом .
Решение.
Из уравнения эллипса для I квадранта имеем . Отсюда по формуле получаем
Применим
подстановку x = a sin t, dx = a cos t dt. Новые пределы интегрирования t = α и t = β определяются
из уравнений 0 = a sin t, a = a sin t.
Можно положить α =
0 и β = π/2.
Новые пределы интегрирования t = α и t = β определяются
из уравнений 0 = a sin t, a = a sin t.
Можно положить α =
0 и β = π/2.
Находим одну четвертую искомой площади
Отсюда S = πab.
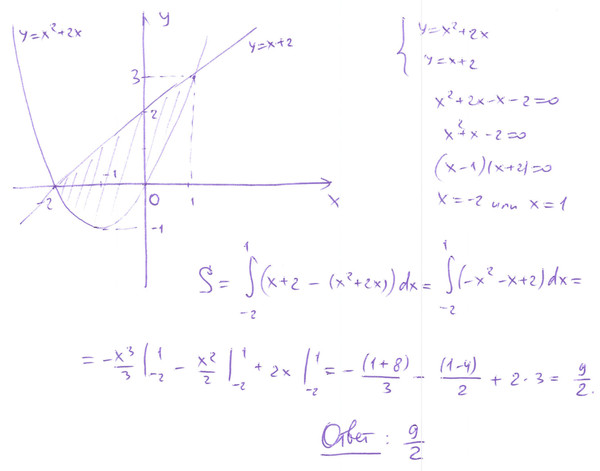
Найти площадь фигуры, ограниченной линиями y = —x2 + x + 4 и y = —x + 1.
Решение.
Найдем
точки пересечения линий y =
—x2 + x +
4, y =
—x +
1, приравнивая ординаты линий: —x2 + x +
4 = —x +
1 или x2 —
2x —
3 = 0. Находим корни x1 =
-1, x2 =
3 и соответствующие им ординаты y1 =
2, y2 =
-2.
По формуле площади фигуры получаем
Определить площадь, ограниченную параболой y = x2 + 1 и прямой x + y = 3.
Решение.
Решая систему уравнений
находим абсциссы точек пересечения x1 = -2 и x2 = 1.
Полагая y2 = 3 — x и y1 = x2 + 1, на основании формулы получаем
Вычислить площадь, заключенную внутри лемнискаты Бернулли r2 = a2cos 2φ.
Решение.
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ1 = ʅ и φ2 = ʆ, выразится интегралом
В силу симметрии кривой определяем сначала одну четвертую искомой площади
Следовательно,
вся площадь равна S = a2.
Вычислить длину дуги астроиды x2/3 + y2/3 = a2/3.
Решение.
Запишем уравнение астроиды в виде
(x1/3)2 + (y1/3)2 = (a1/3)2.
Положим x1/3 = a1/3cos t, y1/3 = a1/3sin t.
Отсюда получаем параметрические уравнения астроиды
x = a cos3t, y = a sin3t, (*)
где 0 ≤ t ≤ 2π.
Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π/2.
Получаем
dx =
-3a cos2t sin t
dt, dy =
3a sin2t cos t
dt.
Отсюда находим
Интегрируя полученное выражение в пределах от 0 до π/2, получаем
Отсюда L = 6a.
Найти площадь, ограниченную спиралью Архимеда
r = aφ и двумя радиусами-векторами, которые соответствуют полярным углам φ1и φ2 (φ1 < φ2).Решение.
Площадь, ограниченная кривой r = f(φ) вычисляется по формуле , где α и β — пределы изменения полярного угла.
Таким образом, получаем
(*)
Из (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ1 = 0; φ2 = 2π):
Аналогичным образом находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда (φ1 = 2π; φ2 = 4π):
Искомая площадь равна разности этих площадей
Вычислить
объем тела, полученного вращением вокруг
оси Ox фигуры,
ограниченной параболами y = x2 и x = y2.
Решение.
Решим систему уравнений
и получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:
Вычислить площадь, ограниченную осью
Ox и синусоидой y = sin x на отрезках: а) [0, π]; б) [0, 2π].Решение.
а) На отрезке [0, π] функция sin x сохраняет знак, и поэтому по формуле , полагая y = sin x, находим
б)
На отрезке [0, 2π],
функция sin x меняет
знак. Для корректного решения задачи,
необходимо отрезок [0, 2π]
разделить на два [0, π]
и [π,
2π],
в каждом из которых функция сохраняет
знак.
Для корректного решения задачи,
необходимо отрезок [0, 2π]
разделить на два [0, π]
и [π,
2π],
в каждом из которых функция сохраняет
знак.
По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус.
В итоге, искомая площадь равна
Определить объем тела, ограниченного поверхностью, полученной от вращения эллипса
Решение.
Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Oxплощади OAB, равной одной четверти площади эллипса, и полученный результат удвоить.
Обозначим объем тела вращения через Vx; тогда на основании формулы имеем , где 0 и a — абсциссы точек B и A. Из уравнения эллипса находим . Отсюда
Таким
образом, искомый объем равен . (При вращении эллипса вокруг малой
оси b,
объем тела равен )
(При вращении эллипса вокруг малой
оси b,
объем тела равен )
Найти площадь, ограниченную параболами y2 = 2px и x2 = 2py.
Решение.
Сначала найдем координаты точек пересечения парабол, чтобы определить отрезок интегрирования. Преобразуя исходные уравнения, получаем и . Приравнивая эти значения, получим или x4 — 8p3x = 0.
Отсюда
x4 — 8p3x = x(x3 — 8p3) = x(x — 2p)(x2 + 2px + 4p2) = 0.
Находим корни уравнений:
Учитывая
то факт, что точка A пересечения
парабол находится в первой четверти,
то пределы интегрирования x =
0 и x =
2p.
Искомую площадь находим по формуле
Вычислить площадь фигуры ограниченной линиями с примерами решения
Содержание:
- Примеры с решением
Пусть требуется найти площадь фигуры, ограниченной графиками функций и . Площадь требуемой фигуры на рисунке можно найти, вычитая из площади площадь
| Каждую площадь можно вычислить как определенный интеграл на заданном промежутке. |
Эти суждения можно обобщить следующим образом.
Так как функции и непрерывны на отрезке и на этом отрезке выполняется условие (т.е.график функции ) расположен выше графика функции то площадь ограниченная графиками функций и прямыми можно выразить следующим выражением:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Графики функций не имеют общих точек.
Примеры с решением
Пример 1.
Найдите площадь, ограниченную графиками функций и и прямыми
Решение:
=
Графики функций пересекаются в двух точках.
Пример 2.
Найдите площадь, ограниченную графиками функций
Решение:
Найдем абсциссы точек пересечения графиков функций.
Полученные значения являются границами определенного интеграла.
Возможно вам будут полезны данные страницы:
Показательное распределение |
Метод неопределенных коэффициентов |
Площадь фигуры ограниченной линиями |
Правило Лопиталя: пример решения |
Пример 3.
Найдите площадь, заключенную между графиками функций и
Решение:
Найдем абсциссы точек пересечени графиков.
Значит, графики пересекаются в точках с абсциссами По графикам функций также видно, что площадь, которую мы должны найти, состоит из площади, ограниченной графиками на промежутке и на промежутке На промежутке выполняется условие на промежутке выполняется условие (разность функций учитываются при записи интеграла).
! Вычислите требуемую площадь при помощи интеграла
Какой результат вы получили?
Пример 4.
Члены школьного клуба юных конструкторов работают над созданием нового двигателя для автомобиля, который будет меньше засорять окружающую среду. Для нового мотора изменение количества частиц (млрд), загрязняющих атмосферу, в год можно выразить следующим образом: Количество загрязняющих частиц, выбрасывамых старым мотором имеет вид:
a) В какой год они будут выбрасывать в атмосферу одинаковое количество частиц?
b) Какова разница между количеством вредных частиц, выброшенных в атмосферу, за этот период
Решение:
а) при удовлетворяющего условию количество вредных частиц будет одинаково.
Значение не соответствует смыслу задачи. На 3-ий год новый мотор будет давать такое же количество вредных частиц, как и старый. b) Разность количества вредных частиц равна разности площадей на промежутке [0;3].
(млрд. частиц)
Пример 5.
Вычислить площадь фигуры, ограниченной параболой и окружностью
Решение:
Сначала схематически изобразим эту площадь. Из рисунка видим
что заданные кривые ограничивают две различающиеся плоские фигуры (меньшую и большую). Каждая из этих фигур, в свою очередь, состоит из двух симметричных относительно оси частей.
Поэтому достаточно вычислить площадь верхней части каждой фигуры и затем умножить ее на два.
Найдем сначала площадь меньшей фигуры. Преобразуем уравнение окружности и определим координаты ее центра и величину радиуса.
Следовательно, центр окружности находится в точке а ее радиус Найдем точки и пересечения обеих линий, решая систему двух
уравнений
Найдем уравнение границы (части окружности) Из условия на ординаты точек границы имеем
по этой же причине уравнение нижней части границы на отрезке
По формуле (1) находим
но
— это площадь четверти окружности. Площадь всей окружности равна Второй интеграл легко вычисляется Теперь найдем искомую площадь
Площадь всей окружности равна Второй интеграл легко вычисляется Теперь найдем искомую площадь
Теперь, чтобы найти площадь большей фигуры, необходимо из площади круга вычесть площадь меньшей фигуры:
Проверим значение первого интеграла
Обозначим
тогда при при (четвертая четверть). Поэтому
Пример 6.
Вычислить площадь фигуры, ограниченной линиями и
Решение:
Второе уравнение запишем так , отсюда следует, что это означает, что вся фигура (парабола) расположена левее точки она симметрична относительно оси так как при замене на уравнение не изменяется. Ветви параболы направлены влево; ее вершина находится в точке Определим точки ее пересечения с осью
Ветви второй параболы направлены также влево, а ее вершина совпадает с началом координат.
Определим точки пересечения этих кривых из решения системы
Одна точка пересечения вторая —
Изобразим эту фигуру на чертеже.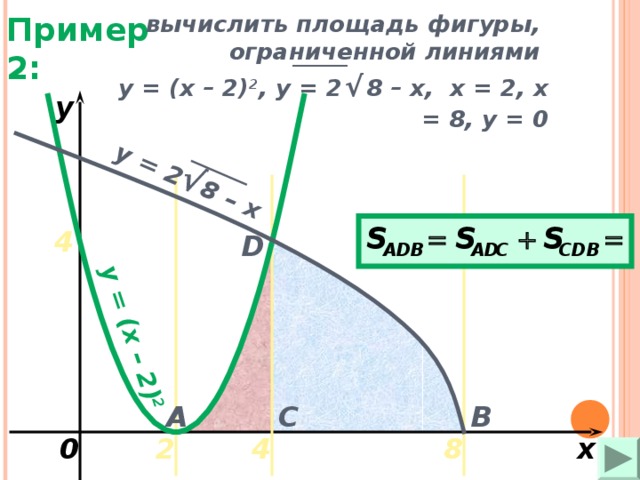 Здесь проще вычислить площадь по формуле (2) т. е.
Здесь проще вычислить площадь по формуле (2) т. е.
Методы вычисления площади фигуры, ограниченной линиями
Существует тип задач из области высшей математики, в которых нужно вычислить площадь фигуры, ограниченной линиями. В этом случае необходимо использовать интегралы. Однако в интернете слишком много неправильных методов решения. Это может существенно замедлить обучение, поэтому следует запомнить алгоритм нахождения площади.
Содержание
- Общие сведения
- Информация об интегралах
- Криволинейные фигуры
- Способы вычисления и рекомендации
- Основной алгоритм
- Примеры решения
- Разновидность параболы
- Гипербола, степенная и прямая
Общие сведения
Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.
Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.
Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.
Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.
Информация об интегралах
С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.
Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.
Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.
Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.
Для нахождения первообразной используется специальная таблица интегралов:
Рисунок 1. Таблица интегралов и их первообразные.
В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Криволинейные фигуры
Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.
Рисунок 2. Фигуры с криволинейными сторонами.
Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.
Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).
Способы вычисления и рекомендации
Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.
Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.
Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.
Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:
Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.
Основной алгоритм
При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:
Алгоритм имеет следующий вид:
Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.
Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.
Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.
После всех операций образуется фигура, которая ограничена линиями. 2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).
2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).
Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.
Предыдущая
МатематикаФормулы площадей всех фигур
Следующая
МатематикаКорень уравнения — определение в математике, формулы нахождения
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 16 из 17Следующая ⇒
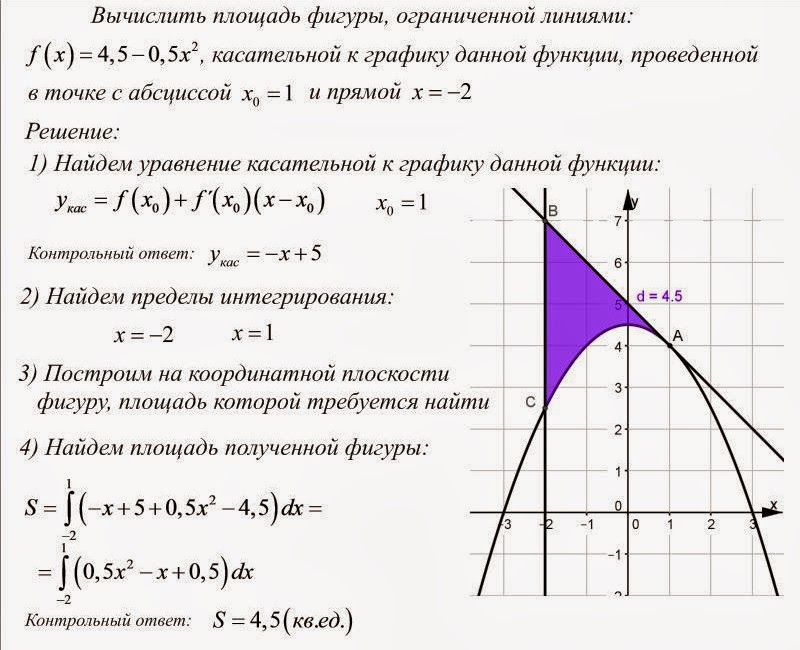
Пример: Найдите площадь фигуры, ограниченной параболой и осью OX.
Пример: Вычислите площадь фигуры, ограниченной линиями , . Решение. Находим точки пересечения линий: . Получаем . Вычисляем площадь: . Пусть функция — непрерывна на [a;b] и для всех . Рассмотрим фигуру Ф, симметричную фигуре F относительно оси OX. , . Таким образом, .
Если конечное число раз меняет знак на отрезке [a;b], то интеграл по отрезку [a;b] разбиваем на сумму интегралов по частичным отрезкам. Интеграл будет положителен на тех отрезках, где , и отрицателен там, где . Тогда сумма площадей вычисляется по формуле: .
2. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями. Пусть криволинейная трапеция ограничена кривой, заданной в параметрической форме где , , .
Пример: Вычислите площадь области, ограниченной эллипсом . Решение. . Площадь криволинейного сектора в полярных координатах.
Пример: Найдите площадь фигуры, ограниченной улиткой Паскаля .
Вычисление длины дуги плоской кривой
Если кривая на отрезке [a;b] – гладкая (т.е. производная непрерывна), то длина соответствующей дуги этой кривой находится по формуле . Пример: Вычислите длину дуги цепной линии от до . Решение. , , Тогда . При параметрическом задании кривой , , где и – непрерывно дифференцируемые функции, длина дуги кривой, соответствующая изменению параметра t от до выражается интегралом . Если гладкая кривая задана в полярных координатах уравнением , где , то длина дуги равна .
Вычисление объёма тела вращения
Если криволинейная трапеция, ограниченная кривой и прямыми x=a, x=b, вращается вокруг оси OX, то объем тела вращения вычисляется по формуле . Если криволинейная трапеция, ограниченная кривой и прямыми y=c, y=d, вращается вокруг оси OY, объем тела вращения равен . Пример: Вычислите объём тела, полученного от вращения фигуры, ограниченной параболой , вокруг оси OX. Решение. .
⇐ Предыдущая891011121314151617Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Калькулятор площади между двумя кривыми
Используйте этот калькулятор площади между двумя кривыми, чтобы найти площадь между двумя кривыми на заданном интервале, соответствующем разнице между определенными интегралами. В координатной плоскости общая площадь занята между двумя кривыми, а калькулятор площади между кривыми вычисляет площадь путем решения определенного интеграла между двумя различными функциями.
Итак, давайте начнем читать, как найти площадь между двумя кривыми, используя определенное интегрирование, но сначала вам нужно рассмотреть некоторые основы прямо сейчас!
Что такое rea Между двумя кривыми? В математике площадь между двумя кривыми можно вычислить с помощью разницы между определенным интегралом двух точек или выражений. В двумерной геометрии площадь может быть выражена областью, покрываемой двумя разными кривыми. Для вычисления площади требуются две функции: f(x) и g(x), а также интегральные пределы от a до b, где b должно быть больше, чем \(a, b>a\) выражения.
В двумерной геометрии площадь может быть выражена областью, покрываемой двумя разными кривыми. Для вычисления площади требуются две функции: f(x) и g(x), а также интегральные пределы от a до b, где b должно быть больше, чем \(a, b>a\) выражения.
\(Y = f (x) \text{ где x} = a, x = b\)
\(Y = f (x)\) между пределами a и b
Формула площади между двумя Кривые:Мы можем найти площади между кривыми, используя стандартную формулу, если у нас есть две разные кривые
$$m = f (x) & m = g (x)$$
(x) \text{ больше} g (x)\)
Таким образом, площадь, ограниченная двумя линиями\( x = a \text{ и} x = b\), равна
$$A = ∫ab[f (x) – g (x)] dx$$
Итак, калькулятор площади между двумя кривыми вычисляет площадь пересечения двух кривых, используя эту стандартную формулу.
Однако онлайн-калькулятор интегралов позволяет вам вычислять интегралы функций по соответствующей переменной.
Вычисление площади между кривыми:Чтобы найти площадь между двумя кривыми, вот простые рекомендации:
- Нужны две кривые: \(y = f (x), \text{ и} y = г (х)\)
- Найдите точки пересечения кривых, добавив одно значение уравнения в другое, и составьте уравнение, которое имеет только одну переменную.

- Решите данное выражение, найдите точки пересечения и нарисуйте график для заданной точки пересечения и кривых.
- Итак, площадь равна \(A = ∫ab [f(x)-g(x)] dx\) и подставим эти значения в данную формулу.
- Затем выполните определенное интегрирование и измените значения, чтобы получить результат.
Вы можете мгновенно рассчитать площадь и определенный интеграл, подставив выражения в калькулятор площади между двумя кривыми. 92/2]30$$
$$= – [(0+0) – (- 33/4*3 – 3/4 * 32/2)$$
$$= – (-27/12 + 3/4 * 9/2)$$
$$A= 27/24$$
Площадь по определенному интегралу равна\( \frac{-27}{24}\).
Кроме того, онлайн-калькулятор производных позволяет определить производную функции по заданной переменной.
Как работает калькулятор rea между двумя кривыми?Калькулятор площади между кривыми найдет площадь между кривыми со следующими шагами:
Ввод:- Введите два разных выражения кривых относительно \(x или y\).

- Установите определенные верхний и нижний пределы для кривых
- Нажмите кнопку расчета для дальнейшего процесса.
Калькулятор отображает следующие результаты для площади между двумя кривыми:
- Отобразите введенные данные в виде правильного уравнения, которое вы введете в соответствующие поля.
- Показывает область, между которой находятся две кривые со всеми шагами интегрального расчета.
Если обе кривые лежат на оси x, площади между кривыми будут отрицательными (-). Однако значение со знаком является окончательным ответом.
Почему мы используем только определенный интеграл для нахождения площади, ограниченной кривыми? Калькулятор площади между кривыми находит площадь по разным функциям, только неопределенные интегралы, потому что неопределенные как раз показывают семейство разных функций, а также используют для нахождения площади между двумя кривыми, которые интегрируют разность выражений.
Неопределенный интеграл показывает семейство различных функций, производными которых являются f. Различия между двумя функциями в семье просто постоянны. А определенный интеграл представляет числа, когда верхний и нижний пределы являются константами.
EndNote:Чтобы найти площадь между кривыми без графика, используйте этот удобный калькулятор площади между двумя кривыми. По сути, площадь между кривой означает величину количества, которая получается произведением величин, обозначенных осями x и y. Таким образом, онлайн-калькулятор площади между кривыми — лучший способ точно указать величину величины.
Ссылка:Из источника Википедии: Единицы, Преобразования, Неметрические единицы, Площадь четырехугольника.
Из источника Brilliant: Площадь между кривой и осью x, Площадь между кривой и линией, Площадь между 2 кривыми.
Из источника Math Online: Areas Between Curves, нижняя кривая g, верхняя кривая f.
Area Between Two Curves Calculator
Related Content
report this ad
y = f(x) =
y = g(x) =
On interval : заключенный в кривые пользовательский ввод
Решение:
Площадь между двумя кривыми Урок
Содержание урока
Что такое площадь между двумя кривыми?
Заштрихованная желтым цветом область на изображении ниже является примером области между двумя кривыми. Эта область представляет собой двумерное пространство, ограниченное кривой верхней функции, кривой нижней функции, левой конечной точкой интервала и правой конечной точкой интервала.
Почему мы изучаем площадь между двумя кривыми?
Когда мы впервые узнаем об интегралах для нахождения площади под кривой, мы получаем первое представление о полезности исчисления для работы со сложными системами реального мира. Основным примером этого является использование суммы Римана для аппроксимации расстояния, пройденного транспортным средством, путем нахождения площади под кривой зависимости скорости от времени.
Основным примером этого является использование суммы Римана для аппроксимации расстояния, пройденного транспортным средством, путем нахождения площади под кривой зависимости скорости от времени.
Но что мы можем сделать, найдя площадь между и кривыми? Ну, скажем, таскаем гоночные машины по трассе по выходным. Перед каждой гонкой мы гарантируем, что наша система сбора данных внутри автомобиля настроена на запись нашей скорости через заданные промежутки времени в течение всей продолжительности каждого заезда против нашего соперника, с которым мы участвуем. У нашего оппонента такая же система сбора данных, которая записывает те же данные в те же промежутки времени.
Гоночная машина на дрэг-стрипе После каждой гонки на четверть мили мы хотели бы узнать дистанцию разрыва между нашей машиной и нашим соперником. Для этого мы собираем данные (скорость в зависимости от времени) от обеих машин и находим площадь 90 209 между 90 210 двумя кривыми скорости на протяжении всего рассматриваемого пробега на четверть мили. Это покажет нам взаимное смещение наших машин, когда победитель доедет до финиша.
Это покажет нам взаимное смещение наших машин, когда победитель доедет до финиша.
Другими словами, найдя площадь между этими двумя кривыми скорости, мы можем определить расстояние разрыва между двумя автомобилями в течение заданного интервала времени в гонке. 9{b} \left( \text{Верхняя функция} – \text{Нижняя функция} \right) \; dx, \hspace{3ex} a \leq x \leq b \end{align}$$
Где A — площадь между кривыми, a — левая конечная точка интервала, b — правая конечная точка интервала, Верхняя функция — это функция x , которая имеет большее значение на интервале, а Нижняя функция — это функция x , которая имеет меньшее значение на интервале.
Мы можем указать интервал x = [a, b] (что эквивалентно a ≤ x ≤ b ) при нахождении площади между двумя кривыми. Однако, если две кривые имеют по крайней мере две точки пересечения, мы также можем использовать интервал, определяющий площадь, заключенную между двумя кривыми.
Давайте посмотрим на изображение ниже в качестве примера. Синяя кривая представляет f(x) = x , а красная кривая представляет g(x) = x 3 . Кривые этих двух функций пересекаются в трех точках: х = -1 , х = 0 и х = 1 . Поэтому площадь, заключенная между ними, определяется интервалом x = [-1, 1] .
Зная интервал, на котором мы работаем, мы должны определить верхнюю и нижнюю функции для подинтервала(ов). В некоторых случаях будет только один подинтервал, который сам является основным интервалом. В других случаях будет более одного подинтервала, где кривые пересекают друг друга и меняют положение в качестве верхней и нижней функций, как, например, на изображении непосредственно выше.
Мы можем визуально определить верхнюю и нижнюю функции для каждого подинтервала, просмотрев график кривых. Если график кривых недоступен, мы можем оценить значение каждой функции в середине каждого подинтервала.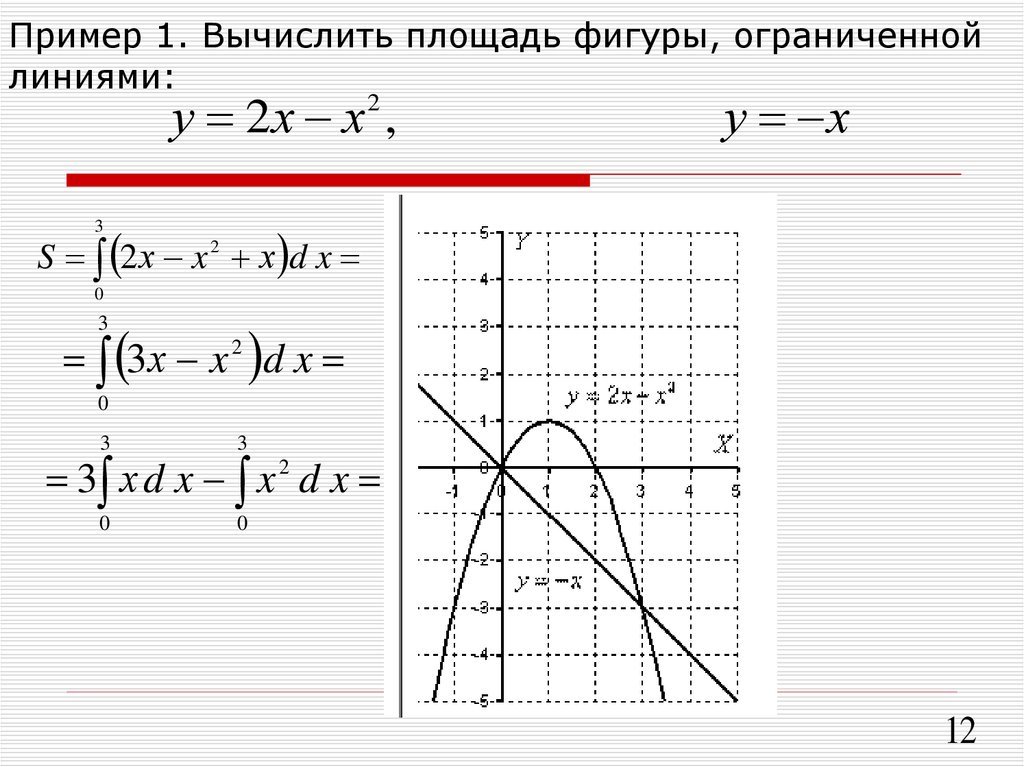 Например, подинтервал x = [2, 4] имеет среднюю точку x = 3 . Поэтому мы подставим x = 3 в каждую функцию и оценим, какое из них имеет большее значение, а какое меньшее в этой точке.
Например, подинтервал x = [2, 4] имеет среднюю точку x = 3 . Поэтому мы подставим x = 3 в каждую функцию и оценим, какое из них имеет большее значение, а какое меньшее в этой точке.
Зная верхнюю и нижнюю функции для одного или нескольких подинтервалов, мы можем установить формулу площади для каждого подинтервала. После решения каждого интеграла формулы площади мы суммируем результаты каждого, чтобы определить общую площадь между кривыми на нашем интервале. Для проблемы с 92 = x\\ \\ & \hspace{3ex} \text{Решая относительно x, получаем: } \: x = 0,00000, \: x = 1,00000\\ \\ & \hspace{3ex} \text{Наш подынтервал (s): } \:x = [0,000, 1,000]\\ \\ \\ & \text{3.) Теперь мы должны определить верхнюю и нижнюю функции для площади} \\ \\ & \hspace{3ex } \text{формульные интегралы). Для этого мы сравним значение каждой} \\ \\ & \hspace{3ex} \text{функции в середине каждого подынтервала.}\\ \\ & \hspace{3ex} \text{3.1) середина подынтервала } x = [0, 1] \text{ находится в точке } x = \frac{0 + 1}{2} = 0,500\\ \\ & \hspace{5ex} \text{Вычисляя каждую функцию в этой получаем:} \\ \\ & \hspace{5ex}f(0,500) = {\left(\frac{1}{2}\right)}^{2} = 0,250, \; g(0,500) = \left(\frac{1}{2}\right) = 0,500\\ \\ & \hspace{5ex} \text{Для} x = [0, 1]:\text{Верхняя функция = } x, \;\text{Нижняя функция = } x^2\\ \\ \\ & \text{4. {1,00000} = 0,16667\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \ hspace{3ex} A = \fbox{0.16667} \end{align}$$ 93\\ \\ & \hspace{3ex} \text{Находя x, получаем: } \: x = -3.00000, \: x = 0.00000, \: x = 3.00000\\ \\ & \hspace{3ex} \text{Наши подинтервалы: } \:x = [-4.000, -3.000], \:x = [-3.000, 0.000], \:x = [0.000, 3.000], \:x = [3.000 , 4.000]\\ \\ \\ & \text{3.) Теперь мы должны определить верхнюю и нижнюю функции для площади} \\ \\ & \hspace{3ex} \text{формула интеграл(ы). Для этого мы сравним значение каждой} \\ \\ & \hspace{3ex} \text{функции в середине каждого подынтервала.}\\ \\ & \hspace{3ex} \text{3.1) середина подинтервала } x = [-4, -3] \text{ находится в } x = \frac{-4 + -3}{2} = -3,500\\ \\ & \hspace{5ex} \text{ Вычисляя каждую функцию в этой точке, мы получаем:} \\ \\ & \hspace{5ex}f(-3,500) = 9{4.00000} = 12.25000\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \hspace{3ex} A = 12.25000 + 20.25000 + 20.
{1,00000} = 0,16667\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \ hspace{3ex} A = \fbox{0.16667} \end{align}$$ 93\\ \\ & \hspace{3ex} \text{Находя x, получаем: } \: x = -3.00000, \: x = 0.00000, \: x = 3.00000\\ \\ & \hspace{3ex} \text{Наши подинтервалы: } \:x = [-4.000, -3.000], \:x = [-3.000, 0.000], \:x = [0.000, 3.000], \:x = [3.000 , 4.000]\\ \\ \\ & \text{3.) Теперь мы должны определить верхнюю и нижнюю функции для площади} \\ \\ & \hspace{3ex} \text{формула интеграл(ы). Для этого мы сравним значение каждой} \\ \\ & \hspace{3ex} \text{функции в середине каждого подынтервала.}\\ \\ & \hspace{3ex} \text{3.1) середина подинтервала } x = [-4, -3] \text{ находится в } x = \frac{-4 + -3}{2} = -3,500\\ \\ & \hspace{5ex} \text{ Вычисляя каждую функцию в этой точке, мы получаем:} \\ \\ & \hspace{5ex}f(-3,500) = 9{4.00000} = 12.25000\\ \\ \\ & \text{5.) Суммируя результаты определенного интеграла, получаем:} \\ \\ & \hspace{3ex} A = 12.25000 + 20.25000 + 20.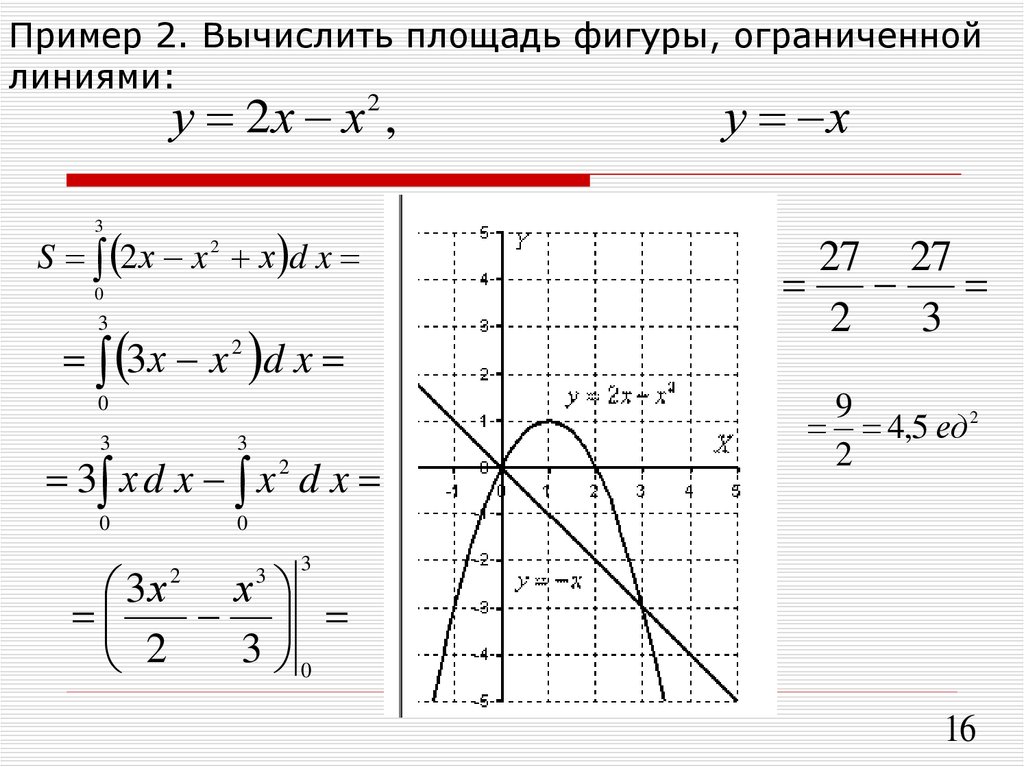 25000 + 12.25000 = \fbox {65.00000}\end{align}$$
25000 + 12.25000 = \fbox {65.00000}\end{align}$$
Как работает калькулятор
сообщить об этом объявлении
Этот калькулятор в основном построен с использованием языков веб-программирования HTML (язык гипертекстовой разметки), CSS (каскадные таблицы стилей) и JS (JavaScript). HTML строит архитектуру, CSS создает все свойства визуального стиля калькулятора, а JS обеспечивает функциональность вычислений.
При нажатии кнопки «Рассчитать» активируется функция JS. Введенные пользователем значения считываются и используются для того же самого процесса, который описан в примерах выше. Различные промежуточные значения сохраняются и форматируются для шагов решения.
Неопределенные интегралы выполняются CAS (система компьютерной алгебры) на основе JS. CAS применяет интегральные правила, рассматривая каждый символ как символ, обеспечивая почти идеальную точность. Этот процесс известен как символьные вычисления.
Окончательный ответ округляется и форматируется, затем форматируются все шаги решения. Ответ и шаги печатаются в области решения и визуализируются механизмом рендеринга LaTeX (язык/технология математического визуального рендеринга).
Ответ и шаги печатаются в области решения и визуализируются механизмом рендеринга LaTeX (язык/технология математического визуального рендеринга).
исчисление — Площадь, заключенная между 3 кривыми
Спрашиваемый
Изменено 4 года, 7 месяцев назад
Просмотрено 24k раз
$\begingroup$
Вопрос: Какова площадь области, ограниченной кривыми:
$$2y = 4\sqrt{x},\quad y = 3,\quad \text{and} \quad 2y + 2x = 6. $$ Я попытался вычислить все определенные интегралы, но я не уверен, какую кривую я должен вычесть, а какая должна быть первой. А еще я немного запутался, потому что там три строчки. Я также не совсем уверен в границах.
Есть идеи?
- исчисление
- интегрирование
- определенные интегралы
- площадь
$\endgroup$
1
$\begingroup$
Подсказка: Разобьем на два интеграла. Один, где $2y+2x=6$, меньше $y=3$, а другой, где $2y=4\sqrt x$, меньше $y=3$. Затем найдите, где пересекаются $2y=4\sqrt x$ и $2y+2x=6$, и это граница между двумя интегралами.
Один, где $2y+2x=6$, меньше $y=3$, а другой, где $2y=4\sqrt x$, меньше $y=3$. Затем найдите, где пересекаются $2y=4\sqrt x$ и $2y+2x=6$, и это граница между двумя интегралами.
Если вам не нужны два интеграла, вы также можете проинтегрировать по $y$, где высота — это разница между $2y=4\sqrt x$ и $2y+2x=6$, а границы взяты из $2$ до $3$.
$\endgroup$
$\begingroup$
Приведенные ответы являются более конкретными, но я хотел дать вам более общий ответ. Когда у вас есть несколько таких линий, они просят вас подумать о форме, которую они образуют. Для любой конкретной части графика будут иметь значение только две кривые. Однако, чтобы выяснить, какие две из трех кривых важны, вы должны построить их, а затем решить для конкретной точки, которую они пересекают.
Вы можете увидеть график здесь:
http://www.wolframalpha.com/input/?i=plot+2y+%3D+4+sqrt(x)+and+y+%3D+3+and+2y+ %2B+2x+%3D+6
Обратите внимание, что он имеет полутреугольную форму. 2=\dfrac 91_0(-x+3-2\sqrt x)dx$$
2=\dfrac 91_0(-x+3-2\sqrt x)dx$$
и площадь $$I=S_1-S_2$$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Репетиторы Колледж-Парка — Блог — Исчисление
Привет, ребята, это Алекс! Я подумал, что начну этот блог с одной из самых популярных (и головокружительных) задач, с которыми сталкиваются мои студенты, изучающие математический анализ. Проблема выглядит примерно так:
Найдите площадь области, ограниченной линиями \(y=2x\), \(y=3x\) и \(y=2\). Вы должны использовать исчисление или вы не получите никакого кредита!
Ого. Сильные слова от парня с зачетной книжкой. Хорошо, надеюсь, вы уже встречались с задачами, которые запрашивают область между две функции . Если нет, вырвите свой учебник ;). Проблемы двухфункциональной области решаются путем интегрирования разницы между «верхней» и «нижней» функциями, например:
Но подождите минутку! Наша проблема в том, что нам дают ТРИ функции, а не две. Как, во имя Бибера, мы можем применить приведенную выше формулу к области, заключенной в три функции?
Я расскажу как.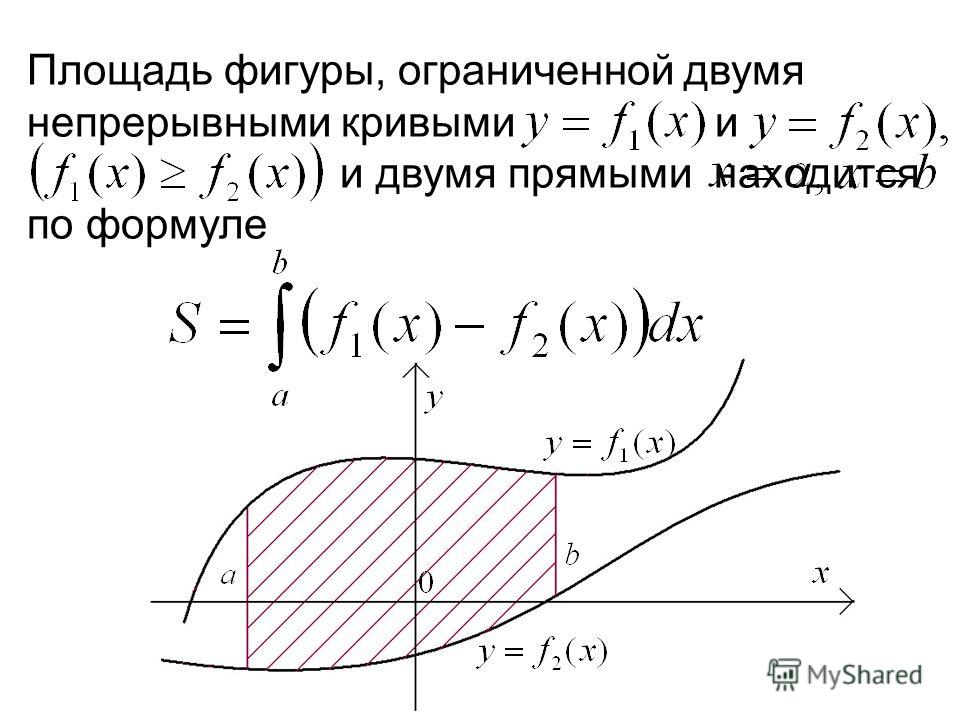 Мы собираемся найти способ разложить на или разбить эту сложную задачу на несколько более мелких и простых задач. Между прочим, умение разбирать задачи является причиной того, что вы обязаны изучать математику для своей специальности, даже если вы никогда больше не увидите другого интеграла за всю свою жизнь. Исчисление — отличный способ научиться более общим навыкам решения задач, математическим или другим.
Мы собираемся найти способ разложить на или разбить эту сложную задачу на несколько более мелких и простых задач. Между прочим, умение разбирать задачи является причиной того, что вы обязаны изучать математику для своей специальности, даже если вы никогда больше не увидите другого интеграла за всю свою жизнь. Исчисление — отличный способ научиться более общим навыкам решения задач, математическим или другим.
Хорошо, вернемся к нашей проблеме. Я повторю это здесь, так как я довольно много болтал с тех пор, как впервые назвал это:
.Найдите площадь области, ограниченной линиями \(y=2x\), \(y=3x\) и \(y=2\). Вы должны использовать исчисление или вы не получите никакого кредита!
Во-первых, я хочу, чтобы вы построили линии на одной оси. Я также хочу, чтобы вы обозначили линии их уравнениями. Попробуйте сделать это сами, прежде чем смотреть на мой график. ПОДСКАЗКА: вы можете изобразить любую линию, выбрав два разных значения \(x\), подставив их в уравнение, чтобы найти соответствующие значения \(y\), начертив эти две точки и проведя через них прямую линию. .
.
Глядя на это изображение, неясно, какая функция является «верхней», а какая «нижней». Строка \(y=2\) выглядит как верхняя функция, а \(y=2x\) — как нижняя, но как насчет \(y=3x\)? Сверху, снизу или вообще где-то еще?
Ответ состоит в том, что \(y=3x\) также находится сверху. Ну, иногда. На самом деле, это зависит от того, на какую часть треугольника мы смотрим. Если мы разрежем эту область в точке пересечения \(y=3x\) и \(y=2\), то часть слева от разреза будет ограничена сверху \(y=3x\). Часть справа от разреза ограничена сверху \(y=2\). Позвольте мне показать вам, что я имею в виду:
Я нарисовал пунктирную линию, чтобы показать, где я вырезал область. Если вы посмотрите на каждую часть отдельно, вы увидите, что теперь каждая из них имеет четкую «верхнюю» и «нижнюю» функцию. Это горячо. Теперь нам просто нужно использовать формулу, чтобы найти площадь каждой части, а затем сложить их вместе, чтобы получить окончательный ответ.
Итак, кусок слева от пунктирной линии ограничен сверху \(y=3x\), а снизу \(y=2x\).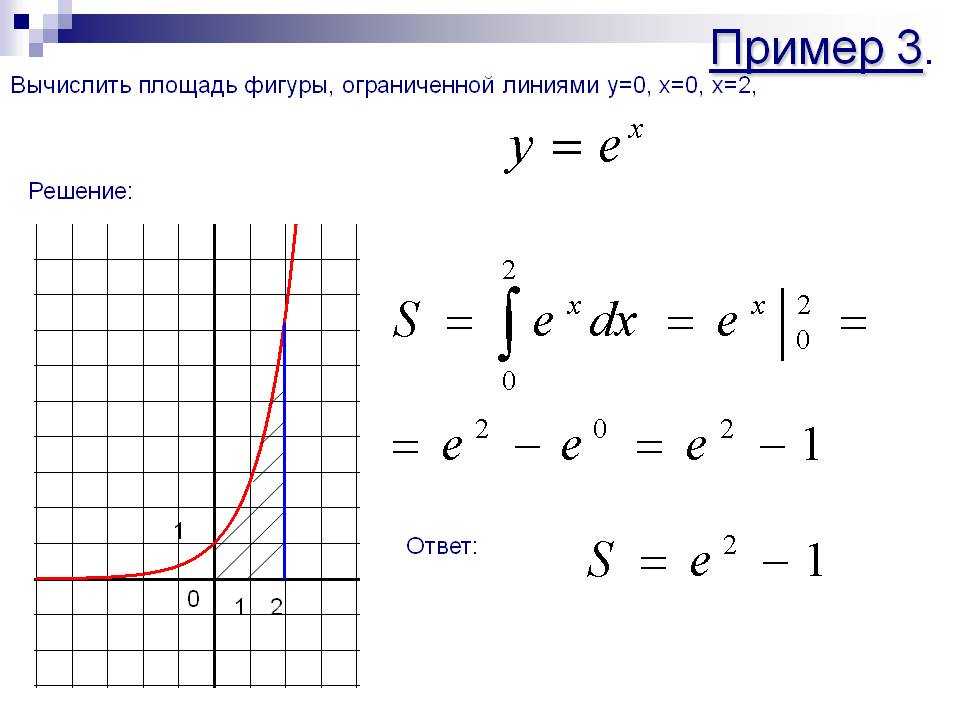 Это дает нам этот интеграл:
Это дает нам этот интеграл:
Кусок справа от пунктирной линии ограничен сверху \(y=2\), а снизу \(y=2x\). Это дает нам интеграл:
Отлично! Мы готовы к интеграции, верно? Держи его там, партнер. Формула площади требует определенного интеграла , а это значит, что нам нужны пределы интегрирования (также известные как «границы»). Хорошо, помните, что наши границы — это просто значения \(x\), которые говорят нам, где начинается и заканчивается область. Чтобы их найти, давайте еще раз посмотрим на график:
Проведя глазами по оси X, левая часть начинается с 0 и заканчивается пунктирной линией. Каково значение x на пунктирной линии, спросите вы? Заметьте, что он проходит через точку пересечения \(y=3x\) и \(y=2\). Чтобы найти значение x этой точки, мы просто приравняем эти два уравнения друг к другу, например:
Правильная часть начинается с пунктирной линии (которую, как мы только что нашли, это \(x=\ frac{2}{3}\) и заканчивается на 1.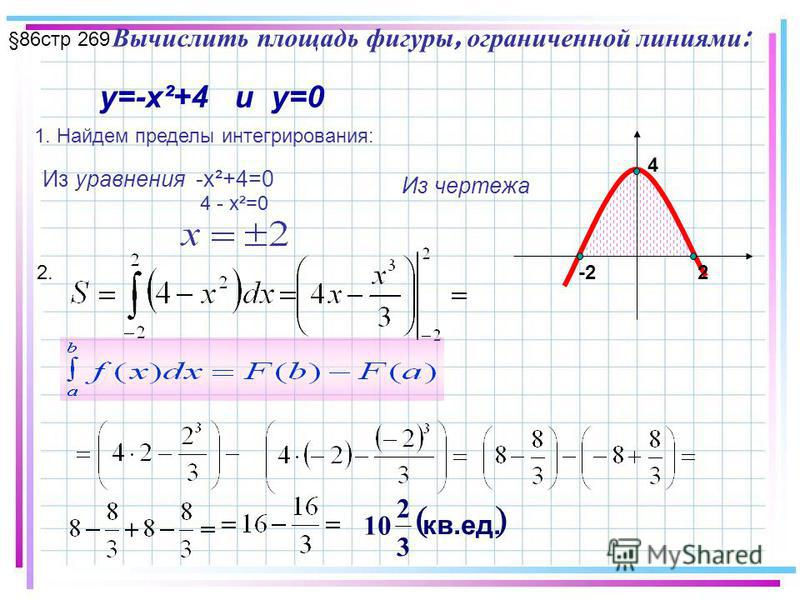 Почему 1? Потому что здесь пересекаются верхняя и нижняя функции, закрывая, таким образом, область. Мы можем показать это математически, установив уравнения верхней и нижней функций равными друг к другу:
Почему 1? Потому что здесь пересекаются верхняя и нижняя функции, закрывая, таким образом, область. Мы можем показать это математически, установив уравнения верхней и нижней функций равными друг к другу:
Хорошо, теперь у нас есть границы (от 0 до \(\frac{2}{3}\) для левой области и от \(\frac{2}{3}\) до 1 для правой область), мы готовы установить и решить наши определенные интегралы. Для левой части получаем:
Для правой части получаем:
Чтобы получить площадь всего региона, мы просто складываем площади отдельных частей:
И вот вы иметь это. Не так уж и плохо, правда? Как я уже говорил, эта задача — отличный пример того, почему мы заставляем студентов, изучающих бизнес и биологию, заниматься исчислением. Конечно, вам, вероятно, никогда не придется находить площадь ограниченной области, когда вы обедаете с Гордоном Гекко или лечите рак, но это учит вас, как решать сложные проблемы, разбивая их на более простые части. И каждый рано или поздно сталкивается с трудной проблемой в жизни.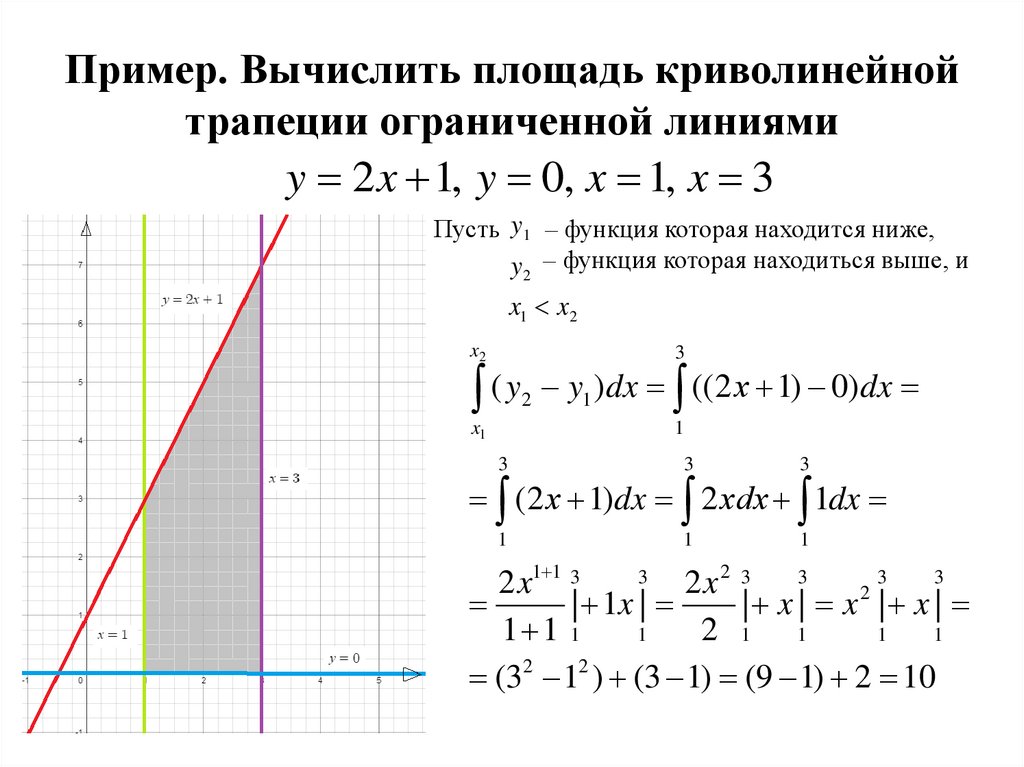
Калькулятор площади между двумя кривыми онлайн, шаг за шагом
Пространство между двумя кривыми Площадь для указанных кривых и пределов вычисляется калькулятором. Определенный интеграл между указанными пределами может быть использован для вычисления площади под кривой.
Важным применением интегрирования является вычисление площади между двумя кривыми. Мы уже знаем, как вычислить площадь под кривой с помощью интегрирования; теперь давайте посмотрим, как найти площадь между двумя пересекающимися кривыми. Это область пространства, которая в заданных пределах лежит между двумя линейными или нелинейными кривыми.
Хотя площадь между двумя кривыми также может быть составной, мы можем легко определить ее с помощью интегрирования, внеся несколько небольших корректировок в известные методы расчета площади под двумя кривыми.
Интегральное исчисление можно использовать для вычисления площади между двумя кривыми, то есть области между двумя пересекающимися кривыми. Когда мы знаем уравнение для двух кривых и места их пересечения, можно использовать интегрирование для определения площади под кривыми. Как видно на рисунке, есть две функции, f(x) и g(x), и мы должны определить площадь между этими двумя кривыми, которая обозначена заштрихованной областью. Затем площадь заштрихованной области можно просто определить с помощью интегрирования. В следующем разделе давайте поговорим подробнее о том, как вычислялась эта площадь.
Когда мы знаем уравнение для двух кривых и места их пересечения, можно использовать интегрирование для определения площади под кривыми. Как видно на рисунке, есть две функции, f(x) и g(x), и мы должны определить площадь между этими двумя кривыми, которая обозначена заштрихованной областью. Затем площадь заштрихованной области можно просто определить с помощью интегрирования. В следующем разделе давайте поговорим подробнее о том, как вычислялась эта площадь.
Содержание
Что такое Калькулятор площади между двумя кривыми?Калькулятор, который помогает определить площадь между двумя кривыми для заданных кривых и ограничений, доступен онлайн. Вы можете быстро получить площадь между двумя кривыми с помощью этого онлайн-калькулятора площадей между кривыми. Введите функцию и предельные значения в предоставленное поле ввода, чтобы использовать эту область между двумя кривыми.
Мы впервые понимаем значение исчисления для работы со сложными реальными системами, когда впервые узнаем об интегралах для определения площади под кривой.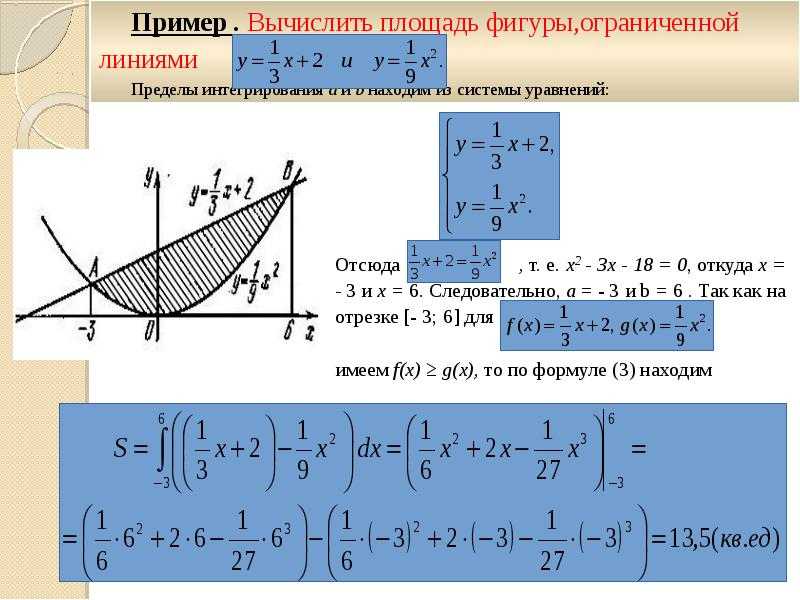 Простая иллюстрация этого — вычисление области под кривой зависимости скорости транспортного средства от времени с использованием суммы Римана для оценки расстояния, пройденного транспортным средством.
Простая иллюстрация этого — вычисление области под кривой зависимости скорости транспортного средства от времени с использованием суммы Римана для оценки расстояния, пройденного транспортным средством.
Читайте также: Притяжательный падеж множественного числа: значение, примеры и прочее
Однако поиск пробела между двумя кривыми бесполезен. Допустим, по выходным мы таскаем гоночные машины по трассе. Перед каждой гонкой мы проверяем, настроено ли оборудование для сбора данных автомобиля на запись нашей скорости через заданные промежутки времени на протяжении каждого заезда против соперников, с которыми мы участвуем в гонках. Те же данные с теми же интервалами записываются и системой сбора данных нашего конкурента.
Нам интересно знать разницу между нашим автомобилем и конкурентами после каждой гонки на четверть мили. Для этого мы собираем данные зависимости скорости от времени для обоих автомобилей и вычисляем площадь между двумя кривыми скорости на протяжении всего периода соответствующего пробега в четверть мили.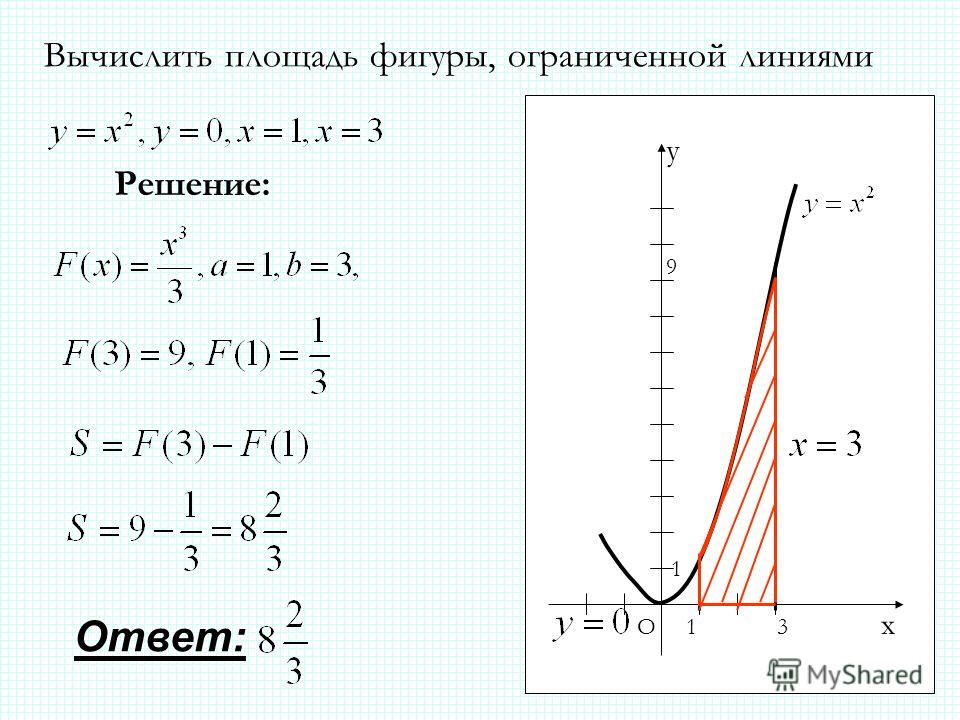 Это покажет, насколько далеко друг от друга находились наши автомобили, когда победитель пересек финишную черту.
Это покажет, насколько далеко друг от друга находились наши автомобили, когда победитель пересек финишную черту.
Другими словами, мы можем рассчитать разрыв между двумя автомобилями в заданной точке гонки, рассчитав площадь между этими двумя кривыми скорости.
Как использовать калькулятор площади между двумя кривыми?Чтобы рассчитать площадь с помощью онлайн-калькулятора площади между двумя кривыми, выполните следующие действия:
Шаг 1: Посетите раздел калькуляторов между двумя кривыми на веб-сайте Cuemath.
Затем, Шаг 2: Введите большую функцию и меньшую функцию в области между двумя изогнутыми калькуляторами, имеющими поля ввода.
Затем, Шаг 3: Введите предельные значения (нижняя и верхняя граница) в области между двумя кривыми в поле ввода калькулятора.
Шаг 4: Чтобы рассчитать площадь для предоставленных кривых и ограничений, нажмите кнопку «Рассчитать».
Затем, Шаг 5: Нажмите кнопку «Сброс», чтобы заполнить новые значения полей после их очистки.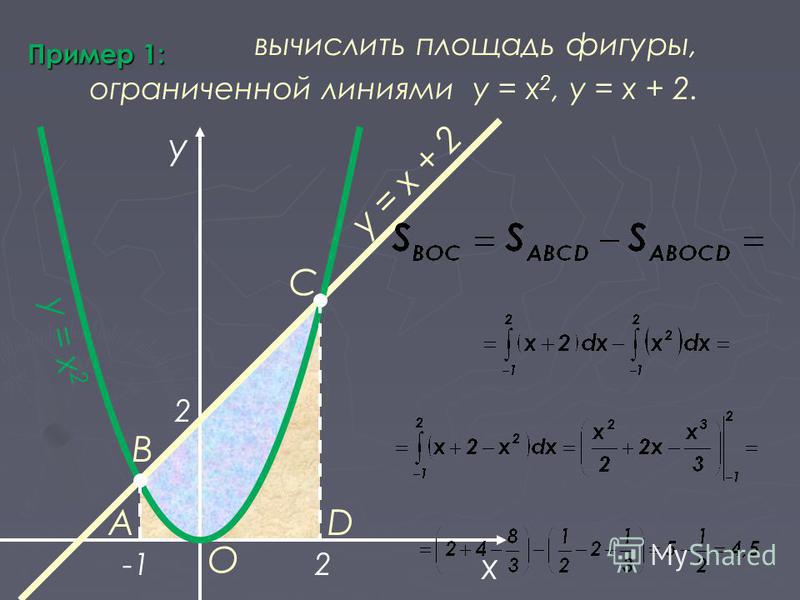
Основная теорема исчисления говорит нам, что для вычисления площади под кривой y = f(x) от x = a до x = b. Оно представлено в виде b∫a f(x)dx
Сначала мы вычисляем интегрирование g(x) для f(x), g(x)= ∫f(x) dx, а затем оцениваем g(b) − g(a ). То есть площадь под кривой f(x) от x = a до x = b равна b∫a f(x)dx = g(b) − g(a)
Пусть y = f(x) и y = g(x) — кривые, а a и b — два предела. Формула для вычисления площади между двумя кривыми имеет вид Для создания этого калькулятора в основном использовался JS (JavaScript). Архитектура калькулятора создается с помощью HTML, все элементы визуального стиля создаются с помощью CSS, а функции расчета предоставляются с помощью JS.
Функция JS запускается при нажатии кнопки «рассчитать». При чтении и использовании значений, введенных пользователем, используется та же самая процедура, которая описана в вышеупомянутых примерах проблем. Для шагов решения подготавливаются и сохраняются несколько промежуточных значений.
CAS на основе JS вычисляет неопределенные интегралы (система компьютерной алгебры). Рассматривая каждый символ как символ и применяя интегральные правила, CAS обеспечивает почти безупречную точность. Термином для этой процедуры является символьное вычисление.
Все этапы решения форматируются после округления и форматирования окончательного ответа. Механизм рендеринга LaTeX (язык/технология математического визуального рендеринга) используется для печати решения и его шагов в области решения.
Калькулятор площади между двумя кривыми с шагами- Найдите расстояние между двумя кривыми, расположенными вдоль линий, используя эти простые правила.
- Даны две кривые P: y = f(x) и Q: y = g (x)
- Заменяя одно значение уравнения другим и делая это уравнение только с одной переменной, вы можете определить точки, где кривая пересекается .
- Найдите точки пересечения, решив это уравнение.
- Для указанных кривых и точек пересечения создайте график.

- Тогда площадь будет равна A = ∫x2x1 [f(x)-g(x)]dx
- Подставьте значения в приведенную выше формулу.
- Решите интегрирование и замените значения, чтобы получить результат.
При попытке вычислить приблизительную площадь двух кривых необходимо сначала разделить область на множество небольших прямоугольных полос, параллельных оси y, в пределах от x = от а до х = б. Эти прямоугольные полоски будут иметь ширину «dx» и высоту «f(x)-g» (x). Используя интегрирование в пределах x = a и x = b, мы теперь можем определить площадь между этими двумя кривыми. Площадь небольшой прямоугольной полоски определяется выражением dx(f(x) – g(x)). Можно использовать следующую формулу, если f(x) и g(x) непрерывны на [a, b] и g(x) < f(x) для каждого x в [a, b].
Площадь = ∫ba [f(x) −g(x)]
Итог:
- Верхняя функция графика, или функция с более высоким значением y для данного x, известна как f.
 (Икс).
(Икс). - Нижняя функция графика, или функция с меньшим значением y для данного x, известна как g. (Икс).
- На графике две отдельные области могут иметь разные верхние и нижние функции. В таких обстоятельствах крайне важно вычислить площадь индивидуально.
- Область над осью Y имеет положительное значение.
- Область ниже оси Y имеет отрицательный знак.
Чтобы определить площадь области, нам пришлось проанализировать два разных интеграла. Однако есть еще один метод, который требует только одного интеграла. Что, если мы рассмотрим кривые как функции от y, а не от x? Проанализируйте рисунок. Функция y= f(x) = x² используется для представления левого графика, который показан красным. Кривая может быть представлена функцией x= v(y)=√ y, и мы могли бы так же легко решить это для x. (Помните, что x= -√y также является допустимым способом записи функции y= f(x)=x² как функции от y.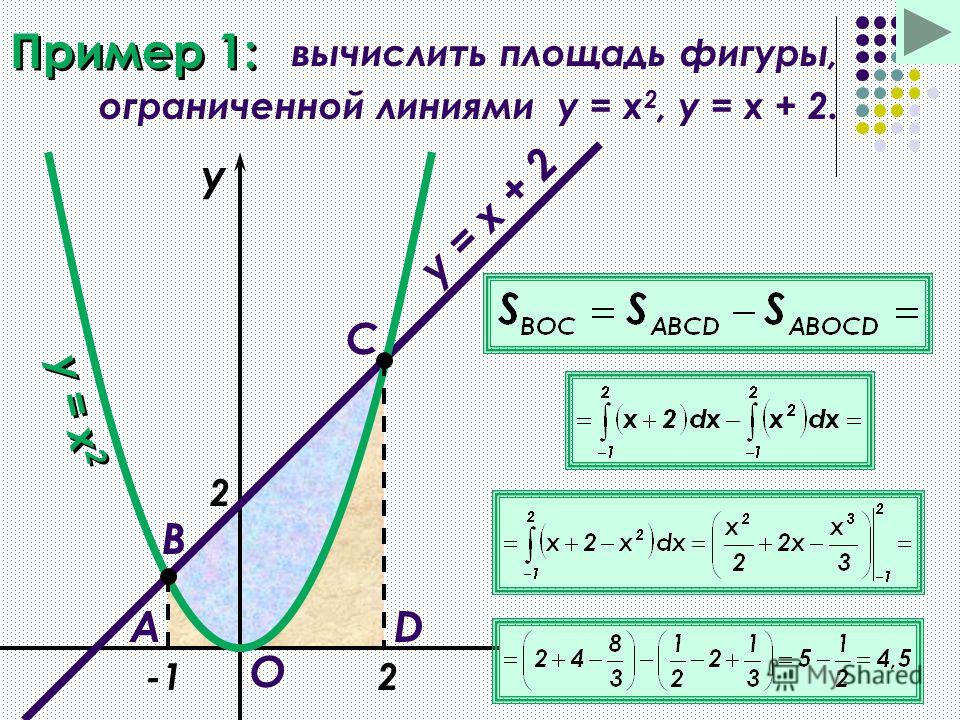
График, однако, ясно показывает, что нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией y= g(x)= 2−x , но также легко может быть представлен как функция x= u(y)= 2−y . Область ограничена слева графиком одной функции и справа графиком другой функции, когда графики рассматриваются как функции от y. В результате есть только один интеграл, который необходимо вычислить, если мы интегрируем по y.
Сводка:
- Предположим, что f(y) имеет наибольшее значение x для заданного y и, следовательно, является правильной функцией на графике.
- Левая функция графика, или g, имеет меньшее значение x для заданного значения y. (у).
- Отдельные функции будут использоваться, если граф имеет разные области. Для каждого региона на графике следует определить отдельные области, если они разные.
- Область имеет положительный знак непосредственно на оси x.
- Область слева от оси x отмечена отрицательным знаком.

Пусть u(y) и v(y) – непрерывные функции на интервале [c,d] такие, что u(y)≥v(y) для всех y∈[c,d] . Мы хотим найти площадь между графиками функций, как показано на рисунке ниже.
На этот раз мы собираемся разделить интервал по оси Y и использовать горизонтальные прямоугольники для аппроксимации области между функциями. Итак, для i=0,1,2,…,n пусть Q=yi – обычное разбиение [c,d] . Затем для i=1,2,…,n выберем точку y∗i∈[yi−1,yi], затем над каждым интервалом [yi−1,yi] построим прямоугольник, выходящий горизонтально из v(y0∗ i) к u(y∗i). На изображении ниже показаны прямоугольники, когда y∗i выбрано в качестве нижней конечной точки интервала и n=10 . На изображении ниже показан репрезентативный прямоугольник в деталях. 9n [u(yi * )-v(yi * )] ∆ y
= int cd [u(y)-v(y)]dy.
Калькулятор площади между двумя полярными кривыми Кроме того, мы можем использовать интегральное исчисление для определения площади пересечения двух полярных кривых.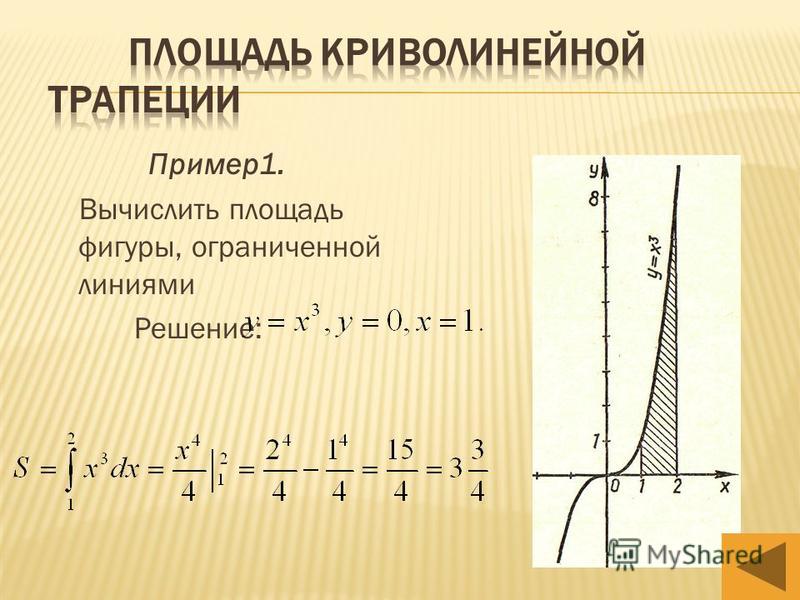 Этот метод используется, когда есть две кривые, координаты которых заданы в полярных координатах, а не в прямоугольных. Мы всегда можем преобразовать полярные координаты в координаты прямоугольника, чтобы решить эту проблему, хотя это уменьшит ее сложность.
Этот метод используется, когда есть две кривые, координаты которых заданы в полярных координатах, а не в прямоугольных. Мы всегда можем преобразовать полярные координаты в координаты прямоугольника, чтобы решить эту проблему, хотя это уменьшит ее сложность.
Допустим, у нас есть две полярные кривые r0 = f(θ) и ri = g(θ), как показано на изображении, и мы хотим найти площадь, заключенную между этими двумя кривыми, такую, что α ≤ θ ≤ β, где [ α, β] — ограниченная область. Таким образом, площадь между кривыми будет равна:
A=½ ∫βα(r²0−r²i)dθ –
Площадь между двумя кривыми Калькулятор Compound Использование вышеупомянутых формул для расчета площадей между двумя составными кривыми, которые пересекаются друг друга приведут к неправильному ответу и заставят кривые двигаться после соединения. Мы оценили отдельные площади между кривыми в каждом сегменте интервалов для кривых, изображенных на изображении. Область между кривыми будет: Пусть f(x) и g(x) непрерывны в интервале [a,b].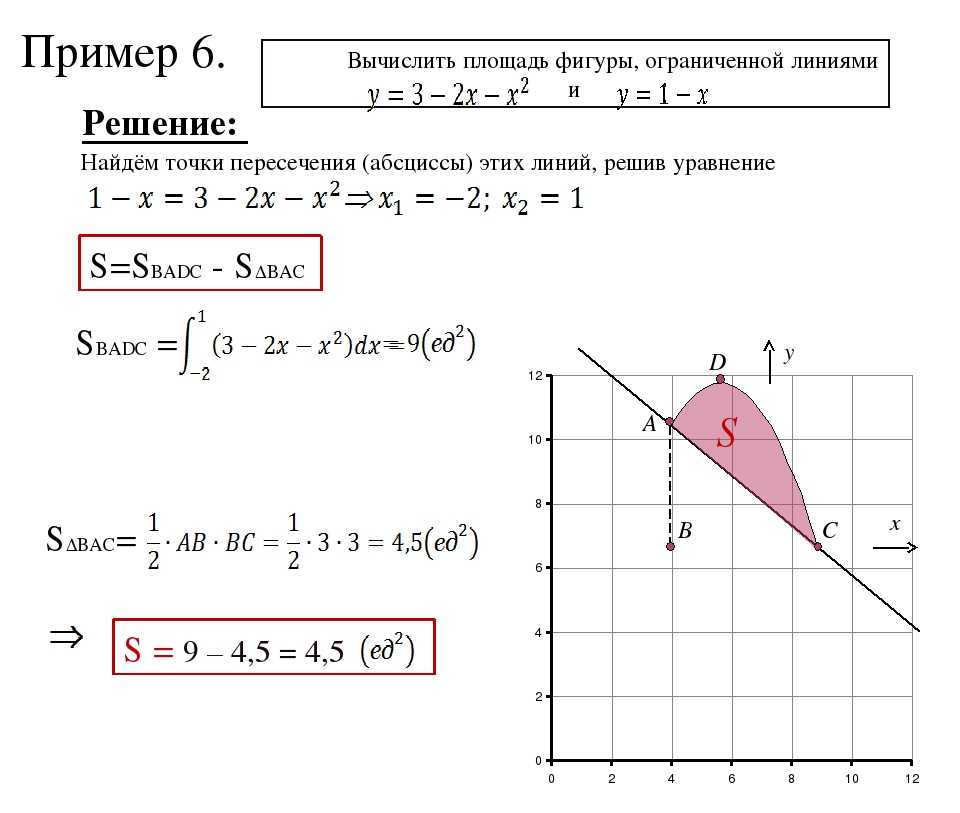
Площадь = If(x) – g(x)/dx
[c, d] g(x) = f(x), поэтому мы разбиваем пределы на две части следующим образом:
Как мы видим в области [a, b], f(x) = g(x) и в области Area = {f(x) = g(x)} dx + {g(x) − f(x)} dx
Как Калькулятор площади между двумя кривыми Первый шаг:A= ∫ (верхняя функция – нижняя функция) dx; a ≤ 2 ≤ 6
Где A — пространство между кривыми, a и b — левая и правая конечные точки интервала соответственно, а Верхняя функция и Нижняя функция — функции от x с большими и меньшими значениями на интервале соответственно.
При вычислении площади между двумя кривыми мы можем указать интервал x = [a, b] (что идентично a < x < b). Мы также можем использовать интервал, определяющий область, которую охватывают две кривые, если они имеют по крайней мере две точки соединения.
Давайте используем изображение ниже в качестве иллюстрации. F(x) = x представлен синей кривой, а g(x) = x³ представлен красной кривой.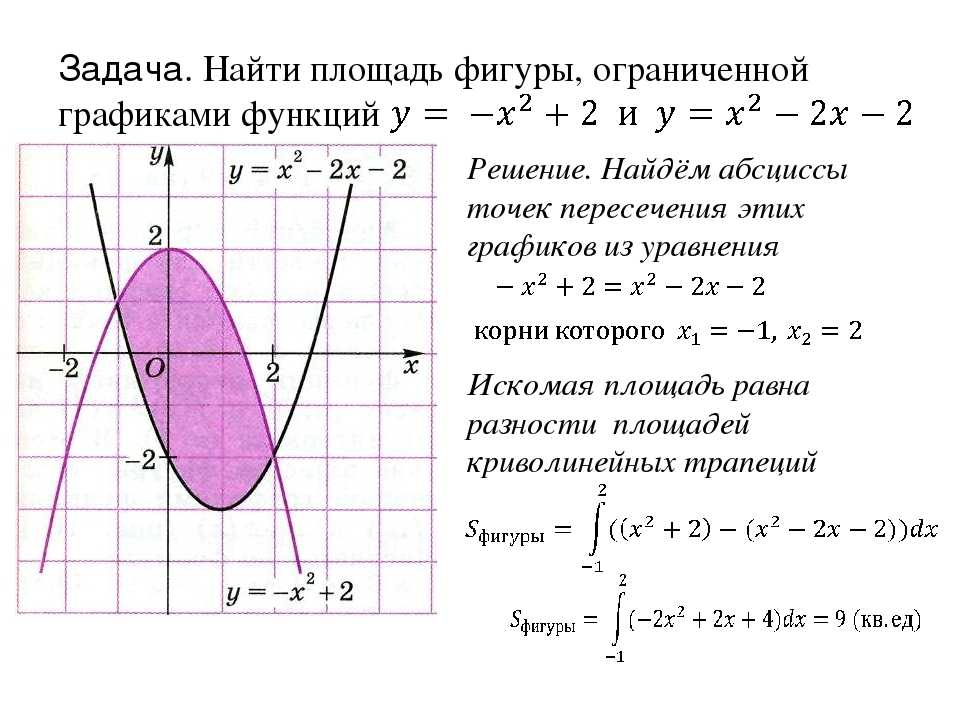 Кривые этих двух функций пересекаются в трех точках: x = -1, x = 0 и x = 1. Следовательно, площадь, заключенная между ними, определяется интервалом x = [-1, 1].
Кривые этих двух функций пересекаются в трех точках: x = -1, x = 0 и x = 1. Следовательно, площадь, заключенная между ними, определяется интервалом x = [-1, 1].
Верхняя и нижняя функции для подинтервала должны быть определены после того, как мы получим интервал, на котором мы решаем (s). В некоторых случаях сам первичный интервал будет служить единственным подинтервалом. В некоторых ситуациях кривые будут пересекаться друг с другом более одного раза и менять положение как верхнюю и нижнюю функции, как показано на иллюстрации непосредственно выше.
Глядя на график кривых, мы можем четко определить верхнюю и нижнюю функции для каждого подинтервала. Мы можем оценить значение каждой функции в середине каждого подинтервала даже без графика кривых. Например, подинтервал x = [2, 4] имеет среднюю точку x = 3. Чтобы определить, какая функция имеет большее и меньшее значение в этот момент, мы подставим x = 3 в каждую из них.
Мы можем составить формулу площади для каждого подинтервала, если нам известны верхняя и нижняя функции для одного или нескольких подинтервалов. Мы складываем решения каждого интеграла формулы площади, чтобы найти общую площадь между кривыми на нашем интервале. Эта сумма будет выглядеть следующим образом для задачи с n подынтервалами:
Мы складываем решения каждого интеграла формулы площади, чтобы найти общую площадь между кривыми на нашем интервале. Эта сумма будет выглядеть следующим образом для задачи с n подынтервалами:
A(total) = A1 + A₂ +…+ An
Пример калькулятора площади между двумя кривымиПример 1: Калькулятор площади между двумя кривыми
Найдите площадь между двумя кривыми f(x) = x² и g(x) = x³ в интервале [0,1], где f(x) ≥ g(x) в заданной области.
Решение:
Дано: f(x) = x² и g(x) = x³
Используя формулу площади между двумя кривыми:
Площадь = ∫ba [f(x)− g(x)] dx
Площадь = ∫10 [x² −x³]dx
= [⅓ x³ − ¼ x⁴]10
= 1/3 – 1/4
= 1/12
Ответ: Площадь между данными кривыми под следующим интервалом 1/12
Пример 2. Калькулятор площади между двумя кривыми
Найдите площадь между кривой r0 = 2cos(θ) и ri= 1 в интервале [−π/3, π/3] и где −π/3 < θ < π/3 и в данной области r0 ≥ ri.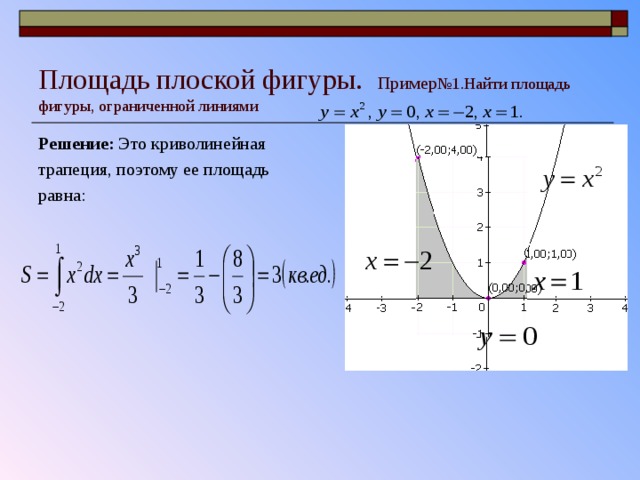
Решение:
Дано: r0 = 2cos(θ) и ri= 1
Используя формулу для площади между двумя полярными кривыми:
A= ½ ∫βα (r20−r2i)dθA
= ½ ∫ /3−π/3 ((2cosθ)2−(1)2)dθA
= ½ ∫π/3−π/3 1+2cos(2θ)dθ
= ½ {θ+sin(2θ)} ∣ π/3−π/3
= π/3+√3/2.
Ответ: Площадь между кривой равна π/3+√3/2 квадратных единиц.
Пример 3. Калькулятор площади между двумя кривыми
Найдите площадь заданных кривых f(x) = x2 + 2x и g(x) = x + 3 для интервала [1, 3] и проверьте ее, используя площадь между двумя кривыми калькулятор
Решение:
Дано: f(x) = x² + 2x и g(x) = x + 3
Площадь=∫ba [f(x) − g(x)]
=∫ 31 [(x²+2x) − (x+3)]
=∫31 [(x² + x−3)]
= 6,67
Точно так же вы можете попробовать вычислить площадь между двумя кривыми и найти площадь для:
f(x) = 5x + 6 и g(x) = 6x² для пределов x = от -3 до 1
f (x) = x³ / 2 и g(x) = 5x для пределов от x = 2 до x = 5
Часто задаваемые вопросы о калькуляторе площади между двумя кривымиЧто означает площадь под кривой?
Область, ограниченная кривой, осью и граничными точками, называется «областью под кривой». Используя оси координат и формулу интегрирования, можно получить двумерную площадь под кривой.
Используя оси координат и формулу интегрирования, можно получить двумерную площадь под кривой.
Что представляет площадь под кривой?
Область, ограниченная кривой и осью, которая обозначена ограничивающими точками, представлена областью под кривой. Площадь асимметричной плоской формы в двумерном массиве определяется областью под кривой.
Какова формула расчета площади между двумя кривыми?
Мы можем рассчитать площадь между этими двумя кривыми, используя данную формулу. Если f(y) и g(y) непрерывны на [a, b] и g(y) f(y) для всех y в [a, b], то Area = ∫ba[f(x)−g( х)]дх
Всегда ли площадь между кривыми положительна?
Это всегда будет неотрицательное значение, если между двумя кривыми есть область. Площадь может быть только положительной или нулевой, но никогда отрицательной. Формула для вычисления площади между двумя кривыми: Площадь = ∫ba[f(x)−g(x)]dx, где dx — абсолютное значение площади. Это никогда не будет плохо.
Как найти площадь под кривой?
Для определения площади кривой под ней можно использовать процессы интегрирования или аспирации. Для этого нам потребуется уравнение кривой (y = f(x)), граница оси кривой и ограничения границы кривой. При этом формулу можно использовать для определения площади, ограниченной кривой. A = ∫ba y.dx.
Для этого нам потребуется уравнение кривой (y = f(x)), граница оси кривой и ограничения границы кривой. При этом формулу можно использовать для определения площади, ограниченной кривой. A = ∫ba y.dx.
Какие существуют методы нахождения площади под кривой?
Площадь под кривой можно найти с помощью одного из трех основных подходов. Разбивая пространство на множество крошечных прямоугольников, вычисляют площадь под кривой. Затем площади добавляются, чтобы получить общую площадь. Второй метод включает в себя разрезание пространства на несколько прямоугольников, которые затем соединяются вместе, чтобы создать желаемую область. Использование интеграции для определения местоположения области является третьим подходом.
Какой первый шаг к нахождению площади между двумя кривыми?
Сначала возьмите интегралы обеих кривых. Получив интегралы для обеих кривых, решите их как обычно. Интеграл кривой, расположенной выше на графике, будет затем вычтен из интеграла кривой, расположенной ниже на графике.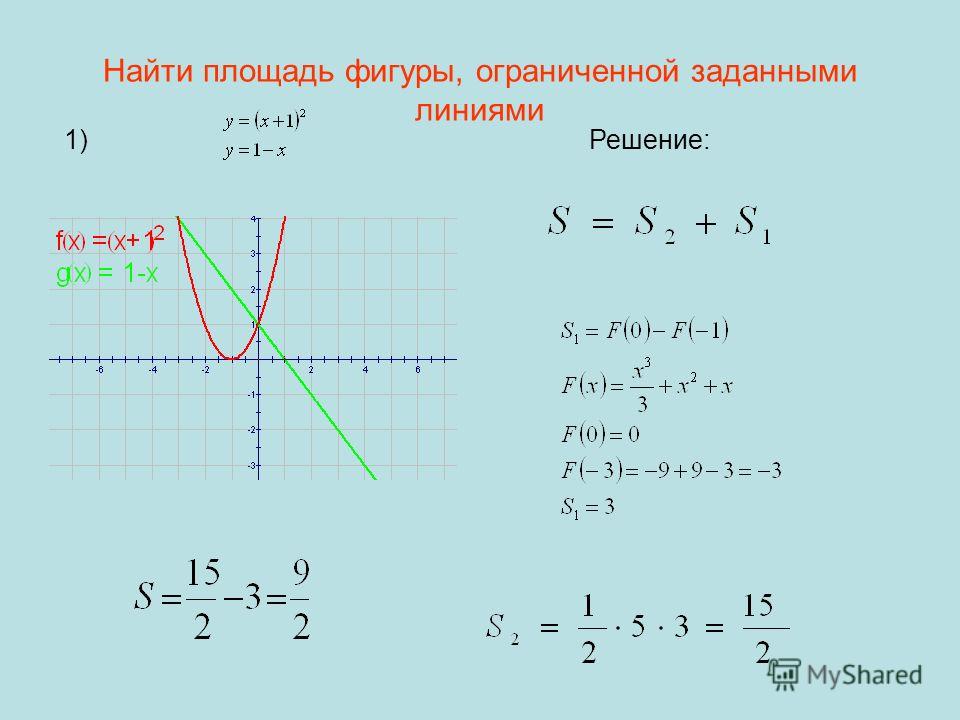
Как вы используете интеграцию для поиска областей?
Вы можете определить площадь под кривой между двумя точками, вычислив определенный интеграл между двумя точками. Проинтегрируйте y = f(x) между a и b, используя предел между a и b, чтобы определить область под кривой y = f. (Икс). В областях ниже оси X будут отображаться отрицательные числа, а в областях выше оси X — положительные значения.
Почему две кривые положительные?
Чтобы обеспечить хороший (неотрицательный) результат для каждого элемента при решении такого рода задач, необходимо подходить к каждому компоненту отдельно и интегрировать верхнюю и нижнюю функции. Независимо от того, где она расположена на плоскости, «Площадь между двумя графиками» по определению положительна.
Как найти площадь между двумя кривыми в Excel?
В пустой ячейке электронной таблицы Excel введите «ЛИНЕЙН(yдиапазон, диапазон, ИСТИНА, ЛОЖЬ)».
Чтобы отразить расположение ваших данных для одного из графиков, измените аргументы команды ЛИНЕЙН.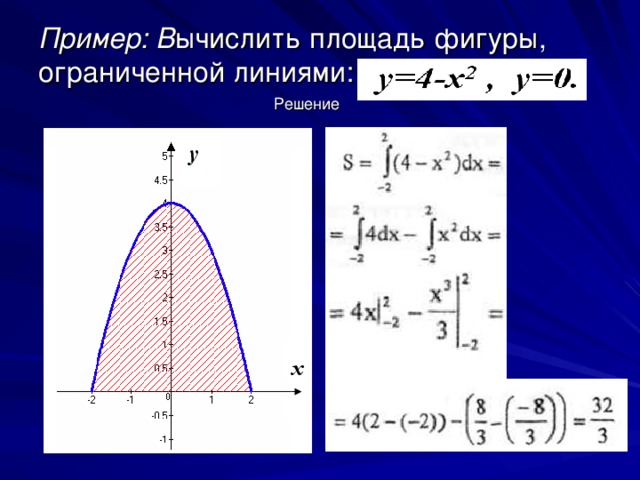
Чтобы получить уравнение для первого набора данных, нажмите «Enter».
Может ли площадь между двумя кривыми быть отрицательной?
Определенный интеграл может иметь отрицательное значение. Результат отрицательный, когда вся площадь интервала находится ниже оси x, но все еще выше кривой.
Как найти площадь вертикального среза?
Площадь между двумя кривыми с использованием вертикальных срезов A = ∫ a b ( g ( x ) − f ( x ) ) dx.
Калькулятор площади под кривой
Знакомство с калькулятором площади под кривой
Калькулятор площади под кривой представляет собой онлайн-инструмент, который используется для расчета определенных интегралов между двумя точками. Этот калькулятор поможет найти определенные интегралы, а также неопределенные интегралы и дает ответ в несколько шагов.
Помогает решать уравнения и дает точные ответы. Определенные интегралы или неопределенные интегралы можно легко вычислить с помощью этого онлайн-калькулятора. Использование этого калькулятора сэкономит ваше время и энергию, которые вы потратили на решение длинных делений или уравнений вручную. Это также бесплатно и просто в использовании.
Использование этого калькулятора сэкономит ваше время и энергию, которые вы потратили на решение длинных делений или уравнений вручную. Это также бесплатно и просто в использовании.
Как найти калькулятор площади под кривой онлайн?
Калькулятор площади под кривой известен как самый продвинутый онлайн-калькулятор, который можно легко найти в Интернете для решения интеграла онлайн. Этот расширенный онлайн-инструмент можно найти или найти с помощью простых шагов. Эти простые и легкие шаги:
- В Интернете Google поможет найти калькулятор интеграла кривой. Прежде всего, вы можете ввести основное ключевое слово этого калькулятора Площадь под кривой Калькулятор в строке поиска Google. Google сразу направит вас на главную страницу калькулятора. Все зависит от вас, чтобы выбрать правильный вариант и выбрать основной калькулятор.
- Google покажет вам различные результаты после ввода площади под калькулятором кривой. Главное при выборе этого калькулятора — понять основные инструкции калькулятора и рекомендации по использованию этого калькулятора.
 Внимательно выбирайте онлайн-калькулятор в соответствии с вашими потребностями.
Внимательно выбирайте онлайн-калькулятор в соответствии с вашими потребностями. - Самый распространенный способ — найти веб-сайт интеграционных калькуляторов и выполнить поиск этого калькулятора прямо здесь. Интеграл калькулятора разработал множество калькуляторов интеграции, из которых вы можете легко найти этот калькулятор. Все эти калькуляторы бесплатны и точны.
Связанный: Также Найдите калькулятор подстановки u или интегральный калькулятор тригонометрической подстановки с шагами в Google для оценки интеграции методами подстановки.
Преимущества использования Калькулятора площади под кривой
Мы знаем, что нахождение площади под кривой — длительная процедура, которую приходится решать вручную. Таким образом, использование этого калькулятора дает различные преимущества, которые можно упомянуть следующим образом:
- Калькулятор площади под кривыми поможет вычислить задачи или уравнения всего за несколько секунд и решить функции шаг за шагом.

- Этот калькулятор помогает сэкономить ваше время и избавляет вас от ручных вычислений.
- Он помогает практиковать понятия площади под кривой онлайн, и вы также можете узнать об этом с помощью этого калькулятора.
- Этот калькулятор предоставляет график и возможные промежуточные шаги метода длинных делений онлайн или уравнения и его возможное количество шагов.
- Он также предоставляет действительную часть, мнимую часть и альтернативную форму определенных интегралов или неопределенных интегралов в результате.
- Этот бесплатный калькулятор помогает вычислять точные результаты.
Чтобы вычислить длинный и сложный интеграл, используйте наш калькулятор интеграла частичной дроби и калькулятор интегрирования по частям с шагами.
Результаты, полученные с помощью калькулятора площади между двумя кривыми
Результаты, полученные с помощью площади под калькулятором кривой , очень точны.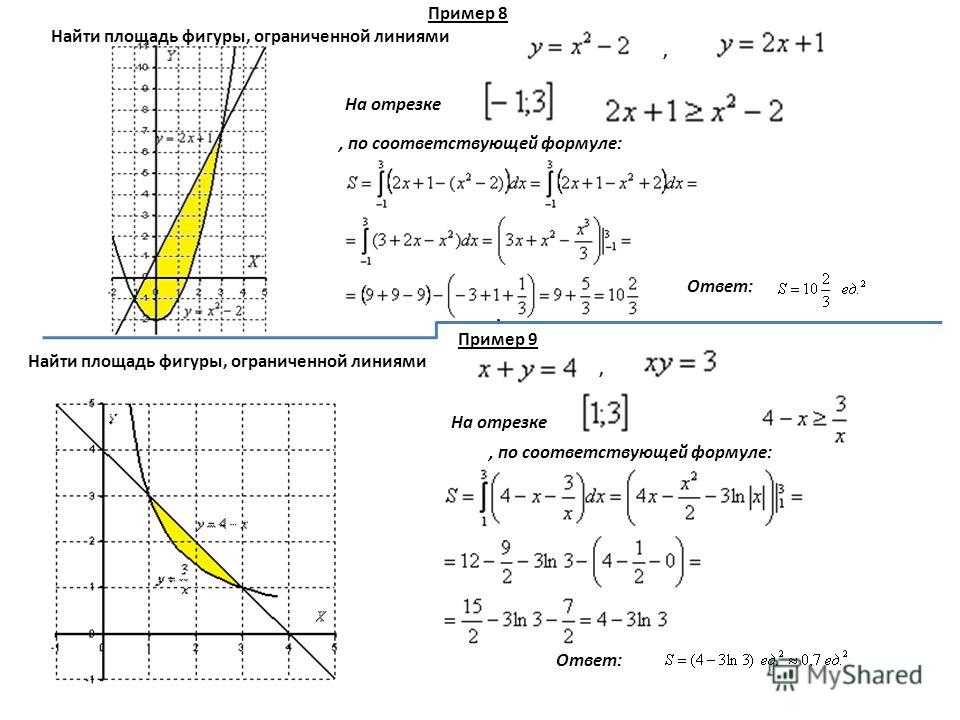 Он дает ответы на каждую функцию шаг за шагом, которые легко понять. Результаты, полученные с помощью этого калькулятора, являются окончательными и содержат простые шаги для правильного понимания этого процесса. Это поможет найти действительную часть, мнимую часть, промежуточные шаги, альтернативную форму интегралов и разложение интегралов в ряды в результатах.
Он дает ответы на каждую функцию шаг за шагом, которые легко понять. Результаты, полученные с помощью этого калькулятора, являются окончательными и содержат простые шаги для правильного понимания этого процесса. Это поможет найти действительную часть, мнимую часть, промежуточные шаги, альтернативную форму интегралов и разложение интегралов в ряды в результатах.
Надежен ли калькулятор площади между кривыми?
Результаты этого калькулятора надежны. Это помогает быстрее вычислять функции и шаг за шагом дает точные результаты. Это помогает тратить время и решать проблемы всего за несколько секунд. Этот калькулятор даст возможность узнать площадь под процессом кривой и предоставит точные результаты, которые легко понять.
Как использовать калькулятор площади между двумя кривыми?
использование площади под калькулятором кривой облегчит вам решение функций или уравнений. У него есть простые инструкции, которым нужно следовать. Вот несколько основных шагов для использования этого калькулятора:
- Первый шаг — ввести функцию из калькулятора или загрузить пример.

- Выберите, хотите ли вы оценивать площадь под функциями кривой как определенный интеграл или неопределенный интеграл.
- Если вы хотите выбрать определенный интеграл, то выберите верхнюю и нижнюю границы для процесса интегрирования, а если вы хотите выбрать неопределенные интегралы, то нет необходимости выбирать верхнюю или нижнюю границу. Он автоматически исчезает после выбора неопределенного интеграла.
- Вы также можете выбрать переменные относительно x, y, z в соответствии с вашей функцией.
- Затем нажмите кнопку «Рассчитать», чтобы обработать функцию. Этот калькулятор выдаст результаты за несколько секунд и даст вам решение шаг за шагом.
Есть много других полезных калькуляторов, которые пригодятся вам при изучении математического анализа. Так же, как вы можете по-разному определить калькулятор суммы Римана или калькулятор правила трапеций для вычисления площади под кривой.
Зачем использовать Калькулятор интеграла кривой?
Калькулятор площади под кривой известен как лучший источник вычисления определенных интегралов между двумя точками, интегрирования, функций, выражений и определенных интегралов или неопределенных интегралов. Это помогает найти площадь под процессом кривой.
Это помогает найти площадь под процессом кривой.
Основным мотивом использования этого калькулятора является достижение наилучших результатов за короткое время. Это помогает в выборе переменных и определенных интегралов, а также неопределенных интегралов в соответствии с вашим выбором расчета. Это помогает в расчете площади под кривой бесплатно и дает простые результаты в несколько шагов.
Таким образом, мы надеемся, что вам понравился один из самых передовых и востребованных инструментов интегралов. Интегральный калькулятор предоставляет множество различных инструментов, которые могут помочь в интеграции. Можно также попробовать калькулятор сходящегося или расходящегося интеграла, который поможет нам вычислить неправильный интеграл функции.
Визуальная форма вашего ввода также показана под строкой ввода, что помогает пользователю анализировать свою подынтегральную функцию под интегралом. Так что продолжайте получать удовольствие, вычисляя интеграл вместе с нами! 9бф(х)dx$$
Если у вас есть значения бесконечных и определенных интегралов, то вы можете найти площадь под кривой калькулятором с шагами онлайн.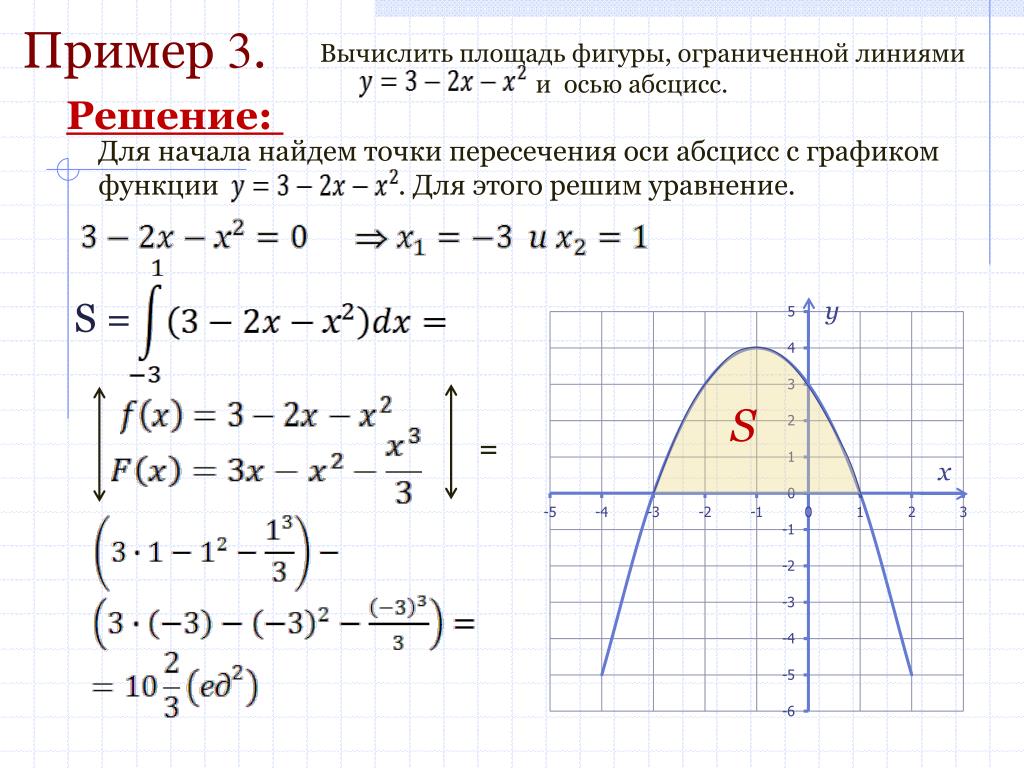
Какова площадь под нормальной кривой, если данный Z-показатель равен 2,14?
Чтобы найти площадь под нормальной кривой с помощью z-показателя, используется таблица z-показателя для нормального распределения. Таким образом, используя таблицу, площадь с z-показателем 2,14 составляет 0,01618. Калькулятор площади под кривой также дает точные результаты.
Когда площадь под кривой имеет отрицательное значение?
После интегрирования площадь под кривой может быть отрицательной. Отрицательный знак с площадью указывает на то, что площадь кривой, лежащей ниже оси x, больше. Это просто указывает, что область находится ниже оси x. Если вы хотите найти площадь под графиком онлайн, вы можете использовать калькулятор площади под графиком.
Как найти площадь под кривой с помощью интегрирования?
Площадь под кривой легко найти с помощью метода интегралов, если известны границы кривой. Вы можете найти площадь под кривой онлайн с помощью калькулятора интегральной площади.

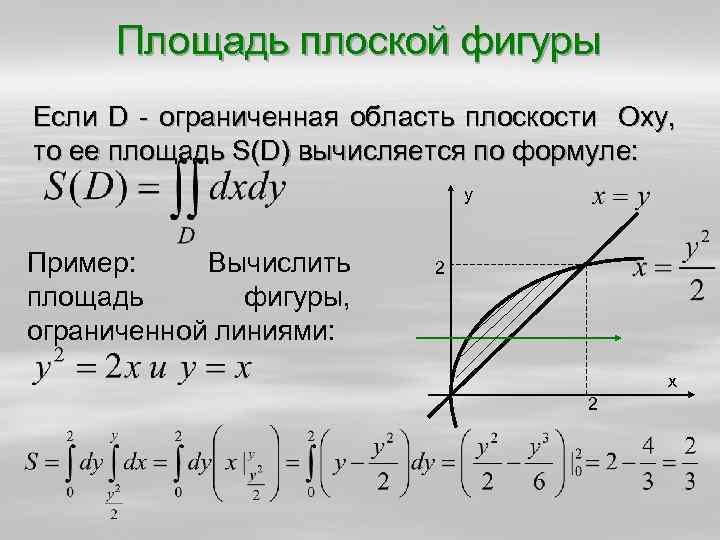
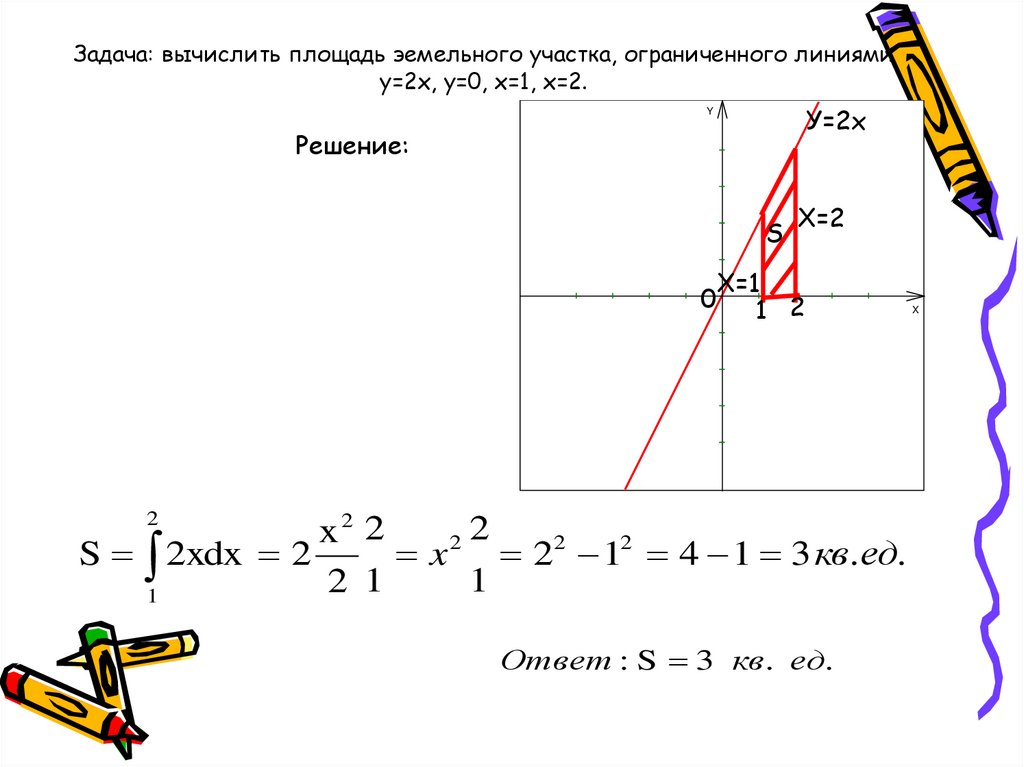 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
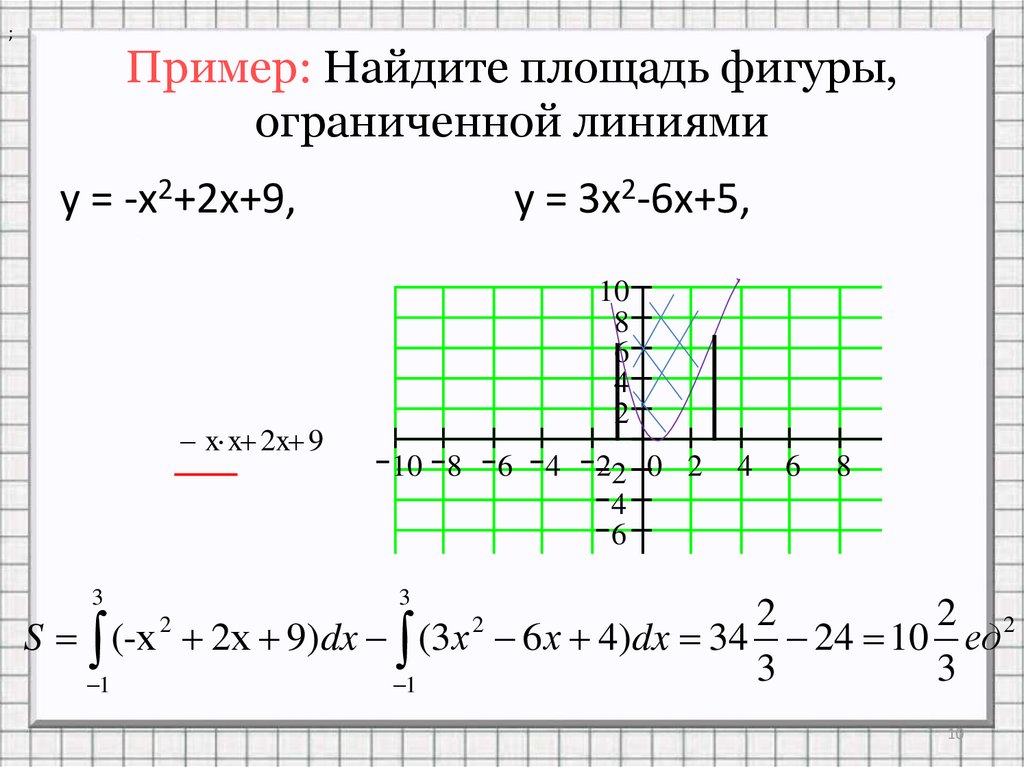
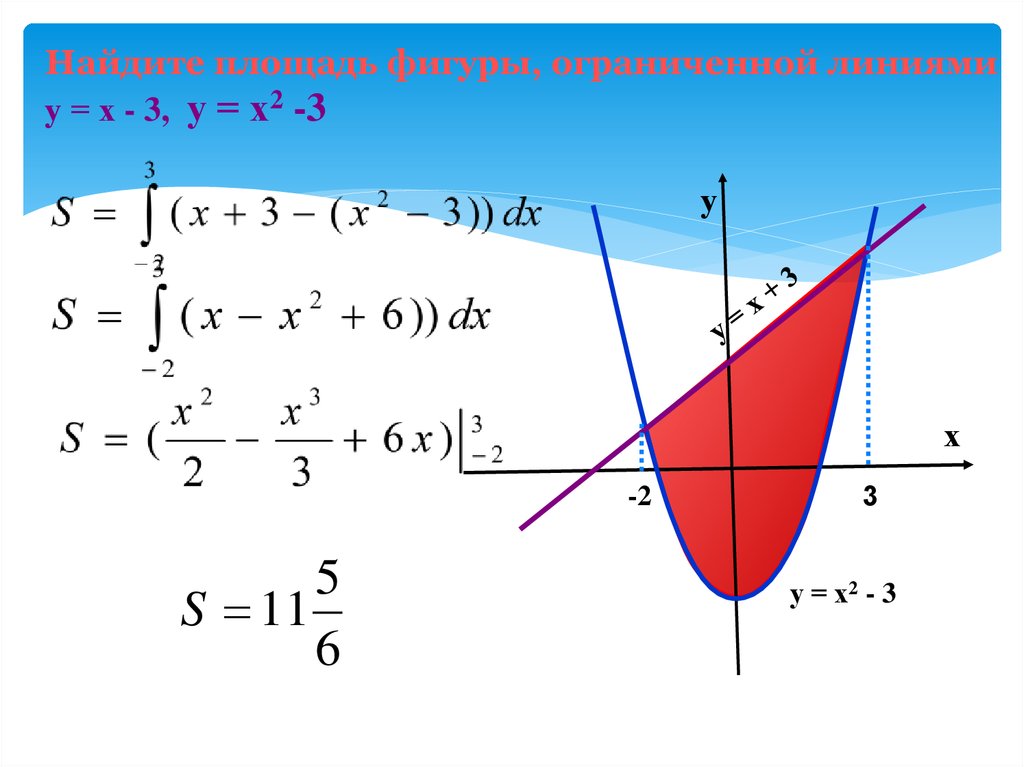 Так как , а , получаем: . Таким образом,
.
Так как , а , получаем: . Таким образом,
.
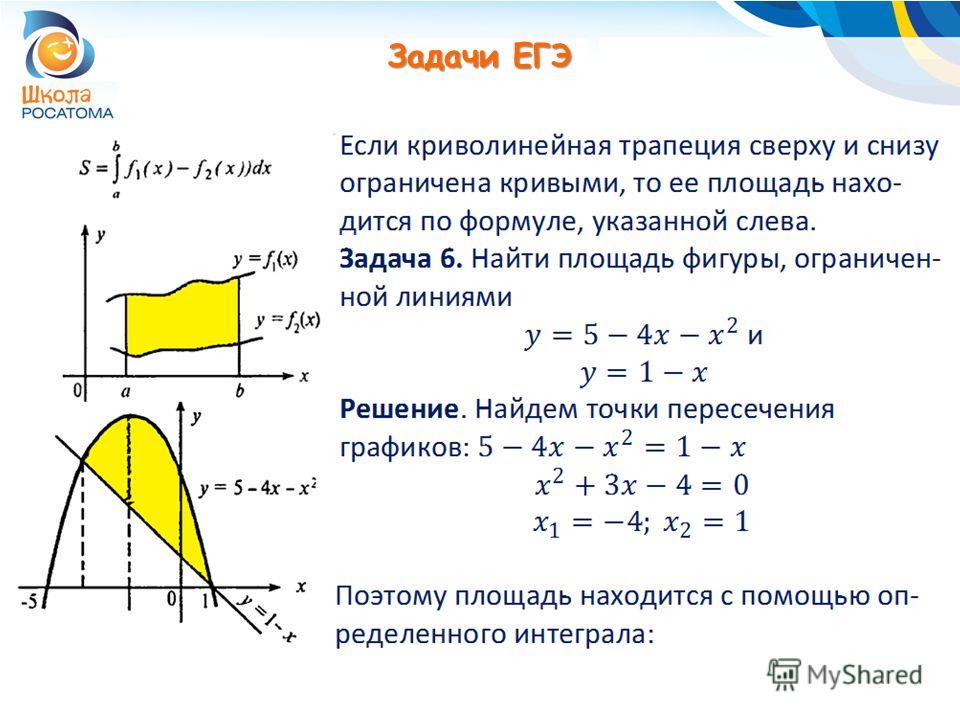
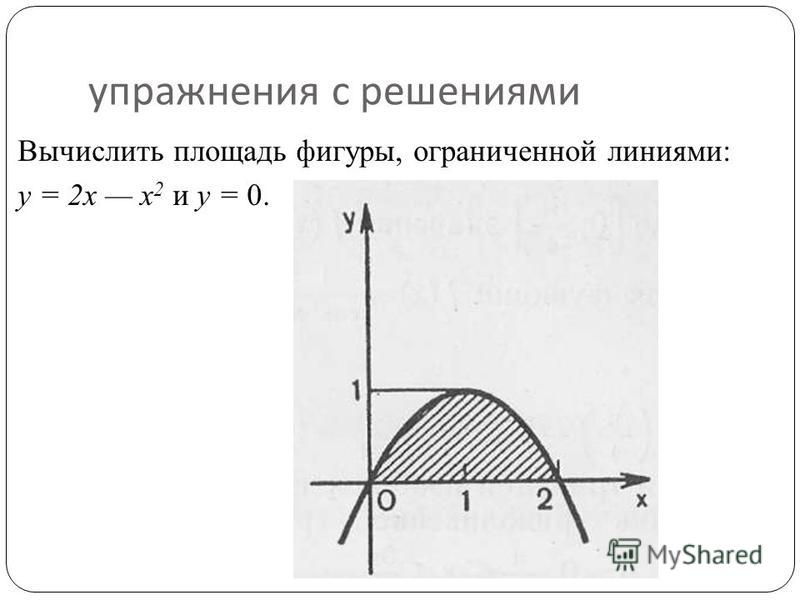 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.012 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.012 с.)


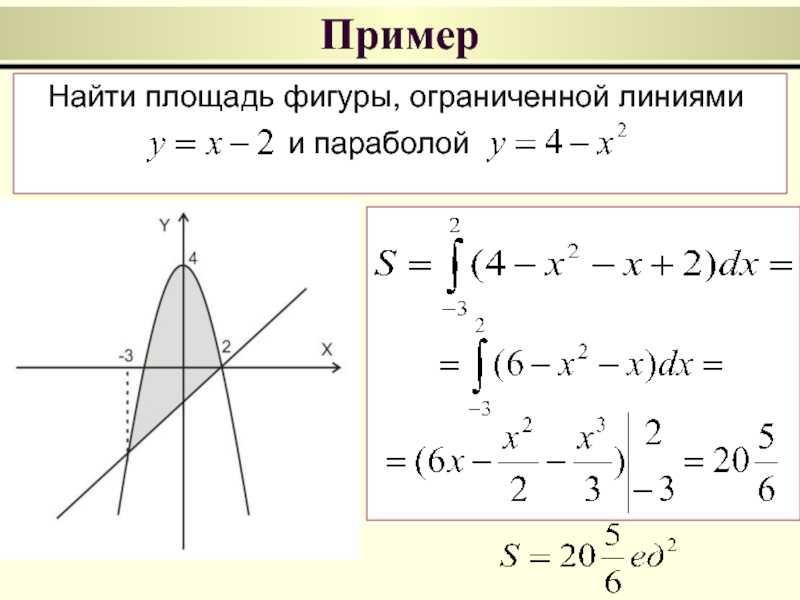 (Икс).
(Икс).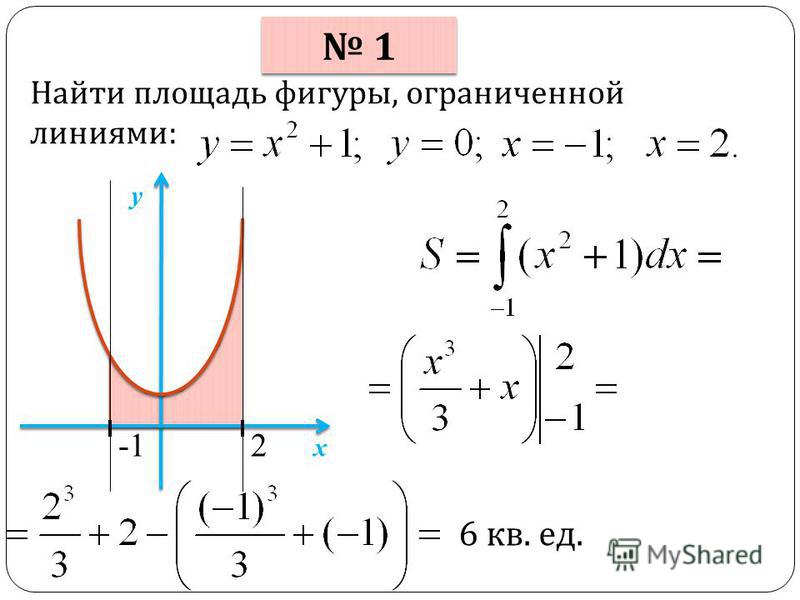
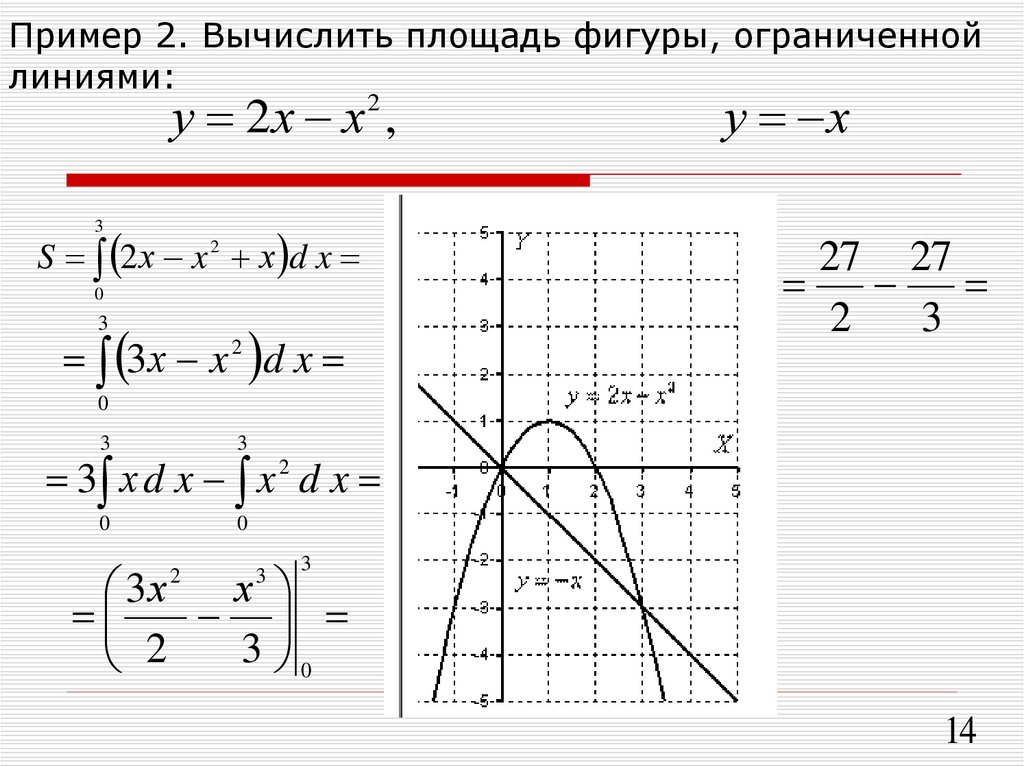 Внимательно выбирайте онлайн-калькулятор в соответствии с вашими потребностями.
Внимательно выбирайте онлайн-калькулятор в соответствии с вашими потребностями.