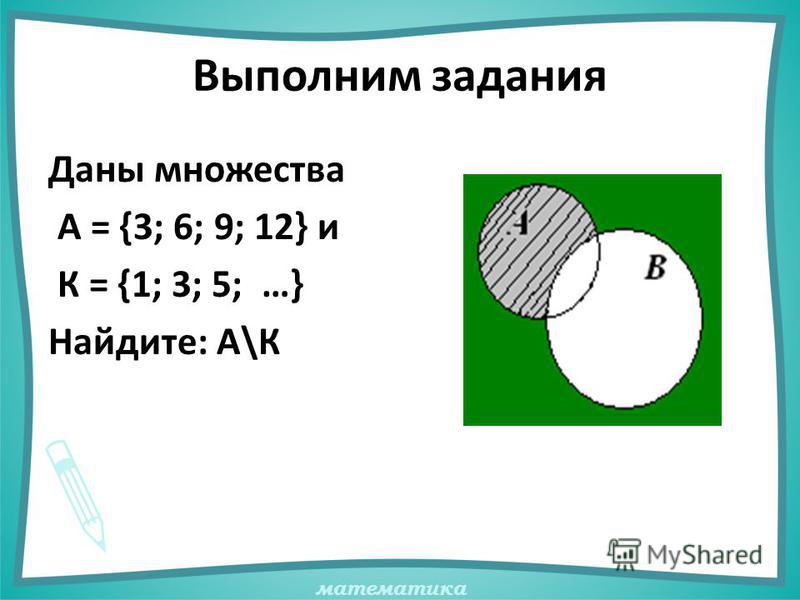
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
Стр 1 из 9Следующая ⇒ Основные понятия теории множеств Вопрос 1: Заданы множества А = {1,2,3} и B = {1,2,3,4,5}, тогда верным для них будет утверждение … Множество А включает в себя множество В + Множество А есть подмножество множества В Множества А и В не имеют общих элементов Множества А и В равны
Вопрос 2: Заданы множества A = {1,3,5} и B = {3,1,5}, тогда верным для них будет утверждение … + Множество B есть подмножество множества А + Множество А есть подмножество множества В Множества А и В не имеют общих элементов + Множества А и В равны
Вопрос 3: Заданы множества A = {1,3,5,7,8} и B = {1,5,7}, тогда верным для них будет утверждение … + Множество А включает в себя множество В Множество А есть подмножество множества В Множества А и В не имеют общих элементов Множества А и В равны
Вопрос 4: 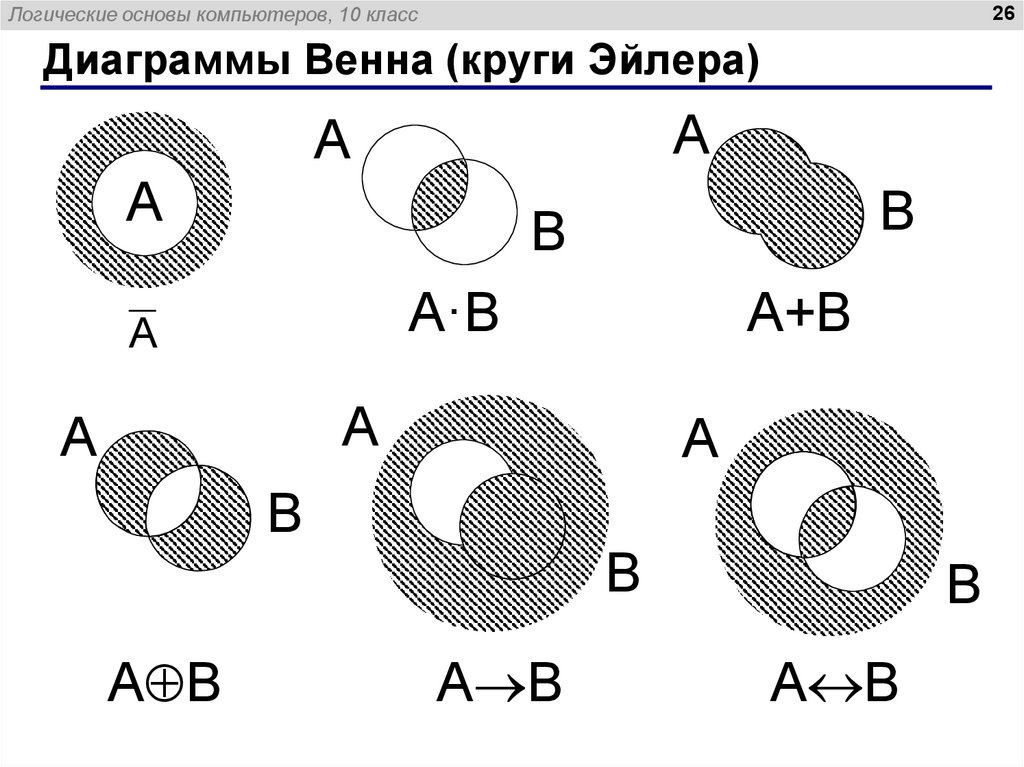 Верным для них будет утверждение … Верным для них будет утверждение …Множество А включает в себя множество В Множество А есть подмножество множества В + Множества А и В не имеют общих элементов Множества А и В равны
Вопрос 5: Пусть М – множество студентов факультета, N – множество студентов факультета, получающих стипендию. Тогда разностью M\N будет … множество студентов факультета множество студентов факультета, получающих стипендию + множество студентов факультета, не получающих стипендию пустое множество
Вопрос 6: Пусть М – множество студентов факультета получающих стипендию, N – множество студентов факультета не получающих стипендию. Тогда объединением M U N будет … + множество студентов факультета множество студентов факультета, получающих стипендию множество студентов факультета, не получающих стипендию пустое множество
Вопрос 7: Пусть М – множество студентов факультета получающих стипендию, N – множество студентов факультета не получающих стипендию. множество студентов факультета множество студентов факультета, получающих стипендию множество студентов факультета, не получающих стипендию + пустое множество
Вопрос 8: Высказывание «Множество A не является подмножеством множества B» истинно для пары множеств … + A={2, 4, 6, 7}, B={4, 7} A={6, 0, 3}, B={0, 3, 6} A={2, 5}, B={1, 2, 5, 0}
Вопрос 9: Даны множества A={б, в, г}, B={б, в}, C={в}. Для заданных множеств будут верны утверждения, что … множества A и B равны + множество C включено в множество A множество A включено в множество C + множества A и B не равны + множество C есть подмножество множества B
Основные операции над множествами. Диаграммы Эйлера-Венна Вопрос 10: Даны множества: A={1, 4, 6, 8, 9}, B={1, 6, 9}, C={4, 8}. Тогда для них истинно высказывание … C=AÈB B=AÇC + A=BÈC A=CÇB
Вопрос 11: Даны множества C={1, 3, 6, 8} и D={1, 6, 9}. {3, 8} + {1, 3, 6, 8, 9} {1, 6} {9}
Бинарные отношения Вопрос 12: Если отношение задано равенством «x-3y=2», то данному отношению принадлежат пары чисел … + (5, 1) (1, 5) (0, 2) + (2, 0)
Вопрос 13: Если отношение задано равенством «y>2x», то данному отношению принадлежат пары чисел … (10, 3) + (1, 5) (2, 4) + (3, 10)
Основные понятия теории вероятностей. Свойства вероятностей Вопрос 61: Игральную кость бросают один раз. Чему равна вероятность того, что выпадет число очков равное 5? + 1/6 2/6
Вопрос 62: Игральную кость бросают один раз. Чему равна вероятность того, что выпадет число очков больше 4? + 2/6 1/6
Вопрос 63: Игральную кость бросают один раз. + 0 1/6 2/3
Вопрос 64: Игральную кость бросают один раз. Чему равна вероятность того, что выпадет число очков меньше 7? + 1 1/6 2/6
Вопрос 65: Как называется событие, вероятность которого равна 0? достоверное + невозможное случайное
Вопрос 66: Как называется событие, вероятность которого равна 1? + достоверное невозможное случайное
Вопрос 67: Как называется событие, вероятность которого больше нуля, но меньше единицы? достоверное невозможное + случайное
Вопрос 68: В мешке лежат 1 белый и 3 черных шара. Каким будет событие: ʺИз мешка вынули 2 белых шараʺ? случайное достоверное + невозможное
Вопрос 69: В мешке лежат 1 белый и 3 черных шара. случайное + достоверное невозможное
Вопрос 70: В урне лежат белые и черные шары. Всего в урне 15 шаров. Вероятность извлечения белого шара равна 7/15. Чему равна вероятность извлечения черного шара?7/15 + 8/15
Вопрос 71: Вероятность наступления некоторого события не может быть равна … + 2 1/2
Вопрос 72: Два стрелка, для которых вероятность попадания в мишень равна 0,8 и 0,7, производят по одному выстрелу в мишень. Чему равна вероятность попадания в мишень обоими стрелками? + 0,56 0,94 0,8 0,7
Вопрос 73: Для посева берут семена из двух пакетов. Вероятность прорастания семян в первом и втором пакетах соответственно равна 0,9 и 0,7. Если взять по одному семени из каждого пакета, то вероятность того, что оба они прорастут, равна … + 0,63 0,8 0,97 0,7
Вопрос 74: На завтрак студент может выбрать кекс, бутерброд, пиццу или булочку, а запить их он может кофе, соком или кефиром. + 12
Вопрос 75: Исходом, благоприятствующим событию «выпало нечетное число очков» при подбрасывании игрального кубика, является цифра … + 1
Вопрос 76: Непрерывной случайной величиной является … X – число зерен в случайно взятом колоске ржи X – количество покупателей в определенный день работы магазина X – число букв в русском алфавите + X – длительность бесперебойной работы купленного телевизора
Вопрос 77: Попадание и промах при одном выстреле являются событиями … совместными не противоположными + несовместными независимыми
Вопрос 78: Невозможными являются следующие два события: + появление двух очков при бросании трех игральных кубиков + появление девятнадцати очков при бросании трех игральных кубиков появление двенадцати очков при бросании трех игральных кубиков появление не менее 3 и не более 18 очков при бросании трех игральных кубиков
Вопрос 79: Вероятность наступления некоторого события не может быть равна … + -0,5 + 4/3 +1,2 0,3
Вопрос 80: Вероятность наступления некоторого события не может быть равна… 0,2 0,3 +1,3
Вопрос 81: В урне 10 белых шаров. «События А и В равновероятны» «Вероятность события А равно 0» + «Событие А достоверно» «Событие В достоверно»
Вопрос 82: В ящике 10 качественных и 5 бракованных деталей. Опыт состоит в выборе только одной детали. Событие A – «Вынули качественную деталь». Событие B – «Вынули бракованную деталь». Тогда для этих событий неверным будет утверждение: «События A и B несовместны» + «Событие A невозможно» + «Событие B невозможно» + «События A и B равновероятны»
Вопрос 83: Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков меньшее, чем 4, равна… 5/6 4/5 + 1/2 2/3
Вопрос 84: Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет четное число очков, равна… + 1/2 1/3 2/3 1/6
Вопрос 85: Некоторый спортсмен выиграет чемпионат Европы с вероятностью 0,9, а чемпионат мира – с вероятностью 0,8. + 0,72 1,7 0,85 0,8
Вопрос 86: Три стрелка стреляют по одной мишени, и каждый попадает или промахивается независимо от результатов выстрелов других стрелков. Вероятности попадания в мишень для каждого из стрелков, соответственно равны: 0,8; 0,7; 0,5. Определить вероятность события: все три стрелка попали в мишень. + 0,28 0,56 0,35 0,4
Вопрос 87: В ящике 10 качественных ламп. Опыт состоит в выборе только одной лампы. Событие А – «Вынули качественную лампу». Событие В – «Вынули бракованную лампу». Тогда для этих событий верным будет утверждение: «События А и В равновероятны» «Вероятность события В больше вероятности события А» «Событие А невозможно» + «Событие А достоверно»
Вопрос 88: Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков, меньшее, чем 5, равна… 1/3 5/6 + 2/3
Вопрос 89: Первый студент успешно ответит на данный текст с вероятностью 0,5; второй – с вероятностью 0,7. 1,2 0,035 0,7 + 0,35
Дисперсия Вопрос 104: Дисперсия случайной величины D(X)=6,25. Найти среднее квадратическое отклонение s(X). + 2,5 39,06
Вопрос 105: Дисперсия случайной величины D(X)=6. Найти среднее квадратическое отклонение s(X). 2,5 + 3
Вопрос 106: Дисперсия случайной величины D(X)=1,44. Найти среднее квадратическое отклонение s(X). + 1,2 2,07 1,44 2,88
Математическая статистика. Основные понятия и определения Вопрос 107: Дана выборка 10, 11, 12, 11, 10, 14, 10. Тогда его выборочная мода равна … 11,29 + 10
Вопрос 108: Дана выборка 10, 11, 12, 11, 11, 14, 10. Тогда его выборочная мода равна … 11,29 + 11
Вопрос 109: Дана выборка 12, 11, 12, 13, 10, 14, 15. + 12
Вопрос 110: Дана выборка 12, 11, 12, 12, 10, 14, 15. Тогда его выборочная мода равна … + 12
Вопрос 111: Дана выборка 8, 8, 9, 9, 9, 10, 11. Тогда его выборочная мода равна … + 9
Вопрос 112: Дана выборка: 1,5; 1,6; 1,6; 1,4; 1,7; 1,6; 1,7; 1,4. Её выборочная мода равна … 1,75 1,4 +1,6 1,7
Вопрос 113: Дана выборка 12, 11, 10, 12, 13. Тогда его выборочная медиана равна … + 12
Вопрос 114: Дана выборка 10, 11, 12, 10, 13. Тогда его выборочная медиана равна … + 11 11,2
Вопрос 115: Дана выборка 10, 11, 11, 12, 10, 13. Тогда его выборочная медиана равна … +11 10,5
Вопрос 116: Дана выборка: -10; -11; 12; -14; -14; -13; 15; -11; -11. Ее выборочная медиана равна … + -11 12,33
Вопрос 117: Укажите статистические исследования, в которых объем выборки одинаковый. + При изучении работы магазина количество посетителей в обследуемые дни составило: 35, 47, 84, 33, 71, 25, 49, 57. + В результате тестирования студенты показали следующие баллы: 5, 1, 3, 4, 0, 1, 2, 5. При медицинском обследовании больных получены следующие результаты взвешивания в килограммах: 44, 52, 66, 48, 76, 93, 69, 84, 82. При изучении длительности случайно отобранных фильмов получены следующие результаты в минутах: 120, 99, 124, 86, 94, 112, 106.
Вопрос 118: В концерте принимали участие артисты, следующего возраста 55, 40, 18, 22, 23, 41, 22. Объем данной выборки составил … + 7 31,57
Вопрос 119: Дан вариационный ряд 4, 5, 6, 8, 10, 11, 11, 12. Тогда медиана данного ряда равна … + 9
Вопрос 120: Дан вариационный ряд 11, 12, 13, 15, 17, 19, 22, 22, 24, 25. Тогда медиана данного ряда равна … + 18
Вопрос 121: Дан вариационный ряд 20, 23, 45, 45, 48, 50, 62, 70, 74. + 48
Вопрос 122: Дан вариационный ряд 1, 2, 2, 2, 4, 7, 7. Тогда мода данного ряда равна … + 2
Вопрос 123: Медиана вариационного ряда 3, 5, 6, 7, 8, 9 равна … + 6,5
Вопрос 124: Выборочная средняя равна 6 для выборки, заданной вариационным рядом … + 1, 2, 4, 4, 7, 7, 8, 9, 9, 9 1, 2, 4, 5, 6, 6, 6, 6, 7, 7 4, 4, 5, 5, 6, 7, 9, 10, 10, 10 3, 4, 4, 5, 5, 6, 6, 8, 9, 9
Вопрос 125: Средняя выборочная вариационного ряда 3, 4, 5, 5, 6, 6, 6, 7, 9, 9 равна … + 6
Вопрос 126: Дана выборка 10, 11, 12, 12, 14. Тогда его выборочная мода равна … + 12
Вопрос 127: Дана выборка 10, 11, 12, 12, 14, 14, 14. Тогда его выборочная мода равна … + 14
Вопрос 128: Дана выборка 10, 10, 10, 12, 14, 13. Тогда его выборочная мода равна … + 10
Вопрос 129: Дана выборка 10, 11, 11, 11, 11, 12, 14, 14. + 11
Вопрос 130: Дана выборка 1, 1, 2, 2, 2, 4, 14, 12. Тогда его выборочная мода равна … +2
Вопрос 131: Дана выборка 10, 11, 12, 10, 13. Тогда его выборочная медиана равна … + 11
Вопрос 132: Дана выборка 10, 12, 12, 10, 13. Тогда его выборочная медиана равна … + 12
Вопрос 133: Дана выборка 10, 10, 11, 12, 13. Тогда его выборочная медиана равна … + 11
Вопрос 134: Дана выборка 4, 5, 6, 7, 8. Тогда его выборочная медиана равна … + 6
Вопрос 135: Дана выборка 1, 2, 3, 4, 5. Тогда его выборочная медиана равна … + 3
Вопрос 136: Дана выборка 1, 3, 4, 5. Тогда его выборочная медиана равна … + 3,5
Тема: Предмет теории вероятностей.
Вопрос: Монета брошена два раза. А) 1/4; Б) 2/4; В) 0,25; Г) 0,75; Д) 3/4. Вопрос: По эмпирическому подходу вероятность события рассчитывается (статистическое определение вероятности): А) Б) Как отношение числа опытов в которых событие А наступила, к общему числу исходов при проведении опытов В) как степень уверенности наступления того и иного события. Г) нет правильного ответа.
Вопрос: В классическом подходе вероятность события рассчитывается: А) Как отношение числа равновероятных благоприятных исходов наступления события А к общему числу возможных исходов Б) В) как степень уверенности наступления того и иного события. Г) нет правильного ответа.
Вопрос: Какова вероятность того, что при двух подбрасываниях одной игральной кости выпадет сумма очков, равная 13? А) 0 Б) 1/13 В) 1/18 Г) 1/36
Вопрос: Могут ли быть противоположными события С и D, если Р(С) = 0,12; P(D) = 0,78 А) Нет Б) Да
Вопрос: Какие значения может принимать вероятность? А) (-1;1) Б) [0;1] В) (0;1) Г) [-1;1]
Вопрос: Пространство элементарных событий – это. А) любое действие, которое приводит к определенному набору результатов. Б) конкретные результаты испытаний или их сочетание. В) множество всех возможных результатов эксперимента
Вопрос: Два события называются несовместными, если: А) вероятность появления каждого из них не зависит от того, появилось другое событие или нет. Б) появление одного из них исключает появление другого в одном и том же испытании. В) при рассмотрении группы событий может произойти только одно из них, а никакие другие события, не входящие в рассматриваемую группу, произойти не могут. Г) событие А происходит тогда и только тогда, когда происходит событие В.
Вопрос: Два события называются независимыми, если: А) вероятность появления каждого из них не зависит от того, появилось другое событие или нет. Б) появление одного из них исключает появление другого в одном и том же испытании. В) при рассмотрении группы событий может произойти только одно из них, а никакие другие события, не входящие в рассматриваемую группу, произойти не могут. Г) событие А происходит тогда и только тогда, когда происходит событие В.
Вопрос: Монета брошена 3 раза. Пусть А, В, С — события, состояние в появлении герба соответственно в первом, втором и третьем испытаниях. Ясно, что эти события являются А) Несовместными Б) Независимыми В) Зависимыми Г) Противоположными
Вопрос: Пр о с т р а н с т в о м э л е м е н т а р н ы х и с х о д о в называется множество, содержащее все возможные результаты данного случайного эксперимента. Элементы этого множества называют э ле ме нт а р ны м и ис х о д а м и. Отношение числа исходов, благоприятствующих появлению события А к общему числу исходов называется А) Вероятностью события А Б) Траекторией события А В) Величиной события А Г) Показателем события А
Вопрос: Выберите неверное утверждение: А) Событие, противоположное достоверному, является невозможным Б) Сумма вероятностей двух противоположных событий равна единице В) Если два события единственно возможны и несовместны, то они называются противоположными Г) Вероятность появления одного из противоположных событий всегда больше вероятности другого.
Вопрос: Заданы множества А = {1, 3, 4}, В = {2, 3, 1, 4}, тогда для них будет неверным утверждением А) множество А есть подмножество множества В; Б) множества А, В пересекаются В) множество А не равно множеству В Г) А и В не имеют общих элементов
Вопрос: Подбрасывают монету. События А = { выпал герб}, В = {выпала цифра}. Тогда верным для этих событий будет утверждение А) событие А тождественно событию В Б) А и В не имеют общих элементов В) события А и В несовместны; Г) А и В противоположны
Вопрос: События образуют ……….группу событий, если в результате испытаний появится хотя бы одно из них А) Независимую Б) Зависимую В) Полную Г) Совместную
Вопрос: Брошена монета. Появление герба исключает появление надписи. События «появился герб» и «появилась надпись» А) независимые Б) совместные В) несовместные Г) противоположные
Вопрос: Какова вероятность приземления парашютиста в заштрихованную область А) 11/36 Б) 1/36 В) 1/6 Г) 1/5
Вопрос: Вероятность события A при условии, что произошло событие B, называется А) Противоположной Б) Несовместной В) Условной Г) независимой
Вопрос: В урне 5 красных, 2 синих и 3 белых шара. вынутый шар не синий вынутый шар разноцветный (красно-белый) шар с четным номером — красный или белый + вынутый шар либо красного цвета, либо белого
Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события AD? + синий шар с четным номером либо шар с четным номером, либо он синий шар с четным номером и не синий синий шар с нечетным номером
Вопрос: В урне 5 красных, 2 синих и 3 белых шара. синий шар с четным номером кратный трем синий шар с четным номером кратный трем синий шар с номером 6 + синий шар с четным номером, но не кратным трем
Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события A + B ? шар с четным кратным трем номером синий шар с четным номером шар с номером 6 + шар с номером кратным трем или двум
Вопрос: Событие А означает, что хотя бы один из трех проверенных приборов бракованный, событие В – все три прибора стандартные. А. все три прибора стандартны и бракованы Б. среди трех стандартных приборов один бракованный + В. хотя бы один из трех приборов стандартный или бракованный Г. Среди трех бракованных изделий есть стандартный Д. среди трех стандартных приборов есть хотя бы один бракованный
Вопрос: Событие А означает, что хотя бы один из трех проверенных приборов бракованный, событие В – все три прибора стандартные. Что означает событие АВ? А. все три прибора стандартны и бракованы Б. среди трех стандартных приборов один бракованный В. хотя бы один из трех приборов стандартный или бракованный Г. Среди трех бракованных изделий есть стандартный +Д. среди трех стандартных приборов есть хотя бы один бракованный
Вопрос: В урне 5 белых, 3 черных, 4 красных шаров. Вероятность того, что из урны вынут белый или черный шар равна А) ¼ Б) 15/8 + В) 2/3 Г) 5/12
123456789Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 2171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Дискретная математика 01
Контрольная работа № 1
1. Даны множества A И B. Изобразить и записать с указанием характеристического свойства результат каждой операции:
А) AÈB ; б) AÇB; в) A \ B; г) B \ A; д) ; е) ; ж) A´ B; з) B´ A.
A = {X| xÎR, X > 2}, B = {X| xÎR,-5 £ X £ 8}
Решение:
Изобразим на числовой прямой множества А и В:
Тогда
А) AÈB= ;
Б) AÇB= ;
В) A \ B= ;
Г) B \ A= ;
Д) = ;
Е) = ;
Ж) A´ B= ;
З) B´ A= .
2. На диаграммах Эйлера-Венна изобразить результат операций, предварительно указав порядок действий в формуле.
Решение:
Порядок действий:
1.
2.
3.
4.
Изобразим на диаграмме Эйлера–Венна:
1.
2.
3.
4.
3. Упростить выражения, используя законы алгебры множеств
Решение:
.
4. На множестве M Бинарное отношение RÍ M´M Задано характеристическим свойством. Представить отношение R Другими возможными способами. Выяснить какими свойствами оно обладает.
Решение:
Составим таблицу произведений элементов множества М, выделив те пары, которые удовлетворяют характеристическому свойству:
|
-3 |
-2 |
0 |
1 |
2 |
3 | |
|
-3 |
9 |
6 |
0 |
-3 |
-6 |
-9 |
|
-2 |
6 |
4 |
0 |
-2 |
-4 |
-6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
-3 |
-2 |
0 |
1 |
2 |
3 |
|
2 |
-6 |
-4 |
0 |
2 |
4 |
6 |
|
3 |
-9 |
-6 |
0 |
3 |
6 |
9 |
Тогда выпишем в явном виде отношение:
Изобразим графически отношение:
Свойства отношения:
1) Рефлексивность: так как , то данное отношение рефлексивно.
2) Так как , то отношение будет симметричным.
3) Тогда отношение не будет антирефлексивным и антисимметричным.
4) Транзитивность выполняется: при положительном значении хотя бы одной переменной и две другие также будут положительны; при отрицательном значении одной переменной остальные также будут отрицательны. Тогда произведение любой их пары будет положительно.
5. Докажите тождество:
Доказательство:
6. Определите свойства отношений:
.
Решение:
1) Рефлексивность: так как , то данное отношение рефлексивно.
2) Так как из неравенства не следует неравенство , то отношение не будет симметричным.
3) Так как неравенства и могут одновременно выполняться лишь при условии , то отношение антисимметричное.
4) Транзитивность выполняется: .
7. Для отношения, заданного матрицей, определить является ли оно отношением эквивалентности
|
R |
A |
B |
C |
D |
E |
F |
|
A |
1 |
0 |
0 |
0 |
1 |
0 |
|
B |
0 |
1 |
1 |
0 |
0 |
0 |
|
C |
0 |
1 |
1 |
0 |
0 |
0 |
|
D |
0 |
0 |
0 |
1 |
0 |
1 |
|
E |
1 |
0 |
0 |
0 |
1 |
0 |
|
F |
0 |
0 |
0 |
1 |
0 |
1 |
Решение:
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Так как в матрице отношения по главной диагонали стоят все 1, то рефлексивность выполняется.
Так как матрица является симметричной, то отношение также является симметричным.
Исследуем на транзитивность:
Тогда транзитивность выполняется.
Следовательно, данное отношение является отношением эквивалентности.
| < Предыдущая | Следующая > |
|---|
Множества. Операции над множествами — презентация онлайн
1. Множества. Операции над множествами.
«Множествоесть многое,
мыслимое
нами как
единое».
Основоположник
теории множеств
немецкий
математик
Георг Кантор
(1845-1918)
3. Основные определения теории множеств. Примеры
Понятие множества является одним из
фундаментальных
понятий
математики,
которому трудно дать определение. Дело в
том, что определить понятие – это значит
найти такое родовое понятие, в которое это
понятие входит в качестве вида, но
понятие «множество» — это самое широкое
понятие математики и математической
логики, т.
 е. категория, а для категории
е. категория, а для категориинельзя найти более широкое, т.е. родовое
понятие.
Ограничимся
описательным
объяснением этого понятия.
4. Основные определения теории множеств. Примеры
Множество – это набор, совокупностькаких-либо
вполне
различаемых
объектов, называемых его элементами,
обладающими общими для всех их и только
их свойствами, и рассматриваемых как
единое целое.
Примеры:
• множество людей, живущих сейчас в России,
• множество точек данной геометрической фигуры,
• множество решений данного уравнения.
• невозможно говорить о множестве капель в стакане воды, так
как невозможно четко и ясно указать каждую отдельную каплю.
5. Структура множества
Каждое множество состоит из того или иногонабора
объектов,
которые
называются
элементами множества.
Факт, что элемент а принадлежит множеству Х
будем обозначать: а Х.
Порядок элементов в множестве несущественен.
Множества {а, в, с} и {а, с, в} одинаковы.
При этом, нужно иметь ввиду, что элемент а и
множество {а} – это не одно и то же. Первое – это
объект, обозначенный а, второе – это множество,
состоящее из единственного элемента а. Поэтому
можно сказать, что «а принадлежит { а }» – это
истинное суждение. В то время как, «{а}
принадлежит а» — это ложное суждение.
6. Способы задания множества
1.2.
Перечисление элементов множества.
Обычно
перечислением
задают
конечные множества.
Описание свойств, общих для всех
элементов этого множества, и только
этого
множества.
Это
свойство
называется
характеристическим
свойством, а такой способ задания
множества
описанием.
Таким
образом,
можно
задавать
как
конечные,
так
и
бесконечные
множества.
Примерами множеств могут
служить:
а) множество всех натуральных чисел,
б) множество всех целых чисел
(положительных, отрицательных и нуля),
в) множество всех рациональных
чисел,
г) множество всех действительных
чисел,
д) множество площадей треугольников,
е)множество четырехугольников,
8.
 Числовые множества1.
Числовые множества1.Множество НАТУРАЛЬНЫХ чисел N, N={1, 2, 3, 4,
5, …}
2.
Множество ЦЕЛЫХ чисел Z, Z={…, -4, -3, -2, -1, 0,
1, 2, 3, 4, …}
2 1,414213…
3.
Множество РАЦИОНАЛЬНЫХ чисел Q, Q={x| x=p/q,
где p Z, q N}
4.
Множество ИРРАЦИОНАЛЬНЫХ чисел I ,бесконечные непериодические дроби, (
=3,141592…, e=2,718281, …)
,
5.
Множество ДЕЙСТВИТЕЛЬНЫХ чисел R получено
объединением РАЦИОНАЛЬНЫХ и
ИРРАЦИОНАЛЬНЫХ чисел.
6.
Множество КОМПЛЕКСНЫХ чисел C, содержащих
в себе мнимую единицу і, которая является
9. Количество элементов множества
Множества бывают конечными или бесконечными. Если числоэлементов множества конечно – множество называется конечным.
Определение: Количество элементов, составляющих множество,
называется мощностью множества.
Определение: Если между элементами бесконечного множества можно
установить взаимооднозначное соответствие с элементами множества
положительных целых чисел, то говорят, что множество счетно.
Например:
множество действительных чисел — бесконечное множество.
множество чисел, делящихся без остатка на 3 – счетное множество,
множество букв русского алфавита, множество отличников вашей
группы – конечно.
10. Равенство множеств
Определение:Два множества
равны между собой, если они
состоят из одних и тех же
элементов.
Т.е. любой элемент множества Х
является элементом множества Y, и
любой элемент множества Y
является элементом множества Х.
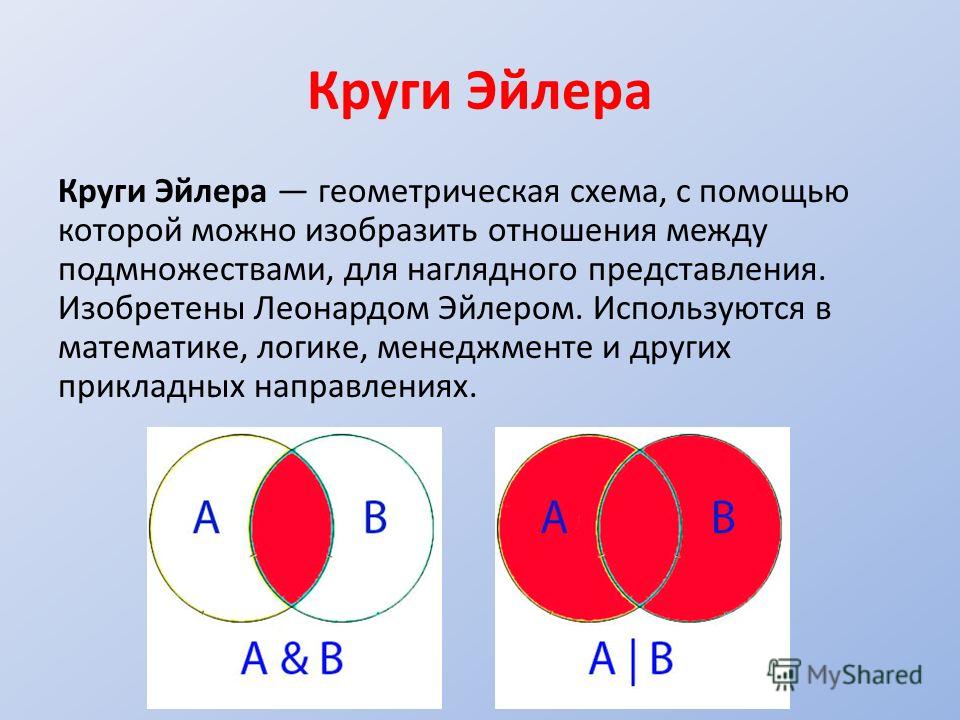
11. Диаграммы Эйлера-Венна
Для наглядногопредставления (графического
изображения) множеств и
результатов операций над
ними удобно пользоваться так
называемыми диаграммами
Эйлера-Венна (кругами
Эйлера).
При этом множества
изображаются на плоскости
в виде замкнутых кругов, а
универсальное множество в
виде прямоугольника.
Элементы множества – точки
внутри соответствующего
круга.
«Парадокс брадобрея».
Одному солдату было приказано брить тех и
только тех солдат его взвода, которые сами
себя не бреют.
 Неисполнение приказа в армии,
Неисполнение приказа в армии,как известно, тягчайшее преступление. Однако
возник вопрос, брить ли этому солдату самого
себя. Если он побреется, то его следует
отнести к множеству солдат, которые сами
себя бреют, а таких брить он не имеет права.
Если же он себя брить не будет, то попадёт во
множество солдат, которые сами себя не
бреют, а таких солдат согласно приказу он
обязан брить. Парадокс.
13. Подмножество. Включение
Определение: Множество A является подмножеством B,если любой элемент множества A принадлежит множеству
B. Это еще называется нестрогим включением A B.
Например:
Пусть Х – множество студентов некоторой группы, Е –
множество отличников этой же группы.
E X т.к. группа может состоять только из отличников.
Когда хотят подчеркнуть, что в множестве B есть
обязательно элементы, отличные от элементов множества
A, то пишут A B. Это называется строгим включением.
Например:
Пусть Х – множество всех студентов ВлГУ, Е – множество
студентов педагогического института.

E X т.к. в множестве всех студентов ВлГУ обязательно есть
элементы E.
14. Пустое множество
Пустое множествоЕсли характеристическим свойством, задающим
множество, А не обладает ни один объект, то
говорят, что множество А пустое.
Понятие пустого множества очень важное понятие.
Оно позволяет описательно задавать множества, не
заботясь, есть ли в этом множестве элементы и
совершенно
спокойно
оперировать
с
этими
множествами. Пустое множество будем считать
конечным множеством.
Например: множество действительных корней
уравнения
2
x 1
пустое.
15. Операции над множествами
16. 1. Пересечение множеств А∩В
Пересечением множества А и В называютмножество,
состоящие из всех общих элементов
множеств А и В (А∩В).
Например,
а) А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то А∩В
=
{3; 9};
17. Непересекающиеся множества
Определение: Множества называютсянепересекающимися, если не имеют
общих элементов, т.
 е. их пересечение
е. их пересечениеравно пустому множеству.
Например:
а) непересекающимися множествами
являются множества отличников группы и
неуспевающих.
б) непересекающимися множествами
являются множества А = {3; 9; 12} и В =
{1; 5; 7; 11}.
18. Свойства пересечения
X∩Y = Y∩X – коммутативность;(X∩Y) ∩Z =X∩ (Y∩Z)=X∩Y∩Z –
ассоциативность;
X∩ = ;
X∩I = Х;
19. 2. Объединение множеств АUВ
Объединением множеств А и В называютмножество, состоящее из всех элементов,
которые принадлежат хотя
бы одному из
этих множеств.
Например,
А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11},
АUВ=?
АUВ = {1; 3; 5; 7; 9; 11; 12}.
20. Свойства объединения
XUY=YUY- коммутативность;
(X UY)UZ =XU (YUZ)=XUYUZ –
ассоциативность;
XU = X;
XUI = I.
21. 3. Разность множеств А\ В
Разность А и В это множество элементов А,не
принадлежащих В.
Например,
А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20},
А\ В={2; 4; 6; 8}.

22. Свойства операции разности
А\В≠ В\А;
А\А=∅;
А\∅=А;
I\А= Ā.
23. 4. Дополнение множеств Ā
Дополнениеммножества
А
называется
разность I \ А. То есть,
дополнением
множества
А
называется
множество,
состоящее
из
всех
элементов
универсального
множества,
не
принадлежащих множеству А.
Например, А = {3; 6; 9; 12} и I =N= {1; 2; 3;
4; 5; 6; …}, Ā=?
Ā = {1; 2; 4; 5; 7; 8; 10; 11; 13; …}.
24. Свойства дополнения
1. Множество X и его дополнениене
X X
имеют общих элементов
2. Любой элемент I принадлежит
или
X X
I
множеству Х или его дополнению.
3. Закон двойного
отрицания
X X
25. Декартово произведение множеств
Фабрика верхнего трикотажа изготовляет мужские пуловеры, женскиекостюмы, кофты и платья следующих расцветок: бордо, синяя,
голубая, зеленая, коричневая, серая.
Посмотрим, какие изделия можно получить, учитывая возможные для них
расцветки.

Обозначим через А множество видов изделий: А={мужской пуловер,
женский костюм, кофта, платье}, через В – множество предлагаемых
расцветок: В={бордо, синяя, голубая, зеленая, коричневая, серая}.
Cоставим список всех пар из элементов
множества В таким образом, что сначала
множества А, затем элемент множества
упорядоченных пар элементов множеств А
можно перечислить с помощью таблицы.
множества А и элементов
будем записывать элемент
В. получим множество С
и В. Возможные изделия
26. Декартово произведение множеств
BA
Мужской
пуловер
Бордо
Пуловербордо
Синяя
Пуловерсиний
Женский
костюм
костюмбордо
Кофта
Кофтабордо
Платье
Платьебордо
Голубая
Зеленая
Кофтазеленая
Коричневая
Серая
Платьекоричневое
Костюмсерый
27. Определение декартова произведения
Декартовым (или прямым) произведениемА×В множества А на множество В
называется
множество
всех
упорядоченных пар, в которых первая
компонента – элемент множества А, а
вторая – элемент множества В.

А×В={(x, y) |x∈A, y∈B}.
Количество элементов в декартовом
произведении двух множеств:
если m(А)=n, m(B)=k, то m(А×В)=n⋅k.
28. Пример декартова произведения
Вычислить количество двухзначныхчисел.
Двухзначное число можно принять за
упорядоченную пару, где на первом
месте может стоять цифра из множества
А={1, 2, 3, 4, 5, 6, 7, 8, 9}, а на втором –
из множества В={0, 1, 2, 3, 4, 5, 6, 7, 8,
9}, т.е. за элемент прямого произведения
этих множеств, тогда получаем:
m(А)=9, m(B)=10, то m(А×В)=9⋅10=90.
Итак, всего имеется 90 различных
двухзначных чисел.
29. Соответствие множеств
Определение.Будем говорить, что между
элементами двух множеств
А и В установлено
соответствие ρ, если в их произведении А×В
выделено некоторое подмножество Ω. Если пара
(a,b)∈Ω⊆Α×Β, это означает по определению, что
элементы a и b множеств А и В находятся в
отношении ρ (пишется aρb).
Пример соответствия.
 Пусть даны множества А –
Пусть даны множества А –студентов и В – множество групп. Утверждение
“студент
a
учится
в группе b” задает
соответствие между множеством студентов и
множеством групп. Здесь а пробегает множество
значений А, b – множество значений В. Такое
соотношение называется бинарным соответствием,
т.е. соответствием между двумя множествами А и В.
30. Пример соответствия множеств
Бинарные соответствия можно задавать таблицами (например,расписание занятий) или ориентированными графами.
Группы
Студенты
1
2
3
Иванов
Петров
Сидоров
И
1
П
2
С
3
31. Отображение множеств f: X→Y
Отображение множеств f:Определение. Если каждому X→Y
элементу x∈X поставлен в соответствие
единственный элемент y∈Y, то такое соответствие называется отображением
множества Х в множество Y. Т.е., каждому элементу х соответствует только
один элемент y.
При таком отображении множества Х в множество Y, элемент y∈Y называется
образом элемента x∈X, а элемент x∈X называется прообразом элемента
y∈Y.
Пример. Пусть Х – множество студентов в аудитории, Y – множество столов в
этой аудитории. Соответствие “студент х сидит за столом y” задает
отображение множества Х в множество Y, так как все студенты сидят за
столом, иногда по двое, по трое и т.д., но есть и пустые столы.
x1
x2
x3
y1
y2
y3
32. Сюръективное отображение
Определение.33. Инъективное отображение
Определение.34. Взаимно-однозначное соответствие
Определение.35. Задания
Задание 11) Задайте множество цифр, с помощью
которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
2) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {- 2, — 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
г) А = {0,1; 0,01; 0,001; 0,0001; …};
д) А = {1/2, 2/3, 3/4, 4/5, … }.
3) Задание с выбором ответа. Даны множества:
М = {5,4,6},
Р = {4,5,6}, Т = {5,6,7}, S =
{4, 6}.
Какое из утверждений неверно?
а) М = Р.
 б) Р ≠ S.
б) Р ≠ S.в) М ≠ Т.
г) Р = Т.
Задание 2
1. Запишите на символическом языке
следующее утверждение:
а) число 10 – натуральное;
б) число – 7 не является натуральным;
в) число – 100 является целым;
г) число 2,5 – не целое.
2. Верно ли, что:
а) – 5
N; б) -5
Z; в) 2,(45)
Q?
3. Верно ли, что:
а) 0,7
{х | х2 – 1 < 0}; б) – 7
{х | х2
+ 16х ≤ — 64}?
Задание 3
1. Даны множества:
А = {10}, В = {10, 15}, С = {5, 10, 15}, D =
{5, 10, 15, 20}.
Поставьте вместо … знак включения (
или
) так,
чтобы получилось верное утверждение:
а) А … D; б) А … В; в) С … А; г) С … В.
2. Даны три множества А = {1, 2, 3, …, 37}, В =
{2, 4, 6, 8, …},
С = {4, 8, 12, 16, …, 36}.
Верно ли, что:
а) А
В; б) В
С; в) С
А; г) С
В?
Задание 4
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8;
11},
С = {5; 11}.
Найдите: 1) А∩В; 2) А∩С; 3) С∩В.
2. Даны множества: А – множества всех
натуральных чисел, кратных 10, В = {1; 2; 3;…,
41}.

Найдите А∩В.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e,
f},
C = {c, e, g, k}. Найдите (А∩В)∩С.
Задание 5
1. Даны множества: А = {2; 3; 8}, В = {2; 3;
8; 11}, С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
2. Даны множества: А = {a, b, c, d}, B = {c,
d, e, f},
C = {c, e, g, k}.
Найдите (АUВ)UС.
41. Решение задач с помощью кругов Эйлера
ЭЙЛЕР Леонард (1707-1783),российский ученый — математик,
механик, физик и астроном.
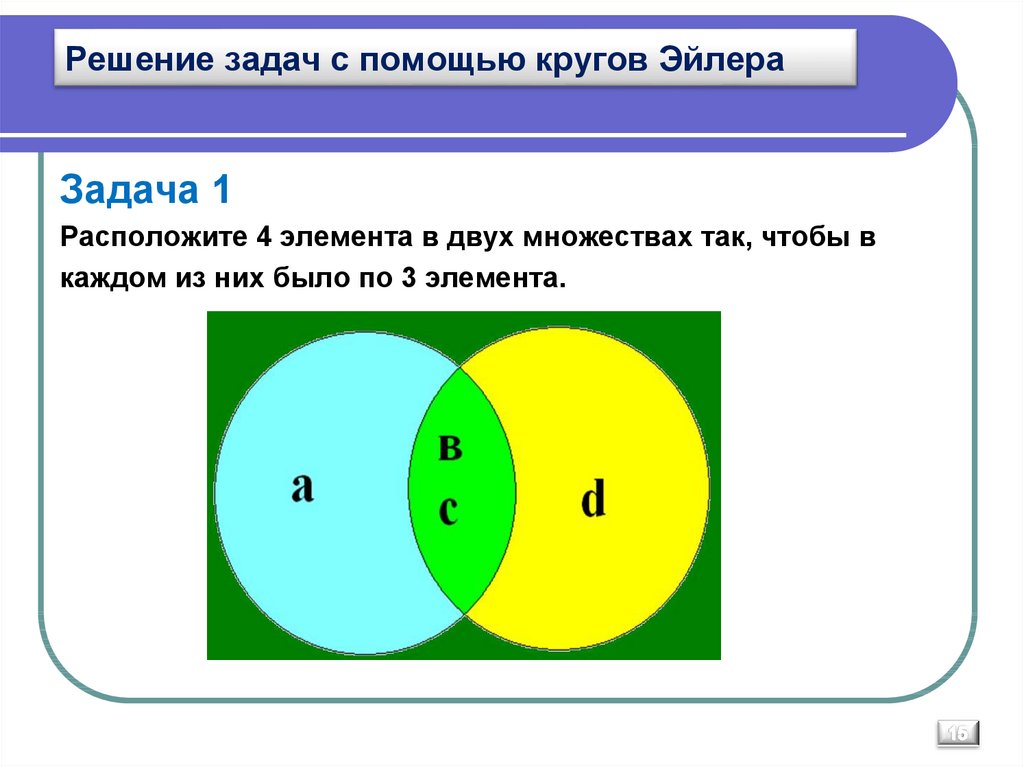
42. Задача 1
Расположите 4 элемента в двух множествахтак, чтобы в
каждом из них было по 3 элемента.
43. Задача 2
Множества А и В содержат соответственно 5и 6 элементов,
а множество А ∩ В – 2 элемента. Сколько
элементов в
множестве А U В?
44. Задача 3
Каждая семья, живущая в нашем доме,выписывает или
газету, или журнал, или и то и другое
вместе. 75 семей
выписывают газету, а 27 семей
выписывают журнал и лишь
13 семей выписывают и журнал, и газету.

Сколько
семей живет в нашем доме?
45. Задача 4
На школьной спартакиаде каждый из 25учеников 9 –го
класса выполнил норматив или по бегу, или по
прыжкам в
высоту. Оба норматива выполнили 7 человек, а
11 учеников
выполнили норматив по бегу, но не выполнили
норматив
по прыжкам в высоту. Сколько учеников
выполнили
норматив: а) по бегу; б) по прыжкам в высоту;
в) по
прыжкам при условии, что не выполнен
норматив по бегу?
46. Задача 5
Из 52 школьников 23 собирают значки, 35собирают марки,
а 16 – и значки, и марки. Остальные не
увлекаются
коллекционированием. Сколько школьников
не
увлекаются коллекционированием?
46
47. Задача 6
Каждый из учеников 9-го класса в зимниеканикулы ровно
два раза был в театре, посмотрев
спектакли А, В или С. При
этом спектакли А, В, С видели
соответственно 25, 12 и 23
ученика. Сколько учеников в классе?
48. Задача 7
В воскресенье 19 учеников нашего классапобывали в
планетарии, 10 – в цирке и 6 – на стадионе.

Планетарий и
цирк посетили 5 учеников; планетарий и
стадион-3; цирк и
стадион -1. Сколько учеников в нашем классе,
если никто не
успел посетить все три места, а три ученика не
посетили ни
одного места?
49. Задача 8
В одном классе 25 учеников. Из них 7 любятгруши,
11 – черешню. Двое любят груши и черешню; 6 –
груши и
яблоки; 5 – яблоки и черешню. Но есть в классе
два ученика,
которые любят всё и четверо таких, что не
любят фруктов
вообще. Сколько учеников этого класса любят
яблоки?
50. Задача 9
На уроке литературы учитель решил узнать, кто из40
учеников 9 –го класса читал книги А, В, С.
Результаты
опроса выглядели так: книгу А прочитали 25
учеников,
книгу В – 22 ученика, книгу С – 22 ученика; одну из
книг А
или В прочитали 33 ученика, одну из книг А или С
прочитали 32 ученика, одну из книг В или С – 31
ученик.
Все три книги прочитали 10 учеников.
Сколько учеников:
а) прочитали только по одной книге;
б) прочитали ровно две книги;
в) не прочили ни одной из указанных книг?
51.
 Задача 9. Решениеа)
Задача 9. Решениеа)учеников
б)
Ответ: 12 учеников
ученика
Ответ: 15
в)
Ответ: 3
52. Задача 10
На зимних каникулах из 36 учащихся класса только двоепросидели дома, а 25 ребят ходили в кино, 15 – в театр,
17 – в цирк. Кино и театр посетили 11 человек, кино и
цирк – 10, театр и цирк – 4.
Сколько ребят побывало и в кино, и в театре, и в цирке?
Литература
[1] Алгебра, 9 класс. В 2 ч. Ч. 2. Задачник для
учащихся общеобразовательных учреждений
/ [А. Г. Мордкович, Л.А. Александрова и др.]
-12-е изд., испр. — М.: Мнемозина, 2010.
[2] Занимательная математика. 5 – 11 классы.
Авт.- сост. Т.Д. Гаврилова. – Волгоград:
Учитель, 2005. – 96 с.
[3] Математика 6 класс: учеб. для
общеобразоват. учреждений / Г.В. Дорофеев,
И.Ф.
Шарыгин, С.Б. Суворова и др./; под ред. Г.В.
Дорофеева, И.Ф. Шарыгина; Рос. акад. наук,
Рос. акад. образования, изд-во
«Просвещение». – 11 –е изд. — М.:
Просвещение, 2010.
 – 303 с.: ил.
– 303 с.: ил.53
54. Связь между алгеброй логики и теорией множеств
Дело в том, что термин алгебра в своем роде имянарицательное. Под ним понимается раздел
математики, изучающий алгебраические операции,
а природа объектов, к которым применяются эти
операции, не важна. Говоря об алгебре логики или
об алгебре множеств, мы более всего уделяли
внимание операциям, определенным над
допустимыми в данной теории объектами,
свойствам этих операций. Еще одним хорошо
известным вам примером алгебры, является
алгебра чисел, к которой все выписанные законы
также применимы. Проводя аналогии между этими
алгебрами, мы можем сказать
№ 5.
В классе 30 человек, каждый
из которых поёт или танцует.
Известно, что поют 17
человек, а танцевать умеют
19 человек. Сколько человек
поёт и танцует
одновременно?
56. Решение 1.
Пусть А — это множество учеников, умеющих петь.Количество элементов в нём по условию равно n = 17.

Пусть В — множество учеников, умеющих танцевать.
Количество элементов в нём — m = 18. Множество А В
совпадает со всем классом, т.к. каждый ученик в классе
поёт или танцует. А В — это множество тех учеников
класса, которые поют и танцуют одновременно. Пусть их
количество равно k.
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют одновременно.
57. Решение 2.
Сначала заметим, что из 30 человекне умеют петь 30 — 17 = 13 человек.
Все они умеют танцевать, т.к. по
условию каждый ученик класса поёт
или танцует. Всего умеют танцевать
19 человек, из них 13 не умеют петь,
значит, танцевать и петь
одновременно умеют 19-13 = 6
человек.
На фирме работают 67 человек. Из
них 47 знают английский язык, 35 немецкий язык, а 23 — оба языка.
Сколько человек в фирме не знают
ни английского, ни немецкого
языков?
59. Решение.
n ( А) = 47 – знают английский языкn ( В) = 35- знают немецкий язык
n ( C)= x – не знают ни английский, ни
немецкий язык
n (A B )= 23 – знают английский и
немецкий языки
n ( A B C) = 67 – работники фирмы
67 = 47 +35 – 23 +x
x=8
Ответ: 8 человек не знают ни английский, ни
немецкий язык.
№ 7.
Изобразите с помощью кругов
Эйлера пересечение множеств
K и M, если:
а) K L
б) L K
в) K = L
г) K L =
Решение задачи с помощью
кругов Эйлера.
k
L
L
K
L=K
L
4681
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
МАТЕМАТИКА
ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Методические указания для самостоятельной работы студентов специальности
190601 – Автомобили и автомобильное хозяйство
Воронеж 2010
2
УДК 517.5(075.8)
Котко, Л. А. Математика. Элементы функционального анализа [Текст] : методические указания для самостоятельной работы студентов специальности 190601 – Автомобили и автомобильное хозяйство / Л. А. Котко, С. В. Писарева ; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2010. – 24 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 8 от 23 апреля 2010 г. )
)
Рецензент канд. физ.-мат. наук, доц. кафедры цифровых технологий ВГУ С.А. Скляднев
3
1.МНОЖЕСТВА
1.1Множества
Множества, как правило, обозначают прописными буквами некоторого алфавита A, B, C, N. R… Элементы множества обычно обозначают строчными буквами a, p, e, x, t… Знак обозначает принадлежность;
читается «элемент x принадлежит множеству M»; читается «элемент x
не принадлежит множеству M».
Буквами N, Z, Q, R обозначают, как правило, множества натуральных, целых, рациональных и действительных чисел соответственно.
Перечислим некоторые, наиболее употребляемые, способы задания множеств:
а) множество может быть задано путем перечисления всех его элементов; например, множество всех цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; множество лиц, присутствующих в комнате {Коля, Володя, Ира, Лена, Оля}; множество всех трехзначных чисел в двоичной системе исчисления {100, 101, 110, 111} и т.п.
b) Множество M может быть задано путем формулирования некоторого
характеристического | свойства | P(x), которым обладают элементы множества | |||
(и только они одни): |
| или | . |
| |
Например, | множество | Е | корней | уравнения | , |
где |
|
| можно составить следующим образом: | ||
Е={x| | }. |
|
|
|
Множество А точек отрезка [0, 1] задается так: | A={x: 0 | }. | ||
c) Множество M может быть задано путем определения его элементов по | ||||
уже известному множеству T. |
|
|
| |
Например, | считая | заданным | множество | целых |
чисел |
| , определим множество | степеней | |
числа 2: |
|
| . |
|
4
Пустым называется множество, не содержащее никаких элементов. Оно обозначается символоми содержится в любом множестве.
Множества A и B называются равными, если они состоят из одних и тех же элементов.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A содержится в множестве B (пишут ) или, что то же, множество B содержит множество A (пишут ). В этих случаях говорят, что множество A является подмножеством множества B.
1.2 Операции над множествами
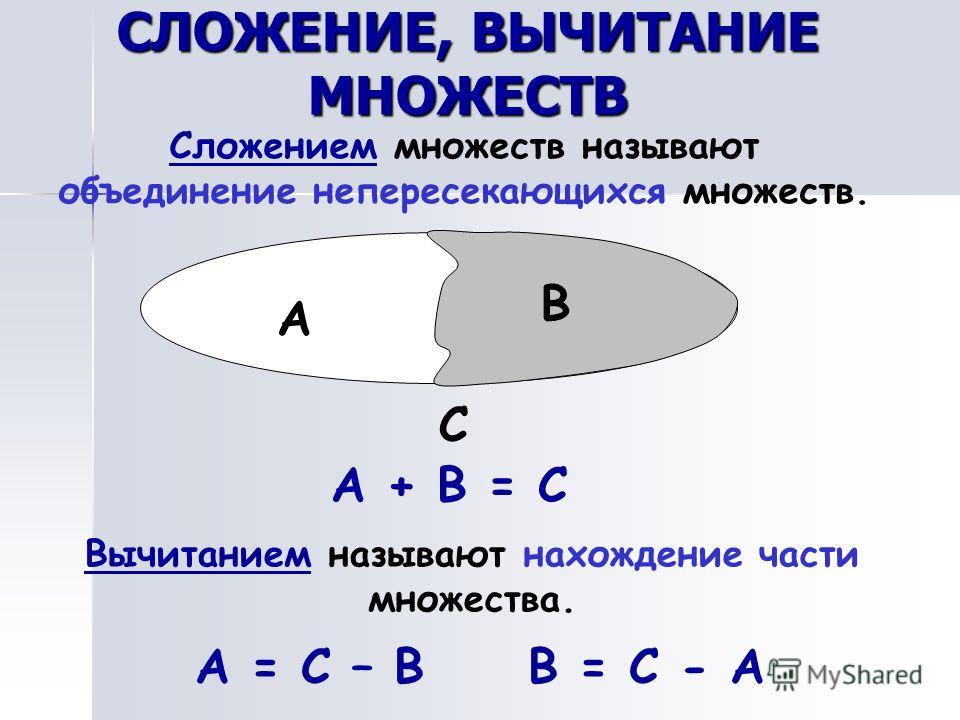
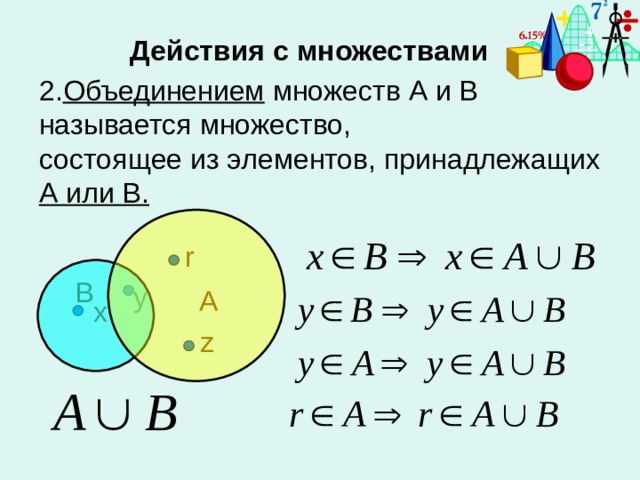
Пусть А и В – произвольные множества; их суммой или объединением называют множество, состоящее из всех элементов, принадлежащих
хотя бы одному из множеств А и В (см. рис. 1).
Аналогично определяется объединение любого (конечного или бесконечного) числа множеств. Пусть – произвольные множества.
Объединением множеств называется множество элементов, каждый из которых принадлежит хотя бы одному из множеств , или
.
Очевидно, что для любого А выполняется.
A A
B B
Рис. 1 | Рис. 2 |
5
Пересечением множеств А и В называется множество, состоящее
из всех элементов, принадлежащих как А, так и В (см. рис. 2).
Например, пересечение множества всех четных чисел и множества всех чисел, делящихся без остатка на три, состоит из всех целых чисел, делящихся
без остатка на шесть. |
|
| |
Если множества С и D не имеют общих элементов, то | . | ||
В этом случае множества С и D называются непересекающимися. |
| ||
Полезно отметить, что | . |
| |
Пересечением любого (конечного или бесконечного) числа множеств | |||
| называется множество | элементов, принадлежащих каждому | из |
множеств | , или |
|
|
|
| . |
|
Разностью множеств А и В (обозначается А\В) называют множество, |
| ||
состоящее из тех элементов множества А, которые не принадлежат множеству В (см. рис. 3). Ясно, что А\А=.
Если В , то А\В называют дополнением множества В до множества | |
А (см. рис. 4). |
|
А | А |
| В |
| В |
А\В |
|
| А\В |
Рис. 3 | Рис. 4 |
В случае, когда рассматриваются различные подмножества множества А | |
(и только они одни), дополнение множества В до множества А называют просто дополнением.
6
Очевидно, что для любого множества А выполняется АА. Принято также считать, по определению, что пустое множество является подмножеством каждого множества: А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А, и существует элемент x такой, что x не принадлежит А, то А называется собственным подмножеством множества В.
Принято также считать, по определению, что пустое множество является подмножеством каждого множества: А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А, и существует элемент x такой, что x не принадлежит А, то А называется собственным подмножеством множества В.
Пример 1. Даны множества А, В и С. С помощью операций объединения и пересечения записать множество, состоящее из элементов, принадлежащих:
1) всем трем множествам; 2) хотя бы одному множеству; 3) по крайней мере двум этим множествам.
Решение. 1) (АВ) С;
2)(АВ) С;
3)(АВ) (СВ) (АС).
Пример 2. Найти АВ, АВ, А\В, В\А, если А={-4, -3, -2, -1, 0, 1}, B={-1, 0, 1, 2, 3}.
Решение. АВ={-4, -3, -2, -1, 0, 1, 2, 3}, АВ={-1, 0, 1}, А\В={-4, -3, -2}, В\А={2, 3}.
1.3 Эквивалентные множества
Говорят, что между множествами А и В установлено взаимно однозначное соответствие, если каждому элементу множества А сопоставлен один и только один элемент множества В так, что различным элементам множества А сопоставлены различные элементы множества В и каждый элемент множества В оказывается сопоставленным некоторому элементу множества А.
Множества, между которыми установлено взаимно однозначное соответствие, называют эквивалентными.
Если множества А и В эквивалентны, то пишут А В.
7
Если А, и В не эквивалентно А, то говорят, что множество
А имеет меньшую мощность, чем множество В.
Множество А называется конечным, если существует такое число nN,
что А {1, 2, 3,…,n}.
В этом случае говорят, что множество А содержит n элементов или что множество А имеет мощность n.
Мощность пустого множества принимается равной нулю. Множество, не являющееся конечным, называется бесконечным. Множество А называется счетным, если АN .
Множество называется несчетным, если оно имеет мощность, большую, чем мощность множества N.
Теоремы Кантора.
1.Множество всех рациональных чисел счетно.
2.Множество всех действительных чисел несчетно.
| Множество А называется множеством мощности | континуума, | если | ||||
А . |
|
|
|
|
|
|
|
| 1.4 Бинарные отношения |
|
|
|
|
| |
| Прямым | произведением | двух множеств | A={ |
|
| } и |
B={ |
| } называется | множество A | упорядоченных | пар | вида | |
( | ), где |
| . |
|
|
|
|
| Прямым | произведением | k множеств |
|
| называется | |
множество |
| упорядоченных | наборов | ( |
| ) | |
длины k, где |
| . |
|
|
|
| |
| Эти определения кратко можно записать так: |
|
|
|
| ||
| A |
|
|
|
|
|
|
.
Пример 1. Перечислите элементы множеств A, B:
8
1)A={1, 2}, B={3, 4, 5};
2)A=, B={1, 2, 3, 4}.
Решение. По определению
Порядок построения данного множества будет следующий: вначале перечислим все пары, первый элемент которых равен первому элементу множества А, а второй берется из множества В в том порядке, в котором они записаны в множестве В, затем аналогично берем второй элемент из А и составляем пары со всеми элементами из В и т.д.
Аналогичен и метод построения множества
1) | , | . |
2)=поскольку множество А пусто и мы не можем
составить ни одной пары.
Теорема 1. Мощность прямого произведения конечного числа конечных множеств равна произведению мощностей этих множеств.
Множество называется k-ой степенью множества A. Из теоремы о мощности прямого произведения следует:
Пример 2. Пусть A={3, 4}. Перечислите элементы множества. Решение. По определению
=
Пример 3. Пусть E={0, 1}. Найти мощность множества
|
|
| 9 |
|
|
|
|
| Решение. |
|
|
|
| , | откуда |
следует | , т.е. мощность множества всех наборов длины n из | ||||||
нулей и единиц равна | . |
|
|
|
|
| |
| Подмножество | множества |
|
| называется n | — местным | |
отношением на множестве A. |
|
|
|
|
| ||
| Говорят, что элементы |
| находятся в отношении | , если | |||
|
| . |
|
|
|
|
|
| Одноместное отношение – | это | просто | подмножество | множества | ||
A ( | ) , Такие | отношения | называют | свойствами или | признаками, | ||
например, свойство четности чисел, признак делимости на три и т. |
| ||||||
| Наиболее часто встречающимися | являются двуместные или бинарные | |||||
отношения. Ниже мы будем рассматривать только бинарные отношения. Если
a и b находятся в отношении , то пишут | или a . |
Примерами отношений на множестве вещественных чисел являются | |
отношения: « », « », « > », « < », | « = ». На множестве натуральных |
чисел рассмотрим отношения: а) иметь один и тот же остаток от деления на пять; 2) иметь общий делитель, отличный от единицы. На множестве плоских
прямых | отметим | отношения | параллельности, | перпендикулярности, | |||||
симметричности относительно начала координат и др. |
|
| |||||||
Областью | определения | отношения | на множестве A называется | ||||||
множество тех |
|
| , для которых существует | такое | , что | . | |||
Областью значений отношения | на множестве A называется множество | ||||||||
тех значений |
|
| , для которых существует такое | , что | . | ||||
Поскольку | отношения | на множестве | являются подмножествами | ||||||
множества |
| , для них можно определить те же операции, что и для множеств: | |||||||
объединение, | пересечение, дополнение, разность. | отношение « | » на | ||||||
множестве натуральных чисел является объединением отношений « < » и « = ». Отношение « > » является дополнением отношения « », а отношение
| 10 |
|
равенства « = » является пересечением отношений « | » и « » на множестве | |
действительных чисел. |
|
|
Отношение | на множестве A называется | рефлексивным, если |
для | , и антирефлексивным в противоположном случае: | |
для | . |
|
Примерами рефлексивных отношений являются отношения « », « = » и « » на произвольном числовом множестве.
Отношения | « x < y », «быть сыном», «быть старше» являются | |||
примерами антирефлексивных отношений. |
|
| ||
Отношение | на множестве | A называется симметричным, если из | ||
следует | . | Отношение | называется | |
антисимметричным, еслииз | и |
| следует x=y. | |
Отношения «жить в одном городе», «иметь общий делитель, отличный от единицы» на множестве целых чисел, «быть симметричным относительно оси» на множестве точек плоскости являются примерами симметричных отношений.
Отношения « », « | » на | являются антисимметричными. |
| |
Отношение | на множестве A называется транзитивным, если для | |||
любых | из | , | следует | . |
Отношения « < », « », « = » на множестве действительных чисел, отношение параллельности прямых, отношение «быть соседом» являются транзитивными. Отношение перпендикулярности прямых, отношение «иметь общий делитель, отличный от единицы» на множестве натуральных чисел свойством транзитивности не обладают.
Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 4. Для бинарного отношения выясните, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает и какими не обладает.
1) на множестве
А={1, 2, 3};
Дискретная математика — тест 3
Дискретная математика — тест 3Решение тестов Intuit
игра брюс 2048
Главная / Алгоритмы и дискретные структуры / Дискретная математика / Тест 3
Упражнение 1:
Номер 1
Даны множества A = {a,b,d,e,f}, B = {b,c,e,g}, С = {a,d,f}. Отметьте верное равенство:
Отметьте верное равенство:
Ответ:
 (1) С = A∩B  
 (2) С = A\B  
 (3) С = A∪B  
 (4) С = B\A  
Номер 2
Даны множества , , .
Отметьте верное равенство:
Ответ:
 (1)  
 (2)  
 (3)  
 (4)  
Номер 3
Даны множества A = {a,b,d,e}, B = {b,c,e,f,g}, С = {c,f,g}. Отметьте верное равенство:
Отметьте верное равенство:
Ответ:
 (1) С = A∩B  
 (2) С = A\B  
 (3) С = A∪B  
 (4) С = B\A  
Упражнение 2:
Номер 1
МножествоAсодержит5элементов, множествоBсодержит8элементов. Сколько элементов может содержать их пересечение?
Ответ:
 (1) 8 элементов
 
 (2) 6 элементов
 
 (3) 5 элементов
 
 (4) 3 элемента
 
Номер 2
Множество A содержит 6 элементов,
множество B содержит 7 элементов. Сколько элементов может содержать их объединение?
Сколько элементов может содержать их объединение?
Ответ:
 (1) 9 элементов
 
 (2) 7 элементов
 
 (3) 6 элементов
 
 (4) 4 элемента
 
Номер 3
Множество A содержит 5 элементов,
множество B содержит 8 элементов. Сколько элементов может содержать разность A\B?
Ответ:
 (1) 0 элементов
 
 (2) 2 элемента
 
 (3) 5 элементов
 
 (4) 8 элементов
 
Упражнение 3:
Номер 1
Множества , , выражены через три других множества
, , следующими равенствами: , , . Отметьте верное равенство:
Отметьте верное равенство:
Ответ:
 (1)  
 (2)  
 (3)  
Номер 2
Множества A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D\(E∪F), B = DE∪DF, C = (D\E)∩(D\F).
Отметьте верное равенство:
Ответ:
 (1) A=B  
 (2) B=C  
 (3) A=C  
Номер 3
Множества A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D∪EF, B = ((D\E)∪E)F, С = DF∪EF. Отметьте верное равенство:
Отметьте верное равенство:
Ответ:
 (1) A=B  
 (2) B=C  
 (3) A=C  
Упражнение 4:
Номер 1
Чему равна проекция множества A = {(1,2),(1,3),(2,3),(3,4)} на первую координату?
Ответ:
 (1) {1,2,3,4}  
 (2) {1,2,3}  
 (3) {2,3,4}  
Номер 2
Чему равна проекция множества A = {(1,3),(2,3),(2,4),(3,1)} на вторую координату?
Ответ:
 (1) {1,2,3,4}  
 (2) {1,2,2,1}  
 (3) {1,3,4,1}  
 (4) {3,3,4,1}  
Номер 3
Чему равна проекция множества A = {(1,4),(2,1),(2,3),(4,3)} на первую координату?
Ответ:
 (1) {1,2,3,4}  
 (2) {1,2,4}  
 (3) {1,3,4}  
Упражнение 5:
Номер 1
СоответствиеGмежду множествамиA = {a,b,c,d,e}иB = {1,2,3,4}задано множеством парG = {(a,1),(b,2),(b,3),(c,1),(c,4),(e,3)}.Какое из множеств является образом элемента
bпри этом соответствии?
Ответ:
 (1) {1,2,3,4}  
 (2) {1,4}  
 (3) {2,3}  
Номер 2
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(a,3),(b,3),(c,1),(e,3),(e,4)}.
Какое из множеств является прообразом элемента 3 при этом соответствии?
Ответ:
 (1) {a,b,c,e}  
 (2) {a,b,e}  
 (3) {a,c}  
Номер 3
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,3),(d,1),(d,4),(e,3)}. Какое из множеств является образом элемента
Какое из множеств является образом элемента d при этом соответствии?
Ответ:
 (1) {1,2,3,4}  
 (2) {1,2,3}  
 (3) {1,4}  
Упражнение 6:
Номер 1
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(d,3)}.
Отметьте верное утверждение:
Ответ:
 (1) G всюду определено;
 
 (2) G функционально;
 
 (3) G сюръективно?
 
Номер 2
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,1),(d,4)}. Отметьте верные утверждения:
Отметьте верные утверждения:
Ответ:
 (1) G всюду определено
 
 (2) G функционально
 
 (3) G обратимо
 
 (4) G взаимно однозначно
 
Номер 3
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(c,1),(c,3),(d,3),(d,4)}. Отметьте верное утверждение:
Отметьте верное утверждение:
Ответ:
 (1) G всюду определено;
 
 (2) G функционально;
 
 (3) G сюръективно?
 
Упражнение 7:
Номер 1
Какие из множеств являются счетными?
Ответ:
 (1) множество натуральных чисел; 
 (2) множество рациональных чисел; 
 (3) множество действительных чисел; 
 (4) множество [0,1]  
Номер 2
Какое из множеств является конечным?
Ответ:
 (1) множество всех натуральных чисел; 
 (2) множество всех рациональных чисел; 
 (3) действительные числа отрезка [0,1] 
 (4) множество {1,2,3} 
Номер 3
Какие из множеств имеют мощность континуума:
Ответ:
 (1) множество натуральных чисел; 
 (2) множество рациональных чисел; 
 (3) множество действительных чисел; 
 (4) множество [0,1]  
Упражнение 8:
Номер 1
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(c,3),(d,3),(d,4)}
и H = {(a,2),(b,1),(c,3),(d,3)}. Какое соответствие функционально?
Какое соответствие функционально?
Ответ:
 (1) G и H  
 (2) только G  
 (3) только H  
 (4) ни G, ни H  
Номер 2
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(b,1),(c,3),(d,4)}
и H = {(a,1),(c,1),(c,3),(d,4)}. Какое соответствие функционально?
Какое соответствие функционально?
Ответ:
 (1) G и H  
 (2) только G  
 (3) только H  
 (4) ни G, ни H  
Номер 3
Между множествами A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(b,1),(c,2),(d,2),(d,3)}
и H = {(a,2),(b,2),(c,4),(d,1)}. Какое соответствие функционально?
Какое соответствие функционально?
Ответ:
 (1) G и H  
 (2) только G  
 (3) только H  
 (4) ни G, ни H  
Упражнение 9:
Номер 1
Функцияf(x1,x2)имеет типA2*B, функцияg(y1,y2)имеет типCA*A.Какой тип имеет функция
f(x1,g(y1,y2))?
Ответ:
 (1) A2*B  
 (2) CA*A  
 (3) ACA*B  
 (4) A2CA*B 
Номер 2
Функция f(x1,x2) имеет тип AB→C,
функция g(y1,y2) имеет тип AC→A. Какой тип имеет функция
Какой тип имеет функция f(g(y1,y2),x2)?
Ответ:
 (1) AB→C  
 (2) AC→A  
 (3) ACB→C  
 (4) ABAC→C  
Номер 3
Функция f(x1,x2) имеет тип AC→B,
функция g(y1,y2) имеет тип AC→C. Какой тип имеет функция
Какой тип имеет функция f(x1,g(y1,y2))?
Ответ:
 (1) AC→B  
 (2) AC→C  
 (3) A2C→B  
 (4) ACAC→C  
Упражнение 10:
Номер 1
Между точками горизонтальной прямой задано отношение «левее»
(x левее y). Отметьте верное утверждение:
Отметьте верное утверждение:
Ответ:
 (1) отношение рефлексивно 
 (2) отношение антирефлексивно 
 (3) отношение симметрично 
 (4) отношение транзитивно 
Номер 2
На множестве действительных чисел задано отношение |x-y|<5.
Отметьте верное утверждение:
Ответ:
 (1) отношение рефлексивно 
 (2) отношение антирефлексивно 
 (3) отношение симметрично 
 (4) отношение транзитивно 
Номер 3
На множестве натуральных чисел задано отношение «x+y
делится на 2». Отметьте верное утверждение:
Отметьте верное утверждение:
Ответ:
 (1) отношение рефлексивно 
 (2) отношение антирефлексивно 
 (3) отношение симметрично 
 (4) отношение транзитивно 
Упражнение 11:
Номер 1
Объединение двух отношений частичного порядка будет отношением частичного порядка ...
Ответ:
 (1) всегда 
 (2) иногда (может быть, а может не быть) 
 (3) никогда 
Номер 2
Каким может быть дополнение к отношению эквивалентности?
Ответ:
 (1) рефлексивным 
 (2) симметричным 
 (3) антисимметричным 
Номер 3
Каким может быть дополнение к отношению строгого порядка?
Ответ:
 (1) рефлексивным 
 (2) симметричным 
 (3) антисимметричным 
Упражнение 12:
Номер 1
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(a,c),(b,c),(c,d)}. Какие пары нужно добавить к
Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
Ответ:
 (1) (d,a)  
 (2) (a,d), (b,d)  
 (3) никакие, так как R транзитивно;
 
 (4) (a,d)  
Номер 2
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,d),(b,d),(d,c)}. Какие пары нужно добавить к
Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
Ответ:
 (1) (c,d)  
 (2) (a,c), (b,c)  
 (3) никакие, так как R транзитивно;
 
 (4) (a,b), (b,a)  
Номер 3
На множестве A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(b,c),(b,d)}. Какие пары нужно добавить к
Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
Ответ:
 (1) (a,c), (a,d)  
 (2) (c,d), (d,c)  
 (3) никакие, так как R транзитивно;
 
 (4) (b,a)  
Главная / Алгоритмы и дискретные структуры / Дискретная математика / Тест 3
1.5: Введение в множества и действительные числа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 23234
Наборы — Введение
Набор представляет собой набор объектов. Объекты в наборе называются его элементов или элементов . Элементами набора могут быть любые типы объектов, включая наборы! Члены набора даже не обязательно должны быть одного типа. Например, набор может состоять из чисел и имен, хотя у него может и не быть значимого применения.
Объекты в наборе называются его элементов или элементов . Элементами набора могут быть любые типы объектов, включая наборы! Члены набора даже не обязательно должны быть одного типа. Например, набор может состоять из чисел и имен, хотя у него может и не быть значимого применения.
Мы обычно используем заглавные буквы, такие как \(A\), \(B\), \(C\), \(S\) и \(T\) для представления множеств, и обозначаем их общие элементы их соответствующие строчные буквы \(a\), \(b\), \(c\), \(s\) и \(t\) соответственно. Чтобы указать, что \(b\) является элементом множества \(B\), мы принимаем обозначение \(b\in B\), что означает «\(b\) принадлежит \(B\)» или «\(b\) является элементом \(B\)». Следовательно, сказать \(x\in\mathbb {R}\) — это еще один способ сказать, что \(x\) является действительным числом.
Определение: Подмножество
Множество A является подмножеством множества B тогда и только тогда, когда каждый элемент множества A также входит в множество B.
В символах:
\[A \subset B \iff x\in A \rightarrow x\in B\]
Вещественные числа и некоторые подмножества действительных чисел
Мы обозначаем эти обозначения для некоторых специальных наборов чисел: \[\begin{aligned} \mathbb{N} &=& \mbox{ множество натуральных чисел}, \\ \mathbb{Z} &=& \mbox{множество целых чисел}, \\ \mathbb{Q} &=& \mbox{множество рациональных чисел},\\ \mathbb {R} &=& \mbox{множество действительных чисел}. \end{aligned}\] Все это бесконечные множества, потому что все они содержат бесконечно много элементов. Напротив, конечные множества содержат конечное число элементов.
Мы перечисляем натуральные числа и целые числа, определяя рациональные, действительные и иррациональные числа.
\(\mathbb{N} = \{1, 2, 3,\ldots \}\)
\(\mathbb{Z} = \{\ldots, -3, -2, — 1, 0, 1, 2, 3,\ldots \}\)
Определение — рациональные числа равен нулю). Следовательно, рациональное число может быть записано как \(\frac{m}{n}\) для некоторых целых чисел \(m\) и \(n\), где \(n\neq0\).

Определение — действительные числа
действительных чисел — это числа, соответствующие всем точкам на числовой прямой.
Определение. Иррациональные числа
Иррациональное число – это действительное число, которое нельзя выразить как отношение двух целых чисел; т. е. не рационально.
Замыкание
Определение
Для заданного множества S с бинарной операцией *, S замкнуто по операции * тогда и только тогда, когда \(x*y \in S \mbox{ для каждого }x \in S\mbox{ и для каждого } y\in S\).
Пример \(\PageIndex{1}\)
Предположим, вы складываете любые два целых числа. Всегда ли сумма будет целой?
- Раствор
Да; поэтому множество целых чисел замкнуто относительно сложения.
Предположение
Воспользуемся тем свойством, что множество целых чисел замкнуто относительно сложения, вычитания и умножения.
Альтернативный синтаксис: «замыкание целых чисел при умножении».
Это предположение можно использовать в качестве причины в объяснении или доказательстве.
Пример \(\PageIndex{2}\)
Если \(a,b \in \mathbb{Z}\text{, то }a+b \in \mathbb{Z}\) потому что ?
- Раствор
Набор целых чисел закрыт на сложение.
Обозначение набора
Обозначение списка
Мы можем использовать нотация реестра для описания множества, если оно состоит лишь из небольшого числа элементов. Перечислим все его элементы явно, как в \[A = \mbox{множество натуральных чисел, не превосходящих 7} = \{1,2,3,4,5,6,7\}.\] Для множеств с более элементов, показать первые несколько записей для отображения шаблона и использовать многоточие для обозначения «и так далее». Например, \[\{1,2,3,\ldots,20\}\] представляет собой набор первых 20 положительных целых чисел. Повторяющийся шаблон может быть расширен до бесконечности, как в \[\begin{aligned} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ ldots,-2,-1,0,1,2,\ldots\} \end{выровнено}\]
Повторяющийся шаблон может быть расширен до бесконечности, как в \[\begin{aligned} \mathbb{N} &=& \{1,2,3,\ldots\} \\ \mathbb{Z} &=& \{\ ldots,-2,-1,0,1,2,\ldots\} \end{выровнено}\]
В отношении четности целое число может быть либо четным, либо нечетным. Сейчас мы будем использовать наше общее понимание четных и нечетных значений и определим эти термины позже в этом тексте. Набор четных целых чисел можно описать как \(\{\ldots,-4,-2,0,2,4,\ldots\}\).
Нотация построителя набора
Мы можем использовать нотацию построителя набора для описания набора. Например, набор натуральных чисел определяется как \[\mathbb{N} = \{x\in\mathbb{Z} \mid x>0 \}.\] Здесь вертикальная черта \(\mid\) читается как «такой, что» или «для чего». Следовательно, правая часть уравнения произносится как «множество \(x\), принадлежащих множеству целых чисел, таких что \(x>0\)», или просто «множество целых чисел \(x\ ) такой, что \(x>0\)». В общем, этот описательный метод появляется в формате \[\{\,\mbox{членство}\;\mid\;\mbox{свойства}\,\}.\] Обозначение \(\mid\) означает «такой тот» или «для чего» только тогда, когда он используется в обозначении набора. Это может означать что-то еще в другом контексте. Следовательно, 92\) где \(x\in\mathbb{Z}\). Он представляет собой набор квадратов: \(\{0,1,4,9,16,25,\ldots\}\).
В общем, этот описательный метод появляется в формате \[\{\,\mbox{членство}\;\mid\;\mbox{свойства}\,\}.\] Обозначение \(\mid\) означает «такой тот» или «для чего» только тогда, когда он используется в обозначении набора. Это может означать что-то еще в другом контексте. Следовательно, 92\) где \(x\in\mathbb{Z}\). Он представляет собой набор квадратов: \(\{0,1,4,9,16,25,\ldots\}\).
Пример \(\PageIndex{4}\)
Множество \[\{ 2n \mid n\in\mathbb{Z} \}\] описывает множество четных чисел. Мы также можем записать набор как \(2\mathbb{Z}\).
практическое упражнение \(\PageIndex{3}\label{he:setintro-03}\)
Описать набор \(\{2n+1 \mid n\in\mathbb{Z}\}\) по ростерному методу.
практическое упражнение \(\PageIndex{4}\label{he:setintro-04}\)
Используйте метод реестра для описания набора \(\{3n \mid n\in\mathbb{Z}\}\).
Обозначение интервала
Интервал — это набор действительных чисел, все из которых лежат между двумя действительными числами.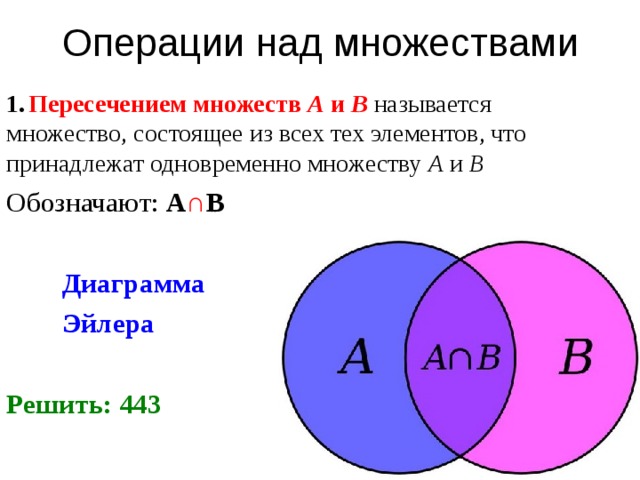 Должны ли конечные точки быть включены или исключены, зависит от того, является ли интервал открытым , закрытым или полуоткрытым . Мы принимаем следующие обозначения интервалов для их описания: \[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a, b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}. \cr}\] Понятно, что \(a\) должно быть меньше чем \(b\). Следовательно, обозначение \((5,3)\) не имеет особого смысла. Как насчет \([3,3]\)? Это может использоваться в некоторых текстах для обозначения \(\ {3\}\), но мы будем использовать \(a < b\) только для интервалов и использовать запись реестра для одиночного числа, такого как \(\{3\}\)9.0038
Должны ли конечные точки быть включены или исключены, зависит от того, является ли интервал открытым , закрытым или полуоткрытым . Мы принимаем следующие обозначения интервалов для их описания: \[\displaylines{ (a,b) = \{x\in\mathbb{R} \mid a < x < b \}, \cr [a, b] = \{x\in\mathbb{R} \mid a\leq x\leq b \}, \cr [a,b) = \{x\in\mathbb{R} \mid a\leq x < b \}, \cr (a,b] = \{x\in\mathbb{R} \mid a < x\leq b \}. \cr}\] Понятно, что \(a\) должно быть меньше чем \(b\). Следовательно, обозначение \((5,3)\) не имеет особого смысла. Как насчет \([3,3]\)? Это может использоваться в некоторых текстах для обозначения \(\ {3\}\), но мы будем использовать \(a < b\) только для интервалов и использовать запись реестра для одиночного числа, такого как \(\{3\}\)9.0038
Интервал содержит не только целые числа, но и все действительные числа между двумя конечными точками. Например, \((1,5)\mathbb \neq \{2,3,4\}\), потому что интервал \((1,5)\) также включает действительные числа, такие как \(1,276\), \ (\sqrt{2}\) и \(\pi\).
Мы можем использовать \(\pm\infty\) в записи интервала: \[\begin{aligned} (a,\infty) &=& \{ x\in\mathbb{R} \mid a
- Решение
По определению интервала находим \[\begin{aligned} {(2,3)} &=& \{x\in\mathbb{R} \mid 2
практическое упражнение \(\PageIndex{5}\label{he:setintro-05}\)
Какой из следующих наборов \[\{x\in\mathbb{Z} \mid 1
практическое упражнение \(\PageIndex{6}\label{he:setintro-06}\)
Объясните, почему \([2,7\,]\mathbb \neq\{2,3,4,5 ,6,7\}\). 9+\).
Практическое упражнение \(\PageIndex{8}\label{he:setintro-08}\)
Как обозначается множество отрицательных целых чисел?
Некоторые математики также используют следующие обозначения: \[\begin{aligned} bS &=& \{ bx \mid x\in S \}, \\ a+bS &=& \{ a+bx \mid x\in С \}. \end{aligned}\] Соответственно, мы можем записать множество четных целых чисел как \(2\mathbb{Z}\), а множество нечетных целых чисел можно представить как \(1+2\mathbb{Z}\ ).
Пример \(\PageIndex{9}\)
\[5\mathbb{Z}=\{\ldots , -15, -10, -5, 0, 5, 10, 15, \ldots\}\]
Существуют три вида действительных чисел: положительные, минус и ноль.
Свойство трихотомии
Для любых двух действительных чисел \(a\) и \(b\) верно одно и только одно из следующих соотношений:
- \(a
- \(а=б\)
- \(а>б.
 \)
\)
Упражнения
Упражнение \(\PageIndex{1}\)
Определите, верны эти утверждения или нет:
- \(0\in\mathbb{Q}\)
- \(0\in\mathbb{Z}\)
- \(-4\in\mathbb{Z}\)
- \(-4\in\mathbb{N}\)
- \(2\in3\mathbb{Z}\)
- \(-18\in3\mathbb{Z}\)
- Ответить
(а) верно (б) верно (в) верно (г) неверно (д) неверно (е) верно
Упражнение \(\PageIndex{2}\)
Определите, верны эти утверждения или нет:
- +\)
- \(0\in\mathbb{N}\)
- \(\пи\в\mathbb{R}\)
- \(\frac{4}{2}\in\mathbb{Q}\)
- \(1,5\дюйма\mathbb{Q}\)
Упражнение \(\PageIndex{3}\label{ex:prop-03}\)
Объясните, почему \(7\mathbb{Q}=\mathbb{Q}\). Верно ли, что \(0\mathbb{Q} = \mathbb{Q}\)?
- Ответить
По определению, рациональное число можно записать как отношение двух целых чисел.
 После умножения числителя на 7 мы все еще имеем отношение двух целых чисел. И наоборот, если для любого рационального числа \(x\) мы можем умножить знаменатель на 7, мы получим другое рациональное число \(y\), такое что \(7y=x\). Следовательно, два набора \(7\mathbb{Q}\) и \(\mathbb{Q}\) содержат один и тот же набор рациональных чисел. Напротив, \(0\mathbb{Q}\) содержит только одно число, а именно 0. Следовательно, \(0\mathbb{Q}\neq\mathbb{Q}\).
После умножения числителя на 7 мы все еще имеем отношение двух целых чисел. И наоборот, если для любого рационального числа \(x\) мы можем умножить знаменатель на 7, мы получим другое рациональное число \(y\), такое что \(7y=x\). Следовательно, два набора \(7\mathbb{Q}\) и \(\mathbb{Q}\) содержат один и тот же набор рациональных чисел. Напротив, \(0\mathbb{Q}\) содержит только одно число, а именно 0. Следовательно, \(0\mathbb{Q}\neq\mathbb{Q}\).
Упражнение \(\PageIndex{4}\label{ex:prop-4}\)
Найдите числа \(k\) такие, что \(k\mathbb{Z}=\mathbb{Z} \).
Упражнение \(\PageIndex{5}\)
Определите, верны эти утверждения или нет:
(См. раздел о замыкании.)
- Множество натуральных чисел замыкается при вычитании.
- Набор целых чисел закрыт при вычитании.
- Множество целых чисел закрыто при делении. 9*}\) закрыто при делении.
- Ответить
(а) неверно (б) верно (в) неверно (г) верно (д) неверно (е) верно
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- да
- Теги

Q1 Запишите кардинальное число каждого из следующих наборов i A 0 1 2 4 ii B 3 1 1 3 5 7 iii C iv D 3…
Перейти к
- Упражнение 10 (А)
- Упражнение 10(Б)
- Упражнение 10 (С)
- Упражнение 10 (Г)
- Упражнение 10 (Д)
- Система счисления (закрепление чувства числа)
- Предварительный расчет
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная > Селина Солюшнс Класс 6 Математика > Глава 10 — Наборы > Упражнение 10 (Д) > Вопрос 1
Вопрос 1 Упражнение 10(E)
В1) Запишите кардинальное число каждого из следующих множеств:
(i) A = {0, 1, 2, 4}
(ii) B = {-3, -1, 1, 3, 5, 7}
(iii) C = {}
( iv) D = {3, 2, 2, 1, 3, 1, 2}
(v) E = {Натуральные числа от 15 до 20}
(vi) F = {Целые числа от 8 до 14}.

Ответ:
Решение 1:
(i) A = {0,1, 2, 4}, т. е. n(A) = 4
(ii) B = {-3, -1, 1, 3, 5, 7} т. е. n(B) = 6
(iii) C = {} т. е. n(C) = 0
(iv) D = {3, 2, 2, 1, 3, 1, 2} = D = {3, 2, 1}, т. е. n(D) = 3
(v) E = {16, 17, 18, 19}, т. е. n(E) = 4
(vi) F = {8, 9, 10, 11, 12, 13, 14}, т. е. n(F) = 7
Стенограмма видео
«Привет всем, добро пожаловать на обучение в лидо тут вопрос написать кардинал количество каждого из следующих наборов, чтобы вы могли см. около шести вопросов здесь и вы должны написать кардинал номер каждого из этих наборов так что вы имеете в виду под количественным числом количественное числительное это представлено как n of a где a — имя набора, который он может отличаться это ряд элементов в наборе хорошо, так вот, когда вы смотрите на квест номер один имеет элементы 0 1 2 и 4, так сколько элементов в установить 4 так какой кардинальный номер карты n равно 4 хорошо теперь второй вопрос b это набор, имеющий элементы минус 3 минус 1 1 3 5 и 7.
 так что это кардинальное число
набора
b сколько там элементов
имея
шесть элементов, поэтому n of b равно шести
теперь третий c равен нулю
установлен
так есть ли какой-либо элемент в нулевом наборе
нет так что такое кардинальность или что такое
номер карты c
такой c это 0, потому что есть
нет элементов в множестве c
теперь d d равно множеству, имеющему
элементы 3
2 2 1 3 1 2
поэтому на самом деле d можно записать как
3 2 и 1 потому что все
остальные элементы такие же, как и у трех
два и один
так сколько всего элементов
три элемента прямо так кардинал
номер множества d
три, как насчет
пятый e представляет собой набор натуральных
числа от 15
а 20 это натуральные числа
между 15 и 20 16
17 18 и 90.
так что такое n из e, сколько элементов
там
четыре, поэтому кардинальное число множества e равно
четыре переходят к последнему набору f
это набор целых чисел от 8 до
14, так что вы можете определить набор
ф с 8
до 14 означает 8
9 10 11
12 13 и 40.
так каково кардинальное число множества f
сколько элементов
один два три четыре пять шесть семь
элементы есть
поэтому кардинальное число смещения f равно
7 хорошо, так что кардинальное число это
количество элементов
в каждом из этих наборов, и я надеюсь, что вы
понял решение
если у вас есть какие-либо сомнения, прокомментируйте ниже и
подпишитесь на этот канал, чтобы получать
регулярные обновления
спасибо»
так что это кардинальное число
набора
b сколько там элементов
имея
шесть элементов, поэтому n of b равно шести
теперь третий c равен нулю
установлен
так есть ли какой-либо элемент в нулевом наборе
нет так что такое кардинальность или что такое
номер карты c
такой c это 0, потому что есть
нет элементов в множестве c
теперь d d равно множеству, имеющему
элементы 3
2 2 1 3 1 2
поэтому на самом деле d можно записать как
3 2 и 1 потому что все
остальные элементы такие же, как и у трех
два и один
так сколько всего элементов
три элемента прямо так кардинал
номер множества d
три, как насчет
пятый e представляет собой набор натуральных
числа от 15
а 20 это натуральные числа
между 15 и 20 16
17 18 и 90.
так что такое n из e, сколько элементов
там
четыре, поэтому кардинальное число множества e равно
четыре переходят к последнему набору f
это набор целых чисел от 8 до
14, так что вы можете определить набор
ф с 8
до 14 означает 8
9 10 11
12 13 и 40.
так каково кардинальное число множества f
сколько элементов
один два три четыре пять шесть семь
элементы есть
поэтому кардинальное число смещения f равно
7 хорошо, так что кардинальное число это
количество элементов
в каждом из этих наборов, и я надеюсь, что вы
понял решение
если у вас есть какие-либо сомнения, прокомментируйте ниже и
подпишитесь на этот канал, чтобы получать
регулярные обновления
спасибо»Связанные вопросы
Q2) Дано: (i) A = {Натуральные числа меньше 10} B = {Буквы слова «КУКЛА»} C = {Квадраты f.
 ..
..Q3) Укажите верно или неверно каждое из следующих утверждений. Исправьте неверное утверждение. (i) Если A = {0}, то…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 10(A)
Упражнение 10(B)
Упражнение 10(C)
Упражнение 10(D)
Упражнение 10(E)
Количество)Оценка
Числа в Индии и международной системе (со сравнением)
Разрядное значение
Натуральные числа и целые числа (включая паттерны)
Отрицательные числа и целые числа
Номерная линия
HCF и LCM
Игра с числами
Установки
Соотношение
Продовольствие (в том числе Word)
.

Proport (включая Word)
. Дроби
Десятичные дроби
Проценты
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (относящиеся к алгебраическим выражениям)
Подстановка (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая вычисление)
Простые (линейные) уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы) Свойства углов и линий (включая параллельные линии)
Треугольники (включая типы, свойства и конструкцию)
Четырехугольник
Многоугольники
Окружность
Повторное упражнение по симметрии (включая построение симметрии)
Распознавание твердых тел
Периметр и площадь плоских фигур
Обработка данных (включая пиктограмму и гистограмму)
Среднее и медиана
Пустой набор — определение и примеры
В наших предыдущих уроках мы рассмотрели классификацию исчисляемых и неисчисляемых элементов.
 Но в мире математики полно возможностей и открытых дверей. Итак, что происходит, когда элементы для классификации не являются ни исчисляемыми, ни неисчисляемыми?
Но в мире математики полно возможностей и открытых дверей. Итак, что происходит, когда элементы для классификации не являются ни исчисляемыми, ни неисчисляемыми?Мы знаем, что этот вопрос может показаться запутанным, но подобные вопросы порождают новую концепцию в области классификации множеств. Ответ на этот вопрос: пустых наборов.
В этой статье объясняется, что такое пустые наборы, чтобы вы могли лучше понять их и узнать, когда, где и как их использовать.
Пустые множества — это множества, не содержащие элементов. Поскольку эти множества пусты, их также называют пустыми множествами.
В этой статье мы рассмотрим следующие темы:
- Что такое пустой набор?
- Как представить пустой набор?
- Свойства пустых множеств.
- Примеры
- Практические задачи
Мы также предлагаем вам быстро освежить в памяти следующие темы, прежде чем мы начнем углубляться в пустые множества: Бесконечные наборы
Что такое пустой набор?Если вы большой поклонник математики, возможно, вы задавались вопросом: «Что такое пустое множество?» особенно когда вы столкнулись с конкретными проблемами, которые нельзя классифицировать как исчисляемые или неисчисляемые.
 Стандартная классификация, которая помогает нам решать такие проблемы, состоит в том, чтобы классифицировать их по пустым множествам.
Стандартная классификация, которая помогает нам решать такие проблемы, состоит в том, чтобы классифицировать их по пустым множествам.Пустой набор, как следует из названия, пуст и не содержит элементов nts.
Эти наборы созданы для упрощения расчетов и часто используются для классификации нечетных или редких предметов. Некоторые примеры, в которых для классификации используется пустой набор, включают месяц с 32 днями, неделю с 2 понедельниками, собаку с пятью ногами или солнечную систему без планет. С математической точки зрения пустой набор может классифицировать целое число от 7 до 8. Все эти примеры не имеют определенных ответов и, следовательно, классифицируются с использованием пустого набора.
Пустые множества являются уникальными множествами, а также обладают уникальной кардинальностью. Мы определили кардинальность как размер набора или общее количество элементов в наборе в наших предыдущих уроках. Поскольку пустые множества не содержат элементов, их мощность также равна нулю.

Давайте решим пример, чтобы лучше понять пустые множества.
Пример 1
Определите, какое из следующих множеств является пустым:
(i) X = {x : x — натуральное число и 4
(ii) Y = {y : y — простое число и 8
(iii) Количество вагонов с 10 дверями.
Решение
(i) Рассмотрим набор натуральных чисел N, приведенный ниже:
N = {1, 2, 3, 4, 5, 6, …}
Поскольку между 4 и 5 не существует натуральных чисел, поэтому множество X является пустым множеством.
(ii) Рассмотрим множество простых чисел P
P = {2, 3, 5, 7, 11, …}
Поскольку между 8 и 10 не существует простых чисел, множество Y является пустым множеством.
(iii). В реальной жизни, если какой-нибудь производитель автомобилей не создаст прототип, невозможно найти автомобиль с десятью дверями. Итак, множество, содержащее вагоны с десятью дверями, пусто.
Как представить пустой набор?Теперь, когда мы знаем, что такое пустое множество, следующий раздел посвящен его представлению.

Пустые наборы представлены обычными фигурными скобками { }, которые используются для уведомления наборов. Однако, поскольку эти наборы уникальны, их также можно представить специальным символом 9.0029 $\фи$ .
Пустые множества не содержат в себе элементов и представляются пустыми фигурными скобками { }. Рассмотрим пустое множество A, не имеющее элементов. Обозначение этого набора:
A = { }
В предыдущих уроках мы упоминали, что мы также можем представлять бесконечные множества любой буквой, словом или фразой. Таким образом, одно и то же пустое множество A может иметь следующие обозначения:
Пустое множество = { }
Или
X = { }
Мы также можем использовать символ $\phi$ для обозначения пустого множества. Пример показан ниже:
$\phi$ = {x : x кратно 5 и 2
Поскольку между 2 и 4 не существует чисел, кратных 5, то набор является пустым.
Вот несколько примеров пустых множеств:
Пример 2
Определите, пусты ли следующие множества:
(i) A = {x : x – точка пересечения двух параллельных прямых}
(ii) B = {x : x — четное натуральное число, кратное 3}
Решение
(i) Определение параллельных прямых гласит, что эти две прямые никогда не пересекаются и, следовательно, не имеют общей точки .
 Таким образом, данное множество является пустым множеством и может быть записано как:
Таким образом, данное множество является пустым множеством и может быть записано как:A = { }
Или
$\phi$ = {x : x точка пересечения двух параллельных прямых}
(ii) данное множество является пустым множеством, так как не существует четного натурального числа, которое делится на 3. Мы можем переписать его следующим образом:
B = { }
Или
$\phi$ = {x : x — четное натуральное число, делящееся на 3}
Разница между нулевым набором и пустым наборомМногие люди часто ошибочно принимают понятие нулевых множеств и называние их пустыми множествами. Они утверждают, что эти два относятся к аналогичным классификациям. Это неправда. Мы можем лучше понять это, проанализировав определения этих двух множеств.
Пустое множество — это множество, не содержащее элементов, тогда как нулевое множество — это множество, содержащее ноль. При просмотре определений становится очевидным, что пустое множество вообще не содержит элементов, тогда как ноль содержит один элемент, который равен нулю.

Эта разница между двумя наборами делает пустой набор еще более уникальным из-за отсутствия элементов. Следовательно, два набора различны, поскольку один набор не содержит элементов, а другой набор, нулевой набор, содержит один элемент.
Следующий пример поможет нам лучше понять эту разницу.
Пример 3
Рассмотрим множество A = {0} и множество B = {x : x — нечетное число, кратное 2}. Различие между двумя наборами.
Решение
Чтобы различать эти два набора, давайте сначала упростим их:
A = {0}
Из набора B видно, что не существует нечетного числа, которое делится на 2; следовательно, множество B — пустое множество. Множество B можно записать следующим образом:
B = { }
Или
$\phi$ = B
Очевидно, что множество B — пустое множество, тогда как множество A — нулевое множество. В этом основное различие между двумя множествами A и B.
Представление пустого множества с помощью диаграммы ВеннаВенна Диаграммы являются наиболее эффективным средством представления множеств, особенно конечных множеств.
 Эти диаграммы также используются для изображения отношений объединения и пересечения между двумя множествами.
Эти диаграммы также используются для изображения отношений объединения и пересечения между двумя множествами.Пустое множество можно представить с помощью диаграммы Венна и отношения пересечения. Отношение и представление следующие:
Рассмотрим множество A = {1, 3, 5} и множество B = {2, 4, 6}.
Как видно из диаграммы Венна, между двумя множествами нет общих или пересекающихся элементов, следовательно, пересечение между двумя множествами пусто.
A∩B = $\phi$
Рассмотрим пример, относящийся к этому понятию.
Пример 4
Пусть множество A = {3, 6, 9} и множество B = {4, 8, 10}. Найдите пересечение между двумя множествами.
Решение
Мы можем решить этот пример с помощью диаграммы Венна.
Два набора указаны ниже. Из диаграммы Венна видно, что между двумя множествами нет общих или пересекающихся элементов. Следовательно, пересечение двух множеств является пустым множеством.

A∩B = $\phi$
Свойства пустого множестваПустые множества играют феноменальную роль в классификации уникальных и нечетных объектов. Эти пустые множества не только упрощают классификацию, но и помогают нам упростить вычисления. Эти пустые множества важны благодаря некоторым своим свойствам, которые составляют основу соответствующих вычислений. Итак, чтобы лучше понять концепцию пустых множеств, давайте проанализируем эти свойства.
1. Подмножество любого множества:Пустое множество — это подмножество любого множества A.
Мы можем понять это свойство, рассмотрев любое конечное или бесконечное множество A. Если мы наметим все возможные подмножества множества A, то мы всегда будем включать в него пустое множество.
Например, рассмотрим конечное множество A = {1, 3, 5}
Все возможные подмножества этого множества A:
A = $\phi$ , A = {1}, A = {3} , А = {5}, А = {1,3}, А = {3, 5}, А = {1,5}
Мы включили пустое множество в список подмножеств из-за следующего свойства:
$\phi$ ⊂ A
Тот же принцип можно применить и к бесконечным множествам.

Для бесконечных множеств рассмотрим бесконечное множество B = {1, 4, 6, …}.
Список всех возможных подмножеств этого множества следующий:
B = $\phi$, B = {1, 4, ….}, B = {4, 6, …} и т. д.
И ,
$\phi$ ⊂ B
Обратите внимание, что не имеет значения, является ли множество конечным или бесконечным; пустой набор всегда будет подмножеством данного набора.
Давайте рассмотрим пример, чтобы понять это свойство.
Пример 5
Рассмотрим множество X = {2, 4, 6}. Перечислите все его возможные подмножества.
Решение
Чтобы решить этот пример, мы рассмотрим указанное выше свойство.
Список всех подмножеств множества X:
$\phi$, {2}, {4}, {6}, {2, 4}, {4, 6}, {2, 6}
Пустое множество также является подмножеством из-за следующего соотношения:
$\phi$ ⊂ X
2. Объединение с пустым множеством:Объединение любого множества с пустым множеством всегда будет самим множеством.

Рассмотрим конечное множество A. Согласно этому свойству, объединение этого множества A с пустым множеством будет следующим:
A U $\phi$ = A
Поскольку пустое множество вообще не содержит элементов, его объединение с любым набором A дает тот же набор A, что и результаты.
Это множество A может быть как бесконечным, так и конечным. Результат одинаков в обоих случаях, так как пустое множество не содержит элементов.
Давайте решим пример, чтобы проверить это свойство.
Пример 6
Рассмотрим множество A = {1, 2, 3, 4, 5, 6}. Найдите объединение этого множества A с пустым множеством.
Решение
Пустое множество не содержит элементов. Объединение множества A с пустым множеством показано ниже:
A U $\phi$ = {1, 2, 3, 4, 5, 6} U { }
A U $\phi$ = {1, 2, 3, 4, 5, 6}
Это доказывает то свойство, что объединение любого множества с пустым множеством является самим множеством.
3. Пересечение с пустым множеством:
Пересечение любого множества с пустым множеством всегда будет пустым множеством.
Рассмотрим множество A. Согласно этому свойству пересечение имеет вид:
A ∩ = $\phi$
и непустое множество.
Это множество A может быть как конечным, так и бесконечным. Результат одинаков в обоих случаях, так как пустое множество не содержит элементов.
Давайте решим пример, чтобы проверить это свойство.
Пример 7
Рассмотрим множество A = {2, 4, 6, 8}. Найдите его пересечение с пустым множеством.
Решение
Пустое множество не содержит элементов. Пересечение пустого множества с множеством A выглядит следующим образом:
A ∩ $\phi$ = {2, 4, 6, 8}
A ∩ =$\phi$
Поскольку пустое множество не имеет элементы, между набором A и пустым набором не существует общего элемента.
4. Мощность пустого множества:Мощность пустого множества всегда равна нулю.

Мощность определяется как размер набора или общее количество элементов в наборе. Поскольку пустые множества не содержат элементов, они имеют нулевую мощность. Это показано ниже:
|$\phi$| = 0
Следовательно, согласно приведенному выше соотношению, мощность пустого множества всегда будет равна нулю.
Рассмотрим пример на основе этого свойства.
Пример 8
Найдите мощность множества X, где множество X = {x: x является нечетным числом, кратным 10}.
Решение
Для решения этого примера мы сначала упростим набор.
Поскольку нечетных чисел, кратных 10, не существует, следовательно, множество пусто.
Мощность можно найти как:
|$\phi$| = |x : x является нечетным кратным 10|
|$\фи$ | = 0
5. Декартово произведение пустого множества:Декартово произведение пустого множества всегда будет пустым множеством.
Декартово произведение — это произведение двух множеств A и B, в результате которого получаются упорядоченные пары.
 Декартово произведение любого набора с пустым набором всегда будет пустым, потому что пустой набор не содержит элементов.
Декартово произведение любого набора с пустым набором всегда будет пустым, потому что пустой набор не содержит элементов.Таким образом, мы можем заключить:
A x $\phi$ = $\phi$
Рассмотрим пример, основанный на этом свойстве.
Пример 9
Найдите декартово произведение множества A = {1, 2, 3, 4} с пустым множеством.
Решение
Декартово произведение — это произведение двух множеств. Он выполняется следующим образом:
A x $\phi$ = {1, 2, 3, 4} x { }
A x $\phi$ = $\phi$
Результатом является пустое множество, поскольку пустое множество не содержит элементов, и его умножение не дает определенного результата. Это также проверяет свойство.
Чтобы еще больше укрепить понимание и концепцию бесконечного множества, рассмотрите следующие практические задачи.
Практические задачи- Определите, какие из следующих множеств являются пустыми:
}
- Проведите различие между множествами X и Y, где X = {0} и Y = {}.

- Перечислите все возможные подмножества A = {3, 6, 9, …}.
- Найдите объединение и пересечение A = {10, 20, 30, 50} с пустым множеством.
- Найдите мощность B = {количество пересекающихся параллельных прямых на плоскости}
- (i) Пустое множество (ii) Непустое множество
- Нулевое множество, Пустое множество.
- { }, {3,…} и т. д.
- A, пустой набор.
- ноль
Как найти среднее значение набора чисел: формулы и примеры
Вы сдаете SAT или ACT и хотите убедиться, что знаете, как работать с наборами данных? Или, может быть, вы хотите освежить в памяти уроки математики в старшей школе или колледже. Как бы то ни было, важно, чтобы вы знали, как найти среднее значение набора данных.
Мы объясним, для чего в математике используется среднее значение, как вычислить среднее значение и как могут выглядеть проблемы со средним значением.

Что такое среднее значение и для чего оно используется?
Среднее или среднее арифметическое — это среднее значение набора чисел. Более конкретно, это мера «центральной» или типичной тенденции в заданном наборе данных.
Среднее значение — его часто называют просто «средним» — это термин, используемый в статистике и анализе данных. Кроме того, нередко можно услышать слова «среднее» или «среднее» в сочетании с терминами «мода», «медиана» и «диапазон», которые представляют собой другие методы вычисления шаблонов и общих значений в наборах данных.
Вкратце, вот определения этих терминов:
- Режим — значение, которое чаще всего встречается в наборе данных
- Медиана — среднее значение набора данных (при упорядочении от наименьшего значения к наибольшему)
- Диапазон — разница между наибольшим и наименьшим значением в наборе данных .
Итак, какова цель среднего значения? Если у вас есть набор данных с широким диапазоном чисел, , зная среднее значение, может дает вам общее представление о том, как эти числа можно объединить в одно репрезентативное значение.

Например, если вы учитесь в старшей школе и готовитесь к сдаче SAT, вам может быть интересно узнать текущий средний балл SAT. Знание среднего балла дает вам приблизительное представление о том, как большинство студентов, сдающих SAT, набирают по нему баллы.
Как найти среднее значение: обзор
Чтобы найти среднее арифметическое набора данных, все, что вам нужно сделать, это сложите все числа в наборе данных, а затем разделите сумму на общее количество значений.
Давайте рассмотрим пример. Допустим, вам дан следующий набор данных:
$$6, 10, 3, 27, 19, 2, 5, 14$$
Чтобы найти среднее значение, вам сначала нужно сложить все значения в набор данных выглядит следующим образом:
$$6 + 10 + 3 + 27 + 19 + 2 + 5 + 14$$
Обратите внимание, что вам не нужно переставлять значения здесь (хотя вы можете, если хотите ) и может просто добавить их в том порядке, в котором они были вам представлены.

Далее запишите сумму всех значений:
$$6 + 10 + 3 + 27 + 19 + 2 + 5 + 14 = \bo86$$
Последний шаг — взять эту сумму ( 86) и разделите его на количество значений в наборе данных. Поскольку существует восемь различных значений (6, 10, 3, 27, 19, 2, 5, 14), мы будем делить 86 на 8:
86 долларов США / 8 = 10,75 долларов США
Среднее значение или среднее значение для этого набора данных составляет 10,75.
Как вычислить среднее значение: практические вопросы
Теперь, когда вы знаете, как найти среднее значение — другими словами, как вычислить среднее значение заданного набора данных, — пришло время проверить, чему вы научились. В этом разделе мы дадим вам четыре математических вопроса, которые включают в себя нахождение или использование среднего значения.
Первые два вопроса являются нашими собственными, тогда как вторые два являются официальными вопросами SAT/ACT; как таковой, эти два потребуют немного больше размышлений.

Прокрутите вопросы, чтобы найти ответы и объяснения ответов.
Практический вопрос 1
Найдите среднее значение следующего набора чисел: 5, 26, 9, 14, 49, 31, 109, 5.
Практический вопрос 2
Вам дан следующий список чисел: 4, 4, 2, 11, 6, $X$, 1, 3, 2. Среднее арифметическое равно 4. Каково значение $X$?
Практический вопрос 3
Список чисел 41, 35, 30, $X$,$Y$, 15 имеет медиану 25. Форма списка чисел равна 15. До ближайшего целого числа, что означает список?
- 20
- 25
- 26
- 27
- 30
Источник: Официальный практический тест ACT за 2018-19 гг. . Что из следующего должно быть верным в отношении среднего возраста $m$ объединенной группы самцов и самок приматов в заповеднике приматов?
- $м = 17$
- $м > 17$
- $м < 17$
- 15 $ < м < 19 $
Источник: The College Board
Как найти среднее значение: ответы + объяснения понять не только, как найти среднее значение данных, но и как использовать то, что вы знаете о среднем значении, чтобы более эффективно подходить к любым математическим вопросам, связанным со средними значениями.

Вот ответы на четыре практических вопроса, приведенных выше:
- Практический вопрос 1: 31
- Практический вопрос 2: 3
- Практический вопрос 3: C. 26
- Практический вопрос 4: D. $15 < m < 19$
Продолжайте читать, чтобы увидеть объяснение ответа на каждый вопрос.
Практический вопрос 1 Ответ Объяснение
Найдите среднее значение следующего набора чисел: 5, 26, 9, 14, 49, 31, 109, 5,
Это простой вопрос, который просто просит вас вычислить среднее арифметическое заданного набора данных.
Во-первых, сложите все числа в наборе данных (помните, что вам не нужно упорядочивать их в порядке от меньшего к большему — сделайте это, только если вы пытаетесь найти медиану):
$ $5 + 26 + 9 + 14 + 49 + 31 + 109 + 5 = \bo248$$
Затем возьмите эту сумму и разделите ее на количество значений в наборе данных. Здесь всего восемь значений, поэтому мы разделим 248 на 8:9.
 0038
0038$248 / 8 = 31$$
Средний и правильный ответ равен 31.
Практический вопрос 2 Ответ Объяснение 6, $X$, 1, 3, 2. Среднее арифметическое равно 4. Каково значение $X$?
Для этого вопроса вы, по сути, работаете в обратном направлении: вы уже знаете среднее значение и теперь должны использовать это знание, чтобы найти пропущенное значение $X$ в наборе данных.
Вспомните, что для нахождения среднего нужно сложить все числа в наборе, а затем разделить сумму на общее количество значений.
Поскольку мы знаем, что среднее значение равно 4, мы начнем с умножения 4 на количество значений (здесь девять отдельных чисел, включая $X$):
$$4 * 9 = 36$$
Это дает нам сумму набора данных (36). Теперь вопрос превращается в задачу по алгебре, в которой все, что нам нужно сделать, это упростить и решить для $X$:
$$4 + 4 + 2 + 11 + 6 + X + 1 + 3 + 2 = 36$$
$33 + X = 36$$
$$X = 3$$
Правильный ответ: 3.

Практика делает совершенным!
Практический вопрос 3 Ответ Объяснение
Список чисел 41, 35, 30, $X$, $Y$, 15 имеет медиану 25. Режим списка чисел 15. К ближайшему целое число, каково среднее значение списка?
- 20
- 25
- 26
- 27
- 30
Эта сложная на вид математическая задача взята из официального практического теста ACT, поэтому вы можете ожидать, что она будет немного менее прямой, чем ваша типичная задача на среднее арифметическое.
Здесь нам дан набор данных с двумя неизвестными значениями:
41, 35, 30, $X$, $Y$, 15
Нам также предоставлены две важные части информации:
- Режим 15
- Медиана 25
Чтобы определить среднее значение этого набора данных, нам потребуется использовать всю предоставленную нам информацию, а также нужно знать моду и медиану.

Напоминаем, что мода — это значение, которое чаще всего встречается в наборе данных, а медиана — это среднее значение в наборе данных (когда все значения расположены от самого низкого до самого высокого).
Поскольку мода равна 15, это должно означать, что значение 15 встречается в наборе данных не менее двух раз (другими словами, больше раз, чем любое другое значение). В результате мы можем сказать, что заменяем либо $X$, либо $Y$ на 15:9.0038
41, 35, 30, $X$,15,15
Нам также сказали, что медиана равна 25. Чтобы найти медиану, вы должны сначала переставить набор данных в порядке от наименьшего значения к наибольшему.
Поскольку медиана больше 15, но меньше 30, мы должны поместить $X$ между этими двумя значениями. Вот что получится, если переставить значения от низшего к высшему:
15, 15, $X$, 30, 35, 41
Всего имеется шесть значений (включая $X$), что означает, что медианой будет число ровно посередине между третьим и четвертым значениями в наборе данных.
 Короче говоря, 25 (медиана) должно находиться на полпути между $X$ и 30.
Короче говоря, 25 (медиана) должно находиться на полпути между $X$ и 30.Это означает, что $X$ должно равняться 20, так как это отделяет 5 от 20 и 5 от 30 (или на полпути). между двумя значениями).
Теперь у нас есть полный набор данных без неизвестных значений:
15,15, 20, 30, 35, 41
Все, что нам нужно сделать, это использовать эти значения, чтобы найти среднее значение. Начните с добавления их всех:
15+15+20+30+35+41=156
Наконец, разделите сумму на количество значений в наборе данных (это шесть):
156/6=26
Правильный ответ: C. 26.
Практический вопрос 4 Ответ Объяснение
В приматном заповеднике средний возраст всех самцов приматов составляет 15 лет, а средний возраст всех самок приматов — 19 лет. Что из следующего должно быть верным в отношении среднего возраста $m$ объединенной группы самцов и самок приматов в заповеднике приматов?
- $м = 17$
- $м > 17$
- $м < 17$
- 15 $ < м < 19 $
Эта практическая задача является официальным практическим вопросом SAT по математике с веб-сайта Совета колледжей.

В этом математическом вопросе вы не должны искать среднее значение, а вместо этого должны использовать свои знания о двух средних, чтобы объяснить, каким может быть среднее значение большей группы. В частности, нас спрашивают , как мы можем использовать эти два средства, чтобы выразить в алгебраических терминах средний возраст ( $\bi m$ ) для как самцов, так и самок приматов.
Вот что мы знаем: во-первых, средний возраст всех самцов приматов составляет 15 лет. Во-вторых, средний возраст всех самок приматов составляет 19 лет. Это означает, что, как правило, самки приматов на старше , чем самцы приматов.
Поскольку средний возраст самцов приматов (15 лет) ниже, чем у самок приматов (19 лет), мы знаем, что средний возраст обеих групп логически не может превышать 19 лет.годы.
Точно так же, поскольку средний возраст самок приматов больше, чем у самцов, мы знаем, что средний возраст обоих не может быть логически ниже 15 лет.

Таким образом, мы остаемся с пониманием того, что средний возраст самцов и самок приматов вместе должен быть на больше 15 лет (средний возраст самцов), но также на меньше 19 лет (средний возраст самцов). самки).
Это обоснование можно записать в виде следующего неравенства:
$$15 < m < 19$$
Правильный ответ D. 15 < $\bi m$ < 19.
Что дальше?
Чтобы узнать больше о наборах данных, просмотрите наше руководство по лучшим стратегиям для среднего, медианы и моды на SAT Math.
Скоро сдавать SAT или ACT? Тогда вам определенно захочется узнать, по какой математике вы собираетесь сдавать экзамен. Чтобы начать работу, ознакомьтесь с нашими подробными руководствами по разделам SAT Math и ACT Math.
Какие математические формулы важнее всего знать для SAT и ACT? Получите обзор 28 важнейших формул SAT и 31 критической формулы ACT, которые вы должны знать.

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Ханна Муниз
Об авторе
Ханна получила степень магистра японоведения в Мичиганском университете и степень бакалавра в Университете Южной Калифорнии. С 2013 по 2015 год преподавала английский язык в Японии по программе JET. Она увлечена образованием, писательством и путешествиями.
Печать всех подмножеств заданного набора 9н.
Пример
Ввод: S[] = [1,2,3] Выход: [ [], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3] ]
Вы можете решить эту задачу здесь.

Возможные вопросы, которые можно задать интервьюеру —
- Может ли набор решений содержать повторяющиеся подмножества? (Ответ: Нет)
- Можем ли мы напечатать подмножество в любом порядке? (Ответ: Да)
1. Подход с возвратом
Идея решения
Зачем использовать возврат? Потому что техника поиска с возвратом предназначена для того, чтобы генерировать все возможные решения один раз. Если мы разумно разработаем алгоритм, мы сможем заставить логику поиска с возвратом работать на нас и сгенерировать все возможные подмножества.
Идея состоит в том, что если у нас есть N элементов внутри массива, у нас есть ровно два варианта выбора для каждого из них: либо мы включаем этот элемент в наше подмножество, либо не включаем его.
 Таким образом, стратегия «брать или не брать» строит псевдобинарное дерево вариантов, возвращая только листья для каждой комбинации, приводящей к набору мощности.
Таким образом, стратегия «брать или не брать» строит псевдобинарное дерево вариантов, возвращая только листья для каждой комбинации, приводящей к набору мощности.Дерево рекурсии для приведенного выше примера будет выглядеть так:
Шаги решения
Мы могли бы просто создать подмножество разного размера в массиве, т.е. subset[] . Вот шаги для его создания:
- Выберите один элемент из ввода, т.е. subset[len] = S[pos]. Мы можем решить, включать его в текущее подмножество или нет.
- Рекурсивно сформировать подмножество, включая его, т.е. allSubsets(pos+1, len+1, subset)
- Рекурсивно формировать подмножество, исключая его, т. е. allSubsets(pos+1, len, subset)
- Обязательно сгенерируйте каждый набор один раз.
Псевдокод
целое S[N] недействительными allSubsets (int pos, int len, int [] подмножество) { если (поз == Н) { печать (подмножество) возвращаться } // Пробуем текущий элемент в подмножестве. подмножество [длина] = S [поз]
allSubsets(pos+1, len+1, подмножество)
// Пропустить текущий элемент.
allSubsets(pos+1, длина, подмножество)
}
подмножество [длина] = S [поз]
allSubsets(pos+1, len+1, подмножество)
// Пропустить текущий элемент.
allSubsets(pos+1, длина, подмножество)
} 9n)
Пространственная сложность : O(n) для дополнительного подмножества массива.
Критические идеи для размышления
- Почему мы отслеживаем оба случая, когда мы выбираем элемент и когда мы не выбираем элемент?
- Можете ли вы написать рекуррентное соотношение для приведенного выше алгоритма?
- Можете ли вы придумать другой способ реализации этого решения?
- Можно ли решить эту проблему с помощью стека?
- Определите проблемы, которые можно решить с помощью аналогичного подхода.
2. Подход с битовой маскировкой
Идея решения
Таким образом, вместо использования массива мы можем просто использовать одно целое число, отдельные биты которого представляют элементы массива.
 n − 1 (все n битов равны единице).
n − 1 (все n битов равны единице).Установить S[] = [1,2,3] Общее количество подмножеств = pow(2, n) = pow(2, 3) = 8 Значение целых подмножеств 000 -> Пустой набор 001 -> 1 010 -> 2 011 -> 12 100 -> 3 101 -> 13 110 -> 23 111 -> 123Шаги решения
- Получить общее количество подмножеств, 9n
- Loop for index from 0 to subset_size
- Loop for i = 0 to subset_size
- If the ith bit in the index is set then, append ith элемент из массива для этого подмножества.
Псевдокод
Void allSubset(int S[], int n) { int subset_size = pow (2, n) внутренний индекс, я //Выполнить от индекса 000..0 до 111..1 for (индекс от 0 до subset_size) { целое подмножество [n] для (i от 0 до n) { // Проверяем, установлен ли j-й бит в индексе // Если установлено, добавляем j-й элемент в подмножество если (индекс и (1 << я)) подмножество [я] = S [я] } печать (подмножество) } } 9n)Пространственная сложность : O(n)
Критические идеи для размышления
- Что означает оператор «<<»?
- Что представляет каждый установленный бит в промежуточных итерациях?
- Можете ли вы объяснить временную сложность?
- Определите проблемы, которые можно решить с помощью аналогичного подхода.

Предлагаемые проблемы для решения
- Разделите строку так, чтобы каждая строка раздела была палиндромом.
- Сумма подмножеств всех подмножеств массива
- Имея n пар скобок, напишите программу для генерации всех комбинаций правильно сформированных скобок.
- Возвращает все возможные перестановки набор различных целых чисел
- Буквенная комбинация телефонного номера
- Возвращает все возможные комбинации k чисел из 1 2 3 ... n.
- Задача N Queen
- Крыса в лабиринте
Удачного кодирования! Наслаждайтесь алгоритмами!
Онлайн-курс AfterAcademy «Структура данных и алгоритмы» — Прием открытМежквартильный размах (IQR): что это такое и как его найти
Что такое межквартильный размах?
Межквартильный диапазон является мерой того, где в наборе данных находится «средний пятидесятый».
 Если диапазон — это мера того, где в наборе находятся начало и конец, межквартильный диапазон — это мера того, где находится основная часть значений. Вот почему он предпочтительнее многих других показателей распространения, когда сообщается о таких вещах, как успеваемость в школе или результаты SAT.
Если диапазон — это мера того, где в наборе находятся начало и конец, межквартильный диапазон — это мера того, где находится основная часть значений. Вот почему он предпочтительнее многих других показателей распространения, когда сообщается о таких вещах, как успеваемость в школе или результаты SAT.Формула межквартильного диапазона представляет собой первый квартиль, вычтенный из третьего квартиля:
IQR = Q 3 – Q 1 . Посмотрите видео о том, как рассчитать межквартильный размах вручную:
Как найти межквартильный размах
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Состав:
Решение вручную:
- Решите формулу вручную (нечетный набор чисел).
- Что делать, если у меня четный набор чисел?
- Найдите межквартильный диапазон для нечетных наборов чисел: Второй метод
- Межквартильный диапазон блочной диаграммы: как его найти
Использование технологии:
- Межквартильный диапазон в Minitab
- Межквартильный диапазон в Excel
- Межквартильный диапазон в SPSS
- Межквартильный диапазон на TI83
- Q1, Q3 и IQR на TI89
Общая информация:
- Что такое межквартильный диапазон?
- Что такое формула межквартильного диапазона?
- IQR как тест на нормальное распределение
- Для чего используется межквартильный диапазон?
- История межквартильного диапазона.

Шаги:
- Шаг 1: Поставь числа по порядку.
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. - Шаг 2: Найдите медиану .
1, 2, 5, 6, 7 , 9 , 12, 15, 18, 19, 27. - Шаг 3: Заключите в скобки числа выше и ниже медианы.
Не обязательно статистически , но это облегчает обнаружение Q1 и Q3.
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27). - Шаг 4: Найдите Q1 и Q3
Думайте о Q1 как о медиане в нижней половине данных и о Q3 как о медиане в верхней половине данных.
(1, 2, 5 , 6, 7) , 9 , (12, 15, 18 , 19, 27). Q1 = 5 и Q3 = 18. - Шаг 5: Вычтите Q1 из Q3, чтобы найти межквартильный размах .
18 – 5 = 13.
Нравится объяснение? Прочтите «Руководство по статистике практического мошенничества», в котором есть еще сотни пошаговых объяснений, таких как это!
Пример вопроса : Найдите IQR для следующего набора данных: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.

- Шаг 1: Расставьте числа по порядку .
3, 5, 7, 8, 9, 11, 15, 16, 20, 21. - Шаг 2: Сделайте отметку в центре данных :
3, 5, 7, 8, 9, | 11, 15, 16, 20, 21. - Шаг 3: Поместите в круглые скобки числа над и под отметкой, сделанной на шаге 2, — так будет легче найти Q1 и Q3.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). - Шаг 4: Найти Q1 и Q3
Q1 — это медиана (середина) нижней половины данных, а Q3 — это медиана (середина) верхней половины данных.
(3, 5, 7 , 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 и Q3 = 16. - Шаг 5: Вычесть Q1 из Q3 .
16 – 7 = 9.
Это ваш IQR .
Вернуться к началу
Как вы, возможно, уже знаете, в статистике нет ничего «высеченного на камне»: когда некоторые статистики находят межквартильный диапазон для набора нечетных чисел, они включают медиану в оба оба квартили.
 Например, в следующем наборе чисел: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 некоторые статистики разбили бы его на две половины, включая медиану (9) в обеих половинах:
Например, в следующем наборе чисел: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 некоторые статистики разбили бы его на две половины, включая медиану (9) в обеих половинах:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Это приводит к двум половинам с четным набором чисел, поэтому вы можете выполнить описанные выше шаги, чтобы найти ИКР.
Вернуться к началуПосмотрите видео с инструкциями.
Как найти межквартильный диапазон на ящичковой диаграмме
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Межквартильный размах блочной диаграммы: как его найти
Пример вопроса: Найдите межквартильный размах для приведенной выше блочной диаграммы.
Вот и все!
Вернуться к началу
Межквартильный размах в Minitab
Посмотрите видео с пошаговыми инструкциями:Как найти межквартильный размах в Minitab
Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.
Межквартильный диапазон в Minitab: Шаги
Пример вопроса: Найдите межквартильный диапазон в Minitab для среднего балла успеваемости (GPA) в следующем наборе данных:
Средний балл успеваемости (GPA): 1(3.2), 1( 3.1), 2(3.5), 2(2.0), 3(1.9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5( 3,3), 6(3,4), 6(2,6), 6(2,5), 7(2,0), 7(1,5), 8(4,0), 8(2,0).Шаг 1: Введите данные в рабочий лист Minitab . Введите свои данные в один или два столбца.
Шаг 2: Нажмите «Стат.», , затем нажмите «Основная статистика», затем нажмите «Показать описательную статистику», чтобы открыть меню «Описательная статистика».
Шаг 3: Щелкните имя переменной в левом окне , а затем нажмите кнопку «Выбрать», чтобы перенести имя переменной в правое окно.
Шаг 4: Нажмите кнопку «Статистика».
Шаг 5: Отметьте «Межквартильный диапазон».

.Шаг 6: Нажмите кнопку «ОК» (откроется новое окно с результатом). IQR для среднего балла в этом конкретном наборе данных составляет 1,8.
Вот и все!
Совет . Если описательная статистика не отображается в окне, нажмите «Окно» на панели инструментов, затем нажмите «Мозаика». Щелкните окно «Сеанс» (здесь появляется описательная статистика), а затем прокрутите вверх, чтобы просмотреть результаты.
Вернуться к началу
Как найти межквартильный диапазон Excel 2007
Посмотрите видео или прочитайте приведенные ниже шаги, чтобы найти межквартильный диапазон в Excel 2007:
Как найти межквартильный диапазон в Excel
Посмотрите это видео на YouTube.
Шаги:
Шаг 1: Введите данные в один столбец Excel на листе. Например, введите данные в ячейки от A2 до A10. Не оставляйте пробелов в данных.Шаг 2. Щелкните пустую ячейку (например, щелкните ячейку B2) и введите =КВАРТИЛЬ(A2:A10,1) .
 Вам нужно будет заменить A2: A10 фактическими значениями из вашего набора данных. Например, если вы ввели данные в поля от B2 до B50, получится уравнение =QUARTILE(B2:B50,1) . «1» в этой формуле Excel (A2:A10, 1 ) представляет первый квартиль (то есть точку, лежащую в 25% набора данных).
Вам нужно будет заменить A2: A10 фактическими значениями из вашего набора данных. Например, если вы ввели данные в поля от B2 до B50, получится уравнение =QUARTILE(B2:B50,1) . «1» в этой формуле Excel (A2:A10, 1 ) представляет первый квартиль (то есть точку, лежащую в 25% набора данных).Шаг 3. Щелкните вторую пустую ячейку (например, щелкните ячейку B3) и введите =КВАРТИЛЬ(A2:A10,3) . Замените A2:A10 фактическими значениями из вашего набора данных. «3» в этой формуле Excel (A2:A10, 3 ) представляет третий квартиль (т. е. точку, лежащую в 75% набора данных).
Шаг 4. Щелкните третью пустую ячейку (например, щелкните ячейку B4) и введите =B3-B2 . Если ваши функции квартилей из шагов 2 и 3 находятся в разных местах, измените ссылки на ячейки.
Шаг 5: Нажмите клавишу «Ввод». Excel вернет IQR в ячейке, которую вы щелкнули на шаге 4
Вот и все!
Вернуться к началу
Как и большинство технологий, SPSS имеет несколькими способами можно рассчитать IQR.
 Однако, если вы нажмете на наиболее интуитивно понятный способ, который вы ожидаете найти («Описательная статистика»> «Частоты»), сюрпризом будет то, что он не будет отображать IQR (хотя он будет перечислять первый, второй и третий квартили). Вы могли бы пойти по этому маршруту, а затем вычесть третий квартиль из первого, чтобы получить IQR. Однако проще всего найти межквартильный размах в SPSS с помощью команды «Исследовать». Если вы уже ввели данные в свой рабочий лист, перейдите к шагу 3.
Однако, если вы нажмете на наиболее интуитивно понятный способ, который вы ожидаете найти («Описательная статистика»> «Частоты»), сюрпризом будет то, что он не будет отображать IQR (хотя он будет перечислять первый, второй и третий квартили). Вы могли бы пойти по этому маршруту, а затем вычесть третий квартиль из первого, чтобы получить IQR. Однако проще всего найти межквартильный размах в SPSS с помощью команды «Исследовать». Если вы уже ввели данные в свой рабочий лист, перейдите к шагу 3.Посмотрите видео с инструкциями:
Как найти межквартильный диапазон в SPSS
Посмотрите это видео на YouTube.
Шаги не видны? Кликните сюда.
Шаги
Шаг 1: Откройте новый файл данных в SPSS. Нажмите «Файл», наведите указатель мыши на «Создать», а затем нажмите «Данные».
Шаг 2: Введите данные в столбцы рабочего листа. Вы можете использовать столько столбцов, сколько вам нужно, но не оставляйте пустых строк или пробелов между данными.
 См.: Как ввести данные в SPSS.
См.: Как ввести данные в SPSS.Шаг 3: Нажмите «Анализ», , затем наведите указатель мыши на «Описательная статистика». Нажмите «Исследовать», чтобы открыть диалоговое окно «Исследовать».
Шаг 4: Щелкните имя переменной (это просто красивое имя для заголовка столбца), затем щелкните верхнюю стрелку , чтобы переместить переменную в поле «Зависимый список».
Диалоговое окно «Исследовать» переменные.Шаг 5: Нажмите «ОК». Межквартильный диапазон указан в описании 9Коробка 0028.
Совет: В этом примере в таблицу данных введен только один список, но у вас может быть несколько на выбор в зависимости от того, как вы ввели свои данные. Прежде чем продолжить, убедитесь, что вы выбрали правильную переменную (имена столбцов). Если вам нужны более запоминающиеся имена переменных, измените заголовок столбца, нажав кнопку «Просмотр переменных» в самом нижнем левом углу рабочего листа.
 Введите новое имя переменной, а затем вернитесь к просмотру данных, нажав кнопку «Просмотр данных».
Введите новое имя переменной, а затем вернитесь к просмотру данных, нажав кнопку «Просмотр данных».
Вернуться к началу
Представьте себе, что все данные в наборе представляют собой точки на числовой прямой. Например, если в вашем наборе данных есть 3, 7 и 28, представьте их как точки на числовой прямой с центром в 0, но простирающейся как бесконечно ниже нуля, так и бесконечно выше нуля. После нанесения на эту числовую линию наименьшая точка данных и самая большая точка данных в наборе данных создают границы (т.е. нижнюю границу и верхнюю границу) интервала пространства на числовой линии, которая содержит все точки данных в наборе данных. установлен. межквартильный диапазон (IQR) - это длина средних 50% этого интервала пространства.Межквартильный диапазон — это средние 50 % набора данных. Коробка и усы. Изображение от Jhguch на en.wikipedia
. Если вы хотите знать, что IQR находится в формальных терминах, IQR рассчитывается как: разница между третьим или верхним квартилем и первым или нижним квартилем .
 Квартиль — это термин, используемый для описания того, как разделить набор данных на четыре равные части (думаю, квартал ).
Квартиль — это термин, используемый для описания того, как разделить набор данных на четыре равные части (думаю, квартал ).Пример IQR
Если у вас есть набор, содержащий точки данных 1, 3, 5, 7, 8, 10, 11 и 13, первый квартиль равен 4, второй квартиль — 7,5 и третий квартиль — 10,5. Нарисуйте эти точки на числовой прямой, и вы увидите, что эти три числа делят числовую прямую на четверти от 1 до 13. Таким образом, IQR этого набора данных составляет 6,5, рассчитанное как 10,5 минус 4. Первое и третьи квартили также иногда называют 25-м и 75-м процентилями, потому что это эквивалентные цифры, когда набор данных делится на проценты, а не на четверти.
Вернуться к началу
Посмотрите видео с шагами:
TI 83 Межквартильный диапазон
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Хотя на этом веб-сайте можно использовать отличный онлайн-калькулятор межквартильного диапазона, в викторине или тесте его может не быть.
 Большинство инструкторов разрешают использовать TI-83 на тестах, и это даже один из немногих калькуляторов, разрешенных на экзамене AP Statistics. Чтобы найти межквартильный диапазон TI 83, нужно всего лишь ввести список данных и нажать пару кнопок.
Большинство инструкторов разрешают использовать TI-83 на тестах, и это даже один из немногих калькуляторов, разрешенных на экзамене AP Statistics. Чтобы найти межквартильный диапазон TI 83, нужно всего лишь ввести список данных и нажать пару кнопок.Пример задачи: Найдите межквартильный диапазон TI 83 для высот 10 лучших зданий в мире (по состоянию на 2009 г.). Высота (в футах): 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272. калькулятор. Нажмите кнопку STAT, а затем нажмите ENTER. Введите первое число (2717) и нажмите клавишу ВВОД. Продолжайте вводить цифры, нажимая ENTER после каждого ввода.
Шаг 2: Нажмите кнопку STAT.
Шаг 3: Нажмите кнопку со стрелкой вправо (клавиши со стрелками расположены в правом верхнем углу клавиатуры), чтобы выбрать «Расч.».
Шаг 4: Нажмите ENTER, чтобы выделить «1-Var Stats».
Шаг 5: Нажмите ENTER еще раз, чтобы открыть список статистики.

Шаг 6: Прокрутите список с помощью клавиш со стрелками, чтобы найти Q1 и Q3. Запишите эти числа. Вы могли бы скопировать и вставить числа, но, к сожалению, Texas Instruments не упрощает эту задачу:
- С помощью клавиш со стрелками поместите курсор в начало текста
, который вы хотите выделить. - Используя клавиатуру TI, нажмите и удерживайте клавишу Shift, а затем используйте клавиши со стрелками, чтобы выделить текст.
- Отпустите клавишу Shift и клавишу со стрелкой.
Должно появиться меню копирования и вставки, позволяющее копировать и вставлять данные. Вам придется сделать это дважды (каждый раз возвращаясь на ГЛАВНЫЙ экран), поэтому гораздо быстрее просто записать числа.
Шаг 7: Вычтите Q1 из Q3, чтобы найти IQR (сильное> 624 фута для этого набора чисел).
Вот и все!
НаверхПример задачи : Найдите Q 1 , Q 3 и IQR для следующего списка чисел: 1, 9, 2, 3, 7, 8, 9, 2.

Шаг 1: Нажмите APPS. Прокрутите до редактора статистики/списка (используйте клавиши со стрелками на клавиатуре для прокрутки). Нажмите Ввод. Если у вас нет редактора статистики/списков, вы можете скачать его здесь.
Шаг 2: Очистить список редактора данных: нажмите F1 8.
Шаг 3: Нажмите АЛЬФА 9 АЛЬФА 1 ENTER. Это назовет ваш список «IQ».
Шаг 4: Введите свои номера по одному. После каждой записи нажимайте клавишу ENTER . Для нашей группы чисел введите
1,9,2,3,7,8,9,2Шаг 5: Нажмите F4, затем ENTER (для экрана статистики с 1 переменной).
Шаг 6: Скажите калькулятору, что вам нужна статистика для списка под названием «IQ», введя АЛЬФА 9 АЛЬФА 1 в поле «Список:». Калькулятор должен автоматически поставить курсор туда для вас. Дважды нажмите ВВОД.
Шаг 7: Прочитайте результаты.
 Q 1 указан как Q1X (в нашем примере Q1X=2). Q 3 указан как Q3X (Q3X=8,5). Чтобы найти IQR, вычтите Q 1 из Q 3 на главном экране. IQR составляет 8,5-2=6,5.
Q 1 указан как Q1X (в нашем примере Q1X=2). Q 3 указан как Q3X (Q3X=8,5). Чтобы найти IQR, вычтите Q 1 из Q 3 на главном экране. IQR составляет 8,5-2=6,5.Вот и все!
Вернуться к началу
Формула IQR:
IQR = Q 3 – Q 1Где Q 3 — верхний квартиль, а Q — нижний квартиль.
Используйте формулу межквартильного диапазона со средним значением и стандартным отклонением, чтобы проверить, имеет ли популяция нормальное распределение. Формула для определения нормального распределения популяции:
Q 1 – (σ z 1 ) + X
Q 3 – (σ z 3 ) + X
Где Q 1 – первый квартиль, Q 3 – третий квартиль, σ – стандартный отклонение, z — стандартная оценка («z-оценка»), а X — среднее значение. Чтобы определить, нормально ли распределена популяция, решите оба уравнения, а затем сравните результаты. Если есть значительная разница между результатами и первым или третьим квартилями, то население составляет , а не нормально распределенных.
Если есть значительная разница между результатами и первым или третьим квартилями, то население составляет , а не нормально распределенных.Вернуться к началу
IQR используется для измерения степени разброса точек данных в наборе от среднего значения набора данных. Чем выше IQR, тем больше разбросаны точки данных; Напротив, чем меньше IQR, тем больше точек данных сгруппированы вокруг среднего значения. Диапазон IQR — это одно из многих измерений, используемых для измерения того, насколько разбросаны точки данных в наборе данных. Его лучше всего использовать с другими измерениями, такими как медиана и общий диапазон, чтобы построить полную картину тенденции набора данных группироваться вокруг своего среднего значения.
Вернуться к началуОткуда взялся термин межквартильный размах?
Кто изобрел термин «межквартильный диапазон»? Чтобы это выяснить, нам нужно вернуться в 19 век.
Британский врач сэр Дональд Макалистер использовал термины нижний квартиль и верхний квартиль в публикации 1879 года «Закон среднего геометрического».
 проц. Р. Соц. XXIX, с. 374: «Поскольку эти два показателя вместе со средним значением делят кривую возможностей на четыре равные части, я предлагаю называть их «верхним квартилем» и «нижним квартилем» соответственно».
проц. Р. Соц. XXIX, с. 374: «Поскольку эти два показателя вместе со средним значением делят кривую возможностей на четыре равные части, я предлагаю называть их «верхним квартилем» и «нижним квартилем» соответственно». Хотя по профессии он был врачом, он был одарён математикой и получил наивысший балл на выпускных экзаменах по математике в Кембриджском университете в 1877 году. Он говорил на девятнадцати языках, включая английский, чешский и шведский.
Статья Макалистера «Закон среднего геометрического» фактически была ответом на вопрос, заданный Фрэнсисом Гальтоном (изобретателем доски Гальтона). Однако только в 1882 году Гальтон («Отчет антропометрического комитета») использовал значения верхнего и нижнего квартилей, а также термин «межквартильный диапазон», определяемый как удвоенная вероятная ошибка. Гальтон был не только статистиком, но и антропологом, географом, протогенетиком и психометристом, написавшим более 340 книг. Он также ввел статистические термины «корреляция» и «регрессия к среднему».

- \(a

 Все правила по сольфеджио
Все правила по сольфеджио
 Тогда пересечением M и N будет …
Тогда пересечением M и N будет … Тогда их объединение CÈD представляет собой множество …
Тогда их объединение CÈD представляет собой множество …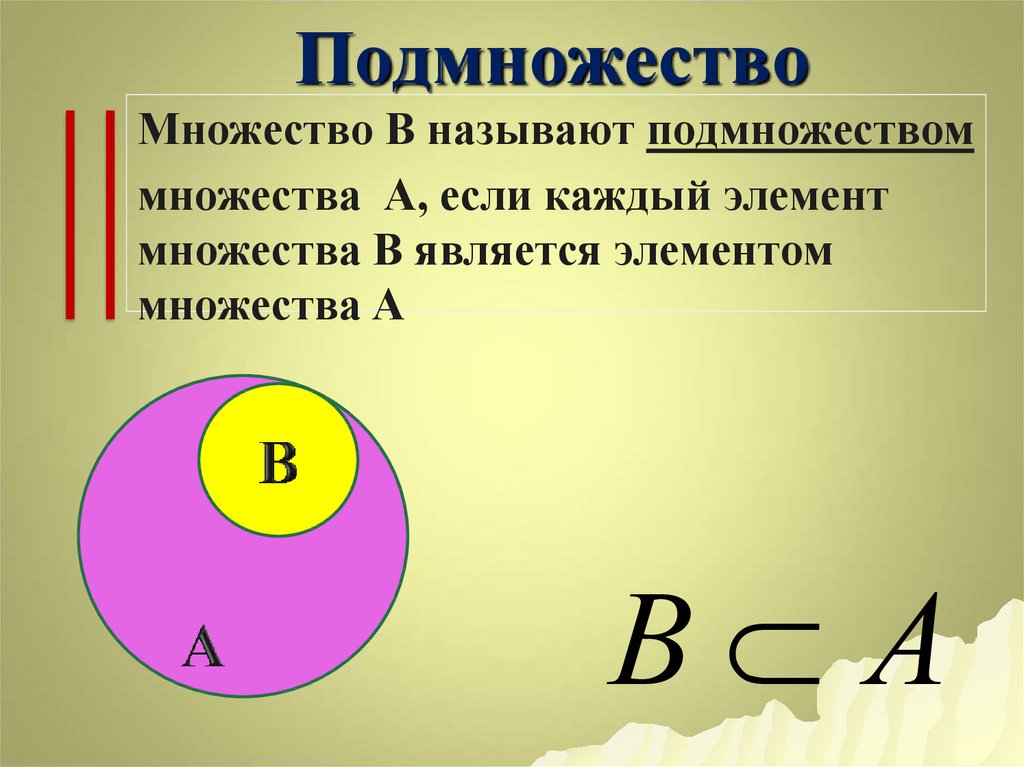 Чему равна вероятность того, что выпадет число очков равное 7?
Чему равна вероятность того, что выпадет число очков равное 7? Каким будет событие: «Из мешка вынули 4 шара, и один оказался белымʺ?
Каким будет событие: «Из мешка вынули 4 шара, и один оказался белымʺ?
 Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение.
Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар». Событие В – «Вынули черный шар». Тогда для этих событий верным будет утверждение.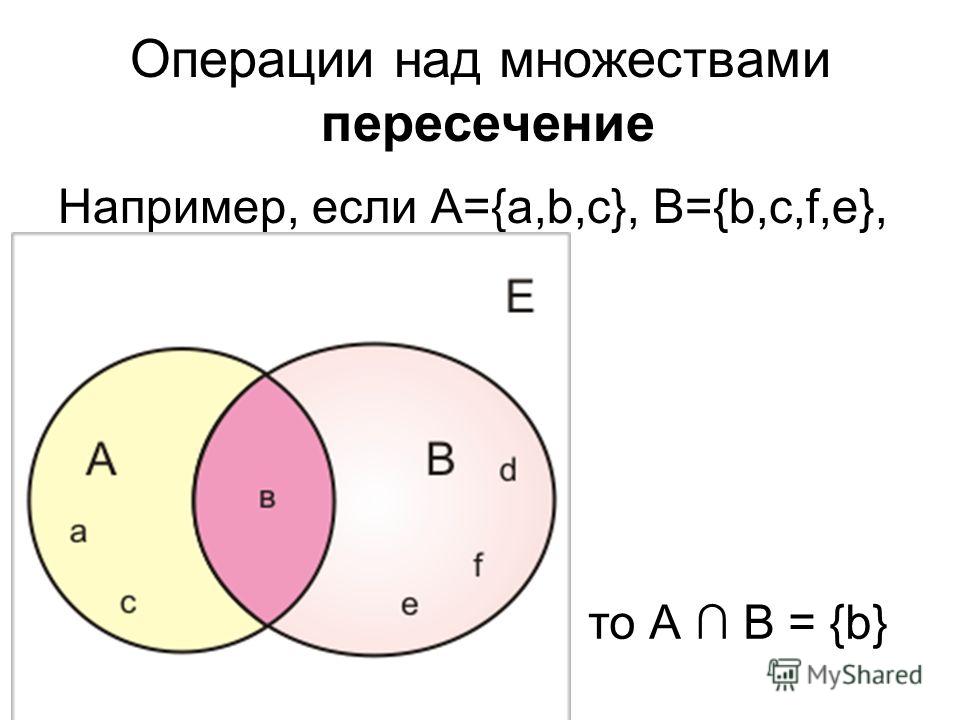 Тогда вероятность выиграть оба чемпионата равна…
Тогда вероятность выиграть оба чемпионата равна… Тогда вероятность того, что оба студента ответят успешно, равна…
Тогда вероятность того, что оба студента ответят успешно, равна…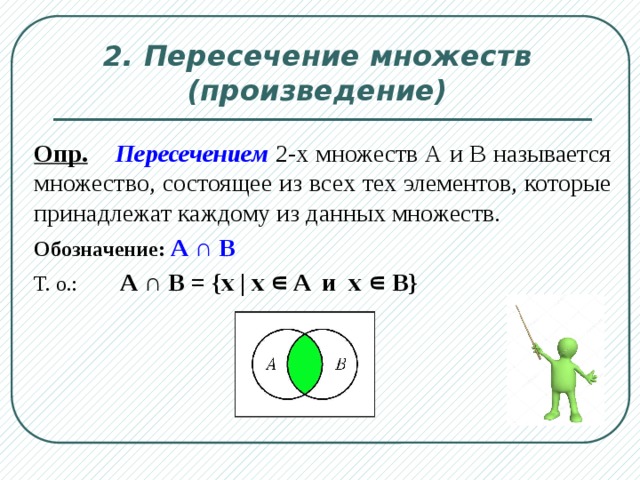 Тогда его выборочная мода равна …
Тогда его выборочная мода равна …
 Тогда медиана данного ряда равна …
Тогда медиана данного ряда равна …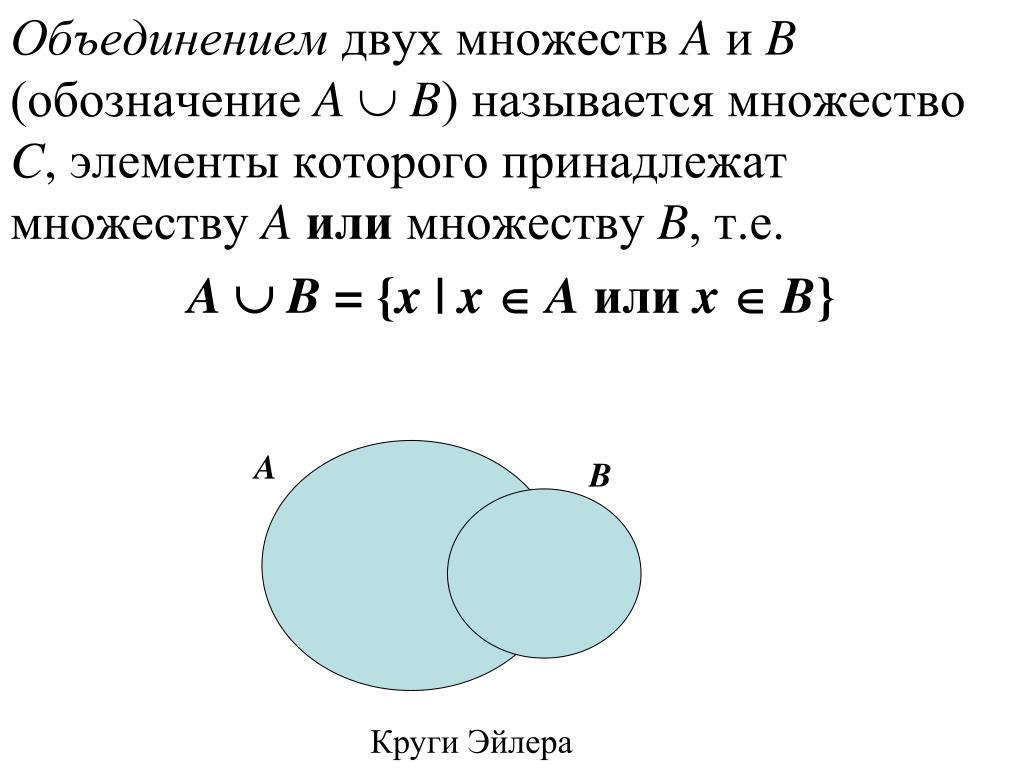 Тогда его выборочная мода равна …
Тогда его выборочная мода равна … Найти вероятность того, что хотя бы один раз выпадет герб.
Найти вероятность того, что хотя бы один раз выпадет герб.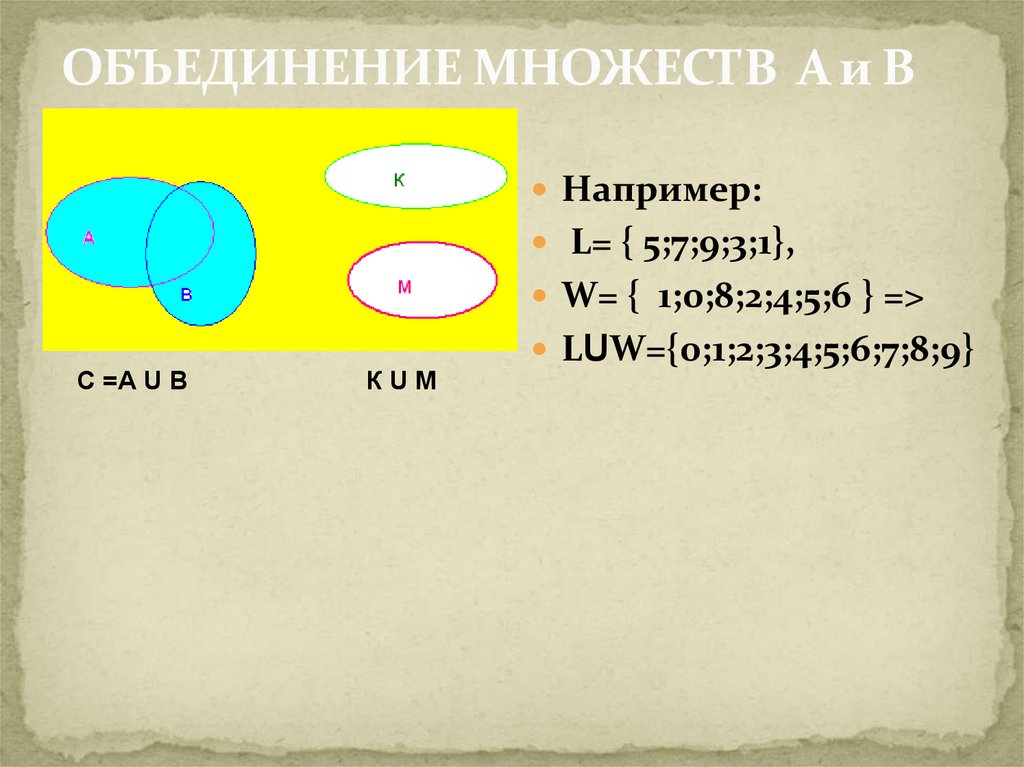 . .
. .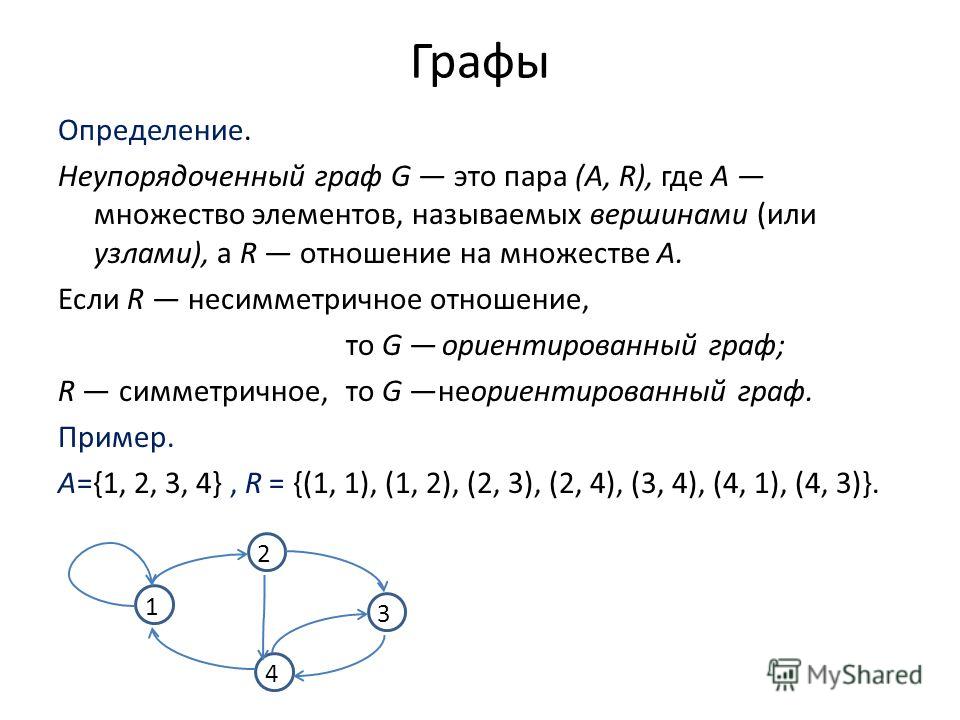
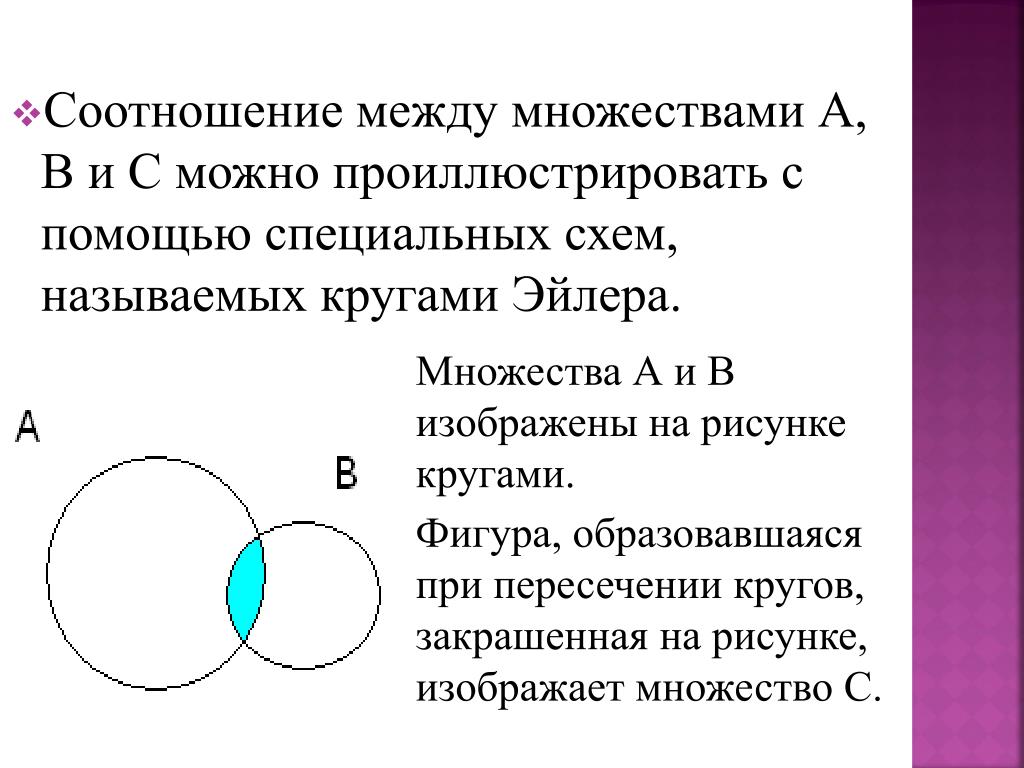
 Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события: C + E?
Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события: C + E? Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события AD \ E ?
Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события AD \ E ? Что означает событие А+В?
Что означает событие А+В? su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.08 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.08 с.)






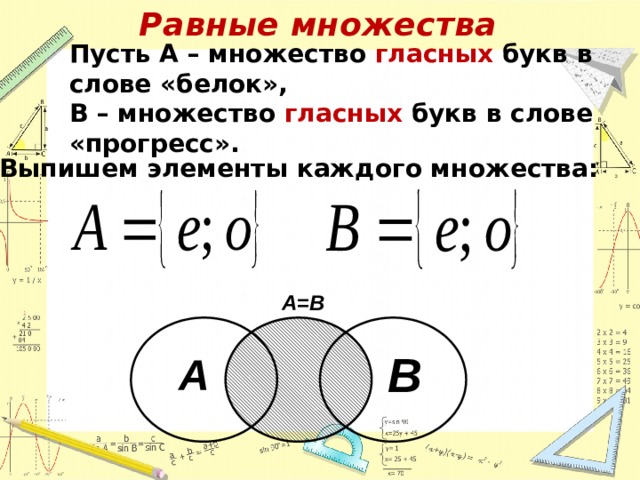 д.
д.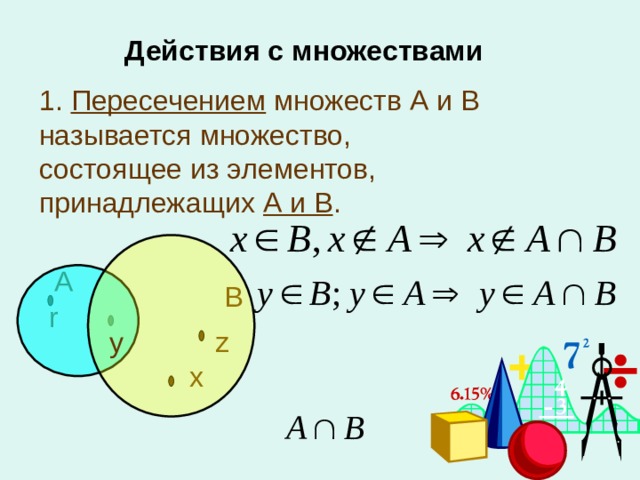
 Так
Так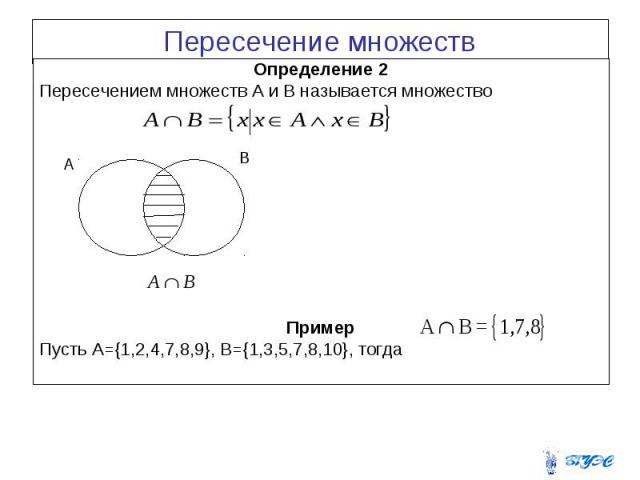

 Отметьте верное равенство:
Отметьте верное равенство:
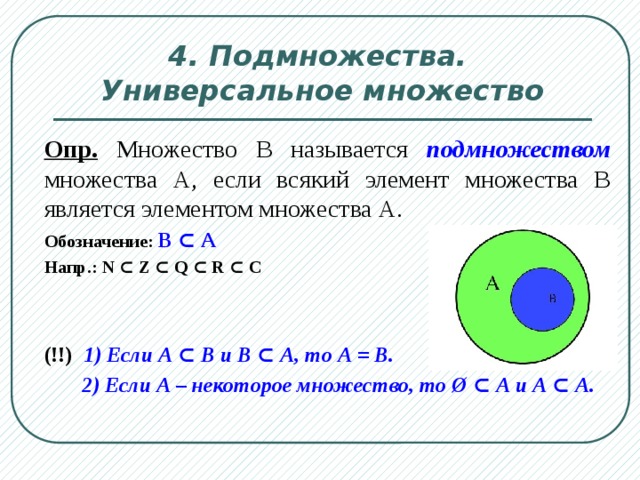 Отметьте верное равенство:
Отметьте верное равенство:
 Сколько элементов может содержать их объединение?
Сколько элементов может содержать их объединение?
 Отметьте верное равенство:
Отметьте верное равенство:
 Отметьте верное равенство:
Отметьте верное равенство:
 Какое из множеств является образом элемента
Какое из множеств является образом элемента  Какое из множеств является образом элемента
Какое из множеств является образом элемента  Отметьте верные утверждения:
Отметьте верные утверждения:
 Отметьте верное утверждение:
Отметьте верное утверждение:
 Какое соответствие функционально?
Какое соответствие функционально?
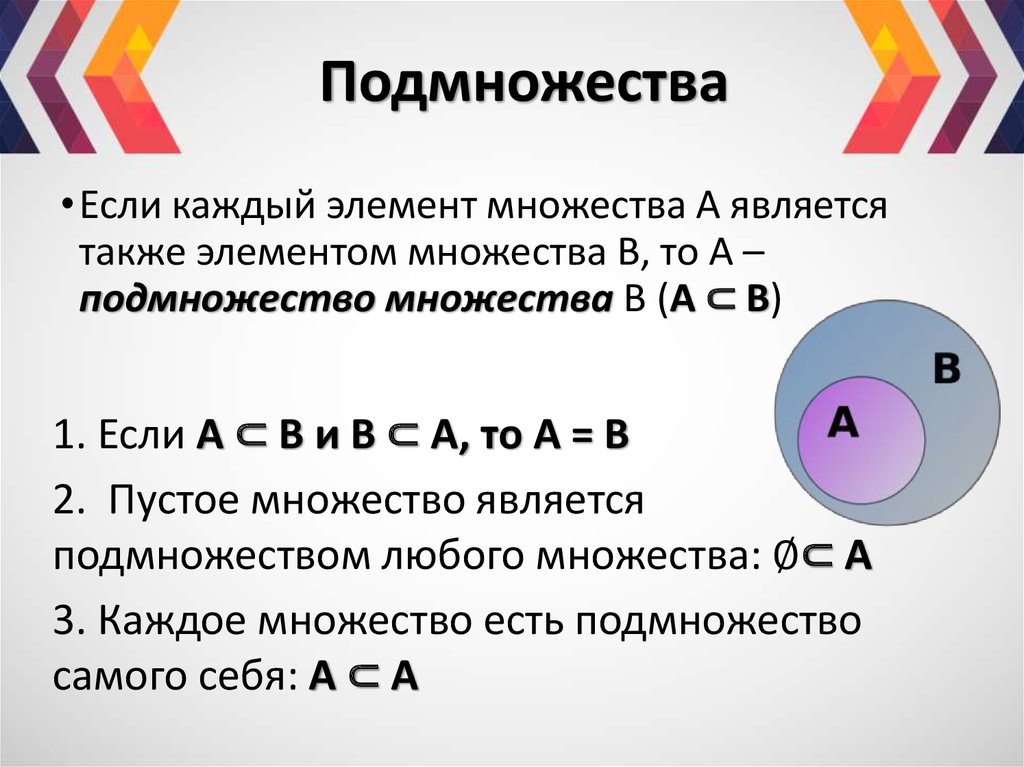 Какое соответствие функционально?
Какое соответствие функционально?
 Какое соответствие функционально?
Какое соответствие функционально?
 Какой тип имеет функция
Какой тип имеет функция  Какой тип имеет функция
Какой тип имеет функция  Какой тип имеет функция
Какой тип имеет функция 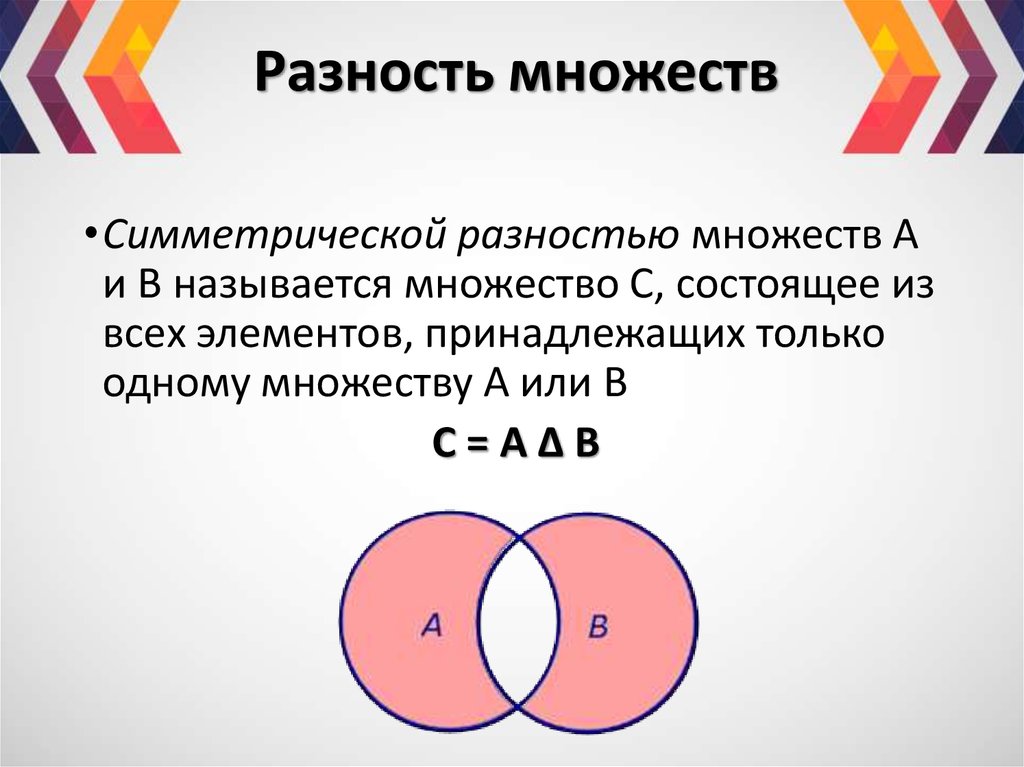 Отметьте верное утверждение:
Отметьте верное утверждение:
 Отметьте верное утверждение:
Отметьте верное утверждение:
 Какие пары нужно добавить к
Какие пары нужно добавить к  Какие пары нужно добавить к
Какие пары нужно добавить к  Какие пары нужно добавить к
Какие пары нужно добавить к  \)
\) После умножения числителя на 7 мы все еще имеем отношение двух целых чисел. И наоборот, если для любого рационального числа \(x\) мы можем умножить знаменатель на 7, мы получим другое рациональное число \(y\), такое что \(7y=x\). Следовательно, два набора \(7\mathbb{Q}\) и \(\mathbb{Q}\) содержат один и тот же набор рациональных чисел. Напротив, \(0\mathbb{Q}\) содержит только одно число, а именно 0. Следовательно, \(0\mathbb{Q}\neq\mathbb{Q}\).
После умножения числителя на 7 мы все еще имеем отношение двух целых чисел. И наоборот, если для любого рационального числа \(x\) мы можем умножить знаменатель на 7, мы получим другое рациональное число \(y\), такое что \(7y=x\). Следовательно, два набора \(7\mathbb{Q}\) и \(\mathbb{Q}\) содержат один и тот же набор рациональных чисел. Напротив, \(0\mathbb{Q}\) содержит только одно число, а именно 0. Следовательно, \(0\mathbb{Q}\neq\mathbb{Q}\).
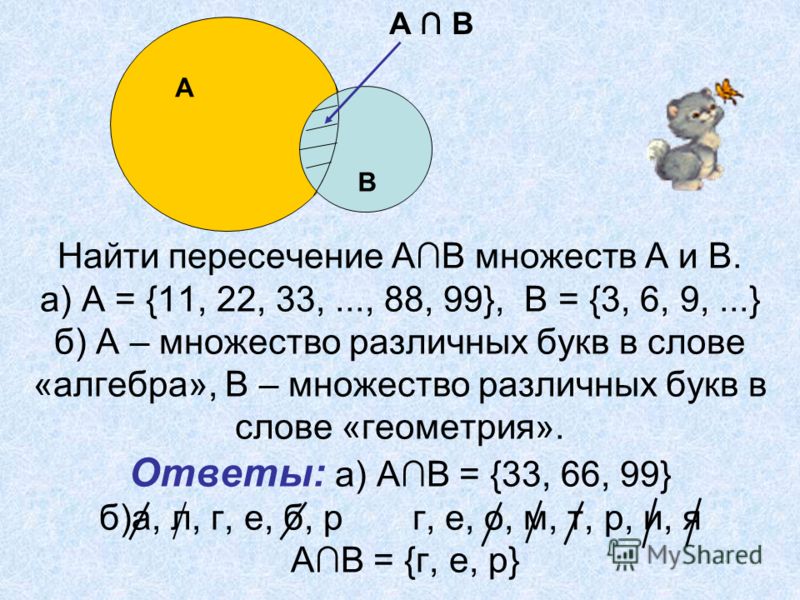
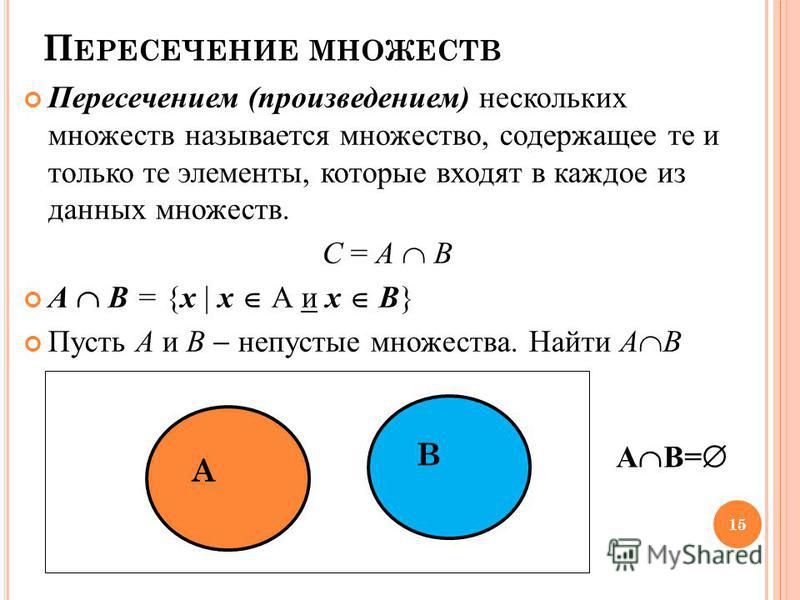 так что это кардинальное число
набора
b сколько там элементов
имея
шесть элементов, поэтому n of b равно шести
теперь третий c равен нулю
установлен
так есть ли какой-либо элемент в нулевом наборе
нет так что такое кардинальность или что такое
номер карты c
такой c это 0, потому что есть
нет элементов в множестве c
теперь d d равно множеству, имеющему
элементы 3
2 2 1 3 1 2
поэтому на самом деле d можно записать как
3 2 и 1 потому что все
остальные элементы такие же, как и у трех
два и один
так сколько всего элементов
три элемента прямо так кардинал
номер множества d
три, как насчет
пятый e представляет собой набор натуральных
числа от 15
а 20 это натуральные числа
между 15 и 20 16
17 18 и 90.
так что такое n из e, сколько элементов
там
четыре, поэтому кардинальное число множества e равно
четыре переходят к последнему набору f
это набор целых чисел от 8 до
14, так что вы можете определить набор
ф с 8
до 14 означает 8
9 10 11
12 13 и 40.
так каково кардинальное число множества f
сколько элементов
один два три четыре пять шесть семь
элементы есть
поэтому кардинальное число смещения f равно
7 хорошо, так что кардинальное число это
количество элементов
в каждом из этих наборов, и я надеюсь, что вы
понял решение
если у вас есть какие-либо сомнения, прокомментируйте ниже и
подпишитесь на этот канал, чтобы получать
регулярные обновления
спасибо»
так что это кардинальное число
набора
b сколько там элементов
имея
шесть элементов, поэтому n of b равно шести
теперь третий c равен нулю
установлен
так есть ли какой-либо элемент в нулевом наборе
нет так что такое кардинальность или что такое
номер карты c
такой c это 0, потому что есть
нет элементов в множестве c
теперь d d равно множеству, имеющему
элементы 3
2 2 1 3 1 2
поэтому на самом деле d можно записать как
3 2 и 1 потому что все
остальные элементы такие же, как и у трех
два и один
так сколько всего элементов
три элемента прямо так кардинал
номер множества d
три, как насчет
пятый e представляет собой набор натуральных
числа от 15
а 20 это натуральные числа
между 15 и 20 16
17 18 и 90.
так что такое n из e, сколько элементов
там
четыре, поэтому кардинальное число множества e равно
четыре переходят к последнему набору f
это набор целых чисел от 8 до
14, так что вы можете определить набор
ф с 8
до 14 означает 8
9 10 11
12 13 и 40.
так каково кардинальное число множества f
сколько элементов
один два три четыре пять шесть семь
элементы есть
поэтому кардинальное число смещения f равно
7 хорошо, так что кардинальное число это
количество элементов
в каждом из этих наборов, и я надеюсь, что вы
понял решение
если у вас есть какие-либо сомнения, прокомментируйте ниже и
подпишитесь на этот канал, чтобы получать
регулярные обновления
спасибо» ..
..
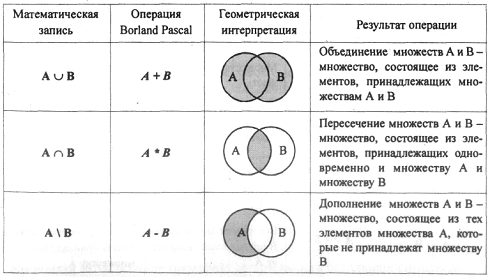 Но в мире математики полно возможностей и открытых дверей. Итак, что происходит, когда элементы для классификации не являются ни исчисляемыми, ни неисчисляемыми?
Но в мире математики полно возможностей и открытых дверей. Итак, что происходит, когда элементы для классификации не являются ни исчисляемыми, ни неисчисляемыми? Стандартная классификация, которая помогает нам решать такие проблемы, состоит в том, чтобы классифицировать их по пустым множествам.
Стандартная классификация, которая помогает нам решать такие проблемы, состоит в том, чтобы классифицировать их по пустым множествам.
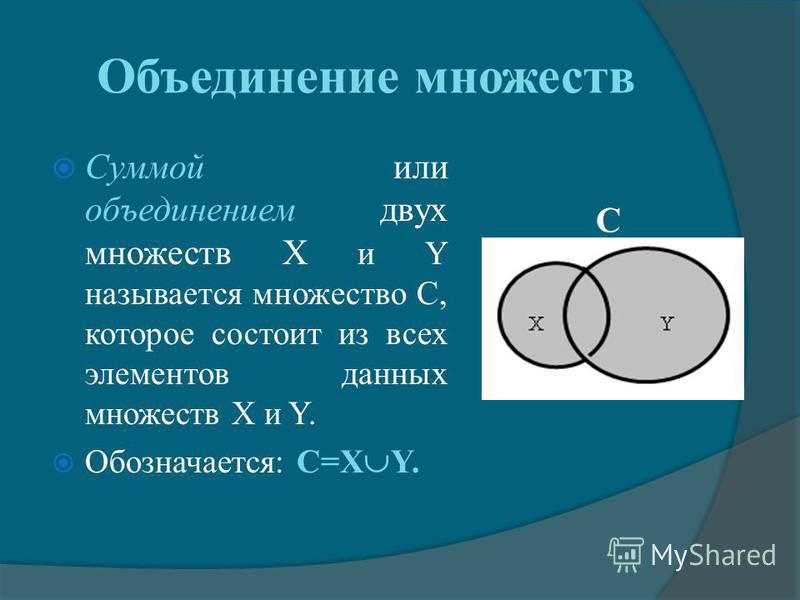
 Таким образом, данное множество является пустым множеством и может быть записано как:
Таким образом, данное множество является пустым множеством и может быть записано как:
 Эти диаграммы также используются для изображения отношений объединения и пересечения между двумя множествами.
Эти диаграммы также используются для изображения отношений объединения и пересечения между двумя множествами.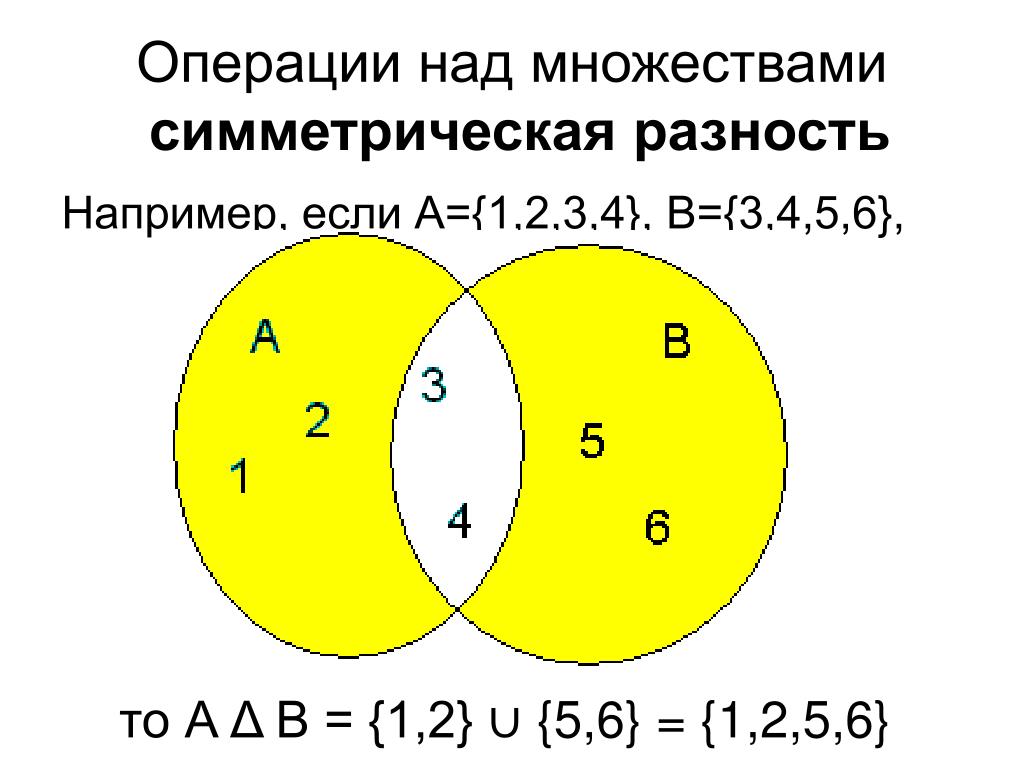


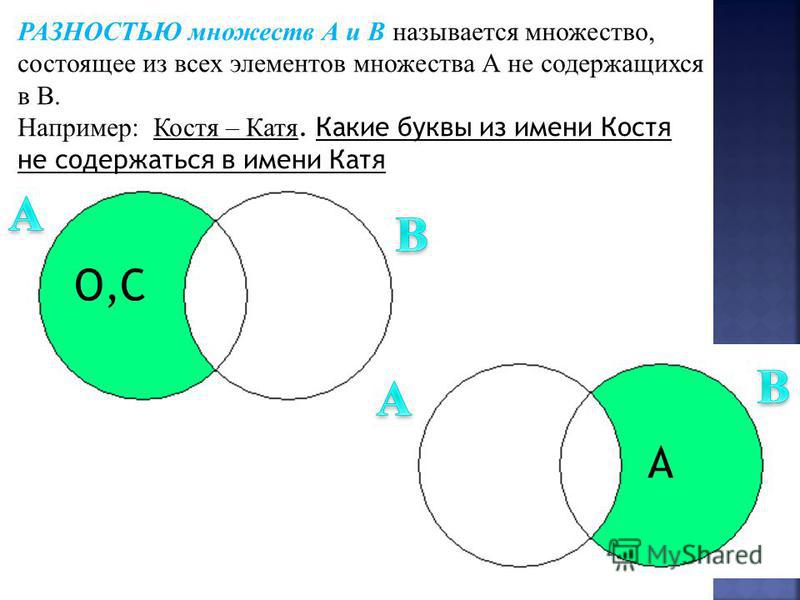

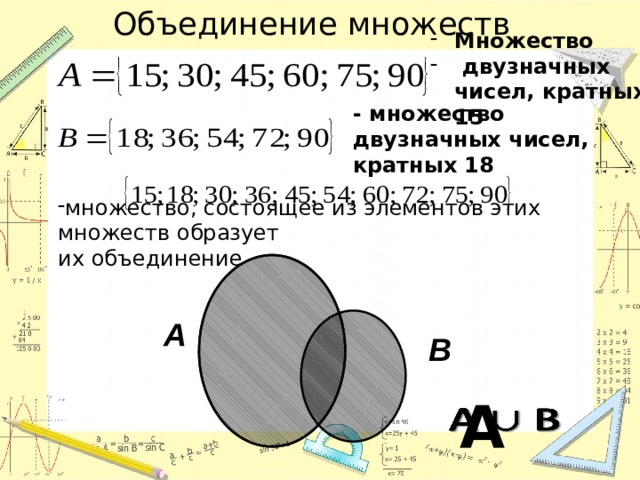 Декартово произведение любого набора с пустым набором всегда будет пустым, потому что пустой набор не содержит элементов.
Декартово произведение любого набора с пустым набором всегда будет пустым, потому что пустой набор не содержит элементов.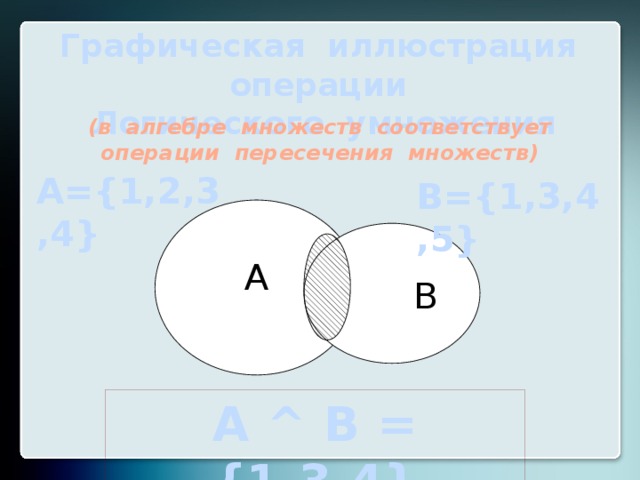
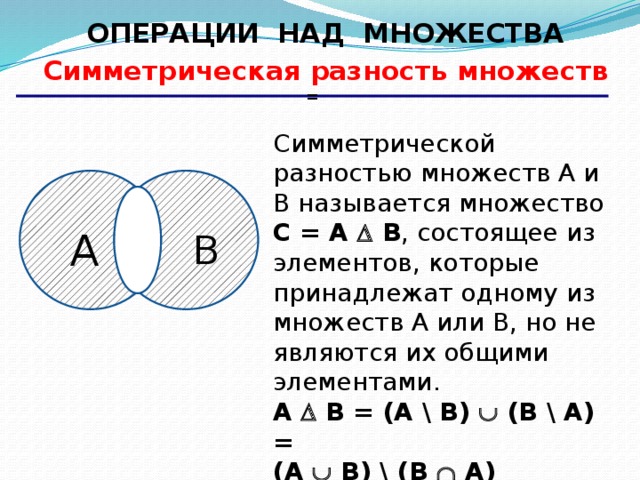


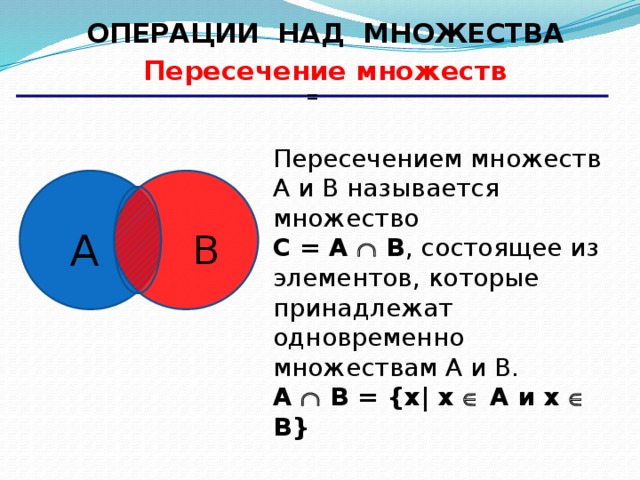
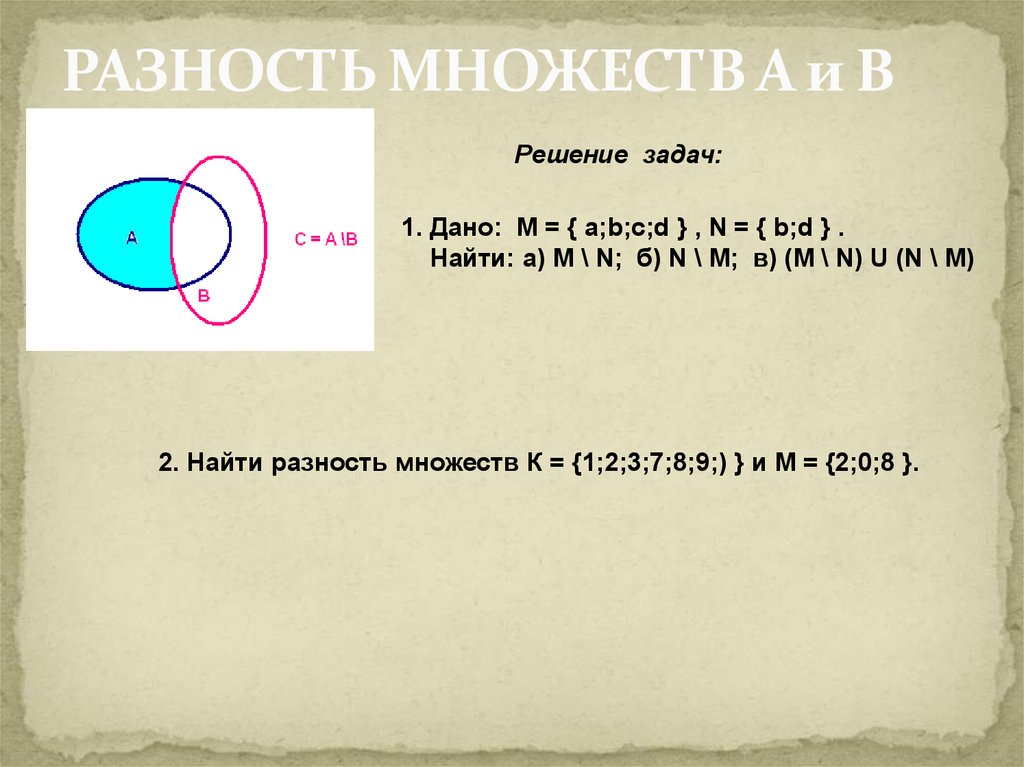
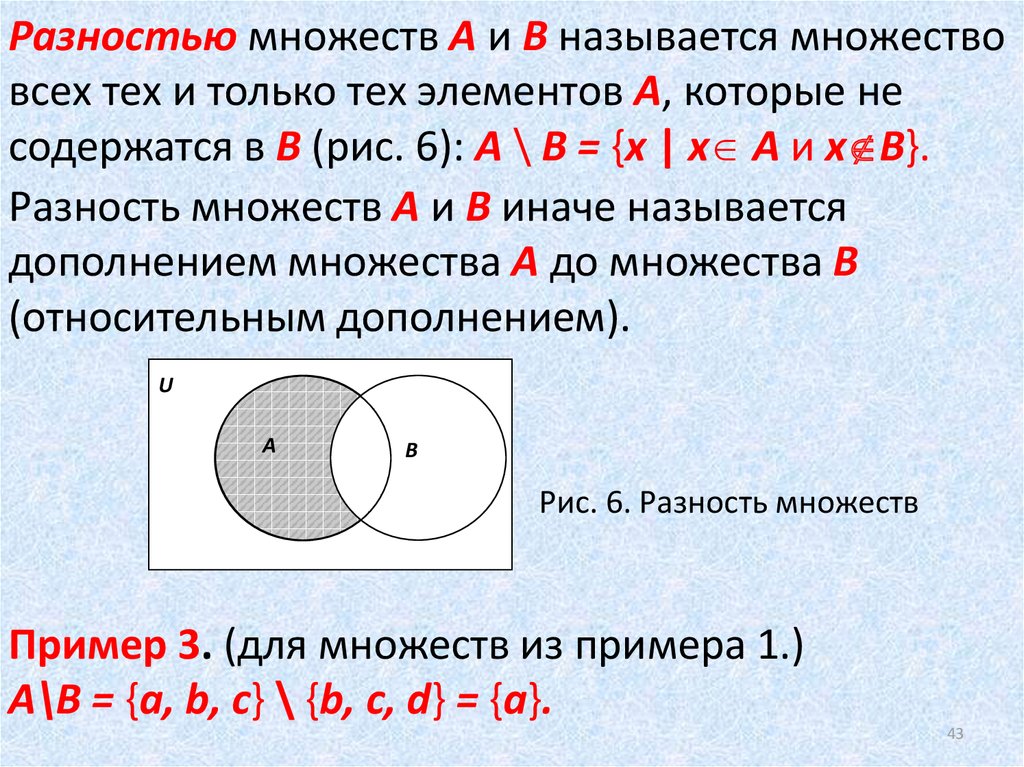 0038
0038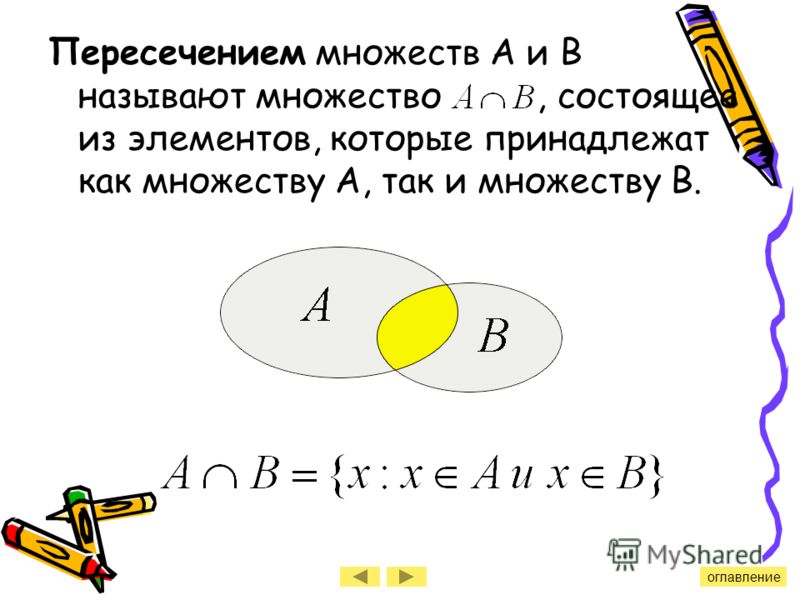

 Короче говоря, 25 (медиана) должно находиться на полпути между $X$ и 30.
Короче говоря, 25 (медиана) должно находиться на полпути между $X$ и 30.

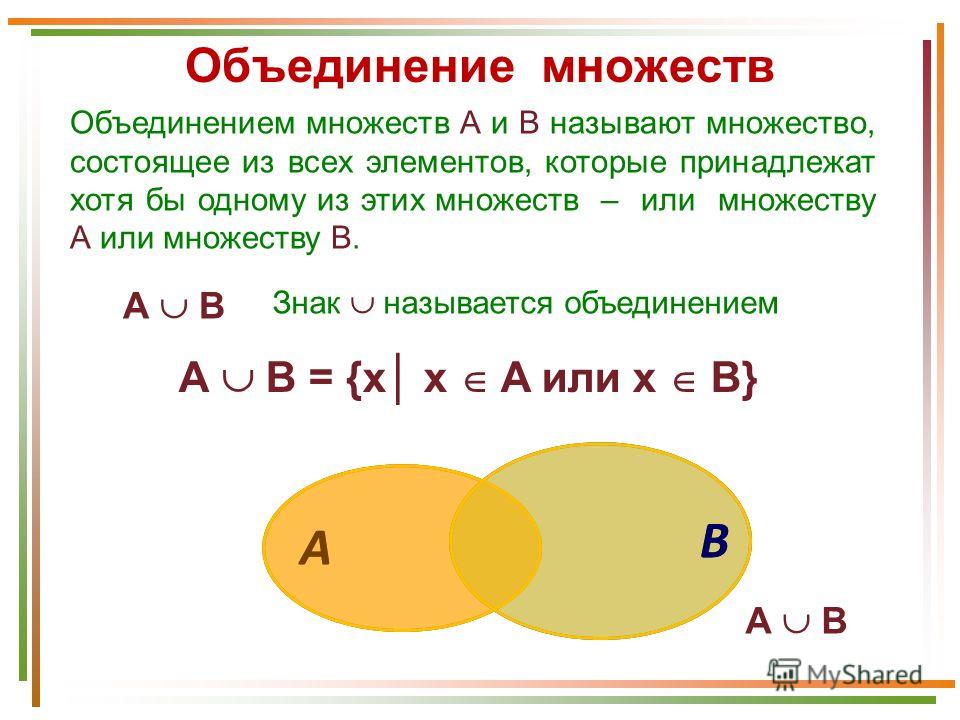

 Таким образом, стратегия «брать или не брать» строит псевдобинарное дерево вариантов, возвращая только листья для каждой комбинации, приводящей к набору мощности.
Таким образом, стратегия «брать или не брать» строит псевдобинарное дерево вариантов, возвращая только листья для каждой комбинации, приводящей к набору мощности. подмножество [длина] = S [поз]
allSubsets(pos+1, len+1, подмножество)
// Пропустить текущий элемент.
allSubsets(pos+1, длина, подмножество)
}
подмножество [длина] = S [поз]
allSubsets(pos+1, len+1, подмножество)
// Пропустить текущий элемент.
allSubsets(pos+1, длина, подмножество)
}  n − 1 (все n битов равны единице).
n − 1 (все n битов равны единице).
 Если диапазон — это мера того, где в наборе находятся начало и конец, межквартильный диапазон — это мера того, где находится основная часть значений. Вот почему он предпочтительнее многих других показателей распространения, когда сообщается о таких вещах, как успеваемость в школе или результаты SAT.
Если диапазон — это мера того, где в наборе находятся начало и конец, межквартильный диапазон — это мера того, где находится основная часть значений. Вот почему он предпочтительнее многих других показателей распространения, когда сообщается о таких вещах, как успеваемость в школе или результаты SAT.

 Например, в следующем наборе чисел: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 некоторые статистики разбили бы его на две половины, включая медиану (9) в обеих половинах:
Например, в следующем наборе чисел: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 некоторые статистики разбили бы его на две половины, включая медиану (9) в обеих половинах: 
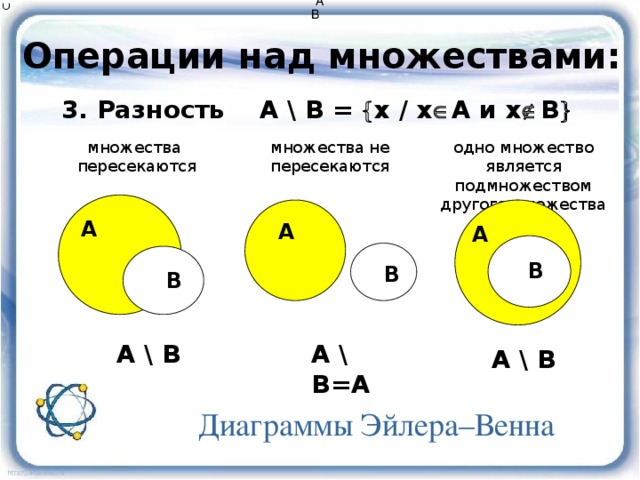
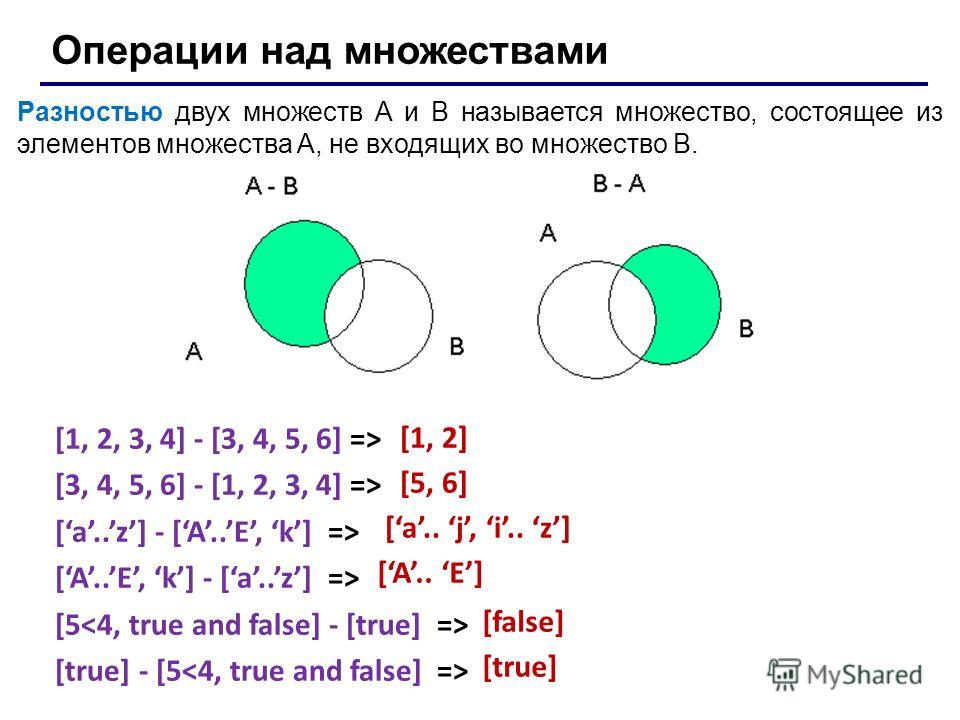 Вам нужно будет заменить A2: A10 фактическими значениями из вашего набора данных. Например, если вы ввели данные в поля от B2 до B50, получится уравнение =QUARTILE(B2:B50,1) . «1» в этой формуле Excel (A2:A10, 1 ) представляет первый квартиль (то есть точку, лежащую в 25% набора данных).
Вам нужно будет заменить A2: A10 фактическими значениями из вашего набора данных. Например, если вы ввели данные в поля от B2 до B50, получится уравнение =QUARTILE(B2:B50,1) . «1» в этой формуле Excel (A2:A10, 1 ) представляет первый квартиль (то есть точку, лежащую в 25% набора данных).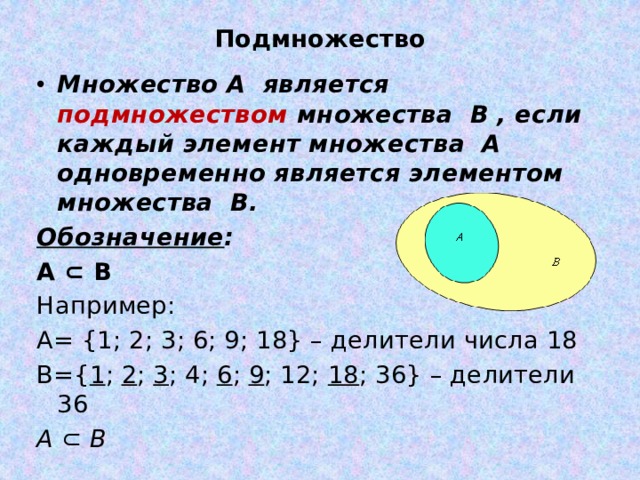 Однако, если вы нажмете на наиболее интуитивно понятный способ, который вы ожидаете найти («Описательная статистика»> «Частоты»), сюрпризом будет то, что он не будет отображать IQR (хотя он будет перечислять первый, второй и третий квартили). Вы могли бы пойти по этому маршруту, а затем вычесть третий квартиль из первого, чтобы получить IQR. Однако проще всего найти межквартильный размах в SPSS с помощью команды «Исследовать». Если вы уже ввели данные в свой рабочий лист, перейдите к шагу 3.
Однако, если вы нажмете на наиболее интуитивно понятный способ, который вы ожидаете найти («Описательная статистика»> «Частоты»), сюрпризом будет то, что он не будет отображать IQR (хотя он будет перечислять первый, второй и третий квартили). Вы могли бы пойти по этому маршруту, а затем вычесть третий квартиль из первого, чтобы получить IQR. Однако проще всего найти межквартильный размах в SPSS с помощью команды «Исследовать». Если вы уже ввели данные в свой рабочий лист, перейдите к шагу 3. См.: Как ввести данные в SPSS.
См.: Как ввести данные в SPSS. Введите новое имя переменной, а затем вернитесь к просмотру данных, нажав кнопку «Просмотр данных».
Введите новое имя переменной, а затем вернитесь к просмотру данных, нажав кнопку «Просмотр данных». 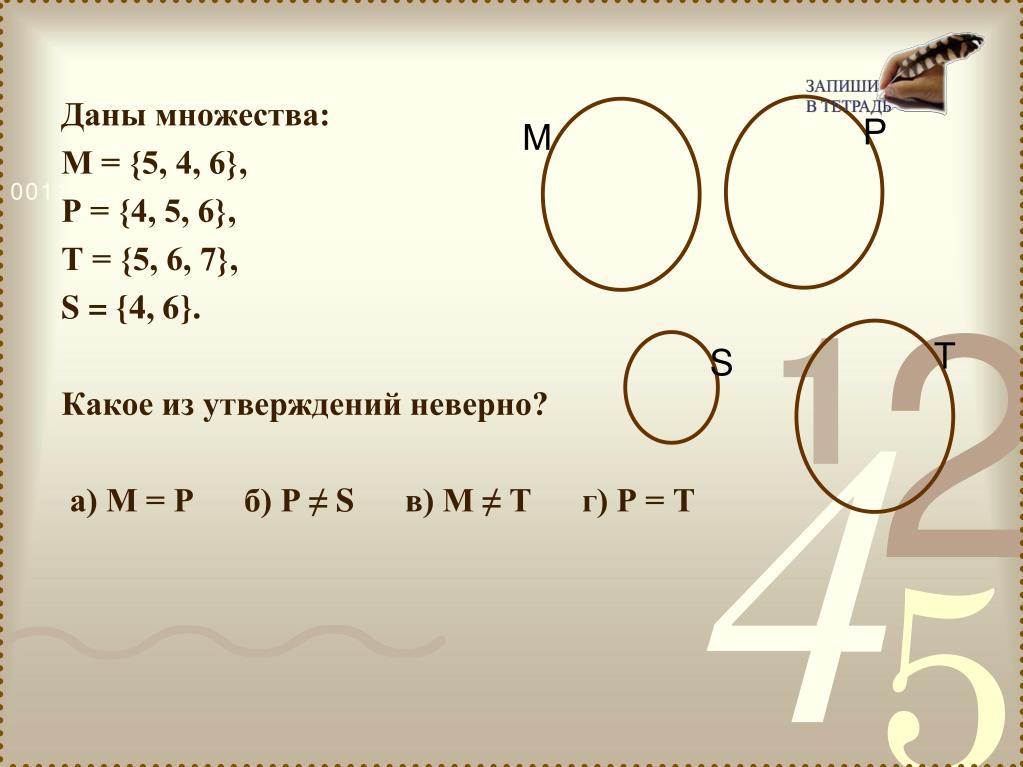 Квартиль — это термин, используемый для описания того, как разделить набор данных на четыре равные части (думаю, квартал ).
Квартиль — это термин, используемый для описания того, как разделить набор данных на четыре равные части (думаю, квартал ).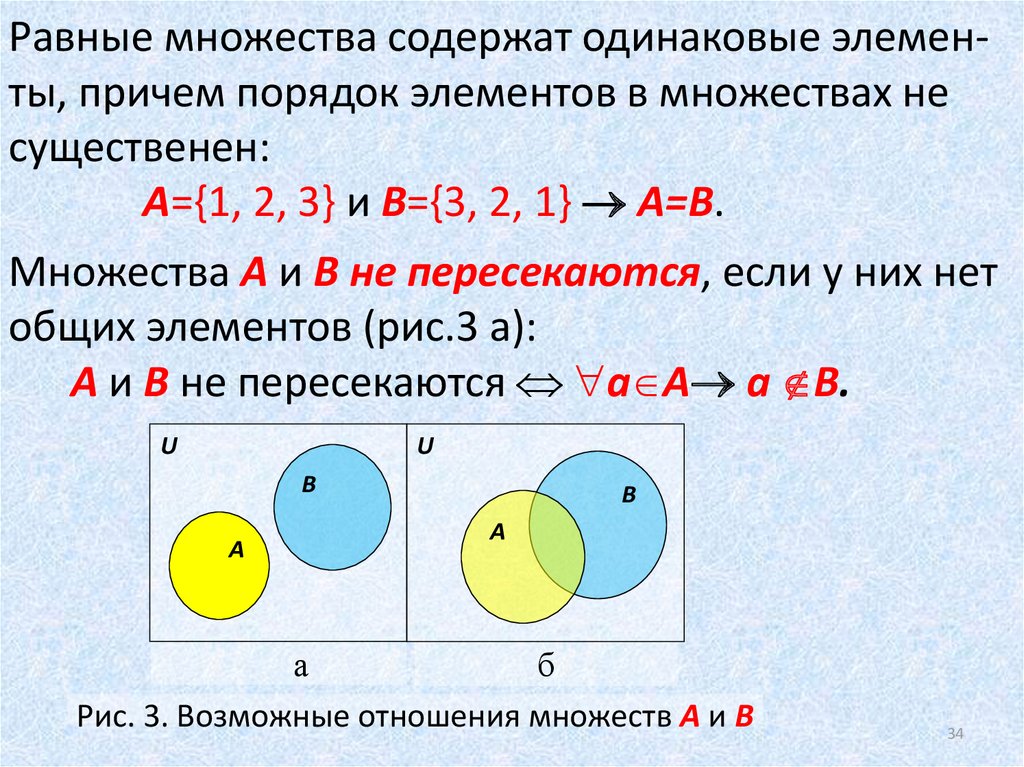 Большинство инструкторов разрешают использовать TI-83 на тестах, и это даже один из немногих калькуляторов, разрешенных на экзамене AP Statistics. Чтобы найти межквартильный диапазон TI 83, нужно всего лишь ввести список данных и нажать пару кнопок.
Большинство инструкторов разрешают использовать TI-83 на тестах, и это даже один из немногих калькуляторов, разрешенных на экзамене AP Statistics. Чтобы найти межквартильный диапазон TI 83, нужно всего лишь ввести список данных и нажать пару кнопок.