Найдем функцию, обратную к данной. Упр 132 параграф 6 Алгебра Алимов 10-11 класс – Рамблер/класс
Найдем функцию, обратную к данной. Упр 132 параграф 6 Алгебра Алимов 10-11 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Вот такое вот ДЗ( Подскажете решение?
Нужно найти функцию, обратную к данной:
2) у = -5х + 4;
5) у = х3 + 1;
6) у = х3- 3
ответы
Хм, я думаю ответ такой:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра.
9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос.
, шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Обратная функция — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.
Базовый уровень Сложные задачи
Обратная функция
Если каждому значению х из некоторого
множества действительных чисел поставлено в
f число у, то, говорят, что на этом множестве
определена функция.
y
y = f(x)
E( f )
0
х
D( f )
x
Если функция у = f ( х ) принимает каждое
своё значение у только при одном значении
х, то эту функцию называют обратимой.
у 2х 2
1
у 2
х
3
у х
у х
х1 у
2
х2 у
Пусть у = f(x) – обратимая функция. Тогда
каждому у из множества значений
функции соответствует одно
определённое число х из области её
определения, такое, что f(x) = y. Это
соответствие определяет функцию х от у,
которую обозначим х = g(y). Поменяем
местами х и у: у = g(x).
Функцию у = g(x) называют обратной к
функции у = f(x).
6. Чтобы найти функцию обратную данной нужно:
1. Область определения обратной функции f -1совпадает с множеством значений исходной f, а
множество значений обратной функции f -1
совпадает с областью определения исходной
функции f:
D(f -1) = E(f), E(f -1) = D(f).
у
у
2
у
1
х 2
у 2
0
2
х
0
1. D(у)=(-∞;2)∪(2;+∞)
1. D(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;0)∪(0;+∞)
2. Е(у)=(-∞;2)∪(2;+∞)
х
1
х
2. Монотонная функция является обратимой:
если функция f возрастает, то обратная к ней
функция f -1 также возрастает;
если функция f убывает, то обратная к ней функция
f -1 также убывает.
у
у=f(x)
y=x2,х<0
3
-2
0
у
у=g(x)
3
х
0
х
-2
у х
1. D(y)=(-∞;0]
1. D(y)=[0;+∞)
1. D(f)=R
1. D(g)=R
2. E(y)=[0;+∞)
2. E(y)=(-∞;0]
2. E(f)=R
2. E(g)=R
3. убывающая
3. убывающая
3. возрастающая 3. возрастающая
3. Если функция имеет обратную, то график
обратной функции симметричен графику данной
функции относительно прямой у = х.
у
(х0;у0)
у=х
у0
(у0;х0)
0
х0
х
12. Для функции, заданной табличным способом, укажите имеет ли она обратную или нет
1.
2.
x
1
2
5
7
x
2
1
0
y
3
4
7
3
y
9
3
1
3.
x
9
3
1
y
2
1
0
-1
-2
-1 -2
13. Установите соответствие между функцией f(x) и обратной к ней функцией g(x)
15. На каждом из заданных промежутках найдите, если это возможно обратную
уу
1
1
0
1
х
0
1
х
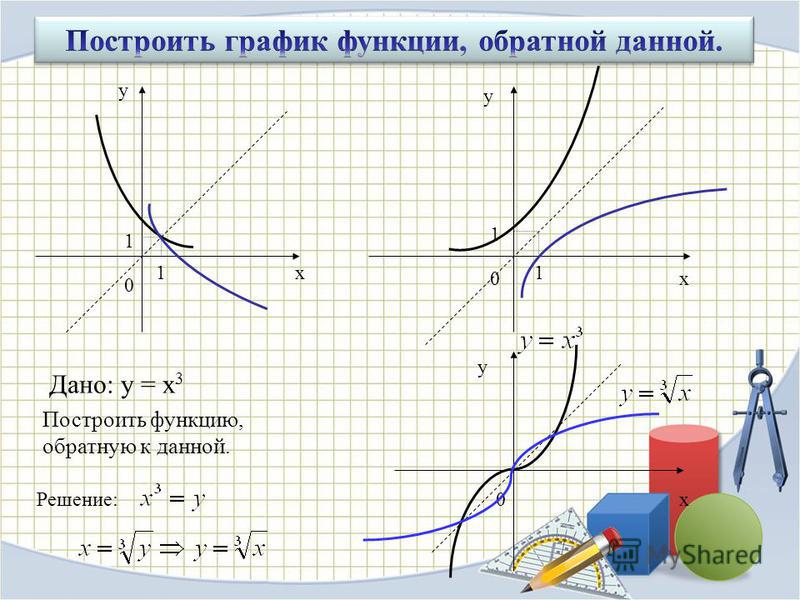
Построить график функции,
обратной данной
English Русский Правила
2,[2,бесконечность)Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Марк М. ответил 14.10.21
Репетитор
4.
9(918)
Математик на пенсии, проф. Очень большой опыт репетиторства по Precalculus.
Об этом репетиторе ›
Об этом репетиторе ›
f(x) = y = (x — 2) 2
Поменяйте местами x и y, чтобы получить x = (y — 2) 2
Найдите y: y — 2 = √x (технически a ± перед подкоренным, но так как x≥2 и мы поменяли местами x и y, то имеем y≥2. Значит, y — 2≥0. Поэтому знак минус перед подкоренным не имеет смысла.
Итак, y = f -1 (x) = √x + 2
Голосовать за 0 голос против
Подробнее
Отчет
Дэниел П. ответил 13.10.21
Репетитор
5 (6)
Степень бакалавра физики по 99-му процентилю на экзамене SAT
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Эмбер,
Итак, у нас есть
f(x) = (x — 2) 2
с доменом = [2,∞)
(x) в качестве входных данных и вернуть вам x в качестве выходных данных.
Если f(x) = (x — 2)
, то обратное выражение f(x) равно
f(f(x)) = x
Чтобы получить последнее выражение, мы просто имеем использовать некоторую алгебру, чтобы получить только x.
(x — 2) 2 = f(x)
x — 2 = √f(x)
x = √f(x) + 2
f(f(x)) = √f( x) + 2
, поэтому обратная функция y(x) будет равна
f(f(x)) = √f(x) + 2
Предположим, что x равно 3, тогда
f (3) = (3 — 2) 2
f(3) = 1
и обратная функция будет
f(f(3)) = √f(3) + 2
f( f(3)) = √1 + 2
f(f(3)) = 1 + 2
f(f(3)) = 3
Вы можете видеть, что в первой функции мы заменили x на 3 и получили 1 на выходе, а во второй функции мы заменили f(x) на 1 и получили обратно 3.
Домен — это все x (ввод) значения, определенные для функции. Обратная функция имеет x в качестве своего выхода, поэтому домен исходной функции становится диапазоном или всеми возможными выходными значениями обратной функции.
Область определения f(x) = [2,∞)
Область определения f(f(x)) = [2,∞)
Область определения f(f(x)) — это область определения f (x) поэтому сначала нам нужно выяснить минимальное и максимальное значения y, возможные для f(x)
Наименьшее значение x равно 2,
f(2) = (2 — 2) 2
f(2) = 0
, а наибольшее число равно бесконечности,
f(∞) = ( ∞ — 2) 2
f(∞) = ∞
Поскольку f(x) имеет область значений [0,∞), f(f(x)) имеет область определения [0,∞)
Поэтому обратная функция f(x) = (x — 2) 2 на области = [2,∞) равна
f(f(x)) = √f(x) + 2
на области [0,∞)
Дайте мне знать, помогло ли это или вам нужны дополнительные разъяснения!
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Обратная функция
Обратная функция — это способ «отменить» функцию. В исходной функции подстановка x возвращает y, но в обратной функции подстановка y (в качестве входных данных) возвращает x (в качестве выходных данных). Если бы функция содержала точку (3,5), ее обратная функция содержала бы точку (5,3).
Если исходной функцией является f(x), то ее обратная функция f -1 (x) не совпадает с .
Чтобы найти обратную функцию, вам нужно сделать противоположное тому, что исходная функция делает с x.
Пример
|
|
Не все функции имеют обратные. Функция должна быть функцией «один к одному», что означает, что каждое значение y имеет в паре уникальное значение x. По сути, одно и то же значение y нельзя использовать дважды. Тест горизонтальной линии может определить, является ли функция взаимно однозначной. Представьте, что вы нашли обратную функцию, которая не является взаимно однозначной. Подстановка значения y из исходной функции может вернуть более одного значения x.
Если функция не является взаимно однозначной, вам необходимо применить ограничения домена, чтобы часть используемой вами функции была взаимно однозначной.
Чтобы найти обратную функцию, выполните следующие действия:
1. В исходном уравнении замените f(x) на y:
на
исходное уравнение с y и каждый y в исходном уравнении с x
Примечание. Гораздо проще найти обратную функцию, имеющую только один член x. Для функций, которые имеют более одного члена x, вам нужно будет найти y, переместив все члены y в одну часть уравнения и выделив y.
Пример
3. Решение для Y:
(1)
(2)
(3)
(4)
(5)
4. Изменение y до F — 1 (x):
5. При необходимости примените ограничения домена.
Поскольку обратная функция вернет x при подстановке y, диапазон исходной функции будет областью ее обратной функции.
Точно так же область определения исходной функции будет областью значений ее обратной.
Если исходная функция не является взаимно однозначной, вам нужно будет ограничить ее домен так, чтобы она была взаимно однозначной, а затем просмотреть диапазон этой части функции.
В этом случае вы знаете, что диапазон исходной функции равен [-3, ∞). Следовательно, область определения обратной функции также будет [-3, ∞).
Посмотрим на график исходной функции и обратной:
|
Если вы заметили, обратная функция (красная) является отражением исходной функции (синяя) по линии y = x. Это верно для всех функций и их обратных.
Вы также можете проверить правильность обратной функции, потому что все функции f(x) и их обратные f -1 (x) будет соответствовать обоим следующим правилам:
(f ∘ f -1 )(x) = x
(f -1 ∘ f)(x) = x
Примечание: «∘» символ указывает составные функции.
По сути, композиция функций включает в себя применение одной функции к результатам другой. Обратитесь к странице составных функций для получения дополнительной информации или освежения знаний о составных функциях.
Причина, по которой приведенные выше правила верны, заключается в том, что функция и обратная ей функция являются отражением друг друга на прямой y = x. Возвращаясь к нашему примеру, мы можем проверить, получили ли мы правильную обратную функцию, используя эти правила.
Вспомним следующее:
и
Сравнивая (f ∘ f -1 )(x) и (f -1 ∘ f)(x), мы видим, что:
15
|
|
Поскольку результатом в обоих случаях является x, это подтверждает, что мы нашли правильное обратное.