Найдите площадь фигуры ограниченной линиями y x 2 y 4: Найти площадь фигуры , ограниченной линиями y = x^2 + 4x ; y = x+4 — Спрашивалка

Определенный интеграл

ВАРИАНТ 1

1. Вычислить площадь фигуры, ограниченной линиями

.

2. Найти длину участка кривой y=arccos e^x, xє[-ln5;-ln2].

3. Найти массу участка кривой, если плотность ,

L: x=tcost; y=tsint; z=t²/2, tє[0;2].

4. Найти массу плоской пластинки, ограниченной линиями

y=4-x², у=0, если плотность p=х²+у.

5. Найти площадь плоской области, ограниченной линиями

r=1+cosφ (кардиоида), (спираль Архимеда), .

11. Найти I_у плоской области, ограниченной линиями

у=х, у=4х-х², если плотность p=4.

Определенный интеграл

ВАРИАНТ 2

1. Вычислить площадь фигуры, ограниченной линиями

ху=12, у=0, х=1, х=е².

2. Найти длину участка кривой x=cost, у=1+sint, z=π/2-t, tє[-π/2; π/2].

3. Найти массу участка кривой, , если плотность

.

4. Найти массу плоской пластинки, ограниченной линиями

y=9-x

2, у=0, если плотность p=2у+х².

5. Найти площадь плоской области, ограниченной линиями

r=2-cosφ, r=cosφ, .

11. Найти М_х плоской области, ограниченной линиями

, у=0, если плотность p=2.

Определенный интеграл

ВАРИАНТ 3

1. Вычислить площадь фигуры, ограниченной линией у²=х²(4-х²).

2. Найти длину участка кривой .

3. Найти массу участка кривой , если плотность .

4. Найти массу плоской пластинки, ограниченной линиями

y=x², 2x+у=3, если плотность p=х²+y.

5. Найти площадь плоской области, ограниченной линиями

r=2sin2φ (1 лепесток), r=1 (r≥1).

11. Найти М_х плоской области, ограниченной линиями,

, если плотность p=3.

Определенный интеграл

ВАРИАНТ 4

1. Вычислить площадь фигуры, ограниченной линиями

у=e^—xsin(x) (первая арка), у=0.

2. Найти длину участка кривой .

3. Найти массу участка кривой

, если плотность .

4. Найти массу плоской пластинки, ограниченной линиями

y=x, x+у=6, y=0, если плотность p=2у+х.

5. Найти площадь плоской области, ограниченной линиями

r=1-соsφ, r=2.

11. Найти I_у участка кривой , если плотность .

Определенный интеграл

ВАРИАНТ 5

1. Вычислить площадь фигуры, ограниченной линиями

.

2. Найти длину участка кривой .

3. Найти массу участка кривой ,

если плотность .

4. Найти массу плоской пластинки, ограниченной линиями

, если плотность .

5. Найти площадь плоской области, ограниченной линиями

.

11. Найти М_х плоской области, ограниченной линиями

, если плотность .

Определенный интеграл

ВАРИАНТ 6

1. Вычислить площадь фигуры, ограниченной линиями

.

2. Найти длину участка кривой .

3. Найти массу участка кривой L, если плотность ,

.

4. Найти массу плоской пластинки, ограниченной линиями

, если плотность .

5. Найти площадь плоской области, ограниченной линиями

(гиперболическая спираль), .

11. Найти М_у плоской области, ограниченной линиями

, если плотность .

AREAS OF BOUNDED REGIONS 21.53 45. Using integration find the area of ​​the..

Home

CBSE

Class 12

Mathematics

Calculus

1. 12 sq. units
2. 4 sq. units
3. 61​ кв. единиц
4. 328​ кв. единиц
5. (π−2)4ab​ кв. единиц 6,4 кв. единиц

Просмотрено: 5,856 студентов

Обновлено: 19 ноября 2022 г. 4 студентов спросили тот же вопрос на Filo

Учитесь на их личных беседах с преподавателями Filo.

26 мин

Загружено на: 19.11.2022

, преподававшегося

Мгновенно подключить с этим репетитором

Connect Now

Всего классов на FILO с этим репетитором — 26876

115

Ар.

Загружено: 18.11.2022

Преподавал

Мгновенно подключитесь к этому репетитору

Подключиться сейчас

85

Поделиться

4 мин

Загружено по телефону: 18.11.2022

, преподававшегося

Connect с мгновенным подключением с этим репетитором

Connect Now

148

Share

5 мин

Загружено на: 11/18/2022

. Преподает

Мгновенно подключитесь к этому репетитору

Подключиться сейчас

129

Поделиться

Практикуйте больше вопросов по исчислению

Вопрос 1

Средний 90:55 Просмотров 90:550003 ∫x2+2x−35x+31​dx равно

1. log(x+7x−5​)2+C
   
2. log(x−5x+7​)2+C
   
3. log(x+7 )3(x−5)2​+C
   
4. log(x+7)2(x−5)3​+C

Тема:

Интегралы

Книга:

IIT-JEE Super Course in Математика — исчисление (Пирсон)

Посмотреть решение

Вопрос 2

Простой

Просмотров: 5640

f(x)=∣x−3∣ … при x=3

1. 0014
2. Непрерывная и дифференцируемая
3. Прерывание и не дифференцируемое
4. Непрерывный и дифференцируемый

Тема:

Непрерывность и дифференцируемость

Просмотр раствора

Вопрос 3

Средний

9003

Вопрос 3

. =I, где B — невырожденная матрица 3×3, такая что ∣B∣=1, тогда det(B−1) равно

1. 0
2. 1
3. 2
4. Ничего из этого

Тема:

Матрицы

Просмотр 2 решений

Вопрос 4

Средний

Просмотров: 5,568

Квадратная неособая матрица A удовлетворяет A2−A01=0,9 A01=0 I−A

2(I−A)​

I+A

2(I+A)​

Тема:

Матрицы

Книга:

)

Посмотреть решение

Посмотреть больше

Студенты, которые задают этот вопрос, также задавали

Вопрос 1

Просмотров: 5 351

10) xy=1, затем y2+dxdy​. i1) Производная функции x+x​​ равна.

. दूसरे शब्दों ब्यूह A तथा आव्यूह −B का योगफल। 7 यदि A=[12​23​31​] तथा B=[3−1​−10​32​] हैं तो 2 A \[ \begin{выровнено} 2 AB= & 2\влево[\begin{массив}{lll} 1 и 2 и 3 \\ 2 и 3 и 1 \end{массив}\right]-\left[\begin{массив}{c} 3\\ -1 \конец{массив}\право.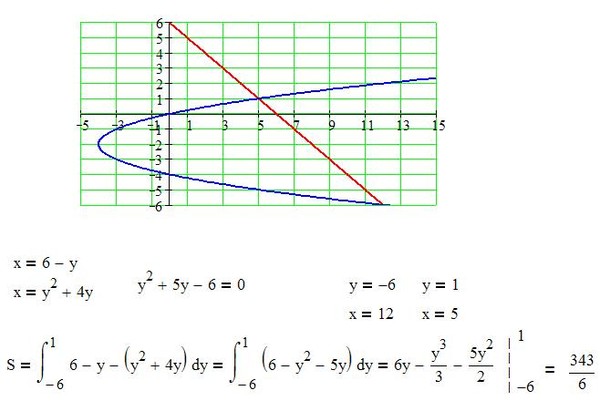

\\ & {\ влево [\ начать {массив} {lll} 2 и 4 и 6 \end{массив}\right]+\left[\begin{массив}{c} -3\ 1 \конец{массив}\справа.} \end{выровнено} \]

Тема:

Calculus

Просмотр решения

Вопрос 3

Просмотры: 5,266

1. सिद्ध कीजिए कि F (x) = x1 द्वा प पाषित फलन f: r. → Р. एकैकी तथा आच्छादक है, जहाँ r, सभी ऋणेतшить वास्तविक सख्याओं का समुच्चय है है।।। है।। है है है यदि प Вивра R. को n से बदल दिया जाए, जबकि सहपшить पू पू पू000 R. ही हे तो भी क क्या यह परिणाम सत्य होगा? 2. निम्नलिखित फलनों की एकैक (инъектив) तथा आच्छादी (Surjective). (i) f(x)=x2 द्वारा प्रदत्त f:N→N फलन है। (iii) f(x)=x2 द्वारा प्रदत्त f:R→R फलन है। (ii) f(x)=x2 द्वारा प्रदत्त f:Z→Z फलन है। (v) f(x)=x3 द्वारा प्रदत्त f:Z→Z फलन है। (iv) f(x)=x3 द्वारा प्रदत्त f:N→N फलन है। 3. सिद्ध कीजिए कि f (x) = [x] द्वारा प्रदत्त महत्तम पू000

Тема:

Исчисление

Посмотреть решение

Вопрос 4

Просмотров: 5 133

14. Периметр треугольника равен 8 см. Если одна из сторон треугольника равна 3 см, каковы будут две другие стороны максимальной площади треугольника? 15. Окно в форме прямоугольника, увенчанного полукруглым проемом. Общий периметр окна 10 метров. Найдите размеры окна, чтобы через него проходило максимальное количество света. [CBSE 2000, ’02, ’06] 16. Из квадратного куска жести со стороной 12 см нужно сделать коробку без крышки, вырезав квадрат из каждого угла и загнув клапаны, чтобы получились стенки. Какую сторону квадрата нужно отрезать, чтобы объем ящика был максимальным? Кроме того, найдите этот максимальный объем. 17. Из заданного картона площадью c2 (квадратных) единиц сделать открытую коробку с квадратным основанием. Покажите, что максимальный объем коробки равен 63​c3​ [CBSE 2001] (кубические) единицы. что сведет к минимуму стоимость металла для изготовления банки. 19. Покажите, что правильный круговой конус с наименьшей кривизной поверхности и данным объемом [CBSE 2007] имеет высоту, равную удвоенному радиусу основания.

Тема:

Calculus

Просмотр решения

Просмотр Подробнее

Текст вопроса	Области граничных областей 21.53 45. Использование интеграции. ​, x2+y2−4x=0 и ось x. [CBSE 2016] УРОВЕНЬ-2 46. Найдите площадь, ограниченную кривыми y=∣x−1∣ и y=−∣x−1∣+1. 47. Найдите площадь, ограниченную кривыми 3×2+5y=32 и y=∣x−2∣. 48. Найдите площадь, ограниченную параболами y=4x−x2 и y=x2−x. 49. В каком отношении ось x делит площадь области, ограниченной параболами y=4x−x2 и y=x2−x? 50. Найдите площадь фигуры, ограниченной кривыми y=∣x−1∣ и y=3−∣x∣. 51. Если площадь, ограниченная параболой y2=4ax и линией y=mx, равна 12a2​ кв. ед., то с помощью интегрирования найдите значение m. 52. Если площадь, ограниченная параболами y2=16ax и x2=16ay,a> 0, равна 31024 квадратных единиц, найдите значение a. ОТВЕТЫ
Обновлено	19 ноября 2022 г.
Topic	Calculus
Subject	Mathematics
Class	Class 12
Answer Type	Video solution: 4
Upvotes	477
Avg . No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт