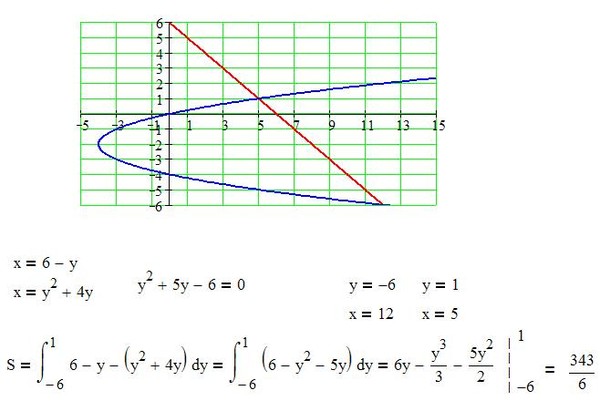
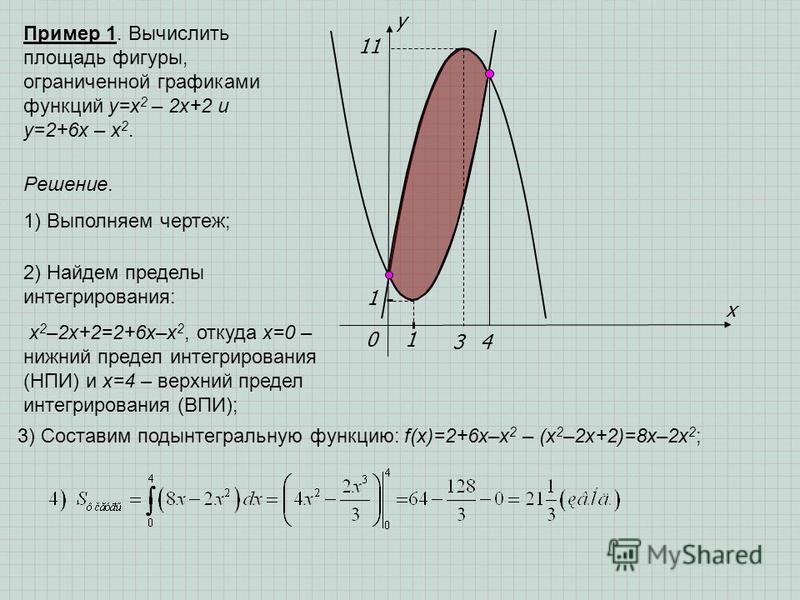
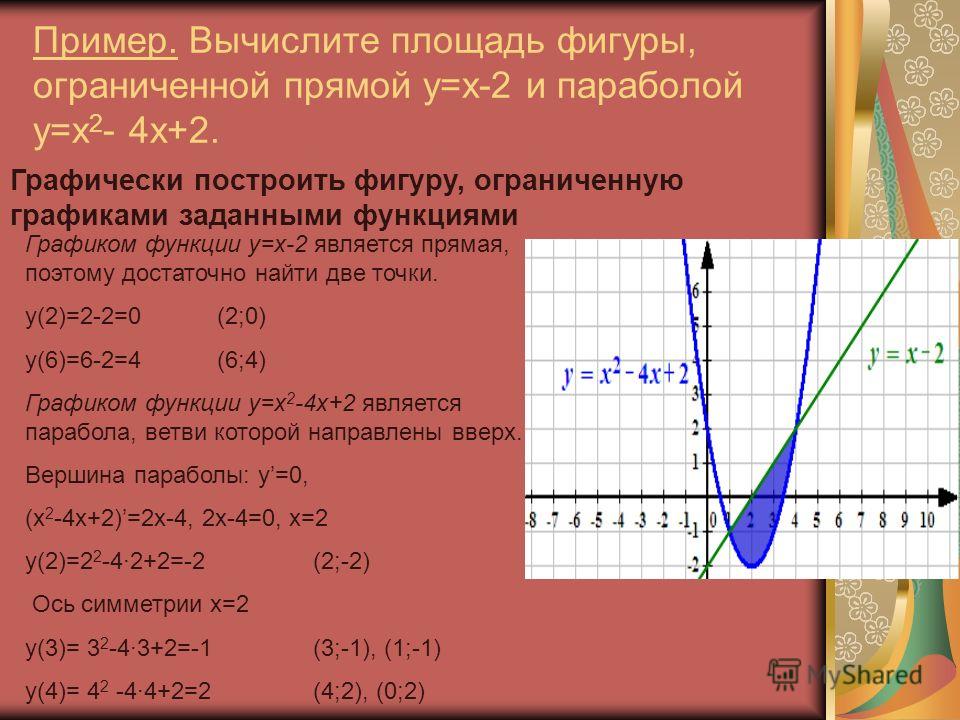
Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
В лесу на разных кустах висят 100 шнурков. Сова утверж-дает, что в среднем три шнурка из четырёх, которые мож-но найти в лесу, ей не подходят,
В клетки таблицы 4×4 вписаны числа (возможно, нецелые) так, что для любой клетки сумма чисел в клетках, соседних с ней по стороне, равна 23. Чему
Пользуйтесь нашим приложением
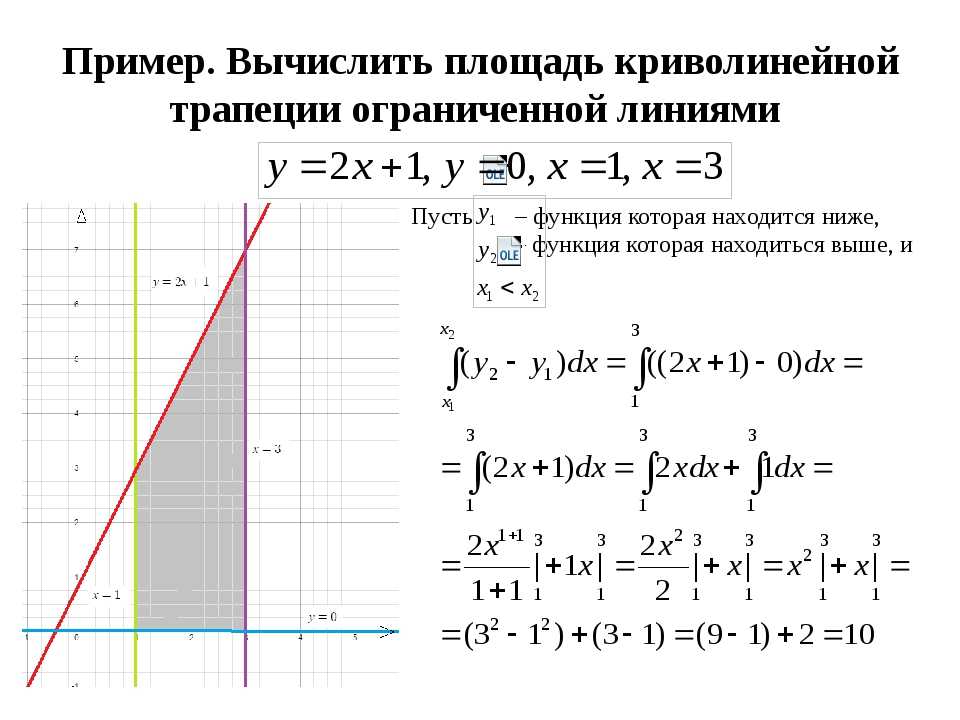
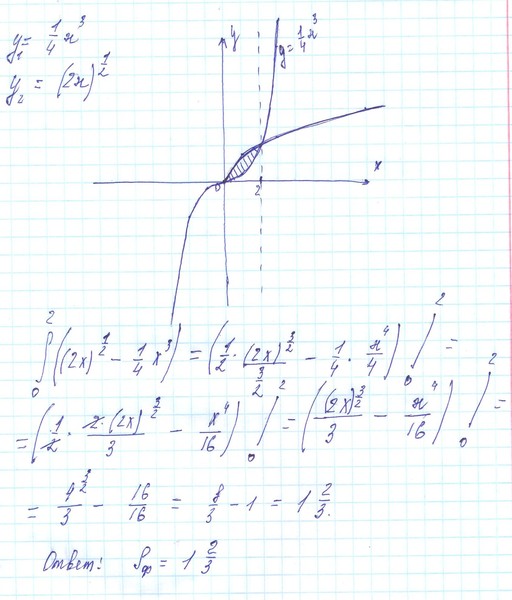
Найдите площадь фигуры, ограниченной графиком функции » задачи
интеграл »
Найдите площадь фигуры, ограниченной линиями: \( y=\frac{16}{x^2}, \\ y=2x, \\ x=4.
 4_0= \\ = \frac{64}{3} -32+20=9 \frac{1}{3} $$
4_0= \\ = \frac{64}{3} -32+20=9 \frac{1}{3} $$В прямоугольник со сторонами 16см и 18см вписывается ромб, вершины которого являются серединами сторон прямоугольника. В полученный ромб аналогичным образом вписывается прямоугольник, а в него снова ромб и так далее. Докажите, что площади полученных фигур образуют геометрическую прогрессию. Найдите знаменатель этой прогрессии
Решение: S₁(данного прямоугольника)=a·b=18·16;
S₂(ромба вписанного в данный прямоугольник)=(1/2)·D₁·D₂=(1/2)·16·18;
S₃=(a/2)(b/2)=(18·16)/4;
S₄=(1/2)·d₁·d₂=(1/2)·(16/2)·(18/2)=(16·18)/8;
q=S₄:S₃=S₃:S₂=S₂:S₁=1/2.
О т в е т. q=1/2.Найдите площадь фигуры, ограниченной линией
модуль их Х + модуль из У=6
Решение: |x|+|y|=6, график так заданной функции будет квадрат с вершинами (6;0)(0;6)(-6;0)(0;-6), что легко установить построив графики данной функции во всех 4 четвертях (квадрантах)
а площадь такого квадрата можно найти из того, что диагональ равна 12
, ну например из теоремы Пифагора следует, что квадрат диагонали квадрата равен удвоенному квадрату стороны, а значит удвоенный квадрат стороны(площадь) равна половине квадрата диагонали
площадь равна 12*12/2=12*6=72
Ответ:72 квадратных единицыВычислите площадь фигуры, ограниченной линиями: а) y=4x-x^2; e=4-x; б) y=x^2, y=2x; в) y=x^2-4x+4, y=4-x^2; г) y=x^2 -2x+2, y=2+6x-x^2;
Решение: 1) пределы интегрирования:
$$ 4x-x^{2}=4-x \\ 4x-x^{2}-4+x=0 \\ x^{2}-5x+4=0, D=25-16=9>0 \\ x_{1}= \frac{5-3}{2}=1 \\ x_{2}= \frac{5+3}{2}=4 \\ S= \int\limits^4_1 {(4x-x^{2}-4+x)} \\, dx= \int\limits^4_1 {(5x-x^{2}-4)} \\, dx= \frac{5x^{2}}{2}-\frac{x^{3}}{3}-4x=\frac{5*4^{2}}{2}-\frac{4^{3}}{3}-4*4-(\frac{5}{2}-\frac{1}{3}-4)=\\=40-\frac{64}{3}-16-\frac{5}{2}+\frac{1}{3}+4=28-\frac{63}{3}-\frac{5}{2}=\\=28-\frac{63*2+15}{6}=28-23. \frac{\pi}{2}_{-\frac{\pi}{2}} {cosx} \, dx = sin\frac{\pi}{2}-sin(-\frac{\pi}{2}))=1-(-1)=2 $$ в)
\frac{\pi}{2}_{-\frac{\pi}{2}} {cosx} \, dx = sin\frac{\pi}{2}-sin(-\frac{\pi}{2}))=1-(-1)=2 $$ в)
1 2 3 > >>
математика — Стр 4
3.Вычисление площадей плоских фигур в декартовой системе координат
Исходя из геометрического смысла определенного интеграла площадь криволинейной трапеции, расположенной выше оси абсцисс ( f ( x ) ≥ 0 ), равна соответствующему оп-
ределенному интегралу:
b
S = ∫ f ( x )dx .
a
В общем случае, площадь фигуры, ограниченной кривыми y = f1( x ) и y = f2 ( x ) , прямыми x = a и x = b , при
| b |
условии, что | f2 ( x ) ≥ f1( x ) , равна S = ∫(f2 ( x ) − f1( x ))dx . |
| a |
Пример |
|
Найти | площадь фигуры, ограниченной линиями |
y = −x2 , y = x − 2 . | |
Решение
Изобразим кривые на чертеже. Решив систему
| y = −x2 |
|
|
| |||||
| y = x − 2 , | получаем координаты двух точек пересе- | |||||||
чения (1; -1) и (-2; -4). Искомая площадь S криволинейно- | |||||||||
го треугольника | можно представить как разность площадей | ||||||||
(рис.3). |
|
|
|
|
|
| |||
1 |
|
|
|
| 1 | ||||
S = ∫( −x2 −( x − 2 ))dx = = ∫(−x2 − x + 2)dx = | |||||||||
| −2 |
|
|
|
|
| −2 | ||
= (− | x3 |
| − | x2 | + 2x) |
| 1−2 = 9 = 4,5 . | ||
|
| ||||||||
|
| ||||||||
3 |
| 2 |
|
|
| 2 | |||
|
|
|
|
|
| 31 | |||
Рис. 3
4.Вычисление площадей плоских фигур в полярной системе координат
Фигура, ограниченная графиком функции (рис.4) r = r(ϕ ) и двумя лучами ϕ = α и ϕ = β , называется криво-
линейным сектором. Его площадь вычисляется по формуле
S = 1 ∫β r2 (ϕ )dϕ . 2 α
32
r(ϕ)
ϕ=β
ϕ=α
Рис.4
Если плоская фигура имеет более сложную форму, то необходимо разбить ее лучами, выходящими из полюса на криволинейные сектора, к которым применять либо полученную формулу, либо формулу для сектора, ограниченного
двумя непрерывными линиями r = r1 ( ϕ) и r = r2 ( ϕ)
(рис. 5).
5).
ϕ=β r1(ϕ)
r2(ϕ) ϕ=α
Рис.5
33
S = 1 ∫β ( r12 (ϕ ) − r2 2 (ϕ ))dϕ . 2 α
Пример
Найти площадь кривой, ограниченной кривой r = 2 cos 3ϕ (рис. 6).
π
6
Рис.6
Решение
Так как площади всех лепестков «трехлепестковой розы» равны, а каждый лепесток симметричен относительно своей оси, то найдем площадь половины одного лепестка и умножим ее на 6, получим площадь искомой фигуры:
|
|
| π | π |
|
S1 | = | 1 | ∫6 | ( 2 cos 3ϕ )2 dϕ = 2∫6 | 1 + cos 6ϕ dϕ = |
|
| 2 | 0 | 0 | 2 |
34
ππ
= (ϕ | 6 | + | sin 6ϕ 6 | ) = ( | π | + 0) | = | π | . | ||
0 | 6 | 0 | 6 | 6 | |||||||
|
|
|
|
|
| ||||||
Тогда площадь всей фигуры равна
S= 6S1 = 6 π6 = π .
5.Вычисление длины дуги плоской кривой
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой y = f ( x ) , где a ≤ x ≤ b .
Если функция | f ( x ) и ее производная непрерывны на | |||||
отрезке [a;b], то кривая АВ имеет длину, равную | ||||||
b |
|
|
|
|
|
|
l = ∫ |
| ′ |
| 2 | dx . |
|
1 +( f ( x )) |
|
| ||||
a |
|
|
|
|
| |
Если линия задана уравнением x = ϕ( y ), | c ≤ y ≤ d , то | |||||
ее длина вычисляется по формуле |
| |||||
d |
|
|
|
|
|
|
l = ∫ |
| ′ |
| 2 | dy . |
|
1 +( ϕ( y )) |
|
| ||||
c |
|
|
|
|
|
|
Если уравнение кривой АВ задано в параметрической | ||||||
x = x( t ) | , α ≤ t ≤ β , причем x( t ), y( t ) | – непрерыв- | ||||
форме | = y( t ) | |||||
y |
|
|
|
|
| |
ные функции с непрерывными производными и a = x(α ) , b = x( β) , то длина кривой АВ находится по формуле
β |
|
|
|
|
|
l = ∫ | ′ | 2 | ′ | 2 | dt . |
( x ( t )) |
| +( y ( t )) |
|
α
35
Примеры
1) Найти длину дуги кривой y = ln( 2x ) на промежутке
3 ≤ x ≤ 8 .
Решение
y′ = |
| 2 |
| = | 1 |
| + | ( y′) | 2 | =1 + | 1 | = | 1 | + x2 |
| ||||||||||||||||||||
|
| x | , 1 |
|
|
|
|
|
|
|
|
|
| и |
| ||||||||||||||||||||
2x |
| x2 |
|
| x2 |
| tdt | ||||||||||||||||||||||||||||
l = ∫ | 1 | + x2 dx | = t = |
| 1 + x | 2 | ; x | = |
|
| t | 2 | −1; dx = | ||||||||||||||||||||||
|
|
|
|
|
|
| t2 −1 = | ||||||||||||||||||||||||||||
| 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 3 |
|
|
|
| x |
|
|
|
| x = 3 t = 2; x = 8 t = 3 |
| |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
3 | t | 2 | dt |
|
|
| 3 |
|
|
|
| 1 |
|
|
|
| 3 + | 1 ln |
|
| t −1 |
|
|
|
| 3 = 1 + | 1 ln 3 . | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
= ∫ |
|
|
| = | ∫( 1 | + |
|
|
|
| )dt = t |
|
|
|
|
|
| ||||||||||||||||||
2 |
|
|
|
|
|
|
| 2 |
|
|
| ||||||||||||||||||||||||
2 | t |
| −1 |
| 2 |
|
| t |
| −1 |
|
|
| 2 |
| 2 |
| t +1 |
|
|
| 2 | 2 2 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||
2) | Найти длину дуги кривой x = 2 cos3 t, y = 2 sin3 t | ||||||||||||||||||||||||||||||||||
при 0 ≤ t ≤ π4 .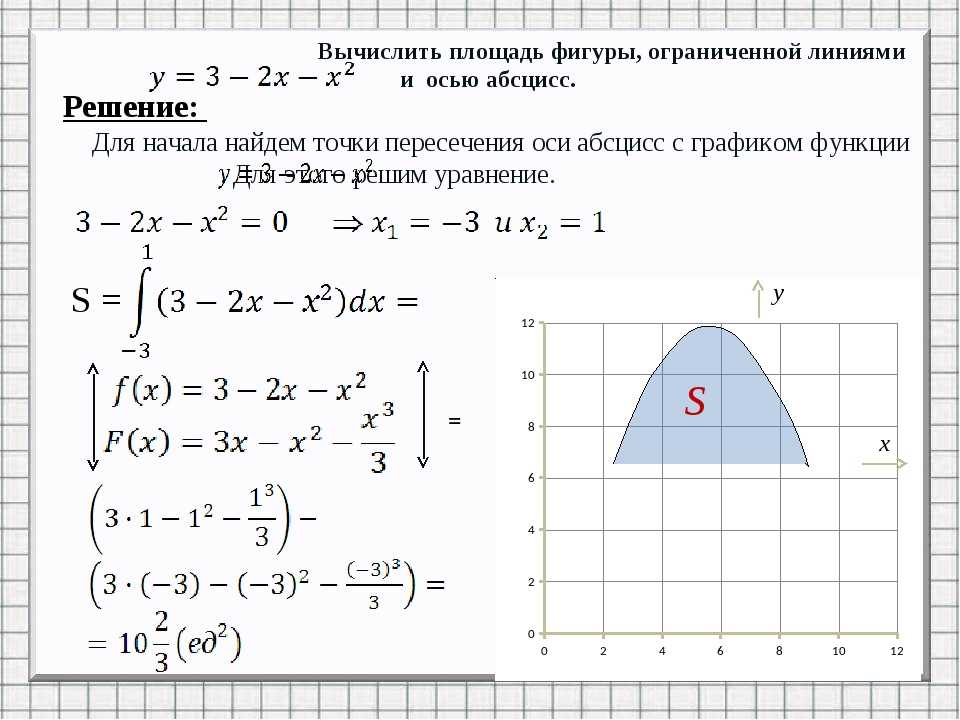
Решение
Найдем значение производных:
x′ = −6 cos2 t sin t , y′ = 6 sin2 t cos t .
π
Отсюда l = ∫4 36 cos4 t sin2 t + 36 sin4 t cos2 tdt =
0
36
π | π | π |
|
|
= ∫4 | 6 cos t sin tdt = 3∫4 | sin 2tdt = − 3 cos 2t 4 = | 3 = 1,5 . | |
0 | 0 | 2 | 0 | 2 |
| 6. Вычисление объема тела вращения | |||
| Объем тела ( рис.7), образованного | вращением во- | ||
круг оси Оx криволинейной трапеции, | ограниченной не- | |||
прерывной кривой | y = f (x) , осью Оx | и прямыми x = a и | ||
b
x = b , вычисляется по формуле Vox = π∫ f 2 ( x )dx .
| a |
y | y=f(x) |
|
Рис. 7
Если криволинейная трапеция ограничена графиком непрерывной функции x = ϕ( y ) и прямыми x = 0, y = c и
y = d( c < d ) , то объем тела, полученного вращением этой трапеции вокруг оси Oy, будет равен
d
Voy = π∫x2 ( y )dy .
c
37
Пример
Найти объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями y = x2 , y = x3 .
Решение
Сделаем рисунок (рис. 8) и убедимся, что искомый объем получится в результате разности двух объемов: объема V1 , полученного от вращения вокруг оси Oy фигуры,
ограниченной линиями x = 3 y , x = 0, y =1, и объема тела
вращения V2 x = 0, y =1 .
Тогда
1
V1 = π∫( 3
0
1
V2 = π∫(
0
фигуры, ограниченной линиями x = y ,
|
|
| 5 |
|
|
|
|
|
|
| |
y ) | 2 | dy = π | 3 y | 3 |
| 1 | = | 3π | ; | ||
| 5 |
|
| 0 |
| 5 | |||||
|
|
|
|
|
|
|
|
| |||
y ) | 2 | dy = π | y2 | 1 | = | π | . |
| |||
| 2 |
| 0 | 2 |
| ||||||
|
|
|
|
|
|
|
| ||||
Окончательно V =V1 −V2 = 35π − π2 = 10π = 0,1π.
38
y=x3 y=x2
Рис. 8
Задания для контрольной работы № 5
201-210. Вычислите несобственный интеграл или установите его расходимость.
| ∞ |
| dx |
|
| ∞ |
|
|
| ||||||
201. | ∫ |
| . |
| 202. ∫ln xdx . | ||||||||||
x(x −1) | |||||||||||||||
| 2 |
|
|
|
| 1 | x | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||
| 4 |
|
| dx |
|
| ∞ | dx | |||||||
203. ∫3 |
|
|
|
| 204. | ||||||||||
|
| . |
|
| . |
| |||||||||
( x −3 )2 | x ln2 x | ||||||||||||||
| ∞ |
|
| dx |
|
| 2 |
| xdx | ||||||
205. | ∫0 |
|
|
|
|
| 206. ∫0 |
| |||||||
|
| . |
| . | |||||||||||
| x2 + 4x +8 | ( x2 − 4 )3 | |||||||||||||
| 1 |
|
| x | 2 | dx 3 . | ∞ |
|
|
| |||||
207. | ∫ |
| 208. ∫xe−x dx . | ||||||||||||
| 0 |
|
| 1 − x |
|
| 0 |
|
|
|
| ||||
39
0 | dx |
|
| ∞ | 6×3 | 2 | +2 | 5 dx . |
209. ∫ |
| . | 210. ∫ |
| ||||
( x + 4 ) | 4 |
| ||||||
−4 |
|
| 1 |
| x |
| ||
211-220. Найдите площадь фигуры, ограниченной линиями. Сделайте чертеж.
Найдите площадь фигуры, ограниченной линиями. Сделайте чертеж.
211. a) y = | x2 | , y = | 4 − 2 x2 | ; | 216. | а) y = x2 −3x, y = 4 −3x; | |||
| |||||||||
| 3 |
| 3 |
|
| б) ρ = 2sin 2ϕ | |||
б) | ρ = 2 +cosϕ . |
|
|
|
|
| |||
|
|
|
|
|
| ||||
212. а) x + y = 2, x = 2, y = 2; | 217. | а) y = 3 − x2 , y =1 − x ; | |||||||
б) ρ =1 +cos 2ϕ . |
|
|
|
| б) ρ = 2cos 2ϕ . | ||||
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
| |
213. | а) 2 y = x2 , y = |
| 3 | − x ; |
|
| а) y = 3×2 +1, y = 3x + 7 ; | ||
|
| 218. | б) ρ = 3cos3ϕ. | ||||||
2 |
| ||||||||
|
|
|
|
|
|
|
| ||
б) ρ = 2 −cosϕ .
214.а) y = 4 – x2, y = x2 –2x; | 219. | а) y = 2x − x2 , y |
б) ρ =1 −sin 2ϕ . | ||
|
| б) ρ =1 −sinϕ . |
215.а) y = (x – 1)2, y2 = x – 1; | 220. | а) y = x2 − 2x, y |
б) ρ = 2 +sinϕ . |
| б) ρ = 2 − sinϕ . |
|
|
=−x ;
=x ;
221-230. Найти длину дуги с помощью определенного интеграла.
221.Кривой x = 2 cos3 t, y = 2 sin3 t , ( 0 ≤ t ≤ π4 ).
222.Кривойx = 5( t − sin t ) , y = 5(1 −cos t), ( 0 ≤ t ≤ π ).
223.Кривой y = ln(sin x ) , ( π4 ≤ t ≤ π2 ).
224.Кривойx = 4(cos t + t sin t ) , y = 4(sin t −t cos t ) , ( 0 ≤ t ≤ 2π ).
40
1.1: Площадь между двумя кривыми
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 501
- Ларри Грин
- Общественный колледж Лейк-Тахо
 \]
\]Приложение
Пусть \(y = f(x)\) будет функцией спроса на продукт и \( у = g(x)\) — функция предложения. Затем мы определяем точку равновесия как пересечение двух кривых. Излишек потребителя определяется площадью выше равновесного значения и ниже кривой спроса, а излишек производителя определяется площадью ниже равновесного значения и выше кривой предложения. 9х \) и \( у = 2х +1 \).
Авторы и авторство
Эта страница под названием 1.1: Area Between Two Curves распространяется по незаявленной лицензии и была создана, изменена и/или курирована Ларри Грином.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ларри Грин
- Показать страницу TOC
- нет
- Теги
- Площадь между двумя кривыми, интегрированная по оси x
- Площадь между двумя кривыми, интегрированная по оси Y
| 1 | Найдите производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d/dx 92) | ||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найдите производную — d/dx | грех(2x) | |
| 23 | Найдите производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найдите производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оцените интеграл 9бесконечность | ||
| 45 | Найдите производную — d/dx | х/2 | |
| 46 | Найдите производную — d/dx | -cos(x) | |
| 47 | Найдите производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найдите производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найдите производную — d/dx | лог х | |
| 86 | Найдите производную — d/dx | арктан(х) | |
| 87 | Найдите производную — d/dx | бревно натуральное 5х93 Целью этого вопроса является нахождение центра масс области, ограниченной кривыми в первом квадранте. Центроид — это центральная точка любой фигуры или объекта, в данном случае — центральная точка любой фигуры, нарисованной в 2D. Другой способ определить центроид — это точка области, в которой область сбалансирована по горизонтали, когда она подвешена к этой точке. Область, определенная в этом вопросе, находится в первом квадранте декартовой плоскости, что означает, что значения по оси x и по оси y точек являются положительными. Область образована двумя кривыми, которые пересекают друг друга в двух разных точках в первом квадранте. Сначала мы найдем площадь A области между точками пересечения двух кривых, а затем найдем центроид, вычислив моменты. Моменты любой области измеряют тенденцию этой области вращаться вокруг начала координат. Centroid C будет: \[ C = \left( \dfrac{M_y}{A}, \dfrac{M_x}{A} \right) \] где $M_x$ и $M_y$ — моменты x и y соответственно. Ответ эксперта: Как обсуждалось выше, область, образованная двумя кривыми, показана на рисунке 1. Мы найдем центр тяжести области, найдя ее площадь и ее моменты. Для этой области будет два момента: $x$-момент и $y$-момент. Делим $y$-момент на площадь, чтобы получить $x$-координату, и делим $x$-момент на площадь, чтобы получить $y$-координату. фигура 1 92 \} \,dx \]Подстановка значений из решенных уравнений, \[ \overline{y} = \dfrac{-0,23}{-0,5} \] \[ \overline{y} = 0,46 \] \[ ( \overline{x} , \overline{y} ) = (0.46, 0.46) \] $( \overline{x} , \overline{y} )$ — координаты центроида данного региона, показанного на рисунке 1. Альтернативное решение:Когда заданы значения моментов области и площади области. Мы можем найти значения центроида, напрямую подставив значения в следующие формулы. 9{9/4}}{9} \Big{]} \] Упрощение, \[ M_y = -0,278 \] Теперь мы можем вычислить координаты центроида $ ( \overline{x} , \ overline{y} )$, используя рассчитанные выше значения площади и момента области. |

 03.17
03.17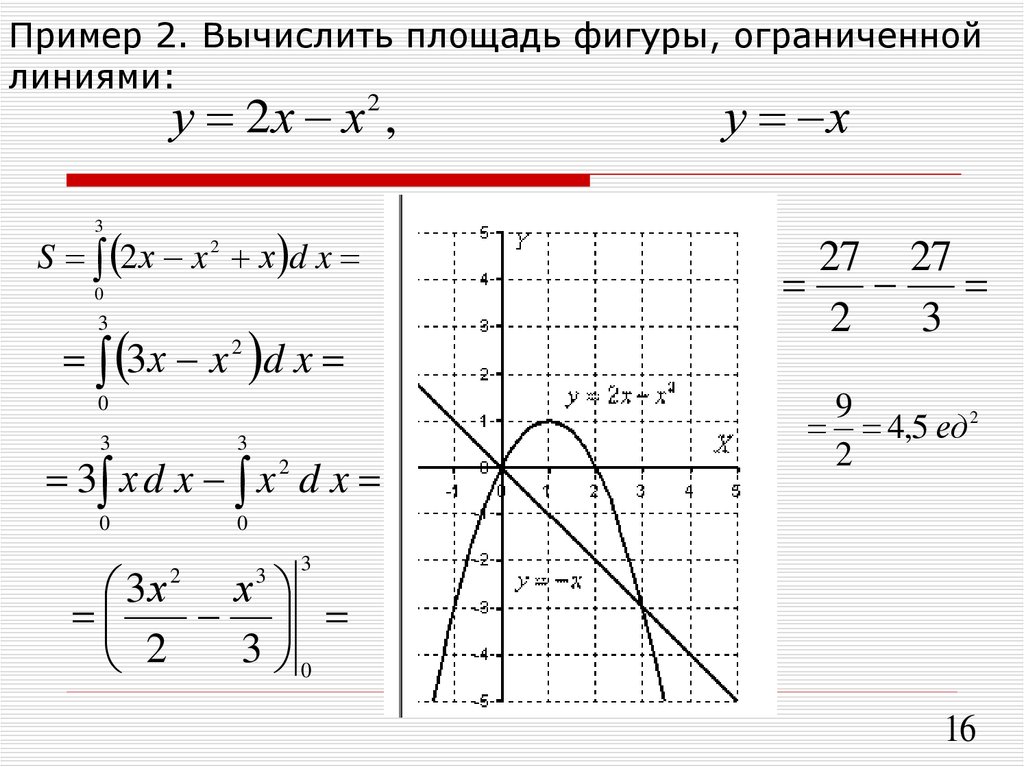 4_0= \\ = \frac{64}{3} -32+20=9 \frac{1}{3} $$
4_0= \\ = \frac{64}{3} -32+20=9 \frac{1}{3} $$ \frac{\pi}{2}_{-\frac{\pi}{2}} {cosx} \, dx = sin\frac{\pi}{2}-sin(-\frac{\pi}{2}))=1-(-1)=2 $$ в)
\frac{\pi}{2}_{-\frac{\pi}{2}} {cosx} \, dx = sin\frac{\pi}{2}-sin(-\frac{\pi}{2}))=1-(-1)=2 $$ в)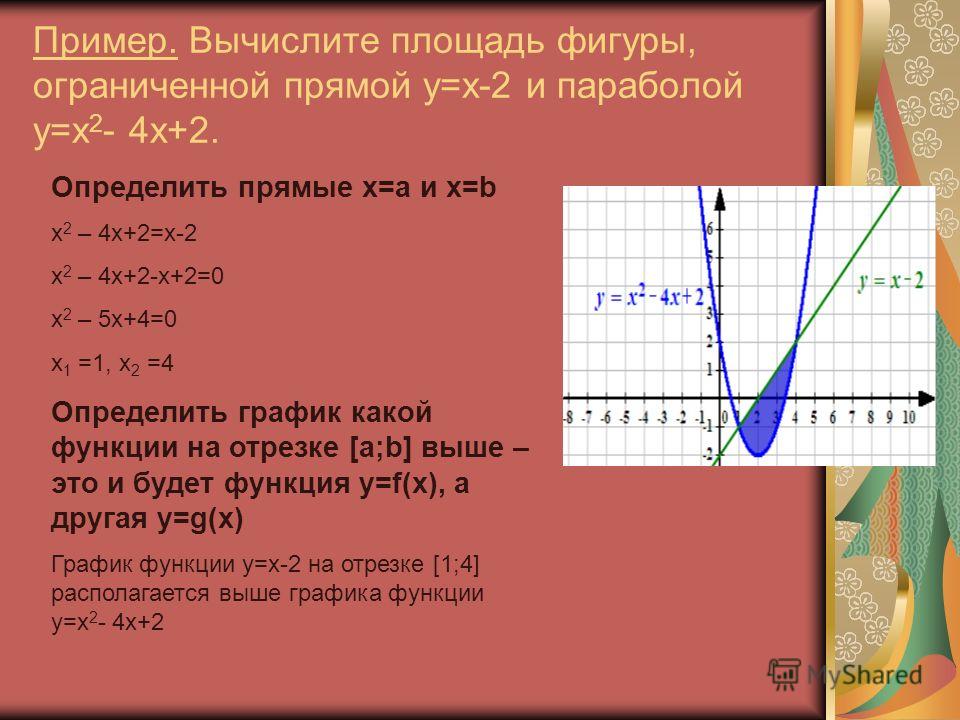



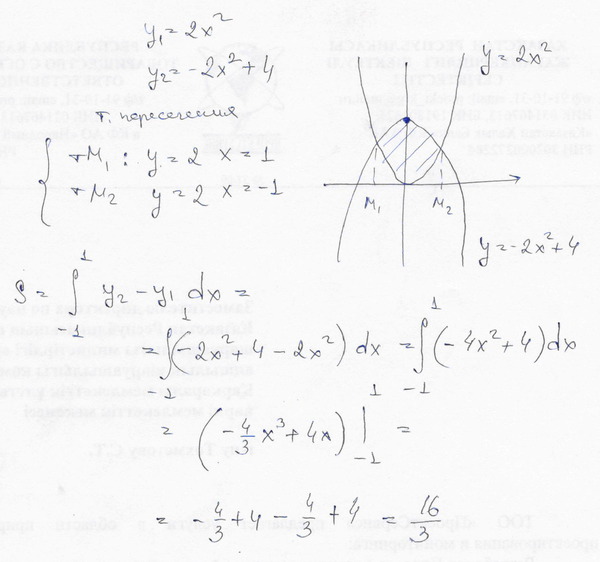

 ∫e
∫e