Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Коля, Дима и Саша собрали.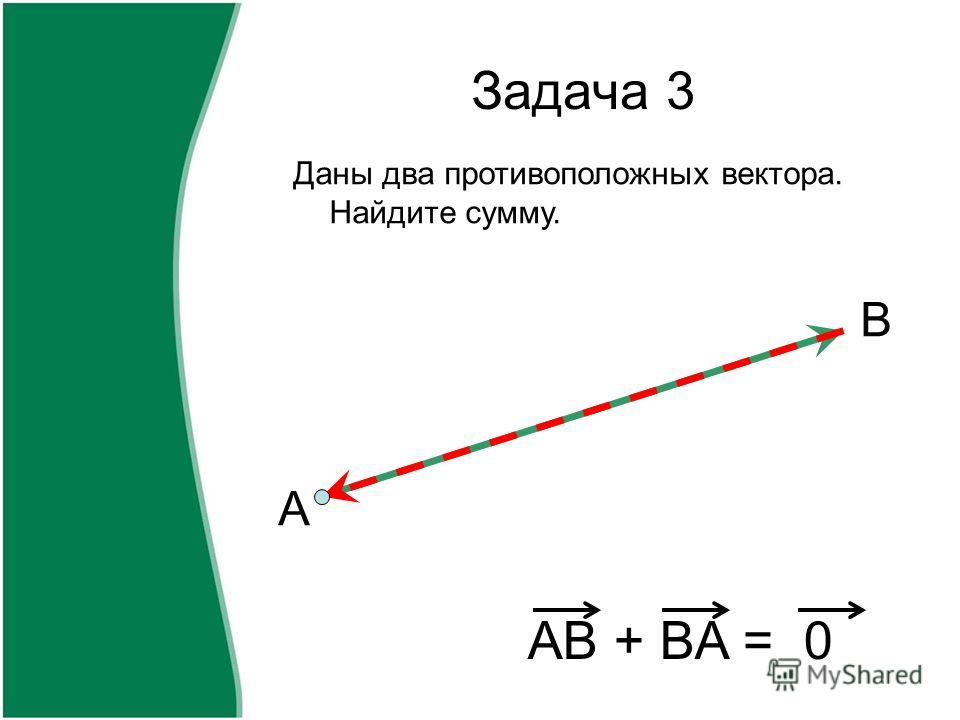 ..
..
Мост длиной 90 метров поезд проезжает за минуту, а мимо телеграфного столба (двигаясь с той же скоростью) проезжает за 4040 секунд. Какова длина поезда?
математика 1 класс. М.И.Моро, С.И. Волкова На каждой корзине записано, сколько в ней яблок. Соедини линией рисунки. на которых нарисовано одинаковое количество яблок, и запиши два верных равенства
Решено
Задача 4-го класса. через иксы решать нельзя. Подскажите пожалуйста!
В одном городе любая улица соединяет либо две различные площади, либо площадь с тупиком, либо два тупика. С любой площади выходит ровно 9 улиц. Всего
Пользуйтесь нашим приложением
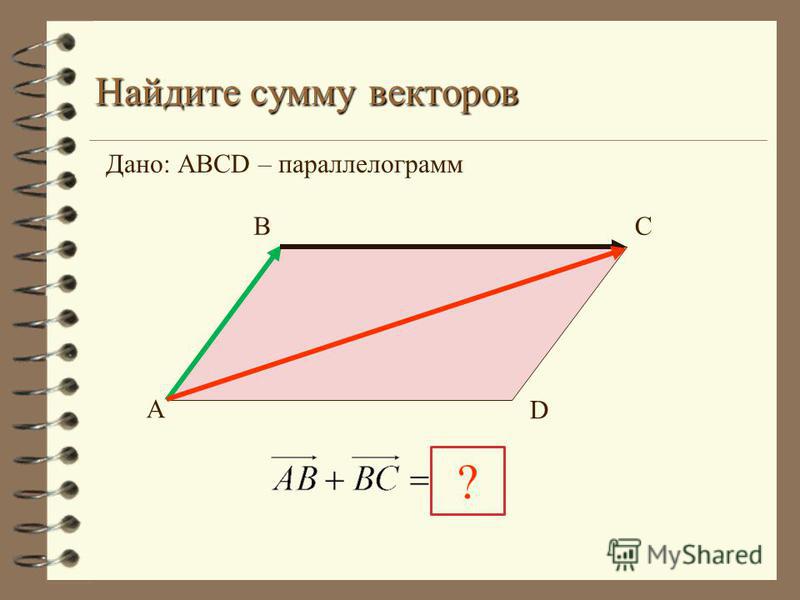
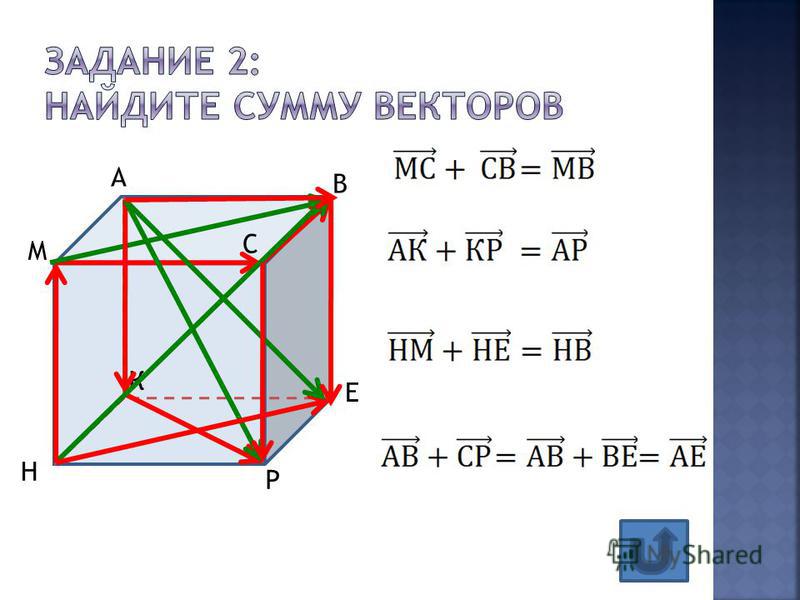
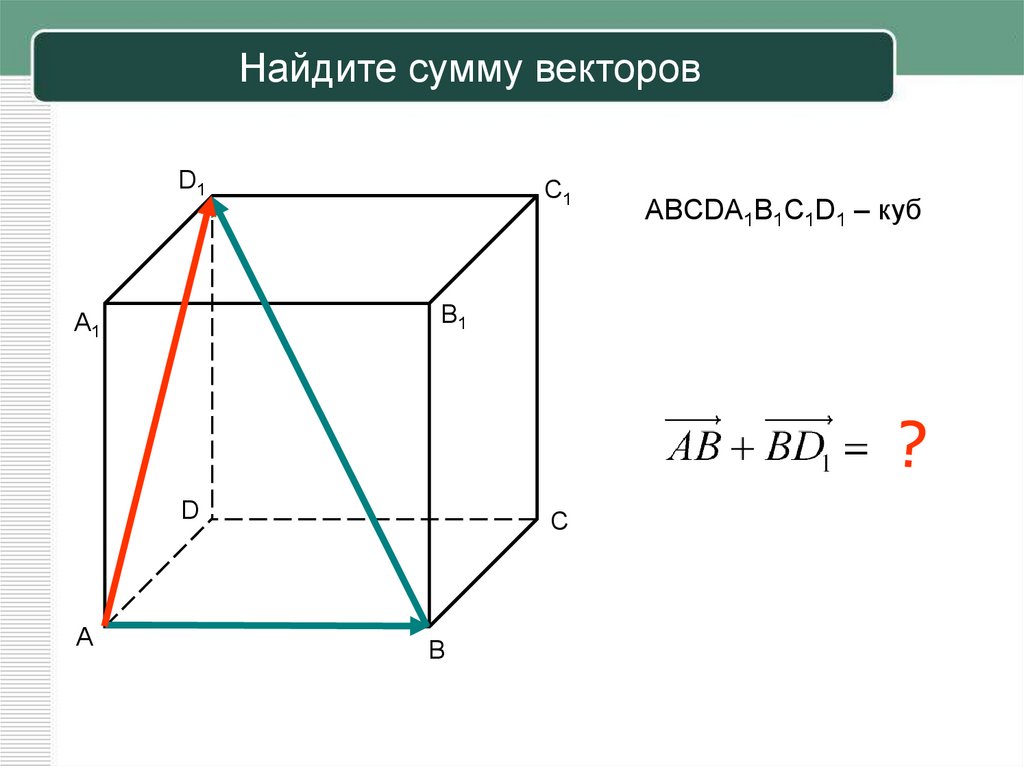
Как найти сумму векторов в пространстве
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической.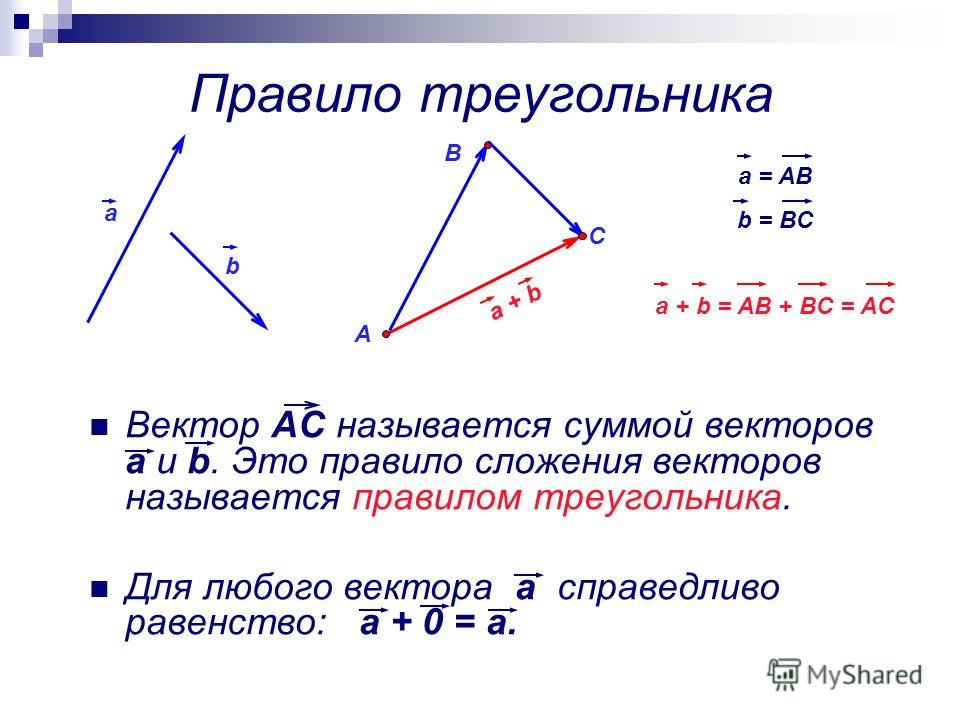 Способ хорош тем, что развивает мозги и пространственное воображение.
Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.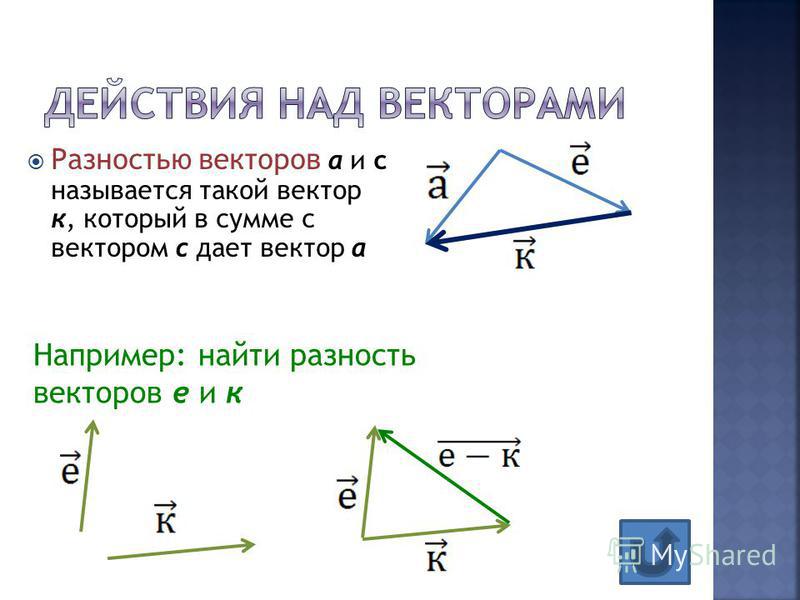
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми.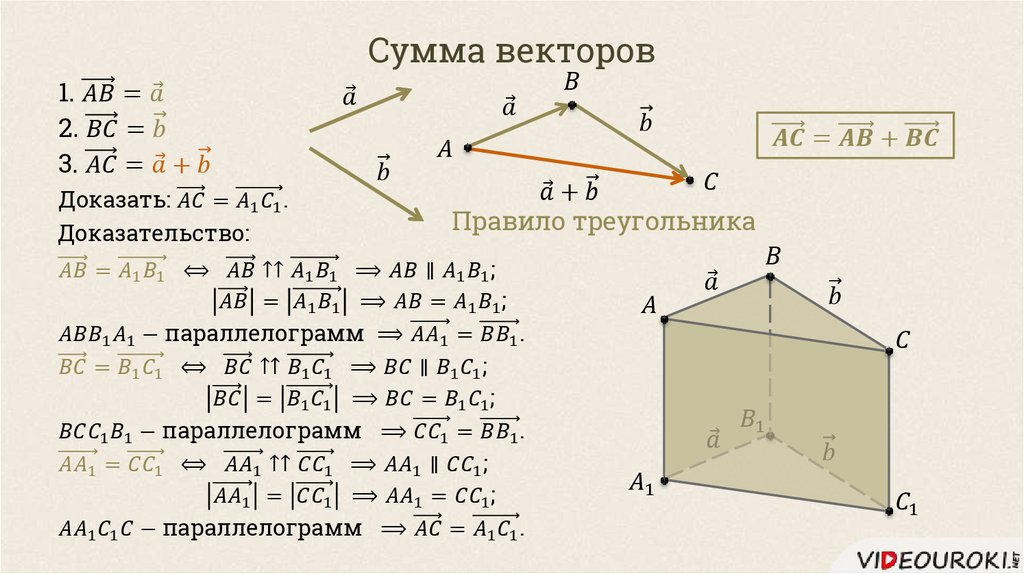 А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему.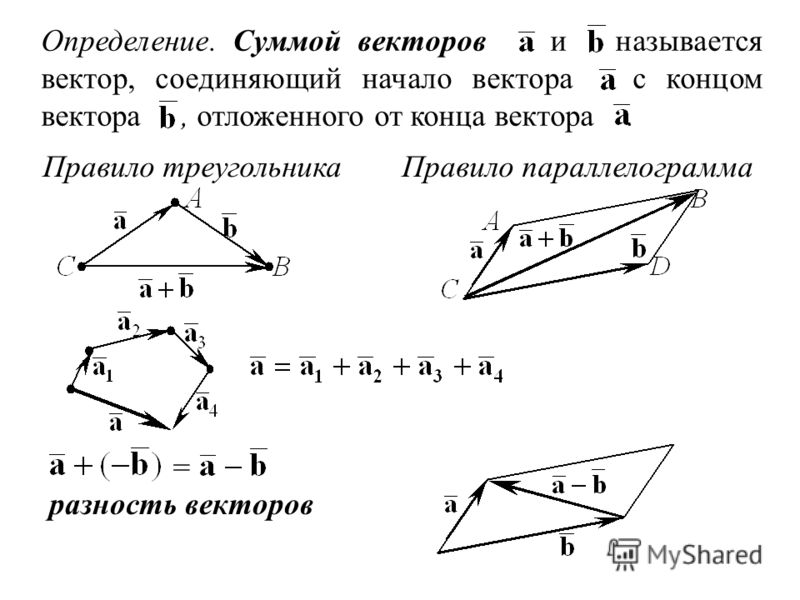 Выберем
Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .
Существование: Имеем два следующих случая:
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .
Из данного выше построения сразу же будет следовать единственность данного вектора.
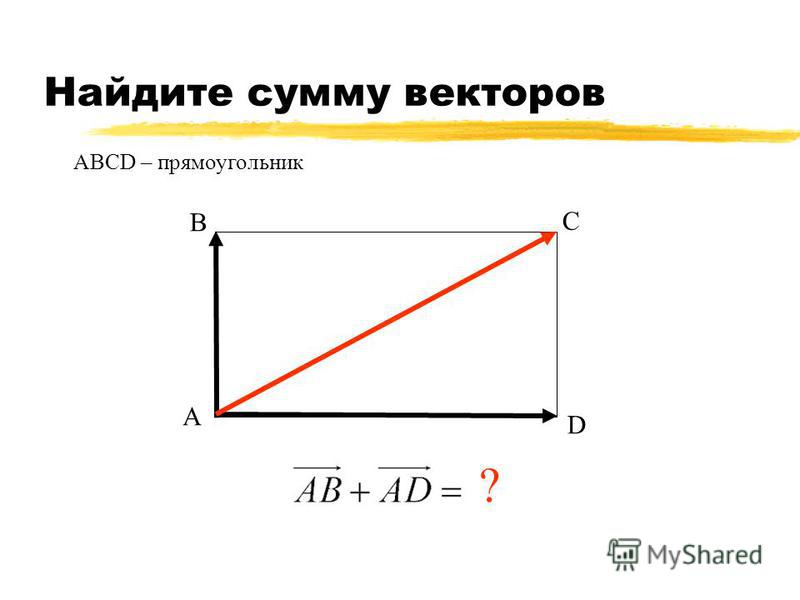
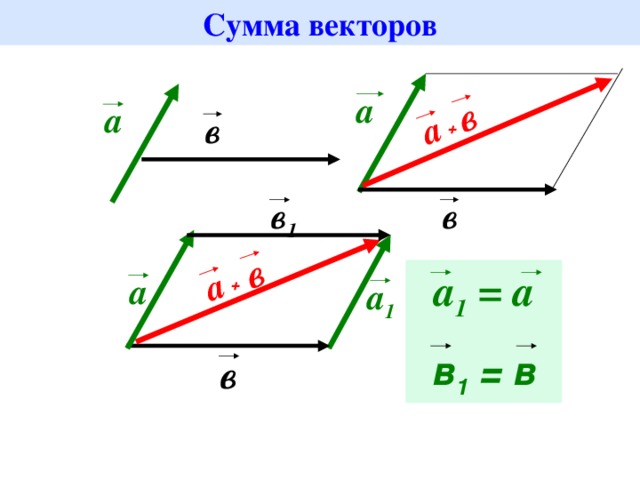
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.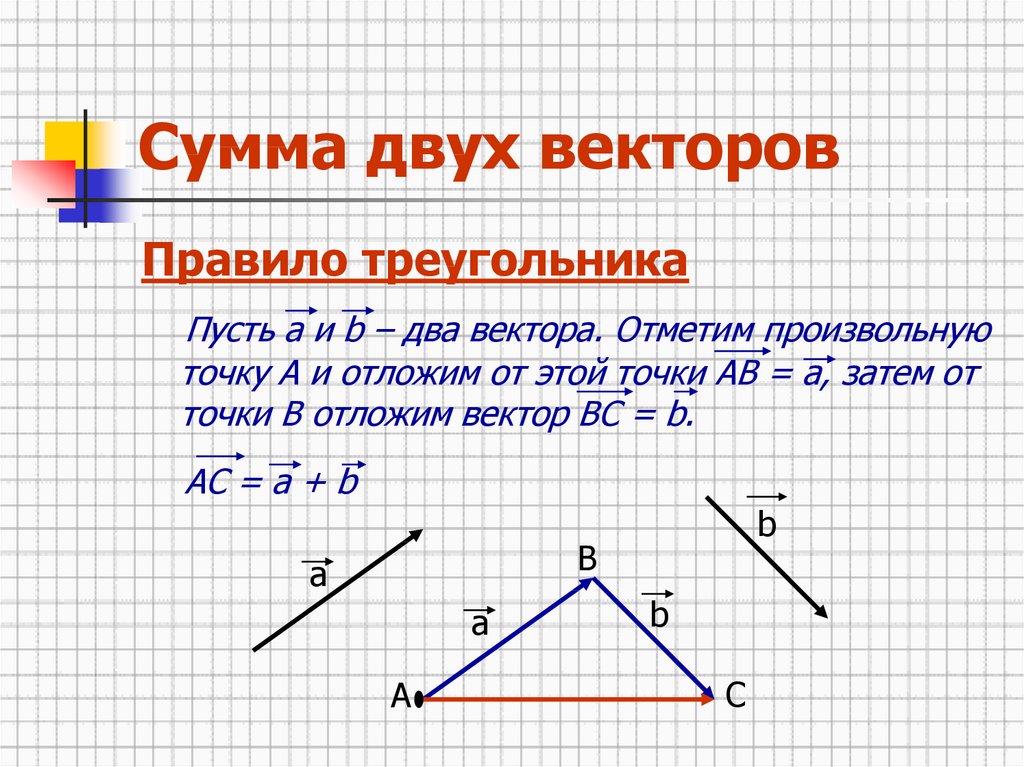
Суммой нескольких векторов ( vec ) , ( vec ) , ( vec,;ldots ) называется вектор ( vec ) , получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( <+ , + , + >
ight) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow ) выполняется равенство
Для произвольных точек ( A, B и C ) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec <0>)
Длина нулевого вектора равна нулю:
( left| vec <0>
ight| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( <— , — , — >
ight) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrow
ight|=left|k
ight||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.
 д..
д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов: .
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
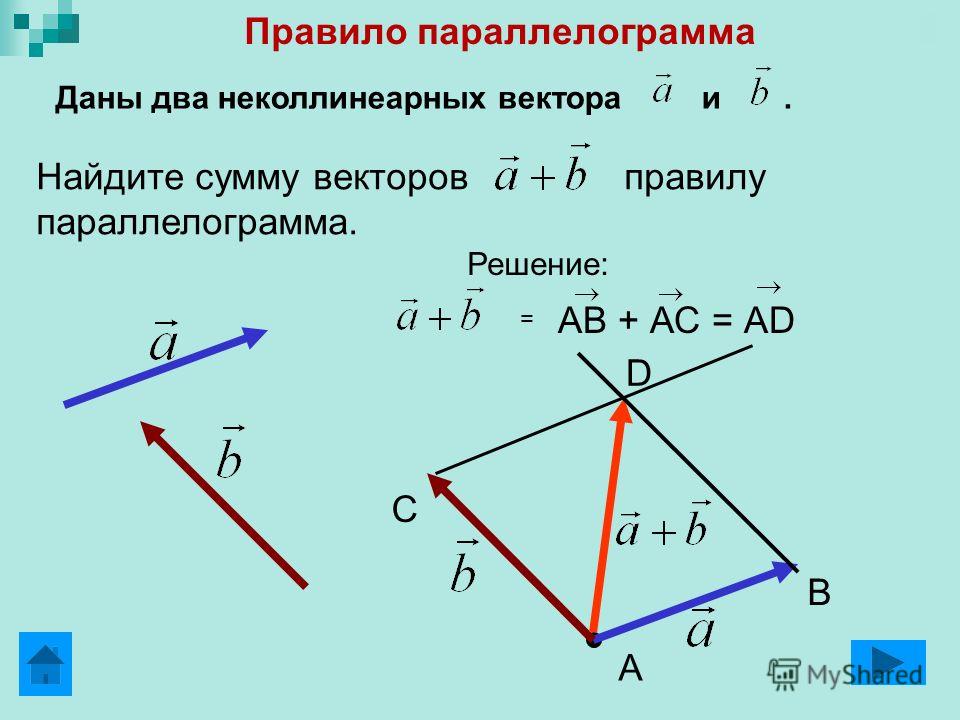
Правило параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

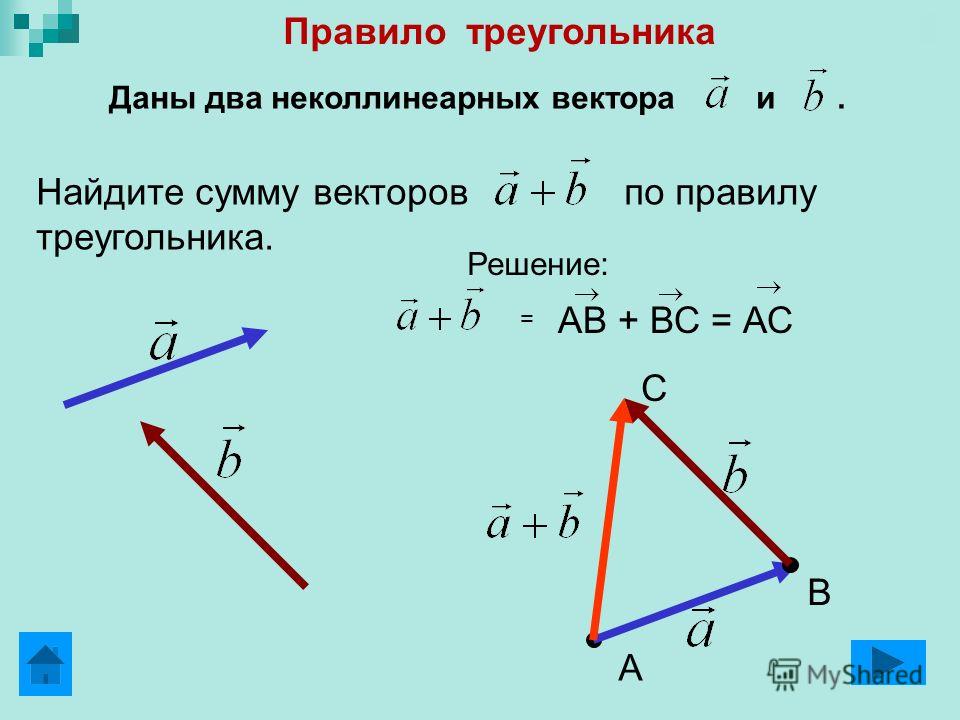
Правило треугольника
Сложение векторов по правилу треугольника заключается в следующем:
- нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
- от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
- результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.
Тригонометрический способ
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
F = числовое значение вектора
α = угол между векторами 1 и 2
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
α = угол между исходными векторами
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Урок 6. Действия над векторами в пространстве
Сумма
векторов, их разность, произведение вектора на число и скалярное произведение
векторов определяется так же, как и на плоскости. Только координат не две, а
три.
Только координат не две, а
три.
Сложение векторов.
Для трёх векторов (АО, ОС, ОО1), которые не лежат в одной плоскости и имеют общее начало О, их сумма изображается диагональю параллелепипеда (ОВ1), построенного на этих векторах, причём начало вектора-суммы совпадает с началом этих векторов.
Координаты
вектора-суммы векторов равны сумме соответствующих координат данных векторов.
Сложение
двух векторов производится покоординатно, то есть, если
то
c = {x3; y3; z3} =
{x1; y1; z1} + {x2; y2; z2} =
{x1 + x2; y1 + y2; z1 + z2}.
Данная формула имеет место для произвольного конечного числа слагаемых.
Правило параллелепипеда сложения векторов.
Пусть даны три вектора
не лежащие в одной плоскости (их называют некомпланарными).
Выполним следующие построения:
1. Отложим от произвольной точки О векторы
2. Построим параллелепипед так, чтобы отрезки
ОА, ОВ, ОС
были его рёбрами.
Из рисунка видно, что
Таким образом, сумма трёх векторов, не параллельных одной плоскости
представляется диагональю параллелепипеда, построенного на данных векторах,
отложенных от одной точки, как на рёбрах.
Получили правило параллелепипеда для сложения векторов в
пространстве.
ПРИМЕР:
Возьмём векторы
Сумма векторов равна:
Вычитание векторов.
Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если
то
c = {x3; y3; z3} =
{x1; y1; z1} – {x2; y2; z2} =
{x1 – x2; y1 – y2; z1 – z2}.
Геометрически два вектора складываются по правилу
параллелограмма с учётом того, что разностью векторов является диагональ,
соединяющая концы векторов, причём результирующий вектор направлен из конца
вычитаемого в конец уменьшаемого вектора.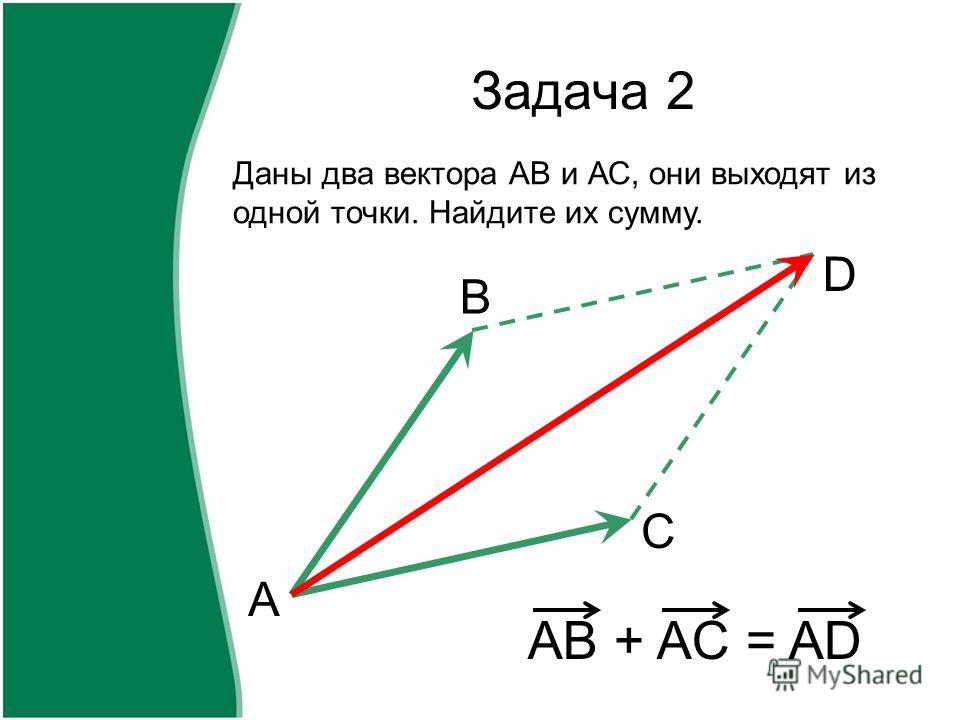
Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координаты его конца вычесть координаты его начала.
Любой вектор пространства
может быть представлен в виде разности двух векторов, исходящих из начала координат:
Координаты векторов
совпадают с координатами точек А и В, так как начало координат
О(0;
0; 0).
Таким образом, по правилу вычитания векторов следует произвести вычитание координат точки А из координат точки В.
Возьмём векторы
Разность векторов равна:
Произведение векторов.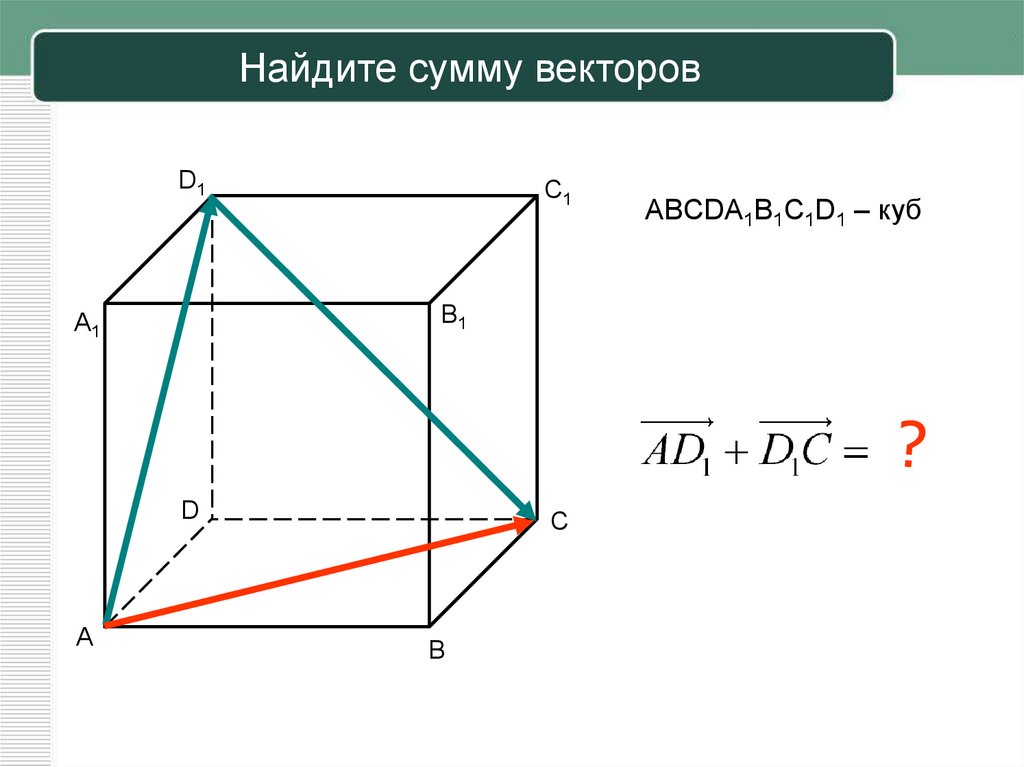
Умножение вектора на
число λ
покоординатно:
При λ ˃ 0 – вектор
сонаправлен
При λ < 0 – вектор
противоположно направлен
При | λ | ˃ 1 – длина вектора
увеличивается в λ раз. При | λ | < 1 – длина вектора
уменьшается в λ раз.
ПРИМЕР:
Даны векторы
Найдите координаты вектора:
РЕШЕНИЕ:
ОТВЕТ:
Скалярное произведение векторов.
Скалярным произведением
векторов
называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть: скалярное произведение двух векторов
Скалярное произведение двух векторов
заданных своими координатами, равно сумме произведений их одноимённых координат, то есть:
ПРИМЕР:
Найдите угол между векторами
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда Откуда ОТВЕТ:
ПРИМЕР:
Найти скалярное произведение векторовесли даны точки:
РЕШЕНИЕ:
Сначала найдём векторы:
По формулеВычислим скалярное произведениеСкалярное
произведение положительно, значит, угол между пространственными векторами
является острым.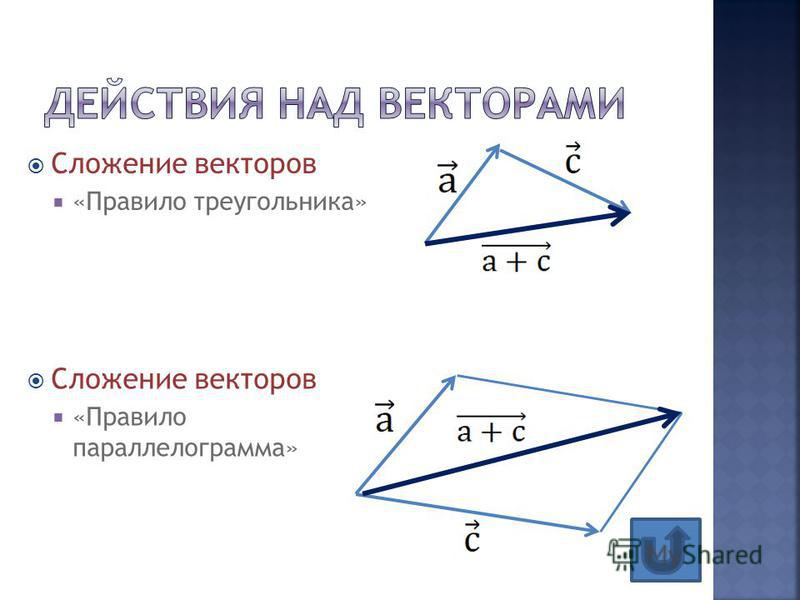
ОТВЕТ: 6
Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол φ = 0, поэтому его косинус равен 1.
Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения.
Если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.
ПРИМЕР:
При каком значении р векторы
взаимно перпендикулярны ?
РЕШЕНИЕ:
Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
3 ∙ р + р ∙ (–2) + (–1) ∙ 5 = 3р – 2р – 5 = р – 5,
тогда
р –
5 = 0.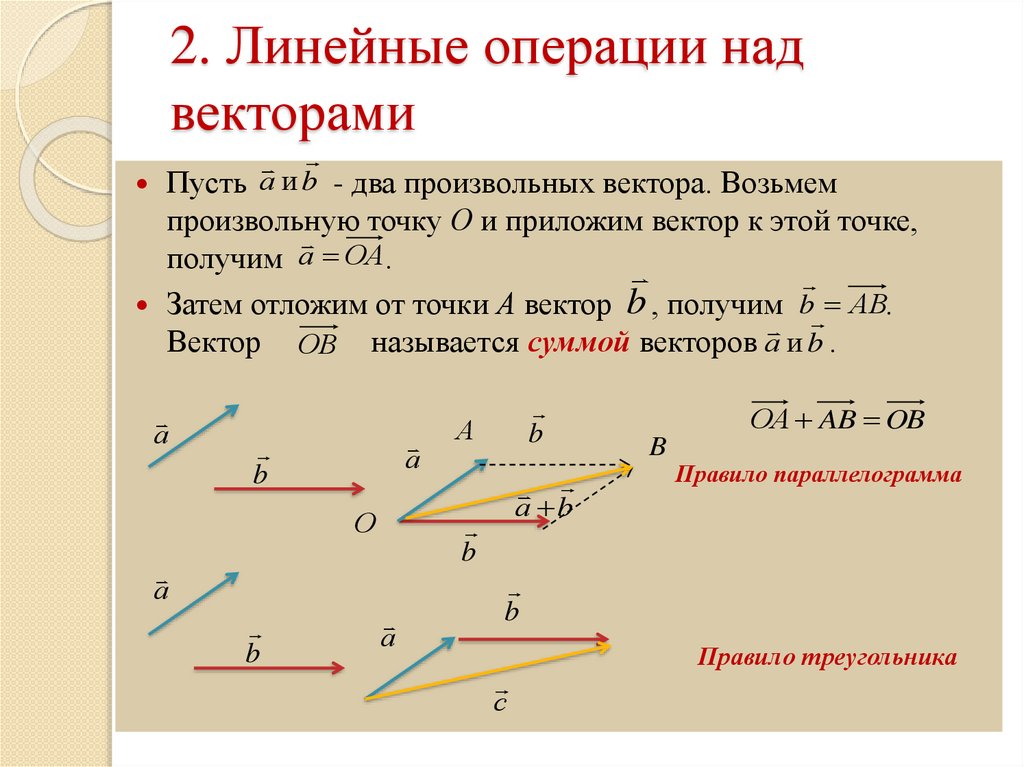
Откуда р = 5.
ОТВЕТ: р = 5
Попарные скалярные произведения единичных орт равны нулю, то есть:
С помощью скалярного произведения векторов можно вычислить угол между ними. Если заданы два ненулевых вектора своими координатами
то косинус угла φ между ними:
то есть
Отсюда следует условие перпендикулярности ненулевых векторов
х1x2 + y1y2 + z1z2 = 0.
С помощью скалярного произведения векторов находят работу постоянной силы
на прямолинейном участке пути. Предположим, что под действием постоянной силы
материальная точка
перемещается прямолинейно из положения А в положение В. Вектор силы
Вектор силы
образует угол φ с вектором перемещения
Физика утверждает, что работа силы
при перемещении
равна
то есть
Следовательно, работа постоянной силы при прямолинейном перемещении точки её приложения равна скалярному произведению вектора силы на вектор перемещения.
Проекции векторов.
Пусть в пространстве задана прямая (ось l), вектор
задан координатами конца и начала. Обозначим проекции точек А и В на ось l соответственно через А‘ и В‘. Проекцией
вектора
на ось l называется длина вектора
взятая со знаком <<+>>, если вектор
и ось l сонаправлены, и со знаком <<–>>, если
противоположно направлены.
Если в качестве оси l взять
некоторый другой вектор
то получим проекцию вектора
на вектор
Нахождение проекции вектора
на направление, заданное вектором
может осуществляться по формуле:
то есть
Некоторые основные свойства проекций.
1. Проекция вектора
на ось l равна произведению модуля вектора
на косинус угла между векторами и осью, то есть
2. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
3. Проекция суммы
нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Свойства векторного произведения.
Если векторы заданы своими координатами:
то векторное произведение находится по формуле:
ПРИМЕР:
Найти векторное произведение векторов:
РЕШЕНИЕ:
Составим определитель и вычислим его:
Смешанное произведение векторов.
Смешанным произведением трёх векторов
называется число, равное скалярному произведению векторов
на вектор
Геометрический смысл смешанного произведения.
Если тройка векторов
правая, то их смешанное произведение равно объёму параллелепипеда построенного на этих векторах:
В случае левой тройки
смешанное произведение указанных векторов равно объёму параллелепипеда со знаком минус:
Если
компланарные, то их смешанное произведение равно нулю.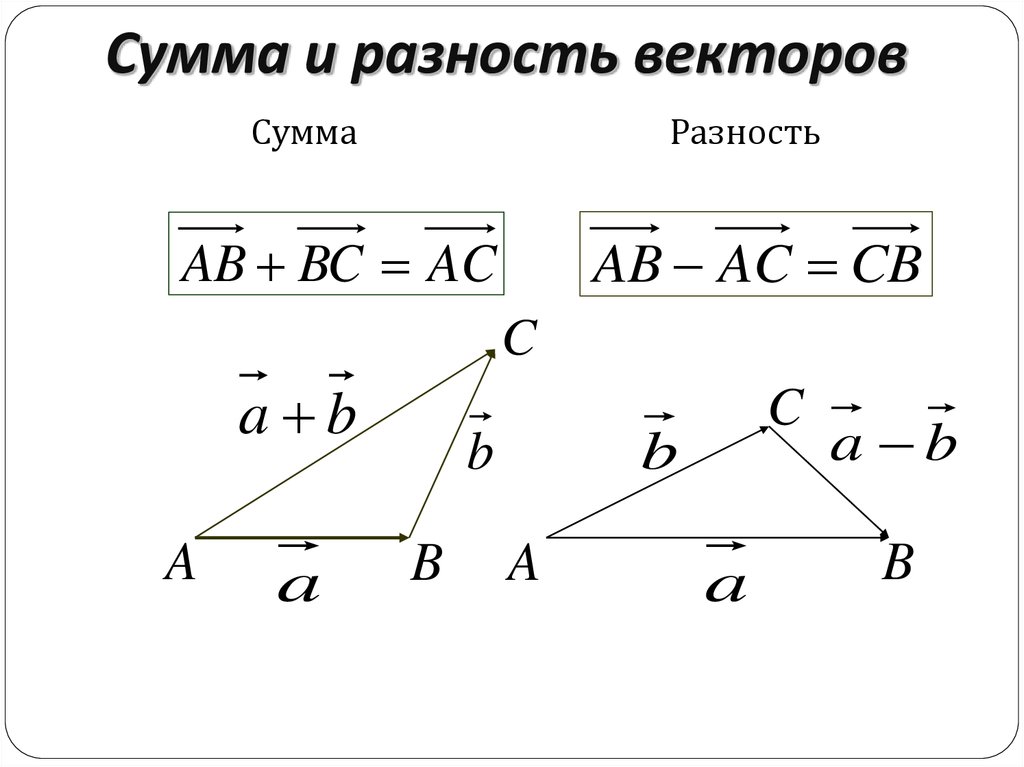 Из выше сказанного можно
сделать вывод, что объём параллелепипеда, построенного на векторах
Из выше сказанного можно
сделать вывод, что объём параллелепипеда, построенного на векторах
равен модулю смешанного произведения этих векторов:
Объём пирамиды, построенный на этой тройке векторов равен:
Свойства смешанного произведения. Три вектора компланарные тогда и только тогда, когда:
Тройка векторов является правой тогда и только тогда, когда
Если же
то векторы
образуют левую тройку векторов.
Если векторы:
заданы своими координатами, то их смешанное произведение вычисляется по формуле:
Задания к уроку 6
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
Как найти сумму векторов
Метод sum() помогает найти сумму группы, сумму определенного столбца фрейма данных.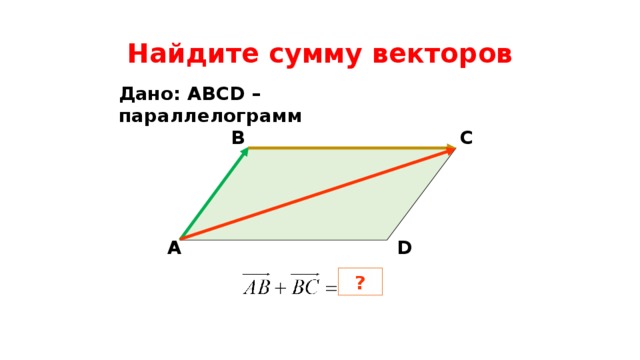 Метод sum() возвращает сумму всех элементов, присутствующих в его аргументах. Если это вектор, то он вернет сумму всех элементов вектора.
Метод sum() возвращает сумму всех элементов, присутствующих в его аргументах. Если это вектор, то он вернет сумму всех элементов вектора.
Функция sum() — это встроенная функция R, которая вычисляет сумму числового входного вектора. Он принимает числовой вектор в качестве аргумента и возвращает сумму элементов вектора. Чтобы вычислить сумму векторов в R, используйте функцию sum().
Синтаксисsum(x, na.rm = FALSE, …)Параметры
- x: числовой вектор.
- rm: следует ли удалить NA; в противном случае будет возвращено NA.
Начнем с вектора. вектор в R – это тип данных для сохранения нескольких элементов в R.
Давайте найдем сумму векторов.
рв <- с(11, 19, 21, 18, 46) #вычисляет сумму значений sum(rv)
Здесь мы определили вектор и использовали метод sum() для вычисления суммы всех элементов вектора.
См. вывод.
[1] 115Передача значения NA в функцию sum()
Если NA присутствует в элементах вектора, то вы не можете получить желаемый результат.
rv <- c(11, 19, NA, 18, 46) #вычисляет сумму векторов с.в. сумма (рв)Выход
[1] Н/П
Ну, мы не ожидали NA вывода. Однако иногда ваш набор данных может содержать значения « NA », т. е. « Not Available ».
Таким образом, если вы добавите значения, включая NA , метод sum() вернет NA вместо вывода числового суммирования.
Но мы можем решить эту проблему, обойдя na.rm = TRUE.
rv <- c(11, 19, NA, 18, 46) # Вычисляет сумму значений сумма (rv, na.rm = ИСТИНА)Вывод
[1] 94Вычисление суммы фрейма данных в R
Чтобы найти сумму значений фрейма данных в R, используйте функцию sum(). Определите data.frame и выполните функцию sum() для столбца.
Определите data.frame и выполните функцию sum() для столбца.
студент <- data.frame(name = c("Санни", "Миа", "Кортни", "Оливия", "Холи"),
enrollno = c(11, 18, 19, 29, 46),
возраст = c(32, 31, 32, 27, 30))
распечатать(студент)
Вывод RScript Pro.R имя enrollno возраст 1 Солнечный 11 32 2 Миа 18 31 3 Кортни 19 32 4 Оливия 29 27 5 Святой 46 30
Найдем сумму столбца enrollno (переменная).
студент <- data.frame(name = c("Санни", "Миа", "Кортни", "Оливия", "Холи"),
enrollno = c(11, 18, 19, 29, 46),
возраст = c(32, 31, 32, 27, 30))
сумма (студент $ enrollno) Чтобы получить доступ к столбцу, используйте $ , а затем имя столбца . Здесь мы находим сумму enrollno значений столбца. См. приведенный ниже вывод.
[1] 123Вычислить сумму по столбцам
Если вы хотите получить сумму определенных столбцов, используйте функцию mapply() .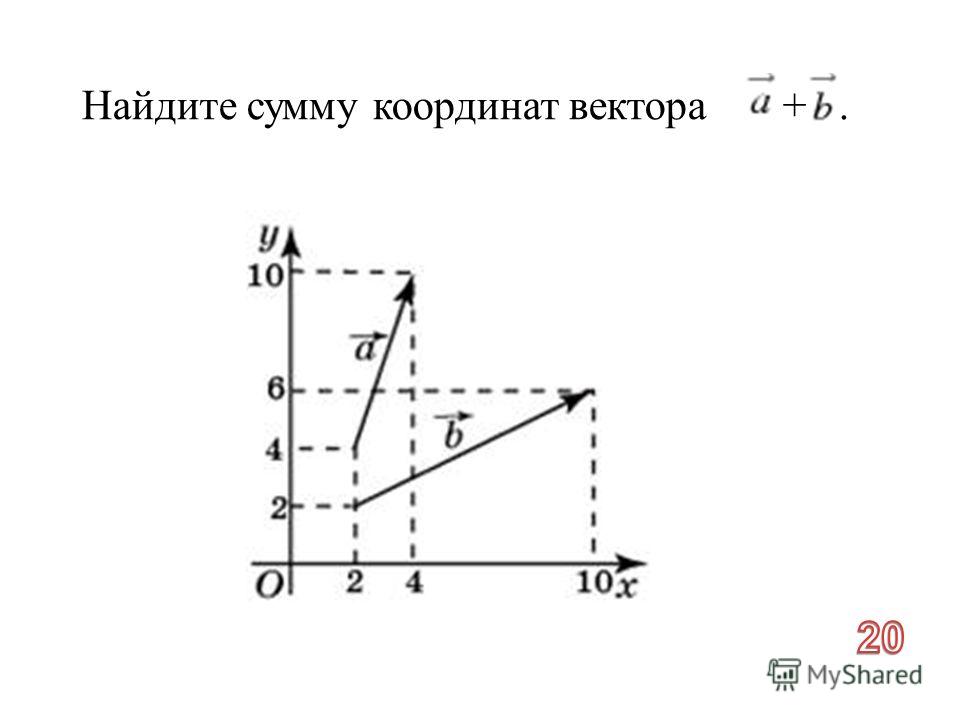 Функция mapply() вычисляет сумму требуемых столбцов.
Функция mapply() вычисляет сумму требуемых столбцов.
студент <- data.frame(name = c("Санни", "Миа", "Кортни", "Оливия", "Холи"),
enrollno = c(11, 18, 19, 29, 46),
возраст = c(32, 31, 32, 27, 30))
mapply (сумма, студент [ c (2, 3)])
Выход enrollno возраст 123 152
Сумма столбца enrollno равна 123, а возраст равен 152. В нашем фрейме данных у нас есть два столбца с числовыми значениями; именно поэтому он не дал нам ошибку. Однако, если каждый столбец не является числовым, это вызовет ошибку.
Сумма столбца по группам в RR имеет встроенную функцию агрегата(), используемую для нахождения суммы столбца по группе.
студент <- data.frame(name = c("Санни", "Миа", "Кортни", "Оливия", "Холи"),
enrollno = c(11, 18, 19, 29, 46),
возраст = c(32, 31, 32, 27, 30))
агрегат (x = студент $ enrollno,
по = список (имя студента $),
FUN = сумма) Выход Группа.1 x 1 святой 46 2 Кортни 19 3 Миа 18 4 Оливия 295 Солнечный 11
В этом примере функция aggregate() вместе с функцией sum() вычисляет сумму группы. Здесь вычисляется сумма столбца «enrollno» для «имя» .
ЗавершениеМетод R sum() используется для нахождения суммы элементов в векторе. В этом руководстве показано, как найти сумму векторов, фрейма данных и его различных вариантов.
Это урок.
Krunal Lathiya
Krunal Lathiya — инженер по информационным технологиям по образованию и веб-разработчик по профессии. Он работал со многими серверными платформами, включая Node.js, PHP и Python. Кроме того, Крунал отлично разбирается в науке о данных и машинном обучении, а также является экспертом в области R Language. Крунал ведет множество блогов по программированию, что свидетельствует о его обширном опыте в этой области.
Скалярное умножение и сложение векторов
Главная > Математика > Предварительное исчисление > Скалярное умножение и сложение векторов
Двумя основными векторными операциями являются скалярное умножение и сложение векторов .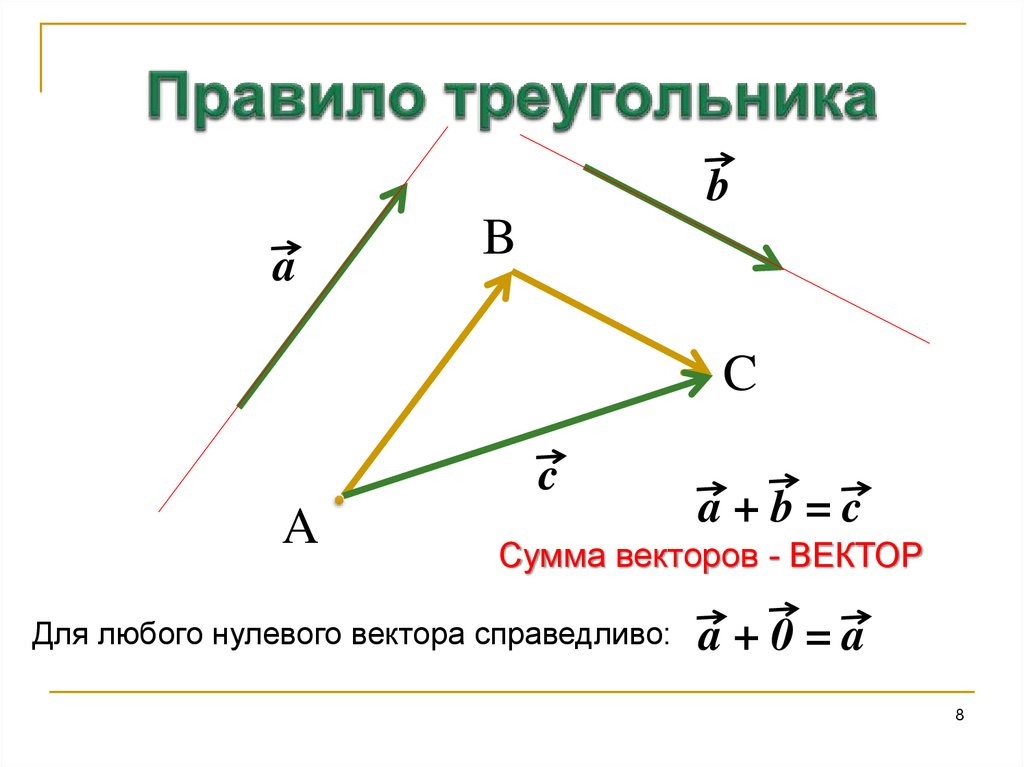 В общем, при работе с векторами числа или константы называются скалярами .
В общем, при работе с векторами числа или константы называются скалярами .
Скалярное умножение — это умножение вектора на скаляр (число или константу). Если вектор v умножить на скаляр k, результатом будет k v . Если k положительно, то k v будет иметь те же направления, что и в . Если k отрицательное, k v будет иметь направление, противоположное v .
СКАЛЯРНОЕ УМНОЖЕНИЕ:
Пусть v = 〈v1,v2〉 и k скаляр.
k v = k〈v1,v2〉 = 〈kv1,kv2〉
Чтобы сложить два вектора u и v , поместите начальную точку второго вектора (без изменения длины или направления) на конечная точка первого вектора. Затем соедините начальную точку первого вектора с концом второго вектора. Эта линия соединения представляет собой сумму двух векторов.
Сумма векторов u и v в компонентном виде равна:
СЛОЖЕНИЕ ВЕКТОРОВ:
〈u1+v1, u2+v2〉
u−v=u+(−v)=〈u1−v1, u2−v2〉
Скалярное умножение и сложение векторов обладают следующими общими свойствами: ДОПОЛНЕНИЕ:
Пусть u , v и w — векторы, а c и d — скаляры.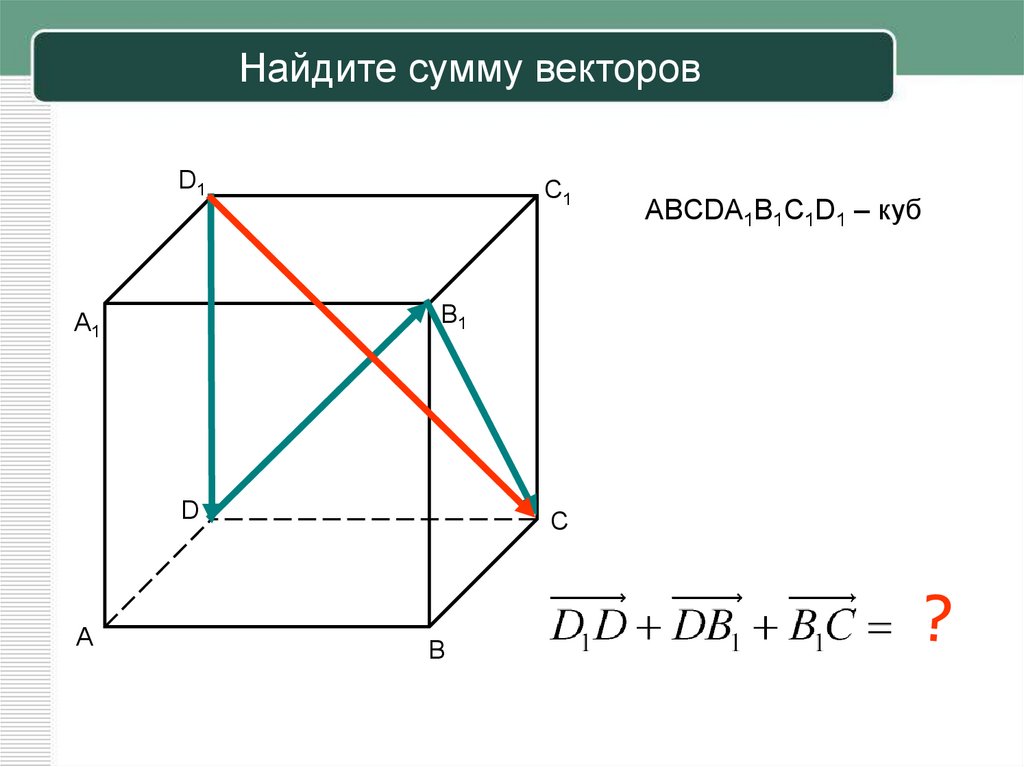
1. U + V = V + U 2. ( U + V ) + W = U + ( V + W )
9. u + 0 = u 4. u + (- u ) = 05. c(d u ) = (cd) u 6 u 9,036 = с и + d и
7. с( и + v ) = с и + с v 8. 1 · u = u , 0 · u = 0
9. ||c v || = |с||| против ||
Давайте рассмотрим пару примеров.
Пример 1: Если u=〈−2,1〉 и v=〈7,−3〉 найти (a) u + v и (b) u - v.
Шаг 1. Вычислите u + v с помощью сложения векторов. Добавьте x-компонент обоих векторов. | u+v=〈−2+7, 1+(−3)〉 u+v=〈5,−2〉 |
Шаг 2: Вычислите u - v с помощью сложения векторов. Помните, что u - v = u + (-v), поэтому вычтите x-компоненту v из и . Сделайте то же самое для y-компонентов. | u−v=u+(−v)=〈−2−7, 1−(−3)〉 u−v=〈−9, 4〉 |
Пример 2: Если u=〈6,15〉 и v=〈−5,20〉 найти (a) 2u + v и (b) 5u - 2v.
Шаг 1: Вычислите 2u + v, используя скалярное умножение и сложение векторов. а) Сначала вычислите 2 u , используя скалярное умножение. б) Затем вычислите 2 u + v , используя сложение векторов. | 2u=2〈6,15〉=〈2 ·6, 2 ·15〉 2u=〈12, 30〉 2u+v=〈12+(−5), 30+20〉 2u+v=〈7,50〉 |
Шаг 2: Вычислите 5u - 2v, используя скалярное умножение и сложение векторов. a) Сначала вычислите 5 u и 2 v , используя скалярное умножение. b) Затем вычислите 5 u +2 v , используя сложение векторов. | 5u=5〈6,15〉=〈5·6, 5·15〉 5u=〈30, 75〉 2v=2〈−5,20〉=〈2··(−5), 2·20〉 2u=〈−10, 40〉 5u−2v=5u+(−2v) 5u−2v=〈30−(−10), 75−40〉 5u−2v=〈40, 35〉 |
Основы работы с запросами | Прометей
- Примеры
- Типы данных языка выражений
- литералов
- Строковые литералы
- Литералы с плавающей запятой
- Селекторы временных рядов
- Мгновенные векторные селекторы
- Селекторы вектора диапазона
- Продолжительность времени
- Модификатор смещения
- @ модификатор
- Подзапрос
- Операторы
- Функции
- Комментарии
- Гочки
- Несвежесть
- Избегайте медленных запросов и перегрузок
Prometheus предоставляет функциональный язык запросов под названием PromQL (Prometheus Query
Язык), который позволяет пользователю выбирать и агрегировать данные временных рядов в реальном времени. время. Результат выражения может быть либо показан в виде графика,
табличные данные в браузере выражений Prometheus или потребляемые внешними
системы через HTTP API.
время. Результат выражения может быть либо показан в виде графика,
табличные данные в браузере выражений Prometheus или потребляемые внешними
системы через HTTP API.
Примеры
Этот документ предназначен для справки. Для обучения может быть проще начни с пары примеров.
Типы данных языка выражений
В языке выражений Prometheus выражение или подвыражение могут оцените один из четырех типов:
- Мгновенный вектор — набор временных рядов, содержащих одну выборку для каждого временного ряда, имеющих одну и ту же метку времени
- Вектор диапазона - набор временных рядов, содержащий диапазон точек данных во времени для каждого временного ряда
- Скаляр - простое числовое значение с плавающей запятой
- String - простое строковое значение; в настоящее время не используется
В зависимости от варианта использования (например, при построении графика или отображении выходных данных
выражение), только некоторые из этих типов являются допустимыми в результате
пользовательское выражение. Например, выражение, возвращающее мгновенный
вектор - единственный тип, который можно напрямую изобразить в виде графика.
Например, выражение, возвращающее мгновенный
вектор - единственный тип, который можно напрямую изобразить в виде графика.
Литералы
Строковые литералы
Строки могут быть указаны как литералы в одинарных, двойных кавычках или обратные кавычки.
PromQL следует тем же правилам экранирования, что и
Идти. В одинарных или двойных кавычках
обратная косая черта начинает управляющую последовательность, за которой могут следовать a , b , f , n , r , t , v или \. Конкретные символы могут быть предоставлены с использованием восьмеричного
( \nnn ) или шестнадцатеричный ( \xnn , \unnnn и \Unnnnnnn ).
Внутри обратных кавычек экранирование не обрабатывается. В отличие от Go, Prometheus не отбрасывает символы новой строки внутри обратных кавычек.
Пример:
"это строка" 'они не экранированы: \n \\ \t' `они не экранированы: \n ' " \t`
Литералы с плавающей запятой
Скалярные значения с плавающей запятой могут быть записаны как целые числа или числа с плавающей запятой в формате (для удобства чтения включены только пробелы):
[-+]?(
[0-9]*\. ?[0-9]+([eE][-+]?[0-9]+)?
| 0[xX][0-9a-fA-F]+
| [нН][аА][нН]
| [ii][nN][fF]
)
?[0-9]+([eE][-+]?[0-9]+)?
| 0[xX][0-9a-fA-F]+
| [нН][аА][нН]
| [ii][nN][fF]
)
Примеры:
23 -2,43 3.4e-9 0x8f -Инф NaN
Селекторы временных рядов
Мгновенные векторные селекторы
Мгновенные селекторы векторов позволяют выбирать набор временных рядов и одно значение выборки для каждого в заданной метке времени (момент): в простейшем форме указывается только имя метрики. Это приводит к мгновенному вектору содержащий элементы для всех временных рядов с этим именем метрики.
В этом примере выбираются все временные ряды с метрикой http_requests_total .
имя:
http_requests_total
Можно дополнительно отфильтровать эти временные ряды, добавив список меток, разделенных запятыми.
сопоставители в фигурных скобках ( {} ).
В этом примере выбираются только временные ряды с http_requests_total имя метрики, у которых также есть метка job , установленная на prometheus , и их группа 9Метка 0512 установлена на canary :
http_requests_total{job="prometheus",group="canary"}
Также возможно отрицательное совпадение значения метки или совпадение значений метки
против регулярных выражений. Существуют следующие операторы сопоставления меток:
Существуют следующие операторы сопоставления меток:
-
=: выберите метки, точно соответствующие предоставленной строке. -
!=: выберите метки, которые не равны предоставленной строке. -
=~: Выберите метки, которые соответствуют регулярному выражению предоставленной строке. 9foo$" .Например, это выбирает все временные ряды
http_requests_totalдляstaging,тестированиеиразработкасред и методов HTTP, отличных отGET.http_requests_total{environment=~"постановка|тестирование|разработка", метод!="GET"}Сопоставители меток, соответствующие пустым значениям меток, также выбирают все временные ряды, которые вообще не имеют конкретной метки. Для одного и того же имени метки может быть несколько сопоставителей.
Векторные селекторы должны либо указывать имя, либо хотя бы один сопоставитель меток который не соответствует пустой строке.
 Следующее выражение недопустимо:
Следующее выражение недопустимо:{job=~".*"} # Плохо!Напротив, эти выражения допустимы, поскольку они оба имеют селектор, который не соответствуют пустым значениям меток.
{job=~".+"} # Хорошо! {job=~".*",method="get"} # Хорошо!Сопоставители меток также можно применять к именам метрик путем сопоставления с внутренним
__имя__ 9этикетка 0512. Например, выражениеhttp_requests_totalэквивалентно{__name__="http_requests_total"}. Также можно использовать сопоставления, отличные от=(!=,=~,!~). Следующее выражение выбирает все метрики, имя которых начинается сjob::{__name__=~"job:.*"}Имя метрики не должно быть одним из ключевых слов
bool,на,игнорируя,группа_слеваигруппа_справа. Следующее выражение является недопустимым:on{} # Плохо!Чтобы обойти это ограничение, используйте метку
__name__:{__name__="on"} # Хорошо!Все регулярные выражения в Prometheus используют RE2 синтаксис.

Селекторы векторов диапазона
Литералы векторов диапазона работают так же, как литералы мгновенных векторов, за исключением того, что они выбрать диапазон выборок назад от текущего момента. Синтаксически время продолжительность добавляется в квадратных скобках (
[]) в конце векторный селектор, чтобы указать, как далеко назад должны быть извлечены значения времени для каждый результирующий элемент вектора диапазона.В этом примере мы выбираем все значения, которые мы записали в течение последних 5 минут для всех временных рядов с именем метрики
http_requests_totalи метка заданияprometheus:http_requests_total{job="prometheus"}[5m]Продолжительность времени
Продолжительность времени указана в виде числа, за которым сразу следует один из следующие единицы:
-
мс- миллисекунды -
с- секунды -
м- минут -
ч- ч -
d- дни - если в сутках всегда 24 часа -
w- недели - при условии, что в неделе всегда 7 дней -
y- годы - при условии, что год всегда равен 365d
Продолжительность времени может быть объединена конкатенацией.
 Установки необходимо заказывать в
от самого длинного до самого короткого. Данный юнит должен появляться только один раз за определенный период времени.
Установки необходимо заказывать в
от самого длинного до самого короткого. Данный юнит должен появляться только один раз за определенный период времени.Вот несколько примеров допустимой продолжительности времени:
5 часов 1ч40м 5м 10 с
Модификатор смещения
Модификатор
offsetпозволяет изменить смещение времени для отдельных мгновенные и диапазонные векторы в запросе.Например, следующее выражение возвращает значение
http_requests_total5 минут в прошлом относительно текущего время оценки запроса:http_requests_total смещение 5 м
Обратите внимание, что смещение
9Модификатор 0512 всегда должен следовать за селектором сразу, т.е. будет правильным следующее:sum(http_requests_total{method="GET"} offset 5m) // ХОРОШО.Хотя следующее будет неверным :
sum(http_requests_total{method="GET"}) offset 5m // INVALID.То же самое работает для векторов диапазона.
 Это возвращает 5-минутную ставку, которая
Это возвращает 5-минутную ставку, которая http_requests_totalнеделю назад:rate(http_requests_total[5m] offset 1w)
Для сравнения с временными сдвигами вперед во времени отрицательное смещение можно указать:
rate(http_requests_total[5m] offset -1w)
Обратите внимание, что это позволяет запросу опережать время его оценки.
@ модификатор
Модификатор
@позволяет изменить время оценки для отдельных мгновений и диапазон векторов в запросе. Время, подаваемое модификатору@является отметкой времени unix и описывается литералом с плавающей запятой.Например, следующее выражение возвращает значение
http_requests_totalв2021-01-04T07:40:00+00:00:http_requests_total @ 1609746000
Обратите внимание, что модификатор
@всегда должен следовать за селектором сразу, т.е. будет правильно:sum(http_requests_total{method="GET"} @ 1609746000) // ХОРОШО.
Хотя следующее будет неверным :
sum(http_requests_total{method="GET"}) @ 1609746000 // НЕДЕЙСТВИТЕЛЬНО.То же самое работает для векторов диапазона. Это возвращает 5-минутную ставку, которая
http_requests_totalимел на2021-01-04T07:40:00+00:00:скорость (http_requests_total[5m] @ 1609746000)
Модификатор
@поддерживает все описанные представления литералов с плавающей запятой выше в пределахint64. Его также можно использовать вместе с модификаторомoffset, где смещение применяется относительно@время модификатора независимо от того, какой модификатор записан первым. Эти 2 запроса дадут один и тот же результат.# смещение после @ http_requests_total @ 1609746000 смещение 5м # смещение перед @ http_requests_total смещение 5 м @ 1609746000
Кроме того,
start()иend()также могут использоваться как значения для модификатора@в качестве специальных значений.
Для запроса диапазона они разрешаются в начало и конец запроса диапазона соответственно и остаются одинаковыми для всех шагов.
Для мгновенного запроса
start()иend()оба разрешаются во время оценки.http_requests_total при запуске() скорость(http_requests_total[5m] @ end())
Обратите внимание, что модификатор
@позволяет запросу опережать время его оценки.Подзапрос
Подзапрос позволяет выполнить мгновенный запрос для заданного диапазона и разрешения. Результатом подзапроса является вектор диапазона.
Синтаксис:
<мгновенный_запрос> '[' <диапазон> ':' [<разрешение>] ']' [ @] [ смещение <длительность> ] -
<разрешение>является необязательным. По умолчанию используется глобальный интервал оценки.
Операторы
Prometheus поддерживает множество бинарных операторов и операторов агрегации. Они описаны подробно на странице операторов языка выражений.

Функции
Prometheus поддерживает несколько функций для работы с данными. Они описаны подробно на странице функций языка выражений.
PromQL поддерживает комментарии к строке, начинающиеся с
#. Пример:# Это комментарий
Попался
Несвежесть
При выполнении запросов выбираются метки времени для выборки данных независимо от фактических текущих данных временного ряда. В основном это поддержка такие случаи, как агрегация (
сумма,avgи т. д.), где несколько агрегированных временные ряды точно не совпадают во времени. Благодаря своей независимости, Prometheus должен присвоить значение этим временным меткам для каждого соответствующего времени. серии. Он делает это, просто беря самую новую выборку до этой метки времени.Если целевая очистка или оценка правила больше не возвращает образец в течение некоторого времени серии, которая присутствовала ранее, эта временная серия будет помечена как устаревшая.
 Если цель удалена, ее ранее возвращенный временной ряд будет помечен как
вскоре после этого устареет.
Если цель удалена, ее ранее возвращенный временной ряд будет помечен как
вскоре после этого устареет.Если запрос оценивается по отметке времени выборки после отметки временного ряда stale, то для этого временного ряда не возвращается никакого значения. Если новые образцы впоследствии принятые для этого временного ряда, они будут возвращены как обычно.
Если образец не найден (по умолчанию) за 5 минут до метки времени выборки, в данный момент времени для этого временного ряда не возвращается никакого значения. Этот фактически означает, что временные ряды «исчезают» с графиков в те моменты времени, когда их последний собранный образец старше 5 минут или после того, как они помечены как устаревшие.
Устаревание не будет помечаться для временных рядов, в которые включены временные метки. их царапины. В этом случае будет применяться только 5-минутный порог.
Предотвращение медленных запросов и перегрузок
Если запрос должен работать с очень большим объемом данных, его графическое представление может время ожидания или перегрузка сервера или браузера.
 Таким образом, при построении запросов
над неизвестными данными, всегда начинайте строить запрос в табличном представлении
Браузер выражений Prometheus, пока набор результатов не покажется разумным
(в лучшем случае сотни, а не тысячи временных рядов). Только после того, как вы отфильтруете
или достаточно агрегировали ваши данные, переключитесь в режим графика. Если выражение
по-прежнему занимает слишком много времени для создания графика ad-hoc, предварительно запишите его с помощью записи
правило.
Таким образом, при построении запросов
над неизвестными данными, всегда начинайте строить запрос в табличном представлении
Браузер выражений Prometheus, пока набор результатов не покажется разумным
(в лучшем случае сотни, а не тысячи временных рядов). Только после того, как вы отфильтруете
или достаточно агрегировали ваши данные, переключитесь в режим графика. Если выражение
по-прежнему занимает слишком много времени для создания графика ad-hoc, предварительно запишите его с помощью записи
правило.Это особенно актуально для языка запросов Prometheus, где Селектор имени метрики, такой как
api_http_requests_total, может расширяться до тысяч временных рядов с разными метками. Также имейте в виду, что выражения, которые агрегирование по многим временным рядам создаст нагрузку на сервер, даже если вывод - это лишь небольшое количество временных рядов. Это похоже на то, как это было бы медленно суммировать все значения столбца в реляционной базе данных, даже если выходное значение - это только одно число.
-

 12.16
12.16 д..
д..
 1 x
1 святой 46
2 Кортни 19
3 Миа 18
4 Оливия 295 Солнечный 11
1 x
1 святой 46
2 Кортни 19
3 Миа 18
4 Оливия 295 Солнечный 11
 Сделайте то же самое для y-компонентов.
Сделайте то же самое для y-компонентов.
 ?[0-9]+([eE][-+]?[0-9]+)?
| 0[xX][0-9a-fA-F]+
| [нН][аА][нН]
| [ii][nN][fF]
)
?[0-9]+([eE][-+]?[0-9]+)?
| 0[xX][0-9a-fA-F]+
| [нН][аА][нН]
| [ii][nN][fF]
)
 Следующее выражение недопустимо:
Следующее выражение недопустимо:
 Установки необходимо заказывать в
от самого длинного до самого короткого. Данный юнит должен появляться только один раз за определенный период времени.
Установки необходимо заказывать в
от самого длинного до самого короткого. Данный юнит должен появляться только один раз за определенный период времени.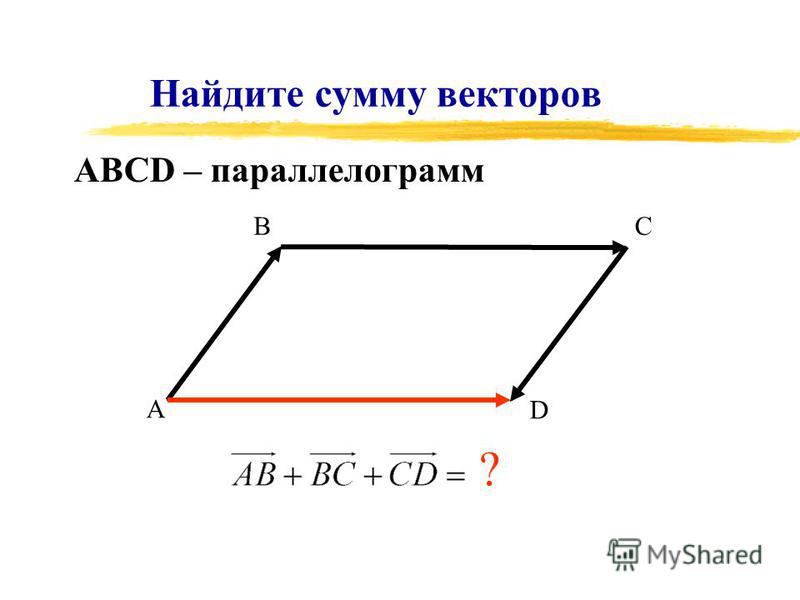 Это возвращает 5-минутную ставку, которая
Это возвращает 5-минутную ставку, которая 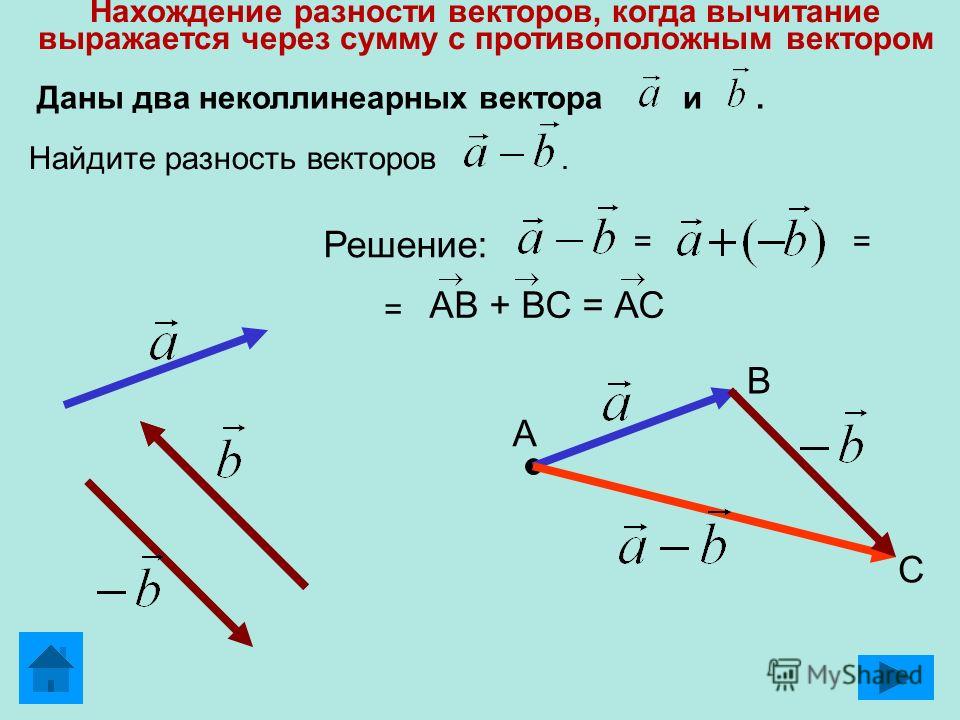
 Если цель удалена, ее ранее возвращенный временной ряд будет помечен как
вскоре после этого устареет.
Если цель удалена, ее ранее возвращенный временной ряд будет помечен как
вскоре после этого устареет. Таким образом, при построении запросов
над неизвестными данными, всегда начинайте строить запрос в табличном представлении
Браузер выражений Prometheus, пока набор результатов не покажется разумным
(в лучшем случае сотни, а не тысячи временных рядов). Только после того, как вы отфильтруете
или достаточно агрегировали ваши данные, переключитесь в режим графика. Если выражение
по-прежнему занимает слишком много времени для создания графика ad-hoc, предварительно запишите его с помощью записи
правило.
Таким образом, при построении запросов
над неизвестными данными, всегда начинайте строить запрос в табличном представлении
Браузер выражений Prometheus, пока набор результатов не покажется разумным
(в лучшем случае сотни, а не тысячи временных рядов). Только после того, как вы отфильтруете
или достаточно агрегировали ваши данные, переключитесь в режим графика. Если выражение
по-прежнему занимает слишком много времени для создания графика ad-hoc, предварительно запишите его с помощью записи
правило.