Найти десятичный логарифм онлайн: Калькулятор десятичный логарифм

Урок 3.

Подготовка к ЕГЭ по математике

Эксперимент

Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами.

Теория

Конспект урока

На предыдущих уроках мы обсуждали показательную функцию, решение показательных уравнений и неравенств.

Определение логарифма

Когда мы обсуждали решение показательных уравнений, то нам всегда удавалось представить обе части в виде степеней с одинаковыми основаниями.

Но вполне логично, что может возникнуть ситуация, когда это сделать не удастся. Например, решить уже рассмотренными методами уравнение  не получится, так как 5 мы пока не умеем представлять в виде степени с основанием 2.

С другой стороны, мы обсуждали тот факт, что показательная функция принимает любое положительное значение. Поэтому, в какой-то точке значение функции  должно равняться 5.

Фактически, мы столкнулись с ситуацией, похожей на извлечение корня – мы точно знали, что есть число, квадрат которого равен 2, но не могли записать его доступными нам методами. В том случае мы поступили следующим образом: ввели новое понятие «корень» и операцию извлечение корня, которая была обратна возведению в степень.

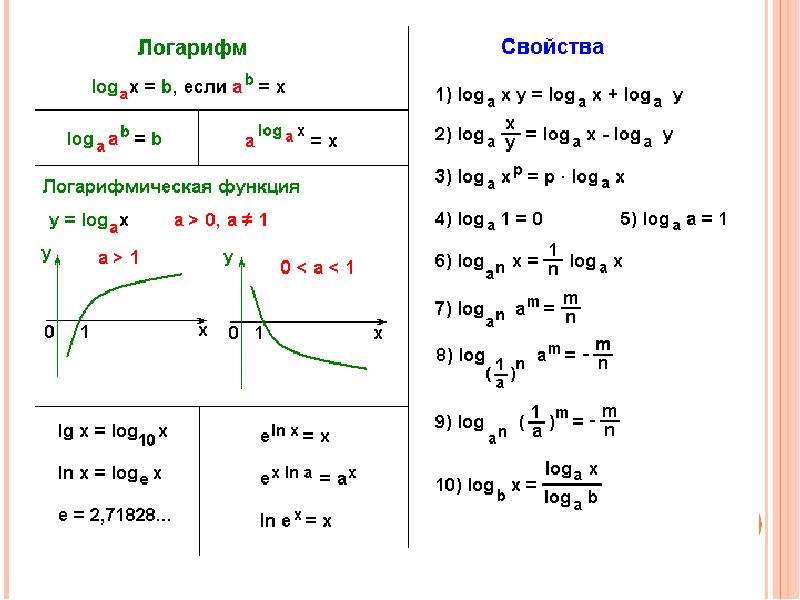
Возвращаясь к нашей проблеме, нам придётся поступить аналогично. Обозначим степень, в которую надо возвести 2, чтобы получить 5, как  – логарифм пяти по основанию 2.

То есть, определение логарифма следующее: для . То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().

Рассмотрим простейшие примеры вычисления логарифмов:

1) , так как .

2) , так как .

3) , так как .

4), так как .

Особые виды логарифмов

Существует два специальных вида логарифмов: десятичный и натуральный.

Десятичный логарифм – это логарифм с основанием 10. Он обозначается следующим образом: .

Натуральный логарифм – это логарифм с основанием  (напомним, что ). Он обозначается следующим образом: .

Основное логарифмическое тождество

Исходя из определения логарифма , легко получить следующее свойство, которое называется основным логарифмическим тождеством. Для этого достаточно подставить вторую формулу в первую. В результате получаем: .

Это выражение называется основным логарифмическим тождеством.

Свойства логарифмов

Давайте сформулируем ещё несколько основных свойств логарифмов ().

1)      (т.к. ),  

2)      

3)    

4)     

5)    Формула перехода к новому основанию:  

6)    (т.к. )

7)    (т.к. )

На этом уроке мы с вами сформулировали определение логарифма, основное логарифмическое тождество и свойства логарифма.

В практической части урока мы научимся вычислять различные логарифмы, а также преобразовывать выражения, содержащие логарифмы.

Полезные ссылки:

1)      Алгебра 11 класс: «Понятие логарифма» 

2)      Алгебра 11 класс: «Понятие логарифма. Простейшие задачи»

3)      Алгебра 11 класс: «Свойства логарифмов. Логарифм произведения и частного» 

4)      Алгебра 11 класс: «Свойства логарифмов. Логарифм степени» 

5)      Алгебра 11 класс: «Свойства логарифмов. Решение более трудных задач» 

6)      Алгебра 11 класс: «Переход к новому основанию логарифма» 

7)      Алгебра 11 класс: «Переход к новому основанию логарифма. Решение задач» 

Видеоурок: Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами. Теория по предмету Алгебра за 11 класс.

МАТЕМАТИКА Форма 2 Тема 4

ЛОГАРИТМЫ

Мы всегда спрашиваем себя, сколько одного числа нужно умножить, чтобы получить другое число? Например; сколько троек нужно умножить, чтобы получить 81? Ответы на все эти вопросы будут даны в этом блоке. Убедитесь, что вы понимаете. Начните читать сейчас……! Стандартная форма

также называется научной нотацией. Это способ записи числа из двух частей. Например,

• цифр (с десятичной запятой после первой цифры), за которыми следует
• X 10 в степени , которая ставит десятичную точку там, где она должна быть (т. е. показывает, на сколько знаков нужно переместить десятичную точку).

Числа в стандартной форме

Запись чисел в стандартной форме

Как записать числа в стандартной форме?

Чтобы вычислить степень числа 10, подумайте, на сколько знаков после запятой нужно переместить:

• Когда число равно 10 или больше, десятичный разряд должен смещаться влево, и степень числа 10 будет положительной. Например; 47 055 = 4,7055 х 10 ⁴
• Когда число меньше 1, десятичная точка должна сместиться вправо, а степень числа 10 будет отрицательной. Например;

0,00025 будет записано как 2,5 x 10 ^-4

Обратите внимание: После ввода числа в экспоненциальном представлении убедитесь, что цифровая часть находится в диапазоне от 1 до 10 (может быть 1, но не 10). А силовая часть точно показывает, на сколько знаков нужно переместить десятичную точку.

Вычисления, включающие умножение и деление чисел, выраженных в стандартной форме

Выполнение вычислений, включающих умножение и деление чисел, выраженных в стандартной форме мы умножаем, чтобы получить другое число. Например; сколько двоек нужно умножить, чтобы получить 16? Ответ: 2 x 2 x 2 x 2 = 16, поэтому нам нужно было умножить 4 двойки, чтобы получить 16. Таким образом, логарифм равен 4.

Как это написать?

^{Мы запишем количество двоек, которое нужно умножить, чтобы получить 16 равно 4, как:}

Две вещи одинаковы:

Число, которое мы умножаем, называется основанием. Таким образом, мы можем сказать: «логарифм 16 по основанию 2 равен 4», или «логарифм 16 по основанию 2 равен 4», или «логарифм 16 по основанию 2 равен 4».

Не то чтобы мы имели дело с 3 числами:

• Основание (число, которое мы умножаем в нашем примере, равно 2)
• Сколько раз использовать его при умножении (в нашем примере это 4 раза, что является логарифмом)
• Число, которое мы хотим получить (в нашем примере это 16)

Существует связь между показателями степени и логарифмами. Показатель степени говорит, сколько раз использовать число при умножении, а логарифм говорит вам, что такое показатель степени. См. Иллюстрацию ниже:

Обычно: A ^x = Y в логарифмической форме: log _A Y = X

Пример 1

Напишите следующие статистики в Logarith.0003

Законы логарифмов

Назовите законы логарифмов

Есть несколько законов логарифмов, которые помогают в их вычислении. Эти законы справедливы только для положительных действительных чисел. Законы таковы:

Проверка законов логарифмов, используя знание показателей

Проверка законов логарифмов, используя знание показателей

Задание 1

Проверка законов логарифмов, используя знание показателей

Законы логарифмов для упрощения логарифмических выражений

Использование законов логарифмов для упрощения логарифмических выражений

Пример 2

Использование законов логарифмов для вычисления следующего:

Решение

Это1 Изменение основания формула изменения основания.

Дано,

, затем находим число, которое является общим основанием для 8 и 4

Пример 3

Решить.

логарифмы для базы 10

Логарифмическое уравнение

Решение логарифмического уравнения

Используйте законы логарифмов для оценки следующих:

Решение

Законы логарифмов для поиска продуктов, котиров Применение законов логарифмов для нахождения произведений, частных, корней и степеней чисел

Здесь мы имеем дело со всеми 4 операциями: сложением, вычитанием, умножением и делением. Все операции такие же, как обычные операции, за исключением деления, когда нам дается отрицательная характеристика. Например; 9Пример 4 . Когда мы хотим прочитать логарифм числа из логарифмической таблицы, мы сначала проверяем, находится ли число между 0 и 10 (но не 0 или 10), потому что таблица состоит только из логарифмов чисел от 0 до 1.

Например; каков логарифм 5,25 из таблицы. Наше число находится между 0 и 1. Смотрим на крайний левый столбец и находим, где 52 (десятичная точка игнорируем). Затем проведите пальцем по этой строке вправо, чтобы найти столбец следующей цифры, в нашем примере это 5. Прочитайте число, где строка 52 встречается со столбцом 5. Логарифм 5,25 равен 0,7202.

Если число состоит из 4 цифр, например 15,27, мы делаем следующее. Прежде всего, проверив наше число, мы видим, что оно больше 10. Число находится между 10 и 100. И мы знаем, что логарифм 10 равен 1, а логарифм 100 равен 2. Итак, логарифм 15,27 находится между 1 и 2. , обычно меньше 2, но больше 1, следовательно, 1.something. Это то, что нам нужно найти в таблице логарифмов. Посмотрите на крайний левый столбец, на строку с номером 15, затем проведите пальцем вправо, чтобы найти столбец с номером 2. Прочитайте число, где ряд 15 встречается со столбцом 2, это число равно 0,1818. Мы остаемся с одной цифрой, равной 7. Если в вашей таблице журналов есть часть с таблицей средних разностей, проведите пальцем к столбцу в этой таблице, отмеченному следующей цифрой числа, которое вы ищете, в нашем примере это 7.

Обратите внимание: если вам дали число, состоящее более чем из 4 цифр, сначала округлите число до 4 цифр, а затем выполните аналогичные процедуры, как описано в примерах выше.

Чтобы найти число, логарифм которого известен, мы можем назвать его муравьиным логарифмом, можно использовать ту же логарифмическую таблицу. Например, чтобы найти число, логарифм которого равен 0,7597, посмотрите в центральную часть таблицы журнала и найдите число (мантисса) 7597. Оно находится на пересечении строки с меткой 57 и столбца 5. Таким образом, число равно 575. Но в чтобы получить правильный ответ, мы должны рассмотреть характеристику нашего логарифма, которая равна 0. Это означает, что наше число находится между 0 и 10, потому что числа, логарифмы которых равны 0.something, находятся между 0 и 10. Следовательно, нам нужно поставить одну десятичную точку слева до нашего числа, чтобы оно находилось в диапазоне от 0 до 10. Следовательно, число будет 5,75, т.е. log 5,75 = 0,759.7, таким образом, антилогарифм 0,7597=5,75.

Как найти ant-log

Шаг 1:  Понять таблицу ant-log. Используйте его, когда у вас есть журнал числа, но не сам номер. муравьиный журнал также известен как обратный журнал.

Шаг 2:  Запишите характеристику. Это число до десятичной точки. Если вы ищете муравьиный журнал 2,8699, характеристика равна 2. Удалите ее из числа, которое вы ищете. Но никогда не забывайте об этом, потому что это будет использоваться позже. Так что лучше, если вы это где-нибудь напишете.

Шаг 3:  Найдите строку в крайнем левом столбце, которая соответствует первым двум числам мантиссы. Наша мантисса равна 8699. Так что проведите пальцем вниз по столбцу, пока не найдете 0,86.

Шаг 4:  Проведите пальцем к столбцу, отмеченному следующей цифрой мантиссы. Для 2,8699 проведите пальцем по строке, отмеченной 0,86, чтобы найти пересечение со столбцом 9. Это читает 7396. Запишите это.

Шаг 5:  Если в таблице ant-log есть таблица средних разностей, проведите пальцем к столбцу в этой таблице, отмеченному следующей цифрой мантиссы. Следите за тем, чтобы палец оставался в том же ряду. В нашем примере проведите пальцем по последнему столбцу таблицы, столбцу 9.. Пересечение строки 0,86 и столбца разности средних 9 равно 15. Запишите это.

Шаг 6:  Сложите два числа, полученные на двух предыдущих шагах. В нашем примере это 7396 и 15. Складываем их, т. е. 7396 + 15 = 7411.

Шаг 7:  Используйте характеристику для размещения десятичной точки. Наша характеристика равна 2, что означает, что наш ответ находится между 100 и 1000, потому что log 100 = 2 и log 1000 = 3. Чтобы число 7411 попало между 100 и 1000, десятичная точка должна быть помещена после 3 цифр. Таким образом, окончательный ответ равен 741,1, следовательно, муравьиный журнал равен 2,869.9 равно 741,1.

Пример 5

Найдите произведение 25,75 × 450.

Раствор;

Из логарифмических законов мы видели, что умножение двух чисел равносильно сложению двух одинаковых чисел. Как это сделать?

Пусть x = 25,75 × 450

log x = log (25,75 × 450)

, что равно

. найдем:

log 25,75 = 1,4108 и log 450 = 2,6532

, таким образом, log x = 1,4108 + 2,6532

log x = 4,0640

, чтобы получить значение x, мы должны найти обратный логарифм 4,0640 или антлог 4,0640

поэтому, x = ant-log 4,0640

x = 11590

, следовательно, 25,75 × 450 = 11590

всегда логарифмические вычисления представлены в табличной форме, чтобы решение не было слишком длинным, как указано выше.

Если представить наш пример в табличной форме, он будет выглядеть так:

Логарифмические таблицы для нахождения корней и степени чисел

Применение логарифмических таблиц для нахождения корней и степеней чисел

Пример 6

Вычисление с использованием логарифмов

Решение

Упражнение 1

245. 750

2. Запишите каждое из следующих чисел десятичными цифрами:

3. Рассчитайте значение x для каждого из следующих:

4. Упростите каждое из следующих, не используя логарифмическую таблицу:

5. Учитывая, что log 2 = 0,3010, log 3 = 0,4771 и log 7 = 0,8451, найдите

6. Найдите log каждого из следующих чисел, используя логарифмическую таблицу:

1. 500
2. 0,00135
3. 52. 25
4. 895000

7. Найдите значение x для каждого из следующих чисел:

1. Log x = 2,8751
2. Лог х = 1,8186

8. Найдите значение каждого из следующих выражений:

10. Определите число,

1. Логарифм по основанию 10 равен -3
2. Логарифм по основанию 5 равен 3

• ПРОЧИТАЙТЕ ТЕМУ 5: 

Калькулятор — журнал(18) — Solumaths

Журнал онлайн-расчетов

Сводка:

Функция журнала вычисляет логарифм числа в режиме онлайн.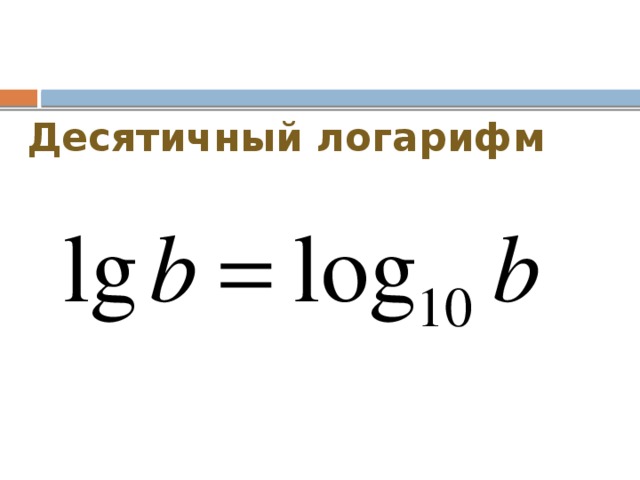

log online

Описание:

Функция логарифма определена для любого числа, принадлежащего интервалу ]0,`+oo`[ это отмечает журнал .

Калькулятор логарифмов позволяет вычислять этого типа логарифмов онлайн .

1. Вычисление логарифма

Для вычисления логарифма числа просто введите число и примените функция лог . Таким образом, для вычисление логарифм числа 1, необходимо ввести журнал(`1`) или непосредственно 1, если лог кнопки уже появляется, возвращается результат 0.

2. Производная логарифма

Производная логарифма равна `1/(x*ln(10))`.

3. Первообразная логарифма

Первообразная логарифма равна `(x*ln(x)-x)/ln(10)`.

4. Пределы логарифмирования

Пределы логарифма существуют при `0` и `+oo`:
• Функция логарифмирования имеет предел в `0`, т.е. `-oo`.
`lim_(x->0)log(x)=-oo`
• Функция логарифмирования имеет предел в `+oo`, который равен `+oo`.
`lim_(x->+oo)log(x)=+oo`

Синтаксис:

log(x), x — число.

Примеры:

log(1), возвращает 0

Производный логарифм:

Чтобы дифференцировать логарифм функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную логарифмической функции

Производная log(x) является производной(`log(x)`)=`1/(ln(10)*x)`

Логарифм первообразной :

Калькулятор первообразной позволяет вычислить первообразную логарифмическая функция.

Первопроизводная log(x) является первообразной(`log(x)`)=`(x*log(x)-x)/ln(10)`

Предельный логарифм :

Калькулятор предела позволяет вычислить пределы функции логарифма.