Наши приборы работают за вас!
Калькуляторы
Калькулятор расчета экспозиционной дозы теплового облучения
Калькулятор помогает рассчитывать экспозиционную дозу теплового облучения, указывает класс условий труда по параметру интенсивность теплового облучения, а также класс условий труда по параметру доза теплового облучения. Необходимо указать интенсивность теплового излучения, длительность воздействия и отметить участки тела, которые подвергаются облучению. Программа выдаст результаты и рекомендации по возможным способам обеспечения допустимых условий труда.
Виброакустический калькулятор НТМ
При обработке результатов измерений уровней звука и ускорения используются операции возведения в степень и логарифмирования. Это неудобно даже с использованием инженерных или научных калькуляторов. Компания НТМ-Защита давно предлагает специализированный калькулятор, делающий такие вычисления не сложнее простых арифметических операций на обычном калькуляторе. Виброакустический калькулятор стал широко распространенным инструментом для многих не только потому, что входит во все комплектации приборов серии АССИСТЕНТ, но и потому, что применим к результатам измерений приборами любых марок и компаний.
Компания НТМ-Защита давно предлагает специализированный калькулятор, делающий такие вычисления не сложнее простых арифметических операций на обычном калькуляторе. Виброакустический калькулятор стал широко распространенным инструментом для многих не только потому, что входит во все комплектации приборов серии АССИСТЕНТ, но и потому, что применим к результатам измерений приборами любых марок и компаний.
Калькулятор-9612
Калькулятор для ГОСТ ISO 9612-2016 «Акустика. Измерение шума для оценки его воздействия на человека. Метод измерения на рабочих местах». Калькулятор-9612 выполняет все вычисления, предусмотренные стандартом.
Калькулятор-20444
Эквивалентный уровень звука транспортного потока на интервале наблюдения определяется по измерениям звукового воздействия единичных проездов транспортных средств разных категорий.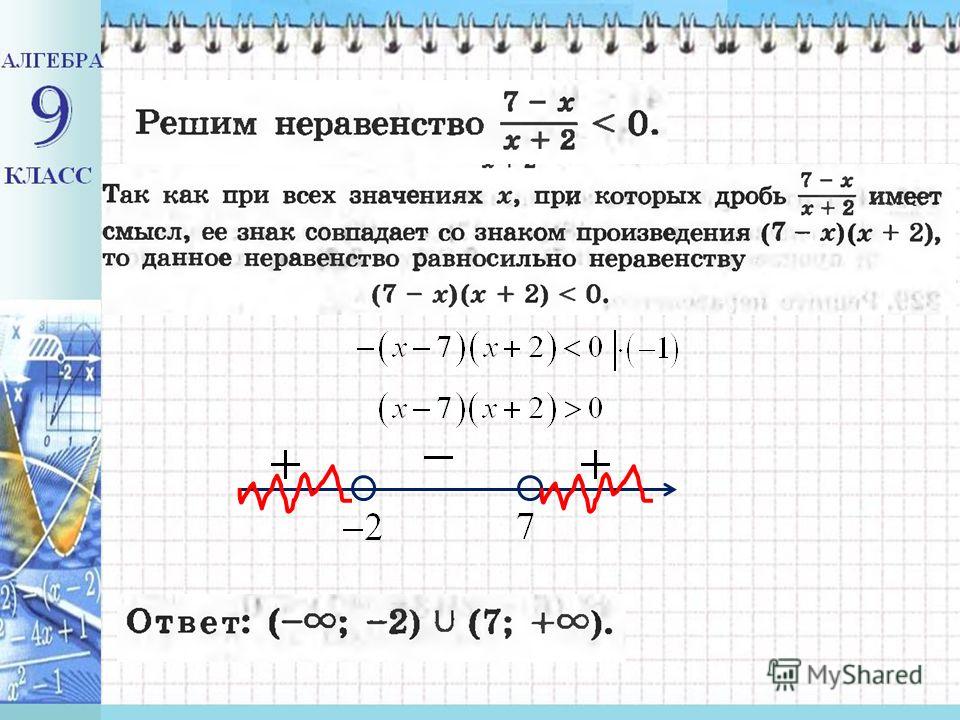 Вариант рекомендован для неинтенсивных транспортных потоков. В расчете используется также число единиц транспорта каждой категории, проходящих мимо точки измерения за интервал наблюдения. Для расчетов по этому методу мы подготовили отдельный калькулятор-20444. Он позволяет вычислить эквивалентный уровень звука транспортного потока на интервале наблюдения и неопределенность результата.
Вариант рекомендован для неинтенсивных транспортных потоков. В расчете используется также число единиц транспорта каждой категории, проходящих мимо точки измерения за интервал наблюдения. Для расчетов по этому методу мы подготовили отдельный калькулятор-20444. Он позволяет вычислить эквивалентный уровень звука транспортного потока на интервале наблюдения и неопределенность результата.
Калькулятор НТМ-Термо
С помощью калькулятора НТМ-Термо можно определить степень вредности микроклиматических условий, действующих на организм человека и рассчитать допустимое пребывание в этих условиях. Подобрать параметры одежды, рассчитать величину дополнительного теплового облучения с целью создания допустимых и оптимальных условий труда. В качестве входной информации требуется ввести значения параметров микроклимата в соответствующие поля.
Калькулятор НТМ-Выбор
Калькулятор НТМ-Выбор помогает осуществить рациональный выбор необходимой аппаратуры. В основу работы программы-калькулятора положена методика, использующая алгоритмы оценки качества, развитые в рамках прикладной квалиметрии.
Лазерный калькулятор
Основная задача калькулятора — определение коэффициента степени опасности лазерного излучения (КСОЛ) при работе оператора с лазерными установками при воздействии на глаза и кожу для конкретной точки контроля.
Онлайн калькулятор по составляющим интервалам
Предназначен для расчета эквивалентного уровня за период оценки, если он состоит из интервалов времени со следующими свойствами. Воздействие фактора на интервале создается одним или несколькими источниками, характерными для этого интервала. В течение интервала генерация воздействующего фактора происходит в типичном для интервала режиме или состоит из ограниченного набора таких режимов. При этом продолжительность составляющих интервалов может быть измерена или установлена в результате анализа ситуации. Например, для эквивалентного уровня звука А и периода оценки, равного рабочей смене, калькулятор составляющих интервалов является аналогом калькулятора-9612.
При этом продолжительность составляющих интервалов может быть измерена или установлена в результате анализа ситуации. Например, для эквивалентного уровня звука А и периода оценки, равного рабочей смене, калькулятор составляющих интервалов является аналогом калькулятора-9612.
Онлайн калькулятор по составляющим событиям
Предназначен для расчета эквивалентного уровня за период оценки, если влияние фактора создается кратковременными событиями, как правило, до нескольких минут. При этом события могут быть разделены на категории так, что уровни воздействия фактора для событий одной категории близки, а число событий каждой категории за период оценки может быть измерено или получено в результате анализа ситуации. Для транспорта примером категорий служат разделение на воздействие пригородных, грузовых, скоростных и других типов железнодорожных составов. Для авиации – разделение на типы ВС, виды ВПО, и т.п. Калькулятор составляющих событий является аналогом калькулятора-20444.
Помогите нам стать лучше!
Оставляйте Ваши комментарии, отзывы и мнения о работе калькуляторов на нашем форуме в разделе “Ваше мнение”
Онлайн калькулятор: Изоляция корней многочлена
УчебаМатематикаАлгебра
Калькуляторы для изоляции вещественных корней полинома методом Штурма и непрерывных дробей (VAS-CF)
Из теоремы Абеля-Руффини, следует, что общее уравнение степени равной 5 или более невозможно решить в радикалах, как например решаются уравнения более низких степеней см. Решение квадратного уравнения, Кубическое уравнение, Решение уравнения 4-й степени.
Для решения уравнений 5-й степени и выше используют численные методы, например: Метод Ньютона, Метод бисекции, Метод хорд или Метод секущих.
Для корректной работы любого численного метода необходимо знать число корней и приближенно знать интервалы, в которых находятся корни уравнения. Калькуляторы представленные ниже, позволяют решить эту задачу. Оба калькулятора находят интервалы корней уравнения, но делают это различными способами.
Калькуляторы представленные ниже, позволяют решить эту задачу. Оба калькулятора находят интервалы корней уравнения, но делают это различными способами.
Первый калькулятор использует более эффективный метод, разработанный Акритасом и Стржебонски. Метод вычисляет диапазоны вещественных корней при помощи непрерывных дробей, основываясь на теореме Винсента1. Метод известен под именем Непрерывные Дроби Винсента-Акритаса-Стржебонски (Vincent-Akritas-Strzebonski Continued Fractions или сокращенно VAS-CF).
Для корректной работы этого метода, входной полином должен быть свободен от квадратов. Для проверки соответствия вашего полинома этому условию используйте Разложение многочлена на свободные от квадратов множители.
Изоляция корней многочлена методом VAS-CF
Многочлен
Коэффициенты многочлена, разделенные пробелом.
Отрицательные значения
Вычислить значения в отрицательной области.
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Следующий калькулятор вычисляет ряд полиномов Штурма и подсчитывает количество изменений знаков значения полиномов в нескольких точках, что дает информацию о числе корней полинома в интервалах, определяемых этими точками, на основе теоремы Штурма2.
Ряд Штурма
Многочлен
Коэффициенты многочлена, разделенные пробелом.
Точность вычисления
Округленно
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
A.G. Akritas, A.W. Strzebonski, P. S. Vigklas, Improving the Performance of the Continued Fractions Method Using New Bounds of Positive Roots, Nonlinear Analysis: Modelling and Control, 2008, Том. 13, N. 3, стр. 265–279 ↩
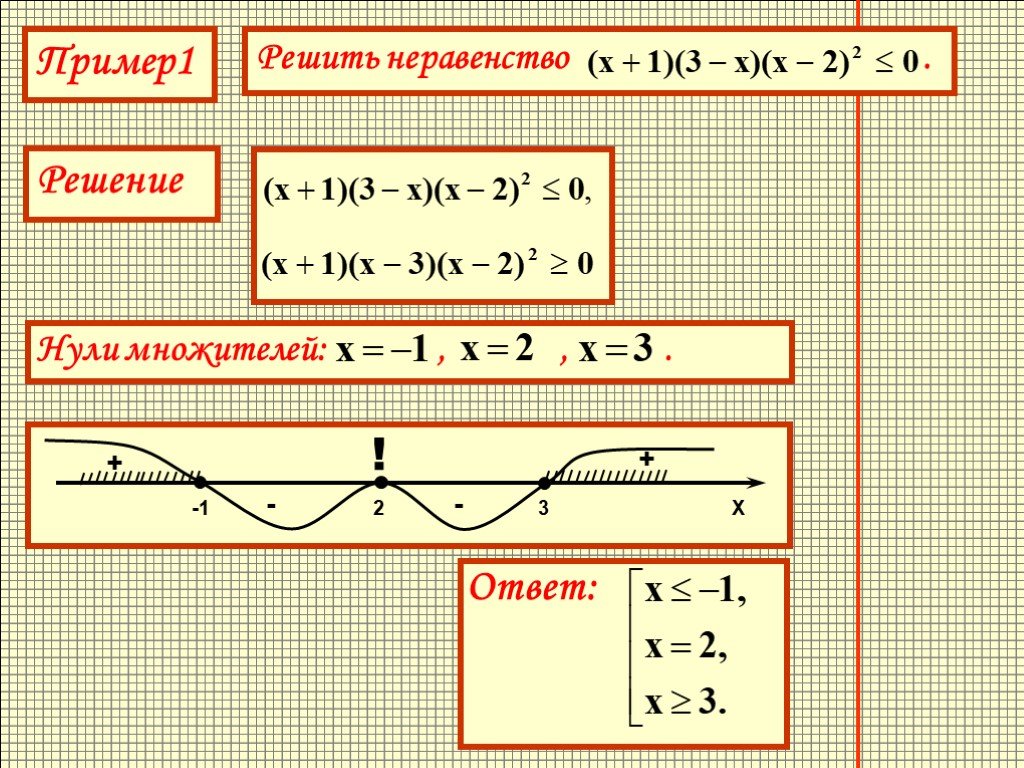
Куликов Л.
 Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979, стр. 521-525 ↩
Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979, стр. 521-525 ↩
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Вычисление корней полинома
- • Метод выделения полного квадрата
- • Сдвиг многочлена
- • Дискриминант
- • Разложение многочлена на свободные от квадратов множители
- • Раздел: Алгебра ( 46 калькуляторов )
#алгебра #многочлен VAS Алгебра границы изоляция корней корень корни Математика метод Штурма многочлен непрерывная дробь полином ряд Штурма теорема Штурма Штурм
PLANETCALC, Изоляция корней многочлена
Anton2020-11-03 14:19:35
Калькулятор доверительного интервала для коэффициента завершения – MeasuringU
Джефф Сауро, доктор философии
1 октября 2005 г.
Используйте этот калькулятор для расчета доверительного интервала и оценки наилучшей точки для наблюдаемой степени завершения.
Вас также может заинтересовать
Загрузите этот калькулятор в файле Excel
Пояснение
Скорректированный метод Вальда следует использовать практически постоянно. Исключения см. ниже.
Подробное обсуждение биномиальных доверительных интервалов для небольших выборок см. в HFES, а обсуждение наилучшей точечной оценки см. в документе JUS.
Скорректированный метод Вальда
Скорректированный интервал Вальда (также называемый модифицированным интервалом Вальда) обеспечивает наилучшее покрытие для указанного интервала, когда количество выборок меньше примерно 150. Другими словами, если вы хотите 95% доверительный интервал, то эта формула даст интервал, который будет содержать наблюдаемую пропорцию в СРЕДНЕМ примерно в 95% случаев. Он использует формулу Вальда, но «скорректирован» тем, что добавляет половину квадрата Z-критического значения к числителю и весь квадрат критического значения к знаменателю перед вычислением интервала, т.
Точный метод
Точный метод был разработан, чтобы гарантировать не менее 95% охвата, в то время как приближенные методы (с поправкой Вальда и оценки) обеспечивают средний охват 95% только в долгосрочной перспективе. Используйте точный метод, когда вам нужно быть уверенным, что вы вычисляете интервал 95% или больше, ошибаясь на консервативной стороне. Например, при уровне заполнения 97,8% и метод Score, и скорректированный метод Вальда имели фактическое покрытие, которое упало до 89. %. Когда риск этого уровня фактического охвата не подходит для приложения, метод Exact обеспечивает необходимую точность. ПРИМЕЧАНИЕ. Мы определили, что существует проблема с нашим кодом для вычисления этого интервала при больших размерах выборки (n>2000). К счастью, при таком большом размере выборки все методы сходятся на одном и том же интервале, поэтому для больших выборок используйте один из других методов.
%. Когда риск этого уровня фактического охвата не подходит для приложения, метод Exact обеспечивает необходимую точность. ПРИМЕЧАНИЕ. Мы определили, что существует проблема с нашим кодом для вычисления этого интервала при больших размерах выборки (n>2000). К счастью, при таком большом размере выборки все методы сходятся на одном и том же интервале, поэтому для больших выборок используйте один из других методов.
Score Method
Score Method обеспечивает лучший охват, чем точный метод и метод Wald, но не соответствует скорректированному методу Wald. Кроме того, его недостатком является сложность вычислений и плохое покрытие некоторых значений, когда коэффициент заполнения составляет около 9.8% или 2%, независимо от размера выборки (Agresti and Coull, 1998). Единственное преимущество использования метода Score заключается в том, что он обеспечивает более точные конечные точки, когда концы интервалов близки к 0 или 1. Для некоторых значений (например, 9/10) скорректированные грубые интервалы Вальда выходят за пределы 0 и 1, и замена >. 999 используется. Для метода оценки верхний интервал равен 0,9975.
999 используется. Для метода оценки верхний интервал равен 0,9975.
Метод Вальда
Метода Вальда следует избегать при расчете доверительных интервалов для коэффициентов завершения с размерами выборки менее 100. Его охват слишком далек от номинального уровня, чтобы обеспечить надежную оценку коэффициента завершения генеральной совокупности. Когда размер выборки превышает 100, все четыре метода сходятся к одинаковым интервалам. Используйте Вальда в качестве точки отсчета или для больших размеров выборки.
* Значения «Погрешности» составляют половину ширины доверительных интервалов. Для скорректированных формул Вальда и Вальда можно использовать пропорцию +/- доверительный интервал. Для точного метода интервалы не симметричны, так как полная пропорция увеличивается от 50% (например, 90% или 15%). Поэтому допустимую погрешность следует использовать только в качестве приближения для точного метода, и следует сообщать фактические значения выше и ниже пропорции.
Когда все пользователи успешно или неуспешно
При небольших размерах выборки часто бывает так, что все пользователи в выборке завершат задачу (коэффициент выполнения 100 %) или все пользователи не справятся с задачей (коэффициент выполнения 0 %). Для этих сценариев часто неприятно сообщать о 100% или 0%. В конце концов, насколько вероятно, что истинный параметр популяции достигает 100% или 0%? Поле «Лучшая оценка» обеспечивает наилучшую точечную оценку в этих условиях и использует для расчета метод Лапласа. Хотя это значение может показаться слишком далеким от наблюдаемых 100 %, его привлекательность заключается в том, что оно зависит от размера выборки: чем больше размер выборки, тем ближе это значение будет к 100 %.
Примечание к расчету: Если наблюдаемая степень завершения равна 100 % или 0 %, двусторонний доверительный интервал невозможен (поскольку у вас не может быть больше 100 % или меньше 0 %). В этих случаях необходимо использовать z-критическое значение для одностороннего доверительного интервала.
Вероятная частота выполнения задач
Два варианта в этом раскрывающемся списке:
Между 0,5 и 1
затем выберите «Между 0,5 и 1» в раскрывающемся списке. См. раздел «Наилучшие оценки» ниже, чтобы узнать, как рассчитывается точечная оценка с помощью этой опции. Неизвестно
Если показатели выполнения вашей задачи обычно принимают широкий диапазон значений, равномерно распределенных между 0 и 1, выберите «Неизвестно» в раскрывающемся списке. Если вы не знаете ни того, ни другого, оставьте значение «Неизвестно». Этот выбор будет использовать метод Лапласа для наилучшей оценки скорости завершения.
Точечные оценки
Принимая во внимание, что доверительный интервал описывает вероятный диапазон или интервал значений, точечная оценка описывает отдельное значение — точка как оценку неизвестного параметра в генеральной совокупности. Вероятность того, что оценка точки выборки совпадает с неизвестной степенью завершения генеральной совокупности, крайне маловероятна. По этой причине вы всегда должны вычислять доверительный интервал, сообщая о степени завершения. Это гораздо более информативно, чем точечная оценка, поскольку она обеспечивает достаточно вероятную границу для степени завершения генеральной совокупности.
Вероятность того, что оценка точки выборки совпадает с неизвестной степенью завершения генеральной совокупности, крайне маловероятна. По этой причине вы всегда должны вычислять доверительный интервал, сообщая о степени завершения. Это гораздо более информативно, чем точечная оценка, поскольку она обеспечивает достаточно вероятную границу для степени завершения генеральной совокупности.
Несмотря на то, что этому методу уделяется мало внимания на вводных занятиях по статистике и он мало повлиял на методы измерения в области инженерии удобства использования, существует богатая история альтернативных методов, разработанных для достижения более точной точечной оценки p, чем простое деление числа успехов. по количеству попыток (например, см. Chew, 1971; Laplace, 1812; Manning & Schutze, 199).9). Эта потребность наиболее очевидна, когда есть экстремальный результат, в частности, когда x=0 (0%) или x=n (100%) — особенно, но не исключительно, когда размеры выборки малы. Ниже подробно описаны четыре метода оценки, которые относятся к ситуациям, более распространенным при тестировании удобства использования:
MLE:(Оценка максимального правдоподобия)(x / n)
MLE представляет собой долю выборки или количество успешных пользователей, деленное на общее количество попыток. Это наиболее распространенная точечная оценка.
Это наиболее распространенная точечная оценка.
Лаплас (x+1)/(n+2)
Известная задача большой выборки возникла в основополагающей работе Лапласа начала 1800-х годов. Он поставил вопрос о том, насколько вы можете быть уверены в том, что солнце взойдет завтра, если вы знаете, что оно всходило каждый день в течение последних 5000 лет (1 825 000 дней). Вы можете быть уверены, что она поднимется, но не можете быть абсолютно уверены. Солнце может взорваться, или большой астероид может разбить Землю на куски. В ответ на этот вопрос он предложил закон наследования Лапласа, который заключается в добавлении единицы к числителю и двух к знаменателю ((x+1)/(n+2)). Применяя эту процедуру, вам будет 99,999945% уверены, что солнце завтра взойдет — близко к 100%, но немного отступили от этой крайности. Величина корректировки больше, когда размеры выборки малы. Например, если вы наблюдаете два успеха из двух и применяете процедуру Лапласа, то ваша оценка p составляет 75% (x+1=3, n+2=4, p=3/4), а не 100%.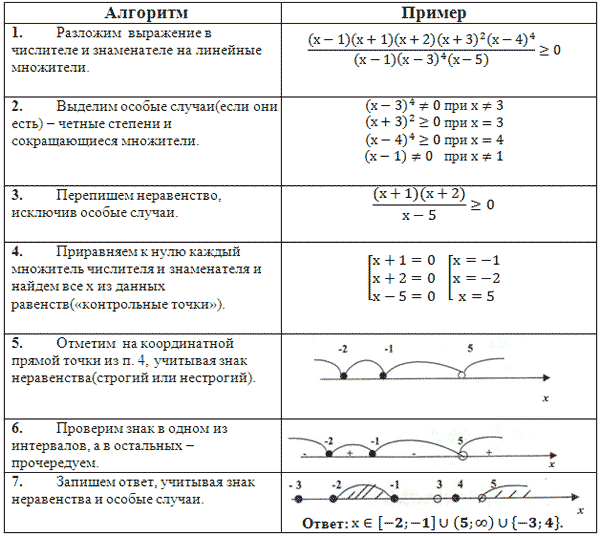
Уилсона (x+z 2 /2)/(n+z 2 )
Точечная оценка Уилсона является средней точкой скорректированного интервала Вальда. Он получается путем прибавления половины критического значения в квадрате к числителю и квадрата критического значения к знаменателю. Услуги Уилсона более консервативны.
Jeffreys (x+.5)/(n+1)
Jeffreys (1961) предложил компромисс между методами Лапласа и MLE. См. ссылку для технических деталей.
Наилучшая оценка
Наилучшая точечная оценка рассчитывается с использованием следующей логики: Если в раскрывающемся списке Вероятная частота заполнения выбрано «Неизвестно», используется метод Лапласа. Чем меньше размер вашей выборки и чем дальше ваша первоначальная оценка p от 0,5, тем больше преимущество над MLE.
Чем меньше размер вашей выборки и чем дальше ваша первоначальная оценка p от 0,5, тем больше преимущество над MLE.
Если в раскрывающемся списке «Вероятная частота завершения популяции» выбрано «От 0,5 до 1», а наблюдаемая скорость завершения составляет:
- Меньше или равно 0,5: используется метод Уилсона.
- Между .5 и .9: используется MLE.
- Более 0,9: используется метод Лапласа (обратите внимание, если 1 > x > 0,9, метод Джефферис также является приемлемой альтернативой).
Нужна дополнительная информация? Обязательно ознакомьтесь с онлайн-руководством по доверительным интервалам.
Ссылки
- Агрести, А., и Коул, Б. (1998). Приблизительный лучше, чем «точный» для интервальной оценки биномиальных пропорций. Американский статистик, 52, 119-126.
- Чу, В. (1971). Точечная оценка параметра биномиального распределения. Американский статистик, 25, 47-50.

- Джеффрис, Х. (1961) Теория вероятностей (3-е изд.), Clarendon Press, Оксфорд, стр. 179.-192.
- Лаплас, PS (1812 г.). Аналитическая теория вероятностей. Париж, Франция: Курсье.
- Льюис, Дж. Р. и Сауро, Дж. (2006) «Когда 100% на самом деле не 100%: повышение точности оценок показателей завершения для небольшой выборки» в Журнале исследований юзабилити, выпуск 3, том. 1, май 2006 г., стр. 136-150
- Manning, C.D., & Schutze, H. (1999). Основы статистической обработки естественного языка. Кембридж, Массачусетс: MIT Press.
- Сауро, Дж. и Льюис, Дж. Р. (2005) «Оценка показателей завершенности по небольшим выборкам с использованием биномиальных доверительных интервалов: сравнения и рекомендации» в Трудах ежегодного собрания Общества человеческого фактора и эргономики (HFES 2005) Орландо, Флорида
Формула метода деления пополам, Калькулятор метода деления пополам, Теория метода деления пополам
Формула метода деления пополам Метод деления пополам — это мощный численный метод для нахождения корней непрерывной функции в заданном интервале. Формула метода деления пополам проста и удобна в реализации, а также гарантирует сходимость к корню. Одним из преимуществ метода является то, что он очень надежен и не требует знания производной функции. Если вы ищете формулу метода деления пополам, прочитайте содержание ниже.
Формула метода деления пополам проста и удобна в реализации, а также гарантирует сходимость к корню. Одним из преимуществ метода является то, что он очень надежен и не требует знания производной функции. Если вы ищете формулу метода деления пополам, прочитайте содержание ниже.
Источник изображения: Fresherslive
Формула метода деления пополам
Метод деления пополам — это численный метод, используемый для аппроксимации корней функции. Метод основан на теореме о промежуточном значении, которая утверждает, что если функция f(x) непрерывна на отрезке [a,b] и принимает на концах значения противоположного знака, то должен быть хотя бы один корень функции на интервале.
Метод деления пополам начинается с деления интервала [a,b] пополам и определения, какая половина интервала содержит корень функции. Если функция имеет противоположные знаки в концах интервала, то по теореме о промежуточном значении должен быть корень функции в интервале. В этом случае метод деления пополам выбирает подынтервал, содержащий корень, и снова делит его пополам и так далее.
Формула для метода деления пополам:
с = (а + b) / 2
где a и b — конечные точки интервала [a,b], а c — его середина. Затем метод деления пополам оценивает функцию в точке с и определяет, имеет ли функция тот же знак в точке с, что и в точках а или b. Если функция имеет тот же знак в точке c, что и в точке a, то корень функции должен находиться в интервале [c, b], а метод деления пополам устанавливает a = c. Если функция имеет тот же знак в точке c, что и в точке b, то корень функции должен находиться в интервале [a, c], а метод деления пополам устанавливает b = c.
Метод деления пополам продолжает делить интервал пополам и оценивать функцию в средней точке, пока не будет достигнут желаемый уровень точности или пока не будет достигнуто максимальное количество итераций. Метод деления пополам — надежный и надежный метод поиска корней функций, но он может медленно сходится, особенно для функций с несколькими корнями или корнями, расположенными очень близко друг к другу.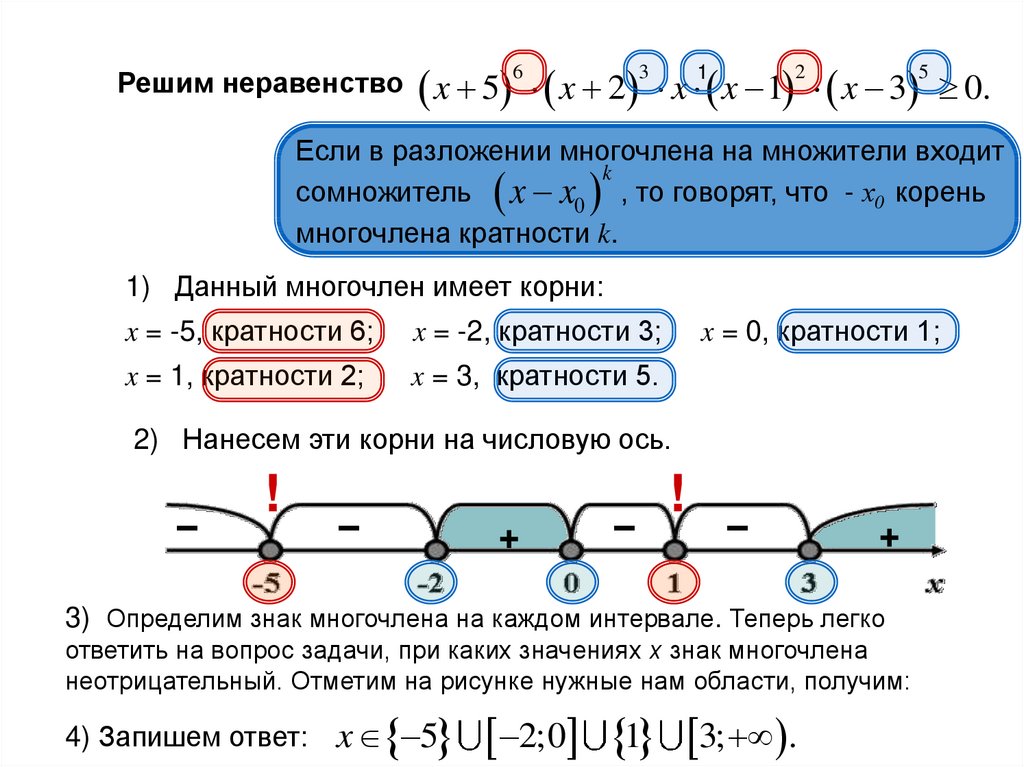
Калькулятор метода деления пополам
Калькулятор метода деления пополам — это программа, использующая метод деления пополам для аппроксимации корней заданной функции. Метод деления пополам — это численный метод, который работает путем деления интервала на два подинтервала и выбора подинтервала, содержащего корень функции. Процесс повторяется путем деления подинтервала пополам и выбора нового подинтервала, содержащего корень, до тех пор, пока не будет достигнут желаемый уровень точности или не будет достигнуто максимальное количество итераций.
Калькулятор метода деления пополам обычно требует, чтобы пользователь ввел функцию, корни которой он хочет найти, интервал [a,b], в котором предположительно находится корень, и желаемый уровень точности. Затем калькулятор будет использовать формулу метода деления пополам, чтобы найти середину интервала [a,b], оценить функцию в средней точке и определить, находится ли корень в левом или правом подынтервале. Процесс повторяется до тех пор, пока не будет достигнут желаемый уровень точности или не будет достигнуто максимальное количество итераций.
Калькулятор метода деления пополам — полезный инструмент для нахождения корней функций, которые не могут быть решены аналитически. Однако важно отметить, что метод деления пополам может медленно сходиться, особенно для функций с несколькими корнями или корнями, расположенными очень близко друг к другу. Таким образом, важно выбрать подходящий интервал и разумное количество итераций, чтобы гарантировать, что метод сходится за разумное время.
Примеры калькулятора метода деления пополам 92 + 2 = 0,578125
Поскольку f(1.25) имеет противоположный знак по сравнению с f(1.5), мы знаем, что корень функции должен находиться в интервале [1.25, 1.5].
- Продолжаем делить интервал пополам и вычислять функцию в средней точке, пока не будет достигнут желаемый уровень точности или не будет достигнуто максимальное количество итераций. В этом случае мы можем продолжать процесс до тех пор, пока размер интервала не станет меньше или равен допуску 0,001: .
- Продолжаем делить интервал пополам и вычислять функцию в средней точке, пока размер интервала не станет меньше или равен допуску 0,001. Продолжаем процесс:
- c = (0,375 + 0,5)/2 = 0,4375, f(0,4375) = -0,3806152344 (корень в [0,375, 0,4375])
- c = (0,375 + 0,4375)/2 = 0,40625, f(0,40625) = -0,0192260742 (корень в [0,40625, 0,4375])
- c = (0,40625 + 0,4375)/2 = 0,421875, f(0,421875) = 0,1616439819 (корень в [0,40625, 0,421875])
- с = (0,40625 + 0,421875)/2 = 0,4140625, f(0,4140625)
- Функция f(x) должна быть непрерывной на интервале [a, b].
- Функции f(a) и f(b) должны иметь противоположные знаки, т. е. f(a) * f(b) < 0. Это условие гарантирует наличие хотя бы одного корня функции в интервале [a, б].
- Функция f(x) должна быть дифференцируемой в интервале (a, b), если для уточнения корневой аппроксимации используется метод Ньютона-Рафсона или любой другой основанный на производной метод.
- Функция f(x) должна быть однозначной функцией в интервале [a, b]. Это означает, что функция не должна иметь кратных корней в интервале.
- Интервал [a, b] должен быть конечным, т. е. a и b должны быть действительными числами.

- Функция f(x) должна быть определена в середине интервала c, т. е. f(c) должна быть корректно определена и конечна.
- Интервал [a, b] не должен содержать особых точек или вертикальных асимптот функции f(x).
- Конечные точки a и b должны быть различными, т. е. a ≠ b. В противном случае интервал не может быть разделен пополам.
- Начните с начального интервала [a, b], содержащего корень функции f(x).
- Вычислите среднюю точку c = (a+b)/2 интервала.
- Оцените функцию в средней точке f(c).

- Если f(c) равно нулю, то мы нашли корень и метод завершает работу.
- Если f(c) имеет тот же знак, что и f(a), обновить интервал до [c, b].
- Если f(c) имеет знак, противоположный f(a), обновите интервал до [a, c].
- Повторяйте шаги 2–6 до тех пор, пока интервал не станет достаточно малым или не будет найден корень в пределах требуемого допуска.
 3 — 3x + 1. Мы будем использовать метод деления пополам, чтобы найти корень с допуском 0,001. Мы начнем с поиска в интервале [0, 1].
93 — 3(0,375) + 1 = 0,34765625
3 — 3x + 1. Мы будем использовать метод деления пополам, чтобы найти корень с допуском 0,001. Мы начнем с поиска в интервале [0, 1].
93 — 3(0,375) + 1 = 0,34765625Поскольку f(0,375) положительна, мы знаем, что корень функции находится в правой половине интервала [0,25, 0,5], поэтому мы обновляем интервал до [0,375, 0,5].
Сколько итераций метода деления пополам?
Количество итераций, требуемых методом деления пополам для нахождения корня функции, зависит от начального интервала и желаемого допуска. В общем случае метод деления пополам сходится линейно, что означает, что количество правильных цифр удваивается с каждой итерацией. Это означает, что если мы хотим найти корень с точностью до n цифр, нам нужно выполнить log2(n) итераций.
9-6. Однако обратите внимание, что это теоретическая оценка, и фактическое количество итераций может варьироваться в зависимости от функции и конкретных значений a и b.
В общем случае метод деления пополам сходится линейно, что означает, что количество правильных цифр удваивается с каждой итерацией. Это означает, что если мы хотим найти корень с точностью до n цифр, нам нужно выполнить log2(n) итераций.
9-6. Однако обратите внимание, что это теоретическая оценка, и фактическое количество итераций может варьироваться в зависимости от функции и конкретных значений a и b.
Что такое формула метода деления пополам Mcq?
Вот формула метода деления пополам в формате вопроса с множественным выбором (MCQ):
Что из следующего является формулой метода деления пополам для нахождения корня функции f(x) в интервале [a, b]?
А) с = (а + b)/2
В) f(c) = (f(a) + f(b))/2
В) с = f(а) + (б — а)/2
D) f(c) = (f(a) + f(b))/f'(c)
Правильный ответ A) c = (a + b)/2. Метод деления пополам находит середину интервала [a, b] и вычисляет функцию в этой точке. Основываясь на знаке функции в средней точке, он обновляет интервал до левой или правой половины текущего интервала и повторяет процесс до тех пор, пока интервал не станет достаточно маленьким или пока не будет найден корень.
Каковы условия для метода деления пополам?
Метод деления пополам — это простой и надежный численный метод нахождения корней непрерывной функции в заданном интервале. Метод работает путем многократного деления интервала пополам и выбора подинтервала, содержащего корень. Вот условия применения метода деления пополам:
Если эти условия соблюдены, то можно использовать метод деления пополам для нахождения корня функции в указанном интервале. Метод гарантирует сходимость к корню и может быть сделан сколь угодно точным, если задать достаточно малый допуск. Эти условия гарантируют, что метод деления пополам будет корректно определен и может использоваться для нахождения корня функции в заданном интервале. Важно проверить эти условия перед применением метода деления пополам, чтобы избежать ошибок или неточностей в аппроксимации корней.
Теория метода деления пополам
Метод деления пополам — это простой и надежный численный метод нахождения корней непрерывной функции в заданном интервале. Метод работает путем многократного деления интервала пополам и выбора подинтервала, содержащего корень. Вот теория метода деления пополам:
Метод работает путем многократного деления интервала пополам и выбора подинтервала, содержащего корень. Вот теория метода деления пополам:
Предположим, мы хотим найти корень непрерывной функции f(x) в интервале [a, b]. Метод деления пополам начинается с деления интервала [a, b] пополам и вычисления функции в средней точке c = (a+b)/2. Если f(c) равно нулю, то мы нашли корень, и метод завершает работу. В противном случае мы проверяем знак f(c) и обновляем интервал до [a, c] или [c, b], в зависимости от того, имеет ли f(c) тот же или противоположный знак, что и f(a).
Мы повторяем этот процесс деления интервала пополам и выбора подинтервала, содержащего корень, до тех пор, пока интервал не станет достаточно маленьким или корень не будет найден в пределах желаемого допуска. Алгоритм можно обобщить следующим образом:
Метод деления пополам гарантирует сходимость к корню, и его можно сделать сколь угодно точным, указав достаточно малый допуск. Этот метод надежен и прост в реализации, но может быть медленным, особенно для функций с несколькими корнями или крутыми склонами. Другие методы, такие как метод Ньютона-Рафсона или метод секущих, могут быть более эффективными для некоторых функций.
Метод деления пополам Численные методы
Метод деления пополам — это численный метод нахождения корней непрерывной функции в заданном интервале. Это один из наиболее широко используемых и надежных численных методов поиска корней, наряду с такими методами, как метод Ньютона-Рафсона и метод секущих.
Метод деления пополам основан на теореме о промежуточном значении, которая утверждает, что если непрерывная функция f(x) принимает противоположные знаки в двух точках a и b, то должен быть хотя бы один корень функции между a и b . Метод деления пополам использует это свойство, многократно деля пополам интервал [a, b] и выбирая подинтервал, содержащий корень.
Алгоритм метода деления пополам прост и легко реализуем. Он включает многократное деление интервала [a, b] пополам и вычисление функции в середине интервала. Основываясь на знаке функции в средней точке, алгоритм выбирает новый интервал и повторяет процесс до тех пор, пока корень не будет найден в пределах желаемого допуска.
Метод деления пополам — надежный метод нахождения корня непрерывной функции в заданном интервале, но он может быть медленным, особенно для функций с несколькими корнями или крутыми наклонами. В таких случаях другие методы, такие как метод Ньютона-Рафсона или метод секущих, могут оказаться более эффективными. Тем не менее, метод деления пополам остается ценным инструментом в наборе численных методов поиска корней и широко используется в различных научных и инженерных приложениях.
Тем не менее, метод деления пополам остается ценным инструментом в наборе численных методов поиска корней и широко используется в различных научных и инженерных приложениях.
Связанные статьи
Формула распределения Пуассона
Формула метода деления пополам – часто задаваемые вопросы
1. Для чего используется метод деления пополам?
Метод деления пополам используется для нахождения корней непрерывной функции в заданном интервале.
2. Какова скорость сходимости метода деления пополам?
Скорость сходимости метода деления пополам является линейной, что означает, что число цифр точности примерно удваивается с каждой итерацией.
3. В чем преимущество метода деления пополам?
Преимущество метода деления пополам в том, что он очень надежен и не требует знания производной функции.
4. В чем недостаток метода деления пополам?
Недостатком метода деления пополам является то, что он может быть медленным, особенно для функций с несколькими корнями или крутыми склонами.
5. Как узнать, когда остановить метод деления пополам?
Метод деления пополам можно остановить, когда абсолютное значение функции в средней точке меньше заданного допуска.
6. Какова роль теоремы о промежуточном значении в методе деления пополам?
Теорема о промежуточном значении используется в методе деления пополам, чтобы гарантировать наличие хотя бы одного корня функции между двумя точками, если функция принимает противоположные знаки в этих точках.
7. Какова формула метода деления пополам?
Формула для метода деления пополам включает вычисление средней точки интервала, оценку функции в средней точке и обновление интервала на основе знака функции в средней точке.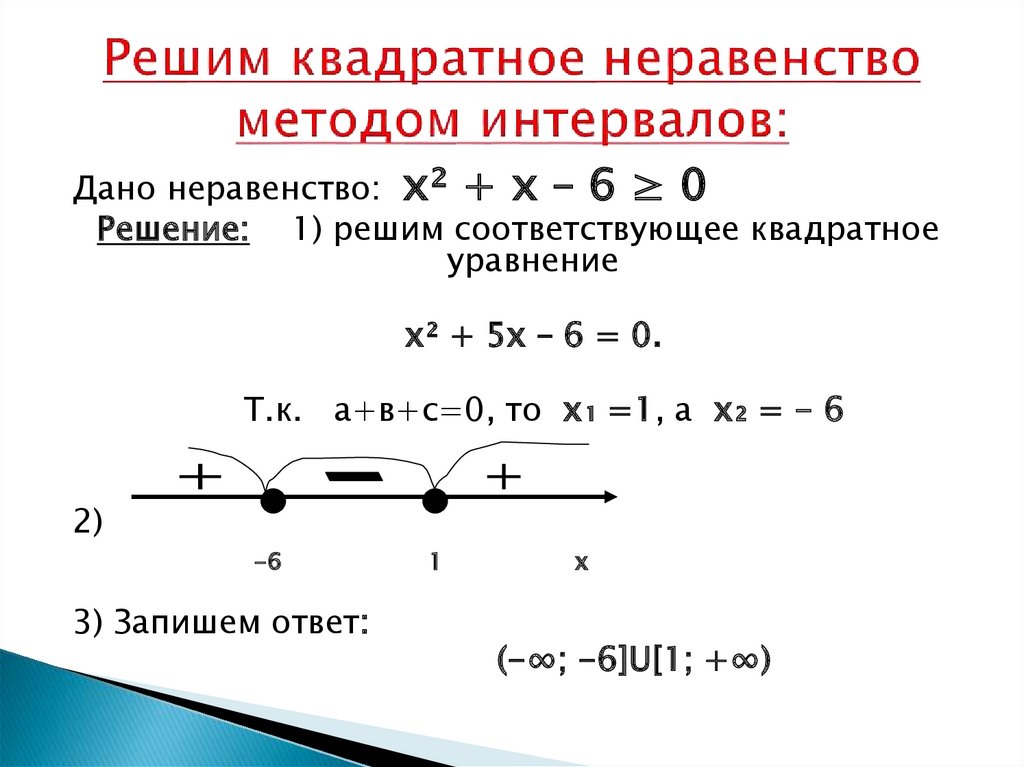

 Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979, стр. 521-525 ↩
Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979, стр. 521-525 ↩

