Найти экстремумы и интервалы монотонности функции онлайн: Интервалы возрастания и убывания функции онлайн

2*arctgh(x)*arcctgh(x)

Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да
• Минимум и максимум функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

Исследование функции с помощью производной

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Тема: исследование
функции с помощью
производной
Чтобы построить график функции, необходимо
исследовать ее свойства с помощью производной.
Вспомним свойства функции, которые
изучались на 1 курсе и добавим некоторые другие.
Возрастающая функция
y
f (x) возрастает

0
x
Убывающая функция
y
0
f (x) убывает
x
Интервалы монотонности функции – это интервалы
возрастания или убывания функции
y
f(x) убывает
f(x) возрастает
-1
0
x
Экстремумы – это максимумы и минимумы функции
max
y
f(x) убывает
f(x) возрастает
f(x) возрастает
0
x
min
Пройдите по ссылкам, посмотрите
2 фрагмента и вспомните
материал первого курса.
https://resh.edu.ru/subject/lesson/3966/start/201135/
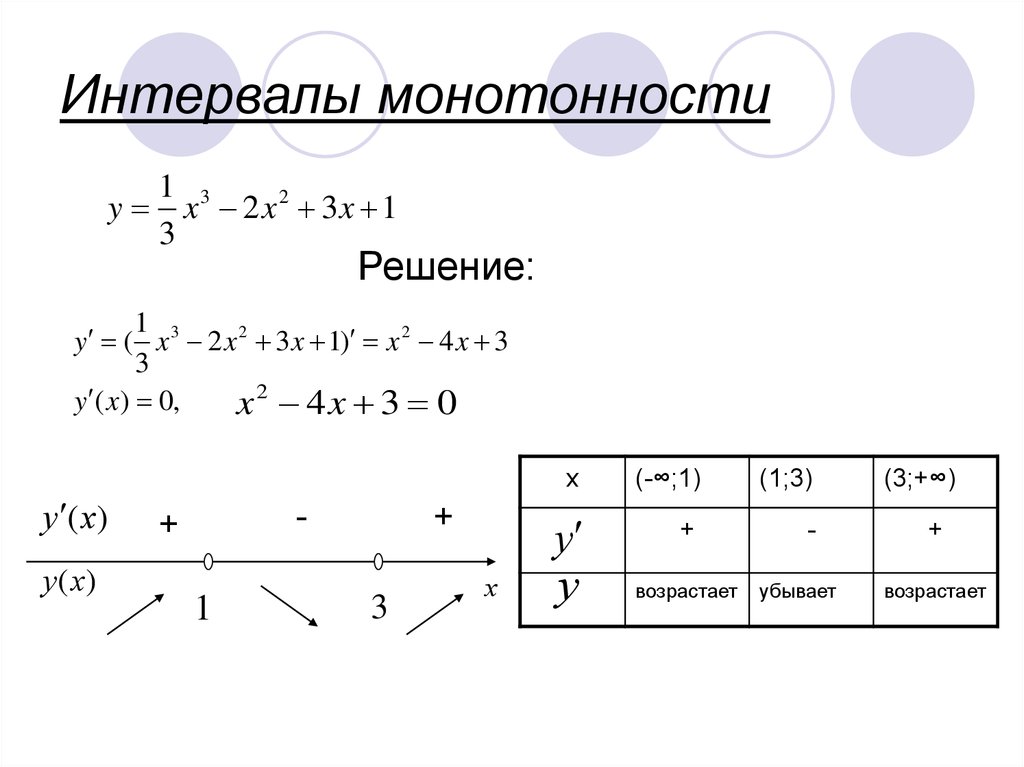
https://resh. edu.ru/subject/lesson/3987/main/273814/
Правило для нахождения
промежутков монотонности функции:
1.Найти первую производную функции .
2. Найти нули и точки разрыва .
3. На числовой прямой изобразить нули первой производной.
4. Определить знак в промежутках, на которые разбита область
определения точками из п.2
5. На интервале, где >0 – функция возрастает,
На интервале, где <0 – функция убывает.
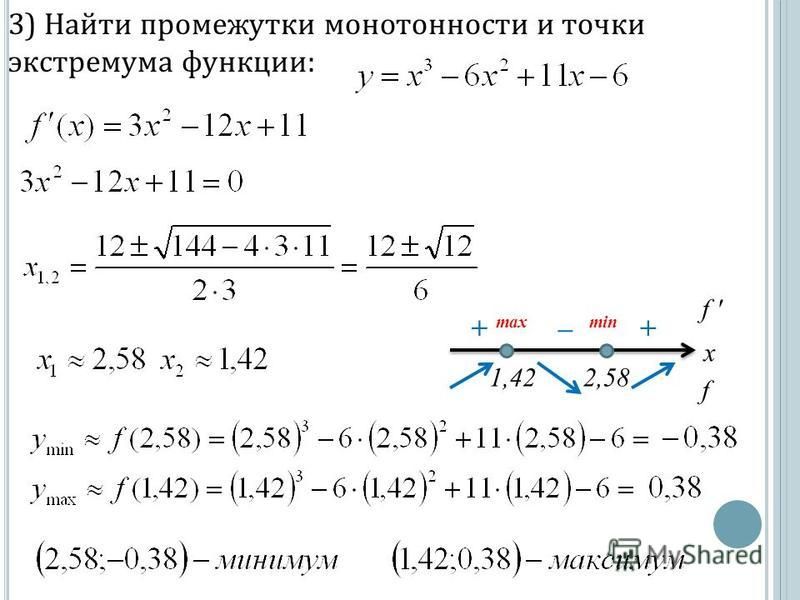
Правило для нахождения экстремумов
функции:
1. Найти первую производную функции .
2. Найти нули и точки разрыва . Это и есть точки,
подозрительные на экстремум.
3. На числовой прямой изобразить эти точки.
4. Определить знак в промежутках, на которые разбита область определения
точками из п.2
5. Если при переходе через точку экстремума знак производной
меняется с «+» на «- », то в данной точке max.
6. Если при переходе через точку экстремума знак производной
меняется с «-» на «+ », то в данной точке min.
Кривая называется выпуклой на
интервале (a;b), если она лежит ниже
касательной, проведенной в любой точке этого
интервала.
y
а
0
b
x
f (x)
Кривая называется вогнутой на интервале (c;d),
если она лежит выше касательной, проведенной в
любой точке этого интервала.
y
f (x)
с
0
d
x
Точкой перегиба графика функции f(x) является
точка x0, которая отделяет интервал выпуклости от
интервала вогнутости.
интервал
выпуклости
y
f (x)
x0
перегиб
0
x
интервал вогнутости

13. Признак выпуклости и вогнутости функции

Если
f ( x) 0 ,то на этом интервале функция вогнута
Если f ( x) 0 , то на этом интервале функция
выпукла.
Признак точки перегиба:
если при переходе через точку x0 вторая
производная меняет знак, то x0 является точкой
перегиба.

14. Правило нахождения интервалов выпуклости(вогнутости) и точек перегиба

1.
2.
3.
4.
5.
6.
7.
Найти область определения функции.
Найти первую производную.
Найти вторую производную.
Найти критические точки — нули второй производной и точки
ее разрыва.
Разбить область определения на промежутки. Определить
знак f ’’(x) в полученных промежутках.
Записать интервалы выпуклости и вогнутости
Определить точки перегиба и найти значения функции в них.

15. Общая схема исследования функции и построение ее графика

1. Найти область определения функции.
2. Периодичность функции
3. Четность/ нечетность функции
Функция является четной, если выполняется условие: f(x)=f(-x),
является нечетной, если выполняется условие f(-x)=-f(x),
4. Найти промежутки знакопостоянства функции.
Для этого найти нули функции . На числовой прямой обозначить
полученные точки и найти знаки функции в каждом из полученных
интервалов.
5. Найти промежутки монотонности функции (возрастание, убывание) с
помощью первой производной.
6. Найти экстремумы функции (максимумы, минимумы)
7. Найти промежутки выпуклости и вогнутости графика функции с
помощью второй производной
8. Найти точки перегиба графика.
9. Используя полученные данные, построить график функции.

English     Русский Правила

Math Tutor — Производные — Обзор методов

Math Tutor — Производные — Обзор методов — Графики

Пусть f — «разумная» функция, что здесь означает, что ее область определения состоит из не более чем счетного числа интервалов, на каждом из которых функция является дифференцируемым. Мы хотим определить интервалы монотонности и локального экстремумы.

Алгоритм:
Шаг 1. Определите интервалы домена f .
Шаг 2. Найдите производную f  ′. Найдите критические точки, то есть точки, где f  ′( x ) = 0 или f  ′ не существует. Эти точки будут разделять интервалы от Шаг 1 в интервалы монотонности.
Кстати, необязательно точно определять точки, где производной не существует. Достаточно включить все точки, где существование сомнительно; если мы добавим дополнительные баллы, они будут сброшены на последующих шагах (см.

соединение соседних интервалов одинаковых монотонность).
Шаг 3. Для каждого интервала шага 2 определить знак производная. Общий метод: подставить точку изнутри такого интервал в f  ′, чтобы найти знак.
Специальный метод для производного инструмента, представляющего собой произведение и/или соотношение факторов: Определите знаки для каждого фактора отдельно, а затем перемножьте знаки используя стандартную алгебру знаков. Лучше всего это сделать с помощью таблицы (см. Пример ниже).
Шаг 4. Определить монотонность по знакам числа ф  ′. функция f возрастает на интервалах, где f  ′ положительна. Оно уменьшается на интервалах, где f  ′ отрицательно.
При наличии двух соседних интервалов одинаковой монотонности проверьте, они могут быть связаны (например, если функция непрерывна в точка встречи двух интервалов, то мы всегда можем соединиться). При написании интервалы в ответе включают конечные точки, где f непрерывны с соответствующей стороны.
Шаг 5. Определение локальных экстремумов. Локальные минимумы – это все точки из область, в которой f меняется с убывающей на возрастающую и непрерывный. Локальные максимумы — это все точки из области, где f изменяется от возрастания к убыванию и является непрерывным. В случае критич. точки, где f не являются непрерывными, необходим дальнейший анализ.

Предысторию этого алгоритма см. Монотонность и локальные экстремумы в Теория — Графика.

Пример: Исследование монотонности и локальных экстремумов

Решение: D (  f  ) = (−∞,−1) ∪ (−1,∞). Мы начинаем с двух интервалы.

Критические точки: f  ′( x ) = 0 выходов x  = −3 и x  = 0; нет точек в области, где производная не существовала бы, следовательно, не было бы другой критической точки. Мы получаем четыре интервала. Мы помещаем их в таблицу, используя закрытые концы, где ф есть непрерывно с соответствующей стороны. В строках ставим отдельные коэффициенты производной и определить их знаки на всех интервалах, затем сделать выводы.

Мы видим два соседних интервала одинаковой монотонности, поэтому мы должны спросить можно ли их подключить. Так как f непрерывно в 0, они могут.

Вывод: f возрастает на (−∞,−3] и на (−1,∞), это убывает на [−3,−1). Имеет локальный максимум f (-3) = -11/8.

Примечание: f также изменяет монотонность при −1, но эта точка не находится в домен, так что это не локальная крайность. Кстати, если вы хотите посмотреть, как это функция выглядит так, ознакомьтесь с примером в Обзор методов — Графики — Обзор).

Примечание: Табличный метод имеет одно особое преимущество, он не необходимо подставить точки из интервалов в производную (или ее факторы). Если множитель линейный, то он меняет знак только один раз, а именно при точка, где этот коэффициент равен нулю. Таким образом, достаточно отметить это деление указать в таблице, а затем поставить один вид знака справа и напротив знаки слева. Должен ли он идти — + или + -? Это легко увидеть, этого достаточно подставить какое-то число, кроме точки деления, один раз можно даже спросить что происходит, когда х растет до бесконечности, становится ли множитель положительным или отрицательный? Для получения дополнительной информации см. Знаковые неравенства в разделе Решение уравнений и неравенства в доп. Эта возможность избегания замены чисел из интервалов может быть весьма полезным в случае, если небольшого интервала, например, нет подходящего целого числа для замены из интервала (2,3).

Другие примеры см. Монотонность и локальные экстремумы в Теория — Графики и соответствующие задачи в Решенные проблемы. 9{5} — 5 х\) , найти все экстремумы и все точки перегиба
, а также интервалы монотонности и интервалы вогнутости.

А теперь я добавляю график функции к экзаменационным вопросам.

Обратите внимание, что на осях нет засечек. Это предотвращает угадывание
ответов, когда ответы представляют собой целые точки. Вот мои мысли, а также
и мысли некоторых моих коллег по поводу этого изменения.

Преимущества включения графика

Я включаю графики, потому что чувствую, что студенты теряются, расставляя критические
точек на числовой прямой и проверяя интервалы между ними. Правда, хотя
это несложная задача, я думаю, что студентов отпугивает ее скучность.
Принимая во внимание, что, глядя на график, построенный на графическом калькуляторе или заданный
вопросом,
учащийся может сразу определить, где функция возрастает или
убывает, вогнута вверх или вогнута вниз, как только он узнает, где
0009 критические точки и потенциальные точки перегиба. Я надеюсь, что это
улучшит понимание учащимися за счет исключения ненужной скуки и сосредоточения внимания на
более важных понятиях.

Теперь я могу использовать графическую утилиту при рассмотрении таких примеров,
не заставляя студентов покупать графические калькуляторы. И я получаю дополнительное время
занятий, потому что мне не нужно проверять знак производных.

Недостатки включения графика и смягчения последствий 9{3} — 2 х\)

, на графике которых
явно не показывает вогнутость. Я могу избежать таких функций на экзаменах, не теряя значения оценки
. А для домашнего задания и в классе графическое изображение первой и второй производных
устранит любую путаницу.

Я спросил у коллег, могут ли они найти еще недостатки в этой идее. Единственное предположение
заключалось в том, что у студентов может быть более слабая связь между положительной первой производной
и возрастающей функцией и т. д. Эту проблему можно было бы предотвратить
, используя дополнительное время занятий для выполнения упражнений, подобных следующим.

• Дан график \(f(x)\) , эскиз \(f'(x)\) и \(f''(x)\) на том же графике.
• Дан график \(f'(x)\) , нарисуйте \(f(x)\) на том же графике.
• Дан график \(f''(x)\) , эскиз \(f'(x)\) и \(f(x)\) на том же графике.

  No related posts.