Докажите что середины сторон пространственного четырехугольника являются: 43. Докажите, что середины сторон пространственного четырехугольника* являются вершинами параллелограмма.

Докажите, что середины сторон пространственного четырехугольника являются… Вопросы и задачи 43, Геометрия, 10-11 класс, Атанасян Л.С.

Докажите, что середины сторон пространственного четырехугольника являются… Вопросы и задачи 43, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Кто смог привести доказаттельства??

Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.
 

Лучший ответ

Почти весь класс смог так-то…

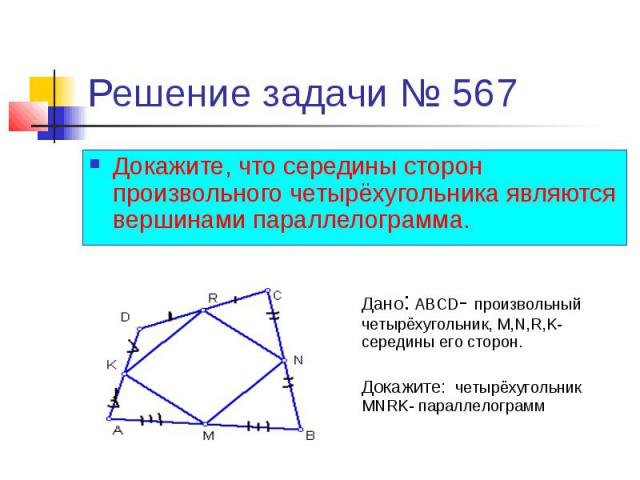
Соединим все вершины пространственного четырехугольника.
НЕ — средняя линия ΔBAD, НЕ || BD; GF — средняя линия ΔBCD, GF || BD.
Значит, НЕ || GF.
GH — средняя линия ΔАВС, GH || АС;
EF- средняя линия ΔADC, EF || АС. Отсюда EF || GH.
4-угольник, у которого противоположные стороны попарно параллельны, называется параллелограммом, следовательно, EFGH — параллелограмм (из параллельности сторон также следует, что че­тырехугольник плоский).

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

ЕГЭ-2017 Цыбулько И.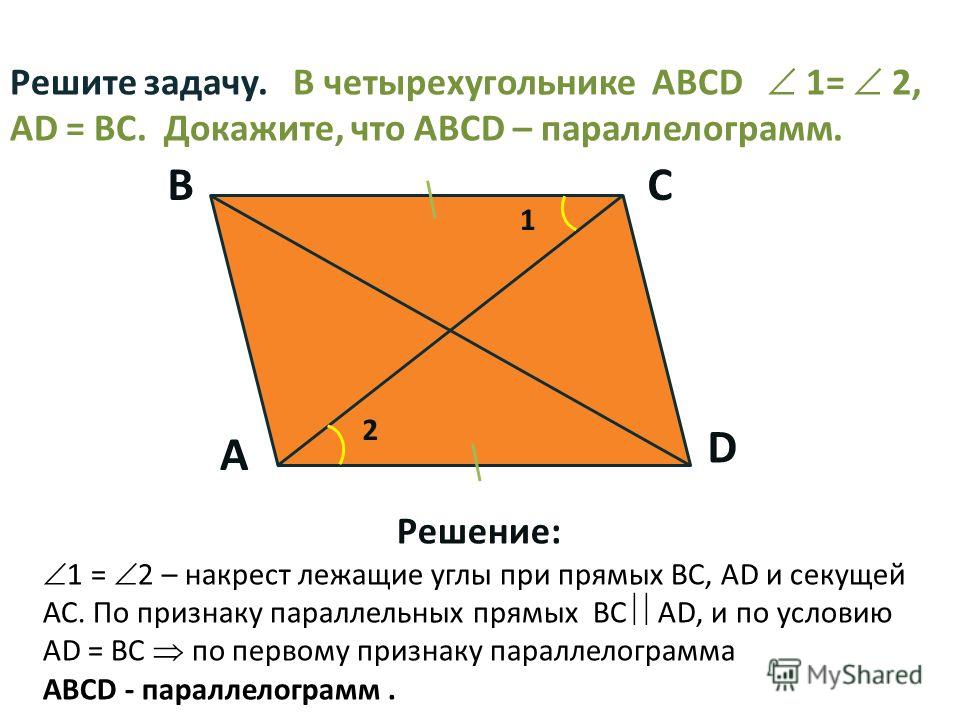 П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Вопросы и задачи к зачетам по геометрии для 10 класса

Вопросы и задачи к зачетам по геометрии для 10 класса

Зачёт по геометрии №1 по теме «Параллельность прямых и плоскостей»

1.Сформулируйте аксиомы стереометрии; разъясните их смысл.

2.Докажите, что через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

3.Докажите, что через две пересекающиеся прямые можно провести плоскость, и притом только одну.

4.Дать определение параллельных прямых в пространстве. Докажите, что через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.

5.Расскажите о взаимном расположении двух прямых в пространстве. Докажите лемму о пересечении плоскости параллельными прямыми.

6.Расскажите о взаимном расположении прямой и плоскости. Докажите признак параллельности прямой и плоскости.

7.Докажите, что если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.

8.Докажите, что если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения параллельна каждой из двух прямых или совпадает с одной из них.

9. Сформулируйте определение скрещивающихся прямых. Докажите признак скрещивающихся прямых.

10. Сформулируйте определение скрещивающихся прямых. Докажите теорему о скрещивающихся прямых.

11. Дайте понятие углов с сонаправленными сторонами. Докажите теорему о равенстве таких углов. Дайте понятие угла между прямыми.

12. Сформулируйте определение параллельных плоскостей. Докажите признак параллельности плоскостей.

13. Сформулируйте определение параллельных плоскостей. Докажите свойства параллельных плоскостей.

14. Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.

15. Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.

16. Две плоскости  пересекаются по прямой

m. Прямая a лежит в плоскости , прямая b — в плоскости. Эти прямые пересекаются в точке A. Докажите, что точка A лежит на прямой  m.

17. Точка M лежит вне плоскости треугольника ABC. Точки P, K, E, H – середины отрезков AB, MA, MC, BC соответственно. Докажите, что четырехугольник PKEH – параллелограмм.

18. Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что m и AC — скрещивающиеся прямые – и найдите угол между ними.

19.  Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что m и AD — скрещивающиеся прямые – и найдите угол между ними, если угол ABC равен 128.

20. Прямая  параллельна одной из двух параллельных плоскостей. Докажите, что прямая  либо параллельна другой плоскости, либо лежит в ней.

21. Докажите, что если плоскость пересекает одну из параллельных плоскостей и , то она пересекает и другую плоскость.

22. Через концы отрезка AB и его середину M  проведены параллельные прямые, пересекающие плоскость  в точках A_1, B_1, M_1.  Найдите длину AA₁, если MM₁=6,3 см; BB₁=10,5 см.

23. Отрезок AB пересекает  плоскость . Через концы отрезка и его середину M проведены параллельные прямые, пересекающие плоскость  в точках A_1, B₁, M_1. Найдите длину отрезка MM₁, если AA₁=5,7 см; BB₁=8,5 см.

24. Через конец A отрезка проведена плоскость. Через конец B и точку C этого отрезка проведены параллельные прямые, пересекающие плоскость в точках B₁ и C₁.

Найдите длину CC₁, если BC:CA = 2:5; BB₁=4,9 см.

25. Дан пространственный четырехугольник ABCD, AC= 10 см, M, AM:MB = 1:4, K, CK:KB = 1:4, P и E – середины сторон AD и DC. Докажите, что MKEP – трапеция и вычислите длину основания MK.

26. Даны параллелограмм ABCD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках A₁, B₁, C₁, D₁. Найдите длину отрезка CC₁, если AA₁ = 3 см, BB₁ = 6 см, DD₁ = 8 см.

27.  Дан треугольник ABC. Плоскость, параллельная прямой BC, пересекает сторону AB в точке B₁, а сторону AC – в точке C₁. Найдите длину отрезка B₁C₁, если BC = 6,3 см,

BB₁:B₁A = 3:4.

28. Параллельные плоскости  и  пересекают сторону AB угла BAC соответственно в точках A₁ и_A

2, а сторону AC  этого угла – соответственно в точках B₁ и B₂ .   Найдите  AA₂ и AB₂, если A₁A₂=2 A₁ A=12см, AB₁=5 см.

29. Параллельные плоскости  и  пересекают сторону AB угла BAC соответственно в точках A₁ и_{A2, а сторону AC  этого угла – соответственно в точках B1 и B2 .  Найдите  A2B2  и AA2, если A1B1=18 см,  A1 A=24см, AA2 =A1A2.}

 

Зачёт по геометрии №2 по теме «Перпендикулярность прямых и плоскостей»

1.Сформулируйте определение перпендикулярности прямой и плоскости. Докажите признак перпендикулярности прямой и плоскости.

2.Докажите теорему о двух параллельных прямых, одна из которых перпендикулярна плоскости.

3. Докажите теорему о двух прямых, перпендикулярных одной и той же плоскости.

4.Сформулируйте понятия перпендикуляра, наклонной и её проекции на плоскость. Докажите теорему о трех перпендикулярах.

5. Докажите теорему, обратную теореме о трех перпендикулярах. Дайте определения расстояния от точки до плоскости, расстояния между параллельными плоскостями, расстояния между скрещивающимися прямыми.

6.Сформулируйте определения двугранного угла, градусной меры двугранного угла, угла между прямой и плоскостью.

 7.Сформулируйте определение перпендикулярных плоскостей. Докажите признак перпендикулярности плоскостей.

8.Сформулируйте определение прямоугольного параллелепипеда. Докажите теорему о квадрате диагонали прямоугольного параллелепипеда.

9. Докажите, что через любую точку, не лежащую на данной прямой, можно провести плоскость, перпендикулярную этой прямой.

10.Плоскости  параллельны, прямые m и n перпендикулярны этим плоскостям. Докажите, что отрезки этих прямых, заключенные между плоскостями, равны.

11.Прямая AM перпендикулярна плоскости квадрата ABCD. Докажите, что прямая BD перпендикулярна плоскости AMC.

12. Докажите, что если плоскости  перпендикулярны прямой a, то они параллельны.

13.Через точку O пересечения диагоналей ромба ABCD проведена прямая OM так, что MA = MC, MB = MD. Докажите, что прямая OM перпендикулярна к плоскости ромба.

14.Из вершины D квадрата ABCD проведен перпендикуляр DM  к плоскости квадрата. Определите площадь треугольника MBC, если AD = 8 см, MD = 6 см.

15.Из вершины A правильного треугольника ABC проведен перпендикуляр AM к его плоскости. Найдите расстояние от точки M до стороны BC, если AB = 4 см, AM = 2 см.

16.Из центра O правильного треугольника ABC проведен перпендикуляр OM к его плоскости. Найдите площадь треугольника MBC, если AB = 6, OM = 4 см.

17.Из точки к плоскости проведены две наклонные длиной 12 и 24 см, проекции которых относятся как 1:7. Найдите расстояние от точки до плоскости.

18.Точка M равноудалена от всех вершин правильного треугольника со стороной 12 см и удалена от плоскости треугольника на расстояние 6 см. Найдите расстояние от точки M до сторон треугольника.

19. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁  АВ=5,  DD₁=2,  B₁C₁=1.

а) Найдите B₁D;  б) Докажите, что плоскости A₁B₁C₁ и ВDD₁ взаимно перпендикулярны.

20.Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см. Найдите расстояние от точки М до плоскости АВС, если АВ=6см.

 

1.Сформулируйте определения двугранного угла, градусной меры двугранного угла. Сформулируйте определения призмы, прямой и правильной призмы, высоты призмы.

2.Сформулируйте определение перпендикулярных плоскостей. Докажите признак перпендикулярности плоскостей.

3.Сформулируйте определение прямоугольного параллелепипеда, его свойства. Докажите теорему о квадрате диагонали прямоугольного параллелепипеда.

4.Сформулируйте определения боковой и полной поверхности призмы.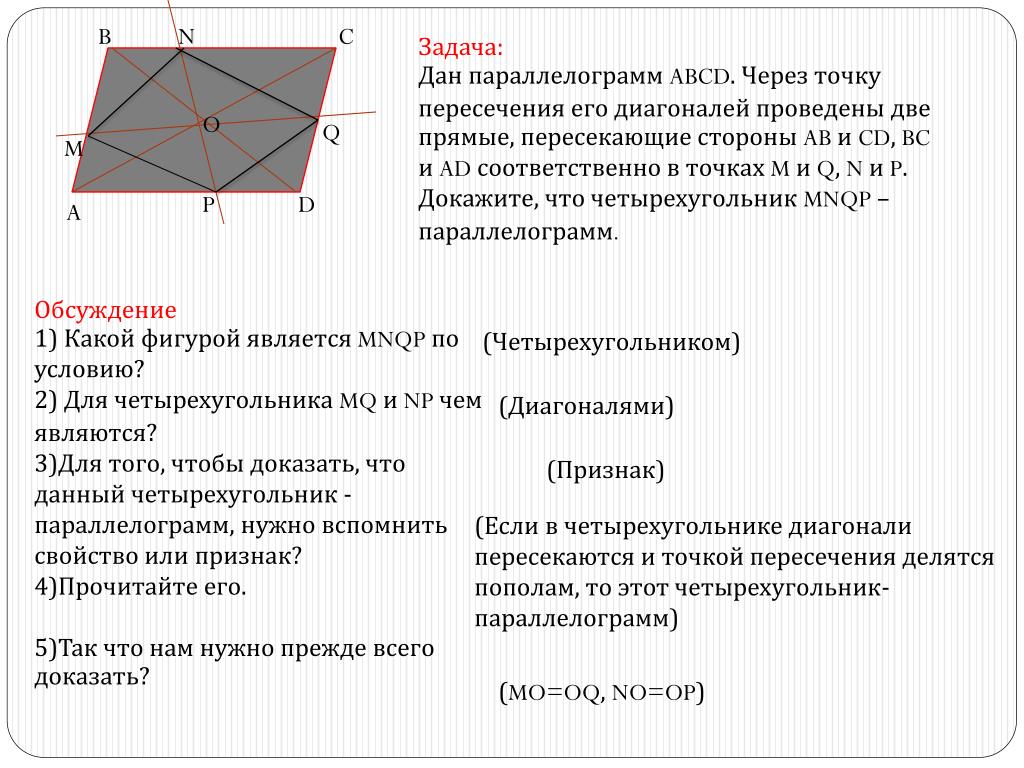 Докажите теорему о площади боковой поверхности прямой призмы.

5.Сформулируйте определения пирамиды, правильной пирамиды, высоты пирамиды, апофемы. Докажите теорему о площади боковой поверхности правильной пирамиды.

6.Сформулируйте определения  пирамиды, правильной пирамиды, усеченной пирамиды, правильной усеченной пирамиды. Докажите теорему о площади боковой поверхности правильной усеченной пирамиды.

7.В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁  АВ=5,  DD₁=2,  B₁C₁=1.

а) Найдите B₁D;  б) Докажите, что плоскости A₁B₁C₁ и ВDD₁ взаимно перпендикулярны.

8.В прямом параллелепипеде АВСDA₁B₁C₁D₁  AB=2, AD=3, ÐВАD=45 , B₁D = Найдите площади боковой и полной поверхностей параллелепипеда.

9.В основании прямого параллелепипеда АВСDA₁B₁C₁D₁ лежит ромб, сторона которого равна 4 см.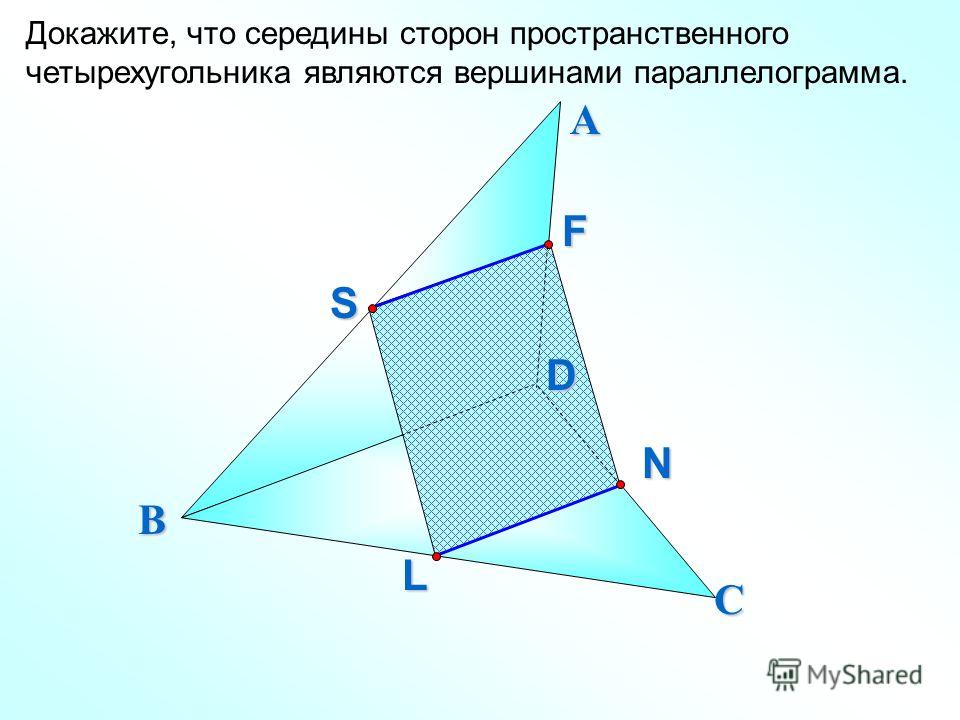 Через ребра АD и B₁C₁ проведена плоскость, составляющая угол 60 с плоскостью основания. Найдите площади боковой и полной поверхностей параллелепипеда, если ÐВАD=45 .

10.В основании прямого параллелепипеда АВСDA₁B₁C₁D₁ лежит параллелограмм, АВ=4 см, АD=6 см, ÐВАD=60 . Через ребра AD и B₁C₁ проведена плоскость под углом 45 к плоскости основания. Найдите площади боковой и полной поверхностей параллелепипеда.

11.В правильной четырехугольной призме АВСDA₁B₁C₁D₁ через диагональ основания ВD и

середину ребра C₁D₁ проведена плоскость. Сторона основания равна 8, а боковое ребро равно 4. Найдите площадь сечения и угол между плоскостью сечения и плоскостью основания.

12.В правильной треугольной пирамиде сторона основания равна 4 см, а высота 6 см.

Найдите площадь поверхности пирамиды.

13.В правильной четырехугольной пирамиде сторона основания равна 5 см, а высота 7 см.

Найдите площадь поверхности пирамиды.

14.В правильной четырехугольной пирамиде боковые грани наклонены к плоскости основания под углом 60. Расстояние от центра основания до боковой грани равно 2 см. Найдите площадь боковой поверхности пирамиды.

15.В правильной треугольной пирамиде боковые грани наклонены к плоскости основания под углом 45. Расстояние от центра основания до боковой грани равно см. Найдите площадь боковой поверхности пирамиды.

16.Основанием тетраэдра DАВС  служит равнобедренный прямоугольный треугольник, ÐАСВ=90 , АС=ВС=6 см. Ребро DВ перпендикулярно плоскости основания. Грань АDС составляет с плоскостью основания угол 60. Найдите площадь боковой поверхности тетраэдра.

17.Боковое ребро пирамиды разделено на четыре равные части, и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400 см². Найдите площади сечений.

18.В правильной усеченной треугольной пирамиде стороны оснований 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.

 

геометрия — Докажите векторными методами, что середины сторон космического четырехугольника образуют параллелограмм.

Задавать вопрос

спросил 5 лет, 4 месяца назад

Изменено 5 лет, 4 месяца назад

Просмотрено 10 тысяч раз

$\begingroup$

Задача

Докажите векторными методами, что середины сторон пространственного четырехугольника образуют параллелограмм.

---

Мое решение

B (Вывод): Середины сторон пространственного четырехугольника образуют параллелограмм.

A (Гипотеза): Пусть $A$, $B$, $C$, $D$ — четыре точки, образующие пространственный четырехугольник.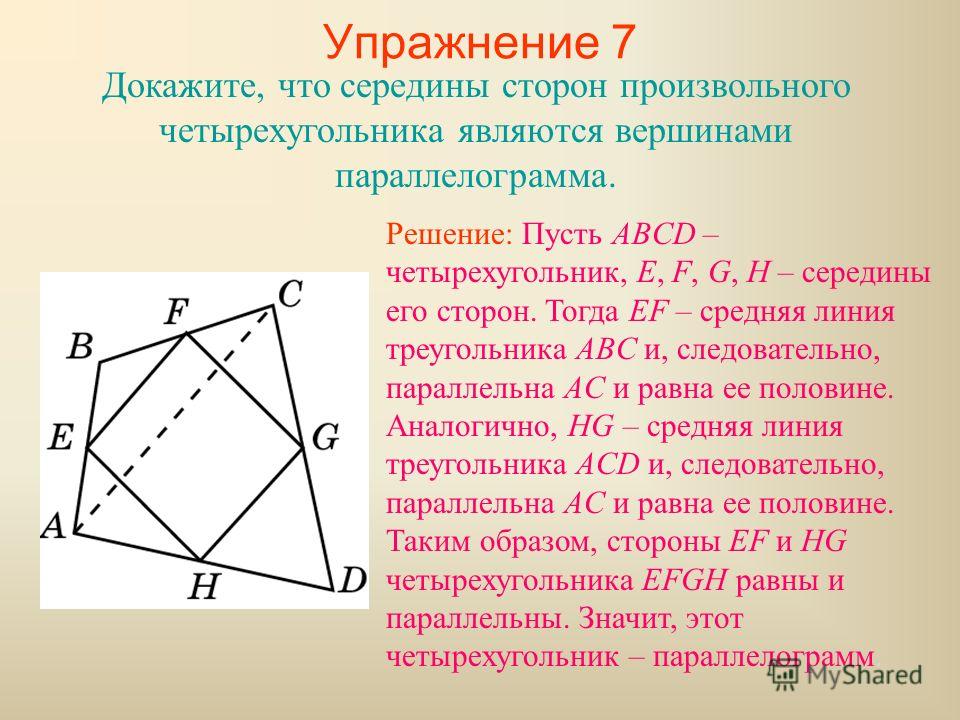

B1: $\dfrac{1}{2} \mathbf{A} + \dfrac{1}{2} \mathbf{B} = \dfrac{1}{2} \mathbf{C} + \ dfrac{1}{2} \mathbf{D}$ , где $\dfrac{1}{2} \mathbf{A} + \dfrac{1}{2} \mathbf{B}$ и $\dfrac{1 {2} \mathbf{C} + \dfrac{1}{2} \mathbf{D}$ равны. То же самое можно сказать и о двух других сторонах.

A1: $\mathbf{A} + \mathbf{B} = \mathbf{C} + \mathbf{D}$ по определению четырехугольников.

$\ подразумевает \dfrac{1}{2} \left( \mathbf{A} + \mathbf{B} \right) = \dfrac{1}{2} \left( \mathbf{C} + \ mathbf{D} \right)$

$\ подразумевает \dfrac{1}{2} \mathbf{A} + \dfrac{1}{2} \mathbf{B} = \dfrac{1}{2} \mathbf{C} + \dfrac{ 1}{2} \mathbf{D}$

$Q.E.D.$

---

Я был бы очень признателен, если бы люди могли проверить правильность моего доказательства.

• геометрия
• доказательство-верификация
• векторы

$\endgroup$

9

$\begingroup$

Подсказка: если ваши четыре точки $a, b, c, d$, то средние точки, расположенные вокруг четырехугольника, равны $$ p = \frac{1}{2}(a+b), q = \frac{1}{2}(b+c), r = \frac{1}{2}(c+d), s = \frac{1}{2}(d+a). $$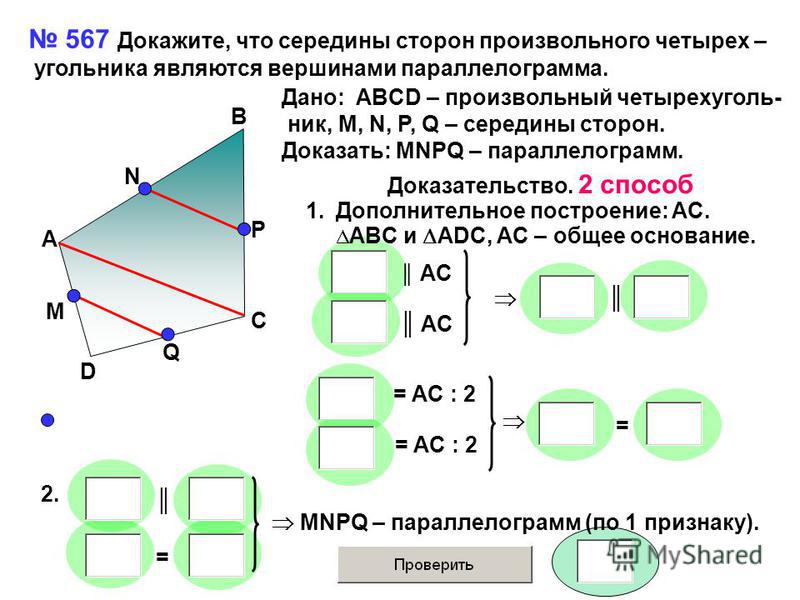

Чтобы $pqrs$ был параллелограммом, нужно, чтобы ребро от $p$ до $q$ имело тот же вектор направления, что и ребро от $s$ до $r$; вам нужно сделать то же самое для ребер от $q$ до $r$ и от $p$ до $s$.

Каков вектор направления ребра от $p$ до $q$? Можете ли вы выразить это через $a, b, c, d$?

$\endgroup$

$\begingroup$

Подсказка:

так как $\vec A+\vec B=\vec C+ \vec D$ имеем:

$$ \frac{1}{2}(\vec A+\vec B)=\frac{1}{2}(\vec C+ \vec D)\iff \frac{1}{2}\vec A +\frac{ 1}{2}\vec B=\frac{1}{2}\vec C+\frac{1}{2}\vec D $$

$\endgroup$

9

$\begingroup$

В общем случае середины любого выпуклого четырехугольника образуют параллелограмм, и это можно довольно легко доказать, проведя диагонали исходного четырехугольника, но я не совсем уверен, что такое пространственный параллелограмм, и не знаю, как докажите это с помощью векторов или проверьте свое доказательство, так как я почти ничего не понимаю в них.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

геометрия — Докажите, что середины сторон четырехугольника лежат на окружности тогда и только тогда, когда четырехугольник ортогонален.

$\begingroup$

Докажите, что середины сторон четырехугольника лежат на окружности тогда и только тогда, когда четырехугольник ортогонален.

Мои усилия:

Для части if я сделал следующее:

Дан ортогональный четырехугольник $ABCD$. Проведем диагонали $AC$ и $BD$, из точки пересечения диагоналей проводим отрезок $OP$, где $P$ является серединой $AD$.

Так как $\Delta AOD$ прямоугольный треугольник, мы имеем, что $OP$ является его медианой, следовательно, $OP=AP=PD$.

Теперь, учитывая, что $\Delta APR \cong \Delta OPR$, по симметрии мы видим, что имеем $AX=XO$, следовательно, $PX$ — высота равнобедренного треугольника $APO$ , и из этого Из факта следует также, что $\Delta APX\cong\Delta OPX$.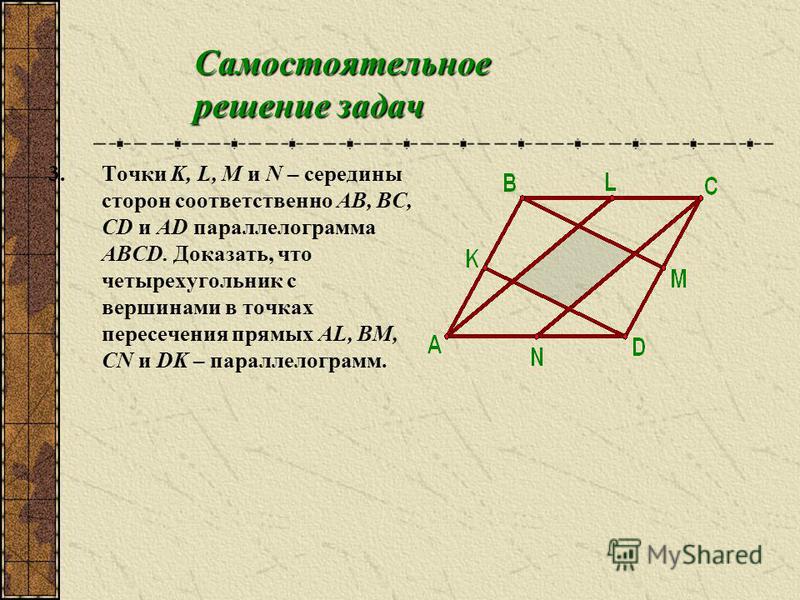

По тому же аргументу $PY$ является высотой равнобедренной $DPO$, поэтому имеем $PY=XO$ и $\Delta DPY \cong \Delta OPY \cong \Delta APX \cong \Delta OPX$.

9\circ$.

Вопрос:

Является ли эта линия рассуждений (наверняка избыточной в какой-то момент) в целом приемлемой? В частности, кто-нибудь может дать мне несколько советов о том, как подойти к , только если часть ? Кроме того, если вы можете дать какие-либо советы о том, как лучше подойти к проблеме, мы будем признательны.

Заранее спасибо и простите меня за любые английские ошибки или если фраза была не совсем ясной (не стесняйтесь редактировать в случае необходимости).

• геометрия
9\circ$.

Следовательно, $PRST$ не является конциклическим.

$\endgroup$

11

$\begingroup$

Дано: ABCD — четырехугольник.

No related posts.