Найти нули функции онлайн: Нули функции онлайн

Свойства функции. Нули функции. Алгебра 7-11 класс смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.

12+

5 месяцев назад

Математика от Баканчиковой269 подписчиков

Алгебра 7-11 класс. Продолжая говорить о свойствах функции, сегодня мы расскажем Вам об одиннадцатом свойстве функции: нулях функции. Мы объясним Вам, что такое нули функции, дадим их определение. На конкретных примерах мы покажем Вам, как нужно находить нули функции, если функция задана таблицей, графиком или формулой, и как правильно записывать ответ. А также поясним Вам, зачем Вас учат решать различные уравнения. 00:00 Начало видео. 00:34 Что такое нули функции? 01:31 Как найти нули функции, заданной таблицей? 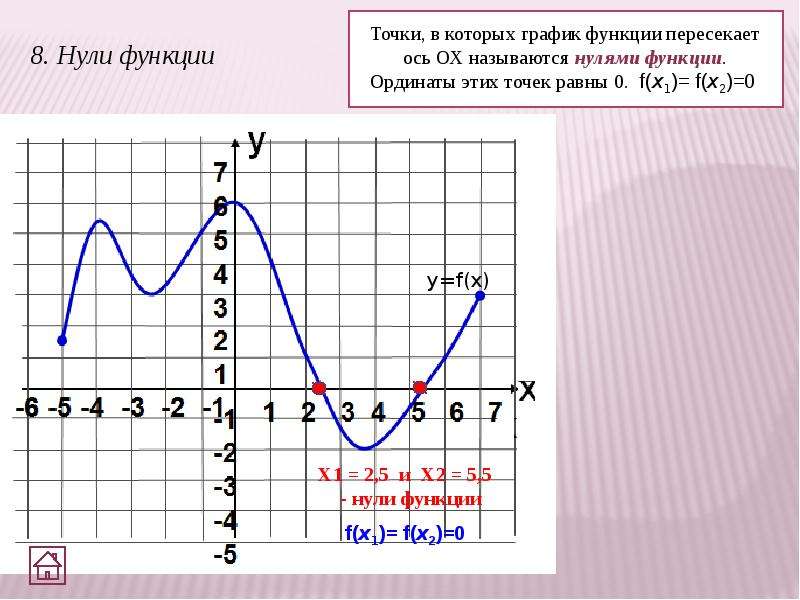02:25 Как найти нули функции, заданной графиком? 04:45 Как найти нули функции, заданной формулой? 08:00 Так зачем нужно уметь решать уравнения? Если Вы впервые на нашем канале и у Вас остались вопросы или Вы хотите освежить в памяти некоторые термины и определения, рекомендуем Вам посмотреть следующие видео: Что такое определение.

37.7. Нули функции. Особые точки

Нули функции. Рассмотрим функциюАналитическую в точкеТочка называется нулем функцииПорядка (или кратности)Когда выполняются условия:

(37.47)

ЕслиТо точкаНазывается простым нулем.

ЗначениеТогда и только тогда является нулем и-го порядка функции f(z), аналитической в точкеКогда в некоторой ее окрестности верно равенство

(37. 48)

Где- функция, аналитическая в точкеИ

Особые точки. Особой точкой функцииНазывается точкаВ которой эта функция не является аналитической. ТочкаНазывается изолированной особой точкой функции, когда существует окрестность этой точки, в которой Аналитическая всюду, кроме. Особая точкаФункцииНазывается устранимой, когда существует конечный предел этой функции в данной точке: ТочкаНазывается полюсом функцииКогда

Для того, чтобы точкаБыла полюсом функцииНеобходимо и достаточно, чтобы эта точка была нулем. функции

(37.49)

ТочкуНазывают полюсом порядкаФункции, когда эта

Точка является нулем порядкаДля функцииВ случае

Полюс называют простым.

Для того, чтобы точкаЯвлялась полюсом порядкаФункции, необходимо и достаточно, чтобы функциюМожно было привести к виду

(37.50)

Где- функция, аналитическая в точкеИ

ТочкаНазывается существенно особой точкой функцииКогда в ней

ФункцияНе имеет ни конечного ни бесконечного предела.

Справедливы следующие утверждения.

1.  ТочкаЯвляется устранимой особой точкой функцииТогда и только тогда, когда ее лорановское разложение в окрестности точкиНе содержит главной части.

2.  ТочкаЯвляется полюсом функцииТогда и только тогда, когда главная часть ее лорановского разложения в окрестности точкиСодержит только конечное число членов:

(37.51)

Наибольший из показателей степени разностиВ знаменателях

Совпадает с порядком полюса.

3.  ТочкаЯвляется существенно особой точкой функцииТогда и только тогда, когда главная часть ее лорановского разложения в окрестности точкиСодержит бесконечное множество членов.

Пример 37.31. Доказать, что точкаЯвляется нулем второго по

Рядка для функции

Разложим в ряды данную функцию и ее первую и вторую производные:

ПосколькуТ. е. выполняются условия (37.47)

При, то— нуль второго порядка для функции

Пример 37.32. Найти порядок нуляДля функции

Использовав разложение функцииВ ряд Тейлора, получим

Таким образом, функция _. j записана в виде (37.48), где- функция, аналитическая в точкеПричемЗначит, точка- нуль

Четвертого порядка для данной функции.

Пример 37.33. Найти нули функцииИ определить их порядки.

КогдаИлиТоЛибоИз первого

Равенства следует, чтоА со второго, что

ПустьТогда функциюМожно представить в виде (37.48):

Где функцияЯвляется аналитической в

ТочкеПричемЗначит, точкаЕсть нуль

Третьего порядка. Аналогично доказывается, что—нуль третьего порядка. ФункцияИмеет нулиДействительно,

Это нули первого порядка для функцииНо

Ибо

Пример 37.34. Доказать, что точкаДля функции

Является устранимой особой точкой.

Действительно, поскольку

То— устранимая особая точка.

Пример 37.35. Найти полюсы функции

Так как для функцииТочки-

Нули первого порядка,—нули второго порядка, то для функции

Точки— полюсы первого порядка, точки- полюсы второго порядка.

Замечание. Если, гдеИ- многочлены,

Не имеющие общих корней, то корни многочлена(и только они) являются полюсами функцииПорядок полюсовСовпадает с кратностью соот

Ветствующих корней многочленаНапример, когда

То- простой полюс,— полюс второго порядка,- полюс третьего порядка Пример 37. 36. Исследовать особые точки функции

Поскольку

Приведем к виду (37.50):

Где- функция, аналитическая в окрестности точкиПричем

Следовательно, точкаЯвляется полюсом второго порядка. Аналогично, записав функциюВ виде

Заключаем, что- простой полюс данной функции.

Пример 37.37. Найти особые точки функцииИ опреде

Лить их типы.

Принимая во внимание, что (см. (37.3))

ПриПолучим

Этот ряд сходится всюду, кроме точкиЕго можно рассматривать как

Разложение функцииВ ряд Лорана в окрестности точкиПоскольку

Главная часть ряда имеет бесконечное множество членов, то точка является существенно особой точкой для функции

Подсчет конечных нулей факториалов

 9332621544394415268169923885626670049071596826438162146859296389521759\
9993229915608941463976156518286253697920827223758251185210916864000000\
000000000000000000
 

 100!
 

 TZF3[n_] := If [n < 5, 0, IntegerDigits[Factorial[n]] // SplitBy[#, 1] & // Part[#, -1] & // Length]
м = 150; ListPlot[{Таблица[TZF1[n], {n, m}], Таблица[TZF2[n], {n, m}],
  Таблица[TZF3[n], {n, m}]}, Соединение -> True, ImageSize -> Большой, PlotRange -> Все]
 

 n = 10000;
Время[TZF1[n]]
Время[TZF2[n]]
Время[TZF3[n]]
{0. 041059, 2499}
{0,000055, 2499}
{0.043205, 2499}
 

 Таблица[{n = случайное целое[10000], r = случайное целое[{5, 30}],
   TZF4[n, r], TZF5[n, r], TZF6[n, r]}, 10] // Форма таблицы
 

 Таблица[{n = RandomInteger[10000], TZF1[n], TZF2[n], TZF3[n],
   TZF4[n, 10], TZF5[n, 10], TZF6[n, 10]}, 10] // Форма таблицы
 

 TZF5[10000, 72]
 

Теорема о нулях для корней полиномиальной функции — Криста Кинг Математика

Теорема о нуле позволяет вычислять корни полиномиальной функции

В этом уроке мы узнаем, как использовать теорему о нуле для вычисления корней факторизованного многочлена.

Мы можем использовать теорему нуля, чтобы найти корни полиномиальной функции после ее факторизации. Когда полином разложен на множители, нулевая теорема говорит нам, что для того, чтобы левая часть была равна ???0???, один или оба множителя должны быть ???0???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Например, если у вас есть факторизованный многочлен

???(2x+5)(x-3)=0???

, то по теореме о нуле мы можем положить каждую часть равной ???0??? найти любые решения уравнения.

Можно сказать,

???2x+5=0???

???2x+5-5=0-5???

???2x=-5???

???\frac{1}{2}\cdot 2x = \frac{1}{2} \cdot -5???

???x=\frac{-5}{2}???

???x=-\frac{5}{2}???

и

???x-3=0???

???x-3+3=0+3???

???х=3???

Пошаговые примеры использования теоремы о нуле

Пройти курс

Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂

Узнать больше 92-13х+36=0???

, и мы учтем левую часть.

???(х-4)(х-9)=0???

Теорема нуля говорит нам, что для того, чтобы левая часть была равна ???0???, один или оба множителя должны быть ???0???. Следовательно, мы можем сказать

???x-4=0???

???x-4+4=0+4???

???х=4???

и

???x-9=0???

???x-9+9=0+9???

???х=9???

Корни ???x=4??? и ???х=9???.