| Основные функции
модуль x: abs(x)
| 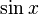 : sin[x] или Sin[x] : sin[x] или Sin[x]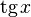 : tan[x] или Tan[x] : tan[x] или Tan[x]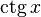 : cot[x] или Cot[x] : cot[x] или Cot[x] : sec[x] или Sec[x] : sec[x] или Sec[x]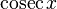 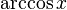 : ArcCos[x] : ArcCos[x]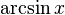 : ArcSin[x] : ArcSin[x]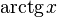 : ArcTan[x] : ArcTan[x]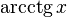 : ArcCot[x] : ArcCot[x]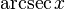 : ArcSec[x] : ArcSec[x]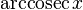 : ArcCsc[x] : ArcCsc[x]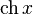 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 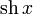 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]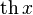 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]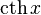 : coth[x] или Coth[x] : coth[x] или Coth[x]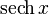 : sech[x] или Sech[x] : sech[x] или Sech[x]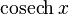 : csch[x] или Csch[е] : csch[x] или Csch[е]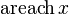 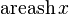 : ArcSinh[x] : ArcSinh[x]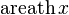 : ArcTanh[x] : ArcTanh[x]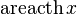 : ArcCoth[x] : ArcCoth[x]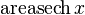 : ArcSech[x] : ArcSech[x]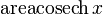 : ArcCsch[x] : ArcCsch[x] |
Вычисление площадей плоских фигур является одним из приложений определенного интеграла.

Для того, чтобы получить площадь фигуры изображенной на рисунке, необходимо вычислить определенный интеграл вида:
Функции f(x) и g(x) как правило, известны из условия задачи, а вот абсциссы их точек пересечения x=a и x=b придется дополнительно найти. Для этого необходимо решить уравнение:
f(x)
=
g(x)
{
x
Описанным выше способом, можно также найти площадь криволинейной трапеции в случае, если графики функций f(x) и g(x) не пересекаются, но точки x=a и x=b заданы по условию задачи:

В этом случае криволинейная трапеция (фигура площадь которой мы вычисляем) образована графиками функций f(x), g(x) и прямыми x=a, x=b.
Онлайн калькулятор, построенный на основе системы Wolfram Alpha, автоматически вычислит площадь фигуры, образованной пересечением двух графиков функций.
∫∫∫ Тройной интеграл — Калькулятор Он-лайн
Введите подинтегральную функцию, для которой надо найти тройной интеграл
Найдём решение тройного интеграла от функции f(x, y, z).
Введите вверхние и нижние пределы для области интегрирования и
подинтегральную функцию для тройного интеграла.
Если подинтегральной функции нету, то укажите 1.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Вычисление объема тела вращения вокруг оси Ох
Пусть график функции y = f(x) вращается вокруг оси Ox, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями x = a, x = b.
Объем тела вращения, образованного вращением графика y=f(x) вокруг оси Ox, может быть вычислен по формуле
Пример 1. Вычислить объем тела, образованного вращением дуги кривой y=x2, x∈[1,3] вокруг оси Оx.
Решение. Данные a=1, b=3, f(x)=x2, подставляем в формулу, получаем
С помощью калькулятора проверяем правильность вычисления объема , а также получаем рисунок тела вращения.
Вычисление объема тела вращения вокруг оси Оy
Пусть график функции x=φ(y) вращается вокруг оси Oy, образуя так называемую поверхность вращения. Определим объем тела, ограниченного этой поверхностью и плоскостями y = c, y = d.
Объем тела вращения, образованного вращением графика x=φ(y) вокруг оси Oy, может быть вычислен по формуле
Пример 2. Вычислить объем тела, образованного вращением дуги кривой x=3y-y2, x∈[1,2] вокруг оси Оx.
Решение. Данные c=1, d=2, φ(y)=3y-y2, подставляем в формулу, получаем
В калькулятор вставляем функцию x=3y-y2, x меняем на y, границы от 1 до 2, проверяем правильность вычисления объема , а также получаем рисунок тела вращения.
Следующая тема: Вычислить длину кривой
Тип урока:
комбинированный.Цель урока: научиться вычислять объемы тел вращения с помощью интегралов.
Задачи:
- закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
- познакомиться с понятием объемной фигуры;
- научиться вычислять объемы тел вращения;
- способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
- воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
Рефлексия. Спокойная мелодия.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее умертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”. (Презентация. Слайд)
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого выполним задание “Исключите лишнее слово”. (Слайд.)
(Учащийся выходит к И.Д.с помощью ластика убирает лишнее слово.)
– Правильно “Дифференциал”. Попробуйте оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным исчислением..
“Математическая гроздь”.
Задание. Восстановите пропуски. (Студент выходит и вписывает ручкой необходимые слова.)
– Реферат о применении интегралов мы заслушаем позже.
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1:
Вычислить площадь фигуры, ограниченной линиямиРешение:
Построим на координатной плоскости графики функций . Выделим площадь фигуры, которую надо найти.III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (Слайд) (На рисунке представлена плоская фигура.)
– Что изображено на втором рисунке? Является ли эта фигура плоской? (Слайд) (На рисунке представлена объемная фигура.)
– В космосе, на земле и в повседневной жизни мы встречаемся не только с плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например объем планеты, каметы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело, насколько они были точны и обоснованны.
Сообщение студентки. (Тюрина Вера.)
1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы. (Слайд 2)
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью, следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного интеграла”. (Слайд)
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
Лабиринт (греческое слово) означает ход в подземелье. Лабиринт– запутанная сеть дорожек, ходов, сообщающихся друг с другом помещений.
Но определение “разбилось”, остались подсказки в виде стрелок.
Задание. Найдите выход из запутанного положения и запишите определение.
Слайд. “Карта инструктаж” Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
Объем тела вращения вычисляется по одной из формул:
1., если вращение криволинейной трапеции вокруг оси ОХ.
2. , если вращение криволинейной трапеции вокруг оси ОУ.
Карту инструктаж получает каждый студент. Преподаватель подчеркивает основные моменты.
– Преподаватель объясняет решение примеров на доске.
Пример.
Рассмотрим отрывок из известной сказки А. С. Пушкина “Сказка о царе Салтане, о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной царевне Лебеде” (Слайд 4):
…..
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
(Слайд 5):
Какими же должен быть объем бочки, чтобы в ней поместились царица и её сын?
– Рассмотрим следующие задания
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y = , x = 4, y = 0.
Решение .
IV. Закрепление нового материала
Пример 2. Вычислить объем тела, образованного вращением лепестка, вокруг оси абсцисс y = x2, y2 = x.
Решение .
Построим графики функции. y = x2, y2 = x. График y2 = x преобразуем к виду y = .
Имеем V = V1 – V2 Вычислим объем каждой функции
– Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей – гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности (рис.8, 9).
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы вокруг ее мнимой оси, как показано на рис. 8, где
Решение.
куб. ед.
Задания по группам. Учащиеся вытягивают жребий с задачами, рисунки выполняют на ватмане, один из представителей группы защищает работу.
1-я группа.
Удар! Удар! Ещё удар!
Летит в ворота мячик – ШАР!
А это– шар арбузный
Зелёный, круглый, вкусный.
Вглядитесь лучше – шар каков!
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.
Найти объем тела, получаемого вращением вокруг оси ОХ функции, ограниченную
Решение.
Ошибка! Закладка не определена.
– Скажите, пожалуйста, где мы встречаемся с данной фигурой?
Дом. задание для 1 группы. ЦИЛИНДР (слайд) .
«Цилиндр – что такое?» – спросил я у папы.
Отец рассмеялся: Цилиндр – это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода – цилиндр,
Труба на нашей крыше – тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой –
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.
– Задание. Домашняя работа составить график функции и вычислить объем .
2-я группа. КОНУС (слайд).
Сказала мама: А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Расскажи ещё про конус.
– Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.
Задание . Вычислить объем тела полученный вращением вокруг оси абсцисс
Дом. задание для 2-й группы. ПИРАМИДА (слайд).
Я видел картину. На этой картине
Стоит ПИРАМИДА в песчаной пустыне.
Всё в пирамиде необычайно,
Какая-то есть в ней загадка и тайна.
А Спасская башня на площади Красной
И детям, и взрослым знакома прекрасно.
Посмотришь на башню – обычная с виду,
А что на вершине у ней? Пирамида!
Задание. Домашняя работа составить график функции и вычислить объем пирамиды
Вывод.
– Объёмы различных тел мы вычисляли опираясь на основную формулу объёмов тел с помощью интеграла.
Это является ещё одним подтверждением того, что определённый интеграл есть некоторый фундамент для изучения математики.
– Ну а теперь давайте немного отдохнем.
Найди пару.
|
Математическое домино мелодия играет.
“Дорога та, что сам искал, вовек не позабудется…”
Исследовательская работа. Применение интеграла в экономике и технике.
Тесты для сильных учащихся и математический футбол.
Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
Д/З. Вычислить объемы тел вращения.
Рефлексия.
Приём рефлексии в форме синквейна (пятистишия).
1-я строка – название темы (одно существительное).
2-я строка – описание темы в двух словах, два прилагательных.
3-я строка – описание действия в рамках этой темы тремя словами.
4-я строка – фраза их четырёх слов, показывает отношение к теме (целое предложение).
5-я строка – синоним, который повторяет суть темы.
- Объем.
- Определенный интеграл, интегрируемая функция.
- Строим, вращаем, вычисляем.
- Тело, полученное вращением криволинейной трапеции (вокруг ее основания).
- Тело вращения (объемное геометрическое тело).
Вывод (слайд).
- Определенный интеграл – это некоторый фундамент для изучения математики, которая вносит незаменимый вклад в решение задач практического содержания.
- Тема “Интеграл” ярко демонстрирует связь математики с физикой, биологией, экономикой и техникой.
- Развитие современной науки немыслимо без использования интеграла. В связи с этим, начинать его изучение необходимо в рамках средне специального образования!
Выставление оценок . (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
Приложение 2.
Вычисление объёмов тел вращения | matematicus.ru
Формула для вычисления объёма тела, получаемого вращением криволинейной трапеции вокруг оси абсцисс OX, ограниченной линиями:
y=f(x) – непрерывная линия, где a≤x≤b
x=a, x=b — прямые
y=0


Аналогично можно записать формулу для определения объём тела, получаемого вращением криволинейной трапеции вокруг оси ординат OX, ограниченной линиями:
x=φ(x) – непрерывная линия, где c≤x≤d
x=c, x=d — прямые
x=0

Для вычисления объёма тела, образованного вращением криволинейной трапеции вокруг оси абсцисс OX и ограниченная кривыми y=f1(x) и y=f2(x) и прямыми x=a и x=b, находится по формуле:

Пример
Найти Vш объем шара, R – радиус шара. Объём шара, образован вращением вокруг оси OX полукруга радиусом R.

Решение

График окружности
Формулы для определения верхней и нижней границы имеют вид:
$$y = \sqrt {{R^2} — {x^2}} $$
$$y = — \sqrt {{R^2} — {x^2}} $$
см. график окружности.
Найдем объем шара:

Объем тела вращения вокруг оси Ox, Oy
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y1(x) и y2(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций yi(x) по переменной x
Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле
Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.
ІV. Найти объемы тел, ограниченными поверхностями, полученными при вращении отрезков следующих линий
Пример 2.139 (2472) Найти объем тела, образованного вращением кривой (нейлоїд) xє[0;a] вокруг оси Ox.
Решение: Складываем подинтегральную функцию:
Пределы интегрирования известны за условием: [0;a].
Найдем объем тела интегрированием:
Всегда помните, что объем измеряется в кубических единицах.
Пример 2.140 (2473) Найти объем тела, образованного вращением кривой y=2x-x^2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:
И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:
б) Вычислим объем тела вращения вокруг оси Oy:
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.
Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:
Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:
б) Выполняем вычисление объема тела при вращении вокруг оси Oy:
Замена переменных помогает найти последний интеграл.
Пример 2.142 (2475) Найти объем тела, образованного вращением кривой
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Чтобы записать подинтегральную функцию найдем разницу квадратов заданных функций:
а)
б) для тела, образованного вращением вокруг оси Oy подинтегральная функция имеет вид
Из условия равенства функций y1(x)=y2(x) определяем пределы интегрирования
x1=0, |x|=a поэтому
Пределы интегрирования :
а)
б)
При :
поэтому принимая во внимание симметрию имеем неравенство .
а) Вычисляем объем тела вращения вокруг оси Ox:
б) Через следующий интеграл определяем объем тела вращения вокруг оси Oy:
Здесь нет сложных моментов при вычислении интеграла.
Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e— x, y=0,
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y2=e-2x;
б) x*y (x) =xe-x.
Запишем пределы интегрирования (известно за условием):
а) Находим объем тела вращения вокруг оси Ox:
б) Найдем объем тела вращения вокруг оси Oy:
Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.
Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x2+(y-b)2=a2, , вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:
При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:
Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:
Внимательно разберите приведенный пример.
90000 Calculus I — Volumes of Solids of Revolution / Method of Rings 90001 Paul’s Online Notes 90002 Notes Quick Nav Download 90003 90004 90005 Go To 90006 90005 Notes 90006 90005 Practice Problems 90006 90005 Assignment Problems 90006 90005 Show / Hide 90006 90015 Show all Solutions / Steps / 90016 etc.90017 90006 90019 Hide all Solutions / Steps / 90016 etc. 90017 90006 90023 90004 90005 Sections 90006 90005 Area Between Curves 90006 90005 Volumes of Solids of Revolution / Method of Cylinders 90006 90005 Chapters 90006 90005 Integrals 90006 90005 Extras 90006 90005 Classes 90006 90005 Algebra 90006 90005 Calculus I 90006 90005 Calculus II 90006 90005 Calculus III 90006 90005 Differential Equations 90006 90005 Extras 90006 90005 Algebra & Trig Review 90006 90005 Common Math Errors 90006 90005 Complex Number Primer 90006 90005 How To Study Math 90006 90005 Cheat Sheets & Tables 90006 90005 Misc 90006 90005 Contact Me 90006 90005 MathJax Help and Configuration 90006 90005 My Students 90006 90023 90004 90005 Notes Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Practice Problems Downloads 90006 90005 Complete Book — Problems Only 90006 90005 Complete Book — Solutions 90006 90085 90005 Current Chapter — Problems Only 90006 90005 Current Chapter — Solutions 90006 90085 90005 Current Section — Problems Only 90006 90005 Current Section — Solutions 90006 90005 Assignment Problems Downloads 90006 90005 Complete Book 90006 90005 Current Chapter 90006 90005 Current Section 90006 90005 Other Items 90006 90005 Get URL’s for Download Items 90006 90023 90004 90005 Print Page in Current Form (Default) 90006 90005 Show all Solutions / Steps and Print Page 90006 90005 Hide all Solutions / Steps and Print Page 90006 90023 90004 90005 Home 90006 90005 Classes 90006 90005 Algebra 90004 90005 Preliminaries 90004 90005 Integer Exponents 90006 90005 Rational Exponents 90006 90005 Radicals 90006 90005 Polynomials 90006 90005 Factoring Polynomials 90006 90005 Rational Expressions 90006 90005 Complex Numbers 90006 90023 90006 90005 Solving Equations and Inequalities 90004 90005 Solutions and Solution Sets 90006 90005 Linear Equations 90006 90005 Applications of Linear Equations 90006 90005 Equations With More Than One Variable 90006 90005 Quadratic Equations — Part I 90006 90005 Quadratic Equations — Part II 90006 90005 Quadratic Equations: A Summary 90006 90005 Applications of Quadratic Equations 90006 90005 Equations Reducible to Quadratic in Form 90006 90005 Equations with Radicals 90006 90005 Linear Inequalities 90006 90005 Polynomial Inequalities 90006 90005 Rational Inequalities 90006 90005 Absolute Value Equations 90006 90005 Absolute Value Inequalities 90006 90023 90006 90005 Graphing and Functions 90004 90005 Graphing 90006 90005 Lines 90006 90005 Circles 90006 90005 The Definition of a Function 90006 90005 Graphing Functions 90006 90005 Combining Functions 90006 90005 Inverse Functions 90006 90023 90006 90005 Common Graphs 90004 90005 Lines, Circles and Piecewise Functions 90006 90005 Parabolas 90006 90005 Ellipses 90006 90023 90006 90023 90006 90023.90000 Volume of a partially filled cylinder with calculator 90001 Volume of a partially filled cylinder with calculator — Math Open Reference 90002 Definition: A shape formed when a cylinder is cut by a plane parallel to the sides of the cylinder. 90003 90002 Try this Drag the orange dots, note how the volume changes. 90003 90002 If we take a horizontal cylinder, and cut it into two pieces using a cut parallel to the sides of the cylinder, we get two horizontal cylinder segments.In the figure above, the bottom one is shown colored blue. The other one is the transparent part on top. 90003 90002 90009 If we look a the end of the cylinder, we see it is a circle cut into two circle segments. See Circle segment definition for more. 90003 90002 Whenever we have a solid whose cross-section is the same along its length, we can always find its volume by multiplying the area of the end by its length. So in this case, the volume of the cylinder segment is the area of the circle segment, times the length.90003 90002 So as a formula the volume of a horizontal cylindrical segment is Where 90014 90015 s 90016 = the area of the circle segment forming the end of the solid, and 90014 90015 l 90016 = the length of the cylinder. 90003 90002 The area of the circle segment can be found using it’s height and the radius of the circle. 90014 See Area of a circle segment given height and radius. 90003 90024 Calculator 90025 90002 Use the calculator below to calculate the volume of a horizontal cylinder segment.It has been set up for the practical case where you are trying to find the volume of liquid is a cylindrical tank by measuring the depth of the liquid. 90003 90002 For convenience, it converts the volume into liquid measures like gallons and liters if you select the desired units. If you do not specify units the volume will be in whatever units you used to input the dimensions. For example, if you used feet, then the volume will be in cubic feet. Use the same units for all three inputs. 90003 90030 90024 As a formula 90025 90014 volume = where: 90014 90015 R 90016 is the 90037 radius 90038 of the cylinder.90014 90015 D 90016 is the depth. 90014 90015 L 90016 is the length of the cylinder 90037 Notes 90038: 90047 90048 The result of the cos 90049 -1 90050 function in the formula is in radians. 90051 90048 The formula uses the radius of the cylinder. This is half its diameter. 90051 90048 All inputs must be in the same units. The result will be in those cubic units. So for example if the inputs are in inches, the result will be in cubic inches. If necessary the result must be converted to liquid volume units such as gallons.90051 90056 90024 Related topics 90025 90002 (C) 2011 Copyright Math Open Reference. 90014 All rights reserved 90003 .90000 Volume of a cylinder with calculator 90001 Volume of a cylinder with calculator — Math Open Reference 90002 Definition: The number of cubic units that will exactly fill a cylinder 90003 90002 Try this Drag the orange dot to resize the cylinder. The volume is calculated as you drag. 90003 90006 How to find the volume of a cylinder 90007 90002 Although a cylinder is technically not a prism, it shares many of the properties of a prism.Like prisms, the volume is found by multiplying the area of one end of the cylinder (base) by its height. 90003 90002 Since the end (base) of a cylinder is a circle, the area of that circle is given by the formula: 90003 90002 Multiplying by the height 90013 h 90014 we get where: 90015 90016 π 90017 is Pi, approximately 3.142 90015 90016 r 90017 is the radius of the circular end of the cylinder 90015 90016 h 90017 height of the cylinder 90015 90003 90006 Calculator 90007 90002 Use the calculator above to calculate height, radius or volume of a cylinder.90003 90002 Enter any two values and the missing one will be calculated. For example: enter the radius and height, and press ‘Calculate’. The volume will be calculated. 90003 90002 Similarly, if you enter the height and volume, the radius needed to get that volume will be calculated. 90003 90006 Volume of a partially filled cylinder 90007 90036 90002 One practical application is where you have horizontal cylindrical tank partly filled with liquid. Using the formula above you can find the volume of the cylinder which gives it’s maximum capacity, but you often need to know the volume of liquid in the tank given the depth of the liquid.90003 90002 This can be done using the methods described in Volume of a horizontal cylindrical segment. 90003 90006 Oblique cylinders 90007 90002 Recall that an oblique cylinder is one that ‘leans over’ — where the top center is not over the base center point. In the figure above check «allow oblique ‘and drag the top orange dot sideways to see an oblique cylinder. 90003 90002 It turns out that the volume formula works just the same for these. You must however use the perpendicular height in the formula.This is the vertical line to left in the figure above. To illustrate this, check ‘Freeze height’. As you drag the top of the cylinder left and right, watch the volume calculation and note that the volume never changes. 90003 90002 See Oblique Cylinders for a deeper discussion on why this is so. 90003 90006 Units 90007 Remember that the radius and the height must be in the same units — convert them if necessary. The resulting volume will be in those cubic units. So, for example if the height and radius are both in centimeters, then the volume will be in cubic centimeters.90006 Things to try 90007 90053 90054 In the figure above, click ‘reset’ and ‘hide details’ 90055 90054 Drag the two dots to alter the size and shape of the cylinder 90055 90054 Calculate the volume of that cylinder 90055 90054 Click ‘show details’ to check your answer. 90055 90062 90006 Related topics 90007 90002 (C) 2011 Copyright Math Open Reference. 90015 All rights reserved 90003 .90000 Volume of a cube with calculator 90001 Volume of a cube with calculator — Math Open Reference 90002 Definition: The number of cubic units that will exactly fill a cube 90003 90002 Try this Drag the orange dot to resize the cube. The volume is calculated as you drag. 90003 90006 How to find the volume of a cube 90007 90002 Recall that a cube has all edges the same length (See Cube definition). The volume of a cube is found by multiplying the length of any edge by itself twice.So if the length of an edge is 4, the volume is 4 x 4 x 4 = 64 90003 90002 Or as a formula: 90003 90012 90013 90014 volume = s 90015 3 90016 90017 90018 where: 90019 90020 s 90021 is the length of any edge of the cube. 90017 90023 90017 90025 90026 90002 In the figure above, drag the orange dot to resize the cube. From the edge length shown, calculate the volume of the cube and verify that it agrees with the calculation in the figure. 90003 90002 When we write 90030 90020 volume = s 90015 3 90016 90021 90035, strictly speaking this should be read as «s to the power 3», but because it is used to calculate the volume of cubes it is usually spoken as «s cubed».90003 90006 Calculator 90007 90002 Use the calculator above to calculate the properties of a cube. 90003 90002 Enter any one value and the others will be calculated. For example, enter the side length and the volume will be calculated. 90003 90002 Similarly, if you enter the surface area, the side length needed to get that area will be calculated. 90003 90006 Some notes on the volume of a cube 90007 90002 Recall that a cube is like an empty box.It has nothing inside, and the walls of the box have zero thickness. So strictly speaking, the cube has zero volume. When we talk about the volume of a cube, we really are talking about how much liquid it can hold, or how many unit cubes would fit inside it. 90003 90002 Think of it this way: if you took a real, empty metal box and melted it down, you would end up with a small blob of metal. If the box was made of metal with zero thickness, you would get no metal at all. That is what we mean when we say a cube has no volume.90003 90002 The strictly correct way of saying it is «the volume enclosed by a cube» — the amount space there is inside it. But many textbooks simply say 90020 «the volume of a cube» 90021 to mean the same thing. However, this is not strictly correct in the mathematical sense. What they usually mean when they say this is the volume 90054 enclosed 90055 by the cube. 90003 90006 Units 90007 Remember that the length of an edge and the volume will be in similar units. So if the edge length is in miles, then the volume will be in cubic miles, and so on.90006 Related topics 90007 90002 (C) 2011 Copyright Math Open Reference. 90019 All rights reserved 90003 .

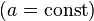
 : x^a
: x^a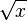 : Sqrt[x]
: Sqrt[x]![\sqrt[n]{x}](/800/600/https/upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n)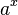 : a^x
: a^x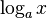 : Log[a, x]
: Log[a, x]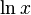 : Log[x]
: Log[x]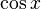 : cos[x] или Cos[x]
: cos[x] или Cos[x]