Найти область определения функции показательной функции: График показательной функции, область определения и область значений функции — задание. Алгебра, 11 класс.

Показательная функция определение, свойства, особенности построения графиков убывающей и возрастающей функций, область определения и применения, формулы, примеры решения

Правильное построение графика показательной функции является не такой простой задачей. Рекомендуется выяснить основные ее свойства, а также разобрать применение в жизненных ситуациях. В интернете информация о ней не систематизирована, и нужно выбирать из нескольких источников, а затем проверять. Начинать изучение следует с базовых понятий, после которых переходить к более сложным элементам.

Общие сведения

Функцией называется закон зависимости одной величины от другой. Выражается она при помощи выражений алгебраического, тригонометрического, иррационального и других типов. Существует два типа переменных, которые встречаются в любых функциях: зависимая и независимая. Последняя называется также аргументом.

Основной особенностью показательной функции считается ее вид, поскольку основанием является число, а степенью — аргумент. n) — 1] / (q — 1), можно без проблем вычислить значение. Первое значение b1 = 1, знаменатель q = 2 3 / 2 2 = 2 2 / 2 = 2 / 1 = 2. Общее число зерен определяется таким образом: S64 = 1 * [(2 64 ) — 1] / (2 — 1) = (2 64 ) — 1. Ученые подсчитали, что такое количество превышает урожай пшеницы на планете за 2008−2009 год в 1800 раз. Если воспользоваться справочником или компьютером, то S64 = 18446744073709551615 — 1 = 18446744073709551614.

Примеры иллюстрируют применение степенной функции в жизни, поскольку она может описывать явления природы, в которой протекают различные процессы. Например, деление клеток злокачественных опухолей, увеличение количества молекул озона при разрядах молнии и так далее.

Представление функции

Математики рекомендуют ознакомиться на начальных этапах с графиком показательной функции и ее свойствами. Графиком называется ее графическое представление в некоторой системе координат. В качестве последней распространена декартовая прямоугольная с двумя осями (ординат — z и абсцисс — y). y относительно y, принимающего нулевое значение: z = a 0 = 1. Искомая точка имеет координаты (0;1).

Построение графиков

Для построения графиков следует рассмотреть два случая, при которых a > 0 (рис. 1) и 0 < a < 1 (рис. 2). Кроме того, можно для сравнения построить частные примеры со следующими условиями:

a < 0 и x > 0 (рис. 3).

a = 0 и x > 0 (рис. 4).

a = 1 и x > 0 (рис. 5).

Для построения графика существуют свои правила, которых рекомендуют придерживаться математики. Процедура осуществляется в двух режимах: схематическом и точном. В первом случае нужно знать свойства. Таблица зависимостей значения от аргумента не составляется. При точном построении необходимо составить таблицу. В ней необходимо рассмотреть около 5-10 значений независимой переменной. Затем все точки отмечаются на декартовой системе координат и плавно соединяются.

Оформление играет очень важную роль, поскольку не допускаются исправления. y (a > 0 и y > 0).

Если рассмотреть пример, в котором y > 0 и 0 < a < 1, то графическое изображение (рис. 2) будет немного другим:

Рисунок 2. График при 0 < a < 1.

При a < 0 и x > 0 график также существенно изменится, поскольку будет постоянно убывать:

Рисунок 3. Графическая иллюстрация при a < 0 и x > 0.

Когда основание равно 0, тогда функция перестает быть показательной, поскольку не соблюдается условие из определения. На рисунке 4 представлен ее график:

Рисунок 4. Графическое представление при a = 0 и x > 0.

Последний случай — основание равно 1. Функция также не является показательной.

Рисунок 5. График при a = 1 и x > 0.

Кроме того, встречаются задачи не только на построение графика, но и на осуществление операций дифференцирования, нахождения производной и первообразной.

Какая из функций является показательной?

Какая из функций является показательной?

функция вида y = a x , где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Как найти область определения показательной функции?

Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией. Область определения показательной функции: D (y)=R – множество всех действительных чисел. Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.

Как определить показательную функцию?

Основные свойства показательной функции y = a x при 0

1. Область определения функции — вся числовая прямая.
2. Область значений функции — промежуток (0;+∞) .
3. Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1 ax2 .
4. При x = 0 значение функции равно 1.

В чем разница между показательной и степенной функцией?

У степенной функции y = xa показатель степени постоянен, а основание степени меняется. Функция, у которой постоянно основание степени, а меняется ее показатель, называется показательной. … При x = 0 показательная функция ax обращается в 1, так как a0 = 1.

Какая показательная функция является возрастающей?

Область определения показательной функции — множество R всех действительных чисел. Множество всех значений показательной функции — множество всех положительных чисел. Показательная функция y = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0

Что называется степенной функцией?

Степенной функцией с вещественным показателем a называется функция y = x n , x > 0. Заметим, что для натуральных n степенная функция определена на всей числовой оси.

Как определить степенную функцию?

Если показатель степени — целое отрицательное число, то степенная функция задаётся формулой y=x−n или y=1/xn. Например, такой вид принимают графики функций y=x−4,y=x−8. Например, такой вид принимают графики функций y=x−5,y=x−11. Функции такого вида называются дробно-линейными.

Как правильно записать область определения функции?

Область определения функции y = sin(x) — множество R действительных чисел. Область определения функции y = cos(x) — так же множество R действительных чисел. Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .

Когда функция называется возрастающей?

Ответ, проверенный экспертом Возрастающая функция — это функция, при которой большему значению аргумента (х) соответствует большее значение функции (y).

Какая функция называется возрастающей?

Функция является возрастающей, если для большего значения аргумента соответствует большее значение заданной функции. Другими словами, если при возрастании значений аргумента значения заданной функции тоже возрастают, то заданная функция возрастает.

Какая функция называется возрастающей на множестве Р?

Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1 , выполнено неравенство f(x2) > f(x1). … Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции.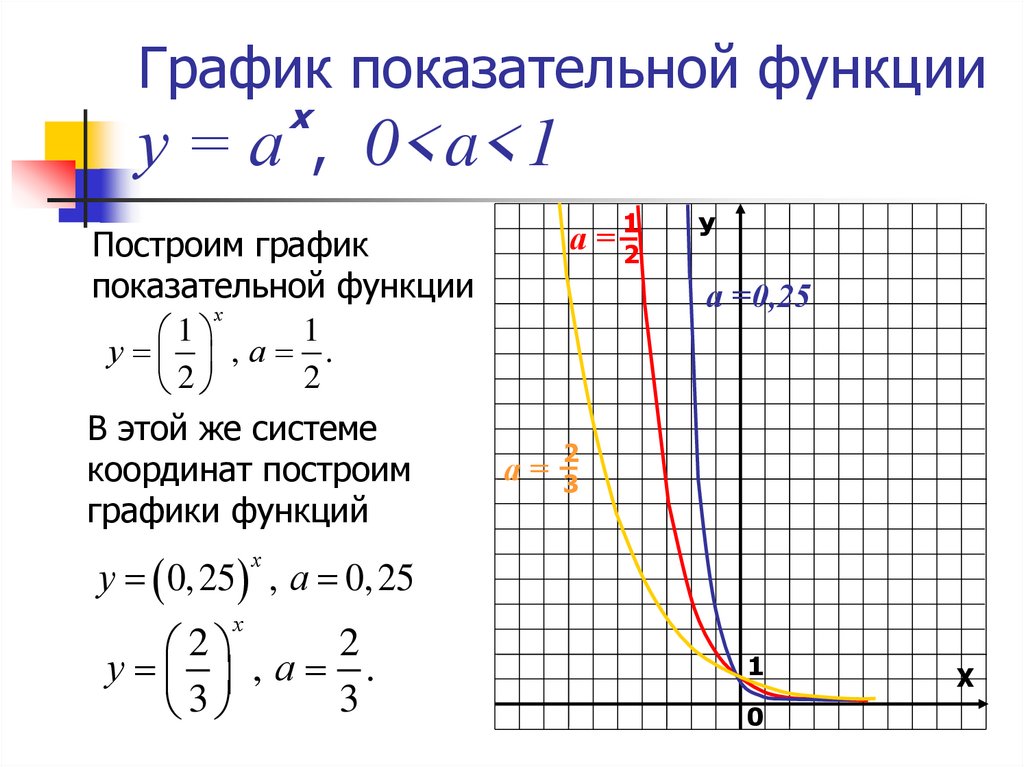

Как определить что функция возрастает?

Вот формулировки признаков возрастания и убывания функции на интервале:

1. если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
2. если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Как определить функцию на монотонность?

Функция называется возрастающей, если большему значению аргумента соответствует большее значения функции. Если x2 > x1, то f(x2 > f(x1) или: чем больше x, тем больше y. Если функция возрастает или убывает на некотором промежутке, то говорят, что она монотонна на данном промежутке.

Как определить возрастает или убывает функция парабола?

Если при возрастании значений аргумента (x) возрастают также значения функции (y), то функция является возрастающей. Если при возрастании значений аргумента (x) значения функции (y) убывают, то функция является убывающей. Чем больше модуль коэффициента | a |, тем ближе к оси Oy расположены ветви параболы.

Как понять что функция монотонна?

Монотонная функция — это функция, которая всё время либо возрастает, либо убывает. Функция y=f(x) называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.

Какая из функций является монотонной?

Определение. Булева функция f(x1, …, xn) называется монотонной (принадлежит классу M), если для любой пары наборов α и β таких, что α β, выполняется условие f(α)≤ f(β) (назовем его условием монотонности).

Как определить является ли Булева функция монотонной?

Существует алгоритм, в котором монотонность булевой функции может быть определена по её вектору значений, путём последовательного его деления пополам и проверки отношения предшествования. Однако, пусть есть функция `f(1101 1110)`. Делим вектор значений пополам и получаем наборы `alpha = (1101)` и `beta = (1110)`.

Как определить является ли последовательность монотонной?

Последовательность {xn} называется монотонной, если она убывающая или возрастающая. Если все элементы последовательности {xn} равны одному и тому же числу, то последовательность называется постоянной. Читать дальше: предел числовой последовательности.

Как определить является ли последовательность ограниченной?

Ограниченные и неограниченные последовательности называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M. называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m.

Что такое монотонная последовательность?

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств.

Что такое сходящаяся последовательность?

Последовательность {xn} называется сходящейся, если существует такое число a∈R такое, что последовательность {xn−a} является бесконечно малой последовательностью.

Что означает последовательность?

В математике последовательность — это пронумерованный набор каких-либо объектов, среди которых допускаются повторения, причём порядок объектов имеет значение. Нумерация чаще всего происходит натуральными числами.

Что такое стационарная последовательность?

Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.

Что такое последовательность?

Последовательность — это такой набор элементов некоторого множества, что: … это число является номером элемента и обозначает позицию данного элемента в последовательности; для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.

Чем отличается последовательность от числового ряда?

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм. … которые в свою очередь образуют новую последовательность.

Как определить последовательность чисел?

Последовательность задается формулой n-го члена: an=f (n). По этой формуле можно найти любой член последовательности.

Что такое последовательность текста?

Последовательность — это признак, который реализуется тогда, когда каждое последующее предложение содержит новую информацию для развертывания содержания текста. В каждом тексте прослеживается логическая последовательность развития мысли.

Что такое текст Назовите основные его характеристики?

Текст (от латинского textus — «ткань», «сплетение», «соединение», «структура», «связь») — это речевое произведение, состоящее из ряда предложений, расположенных в определённой последовательности и объединённых в целое единством темы, основной мысли и с помощью различных языковых средств.

Что такое текст назовите его признаки?

Основные признаки текста: тематическое и композиционное единство всех его частей; наличие смысловой и грамматической связи между частями; смысловая цельность, относительная законченность. Текст может состоять из одного абзаца, а может быть статьёй, докладом, книгой.

Как указать признаки текста?

Основные признаки текста:

• тематическое единство;
• связность;
• последовательность;
• развёрнутость;
• завершённость.

Показательная функция определение, свойства, особенности построения графиков убывающей и возрастающей функций, область определения и применения, формулы, примеры решения

Правильное построение графика показательной функции является не такой простой задачей. Рекомендуется выяснить основные ее свойства, а также разобрать применение в жизненных ситуациях. В интернете информация о ней не систематизирована, и нужно выбирать из нескольких источников, а затем проверять. Начинать изучение следует с базовых понятий, после которых переходить к более сложным элементам.

Содержание

• Общие сведения
• Сферы использования
• Представление функции
  • Основные свойства
  • Доказательства некоторых утверждений
  • Построение графиков
  • Правила дифференцирования
  • Поиск первообразных

Общие сведения

Функцией называется закон зависимости одной величины от другой. Выражается она при помощи выражений алгебраического, тригонометрического, иррационального и других типов. Существует два типа переменных, которые встречаются в любых функциях: зависимая и независимая. Последняя называется также аргументом.

Основной особенностью показательной функции считается ее вид, поскольку основанием является число, а степенью — аргумент. Последним называется независимая переменная, которая может принимать любые значения, кроме превращающих ее значение в пустое множество или неопределенность. n) — 1] / (q — 1), можно без проблем вычислить значение. Первое значение b1 = 1, знаменатель q = 2 ³ / 2 ² = 2 ² / 2 = 2 / 1 = 2. Общее число зерен определяется таким образом: S64 = 1 * [(2 ⁶⁴ ) — 1] / (2 — 1) = (2 ⁶⁴ ) — 1. Ученые подсчитали, что такое количество превышает урожай пшеницы на планете за 2008−2009 год в 1800 раз. Если воспользоваться справочником или компьютером, то S64 = 18446744073709551615 — 1 = 18446744073709551614.

Примеры иллюстрируют применение степенной функции в жизни, поскольку она может описывать явления природы, в которой протекают различные процессы. Например, деление клеток злокачественных опухолей, увеличение количества молекул озона при разрядах молнии и так далее.

Представление функции

Математики рекомендуют ознакомиться на начальных этапах с графиком показательной функции и ее свойствами. Графиком называется ее графическое представление в некоторой системе координат. y относительно y, принимающего нулевое значение: z = a ⁰ = 1. Искомая точка имеет координаты (0;1).

Построение графиков

Для построения графиков следует рассмотреть два случая, при которых a > 0 (рис. 1) и 0 < a < 1 (рис. 2). Кроме того, можно для сравнения построить частные примеры со следующими условиями:

a < 0 и x > 0 (рис. 3).

a = 0 и x > 0 (рис. 4).

a = 1 и x > 0 (рис. 5).

Для построения графика существуют свои правила, которых рекомендуют придерживаться математики. Процедура осуществляется в двух режимах: схематическом и точном. В первом случае нужно знать свойства. Таблица зависимостей значения от аргумента не составляется. При точном построении необходимо составить таблицу. В ней необходимо рассмотреть около 5-10 значений независимой переменной. Затем все точки отмечаются на декартовой системе координат и плавно соединяются.

Оформление играет очень важную роль, поскольку не допускаются исправления. y (a > 0 и y > 0).

Если рассмотреть пример, в котором y > 0 и 0 < a < 1, то графическое изображение (рис. 2) будет немного другим:

Рисунок 2. График при 0 < a < 1.

При a < 0 и x > 0 график также существенно изменится, поскольку будет постоянно убывать:

Рисунок 3. Графическая иллюстрация при a < 0 и x > 0.

Когда основание равно 0, тогда функция перестает быть показательной, поскольку не соблюдается условие из определения. На рисунке 4 представлен ее график:

Рисунок 4. Графическое представление при a = 0 и x > 0.

Последний случай — основание равно 1. Функция также не является показательной.

Рисунок 5. График при a = 1 и x > 0.

Кроме того, встречаются задачи не только на построение графика, но и на осуществление операций дифференцирования, нахождения производной и первообразной.

Предыдущая

АлгебраМножество обозначение, виды, свойства операций, теория, примеры решения множеств натуральных, целых и рациональных чисел, счетных и несчетных множеств

Следующая

АлгебраПравило Лопиталя для вычисления пределов, примеры с подробным решением, доказательство

Область определения и диапазон экспоненциальных функций

Область определения экспоненциальных функций равна всем действительным числам, поскольку у нас нет ограничений на значения, которые может принимать x . Диапазон экспоненциальных функций равен значениям выше или ниже горизонтальной асимптоты.

Здесь мы подробно рассмотрим, как найти область определения и диапазон экспоненциальных функций. Также мы рассмотрим несколько примеров с графиками функций для иллюстрации этих идей.

АЛГЕБРА

Актуально для …

Изучение области и области экспоненциальных функций.

См. примеры

Содержание

АЛГЕБРА

Актуально для …

Изучение области и области экспоненциальных функций.

См. примеры

Как найти область определения и область значений экспоненциальной функции?

Напомним, что домен — это набор входных значений, которые используются для независимой переменной. 9x}$ переведено на 3 единицы влево.

Функция определена для всех действительных чисел, поэтому областью определения функции является множество действительных чисел. x} – 1$?

Решение: Функция может принимать любое значение x в качестве входных данных. Это означает, что областью определения является множество всех действительных чисел.

Функция имеет только отрицательные значения  y . Также мы видим, что у нас есть $latex d=-1$, поэтому горизонтальная асимптота равна $latex y=-1$. Таким образом, все значения меньше -1.

Диапазон представляет собой набор всех действительных чисел $latex \{y \in R | у <-1 \}$.

---

См. также

Хотите узнать больше об области и спектре функций? Взгляните на эти страницы:

• Область определения и область значений графа
• Область определения и область значений линейных функций
• Область определения и область значений квадратичных функций
• Область определения и область значений рациональных функций
• Область определения и область значений тригонометрических функций
• Область значений и области значений логарифмических функций

Изучайте математику с помощью наших дополнительных ресурсов по различным темам

УЗНАТЬ БОЛЬШЕ

Видео

Question: Нахождение области определения и диапазона экспоненциальных функций

Стенограмма видео

Найдите домен и диапазон функция 𝑓 от 𝑥 равна семи в степени 𝑥 плюс пять плюс пять в наборе вещественные числа.

Начнем с того, что напомним себе что мы подразумеваем под доменом и диапазоном функции. Домен по сути является набором возможных значений, которые мы можем ввести в эту функцию, другими словами, множество 𝑥-значения, которые мы можем подставить в функцию 𝑓 от 𝑥. Тогда диапазон представляет собой множество возможные выходные данные функции после того, как значения из домена были заменены. Теперь у нас есть, в частности, экспоненциальная функция здесь. И самая общая форма экспоненциальная функция 𝑔 от 𝑥 равна 𝑏 в степени 𝑥. 𝑏 — действительное число больше, чем ноль и не равен единице.

Итак, начнем с определить, как выглядит график функции 𝑔 от 𝑥. Это позволит выявить его домен и диапазон. Тогда мы можем посмотреть серию преобразования, которые отображают 𝑔 из 𝑥 на 𝑓 из 𝑥, и это даст нам график функция 𝑓 от 𝑥.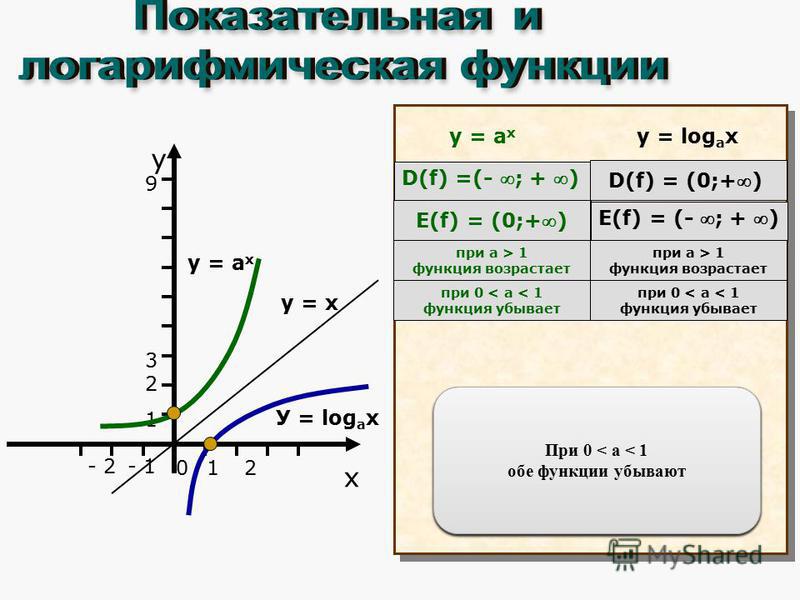 Тогда мы можем найти его домен и диапазон. В частности, мы собираемся начать нарисовав график 𝑔 числа 𝑥 равно семи в степени 𝑥.

Так как основание семь является числом больше единицы, то мы знаем, что имеем экспоненциальный рост вместо экспоненциального разлагаться. График очень похож это. Он проходит через ось 𝑦 в точке один, и он имеет горизонтальную асимптоту, заданную линией 𝑦, равной нулю, или 𝑥-ось. Он также проходит через точку один, семь. Теперь мы можем узнать этот факт, или мы можно заменить 𝑥 равным единице в функцию 𝑔 от 𝑥, и мы действительно получим Семь.

Имея это в виду, давайте определим каковы область определения и область значений функции 𝑔 функции 𝑥. Домен представляет собой множество возможных значения, которые мы можем ввести в функцию. Мы можем думать об этом как о разброс значений в 𝑥-направлении.

Здесь нет никаких ограничений. Мы можем подставить любое 𝑥-значение в функция 𝑔 от 𝑥, и мы всегда будем получать реальный результат. Ассортимент немного другой хотя. Диапазон можно рассматривать как разброс значений в 𝑦-направлении. И мы сказали, что есть горизонтальная асимптота, заданная линией 𝑦, равна нулю. Это означает, что функция 𝑔 от 𝑥 приближается к нулю, но никогда не достигает его. Хотя в другом направлении он направляется в сторону положительного ∞. И так диапазон открыт интервал от нуля до положительных ∞.

Имея это в виду, как нам составить карту функция 𝑔 от 𝑥 равна семи в степени 𝑥 на функцию 𝑓 от 𝑥? Давайте начнем с сопоставления семи с степени 𝑥 на семь в степени 𝑥 плюс пять. Это горизонтальный перевод функция 𝑔 от 𝑥 на пять единиц влево или вектором минус пять, нуль.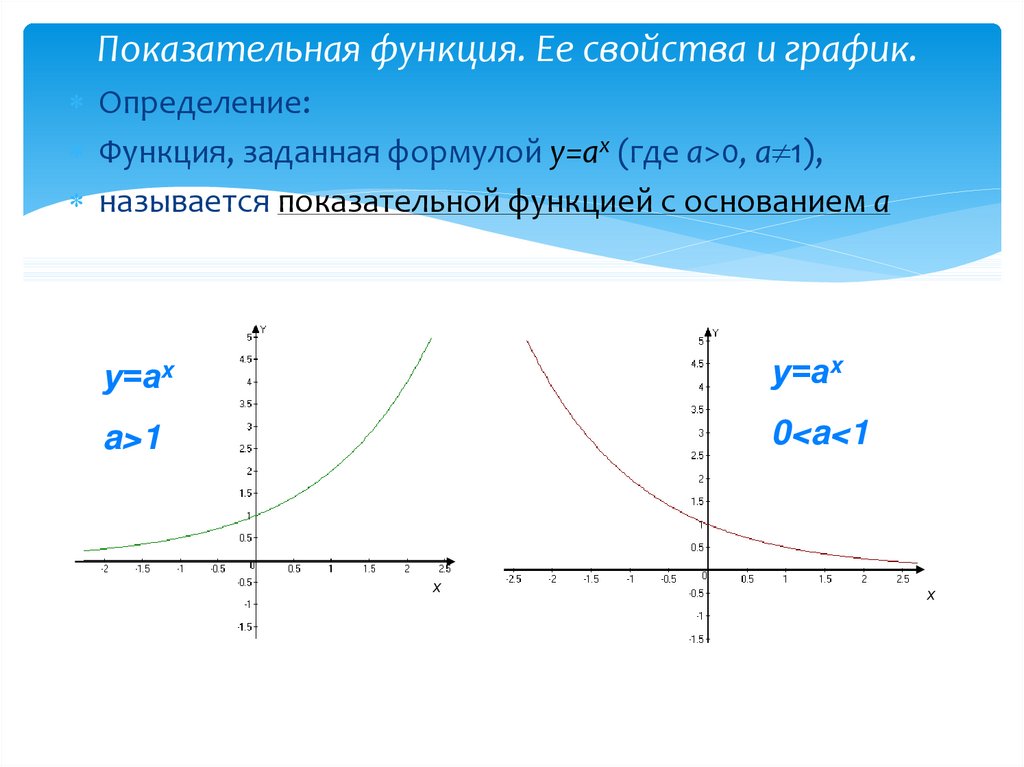

Что произойдет, если мы добавим пять к функция семь в степени 𝑥 плюс пять? ну это вертикаль перевод на пять единиц вверх или по вектору ноль, пять. Таким образом, чтобы отобразить функцию 𝑔 из 𝑥 равно семи в степени 𝑥 на функцию 𝑓 от 𝑥, мы собираемся выполнить два перевода, или мы можем думать об этом как об одном большом переводе. Он переместится на пять единиц влево а затем пять единиц вверх.

На этот раз мы знаем, что у него будет горизонтальная асимптота на пять единиц выше предыдущей. Поскольку предыдущий был предоставлен линия 𝑦 равна нулю, новая асимптота будет иметь уравнение 𝑦 равное пять. И хотя это не совсем необходимо, мы можем найти значение 𝑦-перехвата, подставив 𝑥 равно нулю в функция. Когда мы это делаем, мы получаем семь к пятая степень плюс пять. И мы также можем видеть, что это проходит через точку один, семь в степени шесть плюс пять.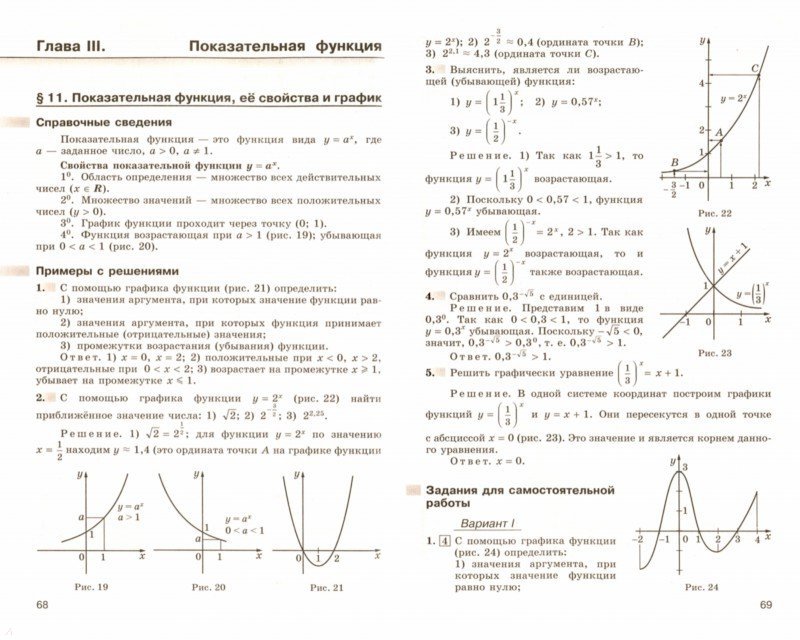

Это найдено путем замены одного в функцию.

У нас теперь, однако, достаточно информацию для определения домена и диапазона этой новой функции. Еще раз, домен может быть рассматривается как распространение значений в 𝑥-направлении. Это еще раз неограниченно. Таким образом, областью 𝑓 of 𝑥 является набор действительных чисел. Диапазон еще раз можно подумать как разброс значений в 𝑦-направлении. На этот раз горизонтальная асимптота задается строкой 𝑦 равно пяти, поэтому 𝑓 из 𝑥 приближается к пяти, но никогда не совсем достигает его. В другом направлении он направляется в сторону положительного ∞. Таким образом, диапазон функции равен открытый интервал от пяти до ∞.

Итак, рассматривая графики и преобразований графиков, мы определили область определения и область значений функции 𝑓 число 𝑥 равно семи в 𝑥 плюс пятая степень плюс пять. Домен представляет собой множество реальных числа, а диапазон — открытый интервал от пяти до ∞.

Экспоненциальные функции (область, диапазон и построение графика) – JDM Educational

Экспоненциальные функции часто встречаются в математике и в природе. Тем не менее, это все еще поднимает вопрос о том, что это за функции и как они выглядят.

Показательная функция имеет вид f(x) = ab ^x , где a — коэффициент, b — основание, а x — показатель степени. Любая экспоненциальная функция имеет область определения всех действительных чисел, но область определения может меняться в зависимости от знака a.

Конечно, вы можете использовать информацию о функции (такую ​​как асимптота и несколько точек на кривой) для построения графика экспоненциальной функции.

В этой статье мы поговорим об экспоненциальных функциях и о том, что они собой представляют. Мы также поговорим об их домене, диапазоне и асимптотах, а также о том, как их изобразить.

Начнем.

Что такое показательная функция?

Экспоненциальная функция имеет вид

• f(x) = ab ^x

, где a — коэффициент, b — основание, а x — показатель степени (обратите внимание, что a и b равны оба действительных числа, где a отлично от нуля, а b положительно).

Например, функция f(x) = 2(3 ^x ) является экспоненциальной функцией с коэффициентом a = 2 и основанием b = 3,

График экспоненциальной функции f(x) = 2(3 ^x ).

Мы всегда можем упростить экспоненциальную функцию до ее простейшей формы f(x) = ab ^x . Например, если у нас есть функция f(x) = 5(2 ^x+3 ), мы можем переписать ее как:

• f(x) = 5(2 ^{x + 3} )   [исходное функция]
• f(x) = 5(2x*2 ³ )   [по правилам экспонент, A ^{B + C} = A ^B A ^c ]
• f(x) = 5(2 ^x *8)   [так как 2 ³ = 8]
• f(x) = 40(2 ^x )  [так как 5 * 8 = 404]  904]  904

Итак, это действительно экспоненциальная функция с a = 40 и b = 2.

График экспоненциальной функции f(x) = 40(2 ^x ).

Обратите внимание, что у нас также может быть отрицательное значение для a. Например, функция f(x) = -4(5 ^x ) имеет a = -4 и b = 5. График будет немного отличаться, так как он будет ниже оси x (из-за того, что что а < 0).

График экспоненциальной функции f(x) = -4(5 ^x ).

Что такое область экспоненциальных функций?

Область экспоненциальной функции состоит из действительных чисел. Причина в том, что любое действительное число является допустимым входом в качестве показателя степени.

Это связано с тем, что b ^x всегда определяется для b > 0, а x — действительное число. На самом деле, когда x = 0, мы получаем b ^x = b ⁰ = 1, и f(0) всегда будет a.

Экспоненциальная функция f(x) = ab ^x является непрерывным, так как не имеет дырок (устранимых разрывов) или вертикальных асимптот (нулевых знаменателей).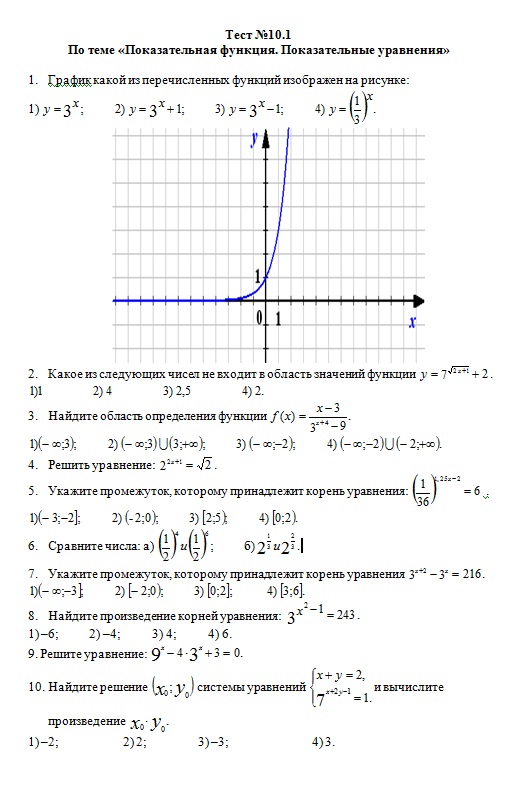

Что такое диапазон экспоненциальных функций?

Диапазон экспоненциальной функции зависит от значений a и b:

• Для b = 1 диапазон f(x) = ab ^x равен просто {a}.
• Для b, отличного от 1, и a > 0 диапазон f(x) = ab ^x равен (0, бесконечность).
• Для b, отличного от 1, и a < 0 диапазон f(x) = ab ^x равен (-бесконечность, 0).

Докажем это для различных случаев.

Случай 1: b = 1

Этот случай прост. Если b = 1, то:

• f(x) = ab ^x
• f(x) = a(1 ^x )   [поскольку b = 1]
• f(x)
• = a   [поскольку 1 ^x = 1 для всех действительных x]

Поскольку f(x) = a для всех действительных x, то диапазоном f(x) является значение {a}.

Случай 2: 0

< b < 1

Сначала мы находим максимальное и минимальное значения для b ^x . Поскольку 0 < b < 1, b ^x будет уменьшаться по мере того, как x принимает большие положительные значения (например, 0,5 ² = 0,25, 0,5 ³ = 0,125 и т. д.).

Значение b ^x всегда будет положительным, поскольку b положительно, но нет предела тому, насколько близко к нулю может быть b ^x . Таким образом, нижняя граница равна 0.

Аналогично, b ^x будет увеличиваться по мере того, как x принимает большие отрицательные значения (например, 0,5 ^-2 = 4, 0,5 ^-3 = 8 и т. д.)

Значение b ^x всегда будет положительным, поскольку b положителен, и нет предела тому, насколько большим может быть b ^x . Таким образом, верхняя граница равна бесконечности.

Итак, мы знаем, что 0 < b ^x < бесконечность.

Если a > 0, то a*0 < a*b ^x < бесконечности или 0 < f(x) < бесконечности.

Если a < 0, то –бесконечность < a*b ^x < 0 или –бесконечность < f(x) < 0.

Итак, диапазон f(x) = ab ^x равен (0, бесконечность) для a > 0 и (-бесконечность, 0) для a < 0,

Случай 3: b > 1

Сначала мы находим максимальное и минимальное значения для b ^x . Поскольку b > 1, b ^x будет увеличиваться по мере того, как x принимает большие положительные значения (например, 2 ² = 4, 2 ³ = 8 и т. д.).

Значение b ^x всегда будет положительным, так как b положительно, и нет ограничений на величину b ^х можно получить. Таким образом, верхняя граница равна бесконечности.

Аналогично, b ^x будет уменьшаться по мере того, как x принимает большие отрицательные значения (например, 2 ^-2 = 0,25, 2 ^-3 = 0,125 и т. д.)

Значение b ^x всегда быть положительным, так как b положительно, но нет предела тому, насколько близко к нулю может быть b ^x . Таким образом, нижняя граница равна нулю.

Итак, мы знаем, что 0 < b ^x < бесконечность.

Если а > 0, то а*0 < а*b ^x < бесконечности или 0 < f(x) < бесконечности.

Если a < 0, то –бесконечность < a*b ^x < 0 или –бесконечность < f(x) < 0.

Итак, диапазон f(x) = ab ^x равен (0 , бесконечность) для a > 0 и (-бесконечность, 0) для a < 0.

Как получить асимптоту экспоненциальной функции

Асимптотой экспоненциальной функции всегда будет горизонтальная линия y = 0. нет вертикальной асимптоты для экспоненциальной функции.

Мы можем сдвигать горизонтальную асимптоту вверх или вниз, если мы добавляем или вычитаем экспоненциальную функцию.

Например:

• Показательная функция f(x) = 3(2 ^x ) имеет горизонтальную асимптоту при y = 0.
• Показательная функция g(x) = 3(2 ) + 4 имеет горизонтальную асимптоту при y = 4.
• Показательная функция h(x) = 3(2 ^x ) – 5 имеет горизонтальную асимптоту при y = -5.

График f(x) = 3(2 ^x ) выделен синим цветом (средняя кривая).
График g(x) = 3(2 ^x ) + 4 выделен красным цветом (верхняя кривая).
График h(x) = 3(2 ^x ) – 5 выделен зеленым цветом (нижняя кривая).

Как построить график экспоненциальной функции

Для построения графика экспоненциальной функции лучше всего использовать следующую информацию:

• Горизонтальная асимптота (y = 0, если только функция не была смещена вверх или вниз).
• Точка пересечения по оси y (точка, где x = 0 – мы можем легко найти координату y, вычислив f(0) = ab ⁰ = a*1 = a).
• Точка, в которой x = 1 (это легко вычислить – мы можем найти координату y, вычислив f(1) = ab ¹ = ab).

Итак, для показательной функции f(x) = ab ^x у нас будет горизонтальная асимптота y = 0 и точки (0, a) и (1, ab).

Пример 1.

График экспоненциальной функции с a > 0

Построим график функции f(x) = 3(2 ^x ), которая имеет a = 3 и b = 2.

Мы знаем, что горизонтальная асимптота находится при y = 0.

Мы также знаем, что одна точка на графике (0, а) = (0, 3).

Еще одна точка на графике: (1, ab) = (1, 3*2) = (1, 6).

Имея эти три фрагмента информации (и зная приблизительную форму экспоненциального графика), мы можем нарисовать кривую.

График показательной функции f(x) = 3(2 ^x ).

Пример 2. Построение графика показательной функции с a

< 0

Построим график функции f(x) = -4(7 ^x ), которая имеет a = -4 и b = 7.

Мы знаем горизонтальную асимптоту находится при y = 0.

Мы также знаем, что одна точка на графике равна (0, a) = (0, -4).

Еще одна точка на графике: (1, ab) = (1, -4*7) = (1, -28).

Имея эти три фрагмента информации (и зная приблизительную форму экспоненциального графика), мы можем нарисовать кривую.

График экспоненциальной функции f(x) = -4(7 ^x ).

Пример 3. График экспоненциальной функции с вертикальным сдвигом

Построим график функции f(x) = 5(2 ^x ) + 3, которая имеет a = 5 и b = 2, со сдвигом по вертикали на 3 единицы вверх.

Мы знаем, что горизонтальная асимптота находится при y = 3.

Мы можем найти одну точку на графике, когда x = 0:

• f(x) = 5(2 ^x ) + 3   [исходная функция ]
• f(0) = 5(2 ⁰ ) + 3   [пусть x = 0]
• f(0) = 5(1) + 3   [так как 2 ⁰ = 1]
• f(0) = 9 3 9 3 Итак, точка (0, 8) находится на графике.

  Мы можем найти другую точку на графике, когда x = 1:

  • f(x) = 5(2 ^x ) + 3  [исходная функция]
  • f(0) = 5(2 ¹ ) + 3   [пусть x = 1]
  • f(0) = 5(2) + 3   [2 ¹ = 2]
  • f(0) = 13

  Итак, точка (1, 13) тоже есть на графике.

  Имея эти три фрагмента информации (и зная приблизительную форму экспоненциального графика), мы можем нарисовать кривую.

  График экспоненциальной функции f(x) = 5(2 ^x ) + 3.

  Заключение

  Теперь вы знаете немного больше об экспоненциальных функциях, а также об их области определения, диапазоне и асимптотах. Вы также знаете, как построить график этих функций, используя некоторую базовую информацию, которую вы можете получить из экспоненциальной функции и ее параметров.

  Здесь вы можете узнать, как найти формулу экспоненциальной функции.

  Вы можете узнать больше о натуральном основании e ~ 2,718 здесь.

  Вы можете узнать о том, когда функция включена (сопоставляется со всем доменом кода) в моей статье здесь.

  Вы можете узнать больше об экспоненциальных функциях в этом ресурсе Университета Ламара.

  О других нелинейных функциях вы можете узнать из моей статьи здесь.

  Вы можете узнать о различиях между доменом и диапазоном здесь.

  No related posts.