Найти область значений функции примеры решения 9 класс: Задачи на нахождение области определения и области значений функции в более сложных случаях 9 класс онлайн-подготовка на

Область определения и область значений функции. | Презентация к уроку по алгебре (9 класс) на тему:

Слайд 1

функция. Область определения функции. Область значений функции. Алгебра 9 класс

Слайд 2

Давайте вспомним: Какую зависимость называют функцией? Как читают запись y = f(x) ? Что называют аргументом функции? Что такое область определения функции? Что называют значением функции? Как читают запись f(2) = 6 и что она означает? Что называют областью значений функции?

Слайд 3

Определение функции. Обозначение функции. у( х ) — функция х — аргумент зависимая переменная независимая переменная

Слайд 4

Область определения функции. Область определения функции у(х) это все значения аргумента — Х Обозначение области определения — D( у )

Слайд 5

Область значений функции. Область значений функции у(х) это все значения — У _ Обозначение области значений — Е ( у )

Слайд 6

x — 4 — 3 — 2 — 1 0 1 2 3 y -8 — 6 — 4 — 2 0 2 4 6

Слайд 8

g(2) = g(- 2) = g(x) = 0 при x = g(x) = 1 при х = или х = D(g) = E(g) =

Слайд 9

f(-3) = f(- 1) = f(x) = — 1,5 при x = f(x) = 2 при х = х = , x = D(f) = E(f) =

Слайд 10

а) f(2) = ? б) D(f) = ? Решение: а) f( 16 ) = ? б) D(f) = ? Решение:

Слайд 11

График функции (х; у)- координаты точки в плоскости у( х )- функция х — аргумент у – ордината точки (координата оси ОУ ) х – абсцисса точки (координата оси ОХ )

Слайд 12

Область определения линейной функции y( х) = k x + b , k≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 13

Область значений линейной функции y( х ) = k x + b , k≠0 y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.

Слайд 14

Область определения линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b D( у ) = (-∞ ; + ∞) х Є (-∞ ; + ∞) -∞ + ∞ -∞ + ∞ О О х 0 х > 0 I ч. II ч. III ч. IV ч.

Слайд 15

Область значений линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b Е ( у ) = b -∞ + ∞ -∞ + ∞ О О I ч. II ч. III ч. IV ч. Е ( у ) = — b b -b

Слайд 16

Область определения прямой пропорциональности y( х) = k x y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 17

Область значений прамой пропорциональности y( х ) = k x y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.

Слайд 18

Область определения обратной пропорциональности , х≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 19

Область значений обратной пропорциональности , х≠0 y x k > 0 y x k 0 y > 0 I ч. III ч. II ч. IV ч.

Слайд 20

Область определения квадратичной функции , а≠0 y x а > 0 y x а 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 21

Область значений квадратичной функции , а≠0 y x а > 0 y x а 0 y

Слайд 22

Область определения функции , х ≥ 0 y x D( у ) = [0; + ∞) ; х Є [0; + ∞) + ∞ О х ≥ 0 I ч.

Слайд 23

Область значений функции , х ≥ 0 y x Е ( у ) = [0; + ∞) ; у(х) Є [0; + ∞) + ∞ О у ≥ 0 I ч.

Слайд 24

Область определения функции у = l х l _ y x D( у ) = (- ∞ ; + ∞) ; х Є (- ∞ ; + ∞) + ∞ О х

Слайд 25

Область значений функции у = l х l _ y x Е ( у ) = [ 0 ; + ∞) ; у(х) Є [ 0 ; + ∞) + ∞ О I ч. у ≥ 0 II ч.

Слайд 26

Область определения функции у = х³ y x D( у ) = (-∞ ; + ∞) ; х Є (-∞ ; + ∞) + ∞ О х ≥ 0 I ч. III ч. х

Слайд 27

Область значений функции у = х³ y x D( у ) = (-∞ ; + ∞) ; у(х) Є (-∞ ; + ∞) + ∞ О у ≥ 0 I ч. III ч. у

Слайд 28

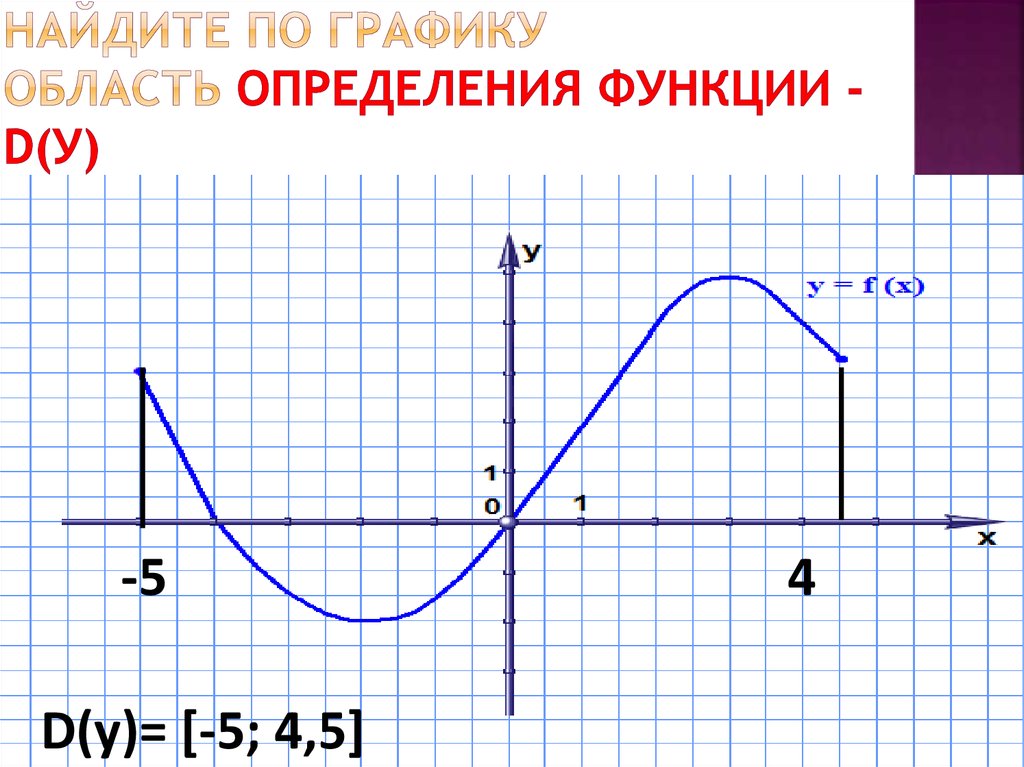
Найдите по графику область определения функции — D( у ) -5 4 D( у )= [ -5 ; 4,5 ]

Слайд 29

Найдите по графику область значений функции — Е ( у ) -2 5 Е ( у )= [ -2 ; 5 ]

Слайд 30

По графику определите промежуток на котором определена данная функция -6 3 D( у )= [ -6 ; 3,5 ]

Слайд 31

По графику определите промежуток на котором определена данная функция -2 4 Е ( у )= [ -2 ; 4 ]

Слайд 32

Найдите по графику область определения функции -5 5 D( у )= [ -5 ; 5 ]

Слайд 33

Найдите по графику область определения функции -2 6 Е ( у )= [ -2 ; 6 ]

Слайд 34

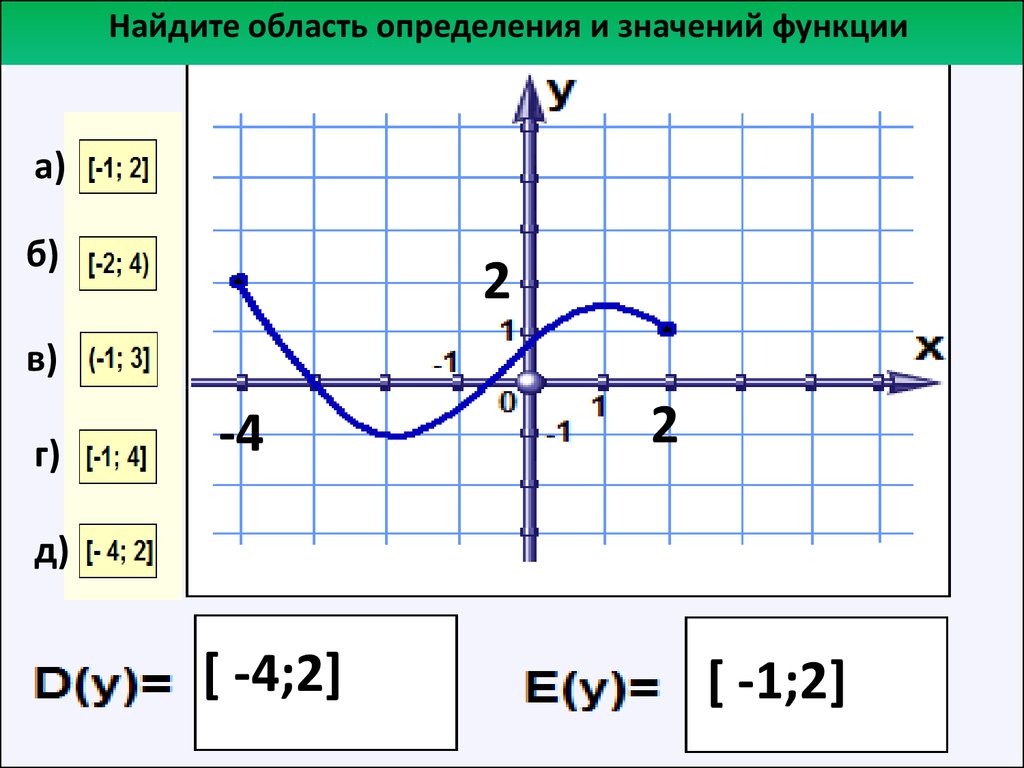
Найдите область определения и значений функции -4 4 [ -4 ; 4) 3 ( — 1;3] а) б) в) г) д)

Слайд 35

Найдите область определения и значений функции 5 ( -1 ; 5 ] -3 4 [ — 3;4) а) б) в) г) д)

Слайд 36

Найдите область определения и значений функции -2 4 [ — 2;4) 4 [ — 1;4] а) б) в) г) д)

Слайд 37

Найдите область определения и значений функции б) в) г) — 4 2 [ -4 ; 2 ] 2 [ -1 ; 2 ] д) а)

Урок 1.

Функция. Область определения и область значений функции

Класс

• 1 класс

• 2 класс

  • Математика
  • Английский язык

• 3 класс

  • Английский язык
  • Русский язык
  • Математика

• 4 класс

  • Математика
  • Русский язык
  • Английский язык

• 5 класс

  • Биология
  • Английский язык
  • Русский язык
  • Математика

• 6 класс

  • Математика
  • Биология
  • Английский язык
  • Русский язык

• 7 класс

  • Химия
  • Английский язык
  • Русский язык
  • Физика
  • Математика
  • Биология

• 8 класс

  • Английский язык
  • Биология
  • Химия
  • Математика
  • Физика
  • Русский язык

• 9 класс

  • Химия
  • Биология
  • Английский язык
  • Физика
  • Русский язык
  • Математика

• 10 класс

  • Биология
  • Математика
  • Физика
  • Химия
  • Английский язык

• 11 класс

  • Химия
  • Английский язык
  • Биология

9 КЛАСС

Урок 1.

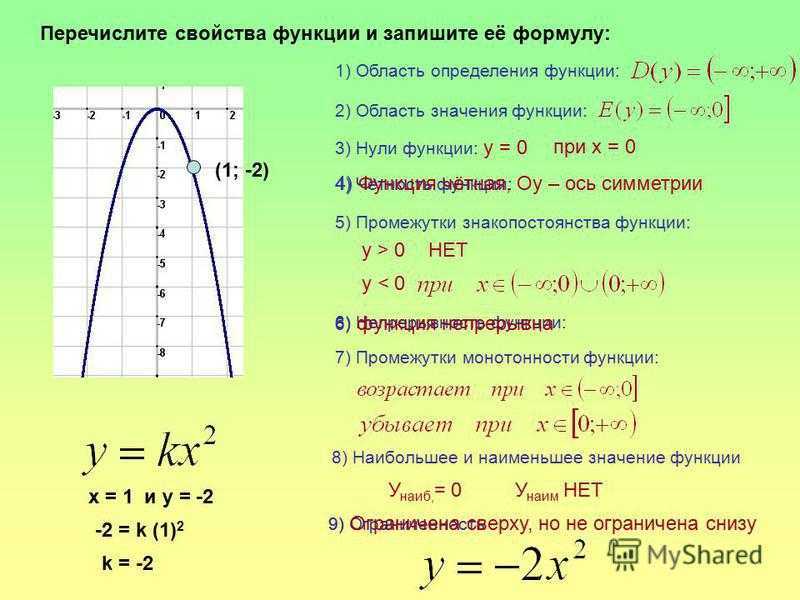Функция. Область определения и область значений функции

Подставить вместо х значения а) -1, б) 0, в) -1/3

Подставьте числа 0; 1,5; и -1 вместо х.

Подставьте вместо х данные значения: а) 5, б) 4, в) 2, г) -3.

Подставьте значения в функцию.

Приравняйте функцию данному числу.

Приравняйте функцию нулю.

Приравняйте функцию данным числам и решите уравнения.

Приравняйте функцию данному числу и решите уравнение.

Найти все значения х, при которых функция существует.

Вспомните разные функции.

Найти значения х, где функция существует.

Изучите график функции.

Возьмите несколько точек и определите, как выглядит график; для пунктов а) и б) достаточно по две точки, для в), г) по четыре.

Найти все х, при которых существует функция. Найти все возможные у.

Изучите правила построения графиков, что такое гипербола, когда и в каких четвертях она находится; для линейной функции - когда она проходит через начало координат, куда и насколько сдвигается при добавлении (вычитании) числа.  
Гипербола с положительным знаком находится в 1 и 3 четвертях, с отрицательным знаком - во 2 и 4 четвертях. 
Если к линейной функции добавить (вычесть из нее) число - она сдвинется на это число вверх (вниз) по оси у. Знак перед слагаемым с х также определяет в каких четвертях проходит график:  с положительным знаком находится в 1 и 3 четвертях, с отрицательным знаком - во 2 и 4 четвертях. 

Проверьте некоторые значения функции.

Восстановите перпендикуляры от оси х и по графику найдите значения х, соответствующие условию.

Постройте таблицу значений.

Будьте внимательны с границами промежутков.

Подставьте соответствующие значения в функцию.

Внимательней со знаками.

Внимательней со знаками.

Проверьте решение подстановкой.

Вопросники:

Вопрос:

Вопрос:

Вопрос:

Вопрос:

Пропуски:

Домен и диапазон функции – объяснение и примеры

В этой статье объясняются домен и диапазон среднего значения функции, а также способы расчета этих двух величин. Прежде чем перейти к теме домена и диапазона, давайте кратко опишем, что такое функция.

В математике мы можем сравнить функцию с машиной, которая производит некоторый результат в соответствии с данным вводом . На примере машины для чеканки монет мы можем проиллюстрировать значение функции следующим образом.

Когда вы вставляете монету в монетоштамповочную машину, в результате получается отштампованный и сплющенный кусок металла. Рассматривая функцию, мы можем связать монету и сплющенный кусок металла с доменом и диапазоном. В этом случае функцией считается машина для чеканки монет.

Точно так же, как машина для чеканки монет, которая может производить только один сплющенный кусок металла за раз, функция работает таким же образом, выдавая один результат за раз.

История функции

Идея функции была введена в начале семнадцатого века, когда Рене Декарт (1596-1650) использовал это понятие в своей книге «Геометрия» (1637) для моделирования математических задач.

Пятьдесят лет спустя, после публикации «Геометрии», Готфрид Вильгельм Лейбниц (1646–1716) ввел термин «функция». Позже Леонард Эйлер (1707-1783) сыграл большую роль, введя технику понятия функции, y = f (x).

Реальное применение функции

Функции очень полезны в математике, потому что они позволяют нам моделировать реальные проблемы в математическом формате.

Вот несколько примеров применения функции.

Длина окружности зависит от ее диаметра или радиуса. Мы можем математически представить это утверждение как:

C(d) =dπ или C(r)=2π⋅r

• Тень

Длина тени объекта является функцией его высоты.

Местоположение движущегося объекта, например автомобиля, зависит от времени.

• Температура

Температура тела зависит от нескольких факторов и исходных данных.

• Деньги

Сложные или простые проценты зависят от времени, основной суммы и процентной ставки.

• Высота объекта

Высота объекта зависит от его/ее возраста и массы тела.

Узнав о функции, теперь можно перейти к вычислению домена и диапазона функции.

Что такое домен и диапазон функции?

Домен функции — это входные числа, которые при подключении к функции определяют результат. Проще говоря, мы можем определить область определения функции как возможные значения x, которые сделают уравнение верным.

Некоторые из случаев, когда функция не будет работать, — это когда уравнение делится на ноль или отрицательный квадратный корень.

Например, f( x ) =  x ² — допустимая функция, поскольку независимо от того, какое значение x можно подставить в уравнение, всегда есть правильный ответ. По этой причине мы можем заключить, что областью определения любой функции являются все действительные числа.

Диапазон функции определяется как набор решений уравнения для данного входа. Другими словами, диапазон — это результат или значение y функции. Для данной функции существует только один диапазон.

Как использовать обозначения интервалов для указания домена и диапазона?

Поскольку диапазон и область значений функции обычно выражаются в интервальной записи, важно обсудить концепцию интервальной записи.

Процедура записи интервалов включает:

• Запишите числа, разделенные запятой, в порядке возрастания.
• Заключите числа в круглые скобки (), чтобы показать, что значение конечной точки не включено.
• Используйте квадратные скобки [] для заключения чисел, когда включено значение конечной точки.

Как найти домен и диапазон функции?

Мы можем определить область определения функции либо алгебраическим, либо графическим методом. Чтобы вычислить область определения функции алгебраически, вы решаете уравнение для определения значений x.

Различные типы функций имеют свои методы определения области определения.

Давайте рассмотрим эти типы функций и то, как вычислить их домен.

Как найти область определения функции без знаменателя и радикалов?

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 1

Найдите область определения f (x) = 5x − 3 ∞)

Диапазон: (−∞, ∞)

Функция с радикалом

Пример 2

Найти область определения функции f(x)=−83×2 4 + 12x + 5

Решение

Функция f(x) = −2x ² + 12x + 5 является квадратичным полиномом, поэтому область определения равна (−∞, ∞)

Как найти область определения рациональной функции с переменной в знаменателе?

Чтобы найти область определения функции этого типа, приравняйте знаменатель к нулю и вычислите значение переменной.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 3

Определить область значений x−4/ (x ² −2x−15)

Решение

Приравнять знаменатель к нулю и найти x (x − 5) (x + 3) = 0

Следовательно, x = −3, x = 5

Чтобы знаменатель не был равен нулю, нам нужно избегать чисел −3 и 5.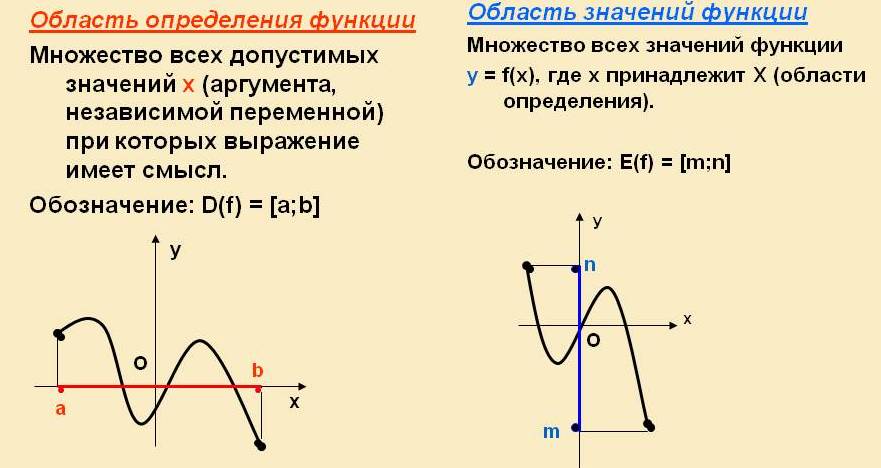 Следовательно, область определения все действительные числа, кроме −3 и 5.

Пример 4

Вычислите область определения и диапазон функции f(x) = -2/x.

Решение

Установите знаменатель равным нулю.

⟹ x = 0

Следовательно, домен: все действительные числа, кроме 0.

Диапазоном являются все действительные значения x, кроме 0.

Пример 5 .

f(x) = 2/(x + 1)

Решение

Приравняйте знаменатель к нулю и найдите x.

х + 1 = 0

= -1

Поскольку при x = -1 функция не определена, областью определения являются все действительные числа, кроме -1. Точно так же диапазоном являются все действительные числа, кроме 0

. Как определить домен для функции с переменной внутри подкоренного знака?

Чтобы найти область определения функции, члены внутри корня задают неравенство > 0 или ≥ 0. Затем определяется значение переменной.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 6

Найдите область определения f(x) = √ (6 + x – x ² )

Решение

Чтобы избежать квадратных корней из отрицательных чисел, мы устанавливаем выражение внутри знака радикала равным ≥ 0.

6 + x – x ² ≥ 0 ⟹ x ² – x – 6≤ 0

⟹ x ² – x – 6= (x – 3) (x +2) = 0

Следовательно, функция равна нулю, если x = 3 или x = -2

Следовательно, домен: [−2, 3]

Пример 7

Найдите область определения f(x) =x/√ (x ² – 9)

Решение

Приведите выражение с радикалом к ​​x ² – 9 > 0 902 переменная, которую нужно получить;

x = 3 или – 3

Следовательно, область определения: (−∞, −3) & (3, ∞)

Пример 8

Найдите область определения f(x) = 1/√ ( x ²  -4)

Решение

Разлагая знаменатель на множители, получаем x ≠ (2, – 2).

Проверьте свой ответ, подставив -3 в выражение перед знаком корня.

⟹ (-3) ²  – 4 = 5

также попробуйте с нулем

⟹ 0 ²  – 4 = -4, поэтому числа от 2 до -2 недействительны

Попробуйте число больше 00 2 ⟹ 3 ²  – 4 = 5. Это верно.

Следовательно, область определения = (-∞, -2) U (2, ∞)

Как найти область определения функции с помощью натурального логарифма (ln)?

Чтобы найти область определения функции с помощью натурального логарифма, присвойте членам в скобках значение >0 и затем решите.

Давайте рассмотрим пример ниже, чтобы понять этот сценарий.

пример 9 + 8

⟹ x > 8

Домен:(8, ∞)

Как найти домен и диапазон отношения?

Отношение — это актив координат x и y. Чтобы найти домен и диапазон в отношении, просто перечислите значения x и y соответственно.

Давайте рассмотрим несколько примеров ниже, чтобы понять этот сценарий.

Пример 10

Укажите область определения и область значений отношения {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3) }

Решение

Список значений x. Домен: {2, 3, 4, 6}

Список значений y. диапазон: {–3, –1, 3, 6}

Пример 11

Найти домен и диапазон отношения {(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}

Решение

Домен {–3, –2, –1, 0, 1, 2} и диапазон {5}

Пример 12

Учитывая, что R = {(4 , 2) (4, -2), (9, 3) (9, -3)}, найти область определения и диапазон R.

Решение

Область определения представляет собой список первых значений, поэтому = {4, 9} и диапазон = {2, -2, 3, -3}

Обратная функция — объяснение, построение графика и примеры решения

Обратная функция — это просто функция, переменная которой находится в знаменатель. Концепция обратной функции может быть легко понята, если учащийся знаком с концепцией обратной вариации, поскольку обратная функция является примером обратной переменной. Взаимные функции имеют стандартный вид, в котором они записываются. Обратные числа — это больше, чем просто сложение и вычитание. Они идут дальше этого, к делению, которое можно определить на графике.

В этой статье мы имеем дело с обратными графами, представляющими собой единицы, где у равно чему-то / х, и здесь мы представляем это что-то буквой а. Таким образом, a может быть любым значением, которое вы можете придумать. Однако наиболее распространенная единица, которую вы увидите, это y = 1 / x. Посмотрим, как он устроен.

Чтобы нарисовать его, вам нужно нарисовать кривую в правом верхнем углу, а затем аналогичную кривую в левом нижнем углу. Таким образом, на самом деле это 2 отдельные части, хотя это всего лишь 1 график. Помимо способности распознавать график, вам также необходимо знать, что он симметричен относительно наклонной угловой линии, проходящей через график y = x, потому что эти части симметричны частям друг друга. И это также симметрично наклонной линии, которая проходит через график под другим углом, y = — x, потому что эти части симметричны частям друг друга.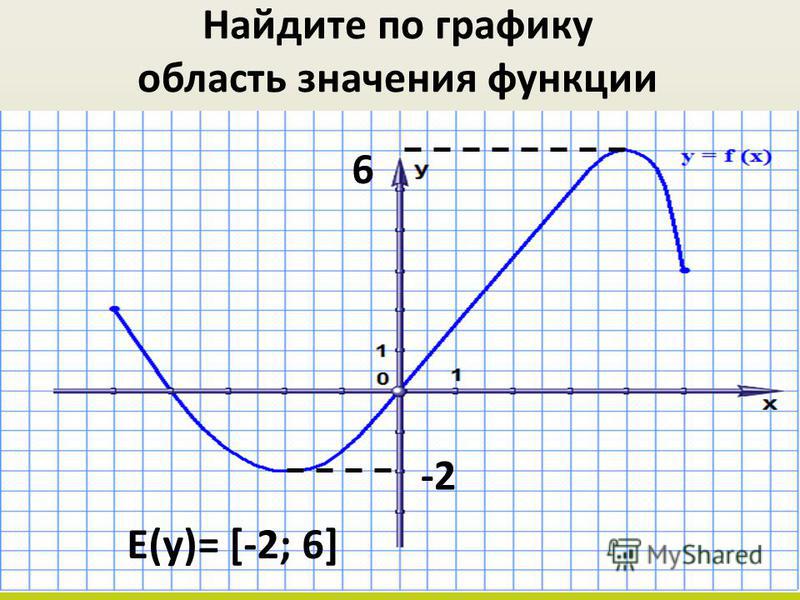

Выберите значения x — 2, 0 и 2. Но вы можете выбрать любые значения, которые появляются на вашем графике. И затем мы можем подставить каждое из этих значений x в уравнение, чтобы выяснить, какими должны быть соответствующие значения y.

Например, чтобы узнать, чему равно y, когда x равно -2, мы просто подставляем -2 в наше уравнение y = 1 / x. Таким образом, получается y = 1/-2, или просто y = минус половина. Итак, мы знаем, что при x = — 2 на нашем графике y должно равняться — половине, что и происходит.

И, наконец, если мы проделаем то же самое для случая, когда x = положительное число 2, мы обнаружим, что y = положительное значение половины. Итак, поскольку полученная нами кривая соответствует тому, что мы ожидаем из нашей таблицы значений, мы можем быть достаточно уверены, что это кривая y = 1/x. 92} \] 

 

\[g(x) = \frac{2}{x + 1} — 4\]

 

\[h(x) = \frac{-3}{x + 4 } + 2\]

 

Как мы видим во всех приведенных выше примерах обратных функций, функции имеют постоянные числители и многочлены в знаменателях.

 

Уравнение обратной функции

Общая форма уравнения обратной функции задается как \[f(x) = \frac{a}{x -h} + k \] 

Где переменные a,h и k — постоянные действительные числа.

 

Как выполнить обратную функцию?

Обратная величина числа может быть определена путем деления переменной на 1. Точно так же обратная величина функции определяется путем деления 1 на выражение функции.

 

Пример:

• Для заданной функции f(y) ее обратная функция равна 1/f(y).

• Произведение f(y) и его обратная функция равна f(y).1/f(y) = 1.

• Дано, 1/f(y), его значение не определено когда f(y)=0,

 

Как построить график обратной функции?

Существуют различные формы взаимных функций. Одна из форм — k/x, где k — действительное число, а значение знаменателя, т. е. x не может быть равно 0. рассматривая различные значения x и y.

 

Value of x	-3	— 2	-1	-1/2	-1/3	1/3	1/2	1	2	3
Value of y	-1/3	-1/2	-1	-2	-3	3	2	1	1/2	1/3

For a given обратная функция f(x) = 1/x, знаменатель ‘x’ не может быть равен нулю, и, аналогично, 1/x также не может быть равен 0.

 

Следовательно, область определения и диапазон обратной функции следующие:

 

Домен — это множество всех действительных чисел, кроме 0, поскольку 1/x не определено. Домен = {x R| x ≠ 0 Подобно домену, диапазон также является набором всех действительных чисел. Следовательно, Диапазон = { x R| x ≠ 0

Из графика обратной функции видно, что кривая никогда не касается оси x и оси y.

 

Ось Y считается вертикальной асимптотой, поскольку кривая приближается, но никогда не касается ее.

 

Аналогично, ось x считается горизонтальной асимптотой, поскольку кривая никогда не касается оси x.

 

Как найти диапазон и область значений обратной функции на графике?

Домен — это набор всех возможных входных значений. Домен графика включает в себя все входные значения, показанные на оси x, тогда как диапазон представляет собой набор всех возможных выходных значений. Если график обратной функции выходит за пределы части графика, мы можем наблюдать, что домен и диапазон могут быть больше, чем видимые значения.

На приведенном выше обратном графике мы можем наблюдать, что график простирается по горизонтали от -5 до правой стороны дальше.

 

Примечание. Область и диапазон обратной функции также записываются от меньших значений к большим или слева направо для области значений и от нижней части графика к нижней части графика для диапазона.

 

Факты для запоминания

• Обратная величина x = 1/x.

• Обратная величина также известна как мультипликативная обратная

• Область определения и область значений обратной функции x = 1/y — это множество всех действительных чисел, кроме 0.

• Асимптота на графике обратной функции — это линия, которая приближается к кривой, но не касается ее . Горизонтальная и вертикальная асимптоты обратной функции f(x) =1/x являются осью x и осью y соответственно.

• Вертикальная асимптота графика обратной функции связана с областью определения, тогда как горизонтальная асимптота связана с диапазоном функции. 92 + 6} \].

   

  Обратная величина 3y равна \[\frac{1}{3y}\].

  2. Определить область определения и область значений обратной функции \[y = \frac{1}{x + 6}\] .

   

  Решение: Чтобы найти область определения и область значений обратной функции, первым делом нужно приравнять значение знаменателя к 0. Соответственно,

  х + 6 = 0

  х = — 6 Область определения обратной функции — это набор всех действительных чисел, кроме значения x = -6.

   

  Область значений обратной функции аналогична области определения обратной функции.

  Чтобы найти диапазон обратных функций, мы определим обратную функцию, поменяв местами x и y.

   

  Получаем,

  \[x = \frac{1}{y + 6}\]

  Решая уравнение относительно y , получаем,

  x(y + 6) = 1

  xy + 6x = 1

  xy = 1 — 6x

  \[y = \frac{(1 — 6x)}{x}\]

   

  Следовательно, обратная функция равна \[y = \frac{(1 — 6x)}{x}\].

   

  Теперь, приравнивая значение знаменателя, получаем x = 0.

   

  Таким образом, область определения обратной функции определяется как множество всех действительных чисел, кроме 0. Поскольку область значений аналогична области определения, можно сказать, что

   

  Областью значений функции \[y = \frac{(1 — 6x)}{x}\] является множество всех действительных чисел, кроме 0.

   

  Соответственно,

  Областью определения является множество всех действительных чисел, кроме значения x = — 6, тогда как диапазоном является множество всех действительных чисел, кроме 0.

   

  3. Найдите горизонтальную и вертикальную асимптоты функции \[f (x) = \frac{2}{x — 6}\].

   

  Решение: Чтобы найти вертикальную асимптоту, мы сначала приравняем значение знаменателя к 0.

  Мы получаем, x — 6 = 0

   

  Следовательно, вертикальная асимптота равна x = 6.

  0

  00405 Чтобы найти горизонтальную асимптоту, нам нужно соблюдать степень многочлена как числителя, так и знаменателя. Так как степень числителя меньше степени знаменателя, то горизонтальная асимптота равна 0,

   

  Соответственно,

  Вертикальная асимптота x = 6,

  Горизонтальная асимптота y = 0,

   

  4.

  No related posts.