Обратные функции | Функции
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
В этом уроке мы узнаем об обратных функциях. Мы разберем, что такое обратная функция и как ее найти.
Такие функции нужны для решения уравнений типа . Например, уравнение можно решить только таким образом.
Что такое обратная функция
Для начала скажем, что обратной называют функцию, которая может превратиться в другую функцию. Проще говоря, если любая функция переводит в , то обратная переведет в .
Если функция обозначается или , то обратная функция обозначается или . Здесь не следует путать с экспонентой или взаимно обратным показателем.
Формальное определение будет звучать так:
Если и — обратные функции, то тогда и только тогда, когда
Обратная функция часто используется в математике — например, в тригонометрии. С ее помощью можно найти меру угла, для которого функция синуса дала значение. Так это выглядит:
Так это выглядит:
градусов
Следовательно,
градусов равен
Как определить обратную функцию
Обычная функция принимает значения, выполняет определенные операции над этими значениями и выдает результат.
Обратная функция согласуется с результирующей, выполняет операции и возвращается к исходной функции. Обратная функция возвращает исходное значение, для которого функция дала выход.
Если рассматривать функции, то и считаются обратными:
Функция, состоящая из своих обратных, возвращает исходное значение. Так это выглядит на практике:
В таком случае является обратной функцией .
Как строить график обратной функции
График обратной функции отражает две вещи:
Эта линия на графике проходит через начало координат и имеет наклон . Она может быть представлена как:
Выражение выше равносильно такому выражению:
Это соотношение немного похоже на
, которое определяет график
. Но обратите внимание на разницу — части
и
поменялись местами.
Когда мы создаем обратную функцию от исходной, меняется и область на графике. Область исходной функции становится областью обратной функции, а область заданной функции становится областью обратной функции.
График обратной функции получается так: нужно взять исходный график и заменить его координаты на относительно прямой .
Переход от функции к обратной функции выглядит так:
Чтобы функция считалась обратной функцией, каждый элемент в диапазоне в должен быть отображен из некоторого элемента в в доменное множество. Такое отношение называется отношением один-один или отношением запрета.
Также обратная функция данной функции имеет область в , связанную с отдельным элементом в в кодоменном множестве. Такое отношение по отношению к данной функции является онто-функцией

А еще существуют биективные функции — так называют обратные функции, которые являются инъюнктивными и сюръективными.
Что такое инверсия функций
Если в результате композиции двух функций и получается тождественная функция , то говорят, что эти две функции являются инверсиями друг друга.
Если применение функции к входу дает выход , то применение другой функции к должно вернуть значение . Следовательно, обратная функция обращает функцию. Область данной функции становится областью обратной функции, а область данной функции становится областью обратной функции.
В общем, обратная функция — это отражение функции начала координат относительно прямой . Ее можно получить, заменив на .
Если даны графики двух функций, можно определить, являются ли они обратными друг другу. Если графики обеих функций симметричны относительно прямой y = x, то мы говорим, что эти две функции являются обратными друг другу. Это объясняется тем, что если лежит на функции, то лежит на ее обратной функции:
Обратная функция — это любая функция, которая никогда не принимает одно и то же значение дважды. Другими словами, для каждого значения
существует только одно значение
. Это означает, что каждый элемент кодомена является образом не более чем одного элемента его области.
Другими словами, для каждого значения
существует только одно значение
. Это означает, что каждый элемент кодомена является образом не более чем одного элемента его области.
Кроме того, обратная функция проходит тесты на вертикальную линию и горизонтальную линию:
Никакая горизонтальная линия не пересекает ее график более одного раза. Таким образом, никакие два элемента в домене не соответствуют одному и тому же элементу в диапазоне
Как найти обратную функцию
Разберемся, как находить обратную функцию. Для этого мы возьмем такой пример:
Пройдем весь процесс по шагам.
Шаг 1. Возьмем заданную функцию и заменим в ней на . Так мы получим такое выражение:
Шаг 2. Далее возьмем функцию . В ней мы заменим на , а — на . Получится такое выражение:
Шаг 3. Далее попробуем решить выражение для . На этом шаге мы получим:
Шаг 4. В конце заменяем
на
. В итоге получаем такой результат:
В итоге получаем такой результат:
Самостоятельная работа
Вопрос №1
Что такое обратная функция?
Нажмите, чтобы увидеть ответОбратная функция — это функция, которая возвращает исходное значение, для которого функция дала выход. Если функция дает на выходе , то обратная функция , то есть вернет значение .
Вопрос №2
Как найти обратную функцию?
Нажмите, чтобы увидеть ответПредположим,
— функция
Пусть
Это обратная функция
Вопрос №3
Являются ли обратная функция и взаимно обратная функция одним и тем же?Нажмите, чтобы увидеть ответНе следует путать обратную функцию и взаимно обратную функцию. Обратная функция возвращает исходное значение, которое было использовано для получения результата, и обозначается .
В свою очередь обратная функция обозначается или .
Вопрос №4
Что является обратной величиной для ?
Нажмите, чтобы увидеть ответПусть
Тогда обратной функцией
будет
Вопрос №5
Как решить обратную функцию тригонометрии?
Нажмите, чтобы увидеть ответЕсли нам нужно найти обратную тригонометрическую функцию
, то значение
равно углу, синус функции которого равен
.
Как известно,
Следовательно,
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
Получить доступ
130
курсов
1000
упражнений
2000+
часов теории
3200
тестов
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно
- 130 курсов, 2000+ часов теории
- 1000 практических заданий в браузере
- 360 000 студентов
Электронная почта *
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Наши выпускники работают в компаниях:
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Алла на 6 лет моложе Веры. Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Решено
Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Сколько существует 2016-значных чисел таких, что при вычёркивании его любой одной цифры получается 2015-значное число, и это 2015-значное число является делителем исходного числа (Напомним, что
Решено
В треугольнике ABC известно что AB=3 BC=8 AC=7. Найдите косинус (COS) угла ABC. Помогите пожалуйста с решением-очень очень нужно. Спасибо.
В стеклянный стакан массой 100 г имеющий температуру 20 градусов цельсия налили воду при температуре 80 градусов цельсия. Через некоторое время…
Пользуйтесь нашим приложением
Нахождение уравнения прямой по двум точкам на обратной — Криста Кинг Математика
Нахождение обратной функции с использованием координатных точек
Здесь мы рассмотрим, как выполнить преобразование из линейной функции и ее обратной, когда нам даны две точки.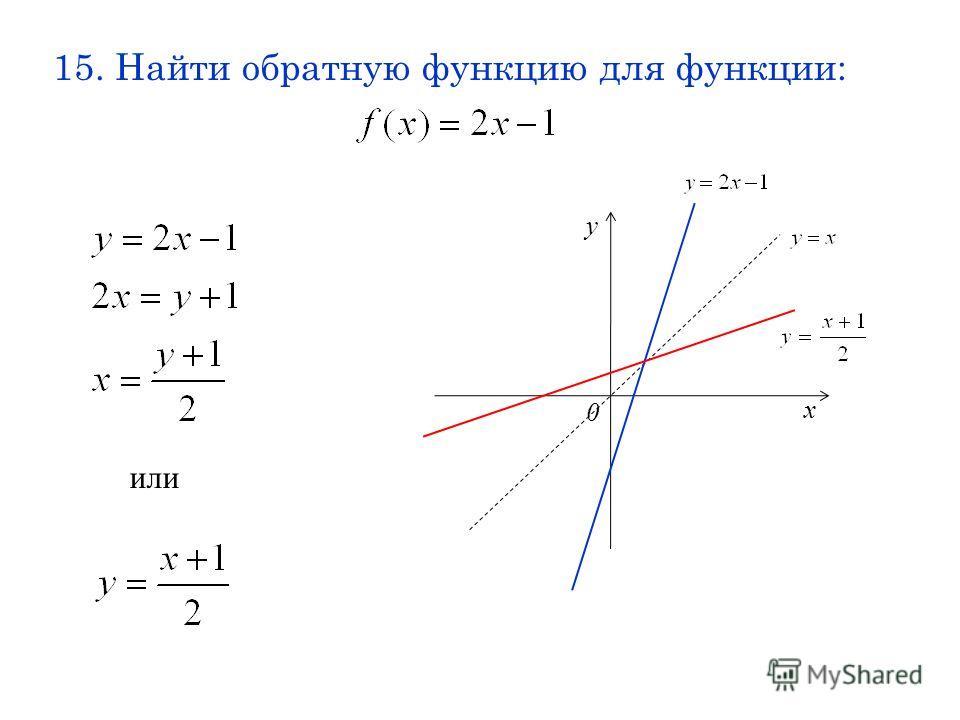 {-1}(x)??? должно быть ???(b_1, a_1)??? и ???(b_2, a_2)???. Это работает очень хорошо, если мы знаем две точки на прямой и хотим найти обратную функцию.
{-1}(x)??? должно быть ???(b_1, a_1)??? и ???(b_2, a_2)???. Это работает очень хорошо, если мы знаем две точки на прямой и хотим найти обратную функцию.
Имея две точки координат на обратной функции, мы можем найти исходную функцию, предполагая, что функции линейны
Пройти курс
Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂
Учить больше
Еще два примера, начиная с точек на обратной функции
9{-1}(x)???, обратное ???f(x)???. Что означает на функцию ???f(x)??? точек будет ???(4,3)??? и ???(5,-1)???. Теперь мы можем использовать эти точки на линии ???f(x)??? найти уравнение прямой. Начнем с нахождения наклона ???m???.???m=\frac{3-(-1)}{4-5}=\frac{4}{-1}=-4???
Найдем ???y???-перехват. Мы можем использовать наклон, который мы только что нашли ???m=-4??? и уравнение линии в форме пересечения наклона, ???y=mx+b???, вместе с точкой, которую нужно решить для ???b??? (давайте использовать ???(4,3)???). {-1}(x)???, поэтому мы будем писать 9{-1}(х)=-2х+4???
{-1}(x)???, поэтому мы будем писать 9{-1}(х)=-2х+4???
Теперь поменяем местами ???x??? и ???й??? чтобы получить ???f(x)???.
???x=-2y+4???
Найдите ???y???.
???x-4=-2y???
???y=-\frac{1}{2}x+2???
Заменить ???y??? с ???f(x)???.
???f(x)=-\frac{1}{2}x+2???
Как видите, существует несколько способов решения подобных проблем. Используйте способ, который лучше всего подходит для вас.
Получить доступ к полному курсу Алгебра 2
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра ii, линейные уравнения, уравнение линии, обратная функция, точки на обратной стороне, координатные точки на обратной стороне
0 лайков9.1 Обратные функции
Неформально две функции $f$ и $g$ являются обратными , если
каждый переворачивает или отменяет другой. Точнее:
9{1/2}=2$.
$\квадрат$
Точнее:
9{1/2}=2$.
$\квадрат$
Проблема в предыдущем примере может быть прослежена до факта, что есть два различных числа с квадратом, равным 4. Получается быть точным описанием функций без обратных.
Определение 9.1.4 Пусть $A$ и $B$ — множества, а $f:A\to B$ — функция. Мы говорим, что $f$ является инъективным или один к одному , если из $f(x)=f(y)$ следует, что $x=y$.
Мы говорим, что $f$ — это сюръективных или на 9.0120 если для для каждого $b\in B$ существует $a\in A$ такое, что $f(a)=b$.
Если $f$ одновременно инъективен и сюръективен, то $f$ биективное или один к одному и на .
$\квадрат$
Нас интересует только случай, когда $A$ и $B$ — множества вещественных чисел, и в этом случае имеется хорошая геометрическая интерпретация приемистость. Часто эту интерпретацию легко использовать для решения является функция или нет 1-1.
Теорема 92 $ не является ни инъективным, ни
сюръективный. Если мы представим $f$ как функцию от $\R$ до
неотрицательные действительные числа, то $f$ сюръективно; другими словами, если
функция не сюръективна, это не главный камень преткновения.
Если мы представим $f$ как функцию от $\R$ до
неотрицательные действительные числа, то $f$ сюръективно; другими словами, если
функция не сюръективна, это не главный камень преткновения.
Функция $f(x)=1/x$ инъективна, но не сюръективен, так как нет значения $x$ такой, что $f(x)=0$.
Функция $f(x) = x(x-1)(x+1)$ сюръективна, но не инъективный; $f(x) =0 $ для трех различных значений $х$. С другой стороны, $\ds\lim_{x\to\infty} f(x)=\infty$ и $\ds\lim _{x\to -\infty} f(x)=-\infty$. Поскольку $f$ непрерывна на $\R$, теорема о промежуточном значении (2.5.6) гарантирует, что $f$ принимает все значения между $-\infty $ и $\infty$. $\квадрат$
Производная дает нам удобный критерий на инъективность без явного поиска точек, где инъективность может не сработать.
Теорема 9.1.8 Если $f$ дифференцируема и $f'(x) >0 $, то $f$ инъективный.
Доказательство. Предположим, что $f(a) = f(b) $ для некоторого $a6.5.1) существует $c\in (a,b) $ такое, что
$f'(c) =(f(b)-f(a))/(b-a)=0$,
что противоречит предположению, что $f'(x) >0$. Следовательно, если $f(a)=f(b)$, то $a=b$.
$\qed$
Следовательно, если $f(a)=f(b)$, то $a=b$.
$\qed$
Точно так же мы можем видеть, что если $f'(x) 93$. Эта $f$ инъективна, хотя вышеуказанная теорема неприменима, так как $f'(0)=0$. Поэтому условия теоремы достаточны, но не необходимы. $\квадрат$
Наше знание производных также может привести нас к выводу, что функция не инъективна.
Теорема 9.1.12 Если $f$ непрерывна и имеет локальный максимум или минимум, то $f$ не является инъективным.
Доказательство. Предположим, что $f$ имеет локальный максимум в точке $х=с$. Тогда в некотором интервале $(c-h, c+h)$ $f(x)\le f(c)$. Пусть $a\in (в-з, в)$. Если $f(a) =f(c)$, то $f$ не инъективен; в противном случае, $f(а)
Пусть $b\in (c,c+h)$. Если $f(b) = f(c)$ или $f(b) =f(a)$, то $f$ не является инъективным. В противном случае либо $f(b)
В любом случае мы видим, что $f$ не является инъективным. $\qed$
Чтобы вернуться к нашему основному интересу, обратным функциям, мы теперь соединим
биекции и инверсии.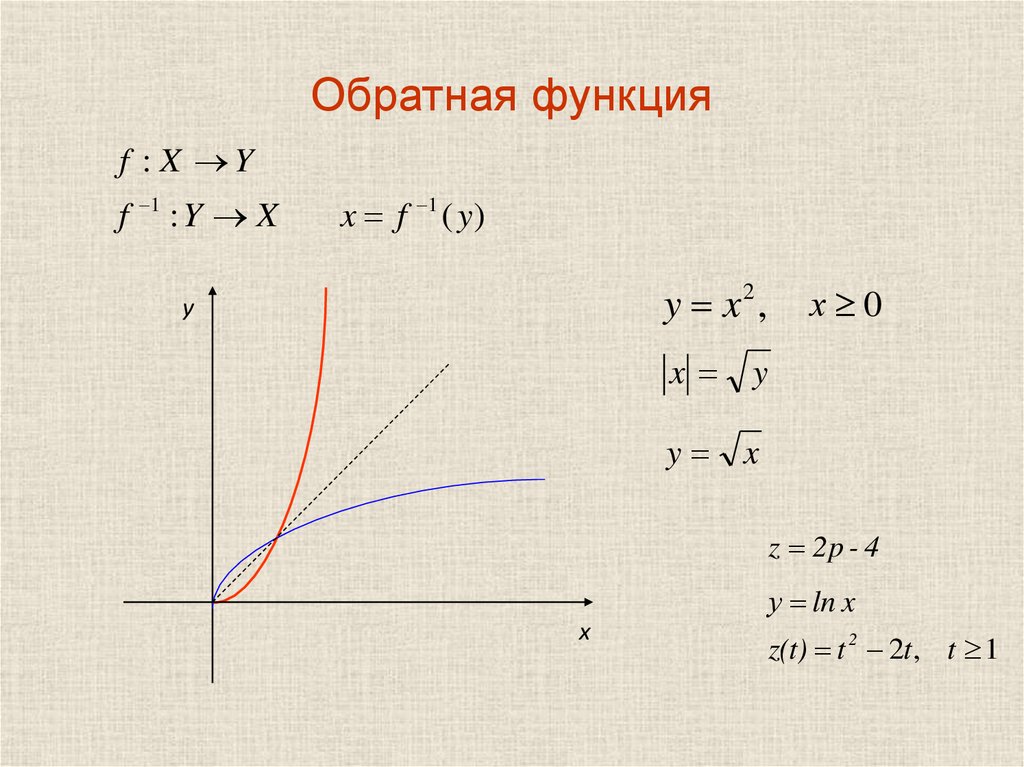
Теорема 9.1.13. Предположим, что $f\colon A\to B$ биекция. Тогда $f$ имеет обратный функция $g\colon B\to A$.
Доказательство. Предположим, что $b\in B$. Так как $f$ на, то существует $a\in A$ такое, что $f(a)=b$. Поскольку $f$ равен 1–1, $a$ — единственный элемент $A$ с таким имущество. Положим $g(b)=a$. Теперь легко увидеть, что для всех $a\in A$ $g(f(a))=a$ и для всех $b\in B$ $f(g(b))=b$. $\qed$ 9Например, можно решить 5=1$.)
К счастью, часто важнее знать, что функция имеет обратное, чтобы иметь возможность придумать явную формулу. Один раз известно, что существует обратная, численные методы часто могут быть используется для получения аппроксимаций обратной функции. Таким образом, теорема 9.1.8 и предложение 9.1.12 обеспечивают полезную Критерии для определения того, является ли функция обратимой.
Перейдем теперь к исчислению обратных функций.
Теорема 9{-1}$ непрерывен на $f(A)$.
Доказательство. Так как $A$ — открытый интервал, а $f$ инъективен и
непрерывным следует из предложения 9.

 ..
.. 12.17
12.17