Найти производную по направлению вектора в точке онлайн калькулятор: Градиент функции онлайн

Содержание

Расчет скорости и ускорения точки по уравнениям ее движения

Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.

Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.

Задача
Движение точки M задано уравнениями:

Требуется:
Установить вид траектории движения точки M, и для момента времени t = t₁ = 0,5 с найти:

положение точки на траектории,
скорость, полное, касательное и нормальное ускорения,
радиус кривизны траектории.

Другие примеры решений >
Помощь с решением задач >

Решение

Расчет траектории движения точки

Уравнения движения можно рассматривать как параметрические уравнения траектории точки.

Другие видео

Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.

Получилось квадратное уравнение. То есть точка движется по параболе.
Построим траекторию движения, рассчитав несколько её точек.

Положение точки на траектории

Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0

а затем, половину секунды.

Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.

Расчет скорости точки

Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.

Здесь i, j — орты осей x и y.
v_x, v_y — проекции вектора скорости на оси координат.

Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.

Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.

Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.

Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.

Рассчитаем модуль вектора скорости

Расчет ускорений точки

Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.

Здесь, a_x, a_y – проекции ускорения точки на оси координат.

В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.

Касательная составляющая полного ускорения это производная скорости точки по времени.

Ее можно рассчитать по этой формуле.

Вектор касательного ускорения всегда направлен по линии вектора скорости.

Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.

Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.

Расчет радиуса кривизны траектории

Осталось найти только радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.

Результаты расчетов

Результаты вычислений для заданного момента времени t₁=0,5c приведены в таблице:

На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.

Вектор v строим по составляющим v_x и v_y, причем этот вектор должен по направлению совпадать с касательной к траектории.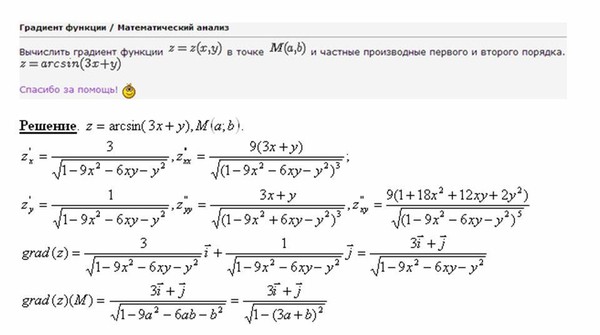

Вектор a строим по составляющим a_x и a_y и затем раскладываем на составляющие векторы a_τ и a_n. Совпадение величин a_τ и a_n, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

Поиск формул и решений задач

Калькулятор производных с шагами | Калькулятор дифференцирования

Введение в калькулятор производных с шагами

В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания.

Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши.

Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию.

Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами.

Формулы, используемые калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$ 92 x $$

Связанный: Нажмите на исчисление, если хотите изучить различные способы нахождения производной функции.

Производные правила, используемые Калькулятором дифференцирования

С помощью производной мы можем найти наклон функции в любой заданной точке. Правила дифференцирования используются для вычисления производной функции. Наиболее важные правила дифференцирования:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d }{dx}g(x) $$

9{n-1} $$

Постоянное множественное правило:

$$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

Здесь c = реальное число

Правило суммы и разности:

Правило продукта:

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{ d}{dx}[f(x)] $$

или

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференциации позволяет пользователям вводить данные в виде уравнения.

Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами.

Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты.

Как найти калькулятор производных?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
Выберите переменную, которую вы хотите дифференцировать.
Выберите, сколько раз вы хотите различать.
Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для закрепления расчетов относительно нормальной линии уравнения, вам нужно попробовать калькулятор уравнения нормальной линии, предлагаемый этим веб-сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

Калькулятор производной в точке

Калькулятор n-й производной
Калькулятор крайних точек
Калькулятор уклона криволинейной линии
Калькулятор производных графиков
Калькулятор производной касательной прямой
Калькулятор 4-й производной
Калькулятор производной обратной функции
Калькулятор второго неявного дифференцирования
Определение калькулятора производной
Калькулятор 5-й производной
Калькулятор 6-й производной

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5. 4x+2.4 $$

Дифференцирование с обеих сторон по ‘x’

$$f'(x) \;=\; d/dx(5.4x+2.4)$$

Имеем,

$$ f'(x) \;=\; d/dx(5.4x)+d/dx(2.4) $$ $$ f'(x) \;=\; 5.4(1)+0 \;=\; 5.4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

Помните, что производная — это вычисление скорости изменения функции.
Применить производную к функции по независимой переменной, входящей в функцию.
Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн.

Что такое производная x?

Производная x равна 1. Она относится к результату, полученному дифференцированием x различными способами. Нахождение скорости изменения функции включает в себя процесс дифференцирования. Таким образом, вы можете найти калькулятор производной для этого процесса. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x?

Поскольку производная экспоненциальной функции с основанием «e» равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (e ^х) = е ^х.

Это может оцениваться в дифференцирующем решателе для перекрестной проверки ответа и его шагов онлайн.

Алан Уокер

Последнее обновление 28 февраля, 2023

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Калькулятор производных с шагами | Дифференциальный калькулятор