Найти смешанное произведение векторов онлайн: Онлайн калькулятор. Смешанное произведение векторов

Как найти смешанное произведение векторов? Ответ на webmath.ru

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

• Формула
• Примеры вычисления смешанного произведения векторов

Формула

Для того чтобы найти смешанное произведение $(\bar{a}$, $\bar{b}$, $\bar{c})$ трех векторов, заданных своими координатами $\bar{a}=\left(a_{x} ; a_{y} ; a_{z}\right), b=\left(b_{x} ; b_{y} ; b_{z}\right)$ и $\bar{c}=\left(c_{x}, c_{y}, c_{z}\right)$ необходимо вычислить следующий определитель, где по строкам записаны координаты заданных векторов, то есть

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{lll}a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z}\end{array}\right|$$

Примеры вычисления смешанного произведения векторов

Пример

Задание. Вычислить смешанное произведение векторов $\bar{a}=(1 ; 3 ; 1)$, $\bar{b}=(2 ; 1 ; 3)$, и $\bar{c}=(3 ; 1 ; 2)$

Решение. Для нахождения смешанного произведения заданных векторов воспользуемся формулой

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{lll}a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z}\end{array}\right|$$

Подставляя координаты заданных векторов, получим:

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{ccc}1 & 3 & 1 \\ 2 & 1 & 3 \\ 3 & 1 & 2\end{array}\right|$$

Определитель вычисляем по правилу треугольника:

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{ccc}1 & 3 & 1 \\ 2 & 1 & 3 \\ 3 & 1 & 2\end{array}\right|=1 \cdot 1 \cdot 2+3 \cdot 3 \cdot 3+2 \cdot 1 \cdot 1-$$ $$-1 \cdot 1 \cdot 3-3 \cdot 2 \cdot 2-3 \cdot 1 \cdot 1=2+27+2-3-12-3=13$$

Ответ. $(\bar{a}, \bar{b}, \bar{c})=13$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Даны три вектора $\bar{a}=(1 ;-2 ; 3), \bar{b}=(3 ;-5 ; 6)$ и $\bar{c}=(5 ;-4 ; 1)$. Проверить, являются ли они компланарными, если нет, определить левую или правую тройку они образуют.

Решение. Найдем смешанное произведение этих векторов. Для этого воспользуемся формулой

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{lll}a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z}\end{array}\right|$$

Подставляя координаты заданных векторов, получим

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{ccc}1 & -2 & 3 \\ 3 & -5 & 6 \\ 5 & -4 & 1\end{array}\right|$$

Определитель вычисляем по правилу треугольника:

$$(\bar{a}, \bar{b}, \bar{c})=\left|\begin{array}{ccc}1 & -2 & 3 \\ 3 & -5 & 6 \\ 5 & -4 & 1\end{array}\right|=1 \cdot(-5) \cdot 1+(-2) \cdot 5 \cdot 6+$$ $$+3 \cdot 3 \cdot(-4)-3 \cdot(-5) \cdot 5-3 \cdot(-2) \cdot 1-1 \cdot 6 \cdot(-4)=$$ $$-5-60-36+75+6+24=4 \neq 0$$

Смешанное произведение заданных векторов не равно нулю, следовательно, векторы некомпланарные. Так как смешанное произведение положительно, то делаем вывод, что заданные векторы образуют правую тройку.

Ответ. Векторы некомпланарны и образуют правую тройку.

Читать дальше: как найти вектор коллинеарный вектору.

Смешанное произведение векторов | Математика

Пусть даны три вектора . Так как для векторов введены два вида произведений — скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:

1)двойное векторное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем векторное произведение полученного вектора на третий из данных векторов.

Например, вначале находится векторное произведение , затем — векторное произведение ;

Помощь с решением задач

2)смешанное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем скалярное произведение полученного вектора на третий из данных векторов.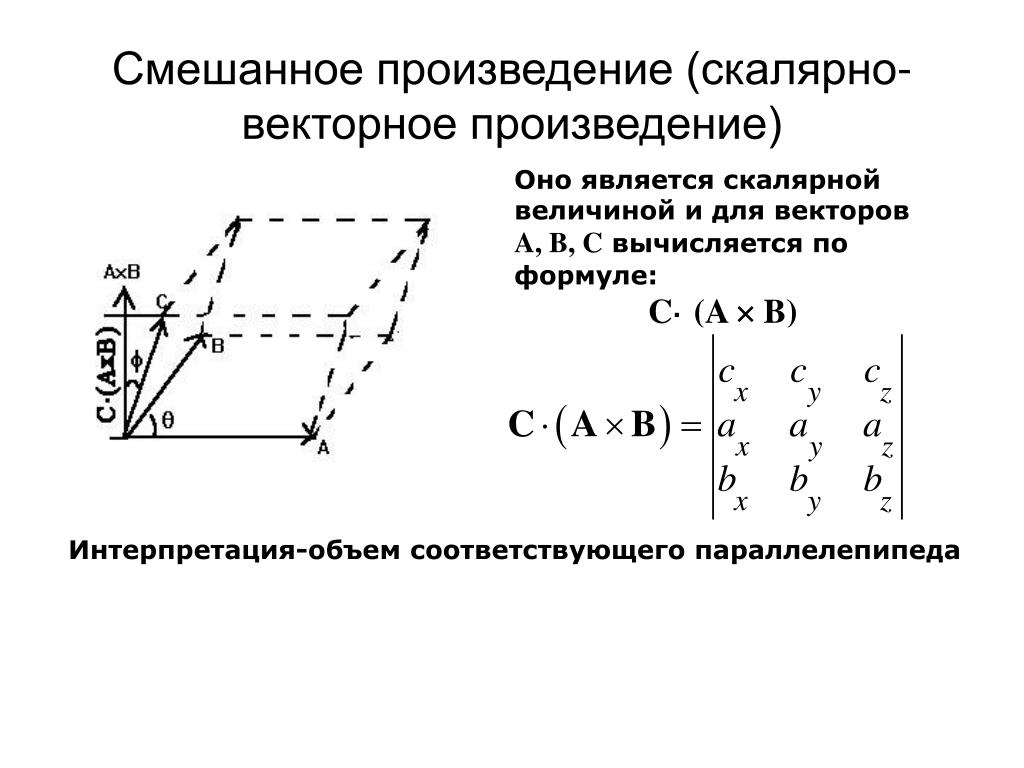

Например, вначале находится векторное произведение , затем — скалярное произведение .

Двойное векторное произведение обозначается в форме или в форме

Ясно, что результатом двойного векторного произведения является вектор.

Смешанное или иначе векторно-скалярное произведение обозначается символом или символом . Результатом смешанного произведения является число.

Пусть требуется определить смешанное произведение векторов, если известны координаты этих векторов

.

Вычислим предварительно Имеем

Воспользовавшись формулой (1.57), найдем

Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме

(1.62)

Формула (1.62) дает выражение для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов записаны соответственно в первой, второй и третьей строках определителя.

Покажем, что для смешанного произведения векторов справедливы равенства

(1.63)

Проверим, например, справедливость равенства Согласно формуле (1.62) имеем

Как известно, при перестановке двух срок определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на , получим

Итак,

Формулы (1.63) проще всего запомнить с помощью правила круговой перестановки векторов, сущность которого пояснена на рис.1.1.25 и 1.1.26.

Рисунки 1.1.25 и 1.1.26

Выясним геометрический смысл смешанного произведения векторов . Отложим векторы от общего начала и построим на этих векторах, как на ребрах, параллелепипед (рис.1.1.27).

Рисунок 1.1.27

Пусть . Тогда, согласно определения векторного произведения векторов, модуль вектора равен площади параллелограмма, построенного на векторах как на сторонах.

Следовательно,

где

Обозначим через высоту параллелепипеда, опущенную из конца вектора на рассматриваемый параллелограмм, и выясним смысл произведения . Вектор перпендикулярен плоскости параллелограмма, тогда

если и

, если

Следовательно, если есть объем параллелепипеда, то

, если и

,если

Итак,

или

(1.64)

Равенство (1.64) означает, что модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах как на ребрах.

Следствие (условие компланарности трех векторов). Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т.е. или в координатной форме

(1.65)

Необходимость Пусть векторы компланарны.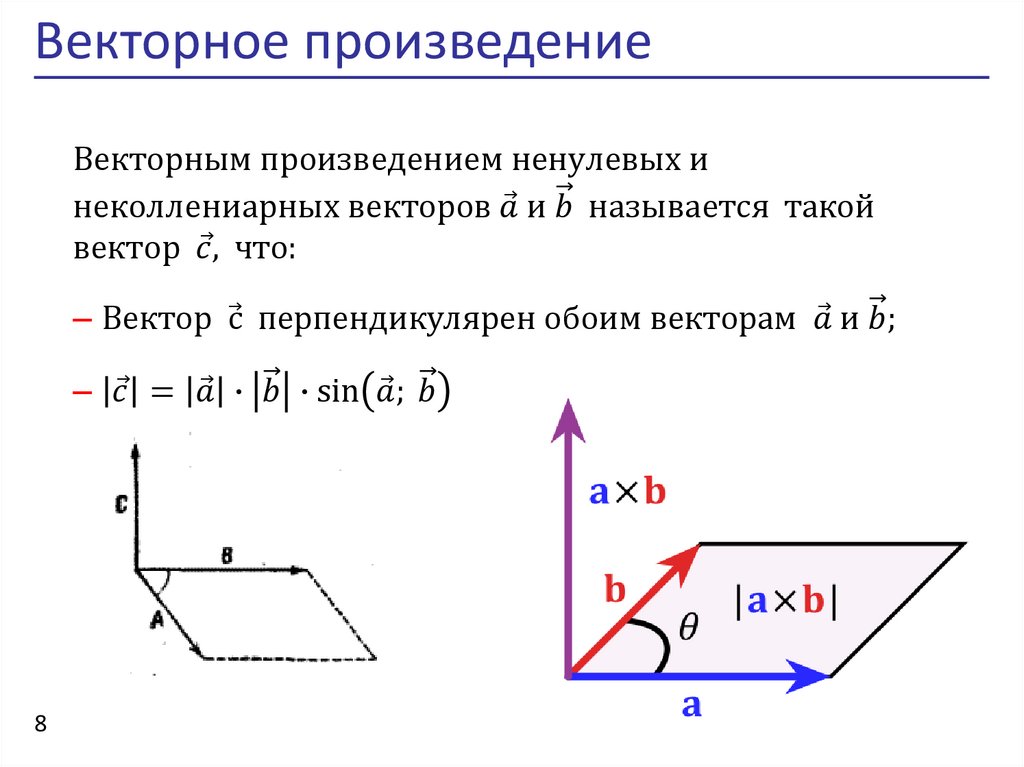 Тогда вектор перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору . Поэтому

Следовательно,

Достаточность Пусть векторы таковы, что

Если предположить, что векторы не компланарны, то на них можно построить параллелепипед с объемом . Но, согласно формуле (64)

Следовательно, или, , что противоречит исходному утверждению.

ПРИМЕР 1.1.26

Вычислить объем треугольной пирамиды с вершинами в точках

Решение. Построим три вектора

с общим началом точкой . На этих векторах, как на ребрах, построим параллелепипед. Его объем равен Объем пирамиды составляет шестую долю объема параллелепипеда. Следовательно,

Ответ: 3

Из геометрического смысла смешанного произведения векторов и рассмотренного примера следует, что оно широко используется при вычислении объемов любых многогранников.

• Матрицы. Определение, виды и основные понятия
• Курс математики

Калькулятор тройного произведения — eMathHelp

Калькулятор вычисляет тройное произведение (как скалярное, так и векторное) трех векторов с указанием шагов.

$$$\mathbf{\vec{u}}$$$:

$$$\langle$$$ $$$\rangle$$$

Через запятую.

$$$\mathbf{\vec{v}}$$$:

$$$\langle$$$ $$$\rangle$$$

Через запятую.

$$$\mathbf{\vec{w}}$$$:

$$$\langle$$$ $$$\rangle$$$

Через запятую.

Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.

Ваш ввод

Вычислить $$$\left\langle -2, 3, 1\right\rangle\cdot \left(\left\langle 7, -4, 0\right\rangle\times \left\ langle -3, 2, 1\right\rangle\right)$$$, $$$\left(\left\langle -2, 3, 1\right\rangle\times \left\langle 7, -4, 0 \right\rangle\right)\cdot \left\langle -3, 2, 1\right\rangle$$$, $$$\left\langle -2, 3, 1\right\rangle\times \left(\ влево\langle 7, -4, 0\вправо\rangle\times \влево\langle -3, 2, 1\вправо\rangle\вправо)$$$ и $$$\влево(\влево\langle -2, 3, 1\право\угол\умножить налево\угол 7, -4, 0\направо\угол\направо)\раз \налево\угол -3, 2, 1\направо\угол. $$$

Решение

• Вычислить скалярное тройное произведение $$$\left\langle -2, 3, 1\right\rangle\cdot \left(\left\langle 7, -4, 0\right \rangle\times \left\langle -3, 2, 1\right\rangle\right).$$$

  $$$\left\langle -2, 3, 1\right\rangle\cdot \left( \left\langle 7, -4, 0\right\rangle\times \left\langle -3, 2, 1\right\rangle\right) = \left\langle -2, 3, 1\right\rangle\cdot \left\langle -4, -7, 2\right\rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

  Далее, $$$\left\langle -2, 3, 1\right\rangle\cdot \left\langle -4, -7, 2\right\rangle = -11$$$ (шаги см. в точках калькулятор продукта).

  Скалярное тройное произведение можно найти как определитель, который имеет три вектора в качестве строк или столбцов.

• Вычислить скалярное тройное произведение $$$\left(\left\langle -2, 3, 1\right\rangle\times \left\langle 7, -4, 0\right\rangle\right)\ cdot \left\langle -3, 2, 1\right\rangle. $$$

  $$$\left(\left\langle -2, 3, 1\right\rangle\times \left\langle 7, -4, 0\right\rangle\right)\cdot \left\langle -3, 2, 1\right\rangle = \left\langle 4, 7, -13\right\rangle\cdot \left\langle -3 , 2, 1\right\rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

  Далее, $$$\left\langle 4, 7, -13\right\rangle\cdot \left\langle -3, 2, 1\right\rangle = -11$$$ (этапы см. в разделе скалярное произведение калькулятор).

  Скалярное тройное произведение можно найти как определитель, который имеет три вектора в качестве строк или столбцов.

• Вычислить векторное тройное произведение $$$\left\langle -2, 3, 1\right\rangle\times \left(\left\langle 7, -4, 0\right\rangle\times \left \langle -3, 2, 1\right\rangle\right).$$$

  $$$\left\langle -2, 3, 1\right\rangle\times \left(\left\langle 7, -4, 0\вправо\угол\раз \влево\лангл -3, 2, 1\вправо\угол\вправо) = \влево\лангл -2, 3, 1\вправо\угол\раз \влево\лангл -4 , -7, 2\right\rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

  Далее, $$$\влево\langle -2, 3, 1\вправо\rangle\times \влево\langle -4, -7, 2\вправо\rangle = \влево\langle 13, 0, 26\вправо \rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

• Вычислить векторное тройное произведение $$$\left(\left\langle -2, 3, 1\right\rangle\times \left\langle 7, -4, 0\right\rangle\right)\ раз \влево\лангле -3, 2, 1\вправо\рангл.$$$

  $$$\влево(\влево\лангле -2, 3, 1\вправо\рангл\раз \влево\лангл 7, -4, 0\вправо\угол\вправо)\раз \влево\лангл -3, 2, 1\вправо\угол = \влево\лангл 4, 7, -13\вправо\угол\раз \влево\лангл -3 , 2, 1\right\rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

  Далее, $$$\влево\langle 4, 7, -13\вправо\rangle\times \влево\langle -3, 2, 1\вправо\rangle = \влево\langle 33, 35, 29\вправо\ rangle$$$ (шаги см. в калькуляторе перекрестного произведения).

Ответ

$$$\left\langle -2, 3, 1\right\rangle\cdot \left(\left\langle 7, -4, 0\right\rangle\times \left \langle -3, 2, 1\right\rangle\right) = -11$$$A

$$$\left(\left\langle -2, 3, 1\right\rangle\times \left \langle 7, -4, 0\right\rangle\right)\cdot \left\langle -3, 2, 1\right\rangle = -11$$$A

$$$\влево\langle -2, 3, 1\вправо\rangle\times \left(\left\langle 7, -4, 0\right\rangle\times \left\langle -3, 2 , 1\right\rangle\right) = \left\langle 13, 0, 26\right\rangle$$$A

$$$\left(\left\langle -2, 3, 1\right\ rangle\times \left\langle 7, -4, 0\right\rangle\right)\times \left\langle -3, 2, 1\right\rangle = \left\langle 33, 35, 29\right\rangle $$$A

векторов — Криста Кинг Математика | Онлайн-помощь по математике

Сообщения с тегами векторов Как найти объем параллелепипеда из его смежных ребер

Если нам нужно найти объем параллелепипеда, и нам даны три его смежных ребра, все, что нам нужно сделать, это найти скалярное тройное произведение трех векторов, определяющих ребра.

Читать больше

Learn mathKrista King 29 июня 2021 математика, выучить онлайн, онлайн курс, онлайн математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, векторы, векторное исчисление, параллелепипед, объем параллелепипеда, объем параллелепипеда, скалярная тройка продукт

Как найти векторы скорости и ускорения

Для данной функции положения r(t), которая моделирует положение объекта во времени, скорость v(t) является производной положения, а ускорение a(t) является производной скорости, что означает, что ускорение также является вторым производная положения. Это означает, что мы можем интегрировать ускорение, чтобы найти скорость, и интегрировать скорость, чтобы найти положение.

Читать больше

Изучение математикиКриста Кинг 23 февраля 2021 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 3, вычисление 3, исчисление iii, вычисление iii, векторы, векторное исчисление, вектор положения, вектор скорости, вектор ускорения, ускорение позиционной скорости , интегрируя ускорение

Определение того, являются ли векторы ортогональными, параллельными или ни тем, ни другим

Мы говорим, что два вектора a и b ортогональны, если они перпендикулярны (их скалярное произведение равно 0), параллельны, если они указывают в одном и том же или противоположном направлении, и никогда не пересекаются друг с другом, в противном случае они не являются ни ортогональными, ни параллельными. Поскольку получить скалярное произведение несложно, хорошей идеей будет завести привычку проверять векторы, чтобы увидеть, ортогональны ли они, а затем, если они не ортогональны, проверить, параллельны ли они.

Читать больше

Изучайте математикуКриста Кинг 8 января 2021 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, вычисление iii, векторное вычисление, векторное исчисление, многомерное исчисление, многомерное вычисление, многомерное исчисление, многомерное вычисление , векторы, ортогональные векторы, параллельные векторы, ортогональные параллельные или ни то, ни другое

Нахождение кривизны векторной функции

Чтобы найти кривизну вектор-функции, нам нужны производная вектор-функции, модуль производной, единичный касательный вектор, его производная и модуль его производной. Получив все эти значения, мы можем использовать их для нахождения кривизны.

Читать больше

Изучение математикиКриста Кинг 26 декабря 2020 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, вычисление iii, векторы, векторные функции, кривизна, кривизна векторной функции, единичный касательный вектор, величина, величина производной, каппа

Комбинации векторов (сложение и вычитание векторов)

Когда мы хотим найти комбинацию двух векторов, мы просто совмещаем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор от начальной точки первого до конечной точки. конечный пункт второго. Мы можем сделать это с любым количеством векторов, мы просто продолжаем сопоставлять начальную точку следующего вектора с конечной точкой предыдущего, а затем рисуем комбинацию из начальной точки самого первого вектора в конечную точку. самого последнего вектора.

Читать больше

Изучайте математикуКриста Кинг 10 октября 2020 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, векторы, векторное исчисление, комбинации векторов, сложение векторов, вычитание векторов, объединение векторов

Производные по направлению в направлении вектора

Производная по направлению функции многих переменных учитывает направление (заданное единичным вектором u), а также частные производные функции по каждой из переменных.

Читать больше

Изучение математикиКриста Кинг 13 сентября 2020 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, вычисление 3, вычисление iii, частные производные, производные по направлению, векторы, производная по направлению в направлении вектора, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление

Скалярное произведение двух векторов

Чтобы взять скалярное произведение двух векторов, умножьте одинаковые координаты векторов, а затем сложите произведения вместе. Другими словами, умножьте координаты x двух векторов, затем добавьте результат к произведению координат y. Для заданных векторов в трехмерном пространстве также добавьте произведение координат z.

Читать больше

Изучайте математикуКриста Кинг 18 августа 2020 г.