Найдите тангенс альфа если синус
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-03
В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.
Относительную сложность могут вызывать следующие:
— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений
Если перечислить все группы задач, то они довольно разнообразны.
Они включают в себя: ПОКАЗАТЬ/СКРЫТЬ
Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!
Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях.
ЭТО ВАЖНО!!!
Как осознать эту информацию и понять следствием чего она является – об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:
Основное тригонометрическое тождество:
Формулы тангенса и котангенса:
Выполняются элементарные алгебраические преобразования:
1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.
В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.
Найдите тангенс альфа, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Косинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение синуса. Затем подставить их в формулу тангенса.
Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи).
Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:
Таким образом:
Ответ: – 0,5
Найдите tg α, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Cинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение косинуса. Затем подставить их в формулу тангенса.
Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому
Таким образом:
Ответ: – 0,25
Найдите 5·cos α, если синус альфа
Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos2x = 1– sin2x и
Определим знак косинуса.
Угол принадлежит интервалу (3Пи/2;2Пи).
Это интервал от 270 до 360 градусов (четвёртая четверть). Значение косинуса в этой четверти положительное, поэтому:
Таким образом, 5·cos α = 5∙0,7 = 3,5
Ответ: 3,5
Найдите 0,1·sin α, если
Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin2x = 1– cos2x и
Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).
Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:
Таким образом 0,1·sin α = 0,1∙0,3 = 0,03
Ответ: 0,03
Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:
65217. Найдите tg2 α, если 3sin2 α + 8 cos2 α = 7
Требуется найти квадрат тангенса.
Разделим обе части уравнения на cos2 α, получим:
Второй способ:
Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:
Ответ: 0, 25
65269. Найдите
Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:
Ответ: – 0,5
65273. Найдите
Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на cosα), получим:
Подставим значение тангенса данное в условии, получим:
*Косинус у нас сократился.
Ответ: 4
65363. Найдите tg α, если
В левой части в числителе и знаменателе вынесем cosα за скобки, получим:
Ответ: 0,4
65423.
Найдите tg α, если
Умножим обе части уравнения на 4 (2sinα+cosα+1)
Ответ: –1,9
26775. Найдите tg α, если
Посмотреть решение
26776. Найдите tg α, если
Посмотреть решение
26777. Найдите 3cos α, если
Посмотреть решение
26778. Найдите 5sin α, если
Посмотреть решение
26787. Найдите tg2 α, если
Посмотреть решение
26788. Найдите
Посмотреть решение
26789. Найдите
Посмотреть решение
26790. Найдите tg α, если
Посмотреть решение
26791. Найдите tg α, если
Посмотреть решение
Подведём итог, для решения подобных примеров вы:
1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны!!!
Надеюсь, что материал был для вас полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Выражения | ЕГЭ-№6Тригонометрия
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
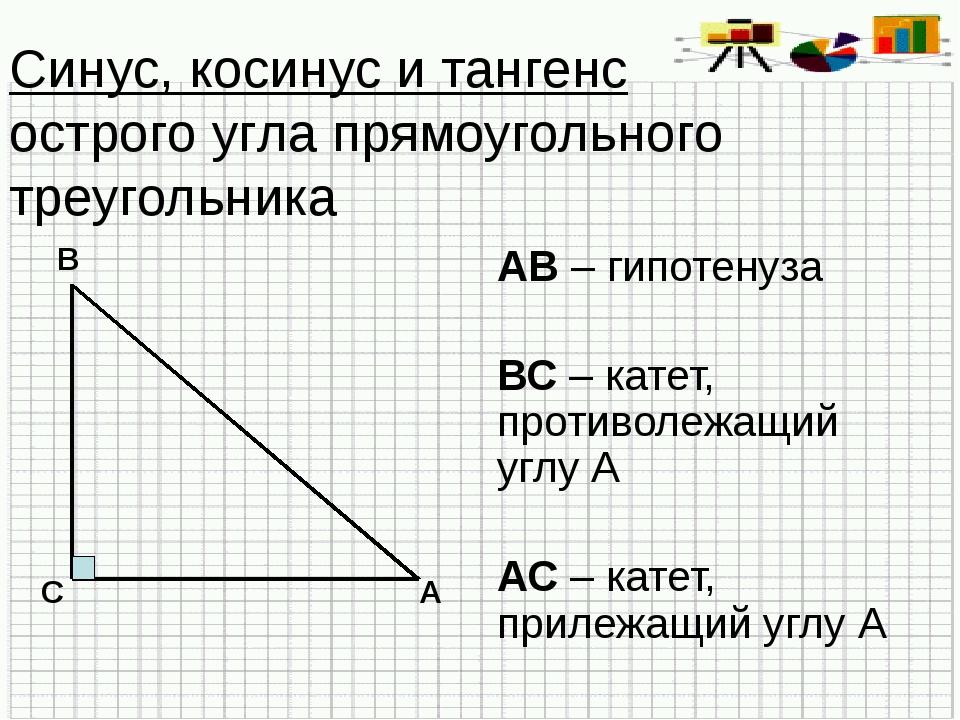
Синус, косинус и тангенс острого угла прямоугольного треугольника
Урок 25. Геометрия 8 класс ФГОС
На этом уроке мы повторим основные элементы прямоугольного треугольника. Введем понятие прилежащего и противолежащего катетов. Познакомимся с синусом, косинусом и тангенсом, понятиями, которые связывают острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Выведем две формулы для нахождения тангенса острого угла прямоугольного треугольника.
Докажем основное тригонометрическое тождество. Подробно рассмотрим примеры, в которых надо найти синусы, косинусы и тангенсы острых углов прямоугольного треугольника.
Конспект урока «Синус, косинус и тангенс острого угла прямоугольного треугольника»
На этом уроке мы познакомимся с синусом, косинусом и тангенсом, понятиями, которые связывают острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника.
Прежде всего, давайте повторим основные сведения о прямоугольном треугольнике. Пусть нам дан прямоугольный треугольник ABC. Вершина C, угол С= 90º – прямой, гипотенуза с. Вершина А, угол α — острый, катет
Напомним, что сумма
углов треугольника равна 180º, значит, сумма острых углов прямоугольного
треугольника равна 90º. Мы знаем, что стороны прямоугольного треугольника
связаны между собой теоремой Пифагора.
Катет, BC является противолежащим для угла А, катет AC является прилежащим для угла А. Аналогично, катет AC является противолежащим для угла B, катет BC является прилежащим для угла B.
А теперь давайте подумаем, а можно ли связать между собой стороны и углы прямоугольного треугольника?
Давайте, посмотрим на два прямоугольных треугольника с острыми углами 30º и 60º.
И давайте, попробуем найти отношение катета, противолежащего углу в тридцать градусов к гипотенузе одного и второго треугольника.Мы видим, что это отношение одинаково в обоих треугольниках.
Теперь давайте найдем отношение катета, прилежащего к углу в тридцать градусов. И опять получили одинаковые отношения.
;
Теперь давайте найдем отношение противолежащего катета к прилежащему. И снова у нас получились одинаковые отношения.
;
Теперь давайте,
рассмотрим два прямоугольных равнобедренных треугольника.
Острые углы этих
треугольников равны по 45º. Находя для них такие же отношения, получим,
что и в этом случае эти отношения для обоих треугольников равны.
= ;
= ;
;
Учеными было сделано предположение, что эти отношения не зависят от величины сторон прямоугольного треугольника, а зависят от величины острых углов прямоугольного треугольника. Для этих отношений были введены специальные названия и обозначения.
Определение: синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Определение: косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Определение: тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Теперь давайте
попробуем найти отношение синуса угла α к косинусу того же угла.
; ;
Сравним полученную формулу с формулой тангенса угла α и увидим, что можно записать, что тангенс угла альфа равен отношению синуса угла альфа к косинусу угла альфа.;
Задача. Найти треугольника с прямым углом , если см, см.
Решение.
(см)
Ответ: .
Из определения синуса,
Из определения тангенса угла А можно получить формулу, которая связывает два катета прямоугольного треугольника. Получим, что катет a равен произведению катета b на тангенс противолежащего угла.
Задача. Пусть в прямоугольном треугольнике, один из катетов равен см, а противолежащий угол равен . Выразить второй катет, противолежащий ему угол и гипотенузу через известный катет и угол, и найти их значение.
Решение.
Ответ: .
Теперь давайте докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Пусть нам даны два прямоугольных треугольника ABC и A1B1C1 с прямыми углами C и C1 и равными острыми углами А и A1. Очевидно, что углы B и B1 также будут равны. То есть наши треугольники подобны по первому признаку подобия (если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны).
Значит, справедливы равенства
Из этих равенств несложно вывести равенство отношения а эти отношения есть ничто иное как синус угла А и синус угла A1. То есть можно записать, что .
Аналогично, можно
вывести равенство отношения то
есть равенство .
Теперь, давайте попробуем доказать справедливость равенства:
Рассмотрим прямоугольный треугольник ABC.
Таким образом, справедливость равенства доказана.
Это равенство называют основным тригонометрическим тождеством. Синус, косинус, тангенс – тригонометрические функции.
Слово «тригонометрия» происходит от греческих слов «треугольники» и «измеряю». «Тригонометрия» — раздел математики, в котором изучают тригонометрические функции и их использование в геометрии.
Задача. Найти если .
Решение
или
Повторим главное:
синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе;
косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе;
тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему;
Синус и косинус
одного и того же угла связаны между собой основным тригонометрическим
тождеством.
Предыдущий урок 24 О подобии произвольных фигур
Следующий урок 26 Значения синуса, косинуса и тангенса для углов 30, 45 и 60
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Синус, косинус и тангенс » Ярно Воуда
1. ВведениеСинус, косинус и тангенс — это функции, которые мы используем в математике для вычисления углов и сторон треугольников. На вашем калькуляторе эти функции кратко записываются как «sin», «cos» и «tan»,
Легенда • = Умножение
∠ = Угол
≈ = Приблизительно равно
- Вы можете применять синус, косинус и тангенс только к прямоугольным треугольникам .
- Проверьте, настроен ли ваш калькулятор на «градусы» или «радианы» в зависимости от необходимого решения. Вы можете изменить этот параметр, нажимая кнопку «Mode» на вашем калькуляторе, пока не увидите «Deg» или «Rad». Выберите тот, который вам нужен.
Прямоугольные треугольники:
Эти треугольники всегда имеют один угол 90 градусов (два других угла вместе также равны 90 градусов). Угол 90 градусов называется прямым углом.
Сумма углов:
Треугольник — это фигура с тремя углами. Если вы сложите все углы вместе, вы всегда получите в сумме 180 градусов, какой бы формы ни был треугольник.
С помощью синуса, косинуса и тангенса мы определяем отношение углов в прямоугольном треугольнике. Хорошо известным примером прямоугольного треугольника является треугольник со сторонами 3, 4 и 5.
Чтобы вычислить угол с помощью синуса, косинуса или тангенса, нам понадобится длина двух сторон. Каждая сторона прямоугольного треугольника может быть названа гипотенузой, смежной или противоположной. Именование сторон всегда связано с углом, который вы вычисляете.
«Гипотенуза»:
Гипотенуза — самая длинная сторона треугольника. Это сторона, противоположная прямому углу. Гипотенуза также находится рядом со стороной, которую вы пытаетесь вычислить.
«Противоположная сторона»:
Противоположная сторона – это сторона, противоположная данному углу. Это также единственная сторона, не касающаяся вычисляемого угла.
«Смежная сторона »:
Смежная сторона также лежит вдоль угла, который вы пытаетесь рассчитать. Поскольку мы уже знаем, что одна из сторон данного угла является гипотенузой, тогда оставшаяся сторона должна быть прилежащей стороной.
5. Тангенс углаС помощью тангенса можно вычислить угол, зная противоположную и прилежащую стороны.
Формула для вычисления тангенса угла:
Противоположная сторона / Прилежащая сторона = Тангенс угла
Число, которое получается при делении двух сторон, называется градиентом. Градиент также называют тангенсом угла. С помощью этого числа вы можете рассчитать угол в градусах.
Чтобы преобразовать тангенс угла в градусы, мы будем использовать арктангенс. Мы делаем это, нажимая кнопки *shift* и *tan* на вашем калькуляторе. Вы увидите, что ваш калькулятор теперь показывает «tan-1».
Если вы сейчас введете тангенс угла, калькулятор рассчитает градус этого угла.
- Другие названия для «tan -1 »: «арктангенс», «арктангенс» или «атан».
Точно так же можно вычислить угол с помощью синуса.
Формула для вычисления синуса угла:
Противоположная сторона / Гипотенуза = Синус угла
Точно так же можно вычислить угол с помощью косинуса.
Формула для вычисления косинуса угла:
Смежная сторона / Гипотенуза = косинус угла
Самый простой способ запомнить это — подумать о «SohCahToa». Это также то, что я использую, чтобы запомнить формулы синуса, косинуса и тангенса. «SohCahToa» — это сокращение от следующего:
Soh… S ine: O противоположная сторона / H ypotenuse
…Cah… 9000 6 C озин: A ближняя сторона / H ypotenuse
…Toa : T angent: O противоположная сторона / A дальняя сторона
Вычисление сторон с касательной Если вы знаете только длину одной стороны и градус угла, вы можете вычислить остальные стороны. Когда вы только нажимаете кнопку *tan* на вашем калькуляторе, а затем угол в градусах, ваш калькулятор рассчитает угол обратно к касательной угла.
Если мы посмотрим на формулу для вычисления тангенса, мы можем заполнить одну из сторон и тангенс угла. В приведенном ниже примере вопрос: Что мы делим на прилежащую сторону, чтобы получить тангенс 0,75.
Давайте сначала рассмотрим упрощенный пример. Что нужно разделить на 2, чтобы получить 5? Ответ: 10. Откуда мы это знаем? 5 • 2 = 10. Мы также можем применить это для вычисления сторон в треугольниках. Тогда имеем: Касательная ангела •прилежащая сторона = противоположная сторона . Так же, как пример ниже.
10.
Формулы Синус угла:
Противоположная сторона / Гипотенуза = Синус угла
Косинус угла:
Прилегающая сторона / Гипотенуза = Косинус угла
Тангенс угла:
Противоположная сторона / Прилежащая сторона = Тангенс угла
.
1. ВведениеDe sinus, cosinus en tangens zijn hulpmiddelen in de wiskunde die je kunt gebruiken om in een rechthoekige driehoek een hoek of een zijde te berekenen. Op je rekenmachine staan deze functies afgekort als «sin», «cos» и «tan».
Легенда • = Vermenigvuldigen
∠ = Hoek
≈ = Ongeveer gelijk aan
- Je kunt sinus, cosinus en tangens alleen toepassen op een rechthoekige driehoek .
- Проверка je rekenmachine op «graden» of «radialen» ingesteld afhankelijk wat voor de uitkomst nodig is. Je kunt dit aanpassen door op de «mode» button op je rekenmachine te drukken totdat je «Deg» of «Rad» ziet staan. Selecteer de optie die je nodig hebt.
Je kunt dit aanpassen door op de «mode» button op je rekenmachine te drukken totdat je «Deg» of «Rad» ziet staan. Selecteer de optie die je nodig hebt. Rechthoekige driehoek:
Deze driehoek heeft altijd één hoek van 90 град (De andere twee hoeken zijn samen 90 град). Де Хук ван 90 классов noem je een rechte hoek.
Hoekensom driehoek:
Een driehoek — это один из видов, встречающихся в общей сложности. Als Je Alle Drie hoeken van een driehoek bij elkaar optelt krijg je altijd 180 град, ват воор vorm de driehoek ook heeft.
Met sinus, cosinus en tangens bepalen we de verhoudingen in een rechthoekige driehoek. Een mooi voorbeeld van een rechthoekige driehoek is de driehoek met de zijden 3, 4 en 5. Als je een andere driehoek neemt met dezelfde verhoudingen zoals 6, 8 en 10.
Zullen de sinus, cosinus en tangens van een bepaalde hoek in beide drie Хекен Хетцельфде зейн. De sinus ван een hoek является kortgezegd де verhouding tussen twee zijdes die een hoek bepalen.
Om van een bepaalde hoek het aantalgrade te bereken met de tangens, sinus of cosinus, hebben we de lengte van twee zijden nodig. Elke zijde in een rechthoekige driehoek kunnen we benoemen als: schuine zijde, aanliggende zijde of overstaande zijde. Het benoemen ван де zijden является altijd gezien vanuit де hoek умереть je wil berekenen.
De «schuine zijde»:
De schuine zijde is altijd de langste zijde. Deze zijde staat in elke rechthoekige driehoek tegenover de rechte hoek фургон 90 град. De schuine zijde ligt ook altijd langs de hoek die je wil berekenen.
De «overstaande zijde»:
De overstaande zijde is de zijde die tegenover de hoek staat die je wil berekenen.
Это ook de enigste zijde die niet langs de gevraagde hoek ligt.
De «aanliggende zijde»:
De aanliggende zijde ligt ook aan de hoek die je wil berekenen. Aangezien we al weten dat één van de zijden langs de hoek de schuine zijde is, moet de overige zijde wel de aanliggende zijde zijn.
Met de tangens kun je, in een rechthoekige driehoek, een hoek berekenen als de overstaande en aanliggende zijden bekend zijn. По формуле hierbij hoort равно volgt:
.Overstaande zijde / Aanliggende zijde = Tangens van de hoek
Het getal dat je krijgt als je met tangens twee zijden door elkaar deelt, это het hellingsgetal van die hoek. Dit hellingsgetal wordt de tangens van de hoek genoemd. Встретил дит Геталь Кун Дже де Граден ван де Хук Берекенен.
Om de tangens van een hoek om te zetten in heaantalgraden, maken we gebruik van de «обратные касательные».
Это мы делаем дверь в машине rekenmachine *shift* en *tan* in te toetsen. Je ziet dat je rekenmachine nu «tan-1» laat zien. Als je nu де тангенс ван een hoek invult berekent де rekenmachine он aantal град ван де хука.
- Andere benamingen voor “tan -1 ” zijn ook wel: “обратные касательные”, “arc tan” слова “atan”.
Op dezelfde manier kun je met sinus een hoek berekenen.
Bij de sinus van een hoek hoort de volgende формула:
Overstaande zijde / Schuine zijde = Sinus van de hoek
Op dezelfde manier kun je met cosinus een hoek berekenen.
Bij de cosinus van een hoek hoort de volgende формула:
Aanliggende zijde / Schuine zijde = Cosinus van de hoek
Совет Dit is niet bepaald het makkelijkste om te onthouden, daarom is het handig om hier een ezelsbruggetje voor te hebben. De meest bekende (en ook degene die ik altijd gebruik) — это «SosCasToa».
Sos… S inus: O verstaande zijde / S chuine zijde
…Cas… C 9003 2 osinus: A anliggende zijde / S chuine zijde
…Toa : T angens: O verstaande zijde / A anliggende zijde
Als je alleen één zijde en hoek ingrade weet, kun je met deze gegeven ook de overige zijden berekenen. Als je nu alleen de *tan* toets indrukt, gevolgd door de hoek в градене, kun je hoek в граде terugrekenen naar de tangens van de hoek.
Также мы де формула voor het berekenen ван де tangens эр weer bij pakken, kunnen мы де twee gegeven invullen.
В het voorbeeld hieronder kunnen мы één van de zijden en de tangens van de hoek invullen. De vraag in dit geval: Wat moeten we delen door de aanliggende zijde, om een tangens van 0.75 te krijgen.
Laten we eerst een simpel voorbeeld erbij pakken met hetzelfde idee. Wat moeten we delen door 2 om 5 te krijgen? Antwoord: 10. Как мы это делаем? 5 • 2 = 10 . Op dezelfde manier kun je ook een onbekende zijde berekenen. Wat we dan krijgen: tangens van een hoek • aanliggende zijde = overstaande zijde . Net als in het voorbeeld hieronder.
10. Формулы Sinus van een hoek:
Overstaande zijde / Schuine zijde = Sinus hoek
Cosinus van een hoek:
Aanliggende zijde / Schuine zijde = Cosinus hoek
Tangens van een hoek:
Overstaande zijde / Aanliggende zijde = Tangens hoek
.
6.5 Соотношения синуса, косинуса и тангенса и приложения тригонометрии – Fanshawe Pre-Health Sciences Mathematics 1
Перейти к содержимомуОжидается, что к концу этого раздела вы сможете
- Находить недостающую сторону прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Найдите недостающий угол прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Решение приложений с помощью тригонометрии прямых углов
Теперь, когда мы знаем основы алгебры и геометрии, связанные с прямоугольным треугольником, мы можем приступить к изучению тригонометрии. Многие реальные жизненные задачи можно представить и решить с помощью прямоугольной тригонометрии.
Отношения синуса, косинуса и тангенса Мы знаем, что любой прямоугольный треугольник имеет три стороны и прямой угол. Сторона, противолежащая прямому углу, называется гипотенузой.
Два других угла в прямоугольном треугольнике — острые углы (с мерой менее [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления.
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника. Две другие стороны называются противоположной стороной и смежной стороной. Названия этих сторон зависят от того, какой из двух острых углов используется в качестве опорного угла.
Рисунок 6.5.1В прямоугольном треугольнике каждая сторона помечена строчной буквой, соответствующей прописной букве противоположной вершины.
Назовите стороны треугольника и найдите гипотенузу, противоположную и прилежащую.
Рисунок 6.5.2 РешениеМы пометили стороны строчными буквами, чтобы они совпадали с прописными буквами противоположной вершины.
[латекс]с[/латекс] является гипотенузой
[латекс]а[/латекс] находится напротив
[латекс]b[/латекс] является смежным
5.31) Обозначьте стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
Рисунок 6.5.4 Решение [латекс]y[/латекс] гипотенуза
[латекс]z[/латекс] противоположно
[латекс]х[/латекс] смежно
Тригонометрические отношения — это отношения сторон прямоугольного треугольника. Для любого прямоугольного треугольника мы можем определить три основных тригонометрических соотношения: синус, косинус и тангенс.
Давайте обратимся к рисунку 6.5.1 и определим три основных тригонометрических отношения как:
Три основных тригонометрических отношения- [латекс] синус (\ тета) = \ гидроразрыва {\ текст {длина противоположной стороны}} {\ текст {длина стороны гипотенузы}} [/латекс]
- [латекс] косинус (\ тета) = \ гидроразрыва {\ текст {длина прилегающей стороны}} {\ текст {длина стороны гипотенузы}} [/латекс]
- [латекс]тангенс(\тета) = \frac{\text{длина противоположной стороны}}{\text{длина соседней стороны}}[/latex]
Где [латекс]θ[/латекс] — мера опорного угла, измеренная в градусах.
Очень часто мы используем сокращения для синуса, косинуса и тангенса.
- [латекс] грех (\ тета) = \ гидроразрыва {опп} {hyp} [/латекс]
- [латекс] соз (\ тета) = \ гидроразрыва {прил. {hyp} [/латекс]
- [латекс] загар (\ тета) = \ гидроразрыв {опп} {прил} [/латекс]
Некоторые люди помнят определение тригонометрических соотношений как SOH CAH TOA.
Давайте воспользуемся [латекс]\Delta DEF[/латекс] из примера 6.5.2, чтобы найти три отношения.
Для данного треугольника найти отношение синуса, косинуса и тангенса.
Рисунок 6.5.5 Решение[латекс]\begin{align*}sin(\theta) &= \frac{f}{d}\\[2ex]cos(\theta)&= \frac{e} {d}\\[2ex]tan(\theta)&= \frac{f}{e}\end{align*}[/latex]
2) Для данного треугольника найти отношение синуса косинуса и тангенса.
Рисунок 6.5.6 Решение[латекс]\begin{align*}sin(\theta)&= \frac{z}{y}\\[2ex]cos(\theta)&= \frac{x} {y}\\[2ex]tan(\theta)&= \frac{z}{x}\end{align*}[/latex]
В примере 6.
5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс].
При расчетах мы обычно округляем отношения до четырех знаков после запятой, а в конце наш окончательный ответ — до одного знака после запятой, если не указано иное.
Для данного треугольника найти отношения синуса, косинуса и тангенса. При необходимости округлить до четырех знаков после запятой.
Рисунок 6.5.7 РешениеУ нас есть два возможных опорных угла: [латекс]R[/латекс] и [латекс]S[/латекс].
Используя определения, тригонометрические соотношения для угла [латекс]R[/латекс] составляют:
- [латекс]sin(R)= \frac{4}{5} = 0,8[/латекс]
- [латекс] cos(R)= \frac{3}{5} = 0,6[/латекс]
- [латекс]загар(R)=\фракция{4}{3} = 1,3333…[/латекс]
Используя определения, тригонометрические соотношения для угла [латекс]S[/латекс]:
- [латекс]sin(S)= \frac{3}{5} = 0,6[/латекс]
- [латекс] cos(S)= \frac{4}{5} = 0,8[/латекс]
- [латекс]загар(S)= \фракция{3}{4} = 0,75[/латекс]
3) Для данного треугольника найти отношения синуса, косинуса и тангенса.
При необходимости округлить до четырех знаков после запятой.
- [латекс]sin(F)= \frac{8}{10} = 0,8[/латекс]
- [латекс] cos(F)= \frac{6}{10} =0,6[/латекс]
- [латекс]tan(F)= \frac{8}{6} = 1,3333…[/latex]
- [латекс]sin(D)= \frac{6}{10} = 0,6[/латекс]
- [латекс] cos(D)= \frac{8}{10} = 0,8[/латекс]
- [латекс]тангенс(D)= \фракция{6}{8} = 0,75[/латекс]
Теперь воспользуемся научным калькулятором и найдем тригонометрические соотношения. Сможете ли вы найти кнопки sin, cos и tan на своем калькуляторе? Чтобы найти тригонометрические соотношения, убедитесь, что ваш калькулятор находится в режиме градусов.
С помощью калькулятора найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой. 9\circ)=1[/латекс]
Нахождение недостающих сторон прямоугольного треугольника В этом разделе вы будете использовать тригонометрические отношения для решения задач прямоугольного треугольника.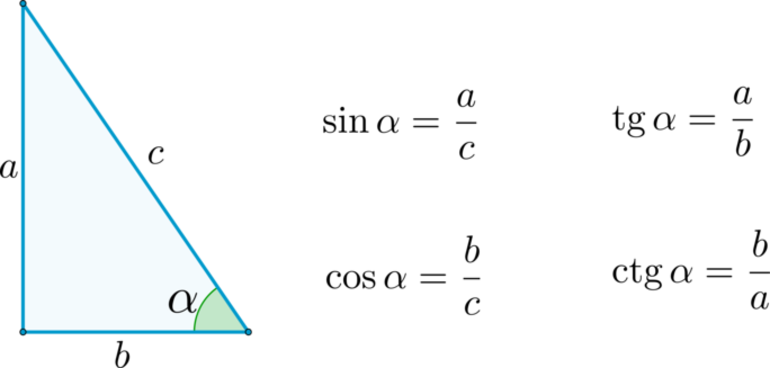
Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
Решить тригонометрические приложения
- Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
- Определите, что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое отношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в соотношение на шаге 4 и убедившись, что он имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением
В следующих нескольких примерах, зная меру одного острого угла и длину одной стороны прямоугольного треугольника, мы решим прямоугольный треугольник относительно недостающих сторон.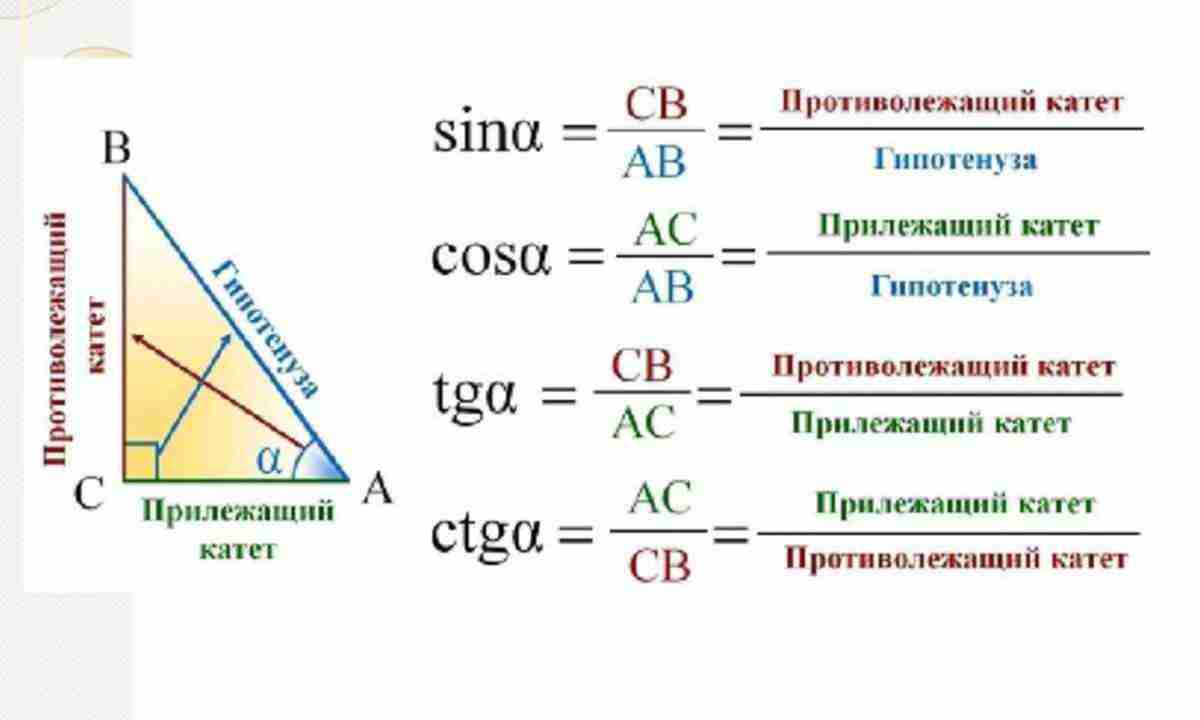
Найти недостающие стороны. Округлите окончательный ответ до двух знаков после запятой
Рисунок 6.5.9 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]Y[/латекс] — это наш опорный угол, [латекс]у[/латекс] — противоположная сторона, [латекс]z[/латекс] — смежная сторона, а [латекс]х=14[/латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
а. Противоположная сторона.
б. Соседняя сторона.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}y&=&?\\z&=&?\end{eqnarray*}[/latex] 9\circ)&=&z\\11.47&=&z\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{align*}\text{a.
}\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
Шаг 7: Ответьте на вопрос полным предложением.
а. Противоположная сторона — [латекс]8.03[/латекс].
б. Соседняя сторона — [латекс]11,47[/латекс].
5) Найдите недостающие стороны. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.10 Решение[латекс]\begin{align*}a &= 20.2\\b &= 16.4\end{align*}[/latex]
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.11 Решение Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]S[/латекс] – это наш опорный угол, [латекс]R[/латекс] – противоположная сторона, [латекс]r = 4[/латекс] – прилежащая сторона, а [латекс]Р[/латекс] это гипотенуза.
Шаг 2: Определите, что вы ищете.
Гипотенуза.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}p&=&?\end{eqnarray*}[/latex] 9\circ)&=&\frac{4}{p}\end{eqnarray*}[/latex]
Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}0,8480&=&\frac{4}{p}\\p&=&4,7170\;\;\text{Округление до 4 знаков после запятой}\end{eqnarray*} [/латекс]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{eqnarray*}0.8480&\overset?=&\frac{4}{4.7170}\\0.8480&=&0.8480\checkmark\end{eqnarray*}[/latex]
Шаг 7: Ответьте на вопрос полным предложением.
Гипотенуза равна [латекс]4,7[/латекс]. Окончательный ответ округлить до одного знака после запятой.
6) Найдите гипотенузу.
{-1}[/latex] находятся на вашем научном калькуляторе. . 9\циркуляр[/латекс]
В приведенном ниже примере у нас есть прямоугольный треугольник с двумя заданными сторонами. У нас отсутствуют острые углы. Давайте посмотрим, каковы шаги, чтобы найти недостающие углы.
Найдите недостающий [латекс]\угол Т[/латекс] . Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.13 Решение Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]T[/латекс] — это наш базовый угол, [латекс]t = 7[/латекс] — противолежащая сторона, [латекс]s[/латекс] — прилежащая сторона, а [латекс]r = 11[/ латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]T[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle T&=&?\end{eqnarray*}[/latex] 9\циркуляр[/латекс]
Найдите недостающий угол [латекс]А[/латекс]. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.15 Решение Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]А[/латекс] — это наш опорный угол, [латекс]а = 9[/латекс] — противолежащая сторона, [латекс]с = 5[/латекс] — прилежащая сторона, а [латекс]b[ /латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]А[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle A&=&?\end{eqnarray*}[/latex]
Шаг 4: Найдите требуемое тригонометрическое соотношение.
[латекс]\begin{eqnarray*}tan A&=&\frac{9}{5}\end{eqnarray*}[/latex] 9\circ\end{align*}[/latex]
Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Дается чертеж. Угол [латекс]А[/латекс] — это наш исходный угол, [латекс]а = 8[/латекс] — противоположная сторона, [латекс]b[/латекс] — прилежащая сторона, а [латекс]с[/латекс] ] — гипотенуза.
Шаг 2: Определите, что вы ищете.
\circ)&=&\frac{8}{c}\end{eqnarray*}[/latex]Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}\text{a.}\;0.9004&=&\frac{8}{b}\\0.9004 b&=&8\\b&=&8.8849\\[3ex]\text {b.}\;0,6691&=&\frac{8}{c}\\0,6691 c&=&8\\c&=&11,9563\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
9\circ\end{align*}[/latex]
[latex]\begin{align*}a &= 6\\b &= 15.6\\c &= 16.7\end{align*}[/ латекс]
Решите прямоугольный треугольник. Округлить до двух знаков после запятой.
Рисунок 6.5.19 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Дается чертеж. Пусть угол [латекс]D[/латекс] будет нашим исходным углом, [латекс]d = 4[/латекс] — противолежащая сторона, [латекс]f[/латекс] — прилежащая сторона, а [латекс]е = 9[/latex] — это гипотенуза.
Шаг 2: Определите, что вы ищете.
а. Угол Д.
б. Соседний.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\text{a.}\;\angle D&=&?\\[2ex] \text{b.}\;f&=&?\end{eqnarray*}[/latex ]
Шаг 4: Найдите требуемое тригонометрическое соотношение.
9\circ\end{align*}[/latex]
[latex]\begin{align*}d &= 29,4\\e &= 18,4\\f &= 60,6\end{align*}[/ латекс]
Решение приложений с использованием тригонометрических соотношенийВ предыдущих примерах мы смогли найти недостающие стороны и недостающие углы прямоугольного треугольника. Теперь давайте воспользуемся тригонометрическими отношениями для решения реальных задач.
Многие применения тригонометрических соотношений связаны с пониманием угла подъема или угла наклона. 9\circ[/latex] угол. Какова высота Harbour Centre?
РешениеШаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Рисунок 6.5.23
Угол [латекс]X[/латекс] — это наш исходный угол, [латекс]х[/латекс] — противоположная сторона, [латекс]у = 31[/латекс]м — прилежащая сторона, а [latex]z[/latex] — гипотенуза.
Шаг 2: Определите, что вы ищете. 9\circ)&=&\frac{x}{31}\end{eqnarray*}[/latex]
Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}4.7046&=&\frac{x}{31}\\x&=&145.8426\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{eqnarray*}4.7046&\overset?=&\frac{145.8426}{31}\\4.7046&=&4.7046 \checkmark\end{eqnarray*}[/latex] 9\circ[/latex] угол. Насколько высокое здание?
Раствор[латекс]43,3[/латекс] метра
Томас стоит на вершине здания высотой [латекс]45[/латекс] метров и смотрит на свою подругу, которая стоит на земле в [латексе]22[/латекс] метрах от основания здания. Что такое угол депрессии?
Решение Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Угол [латекс]Y[/латекс] — это наш исходный угол, [латекс]у = 45[/латекс]м — противоположная сторона, [латекс]z = 22[/латекс]м — прилежащая сторона , а [latex]x[/latex] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]Y[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle Y&=&?\end{eqnarray*}[/latex] 9\циркуляр[/латекс]
- Три основных тригонометрических соотношения: (Где [латекс]θ[/латекс] — мера опорного угла, измеренная в градусах).
- [латекс] синус\;\тета = \фракция{\текст{длина противоположной стороны}}{\текст{длина стороны гипотенузы}}[/латекс]
- [латекс]косинус\;\тета = \фракция{\текст{длина прилежащей стороны}}{\текст{длина гипотенузы}}[/латекс]
- [латекс]тангенс\;\тета = \фракция{\текст{длина противоположной стороны}}{\текст{длина соседней стороны}}[/латекс]
- Стратегия решения проблем для приложений тригонометрии
- Прочитайте задачу и убедитесь, что все слова и идеи понятны.
- Прочитайте задачу и убедитесь, что все слова и идеи понятны.
