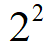Вычислить квадратный корень из числа: примеры, расчеты, калькулятор

Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
- найти квадратные или кубические корни из заданных чисел;
- выполнить математическое действие с дробными степенями.
Как вычислять квадратный корень вручную —методом подбора находить подходящие значения. Рассмотрим, как это делать.
Что такое квадратный корень
Корень n степени натурального числа a — число, n степень которого равна a (подкоренное число). Обозначается корень символом √. Его называют радикалом.
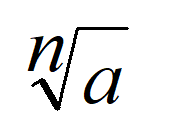
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.
Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
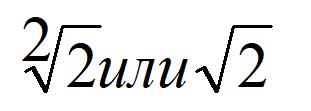
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
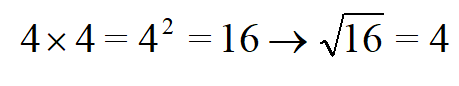
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
Например:
25, 36, 49 — квадратные числа, поскольку:
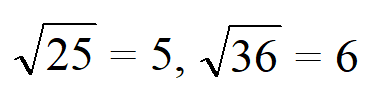
Получается, что квадратные множители — множители, которые являются квадратными числами.
Возьмем 784 и извлечем из него корень.
| Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. | 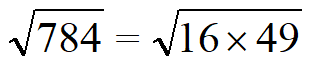 |
| Применим правило
Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ. | 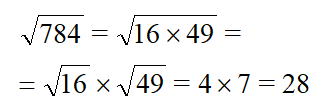 Ответ. |
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
| Раскладываем число 252 на квадратный и обычный множитель. | 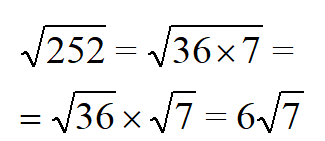 |
| Оцениваем значение корня. Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. | Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4.
Значит
|
| Оцениваем значение | Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76~7. |
| Вычисляем корень | 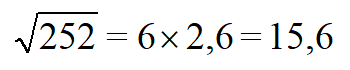 |
Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
| Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. | 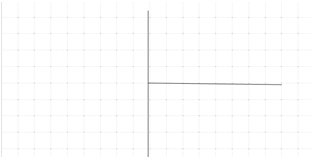 |
| Разбейте подкоренное число на пары чисел. Десятичные дроби делят так: — целую часть справа налево; — число после запятой слева направо. | Пример: 3459842,825694 → 3 45 98 42, 82 56 94 795,28 → 7 95, 28 Допускается, что вначале остается непарное число. |
| Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа. У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 = | 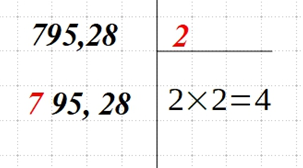 |
| Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_. Примечание: числа должны быть одинаковыми. | 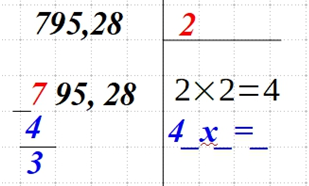 |
| Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева. В нашем случае это 8. | 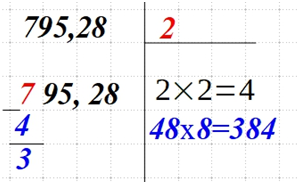 |
| Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева. | 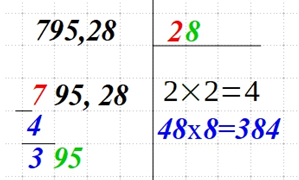 |
| Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками. | 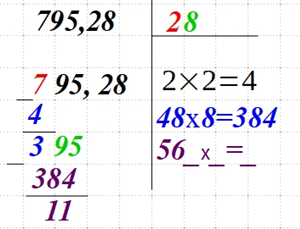 |
| Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева. | 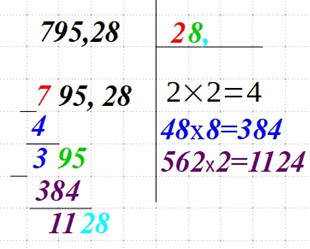 |
| Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. | 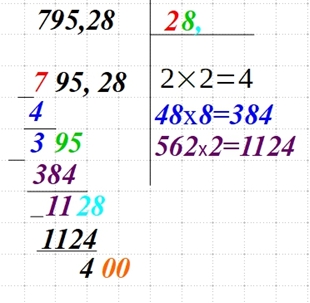 |
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
Алгоритм действий
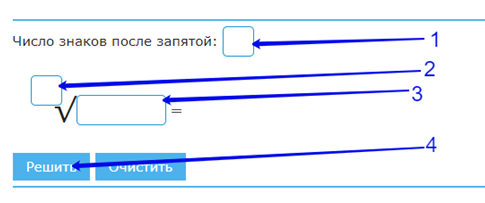
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
4. Нажмите кнопку «Решить».
Вычисление самых сложных математических действий с онлайн калькулятором станет простым! Экономьте время и проводите расчеты с CALCON.RU.

Решение корней в онлайн калькуляторе
Решение корней — одна из многих функций, которой обладает бесплатный калькулятор, размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени калькулятор онлайн посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице кнопки калькулятора онлайн.

Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.

Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).

Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).

Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Выполняя извлечение корня степени, следует помнить, что по свойству корней степень самого корня и степень под корнем по возможности сокращаются на наибольший общий делитель (НОД). Кстати, функционал калькулятора включает также нахождение НОД, подробнее на странице дополнительные функции.
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени:
Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>
Решение корней в онлайн калькуляторе was last modified: 3 марта, 2016 by Admin
Калькуляторы | umath.ru
Популярные
График функцииВычисление логарифма числа
Упрощение выражений
Сокращение дробей
Разложение числа на простые множители
Вычисление функции Эйлера
График функции
Калькулятор процентов
Нахождение точек локального экстремума функции
Нахождение максимума и минимума функции
Пределы, производные, интегралы
Вычисление предела последовательности
Вычисление предела функции
Вычисление производной
Разложение функции в ряд Тейлора, Маклорена
Вычисление неопределённого интеграла
Вычисление определённого интеграла
Дроби
Сокращение арифметических дробей
Приведение дробей к общему знаменателю
Операции с арифметическими дробями
Упрощение алгебраических дробей
Системы счисления
Перевод целых чисел из одной системы счисления в другую
Перевод дробных чисел из одной системы счисления в другую
Теория чисел
Разложение числа на простые множители
Нахождение наибольшего общего делителя
Нахождение наименьшего общего кратного
Вычисление функции Эйлера
Уравнения
Решение квадратного уравнения
Решение кубического уравнения
Упрощение математических выражений
Нахождение неизвестного члена пропорции
Матрицы
Сложение, вычитание матриц
Умножение матриц
Нахождение определителя матрицы
Вычисление обратной матрицы
Возведение матрицы в степень
Корни, степени, логарифмы
Вычисление корня из числа
Возведение числа в степень
Вычисление логарифма числа
Комбинаторика и теория вероятностей
Вычисление факториала числа
Вычисление числа размещений
Вычисление числа сочетаний
Статистика
Вычисление медианы ряда чисел
Вычисление среднего арифметического и среднего геометрического чисел
Вычисление моды и размаха ряда чисел
Геометрия
Вычисление площади треугольника
Нахождение точки пересечения двух прямых
Уравнение прямой на плоскости по двум точкам
Уравнение прямой в пространстве по двум точкам
Тригонометрия
Вычисление синуса, косинуса, тангенса и котангенса
Калькулятор корней онлайн — особенности извлечения корней с подробным объяснением
Калькулятор
Заполните поля для вычисления корня из числа
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни. Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9. Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.
Внесение под знак корня
При решении задач и примеров возникает необходимость вносить под корень множитель. Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 22х3 и 32х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные. Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто.
Калькулятор корня
Калькулятор квадратного корня
Калькулятор кубического корня
Калькулятор общего корня
Калькулятор связанных показателей | Научный калькулятор | Калькулятор журнала
В математике общий корень или корень n th числа a — это другое число b , которое при умножении на себя n раз равно a . В формате уравнения:
n √a = b
б н = а
Оценка корня
Некоторые общие корни включают квадратный корень, где n = 2, и кубический корень, где n = 3.Вычисление квадратных корней и корней n th довольно сложно. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, который не требует глубокого понимания более сложных математических концепций. Для расчета √a:
- Оценить число б
- Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение b и c и использование результата в качестве нового предположения
- Повторите шаг два
| EX: | Найти √27 до 3 знаков после запятой |
| Предположение: 5.125 27 ÷ 5,125 = 5,268 (5,125 + 5,268) / 2 = 5,197 27 ÷ 5,197 = 5,195 (5,195 + 5,197) / 2 = 5,196 27 ÷ 5,196 = 5,196 |
Оценка n th Root
Вычисление корней n th можно выполнить с помощью аналогичного метода, но с изменениями для работы с n .Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n th , даже если использовать калькулятор для промежуточных шагов, значительно утомительнее. Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
- Оценить число б
- Разделите a на b n-1 .Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение: [b × (n-1) + c] / n
- Повторите шаг два
| EX: | Найти 8 √15 до трех знаков после запятой |
| Предположение: 1.432 15 ÷ 1,4327 = 1,405 (1,432 × 7 + 1,405) / 8 = 1,388 15 ÷ 1,388 7 = 1,403 (1,403 × 7 + 1.388) / 8 = 1,402 |
Тогда должно быть ясно, что дальнейшие вычисления приведут к числу, которое округлится до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой.
,Калькулятор квадратного корняИспользование калькулятора
Воспользуйтесь этим калькулятором, чтобы найти главный квадратный корень и корни действительных чисел. Входные данные для подкоренного выражения x могут быть положительными или отрицательными действительными числами. Ответ также скажет вам, вошли ли вы в идеальный квадрат.
Ответ покажет вам комплексные или мнимые решения для квадратных корней из отрицательных действительных чисел. См. Также Упростите калькулятор радикальных выражений, чтобы упростить радикалы вместо поиска дробных (десятичных) ответов.
квадратного корня, четное и нечетное:
Для любого положительного действительного числа существует 2 возможных корня. Положительный корень и отрицательный корень. Учитывая число x , квадратный корень из x — это число a , такое что a 2 = x . Квадратные корни — это особая форма нашего общего калькулятор корней.
«Обратите внимание, что любое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный.Например, квадратные корни из 9 равны -3 и +3, поскольку (-3) 2 = (+3) 2 = 9. Любое неотрицательное действительное число. x имеет уникальный неотрицательный квадратный корень r; это называется главным квадратным корнем ………. Например, главный квадратный корень из 9 равен sqrt (9) = +3, а другой квадратный корень из 9 равен -sqrt (9) = — 3. В общепринятом использовании, если не указано иное, «квадратный корень обычно означает главный квадратный корень» [1].
Калькулятор идеального квадрата
Этот калькулятор также скажет вам, является ли введенное вами число идеальным квадратом или нет.Идеальный квадрат — это число x , где квадратный корень из x — это число a , такое что a 2 = x , а a — целое число. Например, 4, 9 и 16 являются полными квадратами, поскольку их квадратные корни 2, 3 и 4, соответственно, являются целыми числами.
Пример квадратного корня:
- Второй корень из 81, или 81 корень 2, или квадратный корень из 81 записывается как \ (\ sqrt [2] {81} = \ sqrt [] {81} = \ pm 9 \).
- Второй корень из 25 или 25 корень 2, или квадратный корень из 25 записывается как \ (\ sqrt [2] {25} = \ sqrt [] {25} = \ pm 5 \).
- Второй корень из 100, или 100 в корне 2, или квадратный корень из 100 записывается как \ (\ sqrt [2] {100} = \ sqrt [] {100} = \ pm 10 \).
- Второй корень из 10, или 10, радикал 2, или квадратный корень из 10 записывается как \ (\ sqrt [2] {10} = \ sqrt [] {10} = \ pm 3.162278 \).
Для вычисления дробных показателей используйте наш калькулятор для Дробные экспоненты.
Список литературы
[1] Вайсштейн, Эрик В. «Квадратный корень». Из MathWorld — Интернет-ресурс Wolfram. Квадратный корень
Дополнительное чтение квадратных корней:
Math Forum 0 — это идеальный квадрат?
В математике — это весело: корень квадратный
,Онлайн-калькулятор: вычисление выражений
В алгебраическом выражении буквы, представляющие переменные, могут заменять числа. Когда мы подставляем конкретное значение для каждой переменной, а затем выполняем операции, мы оцениваем выражение.
Итак, этот калькулятор вычисляет выражения за вас. Он заменяет каждую букву в выражении присвоенным значением, а затем выполняет операции в выражении, используя правильный порядок операций.
Будьте осторожны с именами переменных и их использованием в выражениях, если вы сделаете ошибку, вы, скорее всего, получите неверные результаты.

Вычисление выражений
добавить import_export mode_edit deleteПеременные
Элементов на странице: chevron_left chevron_rightImport dataImport error
«Используется один из следующих полей данных: , точка с запятой (;) или запятая (,) «Пример: Lorem ipsum; Lorem ipsum
Загрузить данные из файла .csv.
Импорт назад Отмена Точность вычисленияЦифры после десятичной точки: 2
Выражение после замен
сохранить Сохранить расширение Виджет
После замен выражение вычисляется с помощью математического калькулятора. — мощность
Функции:
sqrt — корень квадратный
корень__ n — корень _n_ -й степени, например root3 (x) — кубический корень
exp — экспоненциальная функция
lb — двоичный логарифм (основание 2)
lg — десятичный логарифм (основание 10)
ln — натуральный логарифм (основание e)
log b — логарифм по основанию b , например log7 (x) — логарифм по основанию 7
sin — синус
cos — косинус
tan — тангенс
cot — котангенс
sec — secant
cosec — косеканс
arcsin — arcsine
arccos — arccosine
arctan — arctangent
arccotan — arccotangent
arcsec — arcsecant
arccosec — arccosecant
versin — hansinevers
— покрывает
versin — hansinevers
— покрывает
exsec — exsecant
excsc — excosecant
sh — гиперболический синус
ch — гиперболический косинус
tanh — гиперболический тангенс
coth — гиперболический котангенс
coth — гиперболический котангенс
sech 47__
sech 47__ — гиперболический косеканс
Онлайн калькулятор: Метод секанса
Краткое описание метода секанса можно найти под калькулятором

Метод секанса
Точность вычисленияЦифры после десятичной точки: 4
сохранить Сохранить расширение Виджет
Метод секущей
Метод секущих можно рассматривать как конечно-разностную аппроксимацию метода Ньютона. где производная заменена секущей линией.
Мы используем корень секущей линии (значение x такое, что y = 0) в качестве приближения корня для функции f.
Предположим, у нас есть начальные значения x0 и x1 со значениями функций f (x0) и f (x1).
Секущая имеет уравнение
Корень секущей (где у = 0), следовательно,
Это рекуррентное соотношение для метода секущих. Графическую интерпретацию можно увидеть ниже.
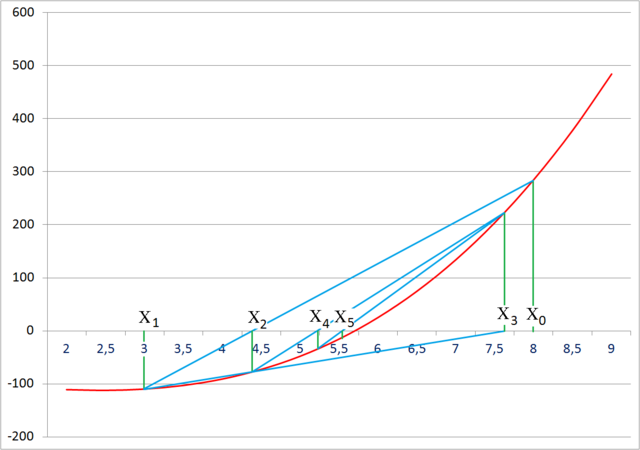
Источник
Метод секущей не требует, чтобы корень оставался заключенным в квадратные скобки, как это делает метод деления пополам (см. Ниже), и, следовательно, он не всегда сходится.
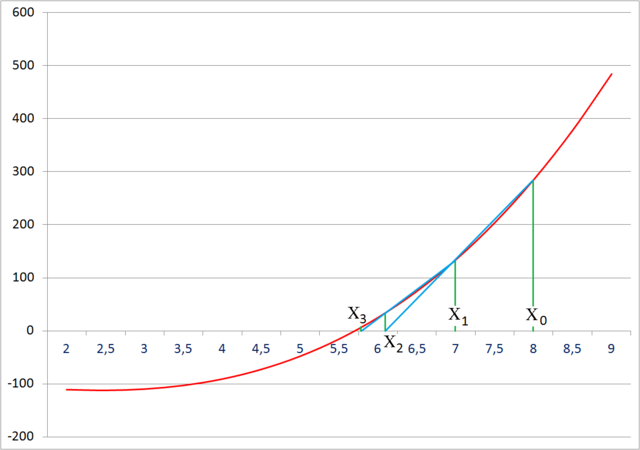
Источник
Как видно из рекуррентного соотношения, метод секущей требует двух начальных значений, x0 и x1, которые в идеале следует выбирать так, чтобы они лежали близко к корню.
Условие допуска может быть либо:
— значение функции меньше ε.
— разница между двумя последовательными хk меньше ε.
Подробнее: Метод секанта
.
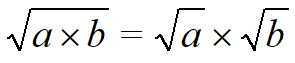
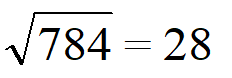
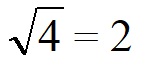
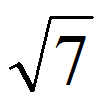 между 2 и 4.
между 2 и 4.