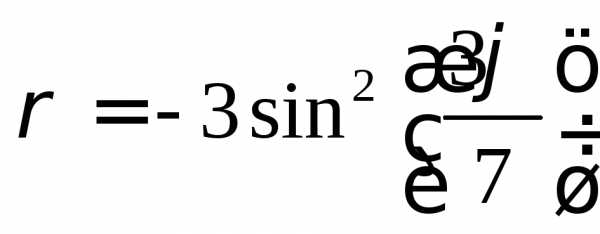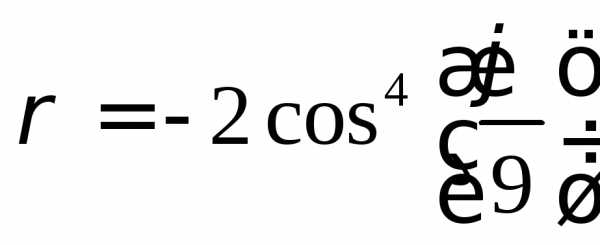ПОСТРОЕНИЕ ФУНКЦИЙ НА ПЛОСКОСТИ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
ПОСТРОЕНИЕ ФУНКЦИЙ НА ПЛОСКОСТИ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Билялова Виктория Мухамедовна
студент, Волжский политехнический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет», РФ, г. Волгоград
Е -mail:
Матвеева Татьяна Александровна
доцент, канд. физ.-мат. наук, Волжский политехнический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет», РФ, г. Волгоград
Е-mail:
Агишева Джамиля Калимулловна
старший преподаватель, Волжский политехнический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет», РФ, г. Волгоград
CREATION OF FUNCTIONS ON THE PLANE, SET PARAMETRICALLY
Bilyalova Viktoriya
student, Volzhsky Politechnical Institute (branch) Volgograd Technical University, Russia, Volgograd
Matveeva Tatyana
associate professor, candidate of physics and mathematics, Volzhsky Politechnical Institute (branch) Volgograd Technical University, Russia, Volgograd
Agisheva Dzhamilya
senior teacher, Volzhsky Politechnical Institute (branch) Volgograd Technical University, Russia, Volgograd
АННОТАЦИЯ
В настоящее время существование большого числа математических пакетов явно упрощают жизнь человека: построение графиков и вычисление расчетов делаются компьютером автоматически. Однако математические пакеты не дают полного истолкования своих действий. Так, мы видим просто построенный график. Но что же скрывается за ним? Почему он выглядит именно так? Ответы на эти вопросы даёт знание дифференциального исчисления. В статье рассматривается исследование и построение функций на плоскости, заданных параметрически.
ABSTRACT
Now existence of a large number of mathematical packages obviously simplify human life: computer performs plotting and implementation of calculations automatically. However, mathematical packages don’t give full interpretation of the actions. So, we see simply constructed graph. But what is behind it? Why does it look quite so? Answers to these questions are given by knowledge of differential calculus. In the article research and creation of the functions on the plane set parametrically are considered.
Ключевые слова: параметрические функция; дифференциальное исчисление.
Keywords: parametrical function; differential calculus.
Довольно часто мы сталкиваемся с тем, что привычные для нас кривые не считаются графиками функций заданных уравнением , так как в декартовой системе координат некоторым абсциссам соответствуют несколько ординат этой кривой. Так, например, обычная окружность не является графиком функции. С точки зрения графического представления у явного задания функции имеются весьма существенные недостатки: каждому значению х соответствует только одно значение у; кривая не может быть замкнутой. В результате явный способ представления функции нельзя применять там, где требуется описание произвольных кривых, которые размещаются в произвольных местах на плоскости.
Альтернативным способом является определение кривой как параметрической функции. У этого способа задания кривой обе координаты имеют равные права. Такая зависимость в общем случае получает вид , где и — функции параметра t.
Сегодня, для решения инженерных задач, построения графиков, проведения математических экспериментов и т.п. существует большое множество математических пакетов, таких как Mathcad, Mathematica, Maple. Система Mathcad — это одна из популярных систем компьютерной математики, которая предназначена для автоматизации решения математических задач в массовом применении в различных областях техники, науки и образования. Выбор системы Mathcad, обусловлен ее распространенностью и возможностью описать математические алгоритмы в естественной математической форме с применением общепринятой символики для математических знаков.
Однако любой математический пакет не предусматривает полного анализа графика, а только предоставляет построенный график, значения функции от разных переменных, оставляя скрытыми от нас вычисления асимптот, точек экстремума, перегиба и т.п.
Для примера построим график функции, заданной в параметрическом виде в среде Mathcad (Рис. 1).
Рисунок 1 График параметрической функции, построенный в математическом пакете Mathcad
По получившемуся графику функции можно предположить, что он имеет горизонтальную, вертикальную и наклонную асимптоты, также наблюдаем точки экстремума и точку возврата, но каким значения параметра t это соответствует «скрыто».
Рассмотрим полное исследование функции с помощью дифференциального исчисления и построение графика функции заданной параметрически:
Область определения: .
Найдем асимптоты данного графика функции. Они играют важную роль при анализе и построении графиков. Различают вертикальные, горизонтальные и наклонные асимптоты.
Вертикальные асимптоты определяются точками разрыва функции . В нашем случае функция имеет точку разрыва , также она является точкой поворота. Тогда , т. е. получаем, что – вертикальная асимптота.
Горизонтальная асимптота в свою очередь определяются точками разрыва функции . Так как имеет разрыв в точке , то получаем .
Таким образом, является горизонтальной асимптотой.
Найдем наклонную асимптоту вида , где
,
.
Подставляя полученные значения в уравнение наклонной асимптоты, имеем
Найдем точки пересечения графика функции с осями координат:
а) с осью Ox: — не имеет корней;
б) с осью Oy: не имеет корней. Таким образом, график функции не пересекает оси координат.
Вычислим первую производную, определим промежутки монотонности и экстремумы функции.
.
При имеем – точку минимума.
При имеем – вертикальную асимптоту.
Вычислим вторую производную, определим промежутки выпуклости-вогнутости графика функции и точки перегиба.
.
При имеем при имеем точку перегиба.
По результатам исследования, заполним таблицу 1.
Таблица 1.
Сводная таблица исследования графика функции
Сначала строим асимптоты, наносим точки локальных максимумов и минимумов функции, точки перегиба и промежуточные точки, опираясь на сводную таблицу исследования функции (рис. 2).
Рисунок 2. График функции
Таким образом, для построения графиков параметрически заданных функций необходимо знание дифференциального исчисления. Математические пакеты удобны только для графической визуализации, но не подходят при поиске значений параметра t для точек экстремума, перегиба и т. п.
Отметим особенности параметрических кривых: обе координаты вычисляются как функции вспомогательного параметра, т. е. они равноправны; кривые имеют более разнообразные формы, чем это позволяют явные уравнения; параметрическое представление важно для пространственных кривых; применение параметрических функций позволяет применять более сложные функции при аппроксимации физических процессов.
Список литературы:
1.Владимирский Б.М. Математика. Общий курс / Б.М. Владимирский. СПб: Лань, 2006. — 960 с.: ил.
2.Письменный Д.Т. Конспект лекций по высшей математике: полный курс 6-е изд., испр. / Д.Т. Письменный. М.: Айрис-пресс, 2007. — 608 с.
3.Матвеева Т.А. Математический анализ в таблицах. Часть 1 [Электронный ресурс]: учебное пособие/Т.А. Матвеева, С.А. Зотова, Д.К. Агишева, В.Б. Светличная //Сборник «Учебные пособия». Серия «Технические дисциплины». Выпуск 1. Волжский: ВПИ (филиал) ВолгГТУ, 2013 г.
4.Мустафина Д.А. Дифференциальное исчисление функции одной и нескольких переменных с приложениями: учеб. пособие Д.А. Мустафина, И.В. Ребро, С.Ю. Кузьмин, Н.Н. Короткова. ВПИ (филиал) ВолгГТУ. Волгоград, 2009. — 118 с.
sibac.info
13. Общая схема исследования функций и построения графиков.
13.1 Общая схема исследования и построения графика функции заданной явно.
Общее исследование функции следует проводить по приведенной ниже схеме:1.Определить область существования функции, область непрерывности, точки разрыва.
2. Найти асимптоты функции.
3. Выяснить вопрос о периодичности.
4. Выяснить вопрос о четности или нечетности.
В случае, если функция окажется четной или нечетнойдостаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
5.Найти точки пересечения графика функции с осями координат:
с осью абсцисс — точки , где-решение уравнения;
с осью ординат- точки , где.
7.Найти интервалы выпуклости и вогнутости, точки перегиба.
8. Составить таблицу
Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | Возрастает или убывает, Выпукла или вогнута | ||||
знак | знак | знак | знак | ||||
знак | знак | знак | знак |
Точки -все найденные в п.6-7 точки, в которых производные обращаются в нуль или не существуют.
9.На основании проведенного исследования построить график заданной функции.
Пример 26
Провести полное исследование и построить график функции .
Решение:
Область определения функции
Точка разрыва функции , функция непрерывна наи.
2. Асимптоты.
Вертикальная асимптота .
Поведение функции в окрестности :
Найдем наклонную асимптоту:
Прямая является наклонной асимптотой заданной кривой.
3. Функция не является периодической.
4. Четность функции
Условие четности или нечетности не выполнено. Заданная функция –функция общего вида.
5. Точки пересечения с осями.
График функции проходит через начало координат.
6. Промежутки монотонности, локальные экстремумы.
Найдем критические точки:
Исследуем знак производной методом интервалов:
знак
Найдем значения функции в критических точках:
7.Промежутки выпуклости и вогнутости. Точки перегиба.
Найдем вторую производную.
Точки, в которых равна нулю или несуществует:
Исследуем знак второй производной методом интервалов:
8. Составляем таблицу.
0 | — | ||||||
+ | 0 | + | — | — | 0 | + | |
— | 0 | + | — | + | + | ||
перегиб | разрыв | Мин. |
13.2 Общая схема исследования и построения графика функции заданной параметрически.
Функция задана параметрически
1.Исследовать область изменения ипри изменении параметра.
2. Найти значения параметра , при которыхи.
3.а)Найти значения параметра , при котрых. Найти вертикальную асимптоту
б) Найти значения параметра , при котрых. Найти наклонную асимптоту
,
4. Вычисляем и.Находим все значения параметра, при которых хотя бы одна из полученных производных обращается в нуль или терпит разрыв. Найденные значения параметра будем называть критическими.По формуле (9) определяем знак производнойв каждом из полученных интервалов.
5. Вычисляем вторую производную по формуле (16) или (17). Определяем значения параметрапри которыхобращается в нуль или терпит разрыв. Определяем промежутки выпукдости вогнутости согласно (40) и (41).
6. Строим таблицу
Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
7. Строим график функции.
Пример 27
Построить кривую (декартов лист), заданную параметрическими уравненниями:
Решение:
1.Обе функции определены при .
При этом
2.при
при .
3.а) При
При этом
Таким образом, вертикальных асимптот график функции не имеет.
б) Найдем наклонную асимптоту:
Таким образом, график функции имеет наклонную асимптоту:
4. Найдем производные и.
Найдем критические значения параметра
При обе производные терпят разрыв.
Таким образом, получаем следующие критические значения параметра :
Найдем по формуле (9):
5. Найдем :
6. Строим таблицу
Область изм. | Область изм. | Область изм. | Знак | Знак | Знак | Знак | Знак | Поведение |
убывает, вогнута | ||||||||
убывает, вогнута | ||||||||
возрастает, вогнута | ||||||||
убывает, вогнута | ||||||||
возрастает, выгнута |
7. Строим график
Задания 11. Провести полное исследование и построить график функции:
1. | 2. | 3. |
4. | 5. | 6. |
7. | 8. | 9. |
10. | 11. | 12. |
studfiles.net
6. Построение графика функции, заданной параметрически.
В среде Mathcad можно также построить график функции, заданной параметрической зависимостью. Чтобы получить такой график нужно:
Задать область изменения переменной t;
Записать аналитические выражения для x(t) и y(t);
Создать поле двумерного графика и указать на оси абсцисс x(t), а на оси ординат — y(t). (См. пример 6 и рис.12).
Пример 6.
рис.12. График функции, заданной параметрически.
7. Построение графика по массиву данных.
Mathcad позволяет построить график не только по аналитическому выражению, но и по массиву данных. Этот массив должен представлять собой матрицу, содержащую два столбца (в первом – абсциссы, а во втором – ординаты). Количество строк этой матрицы равно количеству точек. (См. пример 7). Если вы хотите, чтобы точки на графике обозначались определенными символами и не соединялись линиями, внесите соответствующие изменения в диалоговое окно Formatting Currently Selected X-Y Plot Traces (см. п.2). Полученный график представлен на рис.10.
Пример 7.
р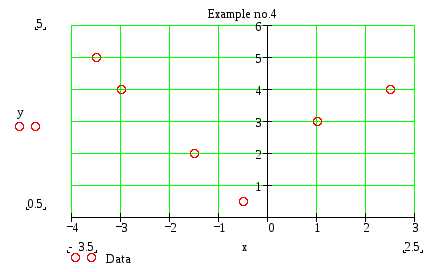 ис.13. График, построенный по матрице данных.
ис.13. График, построенный по матрице данных.
Рассмотрим еще один пример.
Пример 8.
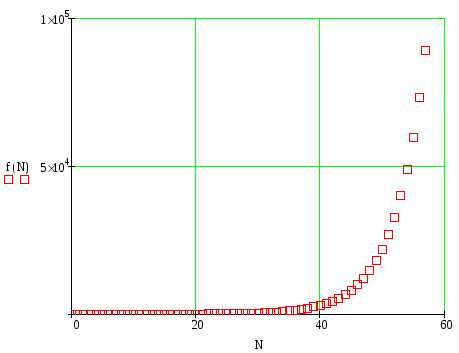
рис.14. График, построенный по массиву данных.
8. Увеличение фрагмента двумерного графика.
Вы можете увеличить интересующий вас фрагмент графического окна, с тем, чтобы более детально изучить поведение кривой на выбранном участке. Для этого сделайте следующее:
Активизируйте поле графика.
Вызовите команду Zoom одним из трех способов:
1) с помощью меню FormatGraphZoom;
2) щелкнув по кнопке “Zoom” из палитры “Graph”;
3) вызвав пункт Zoom из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.
После этого на экране появится диалоговое окно X-Y Zoom.
Выделите мышью тот фрагмент графика, который вы хотели бы увеличить.
Щелкните по кнопке (Zoom) в диалоговом окне X-Y Zoom.
После этого выбранный вами фрагмент будет увеличен до размеров исходного графика (временно). Щелкнув по кнопке (Unzoom) вы вернетесь к выбранному ранее масштабу. Если вы хотите, чтобы на графике остался только выбранный вами фрагмент, щелкните по кнопке “OK”, а кнопка “Cancel” отменяет выполненные ранее действия. Щелкнув по кнопке (Full View) вы выведете на экран всю область графика (т.е. в нашем примере – t от 0 до 10).
9. Считывание координат двумерного графика.
Вы можете узнать координаты любой точки кривой. Для этого:
Активизируйте поле графика.
Вызовите команду Trace одним из трех способов:
1) с помощью меню FormatGraphTrace;
2) щелкнув по кнопке “Trace” из палитры “Graph”;
3) вызвав пункт Trace из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.
После этого на экране появится диалоговое окно X-Y Trace.
Проведите мышью по той кривой в поле графика, координаты точек которой вы хотите узнать. После этого на графике появятся две пунктирные прямые, пересекающиеся на выбранной кривой.
Передвигая это перекрестье мышью или клавишами-стрелками, вы увидите в полях “X-Value”, “Y—Value” или “Y2—Value” координаты точки, на которой оно находится.
Щелкнув по кнопке “Copy X”, “Copy Y” или “Copy Y2” вы скопируете соответствующие координаты в буфер обмена.
Замечание. Если индикатор “Track data points” выключен, вы сможете узнать координаты любой точки поля графика, а не только точек, принадлежащих кривым.
studfiles.net
6. Построение графика функции, заданной параметрически.
В среде Mathcad можно также построить график функции, заданной параметрической зависимостью. Чтобы получить такой график нужно:
Задать область изменения переменной t;
Записать аналитические выражения для x(t) и y(t);
Создать поле двумерного графика и указать на оси абсцисс x(t), а на оси ординат — y(t). (См. пример 6 и рис.12).
Пример 6.
рис.12. График функции, заданной параметрически.
7. Построение графика по массиву данных.
Mathcad позволяет построить график не только по аналитическому выражению, но и по массиву данных. Этот массив должен представлять собой матрицу, содержащую два столбца (в первом – абсциссы, а во втором – ординаты). Количество строк этой матрицы равно количеству точек. (См. пример 7). Если вы хотите, чтобы точки на графике обозначались определенными символами и не соединялись линиями, внесите соответствующие изменения в диалоговое окно Formatting Currently Selected X-Y Plot Traces (см. п.2). Полученный график представлен на рис.10.
Пример 7.
р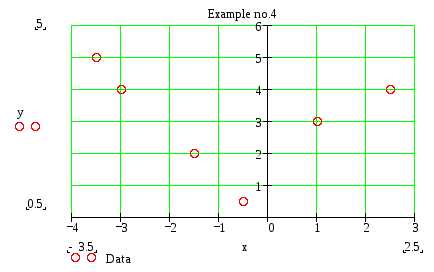 ис.13. График, построенный по матрице данных.
ис.13. График, построенный по матрице данных.
Рассмотрим еще один пример.
Пример 8.
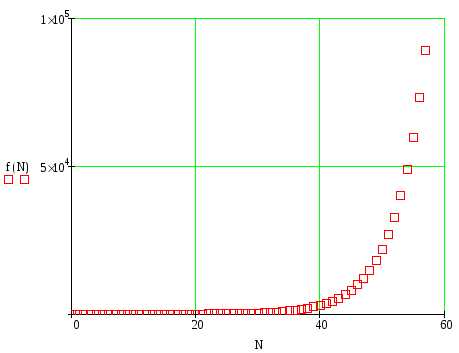
рис.14. График, построенный по массиву данных.
8. Увеличение фрагмента двумерного графика.
Вы можете увеличить интересующий вас фрагмент графического окна, с тем, чтобы более детально изучить поведение кривой на выбранном участке. Для этого сделайте следующее:
Активизируйте поле графика.
Вызовите команду Zoom одним из трех способов:
1) с помощью меню FormatGraphZoom;
2) щелкнув по кнопке “Zoom” из палитры “Graph”;
3) вызвав пункт Zoom из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.
После этого на экране появится диалоговое окно X-Y Zoom.
Выделите мышью тот фрагмент графика, который вы хотели бы увеличить.
Щелкните по кнопке (Zoom) в диалоговом окне X-Y Zoom.
После этого выбранный вами фрагмент будет увеличен до размеров исходного графика (временно). Щелкнув по кнопке (Unzoom) вы вернетесь к выбранному ранее масштабу. Если вы хотите, чтобы на графике остался только выбранный вами фрагмент, щелкните по кнопке “OK”, а кнопка “Cancel” отменяет выполненные ранее действия. Щелкнув по кнопке (Full View) вы выведете на экран всю область графика (т.е. в нашем примере – t от 0 до 10).
9. Считывание координат двумерного графика.
Вы можете узнать координаты любой точки кривой. Для этого:
Активизируйте поле графика.
Вызовите команду Trace одним из трех способов:
1) с помощью меню FormatGraphTrace;
2) щелкнув по кнопке “Trace” из палитры “Graph”;
3) вызвав пункт Trace из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.
После этого на экране появится диалоговое окно X-Y Trace.
Проведите мышью по той кривой в поле графика, координаты точек которой вы хотите узнать. После этого на графике появятся две пунктирные прямые, пересекающиеся на выбранной кривой.
Передвигая это перекрестье мышью или клавишами-стрелками, вы увидите в полях “X-Value”, “Y—Value” или “Y2—Value” координаты точки, на которой оно находится.
Щелкнув по кнопке “Copy X”, “Copy Y” или “Copy Y2” вы скопируете соответствующие координаты в буфер обмена.
Замечание. Если индикатор “Track data points” выключен, вы сможете узнать координаты любой точки поля графика, а не только точек, принадлежащих кривым.
studfiles.net
Построение графиков функций параметрически заданных
22 апр 2011. Первая задача. Найдите синус косинус и тангенс угла при вершине равнобедренного треугольника, периметр которого равен 36 см, а основание — 10 см. Вторая задача. Катет прямоугольного треугольника равен 14 см, а косинус противолежащего угла равен 24/25. Найдите другие стороны.
Построение графиков функций онлайн
Сервис онлайн построения графиков
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Построение графиков функций параметрически заданных
Построение графиков функций онлайн
Сервис онлайн построения графиков
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Построение графиков функций параметрически заданных
6 лучших сервисов для построения графиков функций онлайн
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Kontrolnaya-Rabota. ru
Сервис kontrolnaya-rabota. ru — настоящая находка для нерадивых учащихся. Построение графиков онлайн на этом сайте — целый большой раздел, где рассматривается:
- Построение двухмерного графика функции в декартовых и полярных координатах. Построение графика, заданного параметрически. Построение 3D графиков (поверхностей), заданных уравнением. Построение гистограмм и графиков и по точкам. Построение графиков неявно заданных функций.
Пользователю достаточно ввести в онлайн-программу данные из условия задачи и кликнуть кнопку «Построить график».
Запутаться сложно, так как каждая страница этого раздела сопровождается пояснениями и примерами. Там же даны подсказки, какие символы и сокращения следует использовать при вводе выражений.
При построении 2D-графика в декартовых координатах приводится подробный результат исследования функции, чего не встретишь практически нигде.
Достоинства сервиса kontrolnaya-rabota. ru — возможность пользоваться им без ограничений, выдача результатов с ходом решения, быстрые и точные ответы, наличие других онлайн-калькуляторов для вычисления уравнений, интегралов, неравенств и прочего. А недостаток — в том, что не все чертежи можно масштабировать. Это создает определенные неудобства при копировании.
Веб-сервис Umath. ru — не только набор онлайн-калькуляторов, но и неплохой справочник по математике. Позволяет строить 3 разновидности графиков функций:
- Заданных уравнением. Заданных параметрически. В полярной системе координат.
В отличие от предыдущего, этот веб-сайт дает возможность размещать несколько графиков на одной плоскости (они будут нарисованы разным цветом). Также он позволяет изменять масштаб и смещать положение центра координатного пространства (кнопки управления находятся слева от графика, но можно пользоваться и мышью).
Готовый результат можно скачать на компьютер в виде картинки.
Достоинства Umath. ru — простота применения (на станице есть пояснения, списки функций и констант), масштабирование, возможность оставлять комментарии, пользоваться справочником и другими математическими калькуляторами. Недостаток — ограниченный функционал (к сожалению, нет возможности строить трехмерные графики) и иногда проскакивающие ошибки. Но, надеемся, это временно, так как сервис активно развивается.
Graph. Res
poiskvstavropole.ru
Построение поверхности, заданной параметрически
При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. При этом все три координаты задаются как функции от двух параметров u и v – X(u,v), Y(u,v), Z(u,v). Поверхности задаются значениями координат всех точек. При этом в шаблоне графики указываются три матрицы, хранящие массивы этих координат, X, Y Z.
Сначала необходимо задать векторы значений параметров и
Определить матрицы координат x(u,v), y(u,v) и y(u,v). Ввести как индексные переменные.
Вызвать график поверхности (Graph -> Surface Plot ). В шаблон занести имена матриц. Чтобы получилась фигура вращения, имена вводятся в скобках.
Настроить график.
Пример 3.11
Пример 3.11
На pис.3.28 показано построение объемной фигуры по точкам. (50 точек). Фигура задана параметрически, параметры – углы и. Координаты x,y,z вводятся как индексированные переменные, индексы – ранжированные переменные.
, ,
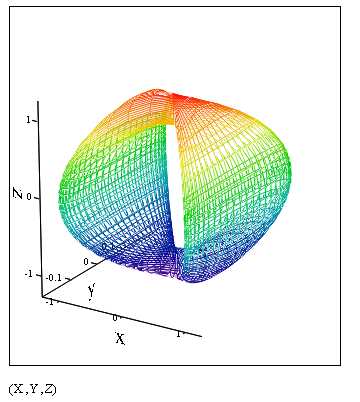
Рис. 3.28. Листинг примера. 3.11. Поверхность задана параметрически
Построение поверхности, заданной в векторной параметрической форме
Построение поверхности, заданной в векторной параметрической форме
Поверхность может быть задана в векторной форме. В этом случае функция вводится в виде матрицы, элементы которой – функции параметров, как и сама поверхность. На pис.3.27 показано построение объемной фигуры примера 3.11, заданной в виде матрицы от параметров — углов и. Количество линий сетки можно изменить в окне форматирования3-D Plot Format, вкладка QuickPlot Data .
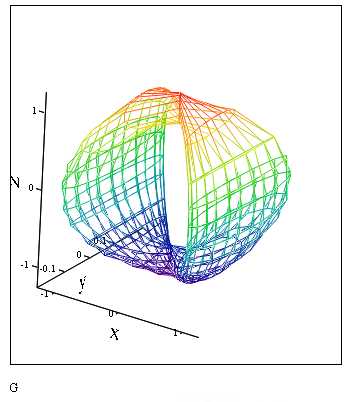
Рис. 3.29. Листинг примера. 3.11. Функция задана в векторной параметрической форме
3D точечный график
Трехмерный график можно представить в виде пространственной кривой. Пространственные кривые задаются, как правило, параметрически, и параметр является непрерывной действительной величиной. Рассмотрим два способа построения.
Пример 3.12
Построить пространственную кривую, у которой координаты определены следующим образом: ,,.
1 способ. Кривая в пространстве задается аналогично параметрическому заданию поверхности (пример 3.11).
Задать значения параметра t в виде ранжированной переменной, для t выбирается номер точки (0-100).
Определить координаты x, y, z как индексированные переменные параметра t.
Вызвать командой с панели Графика Graph / 3D Scatter Plot (график 3D точечный), в шаблон занести имена матриц в скобках (Рис.3.28).
Настроить график в окне форматирования.
На графике показаны максимальные минимальные значения
, ,
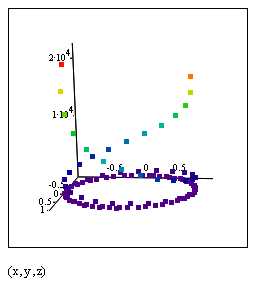
Рис. 3.30. Листинг примера 3.12. Параметрическое задание кривой
2 способ. (Рис.3.31). Векторная форма. Функция задается в виде матрицы-вектора. Для построения графика используется функция CreateSpace()
CreateSpace (R , t0, t1, tgrid, fmap): встроенная функция , создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами ,
t0 и t1 – диапазон изменения параметровй, tgrid – размер сетки переменной, fmap – функция отображения аналогично функции CreateMesh() (необязательный параметр). Аргумент t выбирается из указанного интервала: t0=0 t1=10, сетка tgrid=100 точек. Создает сетку точек на кривой.
, ,
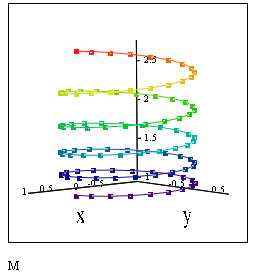
Рис. 3.31. Листинг примера 3.12. Векторное задание кривой. Использование CreateSpace()
studfiles.net
Лабораторная работа №3 Построение графиков функций в MathCad
Цель работы
Овладеть навыками построения графиков в MathCAD.
Задачи:
— умение применять различные способы построения двумерных графиков в Mathcad;
Порядок выполнения
Задание №1: Построить график функции заданный в виде:
а) таблицы:
x | -3.5 | -3 | -1.7 | 0 | 1.1 | 3.7 |
y | 11.21 | 9.99 | 3.6 | 0.65 | -5 | -8.7 |
б) функции y=f(x),
где 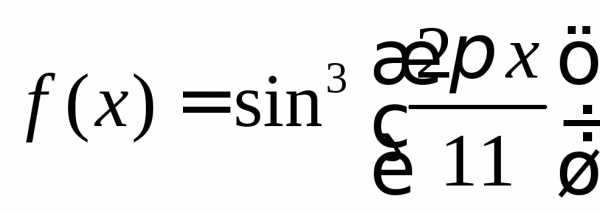 ,
на отрезке [
,
на отрезке [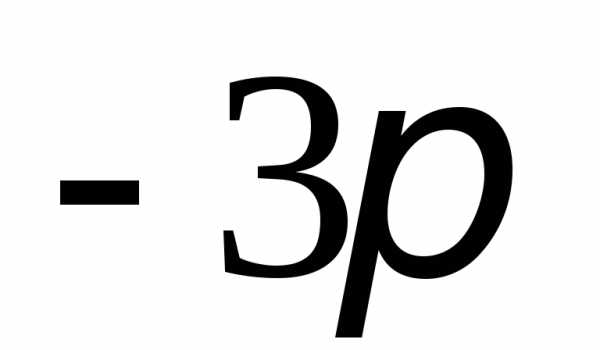 ;
; ]
]
а). 1. Сформировать векторы данных X и Y.
2. Выполнить команды: Добавить – Графики – X—Y график.( рис.10).
3. Ввести исходные данные т.е. в поле оси абсцисс ввести x, а в поле оси ординат y.
4. Нажать Enter (рис.10).
Рис 10. Операции над числами
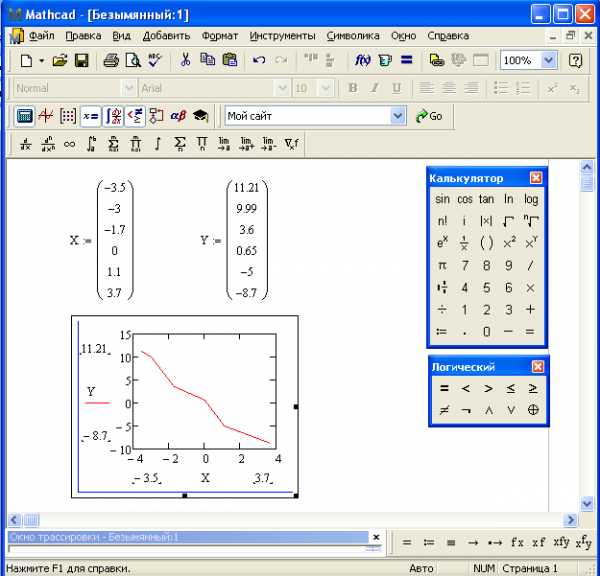
Рис 11. Построение графика
б). 1. Выбрать команды: Добавить – Графики – X—Y график..
2. на оси абсцисс
указать интервал от 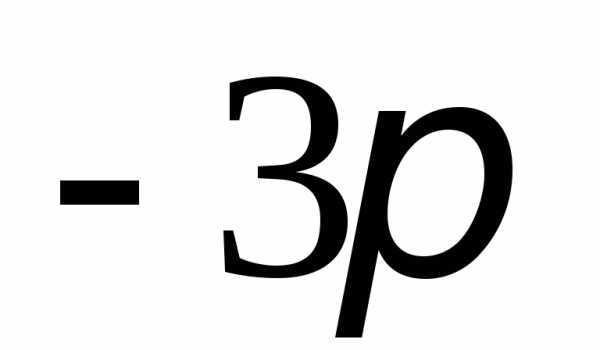 до
до ,
на оси ординат задать функцию.
,
на оси ординат задать функцию.
3. Для ввода 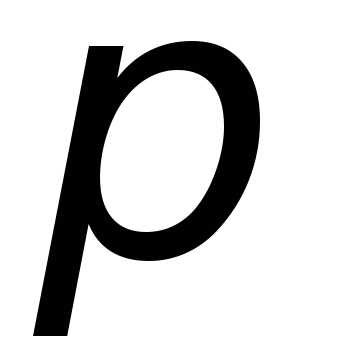 ,
необходимо выбрать:Вид
– панели инструментов – греческая.
,
необходимо выбрать:Вид
– панели инструментов – греческая.
4. Нажать Enter (рис.12).
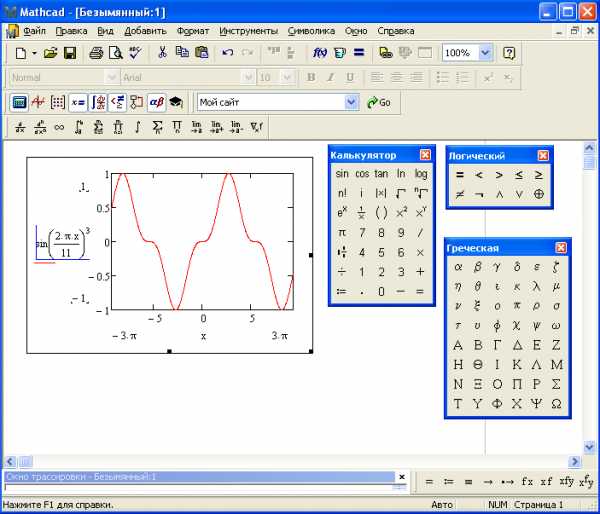
Рис 12. Построение графика
Самостоятельно:
Построить графики функций, заданные в виде таблицы и аналитически:
1.
X | -7.7 | -5 | -3.4 | -2.5 | -1 | 0.8 | 1.3 | 2 | 5 |
Y | 0 | 11 | -5.55 | -6.6 | 6 | 23 | 0 | -7 | -9 |
2.
X | 12 | 11.54 | 8 | 3.43 | 2.54 | 1 | 0.99 | 2.55 | 4.54 |
Y | 11 | 4.876 | 2 | 1.51 | 0 | -3.43 | -5 | -7.76 | -10 |
y=f(x), где
 ,
на отрезке [
,
на отрезке [ ;
; ]
]y=f(x), где
 ,
на отрезке [
,
на отрезке [ ;
; ].
].y=f(x), где
 ,
на отрезке [
,
на отрезке [ ;
; ].
].Построить на одном графике следующие функции:
 ,
, ,
, ,
(рис. 13). Функции перечислить через
запятую.
,
(рис. 13). Функции перечислить через
запятую.
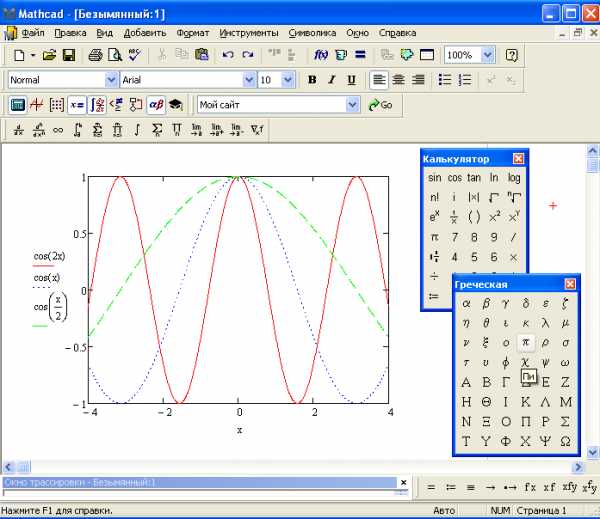
Рис 13. График тригонометрической функции
Задание №2: Построить график функции в полярной системе координат:
Полярная система координат состоит из полюса О и лучей, выходящих из точки О, один из которых, ОХ, называется полярной осью.
График строится
аналогично графику в декартовой системе
координат. Задается: 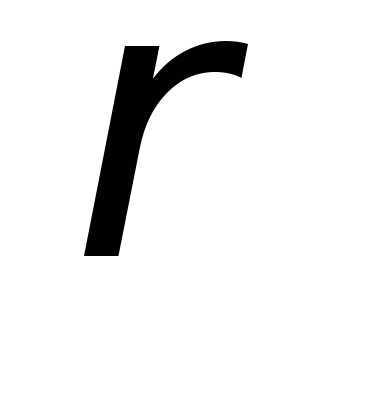 и
и ,
полярными координатами.
,
полярными координатами.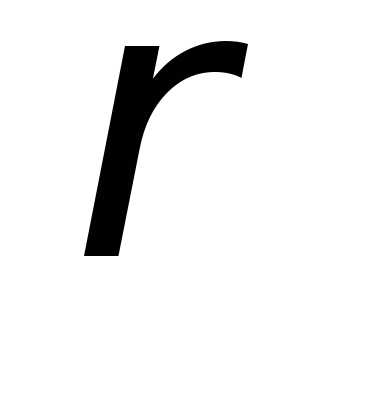 — полярный радиус,
— полярный радиус, — полярный угол.
— полярный угол.
Пример: Построить
график функции:  (рис.14).
(рис.14).
Самостоятельно:
Построить график функции:

Построить график функции:

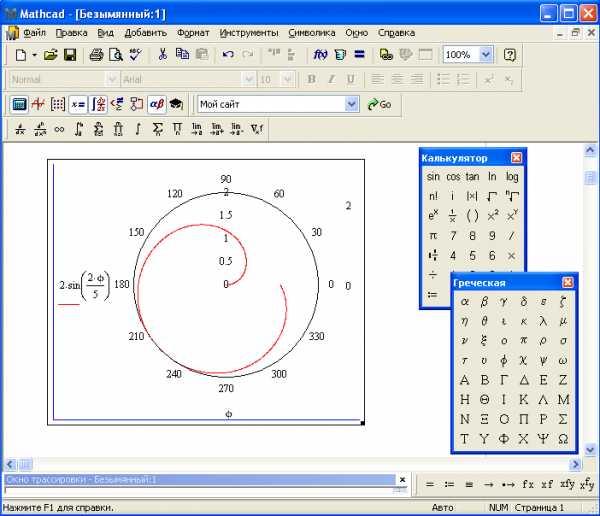
Рис 14. График функции
Задание №3: Построить график функции, заданной параметрически:
Задание функции
при помощи равенств 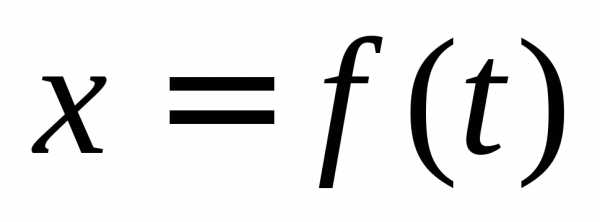 и
и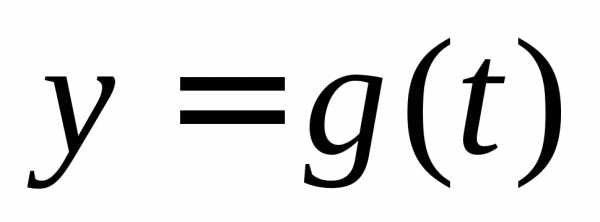 ,
когда
,
когда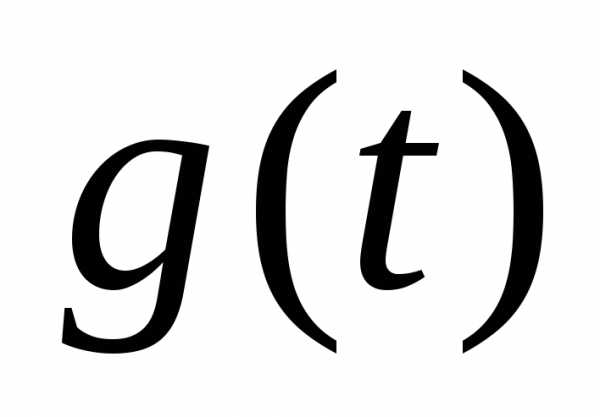 зависит
от
зависит
от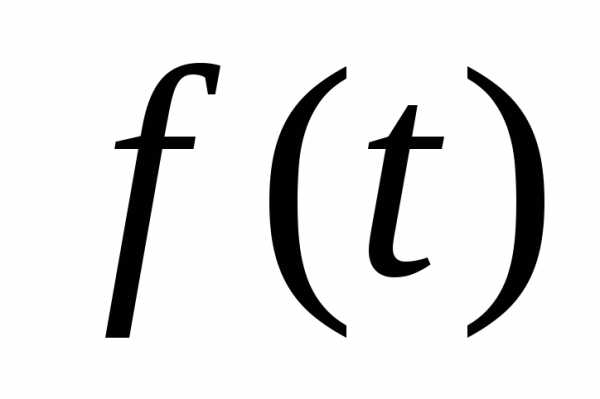 или наоборот, называют параметрическим,
а
или наоборот, называют параметрическим,
а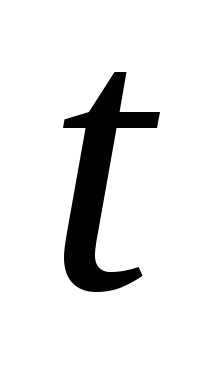 — параметром.
— параметром.
Пример: полукубическая
парабола:
,
параметрически представляется в виде: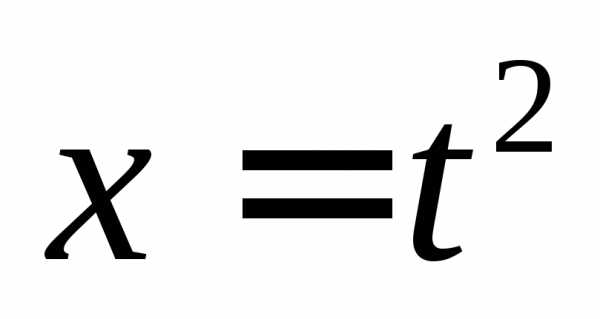 ,
,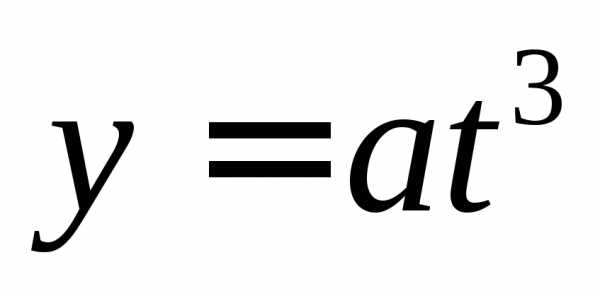 ,
при
,
при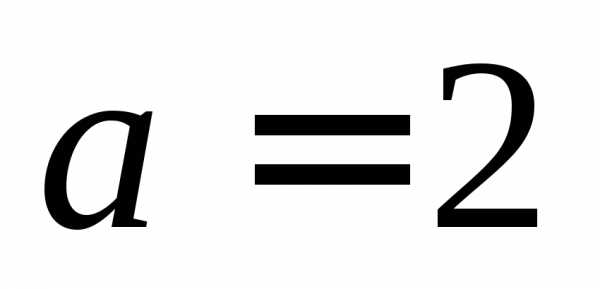 (рис.15).
(рис.15).
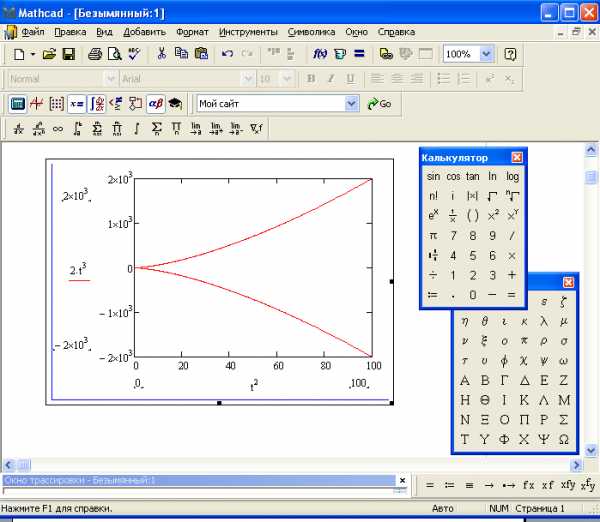
Рис 15. График функции, заданной параметрически
Самостоятельно:
1. Изучить команды трассировки и увеличения построенных графиков.
2. Построить графики функций:
а). 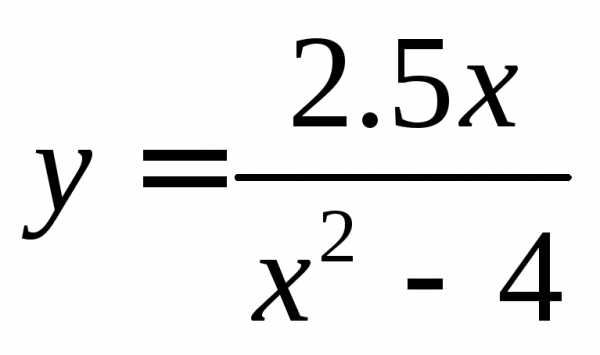
б). 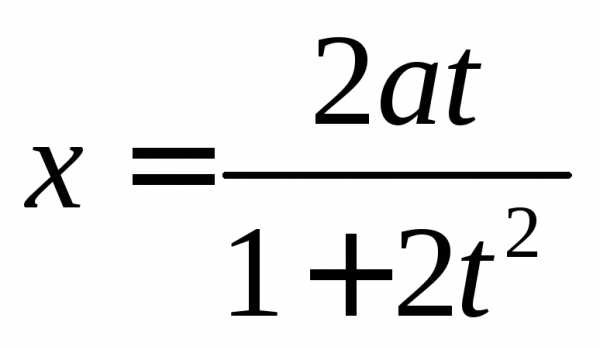 и
и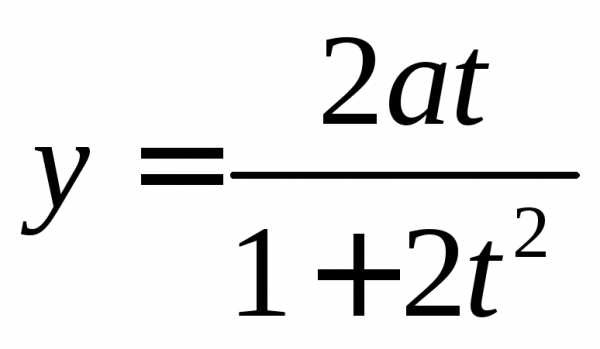 ,
еслии
,
еслии
в). 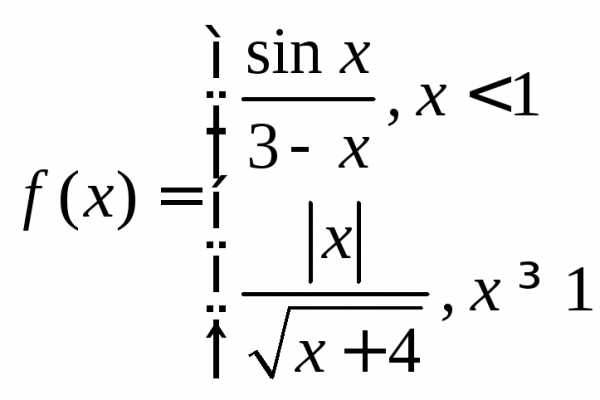
Лабораторная работа №4 Построение трехмерных графиков функций в MathCad
Цель работы
Овладеть навыками построения графиков в MathCAD.
Задачи:
— умение применять различные способы построения трехмерных графиков в Mathcad;
Порядок выполнения
График поверхности (трехмерный) – это график, положение точки в котором определяется значениями трех координат. Прямоугольная система координат в пространстве состоит из начала координат и трех перпендикулярных прямых пространства, не лежащих в одной плоскости и пересекающихся в начале координат.
Функция в пространственной системе координат задается:
1. формулой, функция бывает как явной так и неявной.
2. таблицей с двойным входом, т.е. в верхней строке значения одного аргумента, в левом столбце значения другого, а на пересечении записывают соответствующее значение функции.
3. пространственным графиком, представляет собой поверхность в пространственной системе координат, проекция любой точки поверхности на плоскость служит изображением пары значений аргументов x,y, а аппликата данной точки изображает соответствующее значение функции.
Задание №1:
Построить график функции, заданной в виде таблицы:
1. Для вставки таблицы необходимо выполнить следующие команды: Добавить – Данные – Таблицу.
2. Заполнить таблицу числовыми значениями.
3. Для построения графика необходимо выбрать: Добавить – Графики – График поверхности.( рис. 16).
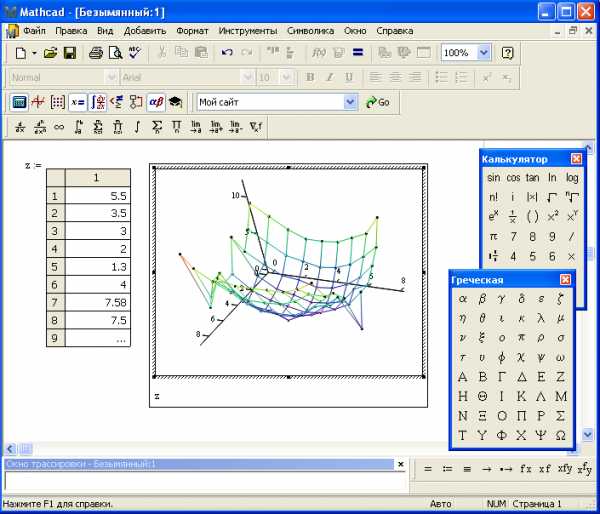
Рис 16. График поверхности
Можно форматировать получившийся график с помощью диалогового окна ( рис. 17) со следующими вкладками:
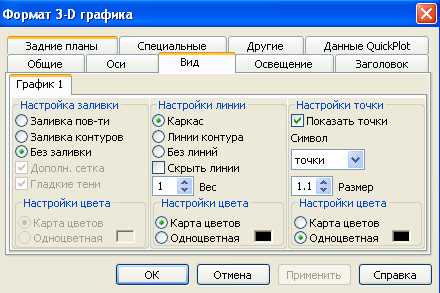
Рис 17. Форматирование графика
Вкладка «Вид» позволяет менять фон графика, заливку, линии. На вкладке «Общие» можно задать угол поворота, угол наклона и вращения, тип графика.
Задание №2:
Построить график функции:
Сначала ввести функцию, затем выбрать Добавить – Графики – График поверхности.( рис. 18).
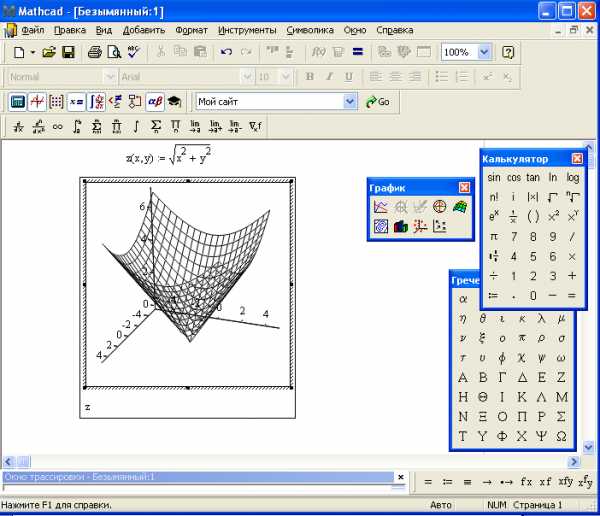
Рис 18. Форматирование графика
Типы графиков:
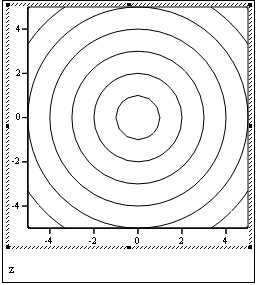
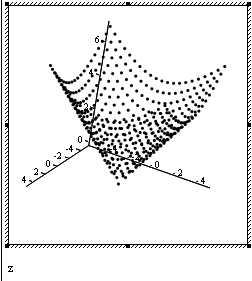
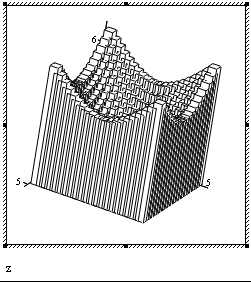
Контурный график Точечные данные График полосы
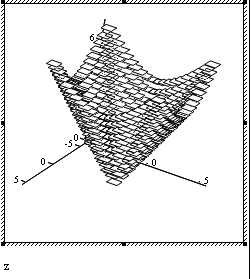
График исправления
Самостоятельно:
1. Построить график функции
2. Построить график функции
3. Построить график функции:
4. Построить график функции:
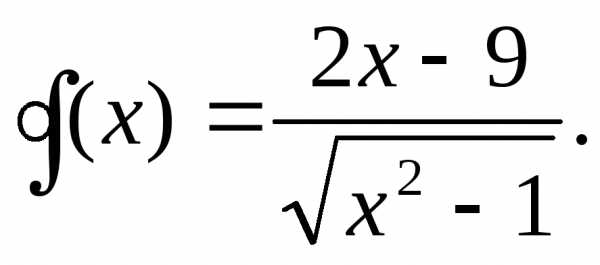
5. Изобразить график:
6. Построить график двух функций в одной области:
7. Изобразить линии, заданные неявно:
8. Построить фигуру, заданную линией:
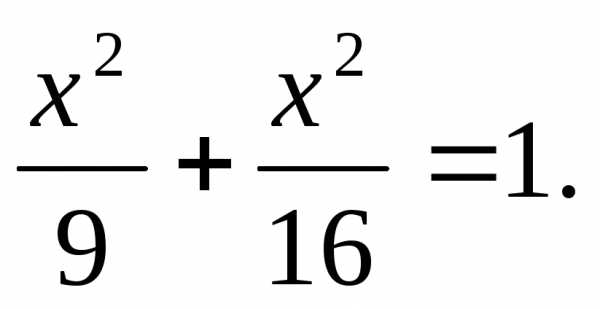
9. Построить на плоскости кривую, заданную в параметрическом виде:
10. Изобразить кривые, заданные в полярных координатах:
studfiles.net

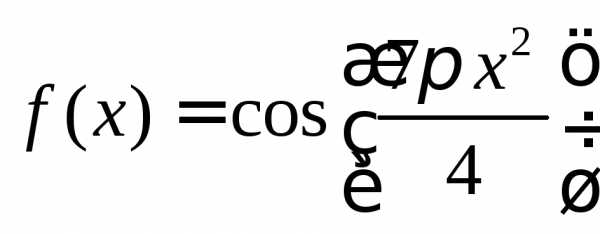 ,
на отрезке [
,
на отрезке [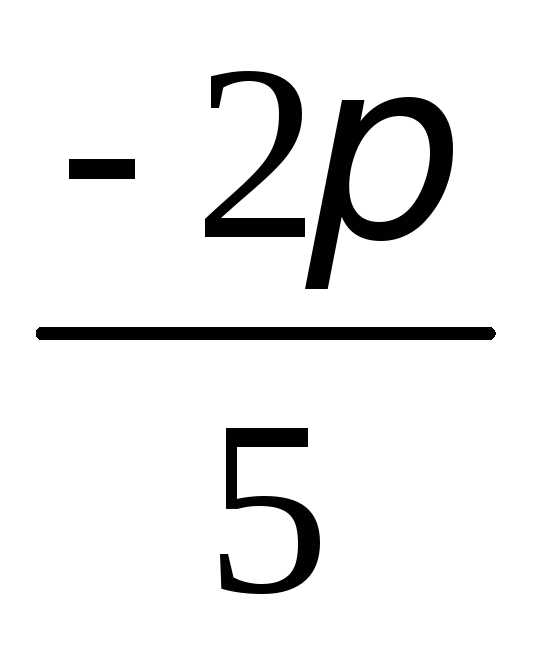 ;
;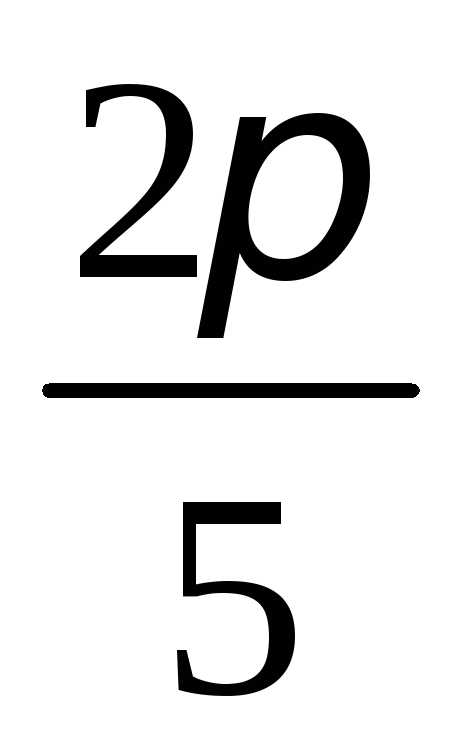 ]
]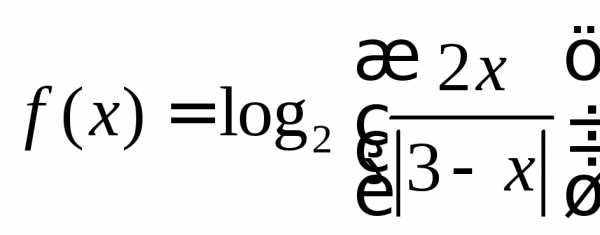 ,
на отрезке [
,
на отрезке [ ;
;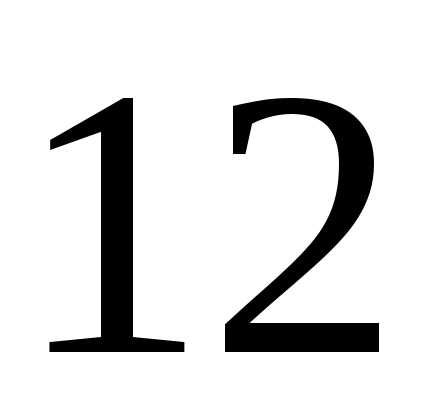 ].
].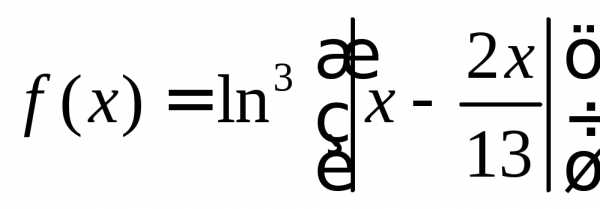 ,
на отрезке [
,
на отрезке [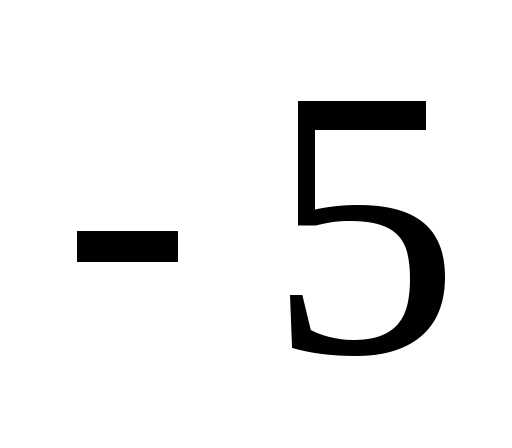 ;
; ].
].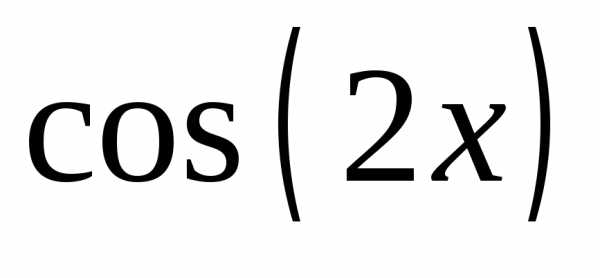 ,
,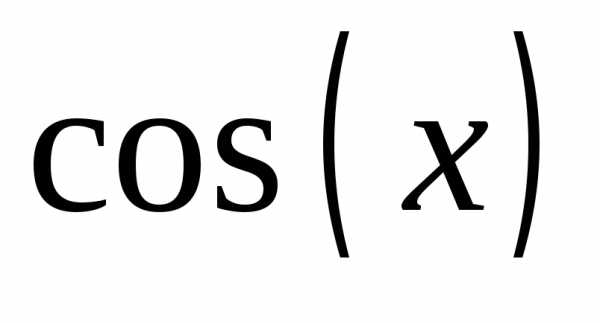 ,
,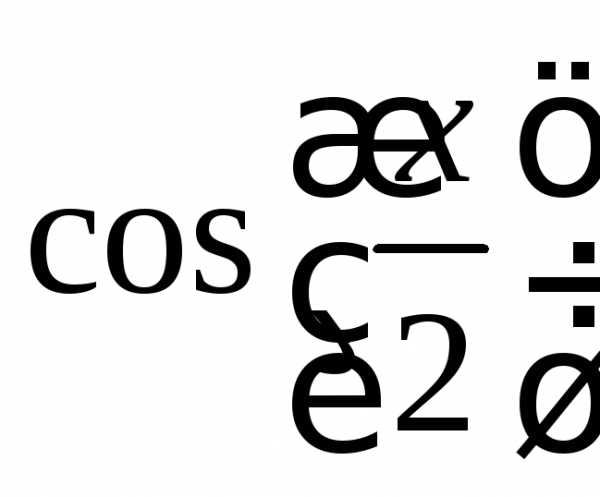 ,
(рис. 13). Функции перечислить через
запятую.
,
(рис. 13). Функции перечислить через
запятую.