Накрест лежащие углы при параллельных прямых равны
☰
Существует теорема о том, что прямые параллельны, если при пересечении их секущей накрест лежащие углы оказываются равными. Здесь дано — равные накрест лежащие углы при секущей, следствие — прямые параллельны.
Существует обратная теорема: накрест лежащие углы при секущей равны, если она пересекает параллельные прямые. В данном случае дано — параллельные прямые, следствие — равенство накрест лежащих углов при секущей.
Не является ли обратная теорема «избыточной»? Нельзя ли просто сказать, что только у параллельных прямых накрест лежащие углы при секущей равны? Но может оказаться, эти углы равны и у каких-то не у параллельных прямых. То есть у параллельных они однозначно равны, но есть еще другие прямые, тоже с равными углами. Обратная теорема исключает такую возможность.
Доказательство обратной теоремы сводится к следующему.
Предполагается обратное, т. е. что при данных параллельных прямых накрест лежащие углы при секущей оказываются не равны. Пусть даны параллельные прямые a и b, которые пересекает секущая c. Предположим, что накрест лежащие углы 1 и 2 не равны друг другу: ∠1 ≠ ∠2.
Через точку пересечения секущей с одной из параллельных прямых (b) проведем прямую d так, чтобы получился равный углу 1 накрест лежащий угол 3: ∠1 = ∠3.
Прямая теорема утверждает, что когда накрест лежащие углы при секущей равны, то прямые параллельны. Значит, прямые a и d параллельны: a || d.
Получается, что через одну точку (в которой пересекаются прямые b, c, d) проведены две параллельные прямые (b и d), которые параллельны прямой a. Однако из ранее доказанной теоремы такого быть не может: через точку, не лежащую на прямой, можно провести только одну параллельную прямую.
Следовательно, предположение о том, что ∠1 ≠ ∠2, не верно. Поэтому ∠1 = ∠2. Нет никакой иной прямой, проходящей через заданную точку, которая давала бы равные углы при секущей, кроме единственной параллельной.
scienceland.info
Свойства углов при параллельных прямых

ТЕОРЕМЫ ОБ УГЛАХ,
ОБРАЗОВАННЫХ ДВУМЯ
ПАРАЛЛЕЛЬНЫМИ
ПРЯМЫМИ
И СЕКУЩЕЙ
22 ЯНВАРЯ 2010Г
Учитель Козина Н.А.

ПОНЯТИЕ ОБРАТНОЙ ТЕОРЕМЫ
ЕСЛИ
Условие
Заключение
ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ,
ТО
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ

ТЕОРЕМа
Свойство
накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
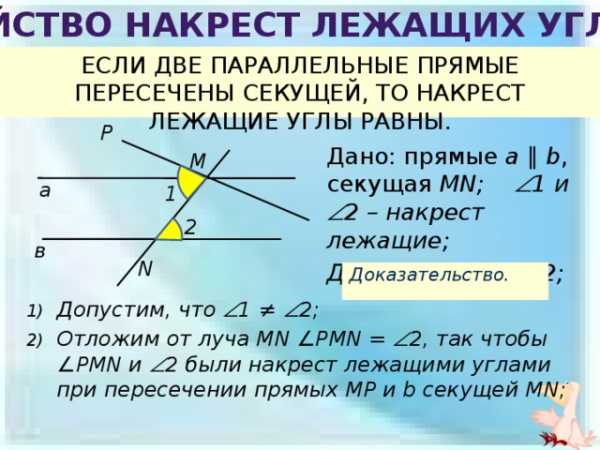
Свойство накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
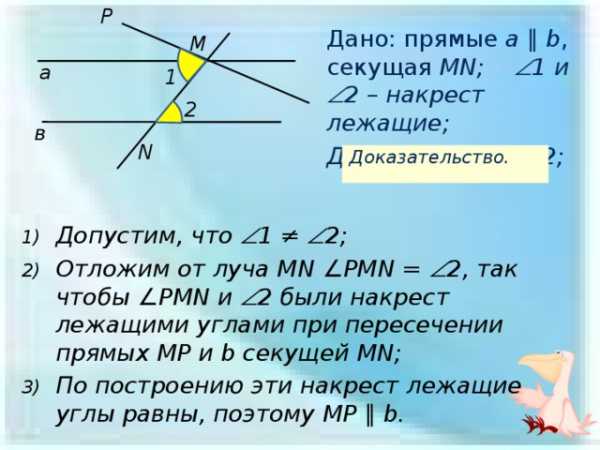
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
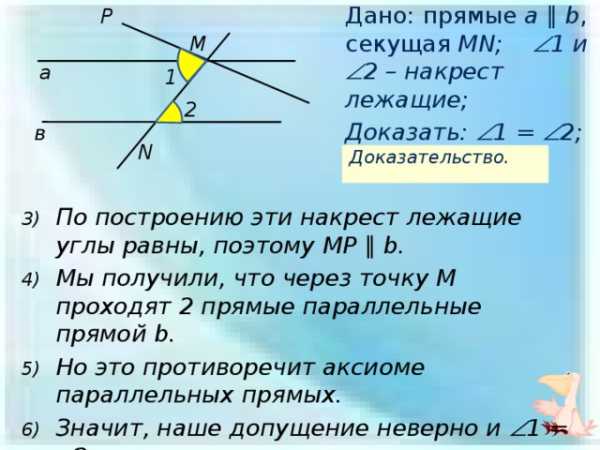
P
Дано: прямые a ∥ b , секущая MN; 1 и
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
- Мы получили, что через точку М проходят 2 прямые параллельные прямой b.
- Но это противоречит аксиоме параллельных прямых.
- Значит, наше допущение неверно и 1 = 2;
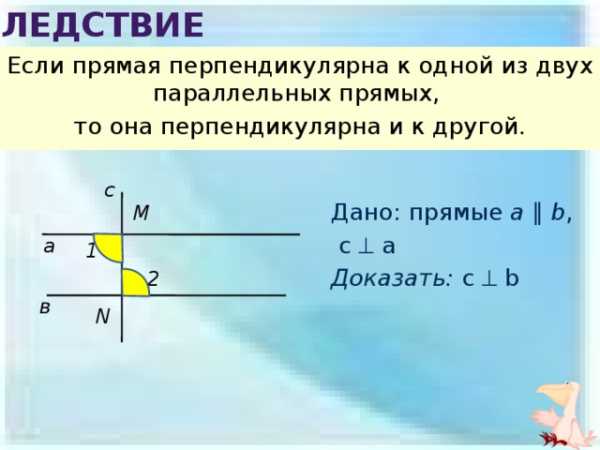
следствие
Если прямая перпендикулярна к одной из двух параллельных прямых,
то она перпендикулярна и к другой.
с
Дано: прямые a ∥ b ,
M
c a
Доказать: c b
а
1
2
в
N
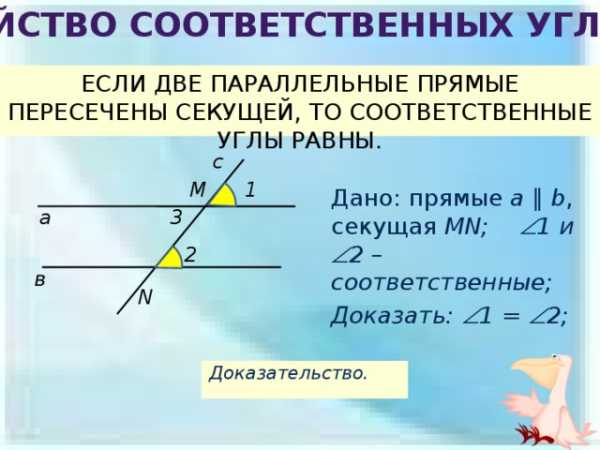
Свойство соответственных углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ.
с
1
M
Дано: прямые a ∥ b , секущая MN; 1 и 2 – соответственные;
Доказать: 1 = 2;
а
3
2
в
N
Доказательство.
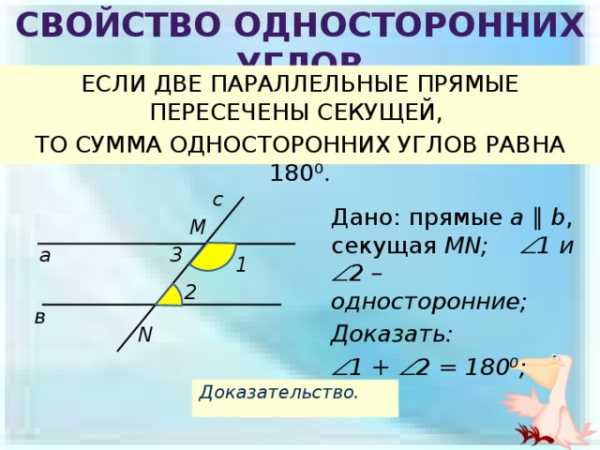
Свойство односторонних углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО СУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰.
с
Дано: прямые a ∥ b , секущая MN; 1 и 2 –односторонние;
Доказать:
1 +
M
а
3
1
2
в
N
Доказательство.

Решение задач
УСТНО
с
4
Дано: прямые a ∥ b ,
1 = 75⁰
Найти: 2, 3, ∠4 .
а
2
3
1
в

Решение задач
УСТНО
с
2
Дано: прямые a ∥ b ,
1 + ∠2 = 160⁰
Найти: 3, 4, ∠5 , ∠6.
а
4
3
5
1
в
6

РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА
ПАРАЛЛЕЛЬНЫХ
ПРЯМЫХ»
- 26 ЯНВАРЯ 2010Г
- Учитель Козина Н.А.
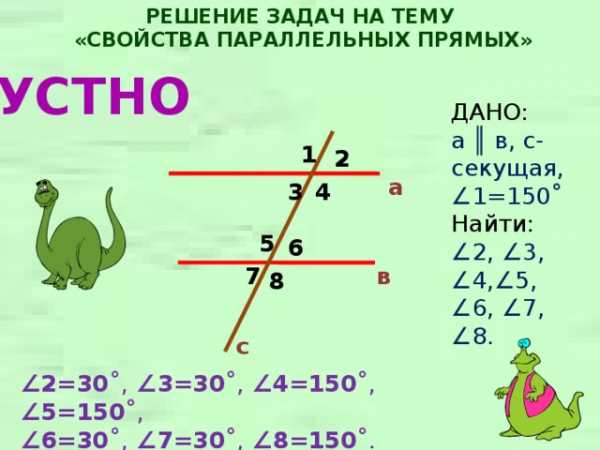
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
ДАНО:
а ║ в, с-секущая, ∠ 1=150˚
Найти:
∠ 2, ∠ 3, ∠ 4, ∠ 5, ∠ 6, ∠ 7, ∠ 8.
1
2
а
3
4
5
6
в
7
8
с
∠ 2=30 ˚, ∠ 3=30 ˚, ∠ 4=150 ˚, ∠ 5=150 ˚,
∠ 6=30 ˚, ∠ 7=30 ˚, ∠8 =150 ˚.
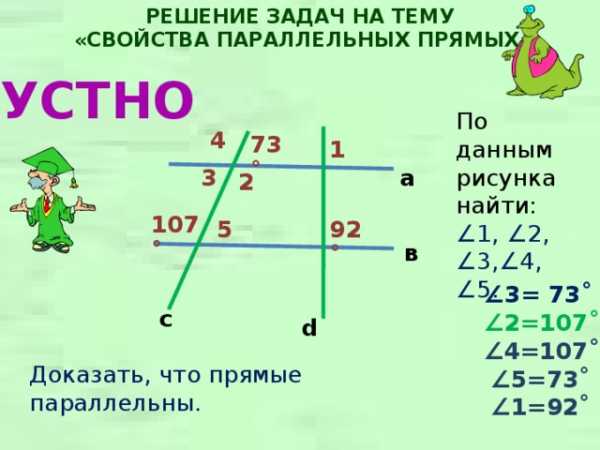
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
По данным рисунка найти:
∠ 1, ∠ 2, ∠ 3, ∠ 4, ∠ 5.
4
73˚
1
3
а
2
107˚
92˚
5
в
∠ 3= 73˚
с
∠ 2=107˚
d
∠ 4=107˚
Доказать, что прямые параллельны.
∠ 5=73˚
∠ 1=92˚
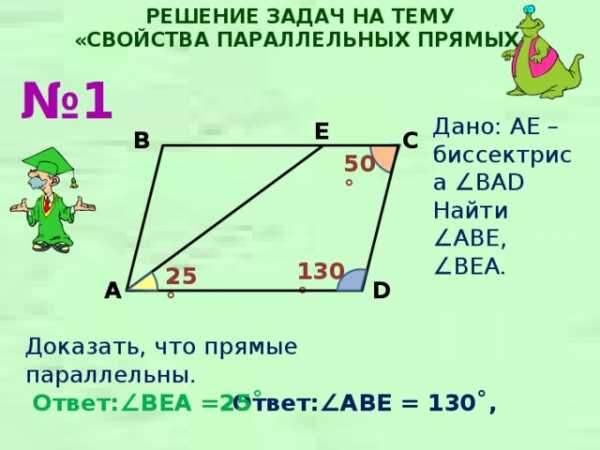
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 1
Дано: AE – биссектриса ∠BAD
Найти
∠ ABE, ∠BEA.
E
C
B
50˚
130˚
25˚
A
D
Доказать, что прямые параллельны.
Ответ:∠ BEA =25˚
Ответ:∠ ABE = 130˚,
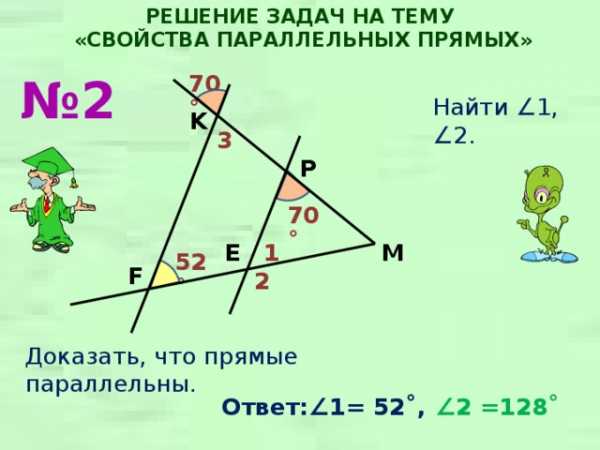
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 2
70˚
Найти ∠1, ∠2.
K
3
P
70˚
E
M
1
52˚
F
2
Доказать, что прямые параллельны.
∠ 2 =128˚
Ответ:∠ 1= 52˚,
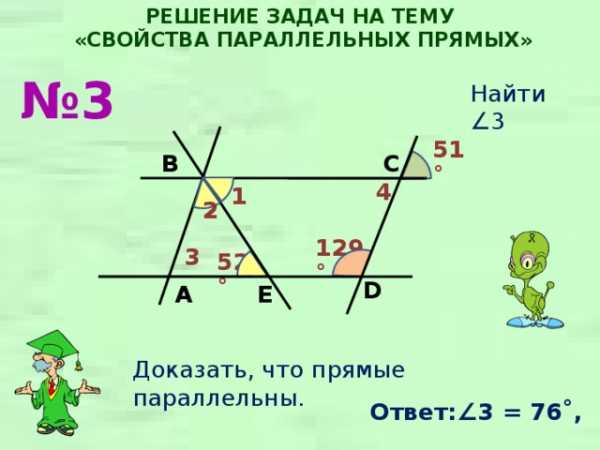
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 3
Найти ∠3
51˚
C
B
4
1
2
129˚
3
52˚
D
E
A
Доказать, что прямые параллельны.
Ответ:∠ 3 = 76˚,
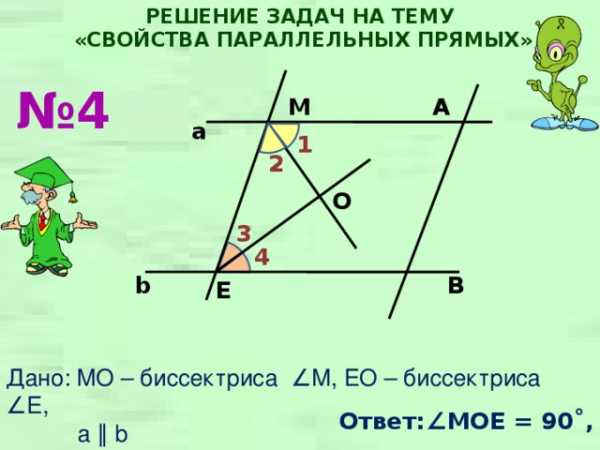
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 4
A
M
a
1
2
O
3
4
B
b
E
Дано: MO – биссектриса ∠M, EO – биссектриса ∠E,
a ∥ b
Найти ∠MOE
Ответ:∠ MOE = 90˚,

РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
САМОСТОЯТЕЛЬНО
№ 5
T
K
N
68˚
1
112˚
4
2
68˚
3
P
M
Доказать, что прямые параллельны.
Дано: PT биссектриса ∠MPT
Найти ∠1
Ответ:∠ 1 = 34˚,

РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
ДОМАШНЕЕ ЗАДАНИЕ
№ 208, 210, 211, 212

videouroki.net
Накрест лежащие углы при параллельных прямых равны — Науколандия
Существует теорема о том, что прямые параллельны, если при пересечении их секущей накрест лежащие углы оказываются равными. Здесь дано — равные накрест лежащие углы при секущей, следствие — прямые параллельны.
Существует обратная теорема: накрест лежащие углы при секущей равны, если она пересекает параллельные прямые. В данном случае дано — параллельные прямые, следствие — равенство накрест лежащих углов при секущей.
Не является ли обратная теорема «избыточной»? Нельзя ли просто сказать, что только у параллельных прямых накрест лежащие углы при секущей равны? Но может оказаться, эти углы равны и у каких-то не у параллельных прямых. То есть у параллельных они однозначно равны, но есть еще другие прямые, тоже с равными углами. Обратная теорема исключает такую возможность.
Доказательство обратной теоремы сводится к следующему.
Предполагается обратное, т. е. что при данных параллельных прямых накрест лежащие углы при секущей оказываются не равны. Пусть даны параллельные прямые a и b, которые пересекает секущая c. Предположим, что накрест лежащие углы 1 и 2 не равны друг другу: ∠1 ≠ ∠2.
Через точку пересечения секущей с одной из параллельных прямых (b) проведем прямую d так, чтобы получился равный углу 1 накрест лежащий угол 3: ∠1 = ∠3.
Прямая теорема утверждает, что когда накрест лежащие углы при секущей равны, то прямые параллельны. Значит, прямые a и d параллельны: a || d.
Получается, что через одну точку (в которой пересекаются прямые b, c, d) проведены две параллельные прямые (b и d), которые параллельны прямой a. Однако из ранее доказанной теоремы такого быть не может: через точку, не лежащую на прямой, можно провести только одну параллельную прямую.
Следовательно, предположение о том, что ∠1 ≠ ∠2, не верно. Поэтому ∠1 = ∠2. Нет никакой иной прямой, проходящей через заданную точку, которая давала бы равные углы при секущей, кроме единственной параллельной.
scienceland.info
докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
угол 2 и угол 3 — вертикальные, то угол 2=углу 3 . угол 1=углу 3 . Углы 1, 3 накрест лежащие, поэтому а параллельна в
Потому что только при параллельных прямых внутренние накрест лежащие углы равны! Это же теорема!
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны (теорема) , Доказательство — ( там ещё рисунок но я его начертить не смогу ХD) уг. 1 = уг. 3 — накрест лежащие, уг. 3 = уг. 2 — вертикальные следует уг. 1 = уг 2- соответственные .
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны (теорема) . И все вот ответ . Но еще нужен рисунок ю
Теорема: Если при пересечениии двух параллельных прямых секущей накрест лежащие углы равны, то прямые параллельны Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b. Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
покажите картинку с доказательвством
рррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррррр
Вообще есть такая теорема — теорема, обратная данной, называется. А вы не знаете, значит молчите.
ооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооого
ееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееееее
Потому что только при параллельных прямых внутренние накрест лежащие углы равны! Это же теорема!
Потому что только при параллельных прямых внутренние накрест лежащие углы равны! Это же теорема!
Потому что только при параллельных прямых внутренние накрест лежащие углы равны! Это же теорема!
touch.otvet.mail.ru
Признаки параллельности двух прямых
В 7 классе мы говорили о том, что две прямые либо имеют только одну общую точку, т. е. пересекаются, либо не имеют общих точек, т. е. не пересекаются.
Определение
Две прямые на плоскости называются параллельными, если они не пересекаются.
Два отрезка называются параллельными, если они лежат на параллельных прямых. Параллельность прямых AB и CD, a и b (отрезков MN и PQ) обозначается так: AB || CD, a || b (MN || PQ).
Рассмотрим прямые a и b, а также прямую c, пересекающую их в двух точках (рис. 10). Прямую c назовем секущей по отношению к прямым a и b. Углы 1 и 3, а также 2 и 4 назовем накрест лежащими углами, образованными при пересечении прямых a и b секущей c.
Теорема
Если при пересечении двух прямых секущей накрест лежащие углы равны, то эти прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей AB накрест лежащие углы 1 и 2 равны (рис. 11, а). Докажем, что прямые a и b параллельны.
Если предположить, что прямые a и b пересекаются в некоторой точке C (рис. 11, б), то получится треугольник ABC, внешний угол которого (угол 1 на рисунке 11, б) равен углу этого треугольника, не смежному с ним. Но этого быть не может. Следовательно, прямые a и b параллельны. Теорема доказана.
При пересечении двух прямых секущей наряду с накрест лежащими углами образуются и другие углы (рис. 12). Назовем углы 1 и 5, 4 и 8, 2 и 6, 3 и 7 соответственными, а углы 4 и 5, 3 и 6 односторонними. Из доказанной теоремы вытекают два следствия.
Следствие 1
Если при пересечении двух прямых секущей соответственные углы равны, то эти прямые параллельны.
Пусть соответственные углы 1 и 2 равны (рис. 13): ∠1 = ∠2. Так как вертикальные углы 2 и 3 равны, то ∠1 = ∠3, т. е. равны накрест лежащие углы 1 и 3. Следовательно, a || b.
Следствие 2
Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то эти прямые параллельны.
Пусть сумма односторонних углов равна 180º (рис. 14): ∠1 + ∠2 = 180º.
Сумма смежных углов 3 и 2 также равна 180º:
∠3 + ∠2 = 180º.
Из этих двух равенств получаем ∠1 = ∠3, т. е. равны накрест лежащие углы 1 и 3.
Следовательно, a || b.
mthm.ru
Если накрест лежащие углы при секущей равны, то прямые параллельны
☰
Пусть даны две прямые a и b, которые пересекаются прямой c. То есть прямая c является секущей для прямых a и b. При этом образуются две пары накрест лежащих углов. Если в любой из этих пар углы равны, то прямые a и b параллельны. На чертеже обозначена одна пара равных между собой накрест лежащих углов.
Дано (условие). Равенство накрест лежащих углов.
Следствие (утверждение; то, что требуется доказать). Параллельность прямых.
Формулировка в виде теоремы. Если при пересечении двух прямых секущей накрест лежащие углы оказываются равны, то значит, эти прямые параллельны.
Доказательство. Воспользуемся методом от противного. Пусть накрест лежащие углы равны, но предложенные прямые не параллельны. Если прямые не параллельны, то они пересекутся в одной точке. На чертеже секущая c пересекает прямые a и b в точках A и B, а сами прямые пересекаются в точке C.
В результате образуется треугольник ABC, у которого угол при вершине B равен внешнему углу при вершине A. Это дано по условию: были даны равные углы при секущей.
Сумма углов в треугольнике равна 180°. Если угол треугольника при вершине B равен x градусов, то два остальных угла треугольника в сумме равны 180 – x.
Так как угол B треугольника равен внешнему углу A, то значит A также равен x градусов. Внутренний угол A и внешний угол A треугольника в сумме составляют 180°, так как это смежные углы. Тогда мы получаем, что внутренний угол A треугольника равен 180 – x. Но этого быть не может, так как 180 – x является суммой углов A и C треугольника.
Такое может быть только в случае, если угол C треугольника равен 0°. Однако такого быть не может, так как в этом случае отрезки AC и BC наложились бы друг на друга. То есть прямая a совпала бы с прямой b. Однако по условию даны разные прямые.
Таким образом доказано, что если накрест лежащие углы равны, то прямые пересекаться не могут. А если прямые не имеют точек пересечения, то они параллельны.
scienceland.info
