Составить уравнение геометрического места точек одинаково удаленных – #158545: : x=4

alexxlab / / Школьная жизнь

Глава 9. Понятие уравнения линии. Задание линии при помощи уравнения

157

Даны точки М1(2; -2), М2(2; 2), М3(2; -1), М4(3; -3), М5(5; -5), М6(3; -2). Установить, какие из данных точек лежат на линии, определенной уравнением , и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже).

158

На линии, определенной уравнением , найти точки, абсциссы которых равны следующим числам: 1). 0; 2). –3; 3). 5; 4). 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5). 3; 6). –5; 7). –8. Какая линия определена данным уравнением? (Изобразить ее на чертеже).

159

Установить, какие линии определяются следующими уравнениями (построить их на чертеже):

159.1

;

159.2

;

159.3

;

159.4

;

159.5

;

159.6

;

159.7

 ;

159.8

;

159.9

;

159.10

;

159.11

;

159.12

 ;

159.13

;

159.14

 ;

159.15

;

159.16

;

159.17

;

159.18

;

159.19

;

159.20

;

159.21

;

159.22

;

159.23

;

159.24

;

159.25

;

159.26

;

159.27

;

159.28

;

159.29

;

159.30

;

159.31

.

160

Даны линии. Определить, какие из них проходят через начало координат.

160.1

;

160.2

;

160.3

;

160.4

;

160.5

.

161

Даны линии. Найти точки их пересечения: а). С осью Ох; б). С осью Оу.

161.1

;

161.2

;

161.3

;

161.4

;

161.5

;

161.6

;

161.7

.

162

Найти точки пересечения двух линий:

162.1

, ;

162.2

 , ;

162.3

, ;

162.4

, .

163

В полярной системе координат даны точки М1(1; /3), М2(2; 0), М3(2, /4), М4(;/6) и М5(1; 2/3). Установить, какие из этих точек лежат на линии, оперделенной в полярных координатаха уравнением , и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже).

164

На линии, определенной уравнением , найти точки, полярные углы которых равны следующим числам: а). , б). ; в). 0; г). . Какая линия определена данным уравнением: (Построить ее на чертеже).

165

На линии, определенной уравнением , найти точки, полярные радиусы которых равны следующим числам: а). 1; б). 2; в). . Какая линия определена данным уравнением? (Построить ее на чертеже).

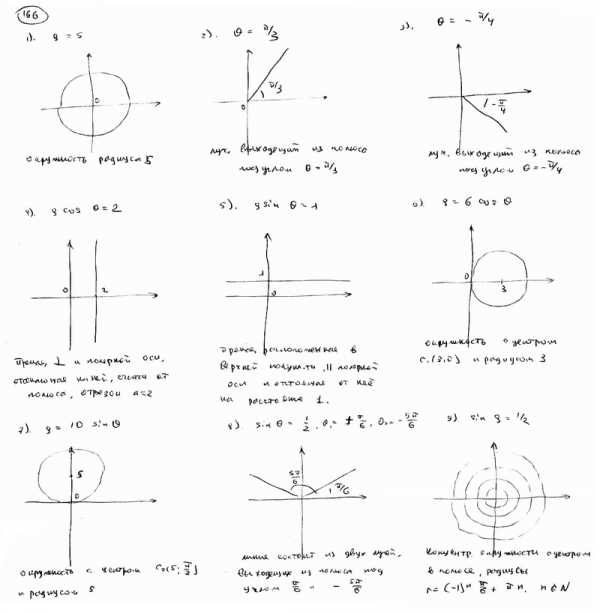
166

Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже):

166.1

;

166.2

;

166.3

;

166.4

;

166.5

;

166.6

;

166.7

;

166.8

;

166.9

.

167

Построить на чертеже следующие спирали Архимеда:

167.1

;

167.2

;

167.3

;

167.4

.

168

Построить на чертеже следующие гиперболические спирали:

168.1

;

168.2

;

168.3

;

168.4

.

169

Построить на чертеже следующие логарифмические спирали:

169.1

 ;

169.2

 .

170

Определить длины отрезков, на которые рассекает спираль Архимеда луч, выходящий из полюса и наклоненный к полярной оси под углом . Сделать чертеж.

171

На спирали Архимеда взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С. Сделать чертеж.

172

На гиперболической спирали найти точку Р, полярный радиус которой равен 12. Сделать чертеж.

173

На логарифмической спирали найти точку Q, полярный радиус которой равен 81. Сделать чертеж.

studfiles.net

составить уравнение геометрического места точек равноудалённых от точки а(-2,5) и данной прямой у= -1 полученное уравнение привести к нормальному виду и

+ 0 — Kbm

05 февр. 2014 г., 14:13:43 (5 лет назад)

Парабола— геометрическое место точек, равноудалённых от данной прямой и данной точки.
y+1=0
A(-2;5)
Пусть  — координаты каждой точки искомой кривой. Расстояние d от точки  до прямой  определяется формулой:

Тогда, используя формулу расстояния между двумя точками, получим:

Возводим обе части в квадрат и получаем уравнение искомой кривой, заменив всюду  на 

Приводим в квадратичную форму  к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы:

Хороший ответ 0 Жалоба Ответить
Имя E-mail
Текст вашего комментария Введите текст с картинки Ответить

matematika.neznaka.ru

Уравнение — геометрическое место — Большая Энциклопедия Нефти и Газа, статья, страница 2

Уравнение — геометрическое место

Cтраница 2

Найти уравнение геометрического места точек, одинаково удаленных от начала координат и от точки А ( — 3, 4) ( фиг.  [16]

Составить уравнение геометрического места точек, обладающих тем свойством, что проекция радиуса-вектора каждой из них на ось х равна четырем единицам. Исследовать, как расположены эти точки в пространстве.  [17]

Составить уравнение геометрического места точек, одинаково удаленных от двух данных прямых: [ ri ] — 0 и [ г, i j ] — i — f j — В полученном уравнении перейти к координатным обозначениям.  [18]

Найти уравнение геометрического места точек, сумма расстояний которых от точек F1 ( 2, 3) и Fz ( 4, 5) есть величина постоянная, равная 10 ( фиг.  [19]

Составить уравнение геометрического места точек, обладающих тем свойством, что проекция радиуса-вектора каждой из них на ось х равна четырем единицам. Исследовать, как расположены эти точки в пространстве.  [20]

Составить уравнение геометрического места точек, одинаково удаленных от двух данных прямых: [ ri ] 0 и [ r, i j ] — i 4 J — В полученном уравнении перейти к координатным обозначениям.  [21]

Написать уравнение геометрического места точек М ( х; у), одинаково удаленных от точки F ( a / 2; а / 21 и от прямой х у 0, и привести его к каноническому виду.  [22]

Написать уравнение геометрического места точек, одинаково удаленных от точки F ( — а; 0; 0) и от плоскости х — а.  [23]

Это есть уравнение геометрического места точек, равноудаленных от центров окружностей, поэтому для наших целей оно будет подходить даже в том случае, если окружности на самом деле не пересекаются.  [24]

При отыскании уравнения геометрического места по данному его свойству не всегда бывает удобно или возможно выразить это свойство непосредственно в виде уравнения, связывающего текущие координаты х, у. В таком случае бывает полезно ввести третью, вспомогательную переменную величину, через которую можно выразить отдельно абсциссу х и ординату у любой точки геометрического места.  [25]

Для вывода уравнения геометрического места точек надо прежде всего установить положение осей координат, Положение осей координат можно, конечно, выбрать как угодно, но при удачном выборе уравнение геометрического места будет проще. Правил, которыми при этом следует руководствоваться, не существует, и умение выбирать надлежащим образом положение осей координат дается только практикой.  [26]

Примерами на составление уравнений геометрических мест могут служить выводы канонических уравнений окружности, эллипса, гиперболы и параболы.  [27]

Зависимость ( 7 — 27) служит уравнением геометрического места кризисных точек семейства кривых Фанно.  [28]

Получив искомое уравнение, доказывают, что это и есть уравнение данного геометрического места, что координаты точек, не принадлежащих данному геометрическому месту, не удовлетворяют найденному уравнению.  [29]

Подставив полученные выражения производных в ( 11), получим уравнение геометрического места шаровых точек. Выбрав любую точку этого геометрического места за центр шарнира С и найдя по формулам ( 10) координаты inapHHpaj В, получим шарнирный четырехзвенник, удовлетворяющий указанным выше условиям.  [30]

Страницы:      1    2    3    4

www.ngpedia.ru

«Аналитическая геометрия»

2.1. Даны три последовательные вершины параллелограмма .

Найти:

1) уравнение стороны ;

2) уравнение высоты, опущенной из вершины на сторону, длину этой высоты;

3) уравнение диагонали ;

4) площадь параллелограмма;

5) угол между диагоналями параллелограмма;

2.1.1.

2.1.2.

2.1.3.

2.1.4.

2.1.5.

2.1.6.

2.1.7.

2.1.8.

2.1.9.

2.1.10.

2.2. Задачи на уравнения прямой и плоскости в пространстве.

2.2.1. Даны две точки: и . Составить урав­нение плоскости, проходящей через т. перпендикулярно к вектору .

2.2.2. Составить уравнение плоскости, которая проходит через т. параллельно плоскости .

2.2.3. Составить канонические уравнения прямой, проходящей через т. параллельно прямой .

2.2.4. Составить уравнение плоскости, проходящей через т. параллельно двум векторам:и.

2.2.5. Составить уравнение плоскости, проходящей через три точки: ,,.

2.2.6. Составить уравнение прямой, проходящей через т. перпендикулярно к плоскости.

2.2.7. Найти угол между прямыми

2.2.8. Составить уравнение плоскости, проходящей через т. перпендикулярно к прямой

2.2.9. Найти точку пересечения прямой и плоскости

2.2.10. При каком значении прямая па­раллельна плоскости ?

2.3. Уравнение кривой 2-го порядка путем выделения полного квад­рата привести к каноническому виду. Построить кривую.

2.3.1.

2.3.2.

2.3.3.

2.3.4.

2.3.5.

2.3.6.

2.3.7.

2.3.8.

2.3.9.

2.3.10.

2.4.1. Составить уравнение геометрического места точек, одинаково удаленных от т. и от оси .

2.4.2. Составить уравнение геометрического места точек, одинаково удаленных от т. и от оси.

2.4.3. Составить уравнение линии, каждая точка которой одинаково удалена от начала координат и точки .

2.4.4. Составить уравнение геометрического места точек, разность расстояний которых до точек иравна 5.

2.4.5. Найти уравнение траектории т. , которая при своем движе­нии остается вдвое дальше от т., чем от прямой.

2.4.6. Найти уравнение траектории т. , которая в каждый момент движения находится вдвое дальше от т. , чем от оси абсцисс.

2.4.7. Составить уравнение геометрического места точек, каждая из которых одинаково удалена от т. и т..

2.4.8. Составить уравнение геометрического места точек, одинаково удаленных от начала координат и от прямой .

2.4.9. Составить уравнение геометрического места точек, сумма квадратов расстояний которых от точк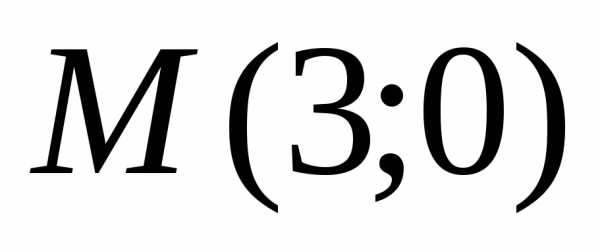и и точкиравна квадрату расстояний между точкам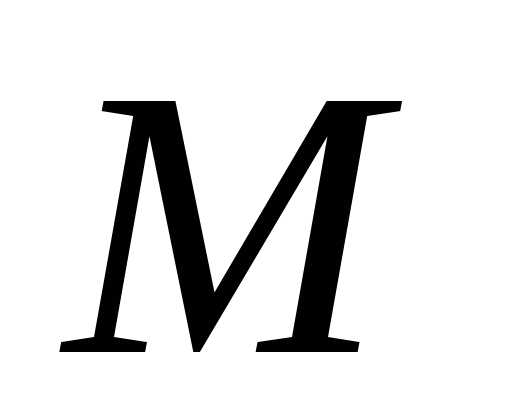ии.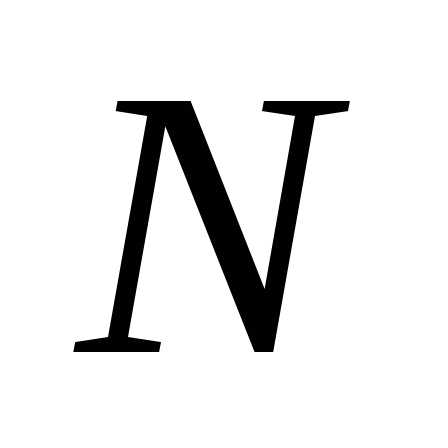

2.4.10. Составить уравнение геометрического места точек, равно­ удаленных от оси и от точки.

2.5. Даны кривые, описанные уравнениями в обобщенной полярной системе координат. Требуется:

1) найти точки, лежащие на кривой, давая значения через промежуток, равный, начиная отдо ;

2) построить кривую, соединив полученные точки линией;

3) составить уравнение этой кривой в прямоугольной декартовой системе координат (полюс совпадает с началом координат, положитель­ная полуось абсцисс берется совпадающей с полярной осью):

2.5.1. 2.5.2.

2.5.3. 2.5.4.

2.5.5. 2.5.6.

2.5.7. 2.5.8.

2.5.9. 2.5.10.

Контрольные вопросы к экзамену

  1. Понятие системы координат. Декартовая и полярная системы координат. Переход из одной системы в другую.

  2. Построение кривой по её уравнению в декартовой и полярной системах координат.

  3. Основные виды уравнений прямой на плоскости и в пространстве. Основные виды уравнений плоскости.

  4. Понятие о кривых второго порядка. Общее уравнение кривой второго порядка.

  5. Эллипс.

  6. Гипербола.

  7. Парабола.

  8. Понятие геометрического места точек. Нахождение уравнения геометрического места точек.

studfiles.net

составить уравнение геометрического места точек равноудалённых от точки а(-2,5) и данной прямой у= -1 полученное уравнение привести к нормальному виду и

+ 0 — Kbm

05 февр. 2014 г., 14:13:43 (5 лет назад)

Парабола— геометрическое место точек, равноудалённых от данной прямой и данной точки.
y+1=0
A(-2;5)
Пусть  — координаты каждой точки искомой кривой. Расстояние d от точки  до прямой  определяется формулой:

Тогда, используя формулу расстояния между двумя точками, получим:

Возводим обе части в квадрат и получаем уравнение искомой кривой, заменив всюду  на 

Приводим в квадратичную форму  к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы:

Хороший ответ 0 Жалоба Ответить
Имя E-mail
Текст вашего комментария Введите текст с картинки Ответить

algebra.neznaka.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *