Онлайн калькулятор: Сложность вычисления школьных примеров
Данный калькулятор пытается оценить сложность вычисления без калькулятора (на листочке) задач с использованием арифметических операций сложения, вычитания, умножения и деления.
Калькулятор определяет количество элементарных операций в примере, дает условную сложность выраженную в миллисекундах, требуемых для вычисления примера. Сложность складывается из суммы элементарных операций, помноженных на коэффициент сложности (время в миллисекундах, требуемое для выполнение операции). Расшифровка элементарных операций дается в таблице в нижней части калькулятора.
Результат вычисления
Количество элементарных операций
Сложность (время вычисления)
Сохранить share extension
Расшифровка операций с указанием сложности.
++ сложность 200, увеличение на единицу, например, при умножении 2003000 — будет одно умножение 23 и 5 раз выполнится подсчет нулей
+ сложность 500, элементарное сложение например 5+4
* сложность 1000, элементарное умножение, например 2*2
/ сложность 1000, деление — операция деления сводится к последовательном выполнении операций умножения и вычитания, при этом мы прикидываем всякий раз какой множитель необходимо выбрать, чтобы произведение получилось чуть меньше или равно текущего делимого. Эта элементарная операция подсчитывается в данной колонке. Необходимые умножения и вычитания подсчитываются дополнительно.
0+ сложность 100, сложение с нулем — частный случай выделен отдельно, так как это более простая операция чем сложение.
0 сложность 100, подстановка нулей
°+ сложность 700, сложение с переносом единицы, например 16+7 — содержит две операции — элементарное сложение и перенос единицы в следующий разряд.
=0 сложность 200, сокращение — операции вычитания равных величин, например 100-100
°- сложность 600, заем единицы при вычитании, например при вычитании 11-9 будет выполнен один заем и одна операция вычитания.
** сложность 400, повторное умножение. часто случается, что при выполнении элементарных ( и не только ) операций умножения выполняются одни и те же операции. Например 2533 будет содержать два элементарных умножения и один повтор, мы просто можем переписать результат умножения 253 еще один раз.
*0 сложность 100, частный случай умножения на ноль
*1 сложность 200, частный случай умножения на единицу
°* сложность 700, перенос при умножении, например 234 — два элементарных умножения плюс один перенос (1) при умножении 34
+- сложность 300, смена знака
<> сложность 500, перестановка вычитаемых, выполняется если мы пытаемся вычесть из меньшего большее
Рассмотрим вычисление сложности на примере (4567+987-8354)*32/25:
Пример содержит все четыре арифметических операции.
Сначала выполняется сложение 4567+987=5554
Запись сложения в столбик
Как видим, в этом примере имеется три элементарных сложения: 7+7, 6+8, 5+9, при выполнении каждого из которых осуществляется перенос единицы в старший разряд.
Затем вычитание 5554-8354=-2800
Запись вычитания в столбик
Так как из меньшего вычитается большее число, результат получается отрицательным, перед вычитанием выполняется перестановка операндов. Первые два разряда 5,4 сокращаются, затем при вычислении 3-5 осуществляется элементарное вычитание с займом единицы, затем просто вычитание 8-1-5=2.
Третьим действием выполняем умножение -2800*32=-89600
Запись умножения в столбик
Так как первый множитель заканчивается нулями, выполняем подсчет их количества, чтобы в конце умножения приписать нули к результату. Затем умножаем 2832. При умножении на 3
Последнее действие — деление -89600/25=-3584
-89600/25=-3584На каждом шаге деления осуществляется подбор множителя таким образом, чтобы произведение его на делитель было близко к числу, составляемому первыми разрядами текущего остатка от деления. Эта операция засчитывается как элементарное деление, после чего выполняется умножение и вычитание, сложность которых рассчитывается по аналогии с предыдущими шагами.
В частности при делении первых разрядов (86) на 25 выбираем множитель = 3. Далее производится умножение 25*3-75, далее вычитание 89-75=14.
Итого при вычислении 89600/25 имеем: 4 деления и 4 вычитания, 8 произведений, 3 сокращения, два умножения с переносом, при умножении с переносом осуществляется одно сложение.
В конечном итоге в ходе вычисления всего примера произведено 52 элементарные операции — с учетом обозначенных весовых коэффициентов, общая сложность составляет 28500. Таким образом для решения данного примера понадобится примерно полминуты (28.5 секунды).
P.S. Все временные оценки и сам алгоритм вычисления сложности сделаны на основе субъективных предположений автора, комментарии и замечания приветствуются.
planetcalc.ru
Помощь по работе с программой LoviOtvet
Ниже приведены наиболее часто встречающиеся вопросы по использованию решебника-калькулятора для школьников и родителей ЛовиОтвет
Ввод данных
Операторы (математические действия)
Кроме основного набора арифметических действий, являющихся базой для всех остальных
вычислений, а именно — деление, вычитание, сложение, умножение Вы сможете оперировать
дробями (в том числе простыми), а также производить вычисления используя тригонометрические функции.
| № | Название | Обозначение | Кол-во аргументов | Приоритет | Пример | Готовность |
|---|---|---|---|---|---|---|
| 1 | Сложение | + | 2 | 1 | x+y | + |
| 2 | Минус | — | 1 или 2 | 1 | x-y | + |
| 3 | Умножение | * | 2 | 2 | x*y | + |
| 4 | Деление | / или : | 2 | 2 | x/y | + |
| 5 | Дробная черта | // | 2 | 4 | 1//3 | + |
| 6 | Разделитель целой и дробной части в смешанной дроби | пробел | 2 | 3 | 1 2//3 | + |
| 7 | Возведение в степень | ^ | 2 | 6 | x^y | + |
| 8 | Равенство | = | 2 | — | x=y | + |
| 9 | Синус | sin | 1 | 5 | sin(x) | + |
| 10 | Косинус | cos | 1 | 5 | cos(x) | + |
| 11 | Тангенс | tan | 1 | 5 | tan(x) | + |
| 12 | Котангенс | ctg | 1 | 5 | ctg(x) | + |
| 13 | Секанс | sec | 1 | 5 | sec(x) | + |
| 14 | Косеканс | csc | 1 | 5 | csc(x) | + |
| 15 | Арксинус | arcsin | 1 | 5 | arcsin(x) | — |
| 16 | Арккосинус | arccos | 1 | 5 | arccos(x) | — |
| 17 | Арктангенс | arctan | 1 | 5 | arctan(x) | — |
| 18 | Арккотангенс | arcctg | 1 | 5 | arcctg(x) | — |
| 19 | Арксеканс | arcsec | 1 | 5 | arcsec(x) | — |
| 20 | Арккосеканс | arccsc | 1 | 5 | arccsc(x) | — |
| 21 | Модуль | abs | 1 | 5 | abs(x) | + |
| 22 | Процент | % | 2 | 5 | x%y | + |
| 23 | Гиперболический синус | sinh | 1 | 5 | sinh(x) | — |
| 24 | Гиперболический косинус | cosh | 1 | 5 | cosh(x) | — |
| 25 | Гиперболический тангенс | tanh | 1 | 5 | tanh(x) | — |
| 26 | Гиперболический котангенс | ctgh | 1 | 5 | ctgh(x) | — |
| 27 | Гиперболический секанс | sech | 1 | 5 | sech(x) | — |
| 28 | Гиперболический косеканс | csch | 1 | 5 | csch(x) | — |
| 29 | Гиперболический арксинус | arcsinh | 1 | 5 | arcsinh(x) | — |
| 30 | Гиперболический арккосинус | arccosh | 1 | 5 | arccosh(x) | — |
| 31 | Гиперболический арктангенс | arctanh | 1 | 5 | arctanh(x) | — |
| 32 | Гиперболический арккотангенс | arcctgh | 1 | 5 | arcctgh(x) | — |
| 33 | Гиперболический арксеканс | arcsech | 1 | 5 | arcsech(x) | — |
| 34 | Гиперболический арккосеканс | arccsch | 1 | 5 | arccsch(x) | — |
| 35 | Целочисленное деление | div | 2 | 2 | (x)div(y) | + |
| 36 | Остаток от деления | mod | 2 | 2 | (x)mod(y) | + |
| 37 | Натуральный логирифм | ln | 1 | 6 | ln(x) | — |
| 38 | Десятичный логарифм | lg | 1 | 6 | lg(x) | — |
| 39 | Логарифм по произвольному основания | log | 2 | 6 | log(x;y) | — |
| 40 | Корень произвольной степени | root | 2 | 6 | (x)root(y) | + |
| 41 | Округление до ближайшего целого | round | 1 | 5 | round(x) | + |
| 42 | Отбрасывание дробной части | trunc | 1 | 5 | trunc(x) | + |
| 43 | Отбрасывание целой части | frac | 1 | 5 | frac(x) | + |
| 44 | Округление до наименьшего целому | ceil | 1 | 5 | ceil(x) | + |
| 45 | Округление до наибольшего целого | floor | 1 | 5 | floor(x) | + |
| 46 | Факториал | ! | 1 | 7 | x! | + |
| 47 | Двойной факториал | ! | 1 | 7 | x!! | + |
Ввод чисел
Ограничения
Максимальное количество значащих цифр в числе — 15, при большем их количестве число будет автоматически округляться.
Примеры:
123456789012345 -> 123456789012345
1234567890123456 -> 1.23456789012346E15
0.123456789012345 -> 0.123456789012345
0.1234567890123456 -> 0.123456789012346
Область допустимых значений для вводимых данных:
[3.37×10-4932;1.18×104932]
При выходе за границы интервала при вводе данных, вычислении ответа либо промежуточных результатов возникает ошибка.
Ввод дробей
Виды дробей:
Десятичная
Десятичным разделителем может являться точка или запятая.
Пример: 1.2
Обыкновенная
Числитель и знаменатель должны являться или натуральными числами (если дробь одноэтажная) или корректными обыкновенными дробями (если дробь многоэтажная).
Пример: 1//3; 1//3//7//9
Смешанная
Дробь состоит и целой части и корректной обыкновенной дроби, которая может быть многоэтажной.
Пример: 1 2//3; 1 3//7//9
Экспоненциальная запись чисел
Экспоненциальной записью называется представление чисел в виде мантиссы и порядка. Удобно для записи очень больших или очень малых чисел. Шаблон записи: MeE, где M — мантисса, а Е — экспонента. Мантисса должна являться рациональным числом, экспонента — целым. Итоговое число N вычисляется как N=M*10^E.
Примеры:
7E6 = 7*106 = 7*1000000 = 7000000
1.23456E-3 = 1.23456*10-3 = 1.23456 * 0.001 = 0.00123456
Ввод переменных
Переменные, или неизвестные, обозначаются прописными или строчными латинскими буквами, возможно с индексом.
Примеры:
х1 — переменная с индексом
х и Х — разные переменные
Ввод математических констант
| Обозначение | Название | Смысл | Значение |
|---|---|---|---|
| pi | Число Пи | Отношение длины окружности к её диаметру | 3,141592653589… |
| e | Число Эйлера | Основание натурального логирифма | 2.718281828459… |
Советы по вводу выражений
Лишних скобок не бывает. Если вы не уверены в том, что программа корректно распознает выражение или правильно выберет порядок действий — поставьте скобки.
Примеры:
sin2^3. Однозначно не сказать, к чему относится вторая степень, к синусу, или к аргументу.
Если подразумевалось, что квадрат относится к синусу, стоит ввести (sin2)^3, в противном случае — sin(2^3) Неоднозначное выражение может вызвать ошибку во время решения, например 2^-3, в
подобных случаях следует с помощью скобок отделять операторы друг от друга: 2^(-3)
Если в выражении много скобок, то легко запутаться в процессе ввода. Поэтому лучше при вводе открывающей скобки, сразу после неё вводить закрывающую, а содержимое писать внутри.
Пример:
Стадии ввода примера (1 2//3+4 5//6)/((3//5+7//8)*4)
1. ()
2. (1 2//3+4 5//6)/()
3. (1 2//3+4 5//6)/(()*4)
4. (1 2//3+4 5//6)/((3//5+7//8)*4)
Режимы решения
Приложение поддерживает 3 режима решения:
— Стандартное решение
— Решение “в столбик”
— Обыкновенные дроби
Если вам необходимы расписанные в виде столбиков арифметические действия, выбирайте режим “решение в столбик”, если решение вашего примера подразумевает использование обыкновенных, а не десятичных дробей, выбирайте режим “обыкновенные дроби”, в остальных случаях вам подойдёт режим стандартного решения.
Работа с интерфейсом программы
Описание интерфейса
Структура результата решения, вложенности
Описание частей решения
Решение состоит из 6 основных частей:
— Выражение — сам введенный пример
— Ответ — результат упрощений без потери точности.
— Решение по действиям — список упрощений, совершенных во время решения
— Решение по шагам — пошаговое изменение выражения под влиянием упрощений.
— Приведение к окончательному ответу. Если ответ можно упростить путём действий с потерей точности
(результатом которого является иррациональная (бесконечная) дробь, которую придется округлить, что и является
этой потерей точности), то это будет произведено в данной секции решения, которая состоит из подразделов:
— Окончательный ответ
— Приведение по действиям
— Приведение по шагам
— Решение уравнения — Решение выражения как уравнения (только для выражений, содержащих знак равенства)
Вложенности
В отличие от предыдущей версии, в этой решение не статично, а представляет собой динамический спискок картинок,
каждый элемент которого может содержать в себе другой подсписок картинок, каждый элемент которого может содержать
в себе другой подсписок… Максимальный уровень вложенности не ограничен.
Что может быть во вложенных элементах:
Побочные части решения (например, итоговый приблизительный результат в секции приведения к окончательному ответу)
Список действий или шагов в секции “решение по действиям/шагам”
Если действие сложное, во вложенных элементах содержатся внутренние операции, которые произведены во время его выполнении.
Примеры:
(x+y)^2
x^2*x^3
5!!
В первом подэлементе будет содержаться выражение, показывающее механизм данного действия, в последующих — его выполнение.
Подробная информация по выполненному действию: столбики для арифметических операций. Запланировано: подробная информация о действиях с обыкновенными дробями, многочленами.
Содержащий подсписок элемент обозначен специальной пиктограммой в левой части:
Элемент, выведенные подэлементы которого можно свернуть, обозначен другой пиктограммой:
При наведении на элемент, который можно свернуть или развернуть, изменяется курсор. Сворачивание или разворачивание происходит по клику. Иерархия элементов отображена с помощью древа вложенностей, нарисованного черным пунктиром.
Охваченные разделы математики
— Действия с натуральными числами
— Действия с десятичными, обыкновенными и смешанными дробями
— Упрощение выражений, действия с многочленами (умножение, деление, приведение подобных членов…)
— Решение линейных и квадратных уравнений
loviotvet.ru
Порядок действий
В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения. Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.
Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.
Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1
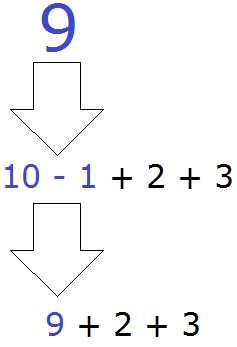
Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:
Осталось простейшее выражение 11 + 3, которое вычисляется легко:
11 + 3 = 14
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
8 + 6 = 14
Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
1) 3250 − 2905 = 345
2) 345 : 5 = 69
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.
В результате будем иметь следующий порядок:
1) 6 411 × 8 = 51 288
2) 51 288 − 40 799 = 10 489
3) 10 489 × 6 = 62 934
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
1) 50 377 + 20 338 = 70 715
2) 1 657 974 : 822 = 2 017
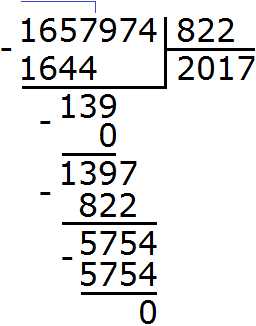
3) 2 017 × 106 = 213 802
4) 213 802−70 715 = 143 087
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
1) 96 : 4 = 24
2)
24 + 3 680 = 3 7043) 14026 − 3 704 = 10 322
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
5 + 2 − 2 − 1
Решение
Задание 2. Найдите значение выражения:
14 + (6 + 2 × 3) − 6
Решение
Задание 3. Найдите значение выражения:
486 : 9 − 288 : 9
Решение
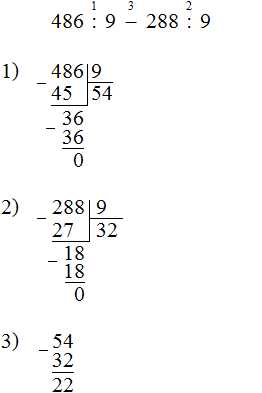
Задание 4. Найдите значение выражения:
756 : 3 : 4 × 28
Решение
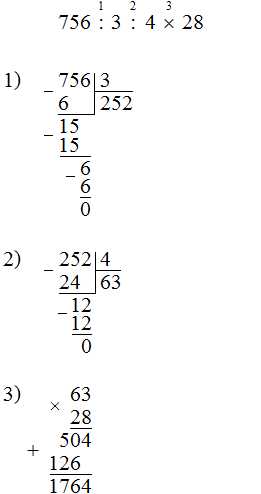
Задание 5. Найдите значение выражения:
807 : 3 − (500 − 58 × 4)
Решение
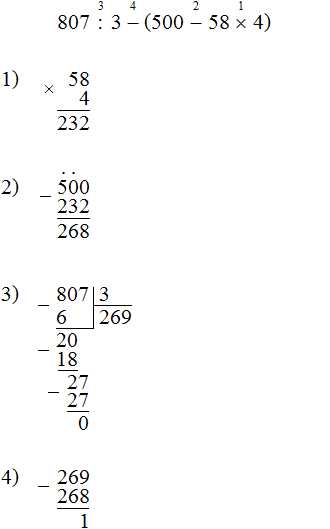
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
• Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
• Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
• Научите ребёнка всегда планировать и нумеровать выполняемые действия.
• Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
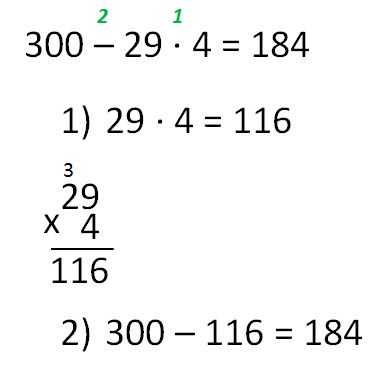
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками
Разберём конкретный пример:
- При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
- Начать следует с умножения, далее – сложение.
- После того, как выражение в скобках решено, приступаем к действиям вне их.
- По правилам порядка действий, следующим шагом будет умножение.
- Завершающим этапом станет вычитание.
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie.info
