Как скобку возвести в степень – Степени и возведение в степень, вторая, третья, четвёртая степени

Возведение степени в степень (формула (an)k=ank)

На этом уроке мы изучим возведение степени в степень. Вначале вспомним определение степени и теоремы об умножении и делении степеней с одинаковым основанием. Далее будет сформулирована теорема о возведении степени в степень. Затем мы приведем примеры ее использования на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач и будем решать типичные примеры с помощью всех теорем.

Напоминание:

Основные определения:

Здесь a – основание степени,

n – показатель степени,

– n-ая степень числа.

Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:

При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.

Теорема 2. Для любого числа а и любых натуральных n и k, таких, что  n > k справедливо равенство:

При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.

На этом уроке будет рассмотрена следующая теорема.

Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:

Вывод: частные случаи подтвердили правильность формулы . Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.

По определению степени:

 

Применим теорему 1:

 

Итак, мы доказали: , где а – любое число, n и k – любые натуральные числа.

Другими словами, чтобы возвести степень в степень показатели нужно перемножить, а основание оставить неизменным.

Пример 1: Упростить.

Для решения следующих примеров воспользуемся свойством .

а)

б)

в)

Комментарий к примеру 1.

Мы написали, что , но в то же время , так как .

Аналогично,   .

В качестве основания может быть любое допустимое алгебраическое выражение:

Пример 2:Упростить.

а)

б)

Пример 3: Вычислить.

а)  

б)  

в)

г). Комментарий:

д). Комментарий:

е). Комментарий:

Пример 4: Упростить.

Для решения следующих примеров будем пользоваться теоремами 1, 2, 3.

а)

б)

в)

г)

д) или быстрее

е) =

Пример 5: Вычислить:

а)= 

 

Список литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Mirurokov.ru (Источник).
2. Школьный помощник (Источник).
3. Интернет-портал Testent.ru (Источник).
4. Фестиваль педагогических идей «Открытый урок» (Источник).

 

Домашнее задание

1. Упростить:
   а)   б)    в)
2.  Вычислить:
   а)   б) ;   в)   
3. Упростить:
   а)   б)     в)              г)
4. Вычислить:
   а)            б)

interneturok.ru

Возведение в степень с помощью научного калькулятора

Nikolay-Monastyrskiy

103

13 подписчиков

24 марта 2014

Многим не раз приходилось решать задачи со степенями. Порой значение степени слишком велико, чтобы решать в уме или на листочке. В таких случаях на помощь приходит научный калькулятор.

Статьи по теме:

Вам понадобится

• — Научный калькулятор;
• — Выражение, которое нужно возвести в степень

Инструкция

К примеру, нужно посчитать такое выражение (см. картинку) Прописываем в научном калькуляторе:
1-(1+0,17)^5 и жмем «=»
Чтобы поставить этот значок «^» нужно нажать на кнопку «X^y»

Если нужно выражение возвести к квадрату, то стоит нажать кнопку «X^2»

Видео по теме

Обратите внимание

Неопытному пользователю легко запутаться в множестве кнопок калькулятора. ))))

Полезный совет

Научный калькулятор — вещь незаменимая в решении сложных и рутинных технических задач.

Совет полезен?

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Как раскрыть скобки?

В данной статье мы подробно рассмотрим основные правила такой важной темы курса математики, как раскрытие скобок. Знать правила раскрытия скобок нужно для того, чтобы верно решать уравнения, в которых они используются. 

Как правильно раскрывать скобки при сложении

Раскрываем скобки, перед которыми стоит знак « + »

Эта самый простой случай, ибо если перед скобками стоит знак сложения, при раскрытии скобок знаки внутри них не меняются. Пример:

(9 + 3) + (1 – 6 + 9) = 9 + 3 + 1 – 6 + 9 = 16.

Как раскрыть скобки, перед которыми стоит знак « — »

В данном случае нужно переписать все слагаемые без скобок, но при этом сменить все знаки внутри них на противоположные. Знаки меняются только у слагаемых из тех скобок, перед которыми стоял знак « — ». Пример:

(9 + 3) — (1 – 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.

Как раскрыть скобки при умножении

Перед скобками стоит число-множитель

В данном случае нужно умножить каждое слагаемое на множитель и раскрыть скобки, не меняя знаков. Если множитель имеет знак « — », то при перемножении знаки слагаемых меняются на противоположные. Пример:

3 * (1 – 6 + 9) = 3 * 1 — 3 * 6 + 3 * 9 = 3 – 18 + 27 = 12.

Как раскрыть две скобки со знаком умножения между ними

В данном случае нужно каждое слагаемое из первых скобок перемножить с каждым слагаемым из вторых скобок и затем сложить полученные результаты. Пример:

(9 + 3) * (1 – 6 + 9) = 9 * 1 + 9 * (- 6) + 9 * 9 + 3 * 1 + 3 * (- 6) + 3 * 9 = 9 – 54 + 81 + 3 – 18 + 27 = 48.

Как раскрыть скобки в квадрате

В случае, если сумма или разность двух слагаемых возведена в квадрат, скобки следует раскрывать по следующей формуле:

( х + у ) ^ 2 = х ^ 2 + 2 * х * у + у ^ 2.

В случае с минусом внутри скобок формула не меняется. Пример:

(9 + 3) ^ 2 = 9 ^ 2 + 2 * 9 * 3 + 3 ^ 2 = 144.

Как раскрыть скобки в другой степени

Если сумма или разность слагаемых возводится, например, в 3 или 4-ю степень, то нужно просто разбить степень скобки на «квадраты». Степени одинаковых множителей складываются, а

elhow.ru

Степень числа — 7 класс — Алгебра — Каталог статей

Степень числа

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4⁶ и произносят «четыре в шестой степени».
4 • 4 • 4 • 4 • 4 • 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:
•    4 — основание степени;
•    6 — показатель степени.
 
В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:

    

• Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

 
Запись aⁿ читается так: «а в степени n» или «n-ая степень числа a».
 

Исключение составляют записи:
•    a² — её можно произносить как «а в квадрате»;
•    a³ — её можно произносить как «а в кубе».
 

Конечно, выражения выше можно читать и по определению степени:
•    a² — «а во второй степени»;
•    a³ — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
    

• Степенью числа «а» с показателем n = 1 является само это число:
• a¹ = a
• Любое число в нулевой степени равно единице.
• a⁰ = 1
• Ноль в любой натуральной степени равен нулю.
• 0ⁿ = 0
• Единица в любой степени равна 1.
• 1ⁿ= 1

Выражение 0⁰ (ноль в нулевой степени) считают лишённым смыслом.
•    (-32)⁰ = 1
•    0²³⁴ = 0
•    1⁴ = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
 

Пример. Возвести в степень.
•    5³ = 5 • 5 • 5 = 125
•    2.5² = 2.5 • 2.5 = 6.25
•    (3)⁴ = 3• 3• 3• 3 = 81
      4       4  4   4  4   256

Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
    

• При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
 

Рассмотрим примеры возведения в степень отрицательных чисел.
 
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
 

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
    
Отрицательное число, возведённое в чётную степень, есть число положительное.

• Отрицательное число, возведённое в нечётную степень, — число отрицательное.
• Квадрат любого числа есть положительное число или нуль, то есть:
• a² ≥ 0 при любом a.

•    2 • (- 3)² = 2 • (- 3) • (- 3) = 2 • 9 = 18
•    — 5 • (- 2)³ = — 5 • (- 8) = 40
 

Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)⁴ и -5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.
 

Вычислить (- 5)⁴ означает найти значение четвёртой степени отрицательного числа.
(- 5)⁴ = (- 5) • (- 5) • (- 5) • (- 5) = 625
 

В то время как найти -5⁴ означает, что пример нужно решать в 2 действия:
1.    Возвести в четвёртую степень положительное число 5. 
5⁴ = 5 • 5 • 5 • 5 = 625
2.    Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание). 

-5⁴ = — 625
Пример. Вычислить: — 6² — (- 1)⁴
— 6² — (- 1)⁴ = — 37

1.    6² = 6 • 6 = 36
2.    -6² = — 36
3.    (- 1)⁴ = (- 1) • (- 1) • (- 1) • (- 1) = 1
4.    — (- 1)⁴ = — 1
5.    — 36 — 1 = — 37
 

Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
    

• В выражениях со степенями, не содержащими скобки, сначала выполняют возведение в степень, затем умножение и деление, а в конце сложение и вычитание.
• Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:
 
 

Cвойства степени

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1 
Произведение степеней
    

• При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
• a^m • aⁿ = a^m+n, где a — любое число, а m, n — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.
Примеры.
•    Упростить выражение. 
b • b² • b³ • b⁴ • b⁵ = b^1+2+3+4+5 = b¹⁵

•    Представить в виде степени. 
6¹⁵• 36 = 6¹⁵ • 6² = 6¹⁵⁺² = 6¹⁷

•    Представить в виде степени. 
(0,8)

3 • (0,8)¹² = (0,8)³⁺¹² = (0,8)¹⁵
    

• Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями. Оно не относится к их сложению.
• Нельзя заменять сумму (3³ + 3²) на 3³. Это понятно, если посчитать 3³ = 27 и 3²= 9; 27 + 9 = 36, а 3⁵ = 243

 

Свойство № 2 
Частное степеней
    

• При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
• a^m • aⁿ = a^m-n, где a — любое число, не равное нулю, а m, n — любые натуральные числа такие, что m > n.

Примеры.
•    Записать частное в виде степени 
(2b)⁵

 : (2b)³ = (2b)^5-3 = (2b)²

•    Пример. Решить уравнение. Используем свойство частного степеней. 
3⁸ : t = 3⁴

t = 3⁸ : 3⁴

t = 3^8-4

t = 3⁴

Ответ: t = 3⁴ = 81
 

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
•    Пример. Упростить выражение. 
4^5m+6 • 4^m+2 : 4^4m+3 = 4^5m+6+m+2 : 4^{4m + 3} = 4^{6m + 8 — 4m — 3}= 4^{2m + 5}

    
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4³ — 4²) на 4¹. Это понятно, если посчитать 4³ = 64 и 4² = 16; 64 — 16 = 48, а 4¹ = 4
Будьте внимательны!
 

Свойство № 3 

Возведение степени в степень
    

• При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
• (aⁿ)^m = a^{n • m}, где a — любое число, а m, n — любые натуральные числа.

•    Пример.
(a⁴)⁶ = a^{4 • 6} = a²⁴
•    Пример. Представить 3²⁰ в виде степени с основанием 32.
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
 
 

Свойства 4 
Степень произведения
    

• При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.
• (a • b)ⁿ = aⁿ • bⁿ, где a, b — любые рациональные числа; n — любое натуральное число.

•    Пример 1.

(6 • a² • b³ • c )² = 6² • a^{2• 2} • b^{3 • 2} • с ^{1 • 2} = 36 a⁴ • b⁶ • с ²

•    Пример 2.

(- x² • y)⁶ = ( (- 1)⁶ • x^{2 • 6} • y^{1 • 6}) = x¹² • y⁶
    
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(aⁿ • bⁿ)= (a • b) ⁿ
 

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
•    Пример. Вычислить.

2⁴ • 5⁴ = (2 • 5)⁴ = 10⁴ = 10 000

•    Пример. Вычислить.

0,5¹⁶ • 2¹⁶ = (0,5 • 2)¹⁶ = 1
 

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4⁵ • 3² = 4³ • 4² • 3² = 4³ • (4 • 3)² = 64 • 12² = 64 • 144 = 9216
 

Пример возведения в степень десятичной дроби.
4²¹ • (-0,25)²⁰ = 4 • 4 ²⁰ • (-0,25) ²⁰ = 4 • (4 • (-0,25))²⁰ = 4 • (- 1)²⁰ = 4 • 1 = 4

Свойства 5
Степень частного (дроби)
    

• Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
• (a : b)ⁿ = aⁿ : bⁿ, где a, b — любые рациональные числа, b ≠ 0, n — любое натуральное число.

•    Пример. Представить выражение в виде частного степеней. 
(5 : 3)¹² = 5¹² : 3¹²
 

Возведение в степень дроби

• При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.

Примеры возведения в степень дроби.

 

Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь. После этого возводим в степень и числитель, и знаменатель.
Пример.

Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.

•    Пример. Найти значение выражения рациональным способом. 

Свойства степеней

 

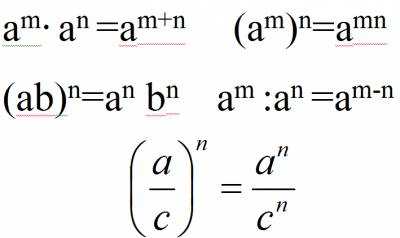
matematik.3dn.ru

что такое возведение в степень

Умножение числа самого на себя столько раз, сколько указано в показателе степени

Возведение в степень -это математическое действие, которое позволяет умножить число само на себбя скокато раз) например 3 во второй степени -это значит три умноженое само на себя =3*3=9 ; 3 в третей степени =3*3*3=27….потом вы будете изучать различные пример со степенями допустим как умножить 3 в третей на 2 в четвёртой и так далее…. так со сложением, вычитанием, делением и умножением, будете знать как возвести степень в степень…. в общем если вы этогоне изучали лутше не забивать голову заранее… ещё всё узнаешь_)

Если возведение в степень это УМНОЖЕНИЕ числа на сомо себя в n-раз, то почему тогда: 1^2=1 (1*1=1) — возведение в степень — умножение само на себя. Тогда и умножение — это возведение в степень: 1*2=2 (хотя должно быть так: 1*2=1^2=1*1=1) — странно, что определение работает только в одну сторону!!! 2*3 должно быть 8, а не 6, раз возведение в степень=умножению. В чём подвох????

touch.otvet.mail.ru