Сочетание без повторений | matematicus.ru
Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.
Обозначение: $С_n^m$
Допустим, имеется три буквы А, В и С.
Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.
При подсчете числа сочетаний элементов — порядок не важен.
Запишем формулу сочетания
Пример 1
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
Пример 2
Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.
Записать все возможные сочетания из указанных букв по три.
Решение
По формуле сочетания имеем,
$C_4^3 =\frac{{4!}}{{\left( {4 — 3} \right)!\cdot3!}} = \frac{{4!}}{{3!}} = \frac{{1\cdot2\cdot3\cdot4}}{{1\cdot2\cdot3}} = 4$
Пример 2
Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?
Решение
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно
Пример 3
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?
Решение
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$
Число способов отбора мужчин, четырех из семи равно $С_7^4$
По формуле комбинаторики – сочетания, группу можно сформировать способами:
Пример 4
Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?
Решение
Число способов выбора офицера: $С_3^1$
сержантов $С_6^2$
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$
Итак, получаем число способов составления суточного наряда
www.matematicus.ru
Сочетания с повторениями
Сочетание с повторениями из n элементов по m(m n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но из m каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если, например, два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Число
сочетаний с повторениями из n элементов
по m будем обозначать символом 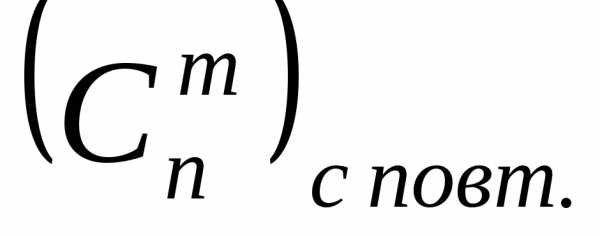 Формула для вычисления числа сочетаний
с повторениями:
Формула для вычисления числа сочетаний
с повторениями:
(1.6)
Замечание: m может быть и больше n.
Пример 1.4. Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?
Решение.
,
где m>n.
Ответ. Существует 84 различных способа выбора пирожных.
1.6. Перестановки
Перестановками из n элементов называются такие соединения, каждое из которых содержит все n элементов, и которые отличаются друг от друга лишь порядком расположения элементов.
Число перестановок их n элементов обозначается символом Рn, это то же самое, что число размещений из n элементов по n в каждом, поэтому
(1.7)
Пример 1.5. Менеджер ежедневно просматривает 6 изданий экономического содержания. Если порядок просмотра изданий случаен, то сколько существует способов его осуществления?
Решение. Способы просмотра изданий различаются только порядком, так как число, а, значит, и состав изданий при каждом способе — неизменны. Следовательно, при решении этой задачи необходимо рассчитать число перестановок.
По условию задачи n = 6.
Следовательно:
.
Ответ. Издания можно просмотреть издания 720 способами.
1.7. Перестановки с повторениями
Число перестановок с повторениями выражается при помощи формулы:
 ,
,(1.8)
где числа повторений.
Пример 1.6. Каким числом способов можно разделить m + n + s предметов на три группы, чтобы в одной группе было m предметов, в другой — n предметов, в третьей — s предметов?
Решение.
Ответ:
1.8. Правила комбинаторики
Правило суммы (принцип логического сложения) | Если объект а может быть выбран m способами, а объект b может быть выбран другими n способами (не такими как а), то выбор элемента а или b из объединенной совокупности может быть осуществлен m+n способами. |
Правило произведения (принцип логического умножения) | Если объект а может быть выбран m способами и после каждого такого выбора объект b может быть выбран |
Задачи к теме 1
1. Для разгрузки поступивших товаров менеджеру требуется выделить 4 из 15 имеющихся рабочих. Сколькими способами можно это сделать, осуществляя отбор в случайном порядке?
2. Сколько существует способов составления в случайном порядке списка из 5 кандидатов для выбора на руководящую должность?
3. Руководством риэлтерской фирмы принято решение о необходимости рекламы нового вида услуг. По расчетам отдела рекламы, выделенных средств хватит для того, чтобы поместить объявления только в 7 из 12 городских газет. Сколько существует способов случайного отбора газет для размещения рекламы?
4. Менеджер по персоналу рассматривает кандидатуры 7 человек, подавших заявления о приеме на работу на должность бухгалтера. Сколько существует способов приглашения кандидатов на собеседование в случайном порядке?
5. Расписание одного дня занятий на II курсе состоит из трех пар. В течение семестра студенты изучают 12 дисциплин. Сколько существует вариантов составления расписания занятий на один из дней недели, если в течение дня проводятся занятия по разным дисциплинам?
6. Покупая карточку лотереи “Спортлото”, игрок должен зачеркнуть 5 из 36 возможных чисел от 1 до 36. Если при розыгрыше тиража лотереи он угадает все 5 чисел, то имеет шанс выиграть значительную сумму денег. Сколько возможных комбинаций можно составить из 36 по 5, если порядок чисел безразличен?
7. а) Сколько различных «слов», каждое из которых содержит 6 букв, можно составить из слова «экспертиза»? б) Сколько различных «слов», каждое из которых содержит 10 букв, можно составить из слова «экспертиза»?
8. Распределение пар в первом круге Уимблдонского турнира проводится методом жеребьевки. Сколько комбинаций пар возможно составить, если в турнире участвуют 20 теннисисток?
9. Администрация города объявила тендер на строительство медицинского центра. В конкурсную комиссию поступило 8 запечатанных пакетов со сметами от различных строительных фирм. Сколько существует способов очередности вскрытия пакетов, если они вскрываются конкурсной комиссией в случайном порядке после окончания срока подачи заявок?
10. Для обнаружения нефти на участке необходимо пробурить до 11 скважин. Однако, компания имеет средства для бурения только 6 скважин. Сколько способов отбора шести различных скважин у компании?
11. В Российской Федерации номерной знак автомобиля каждого региона состоит из трех букв и трех цифр. Чему равно общее число возможных номерных знаков региона, если, для его составления используется 12 букв русского алфавита и 10 цифр. Рассмотрите два случая, когда: а) цифры и буквы в номере не повторяются; б) если повторяются?
12. В финале конкурса телевизионных программ по трем номинациям представлены 9 региональных телерадиокомпаний. Сколько существует вариантов распределения призов, если каждая телерадиокомпания может получить призы по нескольким номинациям и по каждой номинации установлены: а) одинаковые призы? б) различные призы?
13. PIN – код пластиковой карты состоит из 4 цифр. Сколько всевозможных комбинаций PIN – кода существует, если: а) цифры в коде не повторяются? б) повторяются?
14. Издательство планирует выпустить в текущем году 6 различных учебников по статистике. Каким количеством способов можно выбрать 30 экземляров, если в библиотеке университета должны быть представлены все виды изданных учебников по статистике?
15. Сколько различных «слов» можно составить из букв слова «колокол»?
17. В мореплавании принято давать сигналы, используя разноцветные флаги. Сколько сигналов можно составить, используя одновременно 8 флагов, из которых 1 красный, 2 синих, 3 зелёных и 2 белых?
18. Фирма планирует приобрести путевки для отдыха 25 сотрудников. Сколько существует вариантов приобретения путевок, если: а) контракт будет заключен с четырьмя пансионатами? б) с двумя пансионатами?
19. Компьютерный ключ к антивирусной программе состоит из 9 цифр. Сколько существует различных вариантов компьютерных ключей, если: а) цифры ключа не повторяются? б) цифры ключа повторяются?
20. В парфюмерном магазине имеется 5 различных косметических наборов. Фирме необходимо приобрести 18 подарков к празднику. Сколько в таком случае существует вариантов выбора подарков?
studfiles.net
14. СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ | Решение задач по математике и другим пре
Пусть имеются предметы n различных типов. Сколькими способами можно составить из них комбинацию из k элементов, если не принимать во внимание порядок элементов в комбинации, но при этом предметы одного и того же типа могут повторяться? Иными словами, различные комбинации должны отличаться количеством предметов хотя бы одного типа. Такие комбинации называются сочетаниями с повторениями, а их общее число будем обозначать .
Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть сочетаний с повторениями по два элемента: ab, ac, bc, aa, bb, cc.
Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но и k каких угодно и как угодно повторяющихся элементов.
Следует отметить, что если, например, две комбинации по k элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.
Существует специальная формула для вычисления числа сочетаний с повторениями:
(12.1)
Выведем эту формулу. Прежде всего надо занумеровать возможные типы элементов числами от 1 до n (иначе можно оказаться в положении мужа, который никак не мог вспомнить, что ему поручила купить жена: 5 пакетов молока и 2 банки пива или наоборот 2 пакета молока и 5 банок пива). Теперь можно каждую комбинацию зашифровать с помощью последовательности единиц и палочек: для каждого типа с 1-го до n-го по порядку написать столько единиц, сколько предметов этого типа входит в комбинацию, а различные типы отделять друг от друга палочками.
Например, в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:
В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись . Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют).
В результате мы получим столько единиц, сколько предметов входит в комбинацию, т. е. k, а число палочек будет на 1 меньше, чем число типов предметов, т. е. n–1. Таким образом, мы получим перестановки с повторениями из k единиц и n–1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация.
Итак, число сочетаний с повторениями из элементов n типов по k равно числу P(k, n–1) перестановок с повторениями из n–1 палочек и k единиц. А
. Поэтому.
Пример 12.1. В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
Пример 12.2. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? 8 открыток? Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний с повторениями из 10 элементов по 10. Следовательно,
, .
В случае, когда требуется купить 8 различных открыток, получим сочетания без повторений:
.
Пример 12.3. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку , , , , , то существует чисел, удовлетворяющих условию задачи.
Упражнения
12.1. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ: .
12.2. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырёх пирожных?
Ответ: .
12.3. Сколько существует треугольников, длины сторон которых принимают одно из значений 4, 5, 6, 7?
Ответ: .
12.4. Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10?
Ответ: .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Комбинаторика в MS EXCEL. Примеры и методы
Подсчитаем в MS EXCEL количество Сочетаний с повторениями из n по k (выборка с возвращением). Также с помощью формул выведем на лист соответствующие варианты Сочетаний (английский перевод термина: combinations with repetition).
Сочетания с повторениями (выборка с возвращением) — это Сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз.
Примечание: О Сочетаниях без повторений (без возвращения элементов) можно прочитать в статье Сочетания без повторений: Комбинаторика в MS EXCEL
Например, из множества содержащего 3 (n) различных элемента (a, b, c) можно сформировать 6 =ФАКТР(3+2-1) / (ФАКТР (3-1) * ФАКТР (2)) упорядоченных наборов по 2 (k) элемента: аа, ab, ac, bb, bc, сс. В отличие от Сочетаний без повторений наборы аа, bb и сс допустимы. В отличие от Размещений наборы ac и ca считаются одинаковыми (порядок не важен).
В отличие от Сочетаний без повторений, k может быть меньше или больше n. Например, из множества содержащего 2 (n) различных элемента (a, b) можно сформировать 4 =ФАКТР(2+3-1) / (ФАКТР (2-1) * ФАКТР (3)) упорядоченных наборов по 3 (k) элемента (т.е. 4 сочетания с повторениями из 2 по 3): ааa, аab, abb, bbb.
В файле примера MS EXCEL приведен подсчет количества Сочетаний с повторениями и созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания с повторениями.
Задача
В магазине платки 4-х цветов продаются вперемешку в огромной корзине. Женщина не может определиться с выбором, и поэтому решается довериться случаю – выбрать не глядя 3 платка. Определить число различных вариантов покупки 3-х платков.
Так как не важно, в какой последовательности женщина будет выбирать платки, то нам нужно определить число Сочетаний с повторениями покупки 3-х платков 4-х возможных цветов. Т.е. n=4, а k=3. Оказывается, что таких вариантов =(4+3-1)!/(4-1)!/3! равно 20.
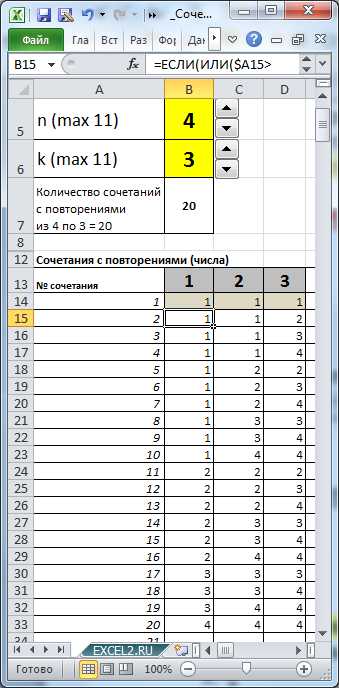
Воспользуемся файлом примера, чтобы убедиться, что мы решили задачу правильно.
По аналогии с решением задачи в статье Размещения без повторений сопоставим произвольным образом 4-м различным цветам числовые значения: 1; 2; 3; 4.
Выставив в ячейках В5 и В6 значения 4 и 3 соответственно, определим все варианты размещений.
Примечание: О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL, а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL.
excel2.ru

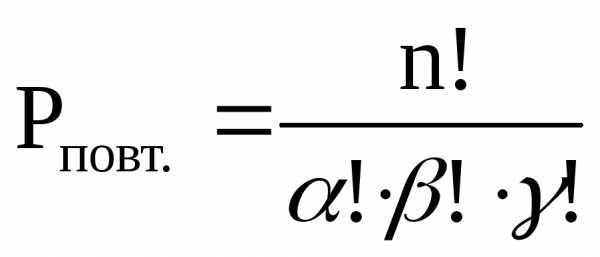 ,
,