sin (п / 2) + cos (п / 2)
Самый простой способ найти значение выражения sin (п / 2) + cos (п / 2) — это воспользоваться таблицей значений тригонометрических функций основных углов.
Согласно таблице sin (п / 2) равен единице, а cos (п / 2) равен нулю. Тогда значение выражения будет вычислено следующим образом:
sin (п / 2) + cos (п / 2) = 1 + 0 = 1.
Но бывают случаи, когда таблицы нет под рукой, значений тригонометрических функций основных углов наизусть не выучили, а найти решение нужно.
Тогда можно использовать тригонометрическую окружность.
Для простоты понимания сначала можно перевести значение радиан в градусы. Для этого воспользуемся тем, что радиан равно 180 градусов. Получим:
Дальше отмечаем на окружности угол радиан или 90 градусов.
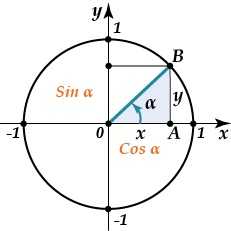
Получаем точку на окружности, которая совпадет с единицей на оси ОУ.
На тригонометрической окружности за значения косинусов отвечает ось Ох, а за значения синусов — ось Оу. Если спроектировать нашу точку на ось Оу, то мы получим значение синуса 90 градусов, равное единице. А спроектировав эту точку на ось Ох получаем значение косинуса, равное нулю. Такой же результат мы получали и с помощью таблицы.
ru.solverbook.com
sin p/2
Чтобы вычислить значение тригонометрического выражения можно применить несколько методов. Рассмотрим их.
1-й метод.
Этот метод используется чаще всего и является одним из простейших для распространенных углов типа . Но для использования этого метода нужно, чтобы была в наличии таблица тригонометрических функций:
По таблице найдем пересечение между функцией синус и аргументом . В результате получим значение , равное 1.
2-й метод.
Он может использоваться в любом случае, особенно, если нет в наличии таблицы. По этому методу можно использовать тригонометрический круг, который позволяет определять значения тригонометрических функций от многих аргументов.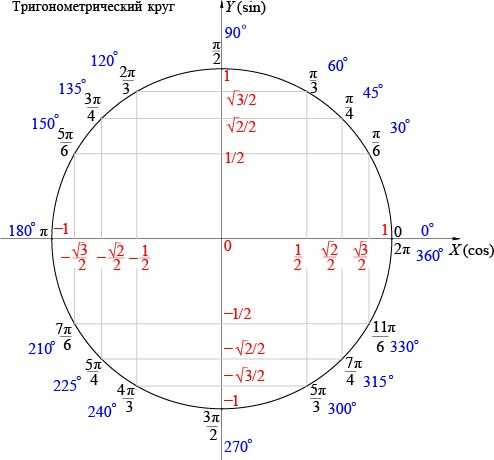
На тригонометрическом круге (или окружности) за значения функции синус отвечает ось ординат. Точка соответствует 90 градусам и на окружности находится на оси ординат в точке 1. Поскольку именно ось ординат содержит значения синусов, то получим, что равно 1.
3-й метод.
Если нет возможности использовать таблицу или тригонометрический круг, то можно воспользоваться синусоидой (графиком функции синус). В некоторых случаях данный метод даже удобнее, чем таблица или тригонометрическая окружность.
По синусоиде найдем, в какой точке функция синус будет соответствовать углу . Получим значение, равное 1.
ru.solverbook.com
sin (x + п / 2)
Задача.
Упростить выражение .
Решение.
Перед упрощением необходимо проанализировать его и обратить внимание на то, из чего оно состоит. Данное выражение является синусом суммы двух различных аргументов.
Тригонометрические формулы содержат варианты для разложения суммы и разности основных тригонометрических функций разных аргументов и носят название формул сложения или разности.
Выше упомянутые формулы используют чаще всего, когда один из аргументов — постоянное число. Например, в данном задании: первым аргументом является неизвестное число х, а вторым — постоянное число . В таких случаях значение тригонометрической функции от постоянного числа можно найти, вследствие чего выражение упростится.
Рассмотрим заданное выражение. Для его упрощения будем использовать соответствующую формулу тригонометрической функции от суммы:
Так как в полученном выражении присутствуют тригонометрические функции, для которых значение может быть вычислено при помощи таблицы тригонометрических функций, вычислим их и подставим в выражение.
Из таблицы получим, что равен нулю, а равен 1. Следовательно:
Ответ. .
ru.solverbook.com
sin(p)^2-sin(p)^2*cos(p)^2 если p=3 (упростите выражение)
Решение
2 2 2 sin (p) - sin (p)*cos (p)
$$- \sin^{2}{\left (p \right )} \cos^{2}{\left (p \right )} + \sin^{2}{\left (p \right )}$$
Подстановка условия[LaTeX]
sin(p)^2 - sin(p)^2*cos(p)^2 при p = 3
sin(p)^2 - sin(p)^2*cos(p)^2
$$- \sin^{2}{\left (p \right )} \cos^{2}{\left (p \right )} + \sin^{2}{\left (p \right )}$$
sin((3))^2 - sin((3))^2*cos((3))^2
$$- \sin^{2}{\left ((3) \right )} \cos^{2}{\left ((3) \right )} + \sin^{2}{\left ((3) \right )}$$
sin(3)^2 - sin(3)^2*cos(3)^2
$$- \sin^{2}{\left (3 \right )} \cos^{2}{\left (3 \right )} + \sin^{2}{\left (3 \right )}$$
sin(3)^2 - cos(3)^2*sin(3)^2
$$- \sin^{2}{\left (3 \right )} \cos^{2}{\left (3 \right )} + \sin^{2}{\left (3 \right )}$$
Численный ответ[LaTeX]
sin(p)^2 - cos(p)^2*sin(p)^2Объединение рациональных выражений
[LaTeX]
2 / 2 \ sin (p)*\1 - cos (p)/
$$\left(- \cos^{2}{\left (p \right )} + 1\right) \sin^{2}{\left (p \right )}$$
Общее упрощение[LaTeX]
$$\sin^{4}{\left (p \right )}$$
Собрать выражение[LaTeX]
3 cos(2*p) cos(4*p) - - -------- + -------- 8 2 8
$$- \frac{1}{2} \cos{\left (2 p \right )} + \frac{1}{8} \cos{\left (4 p \right )} + \frac{3}{8}$$
Комбинаторика[LaTeX]
2 -sin (p)*(1 + cos(p))*(-1 + cos(p))
$$- \left(\cos{\left (p \right )} — 1\right) \left(\cos{\left (p \right )} + 1\right) \sin^{2}{\left (p \right )}$$
Тригонометрическая часть[LaTeX]
$$\sin^{4}{\left (p \right )}$$
www.kontrolnaya-rabota.ru
2*sin(2*p-x)-sin(3*p/2-x)-2*cos(p/2+x) если p=-1/4 (упростите выражение)
Решение
/3*p \ /p \
2*sin(2*p - x) - sin|--- - x| - 2*cos|- + x|
\ 2 / \2 /$$2 \sin{\left (2 p — x \right )} — \sin{\left (\frac{3 p}{2} — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Подстановка условия[LaTeX]
2*sin(2*p - x) - sin((3*p)/2 - x) - 2*cos(p/2 + x) при p = -1/4
2*sin(2*p - x) - sin((3*p)/2 - x) - 2*cos(p/2 + x)
$$2 \sin{\left (2 p — x \right )} — \sin{\left (\frac{3 p}{2} — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
2*sin(2*(-1/4) - x) - sin((3*(-1/4))/2 - x) - 2*cos((-1/4)/2 + x)
$$2 \sin{\left (2 (-1/4) — x \right )} — \sin{\left (\frac{3 (-1/4)}{2} — x \right )} — 2 \cos{\left (\frac{(-1/4)}{2} + x \right )}$$
2*sin(2*(-1)/4 - x) - sin((3*(-1)/4)/2 - x) - 2*cos(-1/8 + x)
$$2 \sin{\left (- x + \frac{-2}{4} \right )} — \sin{\left (- x + \frac{- \frac{3}{4}}{2} 1 \right )} — 2 \cos{\left (x — \frac{1}{8} \right )}$$
-2*cos(-1/8 + x) - 2*sin(1/2 + x) + sin(3/8 + x)
$$\sin{\left (x + \frac{3}{8} \right )} — 2 \sin{\left (x + \frac{1}{2} \right )} — 2 \cos{\left (x — \frac{1}{8} \right )}$$
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Численный ответ[LaTeX]
-sin((3*p)/2 - x) + 2.0*sin(2*p - x) - 2.0*cos(p/2 + x)Рациональный знаменатель
[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Объединение рациональных выражений[LaTeX]
/-2*x + 3*p\ /p + 2*x\
- sin|----------| - 2*cos|-------| + 2*sin(-x + 2*p)
\ 2 / \ 2 / $$2 \sin{\left (2 p — x \right )} — \sin{\left (\frac{1}{2} \left(3 p — 2 x\right) \right )} — 2 \cos{\left (\frac{1}{2} \left(p + 2 x\right) \right )}$$
Общее упрощение[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Собрать выражение[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Общий знаменатель[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Тригонометрическая часть[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(2*p - x)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
Комбинаторика[LaTeX]
/ 3*p\ / p\
- sin|-x + ---| - 2*cos|x + -| + 2*sin(-x + 2*p)
\ 2 / \ 2/ $$- \sin{\left (\frac{3 p}{2} — x \right )} + 2 \sin{\left (2 p — x \right )} — 2 \cos{\left (\frac{p}{2} + x \right )}$$
[LaTeX]
/3*p\ /3*p\ /p\ /p\ cos|---|*sin(x) - cos(x)*sin|---| - 2*cos(x)*cos|-| - 2*cos(2*p)*sin(x) + 2*cos(x)*sin(2*p) + 2*sin(x)*sin|-| \ 2 / \ 2 / \2/ \2/
$$2 \sin{\left (\frac{p}{2} \right )} \sin{\left (x \right )} — \sin{\left (\frac{3 p}{2} \right )} \cos{\left (x \right )} + 2 \sin{\left (2 p \right )} \cos{\left (x \right )} + \sin{\left (x \right )} \cos{\left (\frac{3 p}{2} \right )} — 2 \sin{\left (x \right )} \cos{\left (2 p \right )} — 2 \cos{\left (\frac{p}{2} \right )} \cos{\left (x \right )}$$
www.kontrolnaya-rabota.ru
