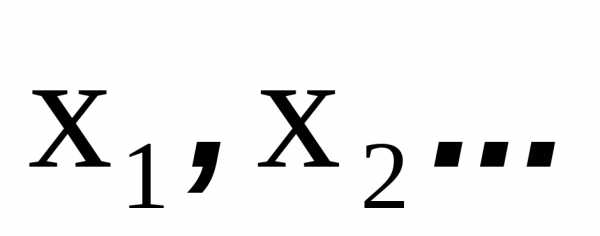Расширенная случайная величина – § 4. Случайные величины, случайные элементы.

§ 4. Случайные величины, случайные элементы.

4.1.Пусть (,F) и (R¹,(R¹)) — измеримыепространства.

Определение.Действительная функция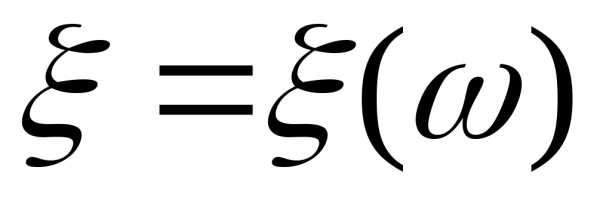определенная (,F), принимающая значения вR¹называетсяF– измеримой илислучайной величиной, если: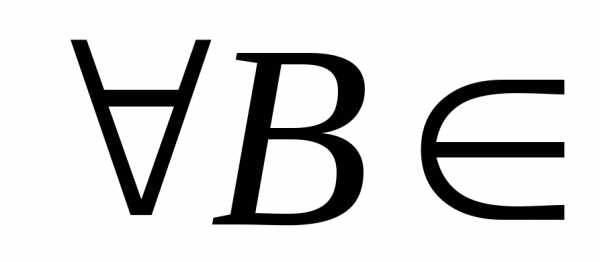(R¹)F(то есть, прообразявляется измеримым множеством в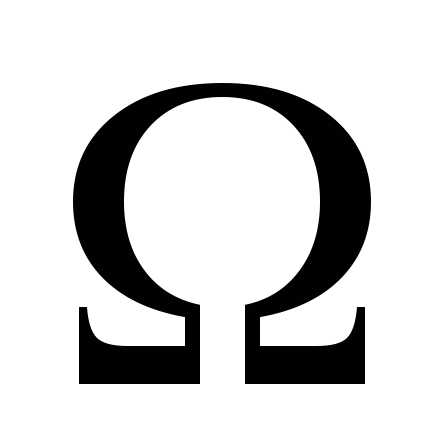

).

Если 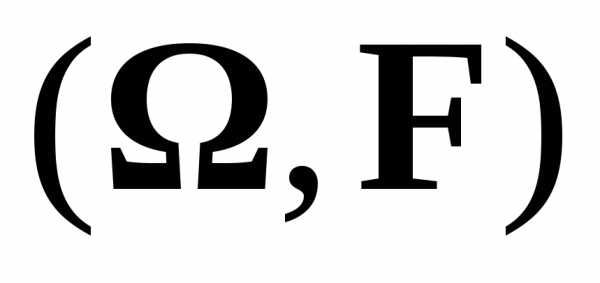=(Rⁿ,(Rⁿ)), то(Rⁿ) – измеримые функции называютсяборелевскими.

Простейшим примером случайной величины является

Определение.Случайная величина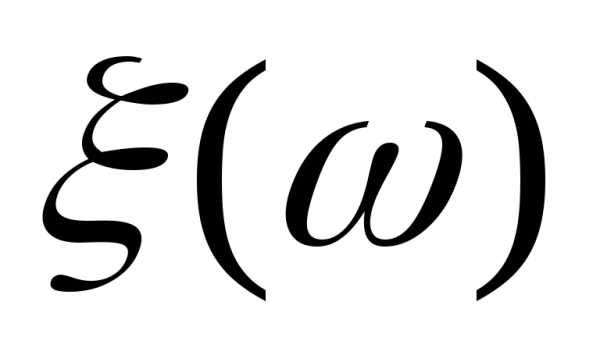представимая в виде

(2)

где

Fназываетсядискретной. Если число слагаемых в сумме в (2) конечно, то случайная величина называетсяпростой.

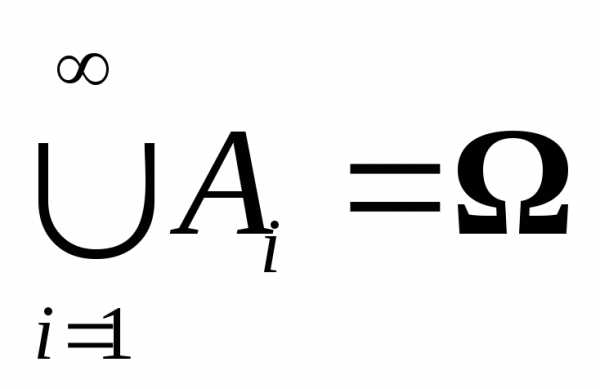
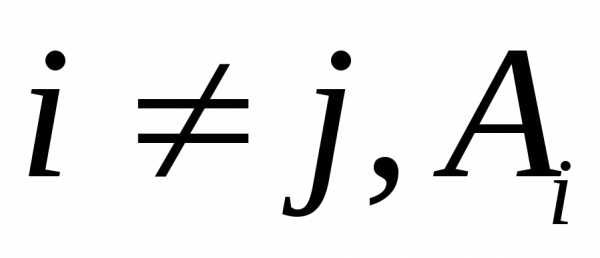
Замечание.Случайная величинаэтонекоторая характеристика эксперимента, результаты которого зависят от случая. Требование измеримости важно. Действительно, если на (,F) задана вероятностная мераР и , тов этом случае можно говорить о вероятности события, состоящегов том, что значение случайной величины принадлежит борелевскому множествуВ.

Определение.Вероятностная мера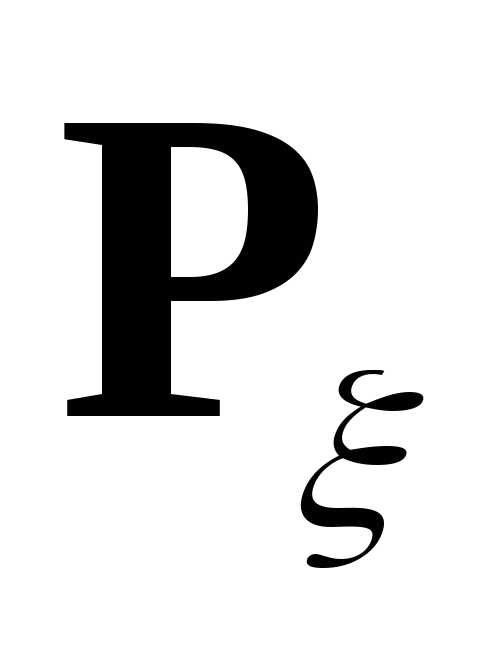на (R,(R)) с,

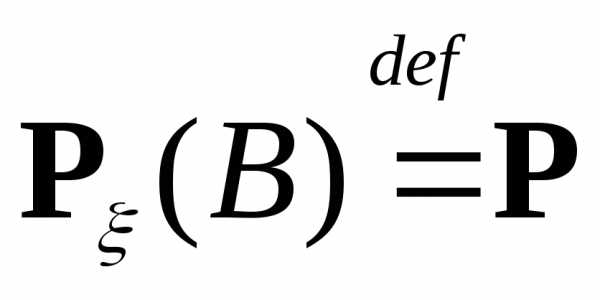(R¹), называетсяраспределением вероятностей случайной величинына (R,(R)).

Определение.Функция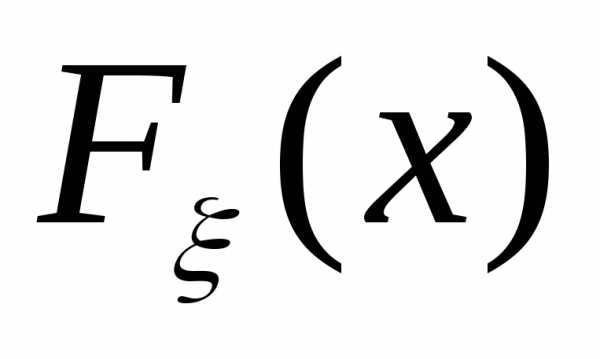Р, где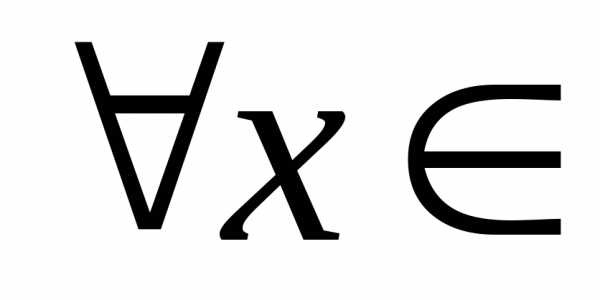R¹, называетсяфункцией распределения случайной величины.

Замечание.Для дискретной случайной величины мера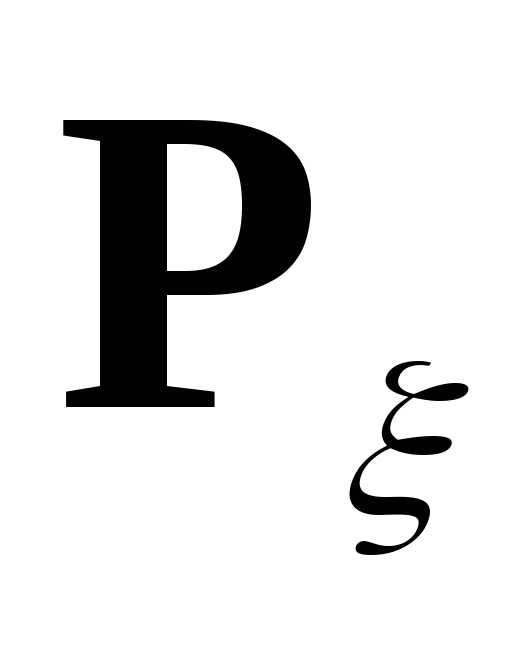сосредоточена не более чем в счетном числе точек и может быть представлена в виде,

где .

Определение. Случайная величина

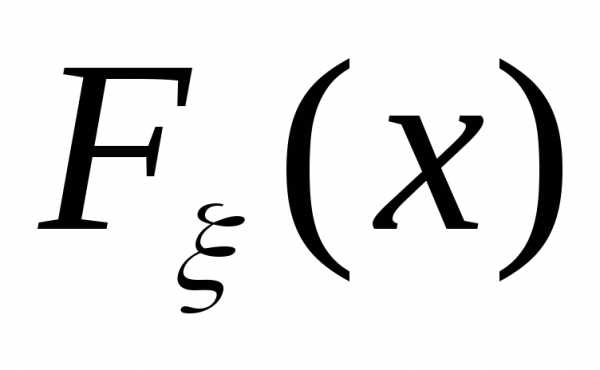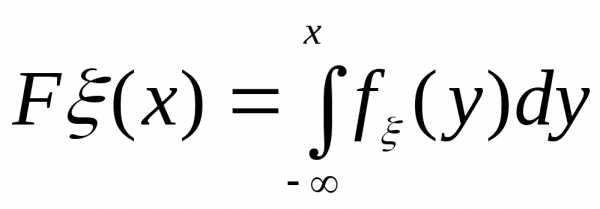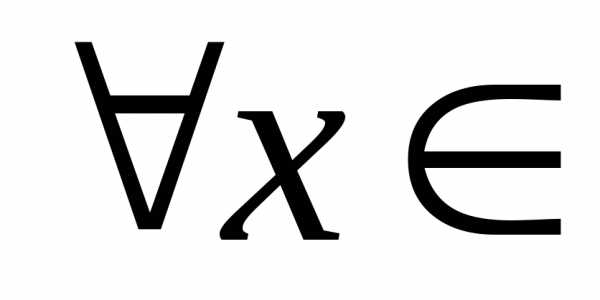называетсянепрерывной, если ее функция распределениянепрерывна. Случайная величинаназываетсяабсолютно непрерывной, если,R¹.

4.2.Вопрос: Когда функцияобозначаемая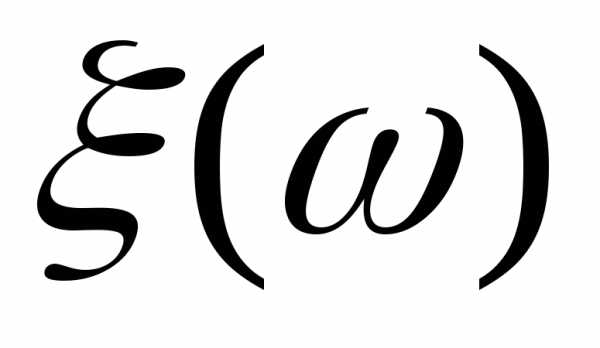является случайной величиной? Для этого надо проверить условиеFдля любого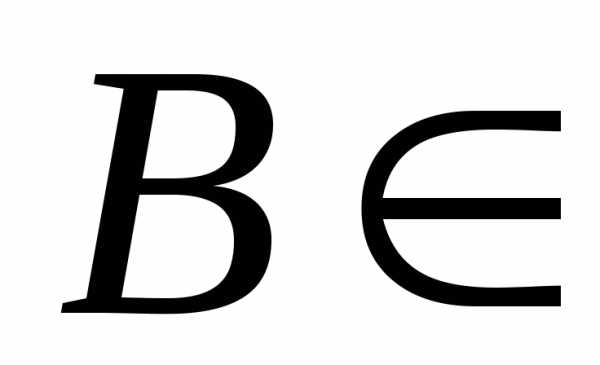(R¹).

Лемма 7.Пусть– некоторая система множеств такая, что

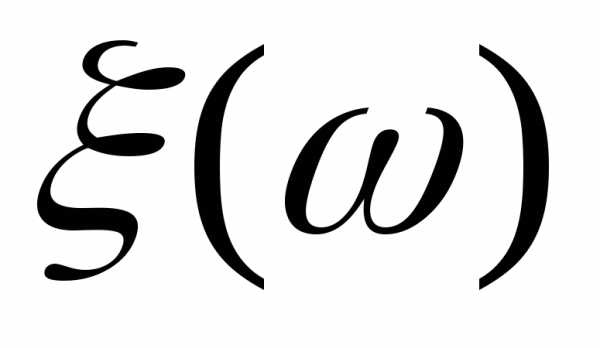()=(R¹). Для того, чтобыбылаF— измеримой необходимо и достаточно, чтобыFдля всех.

Доказательство.Необходимостьочевидна.

Достаточность.Пусть– система борелевских множеств, для которых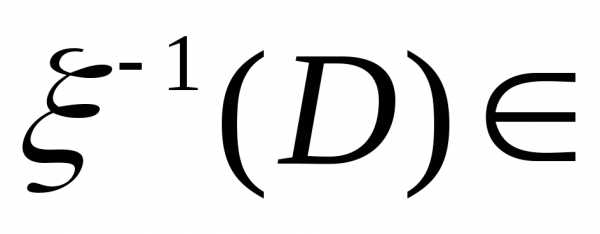F. Известно, что:

i),ii),iii)=.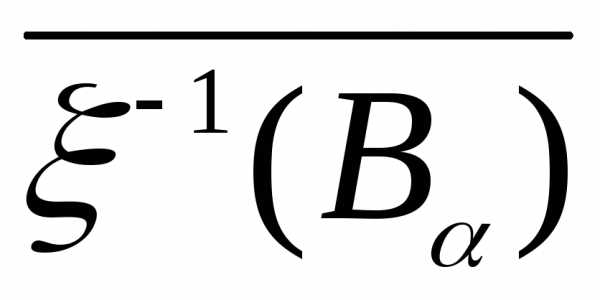

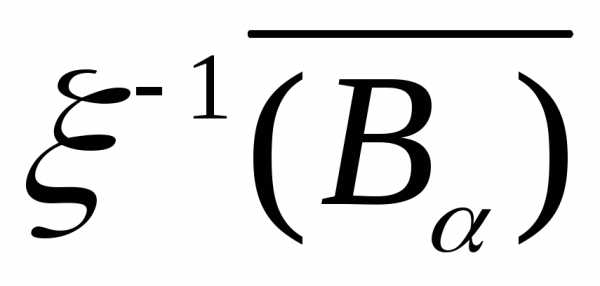Отсюда следует, что система – является-алгеброй, значит

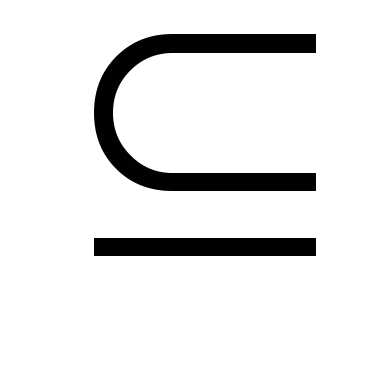
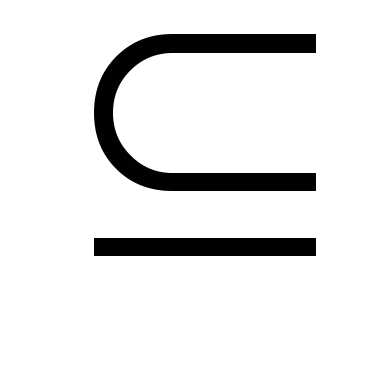(R¹) и(), следовательно=(R¹).

Лемма 8.Пусть: R¹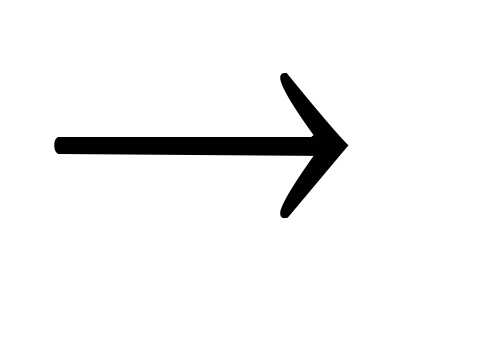R¹— борелевская функция, а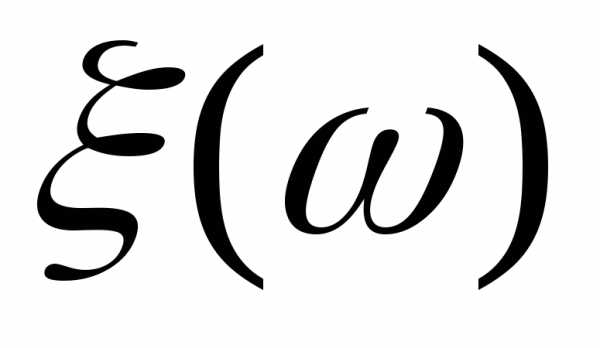— случайная величина. Тогда сложная функция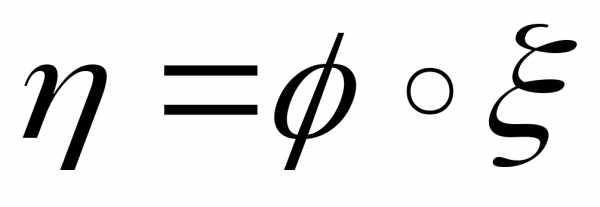(то есть) — случайная величина.

Доказательство. Действительно

,

так как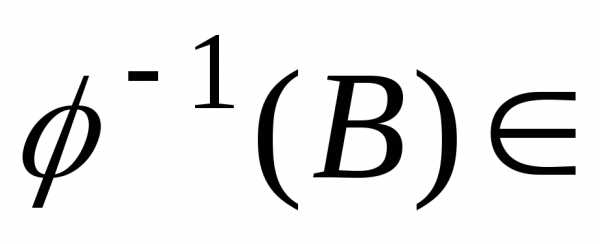

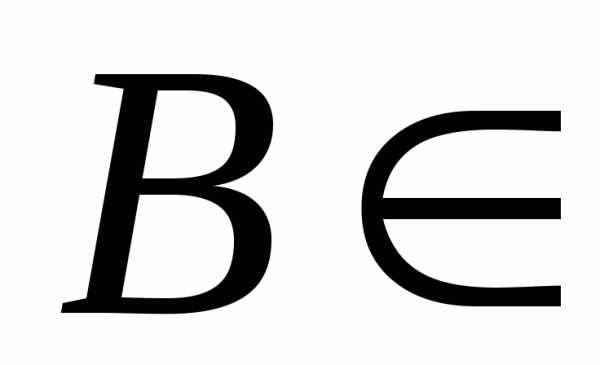(R¹),(R¹).

Доказательство закончено.

Определение. Функция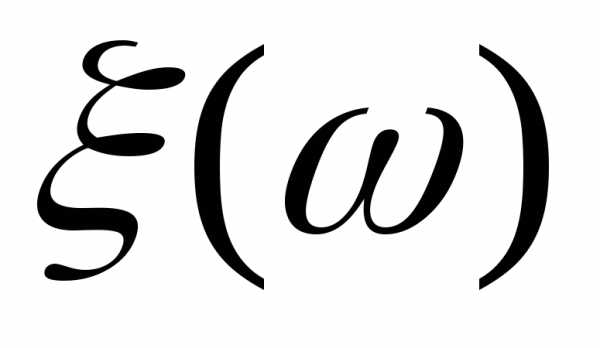на (,F) со значениями в=называетсярасширенной случайной величиной, если: для(R¹)F.

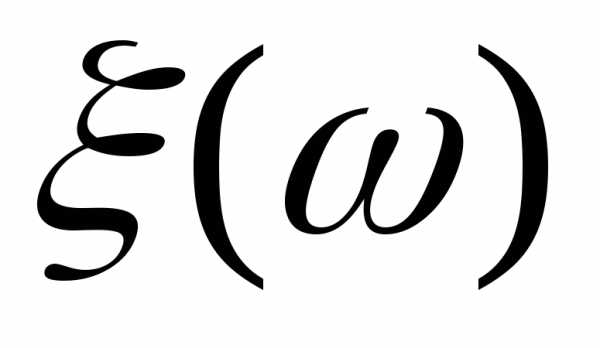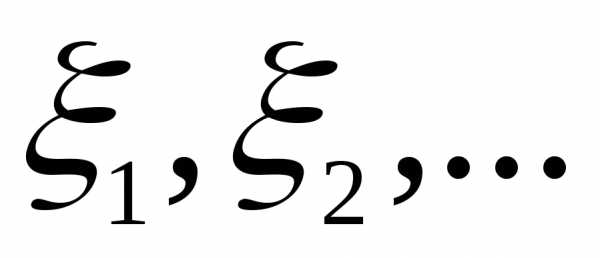Теорема 9. 1) Для любой случайной величинынайдется последовательность простых случайных величинтаких, что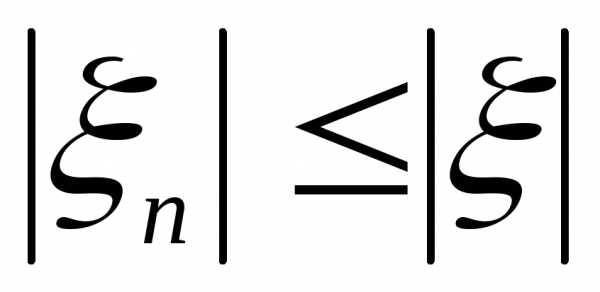

ипридля всех.

2) Если случайная величина , то найдется последовательность простых случайных величин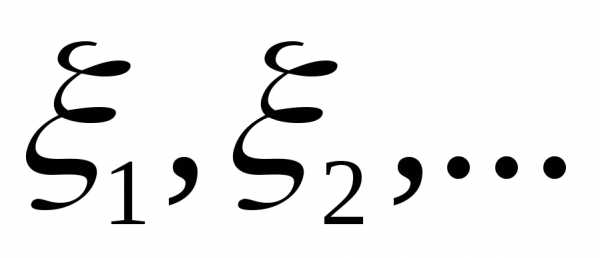таких, чтодля всех.

Доказательство. Начнем с пункта 2). Положим,и

непосредственной проверкой, устанавливается, что для всех. Отсюда следует и доказательство пункта 1) так какможно представить в виде, где.

Теорема 10.Пусть- последовательность расширенных случайных величин и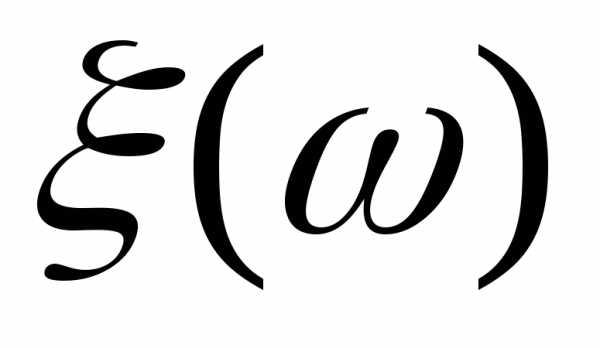=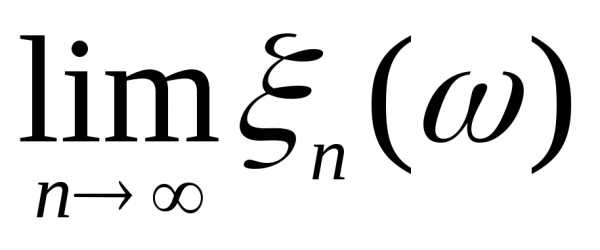. Тогда-расширенная случайная величина.

4.3.Определение. Пусть— случайная величина. Пусть множества извида,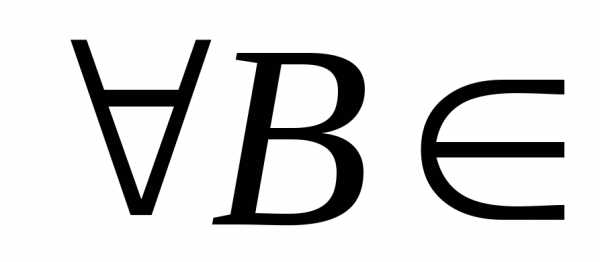(R¹) . Наименьшую-алгебру порожденную такими множествами называют-алгеброй, порожденной случайной величиной

и обозначают ее черезF^.

Если — борелевская функция, то из леммы 7 следует, что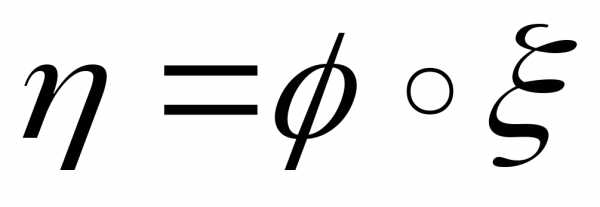— случайная величина, причемF^— измерима. Оказывается, справедливо и обратное утверждение.

Теорема 11.(Бореля). Пусть–измеримая случайная величина. Тогда найдется борелевская функция: R¹R¹ такая, что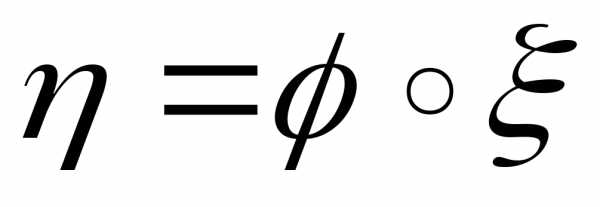, т.е. для каждого. (Докажите самостоятельно.)

4.4.Определение. Пусть (,F) и (E,) — измеримые пространства.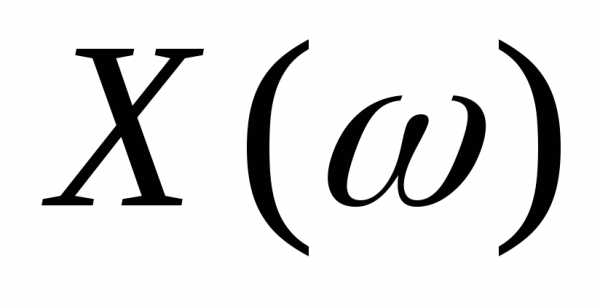определенная напринимающая значения вEназываетсяF/ –измеримой функцией илислучайным элементом(со значениями вE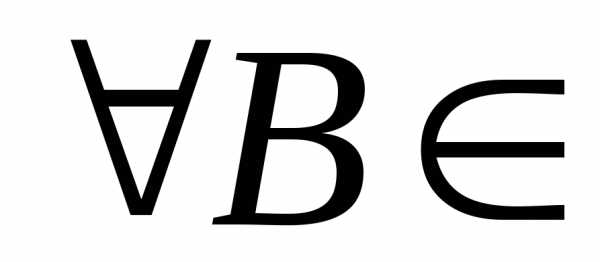F). (3)

Примеры случайных элементов:

1) Если (E,) = (R¹,(R¹)), то определение случайного элемента совпадает с определением случайной величины.

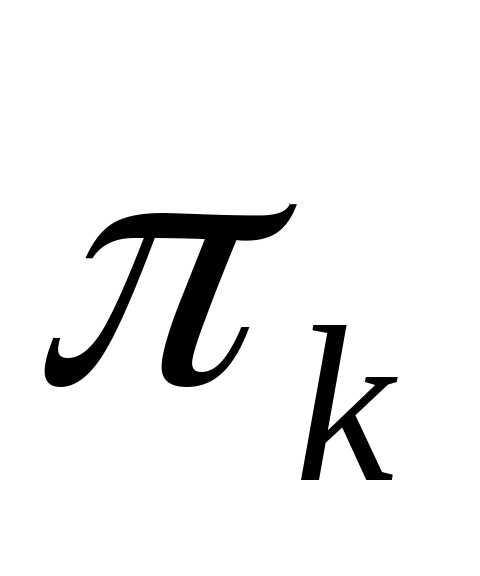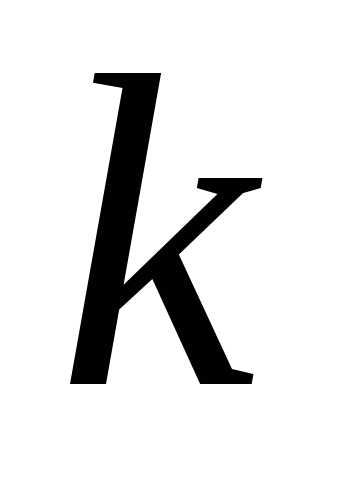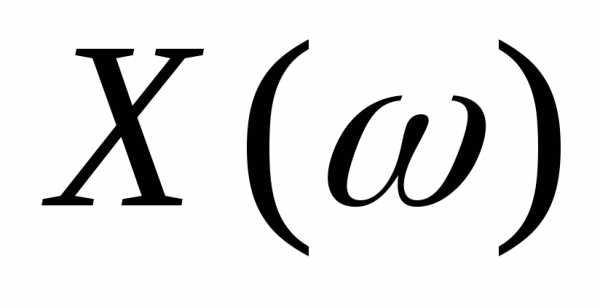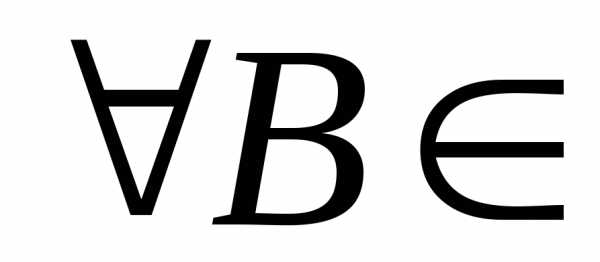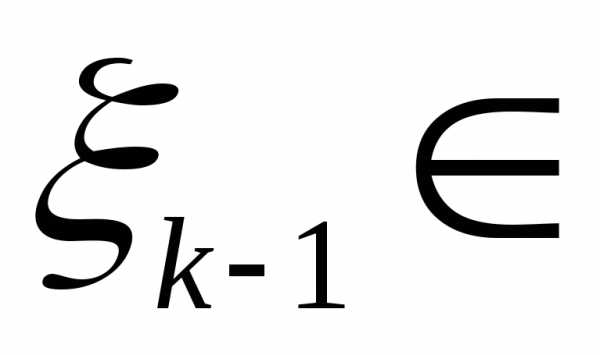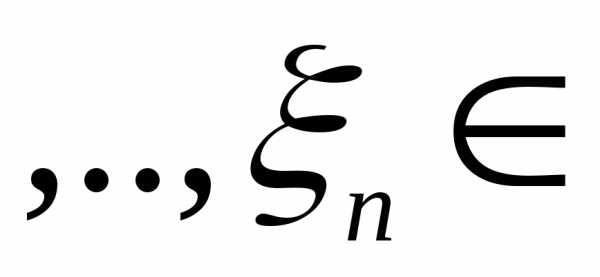2) Пусть (E,) = ( Rⁿ,(Rⁿ)). Тогда случайный элементназываетсяn — мерным случайным вектором. Если— проекцияRⁿна-ую координату, то=, где. Ясно, что— обычные случайные величины. Действительно, для(R¹)R¹,..,R¹,R¹R¹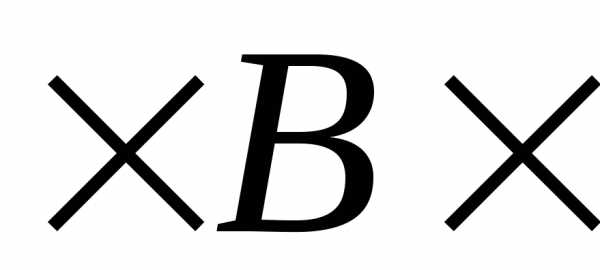}=(R¹R¹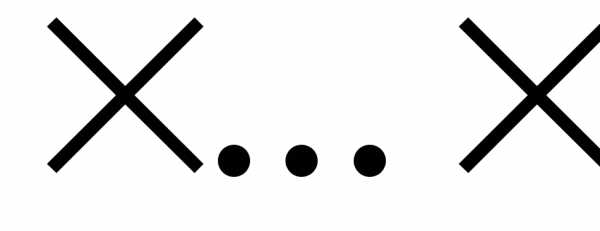R¹R¹)F.

Определение.Упорядоченый набор случайных величин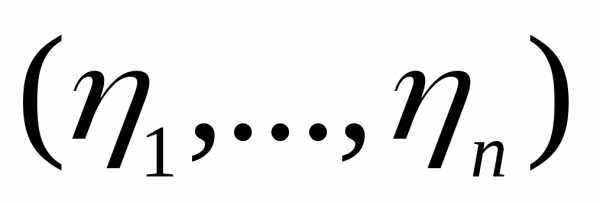будет называться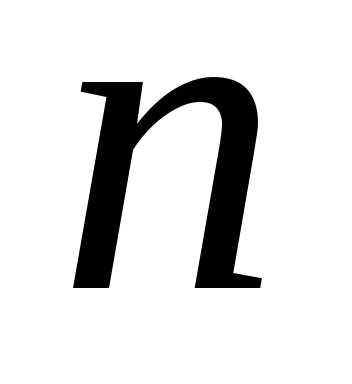— мернымслучайным вектором.

В соответствии с этим определением всякий случайный элемент 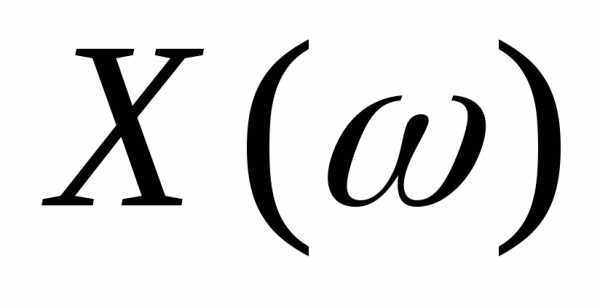со значениями в Rⁿ будет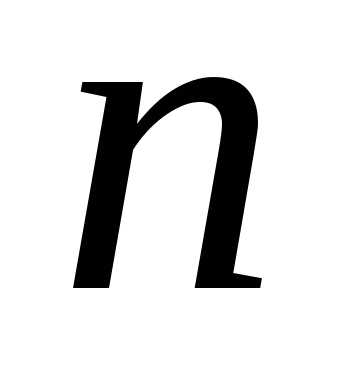— мерным случайным вектором. Справедливо обратноеутверждение: всякий n- мерный случайный вектор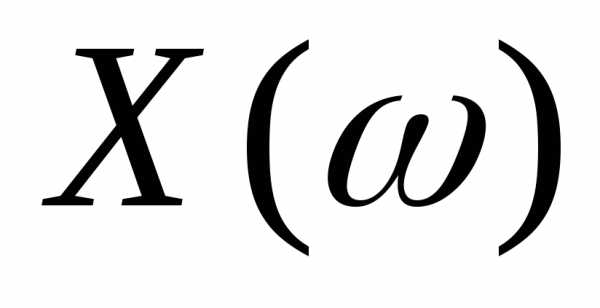=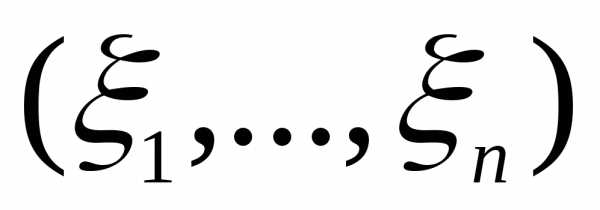есть случайный элемент в Rⁿ. Действительно, если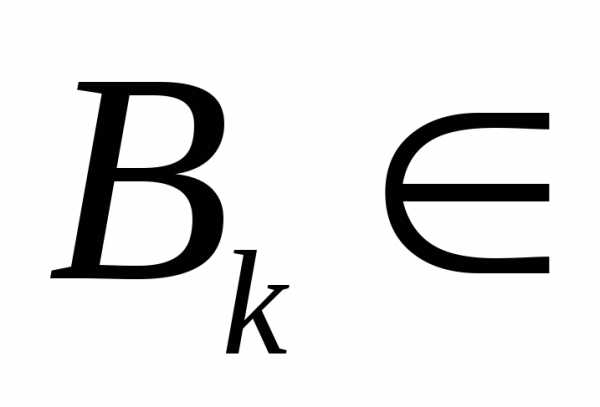(R¹),, тоF, то наименьшая-алгебра,порожденная всеми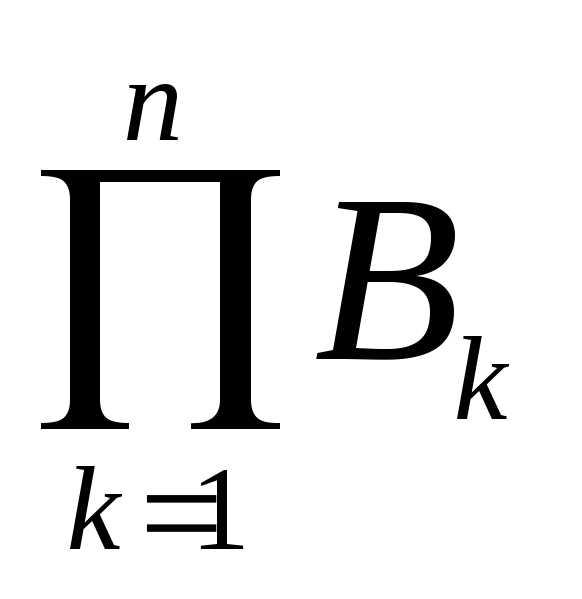совпадает с(Rⁿ). поэтому для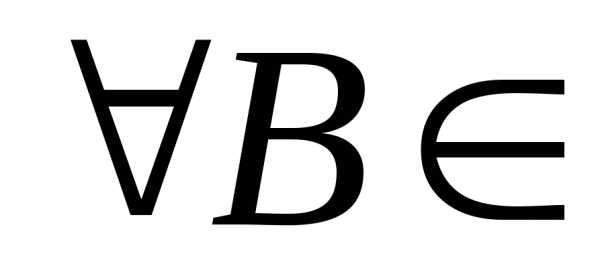(Rⁿ)F.

3) Пусть (E,) = (R^Т,(R^Т)), Т – подмножество числовой прямой. В этом случае всякий случайный элемент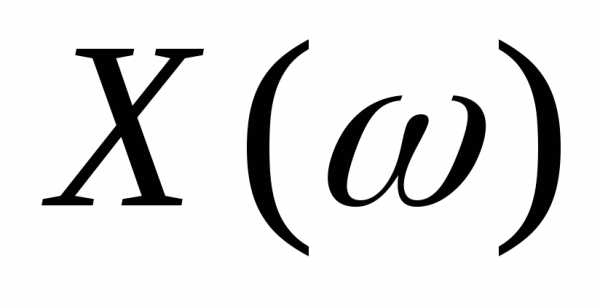представим в видесназывается случайной функцией с временным интерваломТ.

4.5.Определение. Пусть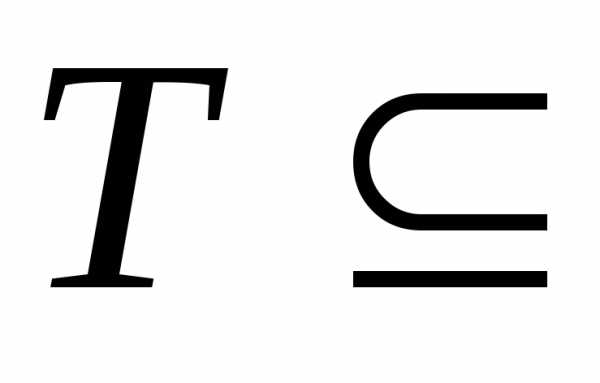R¹. Совокупностьназываетсяслучайным процессомс временным интерваломТ. Если, то- называетсяслучайным процессом с дискретным временем или случайной последовательностью. Если, то- называетсяслучайным процессом с непрерывным временем.

Определение. Пусть- случайный процесс. Для каждогофункция— называетсяреализациейилитраекторией процесса, соответствующего исходу.

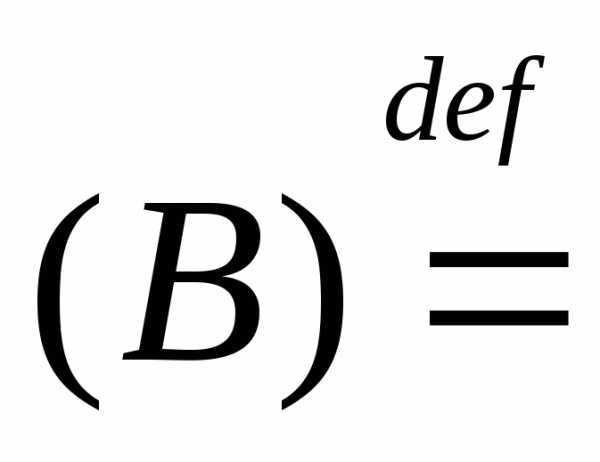Определение. Пусть- случайный процесс. Вероятностная мераРна (R^Т,(R^Т)) сPP,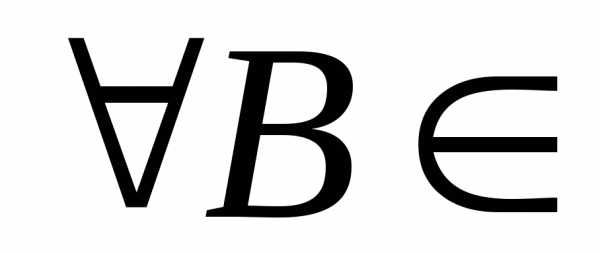(R^Т)называется распределением вероятностей процессаХ.

Определение. Вероятностная мераP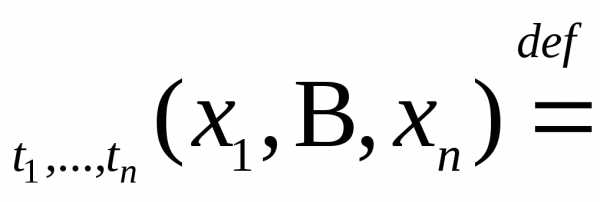P, где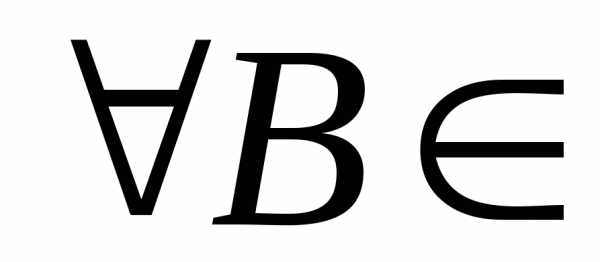(Rⁿ),, называетсяконечномерными распределениями вероятностейслучайного процесса, аn-мерная функция распределения, где, называетсяконечномерными функциями распределения процесса.

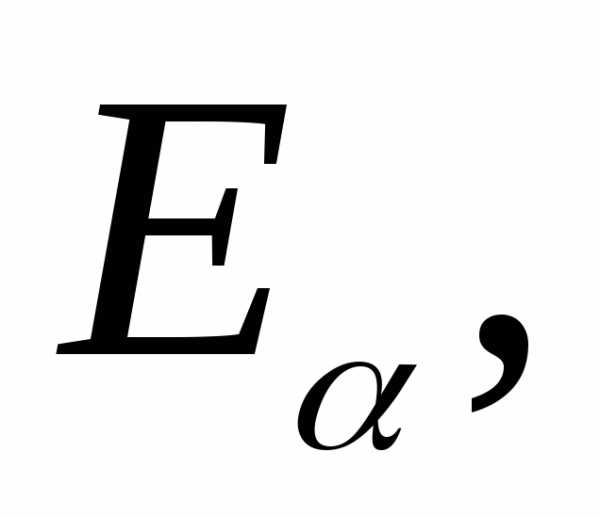
4.6.Определение. Пусть (,F,P) — вероятностное пространство и набор () — измеримых пространств, где— произвольное множество. Будем говорить, что— измеримые функциинезависимы в совокупности, если для любого конечного набораэлементы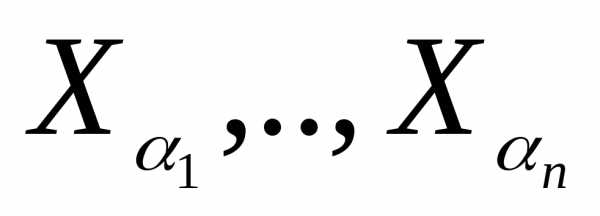— независимы, т.е. дляPP.

Теорема 12. Для того, чтобы случайные величиныбыли независимы в совокупности, необходимо и достаточно, чтобы для любогоRⁿ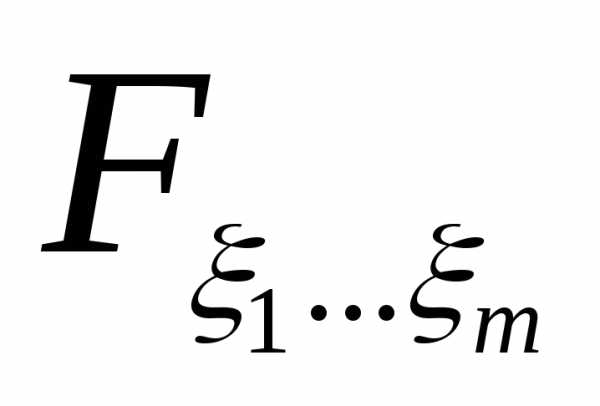, где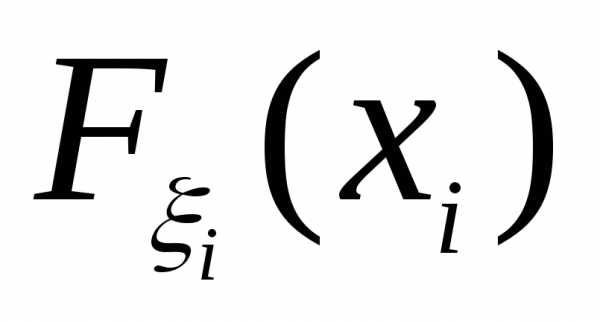. Докажите самостоятельно.

studfiles.net

Случайные величины

7. Дискретная случайная величина

Случайной называют величину, которая в результате испытания примет одно и только одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Обозначают случайные величины буквами Х,Y,Z, а их возможные значения —х,у,z.

Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.

Дискретная случайная величина может быть задана рядом распределения — это соответствие между возможными значениями и их вероятностями:

,.

События образуют полную группу, следовательно, сумма вероятностей этих событий равна единице:

.

Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной — вероятности этих значений, тогда точки с координатами будут изображать полигон распределения вероятностей; соединив же эти точки отрезками прямой, получиммногоугольник распределения вероятностей.

Пример 7.1.ПустьХ— дискретная случайная величина, заданная рядом распределения

Х	–2	–1	0	2	4
Р	0,1	0,2	0,3	0,2	0,2

Построить полигон и многоугольник распределения вероятностей.

Р

.

.

А₄

ешение.На осиХоткладываем значения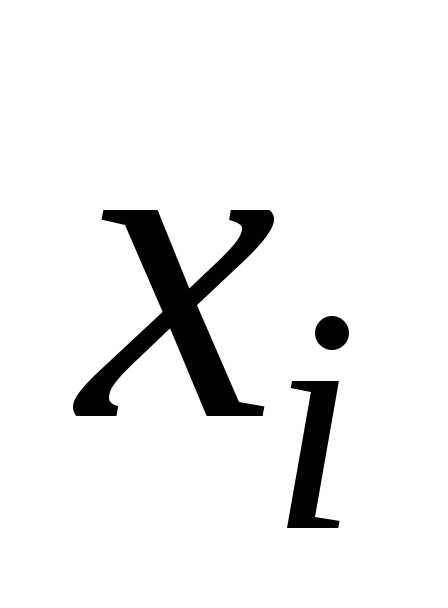, равные –2, –1, 0, 2, 4, а по вертикальной оси вероятности этих значений (рис. 7.1):

Р

.

.

.

А₀

–1

–2

–3

0

1

2

3

4

5

А₁

А₂

А₃

А₅

y

А₆

0,1

0,2

0,3

x

ис. 7.1

Точки изображают полигон распределения, а ломаная— многоугольник распределения вероятностей.

Дискретная случайная величина может быть задана функцией распределения. Функцией распределения случайной величины Хназывается функция, выражающая для каждогохвероятность того, что случайная величинаХпримет значение меньшеех:

Функцию иногда называют интегральной функцией распределения.

Если значения случайной величины — точки на числовой оси, то геометрически функция распределения интерпретируется как вероятность того, что случайная величинаХпопадает левее заданной точких (рис. 7.2):

Рис. 7.2

F(x) обладает свойствами:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:

.

Утверждение следует из того, что функция распределения — это вероятность.

2. Функция распределения есть неубывающая функция на всей числовой оси.

3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна 1, т.е.

;.

4. Вероятность попадания случайной величины в интервал (включая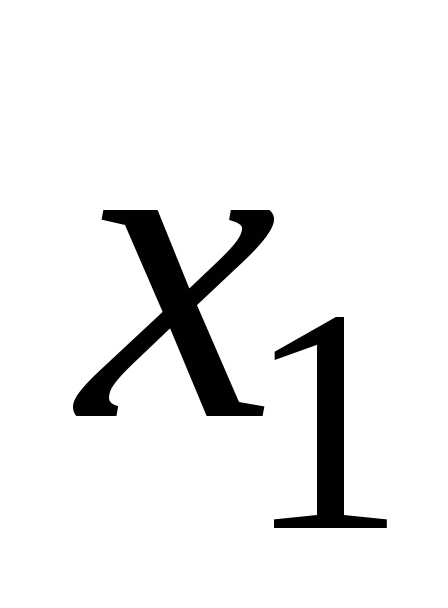) равна приращению ее функции распределения на этом интервале, т.е.

.

Числовые характеристики случайной величины Математическое ожидание м(х) дискретной случайной величины

Пусть случайная величина Хможет принимать только значения, вероятности которых соответственно равны. Тогда математическое ожиданиеМ(Х) случайной величиныХопределяется равенством

.

Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Математическое ожидание приближенно равно среднему арифметическому значений случайной величины: .

studfiles.net

Случайные величины

В данной главе рассматриваются отображения одного вероятностного пространства в другое. Важнейшим случаем такого отображения является отображение основного пространства в пространство действительных чисел или векторов. Возникающие при этом случайные величины, случайные вектора и их распределения являются одними из основных понятий теории вероятностей.

Отображения вероятностных пространств

Дадим формальное определение отображения вероятностного пространства в измеримое пространство

Пусть

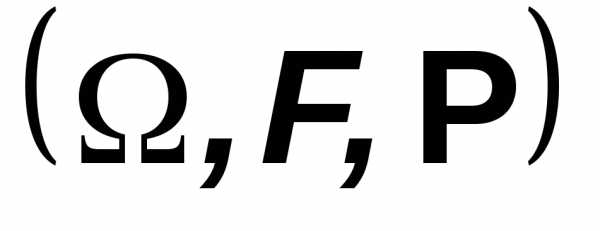
основное вероятностное пространство

измеримое пространство (т.е пара множество и сигма-алгебра)

поточечное отображение (функция), ставящее в соответствие каждому элементарному исходу основного пространства точку x пространства X.

Отображение

называется измеримое отображение, если

множество (прообраз B)

Покажите, что так определенная функция будет вероятностью

Измеримость отображения гарантирует, что функция

определенная на сигма-алгебре

по формуле

будет вероятностью.

Эта функция называется распределение, индуцированное отображением

или просто распределение

Таким образом с каждым отображением

связано новое вероятностное пространство

.

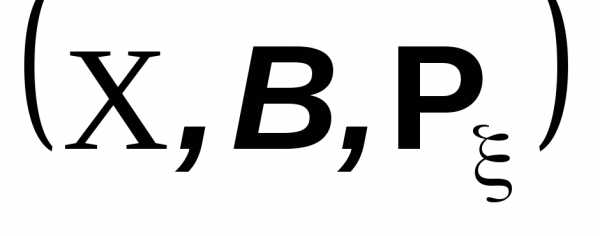Случайная величина

Случайной величиной называется измеримое отображение основного вероятностного пространства в множество действительных чисел. С практической точки зрения случайная величина это числовая характеристика эксперимента. Чтобы дать корректное определение случайной величины, необходимо указать подходящую сигма-алгебру на пространстве действительных чисел. В дальнейшем пространство действительных чисел будем обозначать

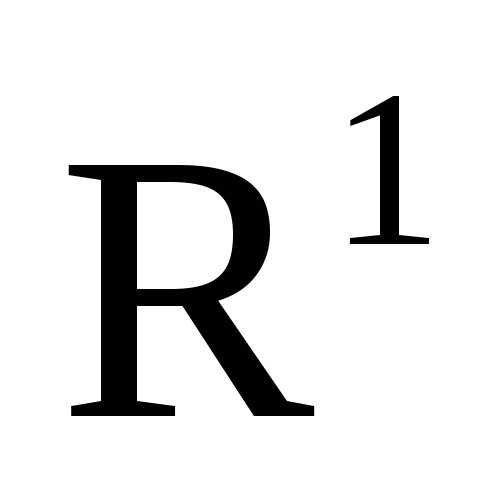
а пространство векторов с n действительными координатами

Борелевская сигма-алгебра

Так как сигма-алгебра на пространстве действительных чисел нужна нам для того, чтобы определить на ней вероятность, то естественно включить в эту сигма-алгебру побольше практически важных множеств. Обозначим

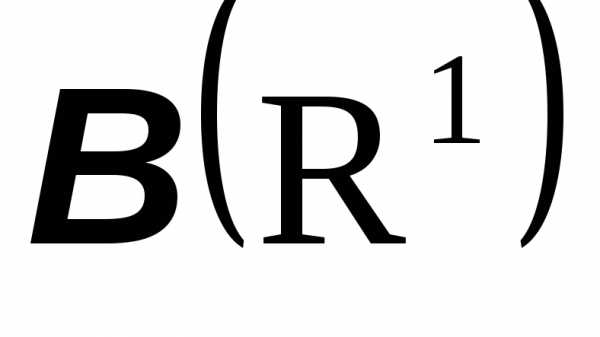
минимальную (которая содержится во всех других) сигма-алгебру, содержащую всевозможные интервалы вида

Эта сигма-алгебра называется борелевская сигма-алгебра). Она содержит все практически важные множества действительной прямой. Множество, принадлежащее борелевской сигма-алгебре называется борелевское множество.

Определение случайной величины

Пусть

основное вероятностное пространство

действительная прямая с борелевской сигма-алгеброй

поточечное измеримое отображение, ставящее в соответствие каждому элементарному исходу основного пространства действительное число. Это отображение называется случайная величина.

Вероятностная мера, определенная на борелевской сигма-алгебре по формуле

называется распределение случайной величины.

Борелевская функция

Заметим, что в определении случайной величины не участвует вероятность. Поэтому в этом определении не требуется указывать, какая вероятность действует на основном пространстве.

Случайная величина, заданная на основном пространстве, которое является действительной прямой с борелевской сигма-алгеброй, называется борелевская функция.

Примеры борелевских функций

Любая непрерывная функция является борелевской.

Функции

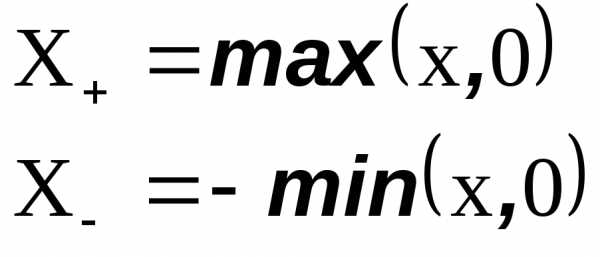
тоже являются борелевскими.

Если f и g – две борелевские функции, то

тоже борелевские, т.к.

Примеры случайных величин

Индикатор события

Пусть A – случайное событие. Тогда функция

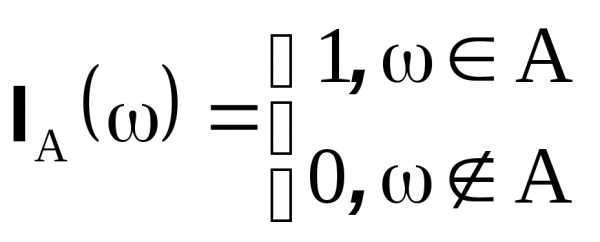
является случайной величиной и называется индикатор события A

Верно и обратное – любая случайная величина принимающая значения 0 или 1 является индикатором некоторого события A.

Часто, для краткости, будем пользоваться обозначением

Простая случайная величина

Пусть

полная группа событий.

Случайная величина

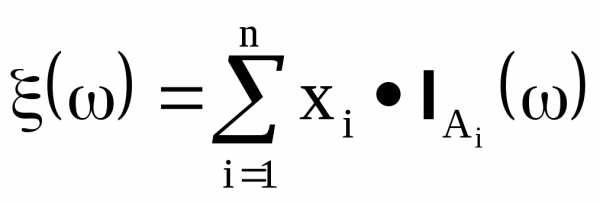
называется простая случайная величина.

Верно и обратное – любая случайная величина принимающая конечное число значений

является простой .

Дискретная случайная величина

Пусть

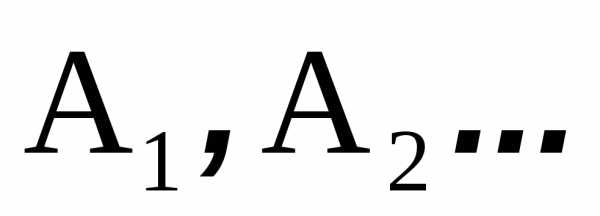
полная группа событий.

Случайная величина

называется дискретная случайная величина.

Верно и обратное – любая случайная величина принимающая конечное или счетное число значений является дискретной.

Случайный вектор

Аналогично одномерному случаю можно определить соответствующие понятия для пространства векторов размерности n. Следует только заменить интервалы на действительной оси прямоугольниками (произведениями интервалов) в пространстве векторов. Получающаяся при этом сигма-алгебра

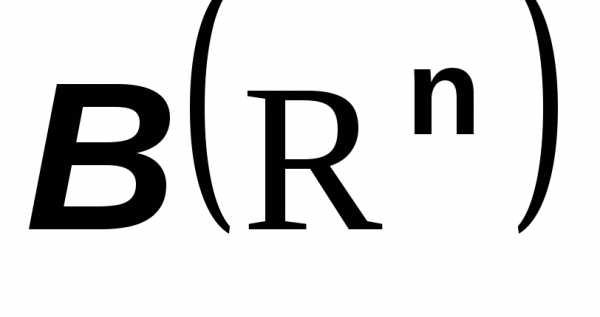
называется борелевской сигма-алгеброй в пространстве

Аналогично даются определения борелевского множества и борелевской функции (как отображения из пространства векторов в пространство действительных чисел). При этом определении координаты случайного вектора будут случайными величинами.

studfiles.net

Случайная величина — это… Что такое Случайная величина?

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Формальное математическое определение следующее: пусть — вероятностное пространство, тогда случайной величиной называется функция , измеримая относительно и борелевской σ-алгебры на . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением.

Определение

Пространство элементарных событий

Пространство элементарных событий в случае бросания игральной кости

Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-либо грани в данном случае в теории вероятностей называется элементарным событием ^[1], то есть

• — грань с одной точкой;
• — грань с двумя точками;
• …
• — грань с шестью точками.

Множество всех граней образует пространство элементарных событий , подмножества которого называются случайными событиями ^[1]. В случае однократного подбрасывания игровой кости примерами событий являются

• выпадение грани с нечётным количеством точек, то есть событие — это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие записывается как множество, содержащее элементарные события: , и . Таким образом, ;
• выпадение грани с чётным количеством точек, то есть событие — это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие записывается как множество, содержащее элементарные события: , и . Таким образом, ;

Алгебра событий

Множество случайных событий образует алгебру событий ^[2], если выполняются следующие условия:

1. содержит пустое множество .
2. Если событие принадлежит , то и его дополнение принадлежит . С помощью кванторов это записывается так:  : .
3. Если и принадлежат , то их объединение также принадлежит . С помощью кванторов это записывается следующим образом () () .

Если вместо третьего условия удовлетворяет другому условию: объединение счётного подсемейства из также принадлежит , то множество случайных событий образует σ-алгебру событий.

-алгебра событий является частным случаем σ-алгебры множеств.

Самая маленькая среди всех возможных -алгебр, элементами которой являются все интервалы на вещественной прямой, называется борелевской σ-алгеброй на множестве вещественных чисел .

Вероятность

Если каждому элементарному событию поставить в соответствие число , для которого выполняется условие:

,

то считается, что заданы вероятности элементарных событий . Вероятность события, как счётного подмножества пространства элементарных событий, определяется как сумма вероятностей тех элементарных событий, которые принадлежат этому событию. Требование счётности важно, так как, иначе сумма будет не определена.

Рассмотрим пример определения вероятности различных случайных событий. Например, если событие является пустым множеством, то его вероятность равна нулю^[3]:

.

Если событием является пространство элементарных событий, то его вероятность равна единице:

.

Вероятность события (подмножества пространства элементарных событий) равна сумме вероятностей тех элементарных событий, которые включает в себя рассматриваемое событие.

Определение случайной величины

Случайной величиной называется функция , измеримая относительно и борелевской σ-алгебры на ^[4].

Случайную величину можно определить и другим эквивалентным способом^[4]. Функция называется случайной величиной, если для любых вещественных чисел и множество событий , таких что , принадлежит .

Примеры

равно среднему арифметическому всех принимаемых значений.

.

,

то есть математическое ожидание не определено.

Классификация

Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).

На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

• Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.
• В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.
• Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.

• Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.

Методы описания

Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.

Если случайная величина дискретная, то полное и однозначное математическое описание её распределения определяется указанием вероятностей всех возможных значений этой случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения.

Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» — с вероятностью q=1-p. Закон распределения в этом случае определяется формулой Бернулли:

.

При стремлении к бесконечности произведение np остаётся равной константе , а закон распределения сходится к закону Пуассона, который описывается следующей формулой:

,

где

Простейшие обобщения

Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,

См. также

Примечания

1. ↑ ^{1 2} Чернова Н. И. Глава 1. § 2. Элементарная теория вероятностей // Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
2. ↑ Чернова Н. И. Глава 3. § 1. Алгебра и сигма-алгебра событий // Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
3. ↑ Чернова Н. И. ГЛАВА 1 § 2. Элементарная теория вероятностей // Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.
4. ↑ ^{1 2} Чернова Н. И. Глава 6. Случайные величины и их распределения § 1. Случайные величины // Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.

Литература

• Гнеденко Б. В. Курс теории вероятности. — 8-е изд. доп. и испр. — М.: Едиториал УРСС, 2005. — 448 с.
• Математический энциклопедический словарь / Гл. ред. Прохоров Ю. В.. — 2-е изд. — М.: «Советская энциклопедия», 1998. — 847 с.
• Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. — Учебное пособие для ВУЗов. — М.: Радио и связь, 1991. — 608 с. — ISBN 5-256-00789-0
• Чернова Н. И. Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с.

Ссылки

dic.academic.ru

1. Определение случайной величины. Виды случайных величин

Одним из основных понятий теории вероятностей является понятие случайной величины.

Примеры случайных величин:

Пример 1 Число родившихся мальчиков (или девочек) среди ста новорожденных.Пример 2 Расстояние, которое пролетит снаряд при выстреле из орудия.

Пример 3 Ошибка измерителя высоты.

Пример4 Число вызовов, поступивших от абонентов на телефонную станцию в течение определенного промежутка времени.

Пример5 Число космических частиц, попадающих на определенный участок земной поверхности в течение определенного промежутка времени.

Пример6 Температура воздуха на следующий день.

Пример7 Число появлений герба при четырех бросаниях монеты.Пример8 Время безотказной работы некоторого прибора.

Приведенные примеры показывают, что со случайными величинами приходится иметь дело в различных областях науки и техники, поэтому понятие случайной величины имеет очень большую практическую значимость.

Определение1.1: Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Более строгое определение случайной величины можно дать следующим образом: Определение1.2:Случайной величиной называется функцияX(ω), определенная на некотором

множестве элементарных событий Ω.

Случайные величины обычно обозначают большими буквами X, Y, Z , а их возможные значения – соответствующими строчными буквамиx, y, z.

Например, если случайная величина X принимает четыре возможных значения, то они будут обозначены какx1 , x2 , x3 , x4.

Дискретные и непрерывные случайные величины

Случайные величины бывают дискретными и непрерывными.

Определение1.3: Случайная величина называетсядискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным).

Дискретными являются случайные величины в примерах 1,4,5,7.

Определение1.4:Случайная величина называетсянепрерывной, если она принимает все значения из некоторого конечного или бесконечного промежутка.

Число возможных значений непрерывной случайной величины бесконечно. Непрерывными являются случайные величины в примерах 2,3,6,8.

Замечание: Более строгое определение непрерывной случайной величины будет дано позднее.

2. Функция распределения вероятностей случайной величины и ее свойства

Для задания случайной величины необходимо знать не только, какие значения может она принимать, но и как часто, то есть с какой вероятностью она принимает эти значения. Для того, чтобы задавать вероятности значений случайных величин, столь разнообразных по своей природе, и притом задавать их одним и тем же способом, вводят понятие функции распределения вероятностей случайной величины или просто функции распределения случайной величины.

studfiles.net

Понятие случайной величины

Глава 3. Принятие решений в условиях риска

3.2.1. Понятие случайной величины

В ситуации риска нам известны исходы той или иной альтернативы и вероятности, с которыми данные исходы могут наступить. То есть нам известно вероятностное распределение исходов, поэтому они могут быть представлены (смоделированы) в виде случайной величины. В этом параграфе мы напомним сведения из теории вероятностей о случайных величинах и способах их определения, которые будут необходимы для дальнейшего изучения материала книги.

Согласно классическому определению, случайной называется величина, значение которой может меняться от опыта к опыту случайным образом. То есть в каждом «испытании» она может принимать одно единственное значение из некоторого множества. При этом нельзя предсказать, какое именно значение она примет.

Случайные величины делятся на дискретные и непрерывные. Дискретная СВ может принимать только конечное или счетное множество значений. Непрерывная СВ может принимать любое значение из некоторого замкнутого или открытого интервала, в том числе и бесконечного.

Наверх

3.2.2. Закон распределения случайной величины

Случайная величина определяется своим законом распределения. Закон распределения считается заданным, если указаны:

• множество возможных значений случайной величины (в т.ч. бесконечное) и
• вероятность попадания случайной величины в произвольную область этого множества, либо закон (формула), позволяющая рассчитать такую вероятность.

По сути, вероятность представляет собой показатель, характеризующий возможность появления случайной величины в данной области.

Наиболее общим и распространенным способом определения вероятностей различных значений случайной величины является задание функции распределения вероятностей, которую сокращенно называют функцией распределения.

Функцией распределения случайной величины Х называется функция F(x), задающая вероятность того, что СВ примет значение меньше конкретного значения х, то есть:

F(x) = P(X < x)

где

Х («икс большое») — обозначает случайную величину,

х («икс маленькое») — конкретное значение из множества возможных значений случайной величины.

Функция распределения неубывающая. При х, стремящемся к минус бесконечности, она стремится к нулю, а при х, стремящемся к плюс бесконечности — к единице.

Форма представления закона распределения случайной величины может быть различна и зависит от того, какая это СВ — дискретная или непрерывная.

Из определения функции распределения следуют следующие зависимости:

вероятность того, что случайная величина примет значения в интервале от а до b:

Р(a ≤ Х < b) = F(b) — F(a)

вероятность того, что случайная величина примет значения не меньше, чем а:

Р(Х ≥ a) = 1 — F(a)

Наверх

3.2.3. Способы представления распределения дискретной случайной величины

Дискретная случайная величина может быть полностью задана своей функцией распределения или рядом (таблицей) распределения. Они могут быть представлены в табличной, аналитической или графической формах.

Допустим, случайная величина Х может принять три возможных значения 25, 45 и 50 с вероятностями 25%, 35% и 40% соответственно. Ряд распределения этой СВ будет выглядеть следующим образом:

xj	25	45	50
pj	0.25	0.35	0.40

Функция распределения этой же случайной величины, которая показывает вероятность непревышения конкретного значения, может быть записана так:

На рис.3.1 представлены графические способы задания закона распределения этой дискретной случайной величины Х.

Рис.3.1. Графики ряда распределения и функции распределения дискретной случайной величины.

На графике ряда распределения вероятности p_j реализации каждого возможного значения х_j представлены столбиками, высота которых равна вероятности. Сумма высот всех М столбиков (т.е. всех вероятностей) равна единице, поскольку они охватывают все возможные значения х:

Иногда вместо столбиков изображают ломанную, соединяющую вероятности реализации значений СВ.

Вероятность того, что дискретная случайная величина примет значение меньше, чем а, равна сумме вероятностей всех исходов, меньших а:

По определению, это равно значению функции распределения в точке х = а. Если мы нанесем на координатную плоскость значения функции распределения, когда х «пробегает» все значения от минус бесконечности до плюс бесконечности, мы получим график функции распределения. Для дискретной СВ он ступенчатый. На интервале от минус бесконечности до первого возможного значения х₁ она равна нулю, поскольку принять какое-либо значение на этом интервале невозможно.

Далее каждое возможное значение х_j увеличивает функцию распределения на величину, равную вероятности наступления этого значения p_j. Между двумя последовательными значениями х_j и x_j+1 функция распределения не изменяется, поскольку других возможных значений х там нет, и скачков не происходит. В конечном итоге, в точке последнего возможного значения х_М происходит скачок на величину вероятности р_М, и функция распределения достигает предельного значения, равного единице. Далее график идет на этом уровне параллельно оси х. Выше он никогда не поднимается, так как вероятность не может быть больше единицы.

Наверх

3.2.4. Способы представления распределения непрерывной случайной величины

Непрерывная случайная величина также задается своей функцией распределения, представленной, как правило, в аналитическом виде. Кроме того, она может быть полностью описана функцией плотности вероятности f(x), которая представляет собой первую производную от функции распределения F(x):

f(x) = F'(x)

Функция плотности вероятности неотрицательна, а ее интеграл в бесконечных пределах равен единице.

Возьмем в качестве примера непрерывную случайную величину, распределенную по нормальному закону.

Ее функция плотности вероятности задается аналитически формулой вида:

Здесь m_X и σ_X параметры распределения. m_X характеризует местоположение центра распределения, а σ_X — рассеивание относительно этого «центра».

Аналитическая запись ее функции распределения выглядит следующим образом:

Графики функции распределения и функции плотности вероятности представлены на рис.3.2.

Рис.3.2 Графики функции плотности вероятности f(x) и функции распределения F(x) непрерывной случайной величины (на примере нормально распределенной случайной величины с параметрами m_X = 5, σ_X = 1).

График функции распределения любой случайной величины всегда неубывающий, стремящийся к единице. Плотность вероятности характеризует «скорость» роста функции распределения. На интервалах, где плотность высокая, функция распределения растет быстрее. Там, где плотность равна к нулю, функция распределения не изменяется, и ее график идет параллельно оси х. В нашем примере наибольшие значения плотность имеет в окрестности точки х = m_X (для нормально распределенных СВ ее еще иногда называют центром рассеивания).

Значение функции распределения F(x) в произвольной точке а равно вероятности того, что случайная величина X примет значение меньше а. Эта вероятность соответствует заштрихованной площади под графиком функции плотности вероятности f(x) на интервале от -∞ до а.

Изложенные в настоящем параграфе сведения о случайных величинах из теории вероятностей понадобятся нам далее для анализа методов принятия решений в условиях риска.

Наверх

Дата обновления: 25.09.2014

risking.ru

Случайные величины

Общие понятия 

Случайное событие является качественной характеристикой случайного результата испытания, но его можно характеризовать количественно, этой количественной характеристикой случайного результата испытания является случайная величина. Определение 1. Случайная величина — это вещественная функция, определенная на множестве исходов, соответствующих данному испытанию. То есть каждому исходу множества- всех исходов испытания ставится в соответствие некоторое действительное число. Случайные величины обозначаются; их возможные значения обозначаются. Рассматриваются два типа случайных величин.Определение 2. Дискретной случайной величиной называется случайная величины, число значений которой  конечно или бесконечно, но счетно. Пример 1. Производится три выстрела по мишени. Пусть случайная величина — число попаданий при трех выстрелах. Она может принимать значения 0,1,2,3, то есть — это дискретная случайная величина.Пример 2. Производятся выстрелы по мишени. Пусть случайная величина — число выстрелов до первого попадания. Она может принимать значения 1,2,3,…, то есть число значений бесконечно, но счетно, значит это  дискретная случайная величина.Определение 3. Непрерывной случайной величиной называется случайная величина, значения которой занимают некоторый интервал(конечный или бесконечный). Пример 3. Автобус некоторого маршрута ходит по расписанию с интервалом 15 минут. Пусть случайная величина — время ожидания пассажиром автобуса. Это непрерывная случайная величина, ее значения занимают отрезок.Пример 4. Работает некоторый прибор. Пусть случайная величина — время безотказной работы данного прибора. Это непрерывная случайная величина, значения которой занимают промежуток.Вопрос. Бросается игральная кость. Выпадение » шестерки» — это: а) дискретная случайная величина; б) непрерывная случайная величина; в) случайное событие; г) неслучайная величина.

а)

б)

в)

г)

Закон распределения дискретной случайной величины

Определение 4. Законом распределение случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Способы или формы представления закона распределения могут быть различными. Закон распределения дискретной случайной величины можно задать с помощью ряда распределения. Рядраспределения — это таблица значений случайной величины и вероятностей, с которыми эти  значения принимаются.

Для того, чтобы подобная таблица являлась рядом распределения дискретной случайной величины, необходимо выполнение следующих условий: 1. значения случайной величины должны быть указаны в возрастающем порядке; 2. ( если множество возможных значений случайной величиныбесконечно, но счетно, то ряддолжен сходиться и его сумма должна равняться 1). Для наглядности ряд распределения можно изобразить графически в видемногоугольника распределения, который представляет из себя ломаную, соединяющую точки с координатами .

Рис.1

Пример 5.Производится три выстрела по мишени. Вероятность попадания при одном выстреле равна 0,7. Пусть случайная величина — число попаданий при трех выстрелах. Построить ряд распределения данной случайной величины.Решение. Данная случайная величина может принимать следующие значения: 0,1,2,3. Найдем вероятности, с которыми эти значения принимаются, они вычисляются по формуле Бернулли: ;;;; Теперь построим ряд распределения:

0 1 2 3 0,027 0,189 0,441 0,343

Вопрос. Данная таблица является рядом распределения.

	1	3	4	6
	0,15	0,2	0,25	0,3

верно

неверно

Функция распределения вероятностей

Для непрерывной случайной величины нельзя построить ряд распределения, так как она может принимать  бесконечное число значений из некоторого промежутка, кроме того, каждое отдельное значение обычно не  обладает никакой отличной от нуля вероятностью. Для непрерывной случайной величины нужен другой способ  задания закона распределения. Общей формой задания закона распределения случайной величины является функция распределения вероятностей. Определение 5. Функцией распределения вероятностей случайной величины называется функция, определяющая вероятность того, что в результате испытания случайная величинапримет значение,  меньшее.

 (1)

Геометрически равенство означает, что если случайная величина — это случайная точка на числовой оси, то — это вероятность того, что в результате испытания случайная точка будет расположена левее точки. Функцию распределения еще принято называть интегральным законом распределения. Из определения следует, что функция распределения существует и для дискретных случайных величин, и для непрерывных. Для дискретных случайных величин формула (1) может быть записана следующим образом:

 (2)

Свойства функции распределения.

1. 2.3.4.- неубывающая функция, то есть если, то. С помощью функции распределения можно найти вероятность попадания случайной величины на некоторый промежуток по формуле:

 (3)

Так как , то формула (3) верна для всех этих случаев.Пример 6. По мишени производится 3 выстрела. Вероятность попадания при одном выстреле 0,7. Найти функцию распределения вероятностей случайной величины — числа попаданий при трех выстрелах.Решение. В примере 5 для данной случайной величины был получен ряд распределения:

	0	1	2	3
	0,027	0,189	0,441	0,343

Используя формулу (2), найдем функцию распределения: 1. если , то; 2. если, то; 3. если, то; 4. если, то; 5. если, то.

Итак, функция распределения аналитически может быть записана так: Теперь построим график этой функции.

Рис.2

То есть функция распределения для дискретной случайной величины является кусочно-постоянной функцией,  имеющей конечное число точек разрыва 1-го рода. Функция распределения непрерывной случайной величины является непрерывной функцией. Пример 7. Дана функция распределения вероятностей непрерывной случайной величины :Найти, построить график функции распределения, вычислить вероятность того, что в результате испытания случайная величинапримет значение в интервале (1;2).Решение. Для нахождения воспользуемся непрерывностью функции распределения:, поэтому, следовательно. Построим график функции распределения:

Рис.3

 

По формуле (3) находим: .

Вопрос. Если случайная величина принимает значения, не большие 4, торавно:

4

5

0

1

Плотность распределения вероятностей

Функция распределения для непрерывной случайной величины является ее исчерпывающей вероятностной характеристикой, но она имеет недостаток, так как по ней трудно судить о характере распределения случайной  величины в небольшой окрестности той или иной точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины в окрестностях различных точек дает функция, которая называется плотностью распределения вероятностей и обозначается .

 (4)

Плотность распределения — это средняя вероятность, которая приходится на единицу длины промежутка . Она указывает на то, как часто случайная величинапоявляется в некоторой окрестности точкипри повторении испытаний. Эту функцию еще называют дифференциальным законом распределения. На рис.4 дан примерный вид функции.

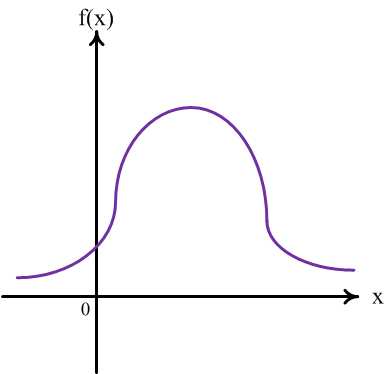
Рис.4

График функции называетсякривой распределения. Так как , то

 (5)

Свойства плотности распределения

1. ; 2.. Геометрически это означает, что площадь под кривой распределения равна 1. Функция распределения и плотность распределения связаны еще одним соотношением:

 (6)

Вероятность того, что случайная величина примет значение из промежутка, можно вычислить с помощью плотности распределения по формуле:

 (7)

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение из промежутка , равна площади криволинейной трапеции с основанием(рис.5).

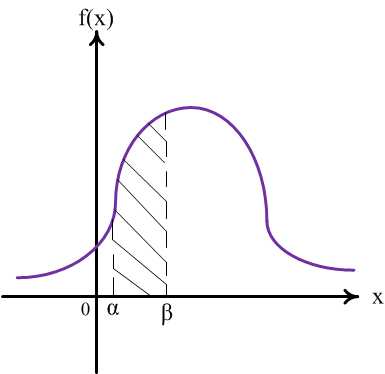
Рис.5

Пример 8. Дана плотность распределения вероятностей непрерывной случайной величины : Найти , построить график функции , найти . Решение. Для нахождения коэффициента воспользуемся свойством 2 плотности распределения, тогда , получаем, что ,  следовательно, . Теперь построим график плотности распределения: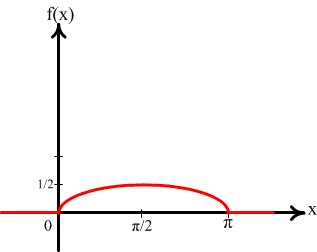

Рис.6

Требуемую вероятность вычисляем по формуле (7): .Вопрос. Для каких случайных величин закон распределения задается с помощью плотности распределения?

Ваш ответ

studfiles.net