Подобные треугольники признаки – Признаки подобия треугольников — урок. Геометрия, 8 класс.

Подобные треугольники. Признаки подобия. Видеоурок. Геометрия 8 Класс

На данном уроке мы рассмотрим подобные треугольники и признаки подобия треугольников. Отметим, что равенство треугольников – это частный случай подобия, и решим несколько примеров.

Тема: Повторение курса геометрии 8 класса

Урок: Подобные треугольники. Признаки подобия

В подобных треугольниках важное место занимает понятие отношения отрезков. Напомним, что отношением отрезков AB и CD называется отношение их длин. Если отношения двух пар отрезков равны, то говорят, что отрезки пропорциональны (см. Рис. 1):

Треугольники  и  в некотором смысле похожи. Если их соответствующие углы равны:

а отношения соответствующих сторон одинаковы:

, k – коэффициент подобия, то треугольники называются подобными:

.

Рис. 1

Треугольник  называется подобным треугольнику  (), если все их соответствующие углы равны между собой, и отношения сходственных сторон (т.е. сторон, лежащих против равных углов) равны.

Отметим, что мы уже имели дело с частным случаем подобия – равенством двух треугольников . Напомним, что два треугольника называются равными, если все их соответствующие углы равны, и все стороны соответственно равны. В данном случае мы имеем дело с подобными треугольниками, коэффициент подобия которых равен единице.

Чтобы установить подобие треугольников, нужно установить справедливость приведенных шести равенств (углов и отношений сторон), но не всегда возможно это сделать. Для этого существуют признаки подобия треугольников.

Всего существует три признака подобия. Перечислим их:

1.      По равенству двух углов: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны:.

2.      По пропорциональности двух сторон и равенству угла между ними: если две стороны одного треугольника пропорциональны соответственно двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны: .

3.      По пропорциональности трёх сторон: если три стороны одного треугольника пропорциональны соответственно трём сторонам другого треугольника, то такие треугольники подобны: .

Пример 1: доказать, что периметр треугольника  относится к периметру треугольника  как коэффициент подобия, если заданные треугольники подобны.

Напомним, что периметр – это сумма линейных элементов, сумма трех сторон треугольника.

Итак, имеем два подобных треугольника: .

Доказать, что .

Доказательство:

Комментарий: мы выразили сторону одного треугольника через сторону второго с помощью коэффициента подобия, записали отношение периметров треугольников, подставили туда полученные выражения, вынесли за скобки общий множитель и сократили дробь.

 

Напомним, что площади подобных треугольников относятся как квадрат коэффициента подобия:

Пояснение: площадь треугольника – это произведение двух линейных элементов – сторона на высоту.

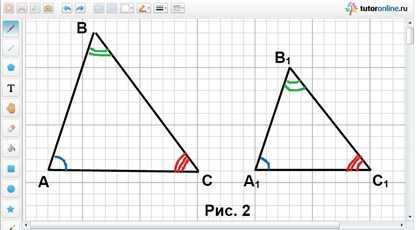
Пример 2 – задача 549: стороны данного треугольника: 15 см, 20 см и 30 см (см. Рис. 2). Найдите стороны треугольника, подобного данному, если его периметр равен 26 см.

В предыдущей задаче мы доказали, что отношение периметров подобных треугольников равно коэффициенту подобия. Периметр треугольника  нам задан, периметр треугольника  мы можем найти, так как нам заданы длины его сторон, таким образом, мы найдем коэффициент подобия и определим искомые длины сторон.

Рис. 2

Итак, мы рассмотрели подобные треугольники, вспомнили, какие треугольники называются подобными и в чем смысл подобия треугольников. Также вспомнили признаки подобия треугольников. Выяснили, что равенство треугольников – это частный случай подобия.

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Fmclass.ru (Источник).
2. Edu.glavsprav.ru (Источник).
3. Dpva.info (Источник).

 

Домашнее задание

1. Задание 1: на стороне ВС треугольника  отмечена точка М так, что треугольники  и  подобны. Найдите АВ, если ВМ = 4 см, СМ = 5 см.
2. Задание 2: диагональ АС трапеции ABCD с основаниями AD = 12 см и ВС = 3 см разделяет ее на два подобных треугольника. Найдите АС.
3. Задание 3: диагональ АС, равная 6 см, разделяет трапецию ABCD на два подобных треугольника. Известны боковые стороны трапеции АВ = 4 см и CD = 6 см. Найдите периметр трапеции.

interneturok.ru

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия

Подобные треугольники

      Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.

Рис.1

      Обозначим

a₁ ,   b₁ ,   c₁

длины сторон треугольника   KLM,   расположенные в порядке возрастания.

      Обозначим

a₂ ,   b₂ ,   c₂

длины сторон треугольника   TRP,   расположенные в порядке возрастания.

      Переобозначим вершины треугольников   KLM   и   TRP   так, как показано на рисунке 2.

Рис.2

      На рисунке 2 треугольник   KLM   обозначается как треугольник   A₁B₁C₁,   а треугольник   TRP   обозначается как треугольник   A₂B₂C₂.

      Определение 1. В треугольниках   A₁B₁C₁   и   A₂B₂C₂,   изображённых на рисунке 2,

• вершины   A₁   и   A₂,   B₁   и   B₂,   C₁   и   C₂   называют сходственными вершинами,
• стороны   A₁B₁   и   A₂B₂,   A₁C₁   и   A₂C₂,   B₁C₁   и   B₂C₂   называют сходственными сторонами,
• углы   A₁   и   A₂,   B₁   и   B₂,   C₁   и   C₂   называют сходственными углами

      Определение 2. Треугольники   A₁B₁C₁   и   A₂B₂C₂   называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.

      Другими словами, треугольники   A₁B₁C₁   и   A₂B₂C₂   подобны, если, во-первых,

а, во-вторых, существует положительное число k, такое, что справедливы равенства:

a1 = k a2 ,   b1 = k b2 ,   c1 = k c2 .

(1)

      Определение 3. В случае, когда треугольники   A₁B₁C₁   и   A₂B₂C₂   подобны, число k, заданное формулами (1), называют коэффициентом подобия треугольников   A₁B₁C₁   и   A₂B₂C₂ .

Признаки подобия треугольников

Название признака	Рисунок	Формулировка признака
Признак подобия треугольников по двум сторонам и углу между ними		Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.
Признак подобия треугольников по двум углам		Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Признак подобия треугольников по трём сторонам		Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны

Признак подобия треугольников по двум сторонам и углу между ними

Формулировка признака подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.

Признак подобия треугольников по двум углам

Формулировка признака подобия: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Признак подобия треугольников по трём сторонам

Формулировка признака подобия: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны

Признаки подобия прямоугольных треугольников

Название признака	Рисунок	Формулировка признака
Признак подобияпрямоугольных треугольников по двум катетам		Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Признак подобия прямоугольных треугольников по острому углу		Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Признак подобия прямоугольных треугольников по гипотенузе и катету		Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Признак подобия прямоугольных треугольников по двум катетам

Формулировка признака подобия прямоугольных треугольников: Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Признак подобия прямоугольных треугольников по острому углу

Формулировка признака подобия прямоугольных треугольников: Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

Признак подобия прямоугольных треугольников по гипотенузе и катету

Формулировка признака подобия прямоугольных треугольников: Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.

      Следствие 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).

Рис.3

      Следствие 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)

Рис.4

     

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Подобие треугольников. Часть 1

Определение и свойства подобных треугольников

Числа a₁, a₂, a₃, …, a_n называются пропорциональными числам b₁, b₂, b₃, …, b_n, если выполняется равенство: a₁/b₁ = а₂/b₂ = a₃/b₃ = … = a_n/b_n = k, где k – некоторое число, которое называют коэффициентом пропорциональности.

Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку

6/-4 = -7,5/5 = 15/-10 = -1,5.

Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.

Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).

Рассмотрим на рис. 1 два треугольника АВС и А₁В₁С₁ с равными попарно углами: A = A₁, B = B₁, C = C₁.

Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными. Так, на рис. 1 стороны AB и A₁B₁, AC и A₁C₁, BC и B₁C₁, сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A₁B₁C₁.

Дадим определение подобных треугольников:

Два треугольника называются подобными

, если их углы попарно равны, а сходственные стороны пропорциональны.

Отношение сходственных сторон подобных треугольников называется коэффициентом подобия.

Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A₁B₁C₁.

Итак, на рис. 2 имеем: Δ ABC ~ Δ A₁B₁C₁

углы A = A₁, B = B₁, C = C₁ и AB/A₁B₁ = ВC/В₁C₁ = АС/А₁С₁ = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.

Замечание 1: Равные треугольники подобны с коэффициентом 1.

Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B

1C₁A₁ некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.

Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.

Сформулируем свойства подобных треугольников:

1. Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.
2. Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Пусть треугольники ABC и A₁B₁C₁ подобны с коэффициентом k (рис. 2).

Докажем, что S_ABC/S_A1B1C1 = k².

Поскольку углы подобных треугольников попарно равны, т.е A = A₁, и по теореме об отношении площадей треугольников, имеющих по равному углу, имеем:

S_ABC/S_A1B1C1 = (AB · AC) / (A₁B₁ · A₁C₁) = AB/A₁B₁ · AC/A₁C₁.  

В силу подобия треугольников AB/A₁B₁ = k и AC/A₁C₁ = k,

поэтому S_ABC/S_A1B1C1 = AB/A₁B

1 · AC/A₁C₁ = k · k = k².

Замечание: Сформулированные выше свойства подобных треугольников справедливы и для произвольных фигур.

Признаки подобия треугольников

Требования, которые предъявляются к подобным треугольникам определением (это равенство углов и пропорциональность сторон) являются избыточными. Устанавливать подобие треугольников можно и по меньшему количеству элементов.

Так, при решении задач чаще всего используется первый признак подобия треугольников, утверждающий, что для подобия двух треугольников достаточно равенства их углов:

Первый признак подобия треугольников (по двум углам): Если два угла одного треугольника соответственно равны двум углам второго треугольника, то эти треугольники подобны (рис. 3).

Пусть даны треугольники Δ ABC, Δ A₁B₁C₁

, в которых углы A = A₁, B = B₁. Необходимо доказать, что Δ ABC ~ Δ A₁B₁C₁.

Доказательство.

1) По теореме о сумме углов треугольника имеем:

угол C = 180^° (угол A + угол B) = 180° (угол A₁ + угол B₁) = угол C₁.

2) По теореме об отношении площадей треугольников, имеющих по равному углу,

S_ABC/S_A1B1C1 = (AB · AC) / (A₁B₁ · A₁C₁) = (AB · ВC) / (A₁B₁ · В₁C₁) = (AС · ВC) / (A₁С₁ · В₁C₁).

3) Из равенства (AB · AC) / (A₁B₁ · A₁C₁) = (AB · ВC) / (A₁B₁ · В₁C₁) следует, что AC/A₁C₁ = BС/В₁С₁.

4) Из равенства (AB · ВC) / (A₁B₁ · В₁C₁) = (AС · ВC) / (A₁С₁ · В₁C₁) следует, что AВ/A₁В₁ = АС/А₁С₁.

Таким образом, у треугольников ABCи A₁B₁C₁ DA = DA₁, DB = DB₁, DC = DC₁, и AB/A₁B₁ = АС/А₁С₁.

5) AB/A₁B₁ = АС/А₁С₁ = ВC/В₁C₁, то есть сходственные стороны пропорциональны. А значит, Δ ABC ~ Δ A₁B₁C₁ по определению.

Теорема о пропорциональных отрезках. Деление отрезка в заданном отношении

Теорема о пропорциональных отрезках является обобщением теоремы Фалеса.

Для использования теоремы Фалеса необходимо, чтобы параллельные прямые, пересекающие две данные прямые, отсекали на одной из них равные отрезки. Обобщенная же теорема Фалеса утверждает, что если параллельные прямые пересекают две данные прямые, то отрезки, отсекаемые ими на одной прямой, пропорциональны отрезкам, отсекаемым на второй прямой.

Теорема о пропорциональных отрезках доказывается аналогично теореме Фалеса (только вместо равенства треугольников здесь используется их подобие).

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса): Параллельные прямые, пересекающие две данные прямые, отсекают на них пропорциональные отрезки.

Свойство медиан треугольника

Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:

Свойство медиан треугольника: Медианы треугольника пересекаются в одной точке, и делятся этой точкой в отношении 2 : 1, считая от вершины (рис. 4).

Точка пересечения медиан называется центроидом треугольника.

Пусть дан Δ ABC, у которого AA₁, BB₁, CC₁ – медианы, кроме того, AA₁∩CC₁ = O. Необходимо доказать, что BB₁ ∩ CC₁ = O и АО/ОА₁ = ВО/ОВ₁ = СО/ОС₁ = 2.

Доказательство.

1) Проведем среднюю линию A₁C₁. По теореме о средней линии треугольника A₁C₁ || AC, и A₁C₁ = AC/2.

2) Треугольники AOC и A₁OC₁ подобны по двум углам (угол AOC = углу A₁OC₁ как вертикальные, угол OAC = углу OA₁C₁ как внутренние накрест лежащие при A₁C₁ || AC и секущей AA₁), следовательно, по определению подобных треугольников АО/А₁О = ОС/ОС₁ = АС/А₁С₁ = 2.

3) Пусть BB₁∩CC₁ = O₁. Аналогично пунктам 1 и 2 можно доказать, что ВО/О₁В₁ = СО₁/О₁С = 2. Но поскольку на отрезке СС₁ существует единственная точка О, делящая его в отношении СО : ОС₁ = 2 : 1, то точки О и О₁ совпадают. Значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2 : 1, считая от вершины.

В курсе геометрии в теме «площади многоугольников» доказывается тот факт, что медиана разбивает произвольный треугольник на две равновеликие части. Кроме того, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников.

 Остались вопросы? Не знаете, как решать задачи на подобие треугольников?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Признаки подобия треугольников — это… Что такое Признаки подобия треугольников?



Признаки подобия треугольников

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.

Признаки подобия треугольников

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, ∠B=∠B₁.

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Второй признак

Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Третий признак

Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Признаки подобия прямоугольных треугольников

1. По острому углу — см. первый признак;
2. По двум катетам — см. второй признак;
3. По катету и гипотенузе — см. второй признак.

Свойства подобных треугольников

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:

Связанные определения

• Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

Литература

• Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.

См. также

Ссылки

Wikimedia Foundation. 2010.

• Признак Абеля
• Признание: Два лица зла (фильм)

Смотреть что такое «Признаки подобия треугольников» в других словарях:

• Признаки равенства треугольников — Стандартные обозначения Треугольник  простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника …   Википедия

• Подобие треугольников — Признаки подобия треугольников геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Преобразование подобия — Подобие  преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k  положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны …   Википедия

• Подобные треугольники — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве)  это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… …   Википедия

• Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие  преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где   положительное число, называемое… …   Википедия

• Подобные фигуры — Подобие  преобразование евклидова пространства, при котором для любых двух точек A, B и их образов A , B имеет место соотношение | A B | = k | AB | , где k  положительное число, называемое коэффициентом подобия. Содержание 1 Примеры 2 Связанны …   Википедия

• подобие — я; ср. 1. Пренебр. Нечто похожее, сходное с чем л. Жалкое п. старинного полонеза. П. человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на себя). 2. Матем …   Энциклопедический словарь

• Площадь треугольника — Стандартные обозначения Треугольник  простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Вершины треугольника …   Википедия

• подобие — я; ср. 1) пренебр. Нечто похожее, сходное с чем л. Жалкое подо/бие старинного полонеза. Подо/бие человеческой фигуры. Не Гамлет, а его бесконечные подобия. Лепить по своему подобию (влияя на кого л., воспитывая кого л., делать его похожим на… …   Словарь многих выражений

dic.academic.ru

8 класс. Геометрия. Подобные треугольники. Признаки подобия треугольников. — Второй и третий признаки подобия треугольников.

Комментарии преподавателя

По­доб­ны­ми на­зы­ва­ют­ся такие тре­уголь­ни­ки, у ко­то­рых углы со­от­вет­ствен­но равны, а сто­ро­ны од­но­го со­от­вет­ствен­но про­пор­ци­о­наль­ны сто­ро­нам дру­го­го тре­уголь­ни­ка (см. рис. 1).

 

Рис. 1. По­доб­ные тре­уголь­ни­ки 

От­но­ше­ние длин сто­рон од­но­го тре­уголь­ни­ка к сход­ствен­ным сто­ро­нам дру­го­го на­зы­ва­ет­ся ко­эф­фи­ци­ен­том по­до­бия (): .

Пер­вый при­знак по­до­бия тре­уголь­ни­ков

Если два угла од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум углам дру­го­го, то такие тре­уголь­ни­ки по­доб­ны (см. рис. 2). 

 

Рис. 2. Пер­вый при­знак по­до­бия тре­уголь­ни­ков

Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны двум дру­гим сто­ро­нам дру­го­го тре­уголь­ни­ка, а углы, за­клю­чён­ные между этими сто­ро­на­ми, равны, то такие тре­уголь­ни­ки по­доб­ны.

Дано: ;  ; ;  (см. рис. 3).

До­ка­зать: по­до­бие дан­ных тре­уголь­ни­ков  . 

 

Рис. 3. Ил­лю­стра­ция к до­ка­за­тель­ству

До­ка­за­тель­ство

Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков, тре­уголь­ни­ки по­доб­ны, если два угла од­но­го со­от­вет­ствен­но равны двум углам дру­го­го. По­это­му для до­ка­за­тель­ства того, что , необ­хо­ди­мо до­ка­зать, что угол  равен углу  (угол  равен углу 

www.kursoteka.ru

Подобные треугольники — это… Что такое Подобные треугольники?



Подобные треугольники

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого.

Признаки подобия треугольников

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Первый признак

Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, ∠B=∠B₁.

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Второй признак

Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, ∠A=∠A₁, = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Третий признак

Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

Признаки подобия прямоугольных треугольников

1. По острому углу — см. первый признак;
2. По двум катетам — см. второй признак;
3. По катету и гипотенузе — см. второй признак.

Свойства подобных треугольников

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:

Связанные определения

• Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

Литература

• Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.: ил.

См. также

Ссылки

Wikimedia Foundation. 2010.

• Подобные фигуры
• Поднять тремя пальцами

Смотреть что такое «Подобные треугольники» в других словарях:

• Признаки подобия треугольников — Подобные треугольники  треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. Содержание 1 Признаки подобия треугольников 1.1 Первый признак …   Википедия

• Теорема Пифагора — Теорема Пифагора  одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 …   Википедия

• Пифагора теорема — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 Формулировки 2 Доказательства …   Википедия

• ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… …   Энциклопедия Кольера

• ПОДОБНЫЙ — ПОДОБНЫЙ, подобная, подобное; подобен, подобна, подобно. 1. кому чему. Сходный, совершенно похожий. Происшествие, подобное этому, было в прошлом году. 2. Такой, этот (о котором говорится). «Где еще мыслимы подобные вещи?» Маяковский. Перечислить… …   Толковый словарь Ушакова

• Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника  перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав …   Википедия

• Теорема Наполеона — Теорема Наполеона  утверждение евклидовой планиметрии о равносторонних треугольниках …   Википедия

• подо́бный — ая, ое; бен, бна, бно. 1. кому чему. Сходный с кем , чем л., похожий на кого , что л. [Белесова:] Если бы вы или кто нибудь из подобных вам людей навещали меня хоть изредка, мне было бы лучше, теплее на душе. А. Островский, Богатые невесты. Он… …   Малый академический словарь

• ПОДОБИЕ — ср. (доба, время, пора, срок, год, година: добрый, удобный, сдобный и пр.) сходство, согласие, одновидность, схожесть. И подобия нет подлинника. | Вещь сделанная по образцу или в подражанье; изображенье чего; образ чего либо. Иссеченное из камня… …   Толковый словарь Даля

• Мгновенный центр скоростей — Мгновенный центр скоростей  при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Содержание 1 Положение… …   Википедия

dic.academic.ru

Свойства

1. Каждая из высот является одновременно биссектрисой и медианой.

2. Центры описанной и вписанной окружностей совпадают.

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

Определение. Треугольник называют прямоугольным, если у него есть прямой угол.

Свойства

1. Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).

2. Сумма двух острых углов прямоугольного треугольника равна прямому углу.

3. Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.

4. Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.

5. Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Рис. 11.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b: a² + b² = c².

Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Признаки равенства прямоугольных треугольников:

1. по катету и гипотенузе;

2. по двум катетам;

3. по катету и острому углу;

4. по гипотенузе и острому углу.

Признаки равенства и подобия треугольников признаки равенства треугольников

Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны (см. рис. 12).

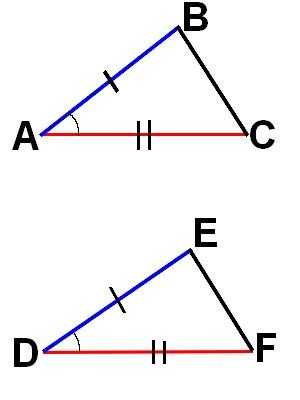
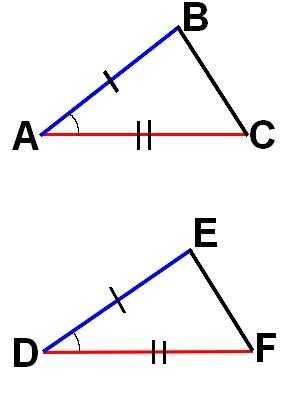
Рис. 12.

AB=DE

AC=DF.

ﮮ A = ﮮ D

ΔABC=Δ DEF по двум сторонам и углу между ними

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны(см. рис. 13.

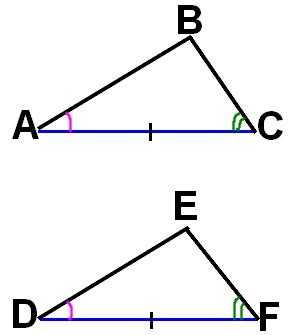
Рис. 13.

AC=DF

ﮮ A = ﮮ D

ﮮ C = ﮮ F

ΔABC=ΔDEF по стороне и прилежащим к ней углам.

Третий признак равенства треугольников

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. (см. рис. 14

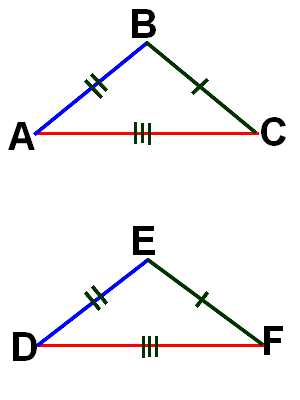
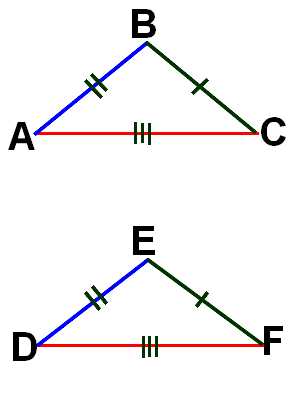
Рис. 14.

AB=DE

BC=EF

AC=DF

ΔABC=ΔDEF по трём сторонам.

Признаки подобия треугольников

Первый признак

Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого треугольника (см. рис. 15).

Рис. 15.

Второй признак

Д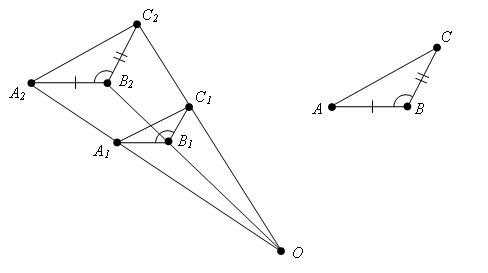ва треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого и углы, образованные этими сторонами в этих треугольниках, равны(см. рис. 16).

Рис. 16.

Третий признак

Два треугольника подобны, если три стороны одного треугольника пропорциональны сторонам другого треугольника (см. рис. 17).

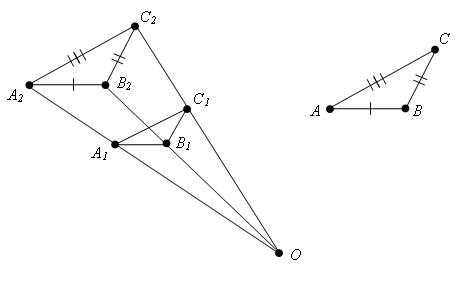
Рис. 17.

Прямоугольные треугольники подобны, если гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

Итак, это треугольник с одной стороны.

Загадки треугольника

С другой стороны треугольник это — тайный оккультный знак, встречающийся во многих цивилизациях. Три угла, три грани — магическое число 3. Не удивительно, что треугольник можно найти на тайных письменах, символах, пентаграммах. И совсем не удивительно, что самые загадочные места и строения могут быть связаны тоже с треугольниками. Например, египетские пирамиды (в Египте треугольник символизировал триаду духовной воли, любви-интуиции и высшего разума человека, то есть его личность и душу.) Или звезда Давида (еврейский символ, образованный наложением двух треугольников). А еще Бермудский треугольник.

Платон утверждал, что вообще вся “Поверхность состоит из треугольников”. На самом деле треугольники используются везде и всюду. Уже со времён палеолита и неолита в древнем искусстве очень широко распространяются изображения равностороннего треугольника. Первобытные люди покрывали сферические сосуды сетью круглых равносторонних треугольников. Символическое изображение треугольника есть в архитектуре и строительстве (пирамиды и др.), во фрагментах одежды и украшениях. Вожди племен североамериканских индейцев носили на груди символ власти: равносторонний треугольник. В Африке женщины туарегов также украшали себя большими пластинами из равносторонних треугольников.

Один из самых загадочных и интересных треугольников– “Бермудский треугольник”. Еще это место называют аномальной зоной.

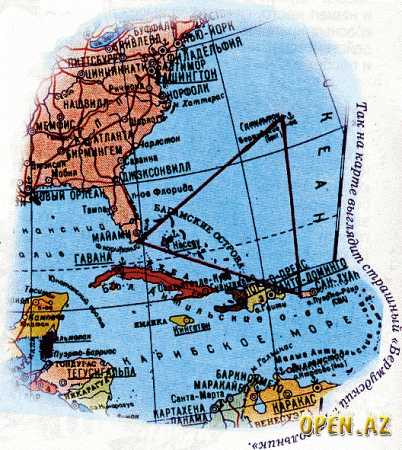
Рис. 18

На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов — большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках не удалось обнаружить ни одного трупа или обломка.

Над океаном плыл рассвет.

Светлело небо, голубея.

Фелюга* шла к Бермудам, нет

Таинственней загадки, злее.

Проникнув в эпицентр Бермуд,

мы видим розу из тумана.

В ней тени кораблей плывут,

«Мэри Селест» без капитана.

Ворота в рай иль ад, не знаем,

но мы войдем туда сейчас.

Сиянье ширится, сгораем…

Не поминайте лихом нас.

Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение — это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь — 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский треугольник” не является географическим.

Древние говорили, что Земля поделена на правильные треугольники, а Платон заявлял, что “Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи”, т.е. 12 пентаграмм.

В свою очередь, каждая пентаграмма делится на треугольники большие и треугольники помельче. Таким образом, поверхность Земли предстает в виде в пересечении вершин треугольников, в которых образуются “энергетические узлы”. Эта идея разработана русскими исследователями Н. Гончаровым, В. Морозовым и В. в соответствии с которой цивилизации развивались в “энергетических узлах”. В пересечении вершин треугольников образуются особенно богатые запасы полезных ископаемых, в некоторых “узлах” порой исчезают материальные предметы (Бермудский треугольник).

Стихи о треугольнике

О, треугольник, как ты прекрасен.

Как красив и богат,

Ибо ты имеешь три стороны.

Три угла, три вершины.

Ты один можешь быть:

И равнобедренным, и равносторонним,

И прямоугольным…

Ибо ты могуч…

…По тебе судят теоремы,

Тебе посвятили три признака равенства.

Ведь, чтобы доказать, что ты равен,

Нужно приложить силы.

Ибо даже медиана, проведенная

К основанию равнобедренного треугольника

Является высотой и биссектрисой.

И не каждый знает, что в треугольнике

Медианы, высоты, биссектрисы

Пересекаются в одной точке.

И что бы мы знали без Великого треугольника!

Ибо даже стол не может стоять на двух ножках.

Ода треугольнику в стихах.

Вы всем известны,

Без вас не обойтись нигде,

Вы так чудесны,

Вы так нужны везде.

Вы — Геометрические фигуры,

Треугольники мои.

“Треугольник, треугольник”.

Самый лучший из фигур,

Ты родился из трех точек

И прекрасных трех прямых.

Но не думайте, ребята,

Треугольник не простой…

Он бывает и прямой,

Равнобедренный…любой!!!

О медиане и …

Медиана – она мышка Яна,

Зацепившись хвостом за вершину,

Спустилась к основанию

Прямо в середину!

Высота стоит столбом – вертикально.

Она измерит даже дом капитально.

Биссектриса — почему так назвали, не пойму…

Потому что, потому

Она ходит по углам

И делит угол пополам.

Биссектриса – это киска,

Которая ловит мышку по углам,

И делит угол пополам!

Медианка – хулиганка

Бросит вещи по углам и

Стороны делит пополам

В треугольнике она стоит

Прямо – как всегда.

Высота, высота!

С высоты глядит на нас:

“С медианой ты не путай,

Есть ведь разница у нас”.

Медиана – как лиана,

Только разница одна –

Из вершины в середину

Не промахнется никогда.

Ода признакам треугольников

О, треугольники, вы так прекрасны,

Три признака ваши для нас не сложны.

Вот первый из них:

Если две стороны и угол между ними

Одного треугольника равны

Двум сторонам и углу между ними другого треугольника,

То такие треугольники равны.

А теперь будьте умны…

Приставьте числительные одна и два

К словам “сторона” и “угла”

И пред ваши очи вмиг

Второй признак подбежит.

А у третьего признака нет углов,

А только три стороны равны.

Третий признак легче всех.

Ну, а вы, мной ободрены,

Додумайте его непременно.

Вы отроки – други, запомните ныне

Сии признаки равенства треугольников.

studfiles.net