Бесплатный графический калькулятор-Graph 2D
Бесплатный графический калькулятор-Graph 2Dx-scale
шкала Y
Это онлайн-образовательные инструменты ( бесплатный онлайн-калькулятор для математической геогебры ) для построения графика математических функций 2D. Его можно использовать в естественнонаучном образовании. Это полезно для студентов и преподавателей естественных наук. Введите любую функцию в поле ввода, а затем нажмите кнопку рисования. Иногда требуется нарисовать график этой функции. Для увеличения этого графика вы можете изменить шкалу x и шкалу y. Он может рисовать алгебраическую функцию, тригонометрическую функцию, обратную круговую функцию, логарифмическую функцию, экспоненциальную функцию, гиперболическую функцию и т. д. Вы можете ознакомиться с руководством пользователя для правильного использования этих онлайн-инструментов.
Чтобы получить обновленный веб-сайт, вы можете очистить данные кэша своего браузера (если вы просматриваете этот веб-сайт в течение многих дней) или просматривать этот веб-сайт с помощью другого веб-браузера. Шаги для очистки chache: 1. на вашем компьютере откройте браузер. 2. В правом верхнем углу нажмите Еще. 3. Щелкните Дополнительные инструменты. Очистить данные просмотра. 4. выберите временной диапазон. 4. Установите флажок «Кэшированные изображения и файлы». 5. Щелкните Очистить данные. В разных браузерах могут быть разные способы.
1. Ссылка на учебник vedio: Учебник Youtube vedio для простых функций 9х вместо е
х5. Для тригонометрической функции вы будете использовать углы в радианах и :
sin(x) вместо sinx, cos(x) вместо cosx
tan(x) вместо tanx,cosec(x) вместо cosecx
sec(x) вместо secx, cot(x) вместо cotx
6.
Для обратной круговой функции вы будете использовать углы в радианах и :asin(x) вместо sin
-1 x, acos(x) вместо cos -1 хatan(x) вместо tan
-1 x, acosec(x) вместо cosec -1 xasec(x) вместо sec
-1 x, acot(x) вместо cot -1 x7. Для гиперболической функции введите:
sinh(x) вместо sinhx, ch(x) вместо coshx
tanh(x) вместо tanhx,cosech(x) вместо cosechx
sech(x) вместо sechx, coth(x) вместо cothx
8. Для обратной гиперболической функции введите:
asinh(x) вместо sinh
-1 x, acosh(x) вместо ch -1 x
9. Если вам нужно написать π, то вы должны написать pi или PI или Pi
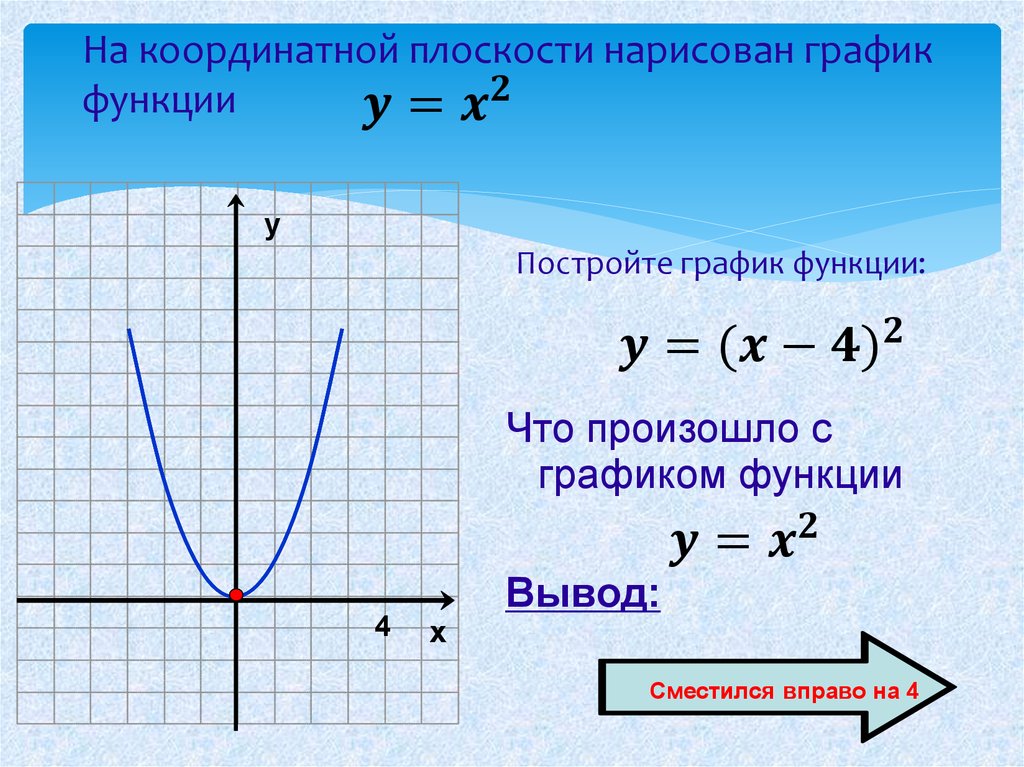
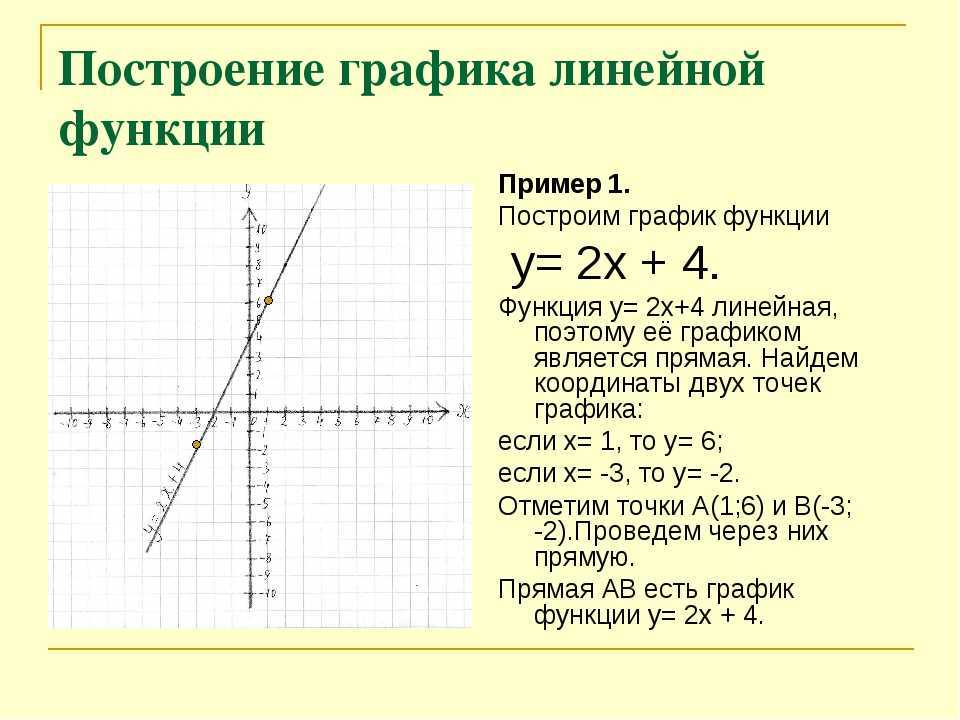
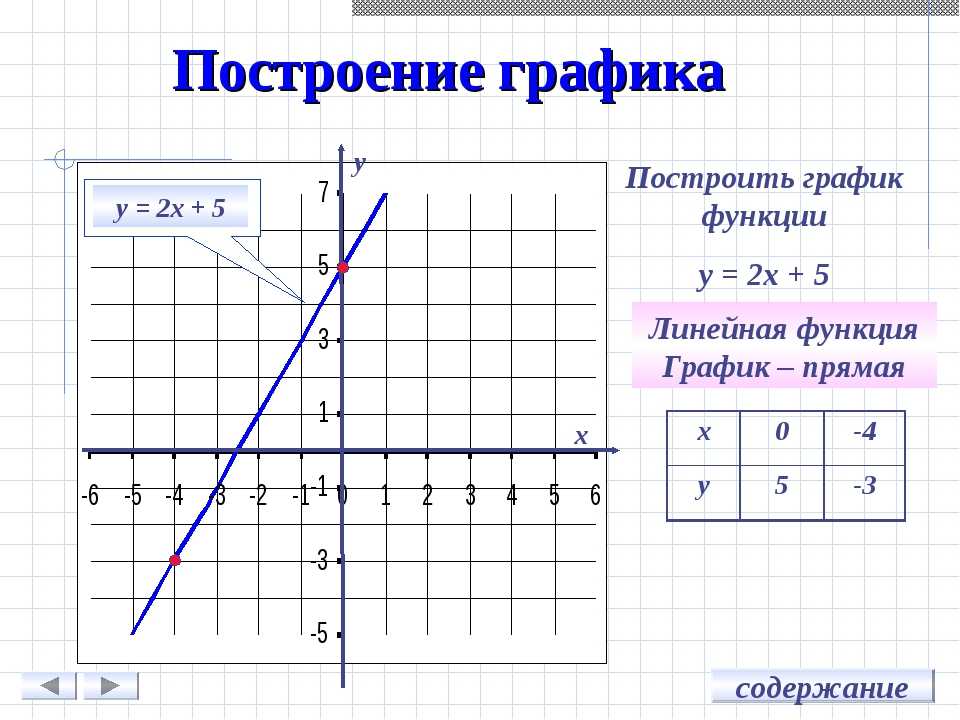
Линейная функция y=f(x)=ax+b всегда представляет собой прямую линию и может быть нарисована путем соединения только двух точек.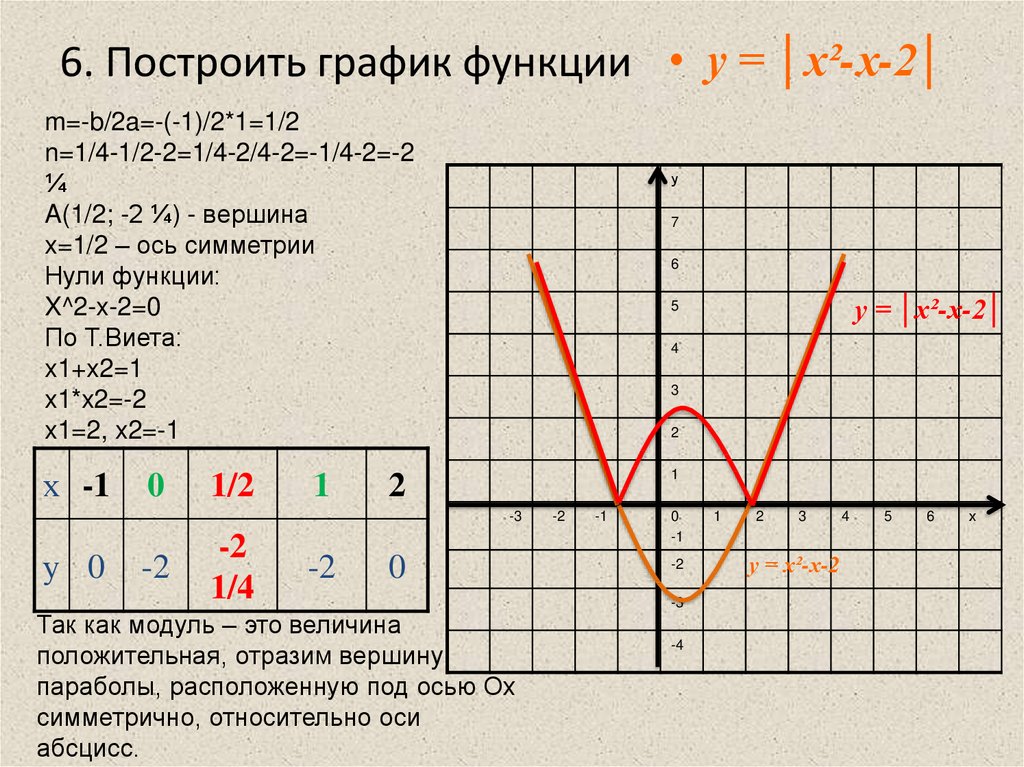
Например, y=f(x)=2x+1 — это линейная функция, которую можно нарисовать, соединив две точки (1,3) и (3,7). Бесплатный графический калькулятор для веб-сайта математического рисования www.graph3d.com может нарисовать любую линейную функцию. Вы можете ввести 2*x+1 в поле ввода, а затем нажать кнопку рисования, чтобы получить график. Вы также можете попробовать рисовать с помощью функции f(x)=x, f(x)=3x+1, f(x)=-2x+3, f(x)=-x-5, f(x)= 5х-1 и т.д. Квадратичная функция y=f(x)=ax 2 +bx+c всегда представляет собой параболу. Если коэффициент x 2 положительный, то парабола будет вогнутой вверх, а отрицательный — парабола вогнутой вниз. Чтобы нарисовать график квадратичной функции вручную, мы найдем две точки, для которых y=f(x)=0, что означает, что парабола проходит через эти две точки, а вогнутость параболы зависит от коэффициента x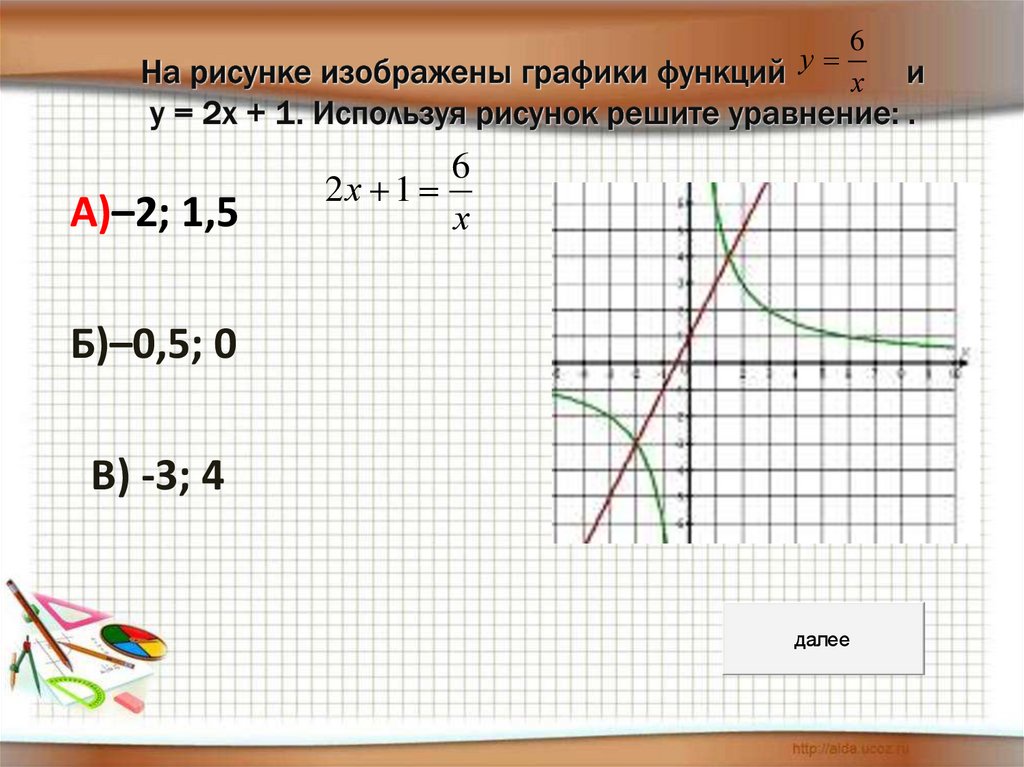 
Так как коэффициент x 2 — это 1, что положительно, поэтому парабола будет вогнутой. Geogebra Бесплатный графический калькулятор для математического веб-сайта рисования графиков www.graph3d.com может нарисовать любую квадратичную функцию. Вы можете ввести x**2-5*x+4 в поле ввода, а затем нажать кнопку рисования, чтобы получить график. Вы также можете попробовать рисовать с помощью функции f(x)=x 2 , f(x)=-x 2 , f(x)=x 2 +5x, f(x)=x 2 -3x, f(x)=x 2 +2x+5 и т.д.
Если мы найдем только одну точку, для которой y=0, то парабола коснется оси x в этой точке. Например, y=f(x)=2(x-2) 2 , есть только одна точка (2, 0), для которой y=0, поэтому парабола касается оси x в (2, 0), которая является критической точкой. Поскольку коэффициент x 2 равен 2, что положительно, парабола будет вогнутой. Бесплатный графический калькулятор для веб-сайта математического рисования www.graph3d.com может нарисовать любую квадратичную функцию.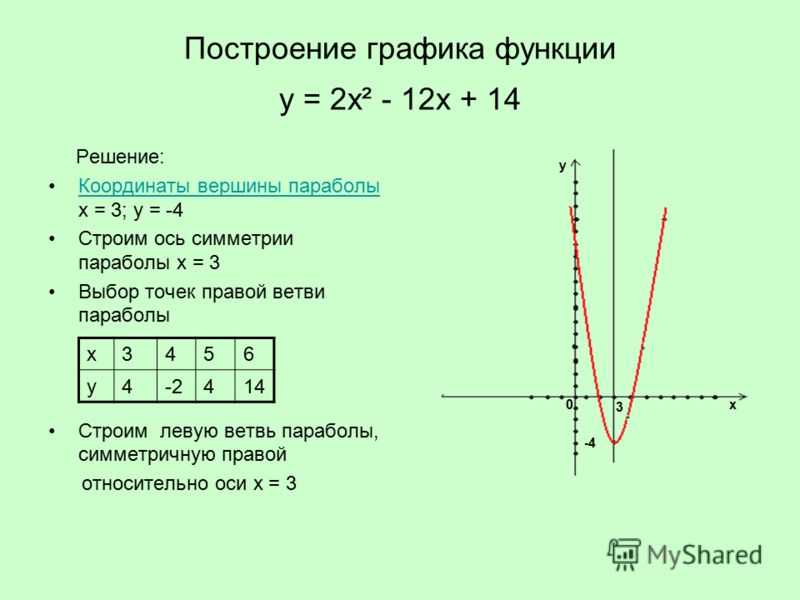
Вы можете ввести 2*(x-2)**2 в поле ввода, а затем нажать кнопку рисования, чтобы получить график.
Если мы не можем найти ни одной точки, для которой y=0, то мы попытаемся получить терм целого квадрата. Например, y=f(x)=x 2 -4x+7=(x-2) 2 +3. Когда x=2, то (x-2) 2 =0 и, следовательно, y=3. Таким образом, точка (2, 3) является критической точкой. Поскольку коэффициент x
Кубическая функция y=f(x)=ax 3 +bx 2 +cx+d представляют собой кривую. Сначала находим значение x, при котором y=0. Если количество одинаковых корней y = 0 нечетное число, то эта точка графика будет пересекаться по оси x и будет четным числом , тогда график коснется оси x.
Если коэффициент x 3 положительный, то кривая будет рисовать от верхней стороны оси x правой стороны, а отрицательный, тогда кривая будет рисовать от нижней стороны оси x правой стороны. Например, y=f(x)=(x-3) 2 (x-7), есть два (четных) одинаковых корня x = 3 и один (нечетный) корень x = 7. Таким образом, кривая касается x = 3 с осью x и пересекает x = 7 с x -ось. Поскольку коэффициент x 3 равен 1, что является положительным, кривая будет рисовать от верхней стороны оси x правой стороны. Бесплатный онлайн-калькулятор по математике для построения графиков на сайте www.graph3d.com может нарисовать любую кубическую функцию. Вы можете ввести (x-3)**2*(x-7) в поле ввода, а затем нажать кнопку рисования, чтобы получить график. Вы также можете попробовать рисовать с помощью функции f(x)=x 3 , f(x)=-x 3 , f(x)=x 3 -4x 2 и т. д.
Рациональная функция y=f(x)=P(x)/Q(x) представляет собой отношение двух многочленов P(x) и Q(x).
Например, y=f(x)=(x 2 +1)/x=x+1/x является рациональной функцией. Имеются две асимптоты y=x и x=0. График этой рациональной функции представляет собой две кривые, расположенные между этими двумя асимптотами. Бесплатный онлайн-калькулятор по математике для построения графиков на сайте www.graph3d.com может нарисовать любую рациональную функцию. Вы можете ввести (x**2+1)/x в поле ввода, а затем нажать кнопку рисования, чтобы получить график. Вы также можете попробовать рисовать с помощью функции f(x)=x-1/x , f(x)=(x+1)/x , f(x)=1/x, f(x)=(x+ 1)(х+3)/(х-2) и т.д.
Тригонометрическая функция – это отношение длин двух сторон прямоугольного треугольника. Ее также называют круговой функцией. Бесплатный онлайн-калькулятор по математике для построения графиков на сайте www.graph3d.com может нарисовать любую тригонометрическую функцию. Вы можете ввести Math.sin(x) в поле ввода, а затем нажать кнопку рисования, чтобы получить график sin(x). Вы также можете изменить масштаб x и y.
Обратная круговая функция — это дуга или обратная тригонометрическая или антитригонометрическая функция. Бесплатный онлайн-калькулятор по математике для построения графиков на веб-сайте www.graph3d.com может нарисовать любую антитригонометрическую функцию или обратную круговую функцию. Вы можете ввести Math.asin(x) в поле ввода, а затем нажать кнопку рисования, чтобы получить график sin -1 (x). Вы также можете изменить шкалу x и шкалу y. Вы также можете попробовать нарисовать с помощью функции f(x)=cos -1 (x), f(x)=tan -1 (x), f(x)=sin -1 (2x) и т. д.
Экспоненциальная функция — это функция, которая обозначается как f(x)=a x =e xlna или f(x)= e x
Бесплатный онлайн-калькулятор по математике для построения графиков на веб-сайте www.graph3d.com может нарисовать любую экспоненциальную функцию. Вы можете ввести Math.exp(x) в поле ввода, а затем нажать кнопку рисования, чтобы получить график e x . Вы также можете изменить шкалу X и шкалу Y. Вы также можете попробовать нарисовать с помощью функции f(x)=e -x , f(x)=e -2x , f(x)=e -3x , f(x)=e 2x , f(x)=e 3x , f(x)=10 x , f(x)=10 -x , f(x)=5 x и т. д. Логарифмическая функция — это функция, которая обозначается как f(x)=log(x) или f(x)= ln(x). Бесплатный онлайн-калькулятор по математике для построения графиков на сайте www.graph3d.com может нарисовать любую логарифмическую функцию. Вы можете ввести log (x) в поле ввода, а затем нажать кнопку рисования, чтобы получить график log (x). Вы также можете изменить шкалу x и шкалу y. Вы также можете попробовать рисовать с помощью функции f(x)=log(2x), f(x)=log(3x-5), f(x)=5log(1-x), f(x)=ln( х), f(x)=ln(5x-2), f(x)=3ln(2x-1), f(x)=2+ln(x),f(x)=2-log(x) и т.
В математике трансцендентная функция — это функция, которая представляет собой комбинацию экспоненциальной функции, логарифмической функции, тригонометрической функции, обратной круговой функции и т. Д., То есть трансцендентная функция не является алгебраической функцией. Например, sin(2x), tan(x), log(x), log(3x), ln(2x), sin -1 (x), кроватка -1 (x), e x , e -2x и т. д. являются трансцендентными функциями. Мы можем нарисовать любой график трансцендентной функции на бесплатном веб-сайте по рисованию графиков www.graph3d.com. Как, например, график f(x)=e 9x+sin(2x) в поле ввода, а затем нажмите кнопку рисования, чтобы получить график. График этой функции приведен ниже.
В математике нечетная функция f(x) — это функция, удовлетворяющая f(-x)=-f(x). Например, sin(x), tan(x), x 3 , x 7 и т. д. являются нечетными функциями. Нечетные функции симметричны относительно начала координат.
Мы можем нарисовать любой график нечетной функции с помощью бесплатного веб-сайта рисования графиков www.graph3d.com. Например, график f(x)=x 3 93 в поле ввода, а затем нажмите кнопку рисования, чтобы получить график нечетной функции f(x)=x 3 . График этой функции приведен ниже.
В математике четная функция f (x) — это функция, удовлетворяющая f (-x) = f (x). Например, cos(x), x 2 , x 4 и т. д. являются четными функциями. Четные функции симметричны относительно оси y. Мы можем нарисовать любой график четной функции на бесплатном веб-сайте по рисованию графиков www.graph3d.com. Как, например, график f(x)=x 92 в поле ввода, а затем нажмите кнопку рисования, чтобы получить график четной функции f(x)=x 4 -x 2 . График этой функции приведен ниже.
В математике гиперболическая функция аналогична тригонометрической функции или круговой функции. Гиперболическая функция определяется комбинацией экспоненциальной функции e x и e -x .
Например, sh(x)=(e x -e -x )/2, cosh(x)=(e x +e -x )/2, th(x)=(e x -e -x )/(e x +e -x ), cosech(x)=2 /(e x -e -x ), sech(x)=2/(e x +e -x ), coth(x)=(e x -e -x )/(е х + е -х ). Мы можем нарисовать любой график гиперболической функции на бесплатном сайте рисования графиков www.graph3d.com. Как, например, график f(x)=coth(x). Для рисования введите coth(x) в поле ввода, а затем нажмите кнопку рисования, чтобы получить график гиперболической функции f(x)=coth(x). График этой функции приведен ниже.
В математике постоянная функция — это функция, диапазон которой представляет собой один элемент во всей области. Например, f(x)=5, f(x)=e, f(x)=π и т. д. являются постоянными функциями. Мы можем нарисовать любой график постоянной функции с помощью бесплатного веб-сайта рисования графиков www.
graph3d.com. Как, например, график f(x)=7. Для рисования введите 7 в поле ввода, а затем нажмите кнопку рисования, чтобы получить график постоянной функции f(x)=7. График этой функции приведен ниже.
В математике квадратный корень функции определяется как f (x) = √ (h (x)), где h (x) — другая функция. Мы можем нарисовать любой двумерный график функции квадратного корня на бесплатном веб-сайте по рисованию графиков www.graph3d.com. Как, например, график f(x)=√(2x+5). Для рисования введите sqrt(2x+5) в поле ввода, а затем нажмите кнопку рисования, чтобы получить график функции квадратного корня f(x)=√(2x+5). График этой функции приведен ниже.
Веб-сайт рисования графиков www.graph3d.com может нарисовать любой график в 2D смешанной функции алгебраической функции и тригонометрической функции. Например, график f(x)=xsin 92 в поле ввода, а затем нажмите кнопку рисования, чтобы получить график смешанной функции f(x)=xsin 2 x. График этой функции приведен ниже.
Область определения функции y=f(x) — это множество всех возможных значений независимой переменной x, а область значений функции y=f(x) — множество всех возможных значений зависимой переменной y. Домен обозначается Domf, а диапазон обозначается Rangf. По графику функции мы можем определить домен и диапазон. Например, y=f(x)=√(x+5). График расположен от -5 до ∞ по горизонтали. Итак, Domf=(-5, ∞). Снова график расположен от 0 до ∞ по вертикали. Итак, Rangf=(0, ∞)
Equation Grapher — Граф неявных функций
Графический редактор уравнений предназначен для построения графиков . уравнения. С помощью графического редактора уравнений вы также можете построить графики неявно определенных функций , стандартных и общих форм конических сечений и кривых уровня .
Устройство для построения уравнений — это устройство для построения графиков , которое рисует график любого уравнения в форме G(x,y) = F(x,y) , где каждая сторона представляет собой выражение, которое может содержать x и y .
Графический редактор уравнений является более общим графическим инструментом, чем графический редактор функций , который рисует только график уравнений в форме y = f(x) , где правая часть представляет собой выражение в x только.
Устройство для построения уравнений также предназначен для построения графиков неявно определенных функций .
Устройство для построения неявных функций можно использовать для построения графиков, например, уравнений линий в стандартных формах и формах точка-наклон .
Для графических уравнений знак равенства должен использоваться для ввода обеих частей уравнения. Это позволяет построить, например, стандартные и общие формы уравнений конических сечений ( окружностей , парабол , гипербол и эллипсов ) и кривых уровня .
Советы: по мере ввода:
- пи заменяется на π .
МышьМатикс! Вы можете использовать мышь для поворота оси, перемещения и изменения масштаба
В дополнение к вводу данных – сначала нажав кнопку ⚙ (шестеренка) – вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивный маркер точек , как описано ниже.
- Щелкните по оси (или рядом с ней) и переместите мышь. Это будет вращать ось . графики перерисовываются в неортогональных декартовых или обобщенных полярных системах координат . Нажмите еще раз, чтобы освободить ось.
- Перетащите мышь на переместите систему координат вместе с графиками.
- Дважды щелкните на холсте до переместить исходную точку туда, где был нажат.
- Удерживая клавишу Alt, щелкните по оси, чтобы изменить масштаб (увеличение в одном направлении) ; в
точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.
Анимация вращения оси: Икс у ► ⬛
сообщение
f(x) =
?
f( ) =
⌨
4 Десятичные разряды
Graph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)
Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°: 92 грех (ху) = потому что (ху)РАД Полярный
🔍+ 1 🔍−
время построения графика (с)
Калькулятор загружается.
Пожалуйста, подождите….
Сделайте это прозрачным
Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осейзаголовок
.
..
Медленный Быстрый
Показать угловые оси Сделанный
Отключить программную клавиатуру
Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.
Графический редактор уравнений прост в использовании ; введите уравнение , например, 3x -2 y = x + 4y в любом поле выражения . Графический редактор уравнений отображает графики по мере ввода (по умолчанию).
- Для графика двух или более уравнений в одной и той же системе координат нажмите » для отображения мультиграфической панели . Панель с несколькими графиками состоит из панелей выражений , который можно добавить или удалить по желанию, нажав + или × . на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
- Можно установить точность графиков, выбрав нужный параметр в раскрывающемся списке Graph Fineness . В целом, чем выше точность, тем больше времени требуется графическому редактору уравнений для построения графиков уравнений.
- Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графическим редактором уравнений . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.Интересные кривые : Нарисуйте любое из выражений под Интересные графики , нажав на него. Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness 9.0008 как «+1» или выше.
Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.