| 1 | Найти число нейтронов | H | |
| 2 | Найти массу одного моля | H_2O | |
| 3 | Баланс | H_2(SO_4)+K(OH)→K_2(SO_4)+H(OH) | |
| 4 | Найти массу одного моля | H | |
| 5 | Найти число нейтронов | Fe | |
| 6 | Найти число нейтронов | Tc | |
| 7 | Найти конфигурацию электронов | H | |
| 8 | Найти число нейтронов | Ca | |
| 9 | Баланс | CH_4+O_2→H_2O+CO_2 | |
| 10 | Найти число нейтронов | C | |
| 11 | Найти число протонов | H | |
| 12 | Найти число нейтронов | O | |
| 13 | Найти массу одного моля | CO_2 | |
| 14 | Баланс | C_8H_18+O_2→CO_2+H_2O | |
| 15 | Найти атомную массу | H | |
| 16 | Определить, растворима ли смесь в воде | H_2O | |
| 17 | Найти конфигурацию электронов | Na | |
| 18 | Найти массу одного атома | H | |
| 19 | Найти число нейтронов | Nb | |
| 20 | Найти число нейтронов | Au | |
| 21 | Найти число нейтронов | Mn | |
| 22 | Найти число нейтронов | Ru | |
| 23 | Найти конфигурацию электронов | ||
| 24 | Найти массовую долю | H_2O | |
| 25 | Определить, растворима ли смесь в воде | NaCl | |
| 26 | Найти эмпирическую/простейшую формулу | H_2O | |
| 27 | Найти степень окисления | H_2O | |
| 28 | Найти конфигурацию электронов | K | |
| 29 | Найти конфигурацию электронов | Mg | |
| 30 | Найти конфигурацию электронов | Ca | |
| 31 | Найти число нейтронов | Rh | |
| 32 | Найти число нейтронов | Na | |
| 33 | Найти число нейтронов | Pt | |
| 34 | Найти число нейтронов | Be | Be |
| 35 | Найти число нейтронов | Cr | |
| 36 | Найти массу одного моля | H_2SO_4 | |
| 37 | Найти массу одного моля | HCl | |
| 38 | Найти массу одного моля | Fe | |
| 39 | Найти массу одного моля | C | |
| 40 | Найти число нейтронов | Cu | |
| 41 | Найти число нейтронов | S | |
| 42 | Найти степень окисления | H | |
| 43 | Баланс | CH_4+O_2→CO_2+H_2O | |
| 44 | Найти атомную массу | O | |
| 45 | Найти атомное число | H | |
| 46 | Найти число нейтронов | Mo | |
| 47 | Найти число нейтронов | Os | |
| 48 | Найти массу одного моля | NaOH | |
| 49 | Найти массу одного моля | O | |
| 50 | Найти конфигурацию электронов | Fe | |
| 51 | Найти конфигурацию электронов | C | |
| 52 | Найти массовую долю | NaCl | |
| 53 | Найти массу одного моля | ||
| 54 | Найти массу одного атома | Na | |
| 55 | Найти число нейтронов | N | |
| 56 | Найти число нейтронов | Li | |
| 57 | Найти число нейтронов | V | |
| 58 | Найти число протонов | N | |
| 59 | Упростить | H^2O | |
| 60 | Упростить | h*2o | |
| 61 | Определить, растворима ли смесь в воде | H | |
| 62 | Найти плотность при стандартной температуре и давлении | H_2O | |
| 63 | Найти степень окисления | NaCl | |
| 64 | Найти атомную массу | He | He |
| 65 | Найти атомную массу | Mg | |
| 66 | Найти число электронов | H | |
| 67 | Найти число электронов | O | |
| 68 | Найти число электронов | S | |
| 69 | Найти число нейтронов | Pd | |
| 70 | Найти число нейтронов | Hg | |
| 71 | Найти число нейтронов | B | |
| 72 | Найти массу одного атома | Li | |
| 73 | Найти эмпирическую формулу | H=12% , C=54% , N=20 | , , |
| 74 | Найти число протонов | Be | Be |
| 75 | Найти массу одного моля | Na | |
| 76 | Найти конфигурацию электронов | Co | |
| 77 | Найти конфигурацию электронов | S | |
| 78 | Баланс | C_2H_6+O_2→CO_2+H_2O | |
| 79 | Баланс | H_2+O_2→H_2O | |
| 80 | Найти конфигурацию электронов | P | |
| 81 | Найти конфигурацию электронов | Pb | |
| 82 | Найти конфигурацию электронов | Al | |
| 83 | Найти конфигурацию электронов | Ar | |
| 84 | Найти массу одного моля | O_2 | |
| 85 | Найти массу одного моля | H_2 | |
| 86 | Найти число нейтронов | K | |
| 87 | Найти число нейтронов | P | |
| 88 | Найти число нейтронов | Mg | |
| 89 | Найти число нейтронов | W | |
| 90 | Найти массу одного атома | C | |
| 91 | Упростить | na+cl | |
| 92 | Определить, растворима ли смесь в воде | H_2SO_4 | |
| 93 | Найти плотность при стандартной температуре и давлении | NaCl | |
| 94 | Найти степень окисления | C_6H_12O_6 | |
| 95 | Найти степень окисления | Na | |
| 96 | Определить, растворима ли смесь в воде | C_6H_12O_6 | |
| 97 | Найти атомную массу | Cl | |
| 98 | Найти атомную массу | Fe | |
| 99 | Найти эмпирическую/простейшую формулу | CO_2 | |
| 100 | Найти число нейтронов | Mt |
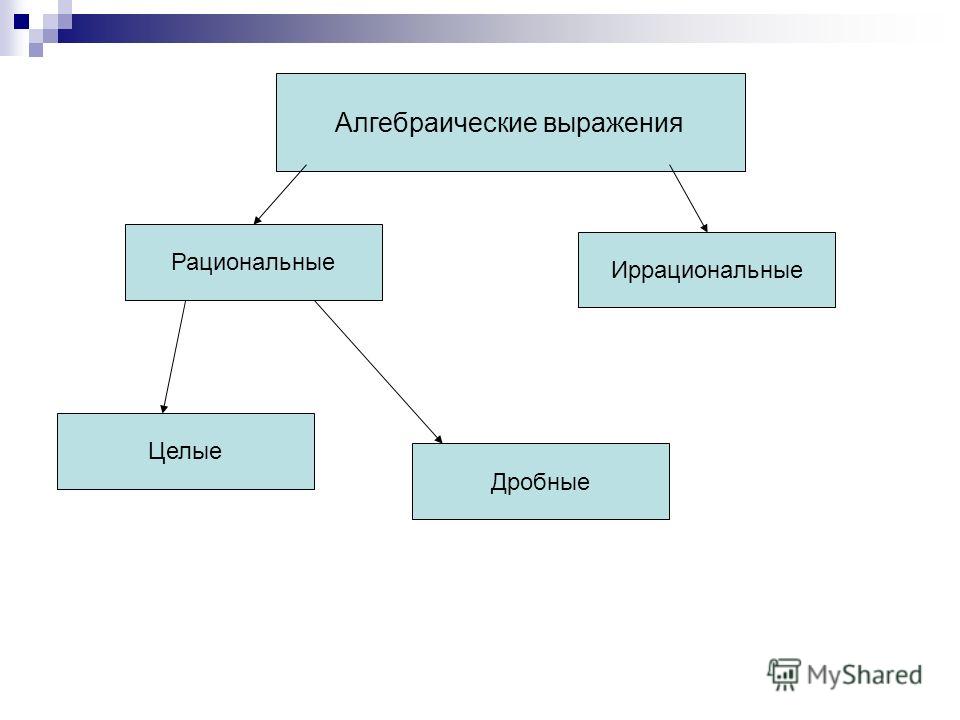
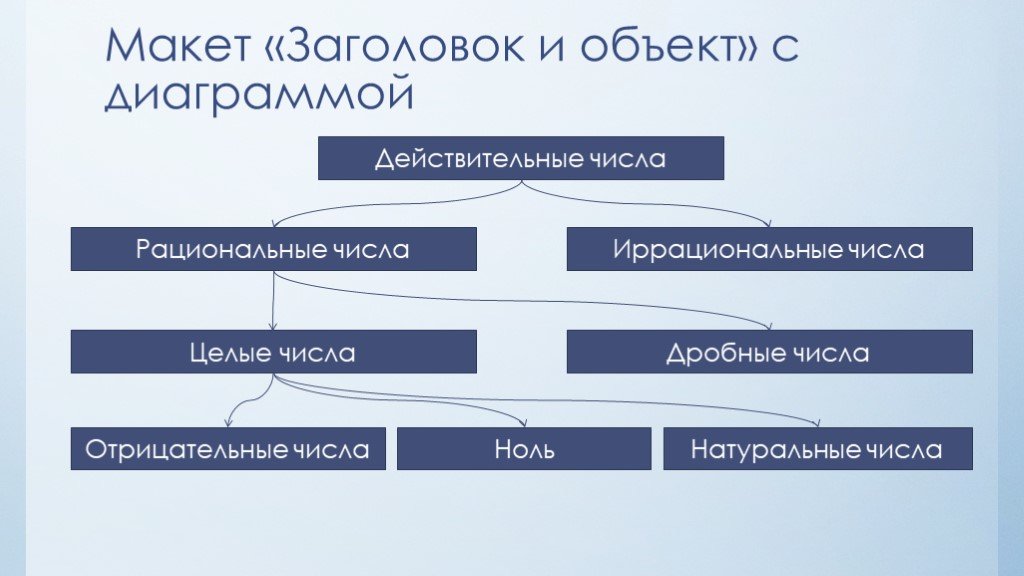
Числа натуральные целые рациональные иррациональные алгебраические трансцендентные.
 Трансцендентное число. Отрывок, характеризующий Трансцендентное число
Трансцендентное число. Отрывок, характеризующий Трансцендентное числоИлья Щуров
Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.
Как «единица» помогла построить первые города и великие империи? Как вдохновляла выдающиеся умы человечества? Какую роль в появлении денег она сыграла? Как «единица» объединилась с нулем, чтобы править современным миром? История единицы неразрывно связана с историей европейской цивилизации. Терри Джонс отправляется в юмористическое путешествие с целью собрать воедино удивительную историю нашего самого простого числа. С помощью компьютерной графики в этой программе единица оживает в самых различных испостасях. Из истории единицы становится ясно, откуда появились современные числа, и каким образом изобретение нуля спасло нас от необходимости сегодня использовать римские цифры.
Жак Сезиано
Мы знаем о Диофанте немного. Кажется, он жил в Александрии. Никто из греческих математиков не упоминает его до IV века, так что он вероятно жил в середине III века. Самая главная работа Диофанта, «Арифметика» (Ἀριθμητικά), состоялась в начале из 13 «книгах» (βιβλία), т. е. главах. Мы сегодня имеем 10 из них, а именно: 6 в греческом тексте и 4 других в средневековом арабском переводе, место которых в середине греческих книг: книги I-III по-гречески, IV-VII по-арабски, VIII-X по-гречески. «Арифметика» Диофанта прежде всего собрание задач, всего около 260. Теории, по правде говоря, нет; имеются только общие инструкции в введении книги, и частные замечания в некоторых задачах, когда нужно. «Арифметика» уже имеет черты алгебраического трактата. Сперва Диофант пользуется разными знаками, чтобы выражать неизвестное и его степени, также и некоторые вычисления; как и все алгебраические символики средних веков, его символика происходит от математических слов. Потом, Диофант объясняет, как решить задачу алгебраическим способом. Но задачи Диофанта не алгебраические в обычном смысле, потому что почти все сводятся к решению неопределённого уравнения или систем таких уравнений.
Самая главная работа Диофанта, «Арифметика» (Ἀριθμητικά), состоялась в начале из 13 «книгах» (βιβλία), т. е. главах. Мы сегодня имеем 10 из них, а именно: 6 в греческом тексте и 4 других в средневековом арабском переводе, место которых в середине греческих книг: книги I-III по-гречески, IV-VII по-арабски, VIII-X по-гречески. «Арифметика» Диофанта прежде всего собрание задач, всего около 260. Теории, по правде говоря, нет; имеются только общие инструкции в введении книги, и частные замечания в некоторых задачах, когда нужно. «Арифметика» уже имеет черты алгебраического трактата. Сперва Диофант пользуется разными знаками, чтобы выражать неизвестное и его степени, также и некоторые вычисления; как и все алгебраические символики средних веков, его символика происходит от математических слов. Потом, Диофант объясняет, как решить задачу алгебраическим способом. Но задачи Диофанта не алгебраические в обычном смысле, потому что почти все сводятся к решению неопределённого уравнения или систем таких уравнений.
Георгий Шабат
Программа курса: История. Первые оценки. Проблема соизмеримости длины окружности с ее диаметром. Бесконечные ряды, произведения и другие выражения для π. Сходимость и ее качество. Выражения, содержащие π. Последовательности, быстро сходящиеся к π. Современные методы вычисления π, использование компьютеров. Об иррациональности и трансцендентности π и некоторых других чисел. Предварительных знаний для понимания курса не требуется.
Ученые из Оксфордского университета заявили, что самым ранним известным употреблением цифры 0 для обозначения отсутствия значения разряда (как в числе 101) следует считать текст индийского манускрипта Бахшали.
Василий Писпанен
Кто не играл в детстве в игру «назови самое большое число»? Миллионы, триллионы и прочие «-оны» представить в уме уже сложно, но мы с вами попробуем разобрать «мастодонта» в математике — число Грэма.
Виктор Клепцын
Действительное число можно сколь угодно точно приблизить рациональными.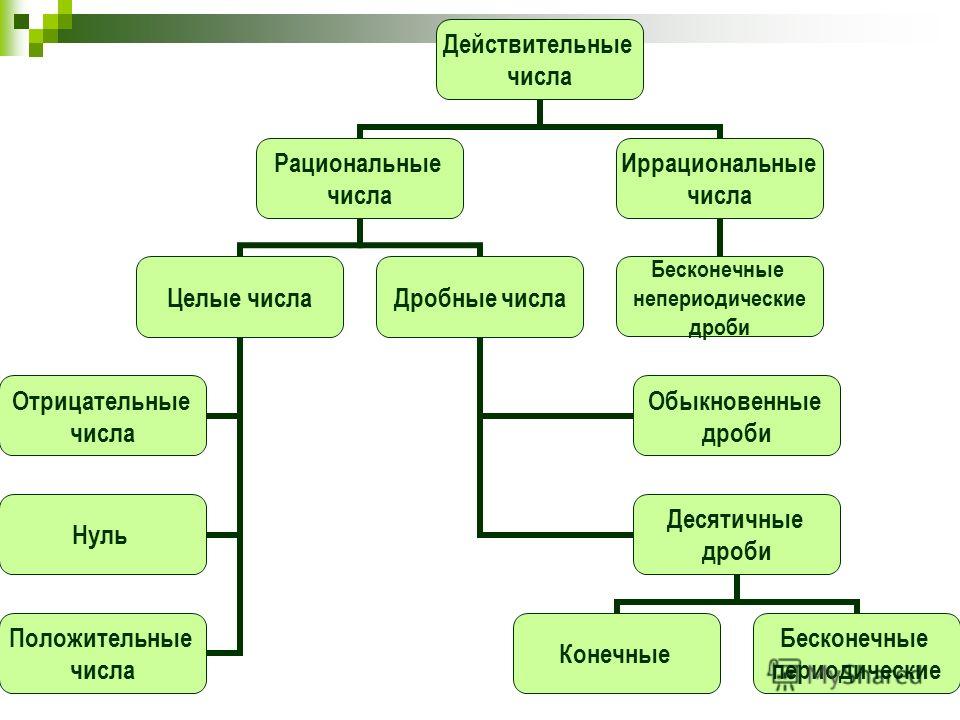 2. Это утверждает теорема Дирихле – и мы начнём курс с её немного нестандартного доказательства.
2. Это утверждает теорема Дирихле – и мы начнём курс с её немного нестандартного доказательства.
В 1980 году Книга рекордов Гиннесса повторила утверждения Гарднера, ещё больше подогрев интерес публики к этому числу. Число Грехема в невообразимое количество раз больше, чем другие хорошо известные большие числа, такие, как гугол, гуголплекс и даже больше, чем число Скьюза и число Мозера. На самом деле вся наблюдаемая вселенная слишком мала для того, чтобы вместить в себя обыкновенную десятичную запись числа Грехема.
Дмитрий Аносов
Лекции читает Аносов Дмитрий Викторович, доктор физико-математических наук, профессор, академик РАН. Летняя школа «Современная математика», г. Дубна. 16-18 июля 2002 г.
Корректно ответить на этот вопрос нельзя, поскольку числовой ряд не имеет верхнего предела. Так, к любому числу достаточно всего лишь прибавить единицу, чтобы получить число ещё большее. Хотя сами числа бесконечны, собственных названий у них не так уж и много, так как большинство из них довольствуются именами, составленными из чисел меньших.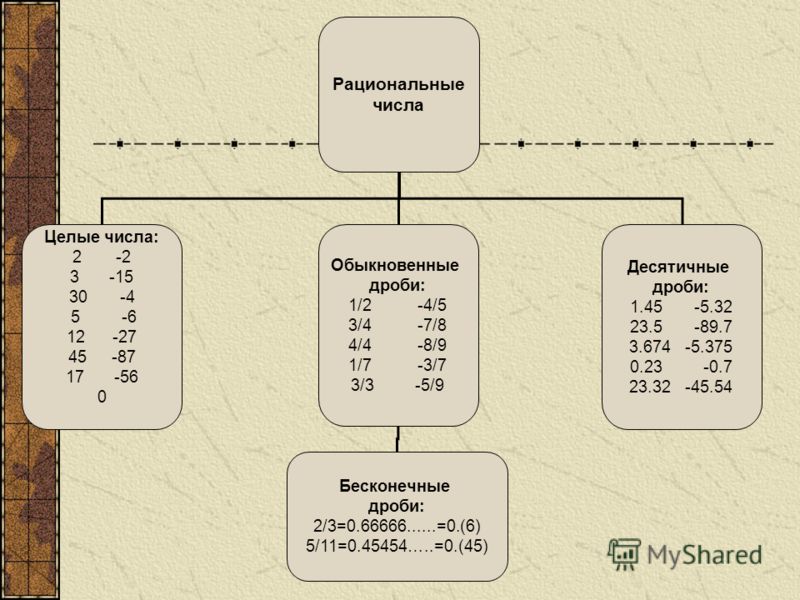
Трансцендентное число
число (действительное или мнимое), не удовлетворяющее никакому алгебраическому уравнению (См. Алгебраическое уравнение) с целыми коэффициентами. Таким образом, Т. ч. противопоставляются алгебраическим числам (См. Алгебраическое число). Существование Т. ч. впервые установил Ж. Лиувилль (1844). Отправной точкой для Лиувилля служила его теорема, согласно которой порядок приближения рациональной дроби с данным знаменателем к данному иррациональному алгебраическому числу не может быть произвольно высоким. Именно, если алгебраическое число а удовлетворяет неприводимому алгебраическому уравнению степени
 Поэтому, если для заданного иррационального числа α можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то α есть Т. ч. Пример такого числа даёт:
Поэтому, если для заданного иррационального числа α можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то α есть Т. ч. Пример такого числа даёт:Другое доказательство существования Т. ч. дал Г. Кантор (1874), заметив, что множество всех алгебраических чисел счётно (то есть все алгебраические числа могут быть перенумерованы; см. Множеств теория), тогда как множество всех действительных чисел несчётно. Отсюда следовало, что множество Т. ч. несчётно, и далее, что Т. ч. составляют основную массу среди множества всех чисел.
Важнейшая задача теории Т. ч. — это выяснение того, являются ли Т. ч. значения аналитических функций, обладающих теми или иными арифметическими и аналитическими свойствами при алгебраических значениях аргумента. Задачи этого рода принадлежат к числу труднейших задач современной математики. В 1873 Ш. Эрмит доказал, что Неперово число
В 1882 немецкий математик Ф. Линдеман получил более общий результат: если α — алгебраическое число, то е α — Т. ч. Результат Липдемана был значительно обобщён немецким математиком К. Зигелем (1930), доказавшим, например, трансцендентность значения широкого класса цилиндрических функций при алгебраических значениях аргумента. В 1900 на математическом конгрессе в Париже Д. Гильберт среди 23 нерешенных проблем математики указал на следующую: является ли трансцендентным числом α β , где α и β — алгебраические числа, причём β — иррациональное число, и, в частности, является ли трансцендентным число е π (проблема трансцендентности чисел вида α β была впервые в частной форме поставлена Л. Эйлер ом, 1744). Полное решение этой проблемы (в утвердительном смысле) удалось получить лишь в 1934 А. О. Гельфонд у. Из открытия Гельфонда, в частности, следует, что все десятичные логарифмы натуральных чисел (то есть «табличные логарифмы») суть Т. ч. Методы теории Т. ч. прилагаются к ряду вопросов решения уравнений в целых числах.
Линдеман получил более общий результат: если α — алгебраическое число, то е α — Т. ч. Результат Липдемана был значительно обобщён немецким математиком К. Зигелем (1930), доказавшим, например, трансцендентность значения широкого класса цилиндрических функций при алгебраических значениях аргумента. В 1900 на математическом конгрессе в Париже Д. Гильберт среди 23 нерешенных проблем математики указал на следующую: является ли трансцендентным числом α β , где α и β — алгебраические числа, причём β — иррациональное число, и, в частности, является ли трансцендентным число е π (проблема трансцендентности чисел вида α β была впервые в частной форме поставлена Л. Эйлер ом, 1744). Полное решение этой проблемы (в утвердительном смысле) удалось получить лишь в 1934 А. О. Гельфонд у. Из открытия Гельфонда, в частности, следует, что все десятичные логарифмы натуральных чисел (то есть «табличные логарифмы») суть Т. ч. Методы теории Т. ч. прилагаются к ряду вопросов решения уравнений в целых числах.
Лит.: Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952.
Большая советская энциклопедия. — М.: Советская энциклопедия . 1969-1978 .
Смотреть что такое «Трансцендентное число» в других словарях:
Число, не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Трансцендентными числами являются: число??3,14159…; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е=2,71828… и др … Большой Энциклопедический словарь
— (от лат. transcendere переходить, превосходить) это вещественное или комплексное число, не являющееся алгебраическим иными словами, число, которое не может быть корнем многочлена с целыми коэффициентами. Содержание 1 Свойства 2… … Википедия
Число, не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Трансцендентными числами являются: число π = 3,14159…; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е = 2,71828. .. и др … Энциклопедический словарь
.. и др … Энциклопедический словарь
Число, не удовлетворяющее никакому алгебр. ур нию с целыми коэффициентами. Т. ч. являются: число ПИ = 3,14159…; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е = 2,71828… и др … Естествознание. Энциклопедический словарь
Число, не являющееся корнем никакого многочлена с целыми коэффициентами. Областью определения таких чисел являются ноля действительных, комплексных и р адических чисел. Существование и явные построения действительных Т. ч. обосновал Ж. Лиувилль… … Математическая энциклопедия
Уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например: Более строгое определение таково: Трансцендентное уравнение это уравнение … Википедия
Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e kt, где k число,… … Энциклопедия Кольера
E математическая константа, основание натурального логарифма, иррациональное и трансцендентное число.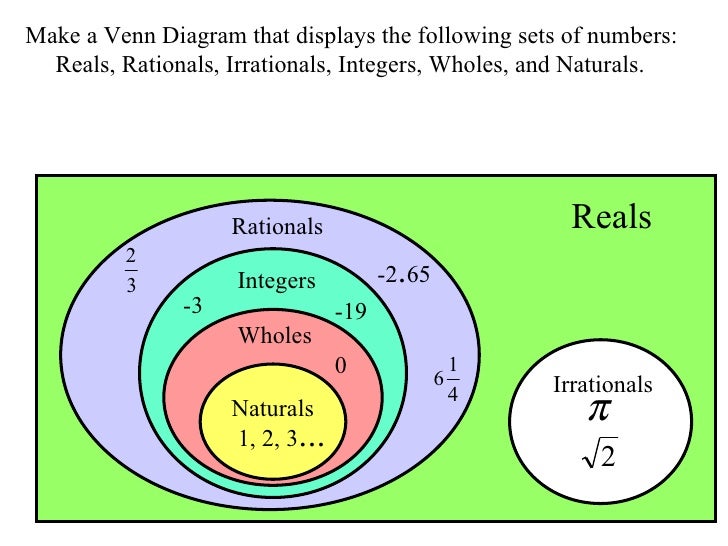 Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
E математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Слово «трансцендентный» обычно ассоциируется с трансцендентальной медитацией и разнообразной эзотерикой. Но чтобы употреблять его правильно, нужно как минимум отличать его от термина «трансцендентальный», а как максимум — вспомнить его роль в работах Канта и других философов.
Это понятие произошло от латинского transcendens — «переступающий», «превосходящий», «выходящий за пределы». В целом он обозначает то, что принципиально недоступно для эмпирического познания или не основано на опыте. Предпосылки термина возникли еще в философии неоплатонизма — основатель направления Плотин создал учение о Едином — всеблагом первоначале, которое невозможно познать ни усилием мысли, ни с помощью чувственного опыта. «Единое не есть сущее, но родитель его» — объясняет философ.
«Единое не есть сущее, но родитель его» — объясняет философ.
Полнее всего термин «трансцендентный» был раскрыт в философии Иммануила Канта, где он использовался для характеристики , существующих независимо от сознания и действующих на наши органы чувств, оставаясь при этом принципиально непознаваемыми, как на практике, так и в теории. Противоположность трансцендентности — : она означает либо неотъемлемость, внутреннюю связь какого-либо качества объекта с самим объектом, либо познаваемость объекта на личном опыте. Например, если предположить, что Вселенная создана по какому-то высшему замыслу, сам замысел для нас трансцендентен — мы можем только строить гипотезы о нем. Но если этот замысел существует в действительности, его последствия для нас имманентны, проявляясь в физических законах и обстоятельствах, в которые мы попадаем. Поэтому в некоторых теологических концепциях Бог трансцендентен и находится вне созданного им бытия.
Некоторые вещи-в-себе все же доступны априорному познанию: например, пространство и время, идеи Бога, добра и красоты, логические категории.
То есть трансцендентальные объекты — это, образно говоря, «предустановленные по умолчанию» в нашем разуме
Представление о трансцендентности существует и в математике: трансцендентное число — это число, которое не может быть вычисленным при помощи алгебры или выраженным алгебраически (то есть, не может быть корнем многочлена с целыми коэффициентами, не тождественного нулю). В их число входят, например, числа π и e.
Понятие, близкое к «трансцендентному», но иное по значению — «трансцендентальное». Изначально оно обозначало просто область отвлеченных умственных категорий, а впоследствии его развил Кант, попав в собственную ловушку: построить философскую систему только на эмпирических данных оказалось невозможно, а никаких других источников опыта, кроме эмпирики он не признавал. Чтобы выкрутиться, философу пришлось допустить, что некоторые вещи-в-себе все же доступны априорному познанию: например, пространство и время, идеи Бога, добра и красоты, логические категории. То есть трансцендентальные объекты — это, образно говоря, «предустановленные по умолчанию» в нашем разуме — при этом информация о них существует сама по себе и не следует из нашего опыта.
То есть трансцендентальные объекты — это, образно говоря, «предустановленные по умолчанию» в нашем разуме — при этом информация о них существует сама по себе и не следует из нашего опыта.
Существует и еще одно родственное понятие — трансценденция. В широком смысле слова оно означает переход границы между двумя разнородными областями, в особенности переход из сферы посюстороннего в сферу потустороннего, трансцендентного. Для простоты возьмем пример из фантастики: параллельный мир для обычного человека — трансцендентное явление. Но когда герой попадает в этот параллельный мир или каким-то образом оказывается способен его воспринимать, это трансценденция. Или более сложный пример из экзистенциальной философии: Жан-Поль Сартр считал, что человек трансцендентен, поскольку он выходит за рамки любого возможного собственного опыта: мы можем изучать себя и окружающий мир с разных сторон, но никогда даже не приблизимся к полному познанию себя. Но одновременно человек обладает способностью к трансценденции: он трансцендирует любую вещь, придавая ей какое-либо значение. Трансценденция — важный элемент и в религии: она помогает человеку освободиться от своей материальной природы и прикоснуться к чему-то запредельному.
Трансценденция — важный элемент и в религии: она помогает человеку освободиться от своей материальной природы и прикоснуться к чему-то запредельному.
Из философии понятие трансцендентальности перекочевало и в психологию: швейцарский психолог Карл Юнг ввел понятие «трансцендентальная функция» — это функция, объединяющая сознательное и бессознательное. В частности, трансцендентальную функцию может выполнять психоаналитик — он помогает пациенту проанализировать образы бессознательного (например, сновидения) и связать их воедино с сознательными процессами в его психике.
Как говорить
Неправильно «Я записалась на занятия по трансцендентной медитации». Правильно — «трансцендентальной».
Правильно «Когда я захожу в храм, я испытываю чувство слияния с чем-то трансцендентным».
Правильно «Искусство трансцендирует знакомые нам предметы из материального мира, наполняя их высшим смыслом».
Трансцендентное число — комплексное число, не являющееся алгебраическим, то есть не являющееся корнем никакого отличного от нуля многочлена с рациональными коэффициентами.
Существование трансцендентных чисел впервые установил Ж. Лиувилль в 1844 г.; он же построил первые примеры таких чисел. Лиувилль заметил, что алебраические числа не могут «слишком хорошо» приближаться рациональными числами . Именно, теорема Лиувилля гласит, что если алгебраическое число является корнем многочлена степени с рациональными коэффициентами, то для любого рационального числа справедливо неравенство
где постоянная зависит только от. Из этого утверждения следует достаточный признак трансцендентности: если число таково, что для любой постоянной существует бесконечное множество рациональных чисел, удовлетворяющих неравенствам
то трансцендентно. Впоследствии такие числа получили название чисел Лиувилля. Примером такого числа является
Другое доказательство существования трансцендентных чисел было получено Г. Кантором в 1874 г. на основе созданной им теории множеств. Кантор доказал счётность множества алгебраических чисел и несчётность множества действительных чисел, откуда следует, что множество трансцендентных чисел несчётно. Однако, в отличие от доказательства Лиувилля, эти рассуждения не позволяют привести пример хотя бы одного такого числа.
Однако, в отличие от доказательства Лиувилля, эти рассуждения не позволяют привести пример хотя бы одного такого числа.
Работа Лиувилля дала начало целому разделу теории трансцендентных чисел — теории приближения алгебраических чисел рациональными или, более общо, алгебраическими числами. Теорема Лиувилля усиливалась и обобщалась в работах многих математиков. Это позволило построить новые примеры трансцендентных чисел. Так, К. Малер показал, что если — непостоянный многочлен, принимающий целые неотрицательные значения при всех натуральных, то для любого натурального число, где — запись числа в системе счисления с основанием, является трансцендентным, но не является числом Лиувилля. Например, при и получаем следующий изящный результат: число
трансцендентно, но не является числом Лиувилля.
В 1873 г. Ш. Эрмит, используя другие идеи, доказал трансцендентность неперова числа (основания натурального логарифма):
Развив идеи Эрмита, Ф. Линдеман в 1882 г. доказал трансцендентность числа, тем самым поставив точку в древней проблеме о квадратуре круга: с помощью циркуля и линейки невозможно построить квадрат, равновеликий (то есть имеющий ту же площадь) данному кругу. Более общо, Линдеман показал, что при любом алгебраическом число трансцендентно. Эквивалентная формулировка: для любого алгебраического числа, отличного от и, его натуральный логарифм является трансцендентым числом.
Более общо, Линдеман показал, что при любом алгебраическом число трансцендентно. Эквивалентная формулировка: для любого алгебраического числа, отличного от и, его натуральный логарифм является трансцендентым числом.
В 1900 г. на конгрессе математиков в Париже Д. Гильберт среди 23 нерешённых проблем математики указал на следующую, в частной форме сформулированную ещё Л. Эйлером :
Пусть и — алгебраические числа, причём трансцендентным? В частности, трансцендентны ли числа и?
Эта проблема может быть переформулирована в следующей форме, близкой к оригинальной формулировке Эйлера:
Пусть и — алгебраические числа, отличные от и, причём отношение их натуральных логарифмов иррационально. Будет ли число трансцендентным?
Первое частичное решение проблемы было получено в 1929 г. А. О. Гельфондом, который, в частности, доказал трансцендентность числа. В 1930 г. Р. О. Кузьмин усовершенствовал метод Гельфонда, в частности, ему удалось доказать трансцендентность числа. Полное решение проблемы Эйлера-Гильберта (в утвердительном смысле) было получено в 1934 г. независимо А. О. Гельфондом и Т. Шнайдером.
Полное решение проблемы Эйлера-Гильберта (в утвердительном смысле) было получено в 1934 г. независимо А. О. Гельфондом и Т. Шнайдером.
А. Бейкер в 1966 обобщил теоремы Линдемана и Гельфонда-Шнайдера, доказав, в частности, трансцендентность произведения произвольного конечного количества чисел вида и с алгебраическими при естественных ограничениях.
В 1996г. Ю.В. Нестеренко доказал алгебраическую независимость значений рядов Эйзенштейна и, в частности, чисел и. Это означает трансцендентность любого числа вида, где отличная от нуля рациональная функция с алгебраическими коэффициентами. Например, трансцендентной будет сумма ряда
В 1929-1930 гг. К. Малер в серии работ предложил новый метод доказательства трансцендентности значений аналитических функций, удовлетворяющих функциональным уравнениям определённого вида (впоследствии такие функции получили название функций Малера).
Методы теории трансцендентных чисел нашли применение и в других разделах математики, в частности в теории диофантовых уравнений.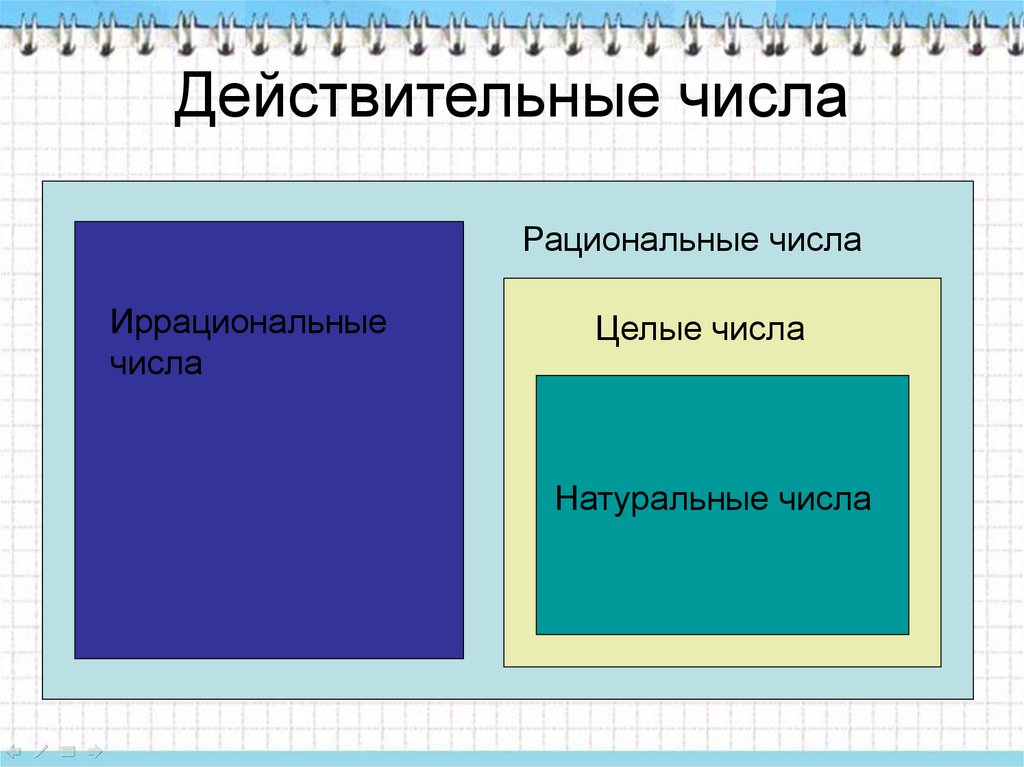
Что это такое и как его использовать
Иррациональный номер Определение: что это такое и как его использовать
Эндрю Ли
23 марта 2021
онлайн -репетиторство
,
Математика
Что иррациональное. числа? Если вы не уверены в разнице между действительными числами, рациональными числами, натуральными числами, комплексными числами и даже мнимыми числами, вы не одиноки. Математика — это один из предметов, где стоит быть точным.
Счет с целыми и натуральными числами
Прежде чем мы дадим определение иррационального числа, рассмотрим целые числа, а также целые и натуральные числа.
Давайте начнем с нескольких основных примеров. Когда вы впервые учитесь считать, скажем, количество имеющихся у вас пальцев, вы используете натуральные или целые числа: 1, 2, 3, 4, 5… и так далее. Это натуральные числа. Целые числа также являются числами без дробей, но целые числа включают 0, а натуральные числа — нет.
Как и целые числа, целые числа не имеют дробей. Однако, в отличие от целых чисел, они включают отрицательные числа: -4, -3, 0, 14 — все это примеры целых чисел.
Определение рационального числа
Рациональное число может быть представлено дробью.
Становясь старше, мы узнаём, что не всё можно сосчитать по пальцам. Например, 0,5 — рациональное число. Это не целое, натуральное или целое число, но его можно выразить как 1/2, что является долей двух других целых чисел: 1 — числитель, а 2 — знаменатель. Итак, 0,5 или 1/2 — рациональное число.
Рациональные числа также можно разделить на два типа: те, которые имеют завершающее десятичное расширение, и те, которые имеют повторяющееся десятичное расширение. Десятичное расширение, когда дробь преобразуется в десятичное число. Десятичное расширение 1/2 равно 0,5. Десятичное расширение 1/3 равно 0,333.
1/2, или 0,5, завершается, поскольку заканчивается на десятой цифре.
1/3 или 0,333 не завершается, потому что «3» повторяется вечно.
Что такое иррациональное число?
По определению иррациональное число не может быть выражено как дробь двух целых чисел. Например, давайте посмотрим на квадратный корень из 2. Несмотря на то, что мы знаем, что число существует, десятичные точки продолжаются бесконечно, поэтому мы не можем полностью раскрыть его.
В зависимости от того, умеете ли вы записывать их в виде дроби, некоторые квадратные и кубические корни рациональны, а некоторые иррациональны.
Примеры иррациональных чисел
Возможно, вам известно больше иррациональных чисел, чем вы думаете.
Пи — отношение длины окружности к ее диаметру. Его десятичные дроби идут бесконечно долго. Вы можете знать первую пару цифр как 3,14.
Число Эйлера E является основанием натуральных логарифмов. Это приблизительно равно 2,718.
Phi, или золотое сечение, — это еще одна дробь, которая не заканчивается, когда она представлена в виде десятичной точки. Ближе всего к 1,618.
Определение иррационального числа и не только
Все эти определения можно рассматривать как подмножества того, что определяет число.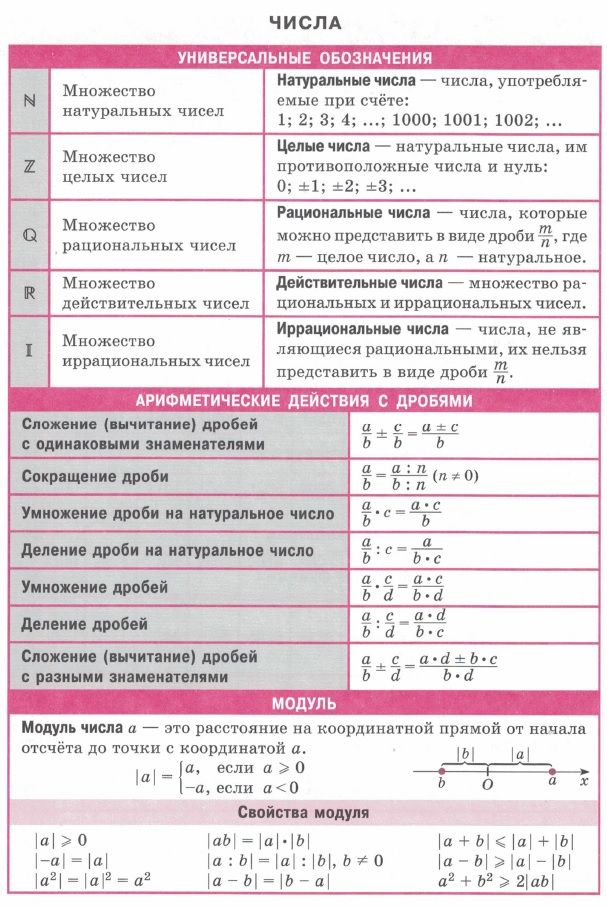 Иррациональные числа не могут быть определены как частное двух целых чисел. С другой стороны, рациональные числа можно разделить на рациональные числа с повторяющимися десятичными знаками и рациональные числа с неповторяющимися десятичными знаками. Натуральные числа и целые числа являются наименьшими подмножествами, а 0 считается целым числом, но не натуральным числом.
Иррациональные числа не могут быть определены как частное двух целых чисел. С другой стороны, рациональные числа можно разделить на рациональные числа с повторяющимися десятичными знаками и рациональные числа с неповторяющимися десятичными знаками. Натуральные числа и целые числа являются наименьшими подмножествами, а 0 считается целым числом, но не натуральным числом.
Дополнительная помощь с домашним заданием по математике
- Как найти сумму конечного геометрического ряда
- Что следует помнить при графическом построении линейных уравнений
- Как освоить квадратичную регрессию
Классификация чисел – MathsTips.com
Ниже приведены классификации чисел.
1. Натуральные числа:
- Каждое из 1,2,3,4,…..,и т.д. является натуральным числом.
- Наименьшее натуральное число равно 1, тогда как наибольшее натуральное число получить невозможно.
- Последовательные натуральные числа отличаются на 1.

- Пусть будет любое натуральное число , тогда натуральные числа, идущие сразу после него, равны и т. д.
2. Четные натуральные числа:
Система натуральных чисел, которые делятся на 2 или кратны 2, называется набором четных чисел.
E= (2,4,6,8,10,12……..)
Существует бесконечное количество четных чисел.
3. Нечетные натуральные числа:
Система натуральных чисел, которые не делятся на 2, называется набором нечетных чисел.
O= (1,3,5,7,9………)
Нечетные числа бесконечны.
Сложив вместе четные и нечетные числа, мы получим натуральные числа.
4. Целые числа:
- 0,1 ,2,3,4,…… и т. д. — целые числа.
- Наименьшее целое число равно нулю, тогда как наибольшее целое число получить невозможно.
- Последовательные целые числа отличаются на 1.
- Все целые числа, кроме нуля, являются натуральными, поэтому:
- Каждое четное натуральное число является четным целым числом
- Каждое нечетное натуральное число является нечетным целым числом.

5. Простые числа:
- Целые числа больше 1, которые делятся только на единицу и само на себя.
- Все остальные простые числа, кроме 2, нечетные. Р= 2,3,5,7,11,13,………. и т. д.
6. Составные числа:
Составное число — это целое число (больше 1), которое не является простым.
Составные числа C= (4,6,8,9 ……..,и т.д.)
7. Целые числа:
- Целые числа состоят из натуральных чисел, нулей и отрицательных натуральных чисел. Таким образом, Z или I = …………………,-4,-3,-2,-1, 0, 1,2,3,4…………….
- Существуют бесконечные целые числа в положительном направлении и бесконечные целые числа в отрицательном направлении.
- Целые положительные числа — это натуральные числа.
Использование целых чисел
Целые числа используются для выражения наших повседневных ситуаций в математических терминах.
- Если прибыль представлена положительными целыми числами, то убытки — отрицательными целыми числами.

- Если высота над уровнем моря выражается положительными целыми числами, то глубина ниже уровня моря выражается отрицательными целыми числами.
- Если повышение цены представлено положительными целыми числами, то снижение цены — отрицательными целыми числами и так далее.
8. Рациональные числа:
Любое число, которое может быть выражено в форме , где a и b оба являются целыми числами, а , является рациональным числом.
- — рациональное число, так как 2, 5 — целые числа, а 5 не равно нулю.
- и т. д. не являются рациональными числами, поскольку эти числа не могут быть выражены как .
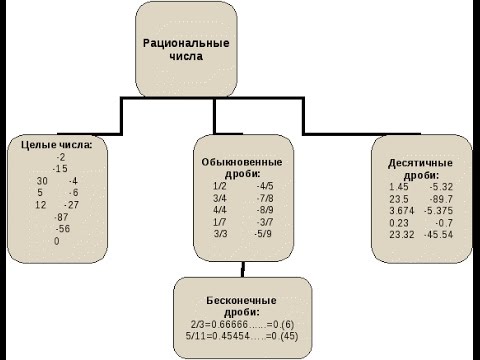
Итак, мы можем сказать, что рациональные числа содержат все целые числа и все дроби (включая десятичные дроби). Существует бесконечное количество рациональных чисел.
- Каждое целое является рациональным числом, но обратное неверно. Тот же результат верен для натуральных чисел, целых чисел, дробей и т. д.
9.


 То есть трансцендентальные объекты — это, образно говоря, «предустановленные по умолчанию» в нашем разуме
То есть трансцендентальные объекты — это, образно говоря, «предустановленные по умолчанию» в нашем разуме