Введение понятий луча и угла.
ГЛАВА 1. Начальные геометрические сведения.
§ 2. Луч и угол.
п. 3. Луч.
Мы уже познакомились с простейшими геометрическими фигурами, теперь будем их постепенно усложнять.
Определение. Лучом (или полупрямой) называется часть прямой, ограниченная одной точкой.
Эта точка называется началом луча (полупрямой).
Луч может обозначаться двумя способами:
Д вумя заглавными латинскими буквами, причём первая из них обозначает начало луча.
Одной маленькой латинской буквой, расположенной на продолжении луча.
О пределение. Дополнительными называются два луча, лежащие на одной прямой, имеющие общее начало, но направленные в разные стороны. Другими словами, это лучи, на которые точка разбивает прямую.
Другими словами, это лучи, на которые точка разбивает прямую.
Лучи и b – дополнительные
Лучи и OB – дополнительные
п. 4. Угол.
Определение. Углом называется геометрическая фигура, которая состоит из точки и двух различных лучей (полупрямых), исходящих из этой точки. Эта точка называется вершиной угла, а лучи – сторонами угла.
Существует три способа обозначения углов.
1. Тремя заглавными латинскими буквами, средняя обозначает его вершину.
2. Одной заглавной латинской буквой, обозначающей вершину угла.
3. Двумя строчными латинскими буквами, обозначающими полупрямые, из которых состоит угол. Они располагаются на продолжении полупрямых.
Виды углов:
1. Острый. Его градусная мера меньше 90°.
2. Тупой.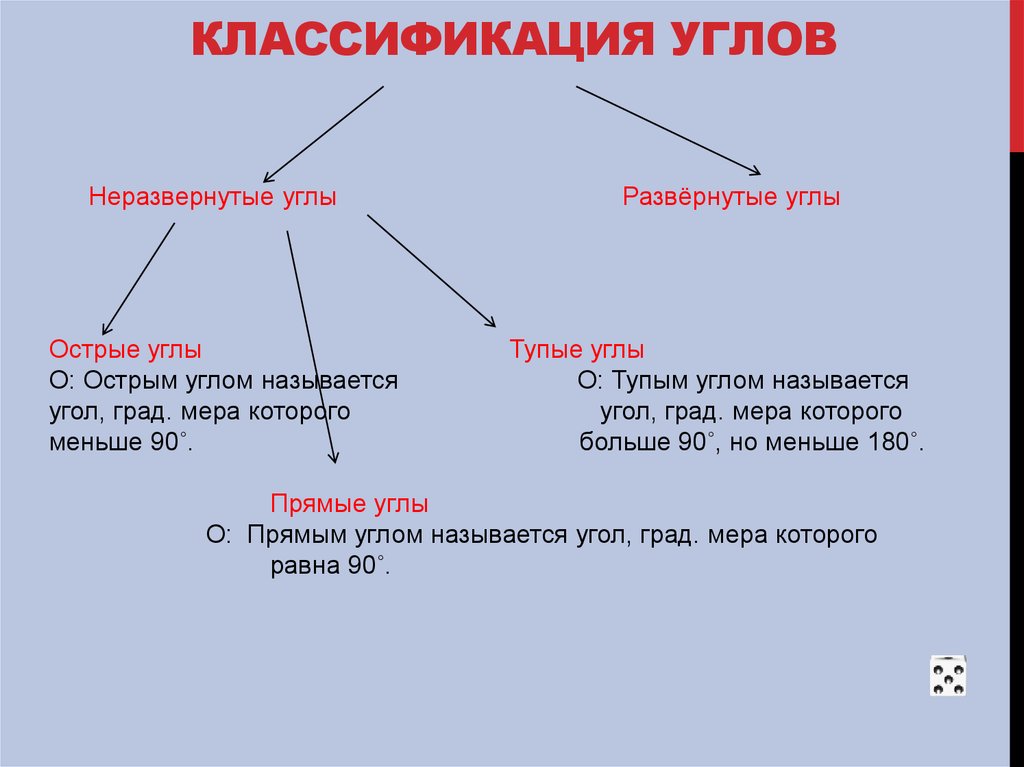 Его градусная мера больше 90°.
Его градусная мера больше 90°.
3. Прямой. Его градусная мера равна 90°.
4. Развёрнутый. Он состоит из двух дополнительных полупрямых и градусная мера его равна 180°.
Любой угол разделяет плоскость на две части. Если этот угол неразвёрнутый, то одна из частей (меньшая) называется внутренней, а другая – внешней областью угла.
а ) Сколько лучей с началом в точке О изображено на рисунке?
б) Сколько углов изображено на этом рисунке?
в) Постройте луч ОМ так, чтобы угол АОМ был развёрнутым.
Начертите угол. Отметьте точку М, которая лежит на стороне угла, точку N, лежащую во внутренней области угла, и точку Е, принадлежащую его внешней области.
а) Сколько лучей с началом в точке О изображено на рисунке?
б) Сколько углов изображено на этом рисунке?
в) Постройте луч ОА так, чтобы угол АОN был развёрнутым.
Начертите угол. Изобразите отрезок: а) все точки которого лежат во внутренней области угла; б) все точки которого лежат во внешней области угла; в) часть точек которого лежит во внутренней области угла.
а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
б) Проведите лучи с началом в точке В, один из которых пересекал бы луч АС, а другой не пересекал бы его.
Даны угол MEF и точка А, лежащая в его внутренней области (рис. 2). Проведите луч с началом в точке Е так, чтобы образовались два угла, такие, что точка А не принадлежала бы их внутренним областям.
а) Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
б) Начертите луч CD, проведите два луча с началом в точке A, один из которых пересекал бы луч CD, а другой не пересекал бы его.
Даны угол EKL и точка M, не лежащая в его внутренней области (рис. 2). Проведите из точки К луч так, чтобы образовалось ещё два угла, такие, что точка М не лежала бы в их внутренней области.
Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч СА, а другой не пересекает луч ВС. Рассмотрите возможные варианты.
Дан неразвёрнутый угол АВС. Проведите лучи с началом в точке В, чтобы образовались при этом шесть углов, из которых один был бы развёрнутым.
Сколько неразвёрнутых и сколько развёрнутых углов изображено на рис. 1?
С началом в точке Е (рис. 2) проведите лучи, один из которых пересекает луч ВС, а другой не пересекает луч АС. Рассмотрите возможные варианты.
Через заданную точку проведите столько прямых, чтобы при их пересечении образовалось шесть углов.
Углы AOB, BOC, COD, DOE и EOA имеют общую вершину О. Прямая а, не проходящая через точку О, пересекает не менее двух лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.
Углы MAF, FAK, KAP, PAQ и QAM имеют общую вершину A. Прямая а, не проходящая через точку A, пересекает не менее трёх лучей, которые являются сторонами этих углов. Рассмотрите все возможные случаи. Сделайте чертежи.
2
Сравнение отрезков и углов
Цели урока:
1) Обучающая: формирование теоретических знаний по теме «Сравнение отрезков и углов»; формирование навыков решения задач на сравнение отрезков и углов.
2) Развивающая: развитие умений применять полученные теоретические знания при выполнении практических заданий.
3) Воспитывающая: воспитание интереса к изучению математики, ответственности, самостоятельности.
Литература: «Геометрия 7 — 9 класс» Л. С. Атанасян и др.
План урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Получение знаний.
4. Закрепление нового материала.
5. Рефлексия.
6. Домашнее задание.
Ход урока:
1. Организационный момент.
Приветствие учащихся. Ставятся цели и определяются задачи урока.
Объявляется тема урока. Учащиеся записывают тему урока и дату в рабочих тетрадях.
2. Актуализация опорных знаний.
Давайте вспомним из материала предыдущего урока, что такое отрезок и угол (Учащимся предлагается ответить на вопросы):
— Что такое отрезок?
— Как можно обозначать отрезки?
— Что называют углом?
— Как обозначают углы?
— Изобразите развёрнутый и неразвёрнутый углы?
Сегодня на уроке мы снова поговорим об отрезках и углах, а точнее выясним, как сравнить два отрезка или два угла. Также познакомимся с новым для вас понятием биссектрисы угла.
Также познакомимся с новым для вас понятием биссектрисы угла.
3. Получение знаний.
Каждому из вас известно, что в окружающем нас мире встречаются предметы, которые имеют одинаковую форму и одинаковые размеры. Например, два одинаковых карандаша, два одинаковых автомобиля, два одинаковых будильника.
В геометрии две фигуры, имеющие одинаковую форму и одинаковые размеры, называют равными.
Давайте возьмём две фигуры F1 и F2 (рисунок 1), вырезанные из бумаги.
Рисунок 1.
Чтобы установить, равны они или нет, наложим одну фигуру на другую. Предположим, что наши фигуры совместились, тогда можем сказать, что они равны.
А вот некоторые фигуры P1 и P2 (рисунок 2).
Рисунок 2.
Если попробуем наложить их друг на друга эти две фигуры, то увидим, что их совместить невозможно, а, следовательно, они не равны.
Можем сделать следующий вывод:
Две геометрические фигуры называются равными, если их можно совместить наложением.
Поговорим, как сравнить два отрезка. Возьмём два произвольных отрезка (рисунок 3).
Рисунок 3.
Чтобы установить, равны данные отрезки или нет, наложим один отрезок на другой так, чтобы конец одного отрезка совместился с концом другого (рисунок 3). При этом совместятся и два других конца отрезков, а, следовательно, отрезки равны.
Теперь возьмём отрезок АВ и отрезок АС (рисунок 4), и наложим их друг на друга таким же образом. Видим, что отрезки не совместились полностью, а значит, они не равны.
Рисунок 4.
Из рисунка также видно, что отрезок АВ составляет часть отрезка АС, поэтому отрезок АВ меньше отрезка АС. Записывают это так: АВ < АС.
Поговорим о том, что же называют серединой отрезка. Рассмотрим отрезок АВ. Отметим на нём точку С, которая делит его на две равные части (рисунок 5). Таким образом, можно сказать, что точка С и есть середина отрезка АВ, т. е. отрезок АС равен отрезку АВ.
Отметим на нём точку С, которая делит его на две равные части (рисунок 5). Таким образом, можно сказать, что точка С и есть середина отрезка АВ, т. е. отрезок АС равен отрезку АВ.
Рисунок 5.
Сформулируем определение:
Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.
Далее рассмотрим два неразвёрнутых угла: угол 1 и угол 2 (рисунок 6). Чтобы установить, равны они или нет, наложим один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон.
Рисунок 6.
Если две другие стороны также совместятся, то и углы полностью совместятся, а, значит, они равны. Но в нашем случае эти стороны не совместились, следовательно, наши углы не равны, и меньшим является угол, который составляет часть другого, а это угол 1.
Записываем это так:
Возьмём неразвёрнутый угол АОС и развёрнутый угол ВОС (рисунок 7), наложим их друг на друга указанным выше способом (рисунок 8), то увидим, что неразвёрнутый угол составляет часть развёрнутого, а, следовательно, развёрнутый угол больше неразвёрнутого, т. е. угол ВОС больше угла АОС.
Рисунок 8.
Следует отметить, что любые два развёрнутых угла, очевидно, равны.
И напоследок, возьмём некоторый угол hk. Проведём луч l из вершины этого угла так, чтобы он разделил его на два равных угла (рисунок 9).
Рисунок 9.
Таким образом, сформулируем следующее определение:
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
В нашем случае луч l — биссектриса угла hk.
4. Закрепление нового материала.
Для закрепления материала учащимся предлагается выполнить следующие практические задания.
Задание 1. На прямой A отмечены точки C и D, которые лежат между точками A и B, точка C лежит между точками А и D, отрезки AD и CB равны. Является ли середина отрезка AB серединой отрезка CD (рисунок 10)?
Рисунок 10.
АD=AC+CD, CB=CD+DB, так как AD=CB, то АС=DB.
Пусть точка О — середина отрезка СD, т. е. СО=OD, CD=CO+OD.
AB=AO+OB, AO=АС+СO, OB=OD+DB. А так как АС=DB и СО=OD, то и АО=ОВ, а следовательно, О является серединой и отрезка АВ.
Задание 2. Углы AOB и COD на рисунке 11 равны, луч OE — биссектриса угла ВОС. Является ли луч OE биссектрисой угла AOD?
Рисунок 11.
Решение: Рассмотрим ∠ AOD.
∠ AOD = ∠ AOE + ∠ EOD. Так как ∠ AOE = ∠ AOВ + ∠ ВOE и ∠EOD= = ∠ EOС + ∠ СOD, причём ∠ AOВ = ∠ СOD (по условию задачи), ∠ ВOE = =∠EOС (так как ОЕ — биссектриса ∠ ВОС), то ∠ AOE = ∠EOD. Следовательно, ОЕ является биссектрисой ∠ AOD.
Так как ∠ AOE = ∠ AOВ + ∠ ВOE и ∠EOD= = ∠ EOС + ∠ СOD, причём ∠ AOВ = ∠ СOD (по условию задачи), ∠ ВOE = =∠EOС (так как ОЕ — биссектриса ∠ ВОС), то ∠ AOE = ∠EOD. Следовательно, ОЕ является биссектрисой ∠ AOD.
5. Рефлексия.
Подводятся итоги урока, обсуждается, что учащиеся узнали. Ребята по кругу высказываются одним предложением, выбирая начало фразы записанной на доске:
1. сегодня я узнал…
2. было интересно…
3. было трудно…
4. я выполнял задания…
5. я понял, что…
6. я научился…
7. у меня получилось …
Оценивается работа учащихся на уроке.
6. Домашнее задание: § 3, № 20, 23
Развернутые состояния в условиях складывания приспосабливаются к специфичным для последовательности конформационным предпочтениям со случайными спиральными размерами
. 2019 18 июня;116(25):12301-12310.
doi: 10. 1073/pnas.1818206116.
Epub 2019 5 июня.
1073/pnas.1818206116.
Epub 2019 5 июня.
Иван Перан 1 , Алекс С Холехаус 2 , Исаак С. Каррико 1 , Рохит В Паппу 3 , Осман Билсел 4 , Дэниел П. Роли 5 6
Принадлежности
- 1 Химический факультет Университета Стоуни-Брук, Стоуни-Брук, Нью-Йорк 11794-3400.
- 2 Департамент биомедицинской инженерии, Центр науки и проектирования живых систем, Вашингтонский университет в Сент-Луисе, Сент-Луис, Миссури 63130.
- 3 Кафедра биомедицинской инженерии, Центр науки и инженерии живых систем, Вашингтонский университет в Сент-Луисе, Сент-Луис, Миссури 63130; pappu@wustl.
 edu [email protected] [email protected].
edu [email protected] [email protected]. - 4 Кафедра биохимии и молекулярной фармакологии, Медицинская школа Массачусетского университета, Вустер, Массачусетс 01605; [email protected] [email protected] [email protected].
- 5 Химический факультет Университета Стоуни-Брук, Стоуни-Брук, Нью-Йорк 11794-3400; [email protected] [email protected] [email protected].
- 6 Институт структурной и молекулярной биологии, Университетский колледж Лондона, Лондон WC1E 6BT1, Соединенное Королевство.
- PMID: 31167941
- PMCID: PMC7056937
- DOI:
10.
 1073/пнас.1818206116
1073/пнас.1818206116
Бесплатная статья ЧВК
Иван Перан и др. Proc Natl Acad Sci U S A. .
Бесплатная статья ЧВК
. 2019 18 июня;116(25):12301-12310.
doi: 10.1073/pnas.1818206116. Epub 2019 5 июня.
Авторы
Иван Перан 1 , Алекс С Холехаус 2 , Исаак С. Каррико 1 , Рохит В Паппу 3 , Осман Билсел 4 , Дэниел П. Роли 5
6
Роли 5
6
Принадлежности
- 1 Химический факультет Университета Стоуни-Брук, Стоуни-Брук, Нью-Йорк 11794-3400.
- 2 Кафедра биомедицинской инженерии, Центр науки и инженерии живых систем, Вашингтонский университет в Сент-Луисе, Сент-Луис, Миссури 63130.
- 3 Кафедра биомедицинской инженерии, Центр науки и инженерии живых систем, Вашингтонский университет в Сент-Луисе, Сент-Луис, Миссури 63130; [email protected] [email protected] [email protected].
- 4 Кафедра биохимии и молекулярной фармакологии, Медицинская школа Массачусетского университета, Вустер, Массачусетс 01605; pappu@wustl.

- 5 Химический факультет Университета Стоуни-Брук, Стоуни-Брук, Нью-Йорк 11794-3400; [email protected] [email protected] [email protected].
- 6 Институт структурной и молекулярной биологии, Университетский колледж Лондона, Лондон WC1E 6BT1, Соединенное Королевство.
- PMID: 31167941
- PMCID: PMC7056937
- DOI: 10.1073/пнас.1818206116
Абстрактный
Белки представляют собой маргинально стабильные молекулы, которые колеблются между свернутым и развернутым состояниями. Здесь мы приводим описание с высоким разрешением развернутых состояний в условиях рефолдинга для N-концевого домена L9.белок (NTL9). Мы используем комбинацию переноса энергии резонанса Ферстера с временным разрешением (FRET), основанного на нескольких парах минимально возмущающих меток, малоуглового рассеяния рентгеновских лучей с временным разрешением (SAXS), моделирования всех атомов и теории полимеров. При разбавлении высоким денатурантом развернутое состояние претерпевает быстрое сокращение. Хотя это сжатие происходит до перехода в складку, развернутое состояние остается значительно более расширенным, чем свернутое состояние, и допускает ряд локальных и нелокальных контактов, включая вторичные структуры и нативные и ненативные взаимодействия. Парадоксально, но, несмотря на заметные конформационные предпочтения, специфичные для последовательности, усредненные по ансамблю свойства развернутых состояний согласуются со свойствами канонических случайных клубков, а именно полимеров в индифферентных (тета) растворителях.
Здесь мы приводим описание с высоким разрешением развернутых состояний в условиях рефолдинга для N-концевого домена L9.белок (NTL9). Мы используем комбинацию переноса энергии резонанса Ферстера с временным разрешением (FRET), основанного на нескольких парах минимально возмущающих меток, малоуглового рассеяния рентгеновских лучей с временным разрешением (SAXS), моделирования всех атомов и теории полимеров. При разбавлении высоким денатурантом развернутое состояние претерпевает быстрое сокращение. Хотя это сжатие происходит до перехода в складку, развернутое состояние остается значительно более расширенным, чем свернутое состояние, и допускает ряд локальных и нелокальных контактов, включая вторичные структуры и нативные и ненативные взаимодействия. Парадоксально, но, несмотря на заметные конформационные предпочтения, специфичные для последовательности, усредненные по ансамблю свойства развернутых состояний согласуются со свойствами канонических случайных клубков, а именно полимеров в индифферентных (тета) растворителях.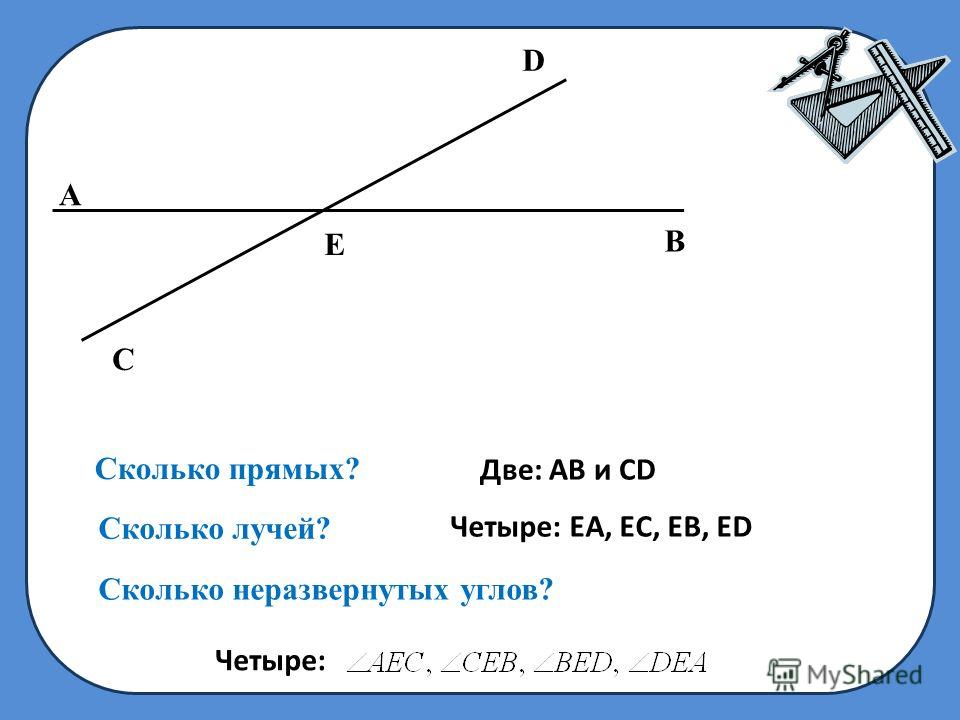
Ключевые слова: ЛАД; переход уплотнения; фолдинг белка; развернутое состояние.
Copyright © 2019 Автор(ы). Опубликовано ПНАС.
Заявление о конфликте интересов
Авторы заявляют об отсутствии конфликта интересов.
Цифры
Рис. 1.
Структура НТЛ9 и…
Рис. 1.
1.
Структура НТЛ9 и точность расчета расстояний в сложенном…
Рисунок 1. Структура NTL9 и точность расчета расстояния в сложенном состоянии. ( A ) Ленточная диаграмма исходного состояния NTL9 (код PDB: 2HBB), показывающая местоположение Trp-25. N-конец помечен. ( B ) Расстояния, полученные с помощью FRET, для исходного состояния NTL9 в сравнении с расстояниями от кольца к кольцу, взятыми из кристаллической структуры, демонстрируя точность, с которой расстояния могут быть определены с помощью Phe  ( C , Внизу , второй ряд) Остатки 2 и 33, а также остатки 2 и 51 использовали для получения дополнительных пар F CN –Trp, и положение этих остатков Trp окрашено в зеленый цвет. ( C , Top
( C , Внизу , второй ряд) Остатки 2 и 33, а также остатки 2 и 51 использовали для получения дополнительных пар F CN –Trp, и положение этих остатков Trp окрашено в зеленый цвет. ( C , Top
Рис. 2.
Репрезентативные измерения времени жизни флуоресценции. Данные…
Рис. 2.
Репрезентативные измерения времени жизни флуоресценции. Данные приведены для пары F CN 10–W25.…
Рис. 2. Репрезентативные измерения времени жизни флуоресценции. Данные приведены для пары F CN 10–W25. Для А и В , кривые соответствия только донора показаны синим цветом, а соответствия кривым донора и акцептора — красным. Остатки показаны ниже. ( A ) Данные о равновесии в 10 М мочевине. (
Остатки показаны ниже. ( A ) Данные о равновесии в 10 М мочевине. (
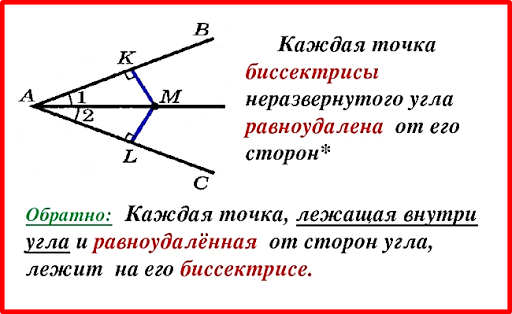
Рис. 3.
( A–F ) FRET обеспечивает…
Рис. 3.
( A–F ) FRET подтверждает наличие уплотнения. Ленточные схемы, иллюстрирующие расположение…
Рис. 3. ( A–F ) FRET свидетельствует об уплотнении. Ленточные диаграммы, иллюстрирующие расположение пар FRET, показаны вместе с распределением расстояний. Красный, развернутое состояние в 10 М мочевине; зеленый, развернутое состояние в 1 М мочевине; черный, в складчатом состоянии в 1 М мочевине. Свернутые и развернутые распределения в 1 М мочевине были извлечены из глобальной аппроксимации данных FRET. Распределение расстояний в развернутом состоянии было смоделировано с использованием червеобразной цепи с параметром диффузии между донором и акцептором в течение времени жизни флуоресценции, в то время как распределение Гаусса использовалось для моделирования распределения в свернутом состоянии.
Рис. 4.
Развернутое состояние 1-M…
Рис. 4.
Развернутое состояние 1-M более компактно, чем развернутое состояние 10-M. В…
Рис. 4. Развернутое состояние 1-M более компактно, чем развернутое состояние 10-M. Развернутое состояние расширено в высокой степени денатурации, но более компактно в низкой степени денатурации, что определяется количественно средними расстояниями в пространстве между парами остатков в зависимости от разделения последовательностей. Свернутое состояние и развернутый ансамбль в 1 М мочевине демонстрируют немонотонную взаимосвязь между разделением последовательностей и пространственным разделением, в то время как ансамбль 10 М мочевины показывает монотонное увеличение расстояния с разделением последовательностей. См. SI Приложение , рис. S7 C для тех же данных, которые включают стандартные полимерные модели.
См. SI Приложение , рис. S7 C для тех же данных, которые включают стандартные полимерные модели.
Рис. 5.
Гинье-анализ данных SAXS…
Рис. 5.
Анализ Гинье данных SAXS. ( A ) Данные непрерывного потока для собственного…
Рис. 5. Анализ Гинье данных SAXS. ( A ) Данные непрерывного потока для нативного состояния в 1 М мочевине. ( B ) Данные непрерывного потока для развернутого состояния в 1 М мочевине. ( C ) Равновесные данные для развернутого состояния в 10 М мочевине. Данные также были проанализированы с использованием независимого эмпирического молекулярного форм-фактора, который дал почти идентичные результаты ( SI Приложение , Таблица S15). ( D ) Сравнение средних радиусов вращения в сложенном и развернутом состояниях. Столбики погрешностей рассчитываются на основе подгонки Гинье.
( D ) Сравнение средних радиусов вращения в сложенном и развернутом состояниях. Столбики погрешностей рассчитываются на основе подгонки Гинье.
Рис. 6.
Сравнение экспериментальных результатов…
Рис. 6.
Сравнение экспериментальных результатов для 1-M мочевины в развернутом состоянии и 375-K…
Рис. 6. Сравнение экспериментальных результатов для развернутого состояния 1-M мочевины и взвешенного ансамбля 375-K (ансамбль в развернутом состоянии в 1M мочевины). ( A ) Расстояния внутри цепи, полученные в результате экспериментов FRET (зеленый цвет), по сравнению с расстоянием C β – C β , извлеченным из развернутого ансамбля (синий). Столбики погрешностей отражают стандартные отклонения базового распределения, связанные с каждым измерением.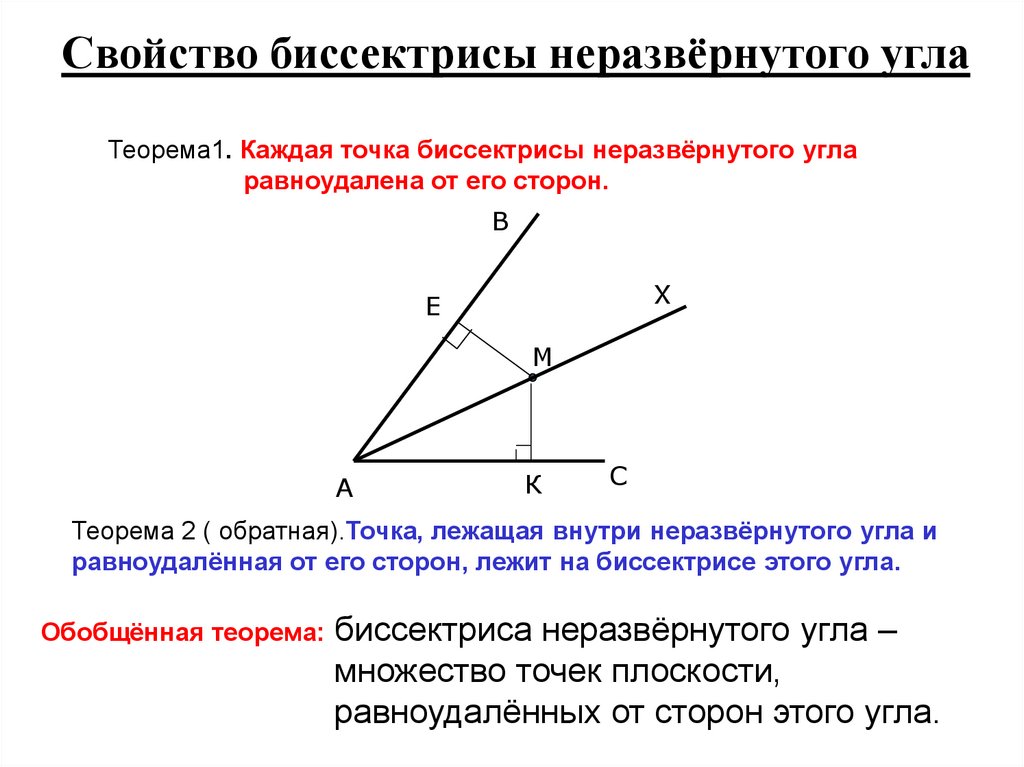 ( B ) Радиус вращения, полученный из SAXS с планками погрешностей, по сравнению с распределением радиусов вращения, полученным в результате моделирования. Данные моделирования как в A , так и в B были извлечены из одного и того же ансамбля, демонстрируя, что FRET, SAXS и моделирование взаимно совместимы.
( B ) Радиус вращения, полученный из SAXS с планками погрешностей, по сравнению с распределением радиусов вращения, полученным в результате моделирования. Данные моделирования как в A , так и в B были извлечены из одного и того же ансамбля, демонстрируя, что FRET, SAXS и моделирование взаимно совместимы.
Рис. 7.
Результаты моделирования и анализа с использованием…
Рис. 7.
Результаты моделирования и анализа с использованием теории полимеров раскрывают детали развернутого…
Рис. 7. Результаты моделирования и анализа с использованием теории полимеров раскрывают детали развернутого состояния в условиях рефолдинга. ( A ) Карта контактов различий, созданная путем взятия карты контактов ансамбля мочевины 1-M и вычитания карты контактов в исходном состоянии. Положительные значения соответствуют неродным взаимодействиям, а отрицательные значения отражают отсутствующие родные контакты. ( B ) Карта контактов различий, полученная путем взятия карты контактов ансамбля мочевины 1-M и вычитания карты контактов мочевины 8-M (48). Положительные значения соответствуют контактам, наблюдаемым при 1 М мочевине, которые не наблюдаются в сильно денатурирующих условиях. В частности, мы наблюдаем обширные контакты, включающие кластер N-концевых гидрофобных остатков (V3, I4, F5, L6) и кластер центральных гидрофобных остатков (F29, L30, F31). ( C ) Нормализованная оценка контакта каждого остатка отражает степень, в которой каждый остаток находится в прямом контакте с любым другим остатком. Внутримолекулярные взаимодействия управляются гидрофобными и ароматическими остатками, как показано упорядочением всех остатков и окраской по их физико-химическим свойствам (черный, гидрофобный/ароматический, зеленый, полярный, фиолетовый, пролин, синий, положительный, красный, отрицательный).
Положительные значения соответствуют неродным взаимодействиям, а отрицательные значения отражают отсутствующие родные контакты. ( B ) Карта контактов различий, полученная путем взятия карты контактов ансамбля мочевины 1-M и вычитания карты контактов мочевины 8-M (48). Положительные значения соответствуют контактам, наблюдаемым при 1 М мочевине, которые не наблюдаются в сильно денатурирующих условиях. В частности, мы наблюдаем обширные контакты, включающие кластер N-концевых гидрофобных остатков (V3, I4, F5, L6) и кластер центральных гидрофобных остатков (F29, L30, F31). ( C ) Нормализованная оценка контакта каждого остатка отражает степень, в которой каждый остаток находится в прямом контакте с любым другим остатком. Внутримолекулярные взаимодействия управляются гидрофобными и ароматическими остатками, как показано упорядочением всех остатков и окраской по их физико-химическим свойствам (черный, гидрофобный/ароматический, зеленый, полярный, фиолетовый, пролин, синий, положительный, красный, отрицательный). В частности, кластер гидрофобных остатков (F31, F29, L30, Y25, L35) в развернутом состоянии вступает в обширные внутримолекулярные взаимодействия и образует в нативной структуре гидрофобный кластер. ( D ) Сравнение профилей внутреннего масштабирования для NTL9 в хорошем растворителе (желтый), в тета-растворителе (розовый) и в комплексе 1-M мочевины (синий). В глобальном усредненном анализе ансамбль 1-M мочевины демонстрирует масштабирование, соответствующее полимеру в тета-растворителе с кажущимся показателем масштабирования 0,48 ± 0,01, несмотря на наличие локальной структуры и дальнодействующих взаимодействий. ( E ) Наличие нативных контактов и вторичной структуры в ансамбле 1-M мочевины в развернутом состоянии. Карта вторичной структуры исходного состояния показана выше для справки. ( F ) Для ансамблей в денатурированном состоянии, созданных между 500 K и 280 K, мы количественно определяем усредненный по ансамблю радиус вращения ( Left ), удельную плотность нативных контактов ( Center ) и кажущийся показатель масштабирования ν приложение ( справа ).
В частности, кластер гидрофобных остатков (F31, F29, L30, Y25, L35) в развернутом состоянии вступает в обширные внутримолекулярные взаимодействия и образует в нативной структуре гидрофобный кластер. ( D ) Сравнение профилей внутреннего масштабирования для NTL9 в хорошем растворителе (желтый), в тета-растворителе (розовый) и в комплексе 1-M мочевины (синий). В глобальном усредненном анализе ансамбль 1-M мочевины демонстрирует масштабирование, соответствующее полимеру в тета-растворителе с кажущимся показателем масштабирования 0,48 ± 0,01, несмотря на наличие локальной структуры и дальнодействующих взаимодействий. ( E ) Наличие нативных контактов и вторичной структуры в ансамбле 1-M мочевины в развернутом состоянии. Карта вторичной структуры исходного состояния показана выше для справки. ( F ) Для ансамблей в денатурированном состоянии, созданных между 500 K и 280 K, мы количественно определяем усредненный по ансамблю радиус вращения ( Left ), удельную плотность нативных контактов ( Center ) и кажущийся показатель масштабирования ν приложение ( справа ). Повторно взвешенный ансамбль выделен пунктирной рамкой и зелеными полосами.
Повторно взвешенный ансамбль выделен пунктирной рамкой и зелеными полосами.
Рис. 8.
Ансамбль развернутого состояния (УЗС) подвергается…
Рис. 8.
Ансамбль развернутого состояния (USE) подвергается непрерывному уменьшению размеров цепи по мере…
Рис. 8. Ансамбль в развернутом состоянии (USE) подвергается постоянному уменьшению размеров цепи в зависимости от снижения концентрации денатуранта. ( A ) SAXS показывает постоянное уменьшение размеров цепи (красные треугольники), тенденция, которая соответствует смоделированным ансамблям в развернутом состоянии. В среднем по ансамблю R g можно оценить по сквозному расстоянию, предполагая, что Rg=Re6.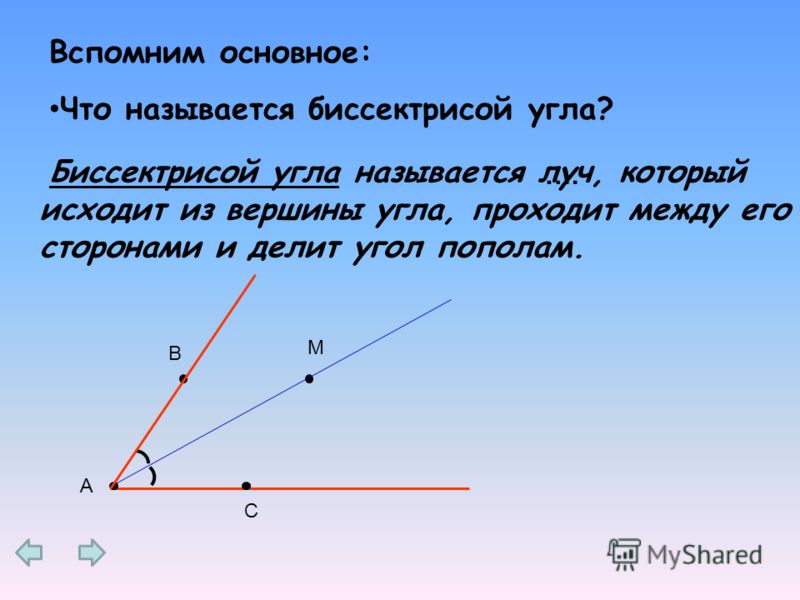 Это приближение работает достаточно хорошо в сильно денатурирующих условиях, но занижает R g в нативных условиях. ( B ) ν app можно оценить по глобальным измерениям или рассчитать непосредственно из ансамбля развернутых состояний. Как и в случае R g , эти приближения для ν приложение хорошо работают в сильно денатурирующих условиях, но в нативных условиях получается диапазон значений ν app .
Это приближение работает достаточно хорошо в сильно денатурирующих условиях, но занижает R g в нативных условиях. ( B ) ν app можно оценить по глобальным измерениям или рассчитать непосредственно из ансамбля развернутых состояний. Как и в случае R g , эти приближения для ν приложение хорошо работают в сильно денатурирующих условиях, но в нативных условиях получается диапазон значений ν app .
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Эксперименты и моделирование показывают, как дальнодействующие контакты могут образовываться в расширенных развернутых белках с незначительной вторичной структурой.
Мэн В., Лайл Н., Луан Б., Роли Д.П., Паппу Р.В. Мэн В. и др. Proc Natl Acad Sci U S A.
 2013 Feb 5;110(6):2123-8. doi: 10.1073/pnas.1216979110. Epub 2013, 22 января.
Proc Natl Acad Sci U S A. 2013.
PMID: 23341588
Бесплатная статья ЧВК.
2013 Feb 5;110(6):2123-8. doi: 10.1073/pnas.1216979110. Epub 2013, 22 января.
Proc Natl Acad Sci U S A. 2013.
PMID: 23341588
Бесплатная статья ЧВК.Холодно-развернутое состояние расширено, но содержит контакты дальнего и среднего радиуса действия и плохо описывается гомополимерными моделями.
Стензоски Н.Е., Цзоу Дж., Писерчио А., Гхош Р., Холехаус А.С., Роли Д.П. Стензоски Н.Е. и соавт. Биохимия. 2020 15 сентября; 59 (36): 3290-3299. doi: 10.1021/acs.biochem.0c00469. Epub 2020 1 сентября. Биохимия. 2020. PMID: 32786415
Малоугловое рассеяние рентгеновских лучей и спектроскопия FRET одиночных молекул дают сильно расходящиеся представления о развернутом состоянии с низким содержанием денатуранта.
Yoo TY, Meisburger SP, Hinshaw J, Pollack L, Haran G, Sosnick TR, Plaxco K.
 Ю ТИ и др.
Дж Мол Биол. 2012 4 мая; 418 (3-4): 226-36. doi: 10.1016/j.jmb.2012.01.016. Epub 2012 27 января.
Дж Мол Биол. 2012.
PMID: 22306460
Бесплатная статья ЧВК.
Ю ТИ и др.
Дж Мол Биол. 2012 4 мая; 418 (3-4): 226-36. doi: 10.1016/j.jmb.2012.01.016. Epub 2012 27 января.
Дж Мол Биол. 2012.
PMID: 22306460
Бесплатная статья ЧВК.Универсальная природа складчатости в контексте сворачивания и эволюции белков.
Тирумалай Д., Саманта Х.С., Мэйти Х., Редди Г. Тирумалай Д. и соавт. Тенденции биохимических наук. 2019 авг; 44 (8): 675-687. doi: 10.1016/j.tibs.2019.04.003. Эпаб 2019 29 мая. Тенденции биохимических наук. 2019. PMID: 31153683 Обзор.
Как, когда и почему коллапсируют белки: отношение к сворачиванию.
Харан Г. Харан Г. Curr Opin Struct Biol. 2012 февраль;22(1):14-20. doi: 10.1016/j.sbi.2011.10.005. Epub 2011 19 ноября. Curr Opin Struct Biol.
 2012.
PMID: 22104965
Бесплатная статья ЧВК.
Обзор.
2012.
PMID: 22104965
Бесплатная статья ЧВК.
Обзор.
Посмотреть все похожие статьи
Цитируется
Биофизика неупорядоченных белков с точки зрения спектроскопии флуоресценции одиночных молекул.
Чубук Дж., Стачелл-Бреретон, доктор медицины, Соранно А. Кубук Дж. и соавт. Очерки биохим. 2022 16 декабря; 66 (7): 875-890. дои: 10.1042/EBC20220065. Очерки биохим. 2022. PMID: 36416865 Бесплатная статья ЧВК.
Конформация белков и биомолекулярные конденсаты.
Vazquez DS, Toledo PL, Gianotti AR, Ermácora MR. Васкес Д.С. и соавт. Curr Res Struct Biol. 2022, 14 сентября; 4: 285-307. дои: 10.1016/j.crstbi.2022.09.004. Электронная коллекция 2022. Curr Res Struct Biol.
 2022.
PMID: 36164646
Бесплатная статья ЧВК.
Обзор.
2022.
PMID: 36164646
Бесплатная статья ЧВК.
Обзор.Онкогенные мутации в ДНК-связывающем домене FOXO1, которые нарушают фолдинг: количественные выводы из экспериментов и молекулярного моделирования.
Новак Д., Цянь Л., Акер Г., Вольц В.А., Бакстер Р.Х.Г. Новак Д. и соавт. Биохимия. 2022 16 августа; 61 (16): 1669-1682. doi: 10.1021/acs.biochem.2c00224. Epub 2022 27 июля. Биохимия. 2022. PMID: 35895105 Бесплатная статья ЧВК.
Остаточная структура в денатурированном состоянии быстро сворачивающегося домена UBA(1) белка эксцизионной репарации ДНК человека HHR23A.
Becht DC, Leavens MJ, Zeng B, Rothfuss MT, Briknarová K, Bowler BE. Бехт Д.К. и др. Биохимия. 2022 3 мая; 61 (9): 767-784. doi: 10.
 1021/acs.biochem.2c00011. Epub 2022 16 апр.
Биохимия. 2022.
PMID: 35430812
1021/acs.biochem.2c00011. Epub 2022 16 апр.
Биохимия. 2022.
PMID: 35430812Модуляция коллапса белковой цепи и стимуляция свертывания с помощью GroEL-ES.
Накви М.М., Авельянеда М.Дж., Рот А., Корс Э.Дж., Роланд А., Сандерликова В., Крамер Г., Рай Х.С., Танс С.Дж. Накви М.М. и др. Научная реклама 2022 4 марта; 8 (9): eabl6293. doi: 10.1126/sciadv.abl6293. Epub 2022 4 марта. Научная реклама 2022. PMID: 35245117 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
Рекомендации
- Левинталь С. Существуют ли пути для сворачивания белков? Дж. Чим. физ. 65, 44–45 (1968).
- Карплюс М.
 , Уивер Д.Л., Динамика сворачивания белков. Природа 260, 404–406 (1976).
—
пабмед
, Уивер Д.Л., Динамика сворачивания белков. Природа 260, 404–406 (1976).
—
пабмед
- Карплюс М.
- Дилл К. А., Доминирующие силы в сворачивании белка. Биохимия 29, 7133–7155 (1990). — пабмед
- Дилл К. А., МакКаллум Дж. Л., Проблема свертывания белка, 50 лет спустя. Наука 338, 1042–1046 (2012). — пабмед
- Чанг Х.
 С., Пиана-Агостинетти С., Шоу Д. Э., Итон В. А., Структурное происхождение медленной диффузии при сворачивании белков. Наука 349, 1504–1510 (2015).
—
ЧВК
—
пабмед
С., Пиана-Агостинетти С., Шоу Д. Э., Итон В. А., Структурное происхождение медленной диффузии при сворачивании белков. Наука 349, 1504–1510 (2015).
—
ЧВК
—
пабмед
- Чанг Х.
Типы публикаций
термины MeSH
вещества
Грантовая поддержка
- WT_/Wellcome Trust/Великобритания
- P41 GM103622/GM/NIGMS NIH HHS/США
- 107927/Z/15/Z/WT_/Wellcome Trust/Великобритания
Первый угол против третьего угла — ортогональные виды
Ортогональные виды позволяют нам представлять 3D-объект в 2D на чертеже.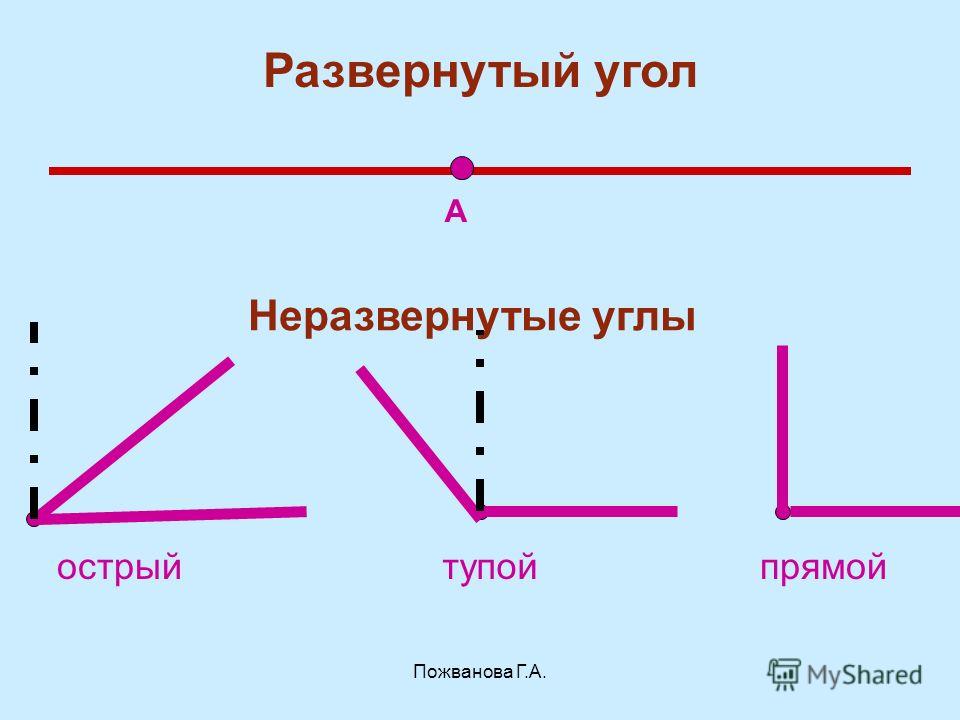 Ортографические виды могут показать нам объект, рассматриваемый с каждого направления. Расположение видов на чертеже зависит от того, используется ли угловая проекция 3 rd или 1 st . Вы можете сказать, какая угловая проекция используется символом, показанным на чертеже.
Ортографические виды могут показать нам объект, рассматриваемый с каждого направления. Расположение видов на чертеже зависит от того, используется ли угловая проекция 3 rd или 1 st . Вы можете сказать, какая угловая проекция используется символом, показанным на чертеже.
Проекция под третьим углом
Проекция под третьим углом может быть визуализирована путем «разворачивания коробки», как если бы сам объект разворачивался, чтобы показать виды с каждой стороны. На рис. 1 показаны виды куба, представленные проекцией под третьим углом.
Рис. 1. Виды в проекции под третьим углом Виды в проекции под третьим углом интуитивно понятны, так как они показывают, что вы смотрите на объект с соответствующей стороны.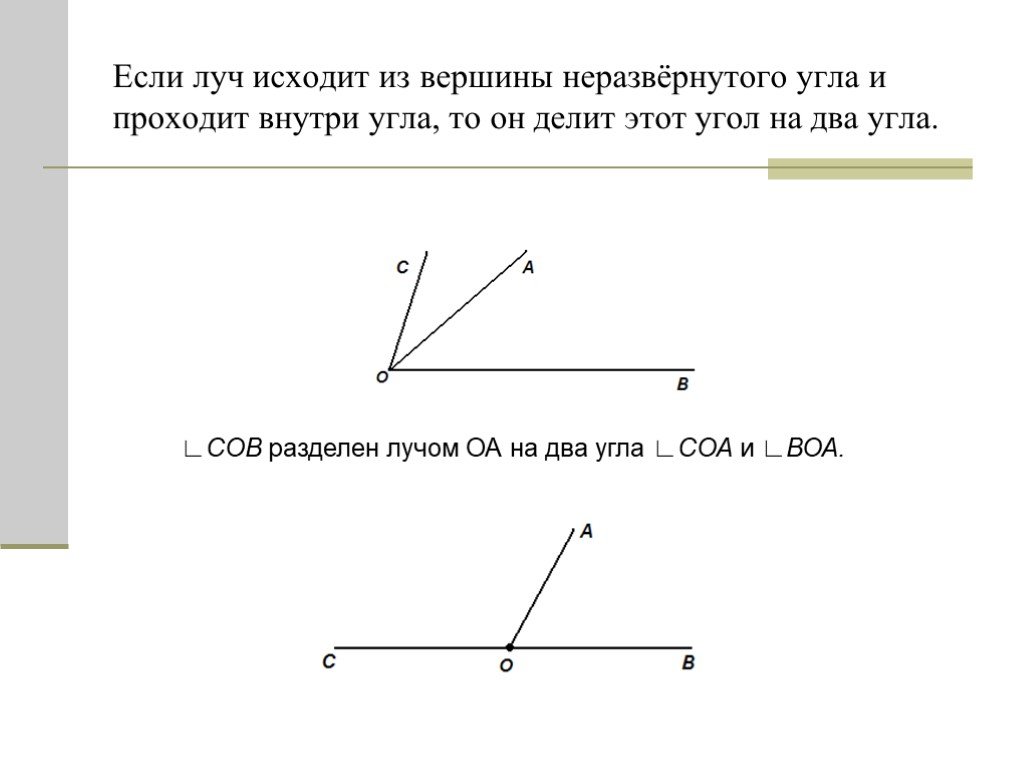 Вид спереди всегда отображается в центре. Вид объекта справа показан справа от вида спереди, вид объекта слева показан слева от вида спереди, а виды сверху и снизу показаны выше и ниже вида спереди , соответственно. Если бы нам нужно было показать вид сзади, вид сзади был бы размещен под видом снизу.
Вид спереди всегда отображается в центре. Вид объекта справа показан справа от вида спереди, вид объекта слева показан слева от вида спереди, а виды сверху и снизу показаны выше и ниже вида спереди , соответственно. Если бы нам нужно было показать вид сзади, вид сзади был бы размещен под видом снизу.
Краткая заметка о представлении символа для третьего угла. На самом деле существует четыре способа представления проекции под третьим углом на отпечатке, и все они приемлемы (рис. 2). Главный вывод здесь заключается в том, что не имеет значения, находится ли «боковой» вид «конуса» справа или слева . Для проекции под третьим углом «заостренный» конец бокового вида конуса в символе всегда указывает вперед/на «круг», как показано на рисунке 2 ниже. Все четыре варианта вполне приемлемы для третьего угла:
Рис. 2. Допустимые представления проекции под третьим углом СимволПроекция под первым углом
Представления под первым углом менее интуитивно понятны.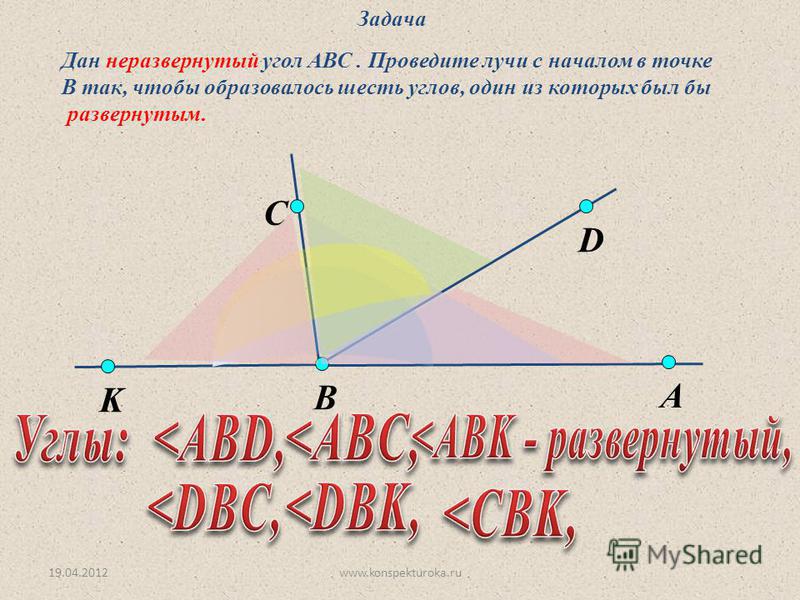 Их можно визуализировать, «опрокинув коробку». На рис. 2 показаны виды куба, представленные проекцией первого угла.
Их можно визуализировать, «опрокинув коробку». На рис. 2 показаны виды куба, представленные проекцией первого угла.
Вид спереди показан в центре, как и в проекции под третьим углом. Чтобы разместить вид на правую сторону, вы должны наклонить коробку так, чтобы правая сторона была обращена к вам. Для этого коробку нужно наклонить влево. Это приводит к тому, что вид справа на объект располагается слева от вида спереди. Повернув коробку лицевой стороной к себе еще раз, наклоните коробку вправо, и левая сторона будет обращена к вам. Таким образом, вид слева будет расположен справа от вида спереди. Этот же метод используется для просмотра сверху и снизу. Повернув перед собой объект, наклоните куб вниз. Теперь у вас есть верхняя сторона, обращенная к вам, при этом вид сверху расположен под видом спереди на чертеже. Если наклонить вид спереди вверх, вид снизу объекта будет обращен к вам, а вид снизу расположен над видом спереди.
Опять же, часто возникает путаница в представлении символов для проекта «Первый угол». Существует четыре способа представления проекции первого угла на отпечатке (рис. 4), и все они приемлемы. Главный вывод здесь заключается в том, что не имеет значения, находится ли «боковой» вид «конуса» справа или слева . Для первого угла «заостренный» конец бокового вида конуса в символе всегда направлен в сторону от передней части/«круга», как показано на рисунке 4 ниже. Все четыре из них вполне приемлемы для Первого Угла.
Рисунок 4. Допустимые представления символа проекции первого угла вид расположен на чертеже. Если человек не знает, какая угловая проекция используется на чертеже, это может привести к путанице. Важно не забывать искать символ проекции и понимать, относится ли символ к третьему или первому виду проекции. Чтобы помочь вам вспомнить, какой символ к какому виду относится, давайте посмотрим на символ для каждого из них.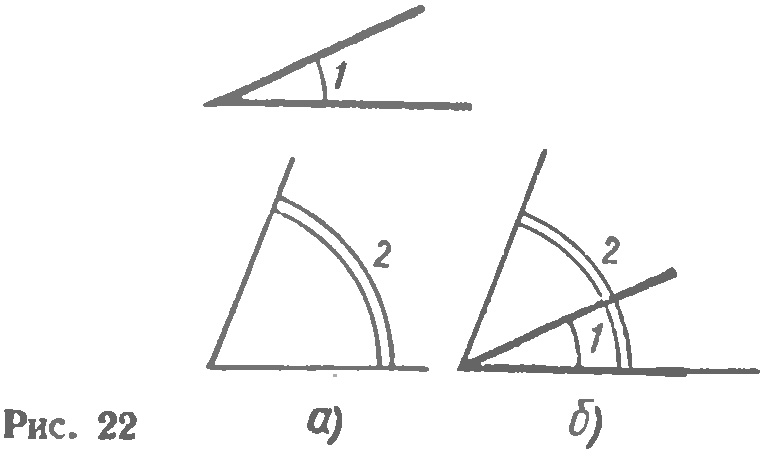 Символ третьего угла показан в верхнем левом углу Рисунка 1. Символ первого угла показан в левом верхнем углу Рисунка 2.
Символ третьего угла показан в верхнем левом углу Рисунка 1. Символ первого угла показан в левом верхнем углу Рисунка 2.
Каждый символ представляет виды конуса с этого угла обзора. Символы третьего и первого угла показывают круговой вид конуса сверху и вид конуса справа. Разница в символах заключается в том, где находится правый вид конуса.
Символ третьего угла показан на рис. 1. Он представлен круговым видом конуса сверху с правым видом конуса справа от него. На виде справа узкий конец конуса направлен в сторону вида сверху.
Символ первого угла, показанный на рис. 2, представляет собой круговой вид конуса сверху с правым видом конуса слева от него. Узкий конец конуса направлен в сторону от вида сверху. Обращая внимание на направление, в котором обращен конус, вы видите, что это не может быть вид слева на проекцию под третьим углом, потому что узкий конец конуса будет указывать на круговой вид сверху. Глядя на форму конуса, вы видите, что это должен быть правильный вид конуса.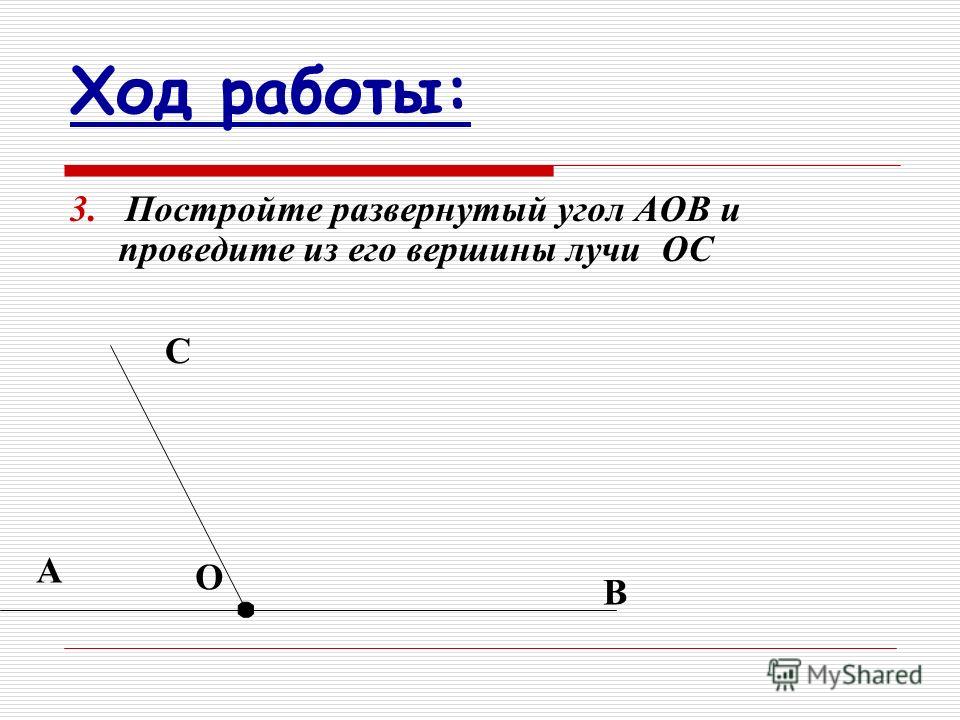

 edu
edu  1073/пнас.1818206116
1073/пнас.1818206116
 2013 Feb 5;110(6):2123-8. doi: 10.1073/pnas.1216979110. Epub 2013, 22 января.
Proc Natl Acad Sci U S A. 2013.
PMID: 23341588
Бесплатная статья ЧВК.
2013 Feb 5;110(6):2123-8. doi: 10.1073/pnas.1216979110. Epub 2013, 22 января.
Proc Natl Acad Sci U S A. 2013.
PMID: 23341588
Бесплатная статья ЧВК. Ю ТИ и др.
Дж Мол Биол. 2012 4 мая; 418 (3-4): 226-36. doi: 10.1016/j.jmb.2012.01.016. Epub 2012 27 января.
Дж Мол Биол. 2012.
PMID: 22306460
Бесплатная статья ЧВК.
Ю ТИ и др.
Дж Мол Биол. 2012 4 мая; 418 (3-4): 226-36. doi: 10.1016/j.jmb.2012.01.016. Epub 2012 27 января.
Дж Мол Биол. 2012.
PMID: 22306460
Бесплатная статья ЧВК. 2012.
PMID: 22104965
Бесплатная статья ЧВК.
Обзор.
2012.
PMID: 22104965
Бесплатная статья ЧВК.
Обзор.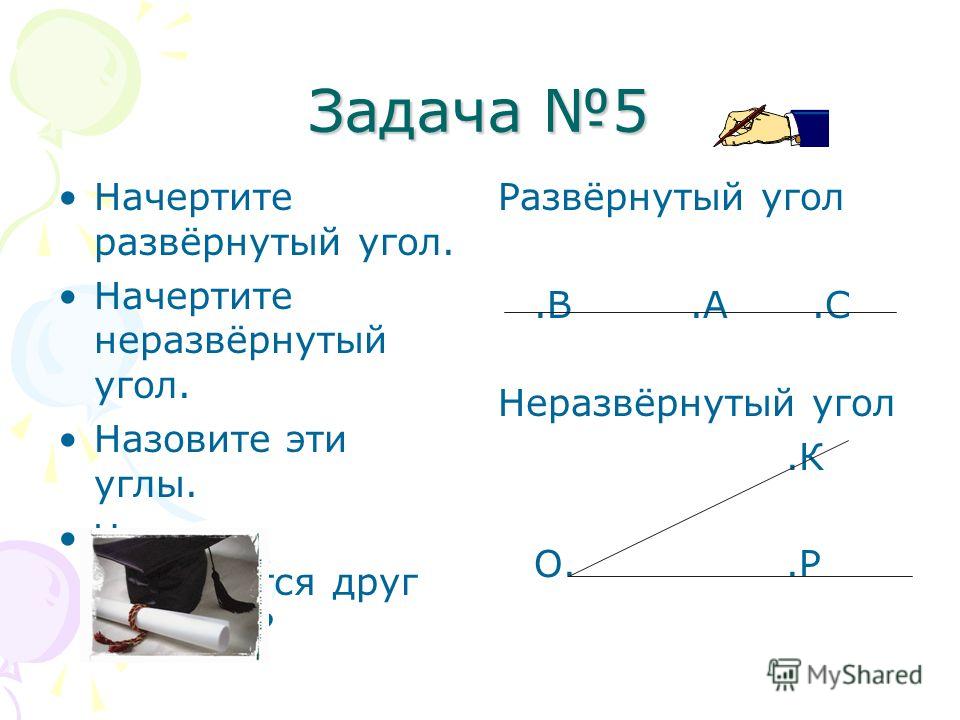 2022.
PMID: 36164646
Бесплатная статья ЧВК.
Обзор.
2022.
PMID: 36164646
Бесплатная статья ЧВК.
Обзор. 1021/acs.biochem.2c00011. Epub 2022 16 апр.
Биохимия. 2022.
PMID: 35430812
1021/acs.biochem.2c00011. Epub 2022 16 апр.
Биохимия. 2022.
PMID: 35430812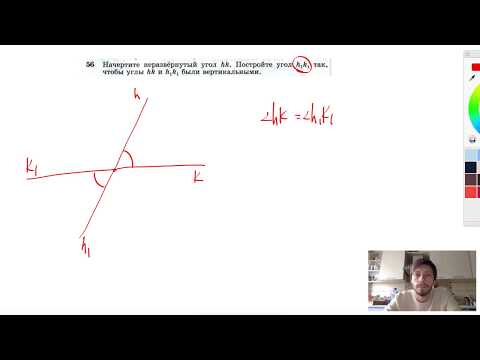 , Уивер Д.Л., Динамика сворачивания белков. Природа 260, 404–406 (1976).
—
пабмед
, Уивер Д.Л., Динамика сворачивания белков. Природа 260, 404–406 (1976).
—
пабмед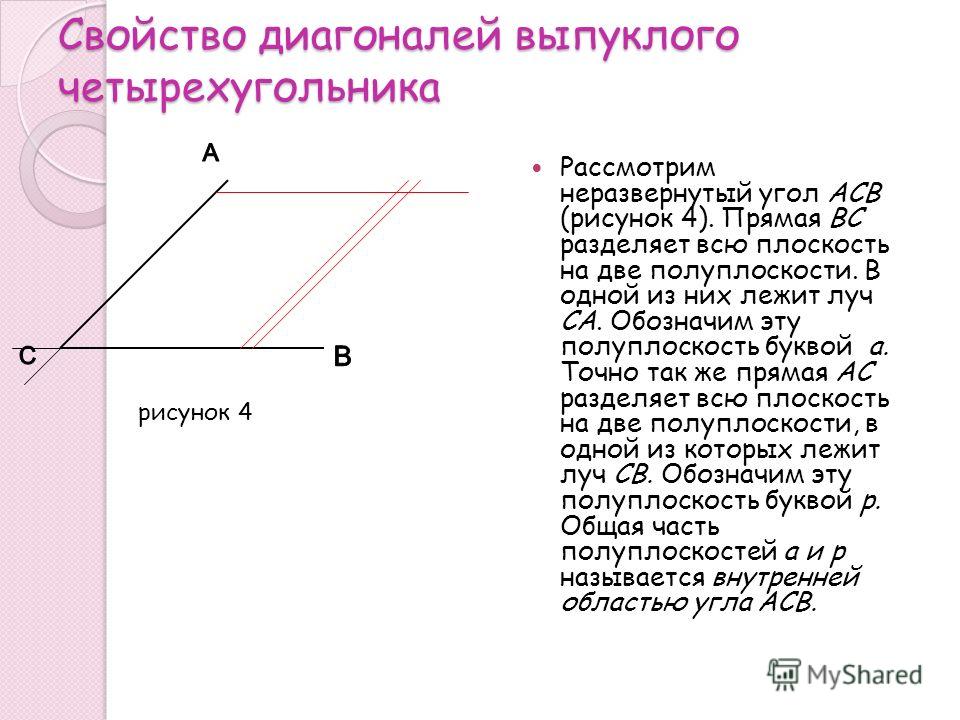 С., Пиана-Агостинетти С., Шоу Д. Э., Итон В. А., Структурное происхождение медленной диффузии при сворачивании белков. Наука 349, 1504–1510 (2015).
—
ЧВК
—
пабмед
С., Пиана-Агостинетти С., Шоу Д. Э., Итон В. А., Структурное происхождение медленной диффузии при сворачивании белков. Наука 349, 1504–1510 (2015).
—
ЧВК
—
пабмед