Когда вектора перпендикулярны: Какие два вектора называются перепендикулярными?

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— 2-е изд.— М.: Просвещение, 1990.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и качал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Предыдущее издание вышло в 1988 году. Оглавление ГЛАВА I. ЧИСЛА 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа § 4. Комплексные числа ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ § 6. Целые рациональные выражения 52. Многочлены. Приведение многочленов к стандартному виду. § 7. Дробные рациональные выражения Глава III. ФУНКЦИИ И ГРАФИКИ § 9. Свойства функций § 10. Виды функций 95. Обратная функция. График обратной функции. 96. Логарифмическая функция. 96. Определение тригонометрических функций. § 11. Преобразования графиков ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. 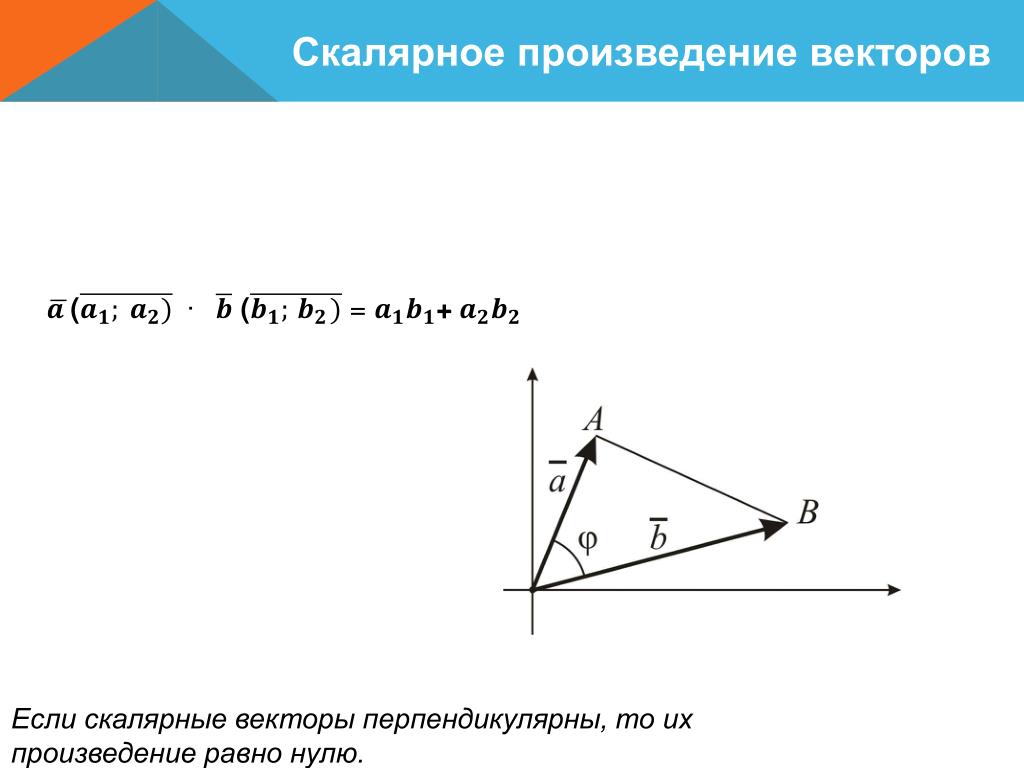Преобразование выражений, содержащих переменную под знаком логарифма § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной § 15. Уравнения с двумя переменными § 16. Системы уравнений Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной § 18. Доказательство неравенств ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности § 20. Предел функции § 21. Производная и ее применения § 22. Первообразная и интеграл ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ § 1. О строении курса геометрии § 2. Основные свойства простейших геометрических фигур § 3. Геометрические построения на плоскости § 4. Четырехугольники § 5. Многоугольники § 6. Решение треугольников 34. Теорема косинусов. Теорема синусов. § 7. Площади плоских фигур 38. Площади подобных фигур. ГЛАВА II. Прямые и плоскости в пространстве § 8. Аксиомы стереометрии и некоторые следствия из них § 9. Параллельность прямых и плоскостей § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники § 12. Тела вращения § 13. Изображение пространственных фигур на плоскости § 14. Объемы тел § 15. Площади поверхностей тел ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве § 17. Уравнения фигур на плоскости § 18. Уравнения фигур в пространстве ГЛАВА V. ПРЕОБРАЗОВАНИЯ ФИГУР § 19. Движение § 20. Подобие фигур ГЛАВА VI. ВЕКТОРЫ § 21. Введение понятия вектора § 22. Операции над векторами ОСНОВНЫЕ ФОРМУЛЫ И СООТНОШЕНИЯ I. Основные законы алгебры ГЕОМЕТРИЯ

Урок 4. Произведение векторов | Уроки математики и физики для школьников и родителей

Умножение вектора на число.

В геометрии часто возникает потребность в сложении двух, трёх или более одинаковых векторов:

и так далее.

Такие суммы, как в алгебре, удобно записывать

и так далее.
Эта процедура подсказывает определение операции умножения вектора на число.
Произведение ненулевого вектора

на число  k – вектор

который сонаправлен с

если  k > 0  и противоположно направлен с

если  k < 0.
Длина вектора

равна

В результате произведения вектора на число всегда получается векторная величина.  

Произведение нулевого вектора на любое число – нулевой вектор. 

Произведение вектора

на число  k  обозначают так:

Произведение числа нуль на любой вектор есть нулевой вектор.

ПРИМЕР:

На рисунке

изображены:

Основные законы умножения вектора на число.

Для операции умножения вектора на число выполняются следующие законы.

– сочетательный закон:

– первый распределительный закон:

– второй распределительный закон:

Здесь  k, l, – любые числа;

– любые векторы.

Если

Умножение вектора на число с помощью координат вектора.

При умножении вектора на число его координаты умножаются на это число, а именно, если

то есть

Или другими словами:

Координаты вектораравняются произведению числа  k  на соответствующие координаты вектораВекторы часто помогают изучать геометрические факты: для этого нужно научиться переводить геометрические факты на векторный язык, и наоборот, уметь векторное выражение перевести на язык геометрии.
Предположим, что нам нужно доказать, что прямые  а  и  b  параллельны.

 Рассмотрим векторы

принадлежащие соответственно прямым  а  и  b.

Векторы

могут иметь и противоположные направления.
Можно доказать, что если векторы

коллинеарны, то по определению коллинеарности векторов получим, что прямые 

а  и  b  параллельны.
Вектор

коллинеарен ненулевому вектору

тогда и только тогда, когда

Два вектора, отложенные от одной и той же точки, лежат на одной прямой тогда и только тогда, когда один из них получается из другого умножением на число.
Другими словами, точка  Х  лежит на прямой  АВ  тогда и только тогда, когда

Скалярное произведение двух векторов.

Угол между двумя векторами с общим началом определяется, как обычный угол.

Если есть два произвольных вектора

то углом между ними называется угол между равными векторами с общим началом.

При этом рассматривают так называемый выпуклый угол (угол, имеющий меньшую величину). Иногда угол между векторами

обозначают так:

Читают: угол между векторами

равен  30°.

Углом между двумя ненулевыми векторами называют угол между соответствующими им направленными отрезками, исходящими из одной точки.

Угол между противоположно направленными векторами равен  180°, а между сонаправленными – 0°.

Скалярное произведение двух ненулевых векторов равняется произведению длин этих векторов на косинус угла между ними.

Если угол между векторами

равен  φ,

то их скалярное произведение

Если хотя бы один из двух векторов нулевой, то скалярное произведение равно  0.

Если векторы

равны, то есть

то пишут

и говорят о скалярном квадрате вектора.

В этом случае  cos φ = 1, то есть

Итак, скалярный квадрат вектора совпадает с квадратом его длины:

Если

и при этом, если

то следует, что

Скалярное умножение связано со сложением векторов (распределительный закон):

Скалярным произведением двух векторов называется число, которое равняется сумме произведений соответствующих координат этих векторов.

Обозначение таково же, как и для произведения чисел.

Если есть векторы

то

Признак перпендикулярности векторов.

Если векторы перпендикулярны,

то их скалярное произведение равняется нулю

И наоборот, если скалярное произведение отличающихся от нуля векторов равняется нулю, то векторы перпендикулярны.

ПРИМЕР:

Необходимо выяснить, будут ли перпендикулярными отрезки  KL  и  MN, если 

К(3; 5), L(–2; 0),

M(8; –1), N(1; 4).

РЕШЕНИЕ:

Здесь речь идёт об обычных отрезках плоскости. Хотя речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы:

Вычислим их скалярное произведение:

Значит, отрезки  KL  и  MN  не перпендикулярны.

ПРИМЕР:

Пусть

Найти вектор:

РЕШЕНИЕ: ОТВЕТ: ПРИМЕР:

Пусть

Найти вектор:

РЕШЕНИЕ:

ОТВЕТ:

ПРИМЕР:

Найдите угол  α  между векторами:

РЕШЕНИЕ:

По определению скалярного произведения

где  α – искомый угол, a  и  b – модули векторовсоответственно.

Отсюда

В свою очередь,

тогдаОтсюда  α ≈ 173°.

Задания к уроку 4

Независимость перпендикулярных составляющих движения

Вектор силы, направленный вверх и вправо, имеет две части – восходящую и правую части. То есть, если вы тянете объект вверх и вправо, то вы оказываете влияние на объект в двух разных направлениях — вверх и вправо. Эти две части двумерного вектора называются компонентами. Компонент описывает действие одного вектора в заданном направлении. Любой вектор силы, приложенный под углом к ​​горизонтали, можно рассматривать как состоящий из двух частей или компонентов. Векторная сумма этих двух составляющих всегда равна силе при данном угле. Это изображено на диаграмме ниже.

 

Любой вектор, будь то вектор силы, вектор смещения, вектор скорости и т. д., направленный под углом, можно рассматривать как состоящий из двух перпендикулярных компонент. Эти два компонента можно представить в виде катетов прямоугольного треугольника, образованного путем проецирования вектора на оси x и y.

Две перпендикулярные части или компоненты вектора не зависят друг от друга. В качестве примера рассмотрим притяжение Фидо. Если горизонтальное притяжение к Фидо увеличится, то Фидо будет ускоряться вправо с большей скоростью; тем не менее, это большее горизонтальное притяжение не окажет никакого вертикального влияния на Фидо. Вытягивание по горизонтали с большей силой не поднимает Фидо вертикально над землей. Изменение горизонтальной составляющей не влияет на вертикальную составляющую. Именно это подразумевается под фразой «перпендикулярные компоненты векторов не зависят друг от друга». Изменение одного компонента не влияет на другой компонент. Изменение компонента повлияет на движение в этом конкретном направлении. Хотя изменение одной из составляющих изменит величину результирующей силы, оно не изменит величину другой составляющей.

Результирующее движение самолета, летящего при наличии бокового ветра, представляет собой комбинацию (или сумму) двух одновременных векторов скорости, перпендикулярных друг другу. Предположим, что самолет пытается лететь на север из Чикаго к границе с Канадой, просто направляя самолет прямо на север. Если самолет встречает боковой ветер, направленный на запад, то результирующая скорость самолета будет северо-западной. Северо-западный вектор скорости состоит из двух компонент: северной составляющей, являющейся следствием двигателя самолета ( плоская скорость ) и западная составляющая, возникающая в результате бокового ветра ( скорость ветра ). Эти два компонента независимы друг от друга. Изменение одного из компонентов не повлияет на другой компонент. Например, если бы скорость ветра увеличилась, то самолет продолжал бы покрывать землю в северном направлении с той же скоростью. Это правда, что изменение скорости ветра заставило бы самолет двигаться дальше на запад; однако самолет по-прежнему летит на север с той же скоростью. Перпендикулярные составляющие движения не влияют друг на друга.

 

Теперь рассмотрим воздушный шар, спускающийся по воздуху к земле при наличии ветра, дующего на восток. Предположим, что скорость воздушного шара вниз составляет 3 м/с, а ветер дует на восток со скоростью 4 м/с. Результирующая скорость воздушного шара будет комбинацией (то есть векторной суммой) этих двух одновременных и независимых векторов скорости. Воздушный шар будет двигаться вниз и на восток.

Если бы скорость ветра увеличилась, воздушный шар начал бы двигаться быстрее в восточном направлении, но его нисходящая скорость не изменилась бы. Если бы воздушный шар находился на высоте 60 метров над землей и двигался вниз со скоростью 3 м/с, то для преодоления этого вертикального расстояния потребовалось бы 20 секунд.

d = v • t So t = d / v = (60 м) / (3 м/с) = 20 секунд

За 20 секунд, за которые воздушный шар пролетит 60 метров к земле, ветер будет нести воздушный шар в восточном направлении. При скорости ветра 4 м/с расстояние, пройденное на восток за 20 секунд, составит 80 метров. Если бы скорость ветра увеличилась со значения 4 м/с до значения 6 м/с, то воздушному шару по-прежнему потребовалось бы 20 секунд, чтобы упасть на 60 метров вниз. На движение вниз влияют только нисходящие компоненты движения. Изменение горизонтальной составляющей движения (например, скорости ветра в восточном направлении) не повлияет на вертикальное движение. Перпендикулярные составляющие движения не зависят друг от друга. Изменение скорости ветра в восточном направлении от значения 4 м/с до значения 6 м/с приведет к тому, что воздушный шар будет унесен на восток только на расстояние 120 метров вместо исходных 80 метров.

 

В последнем разделе Урока 1 обсуждалась тема относительной скорости и движения речного судна. Лодка на реке часто плывет прямо по реке, перпендикулярно ее берегу. Тем не менее, из-за потока воды (то есть течения), движущегося параллельно берегам реки, лодка не приземляется на берег прямо напротив исходной точки. Результирующее движение лодки представляет собой комбинацию (то есть векторную сумму) этих двух одновременных и независимых векторов скорости — скорость лодки плюс скорость реки. На диаграмме справа лодка изображена движущейся через реку на восток, в то время как река течет на юг. Лодка выходит из точки А и направляется к точке В. Но из-за течения реки в южном направлении лодка достигает противоположного берега реки в точке С. Время, необходимое лодке, чтобы пересечь реку с одного берега на другой другая сторона зависит от скорости лодки и ширины реки. Только восточная составляющая движения могла повлиять на время движения на восток через реку.

Предположим, что скорость лодки 4 м/с, а скорость реки 3 м/с. Величину результирующей скорости можно определить равной 5 м/с, используя теорему Пифагора. Время, необходимое лодке для пересечения реки шириной 60 м, будет зависеть от скорости лодки 4 м/с. Чтобы пересечь реку шириной 60 метров, потребуется 15 секунд.

d = v • t Итак, t = d / v = (60 м) / (4 м/с) = 15 секунд

путешествие в восточном направлении.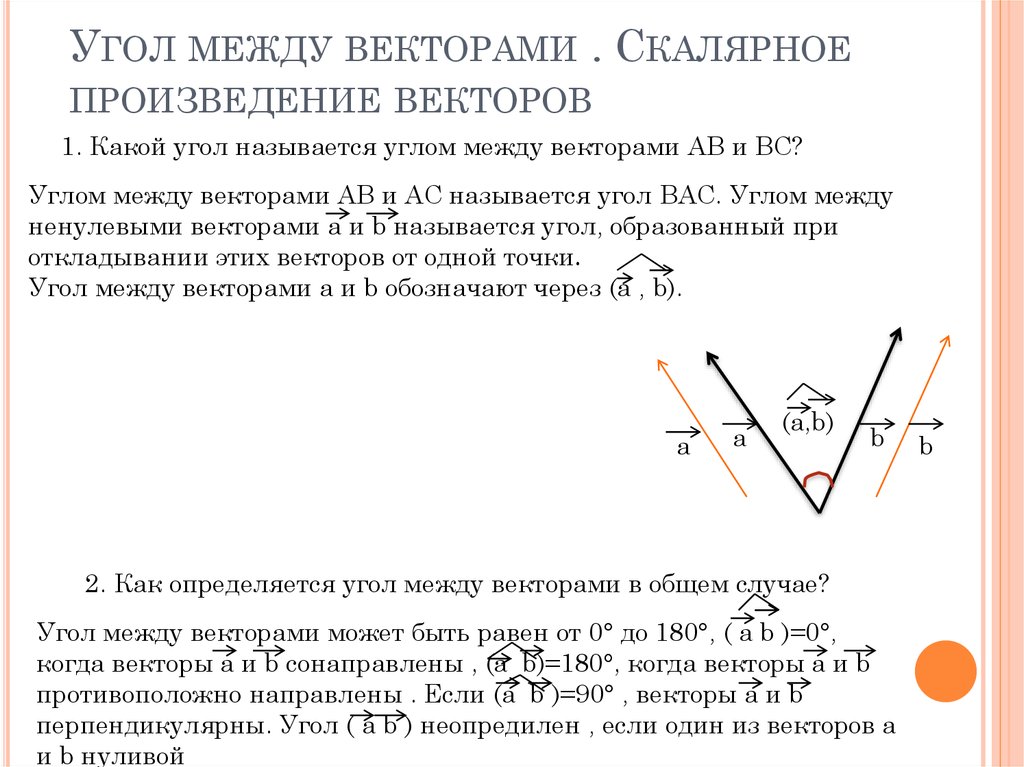 Если бы течение увеличилось так, что скорость реки стала бы 5 м/с, то для пересечения реки по-прежнему потребовалось бы 15 секунд. Перпендикулярные составляющие движения не зависят друг от друга. Увеличение скорости реки просто заставит лодку двигаться дальше в южном направлении в течение этих 15 секунд движения. Изменение южного компонента движения влияет только на южное движение.

 

Все векторы можно рассматривать как имеющие перпендикулярные компоненты. На самом деле, любое движение под углом к ​​горизонтали или вертикали можно рассматривать как имеющее два перпендикулярных движения, происходящих одновременно. Эти перпендикулярные составляющие движения возникают независимо друг от друга. Любая составляющая движения, происходящая строго в горизонтальном направлении, не повлияет на движение в вертикальном направлении. Любое изменение в одном наборе этих компонентов не повлияет на другой набор. На уроке 2 мы применим этот принцип к движению снарядов, которые обычно испытывают как горизонтальное, так и вертикальное движение.

 

Проверьте свое понимание

1. Самолет летит на северо-запад из аэропорта О’Хара в Чикаго со скоростью 400 км/ч в направлении 150 градусов (т. е. 30 градусов к северу от запада). Канадская граница расположена на расстоянии 1500 км к северу от Чикаго. Самолет прибудет в Канаду примерно через ____ часов.

а. 0,13	б. 0,23	в. 0,27
д. 3,75	эл. 4.33	ф. 6.49
г. 7,50
ч. Ни один из них даже близко не стоит.

 

2. Предположим, что рассматриваемый самолет 1 летел со скоростью 358 км/ч в направлении 146 градусов (т. е. 34 градуса к северу от запада). Если канадская граница по-прежнему находится на расстоянии 1500 км к северу от Чикаго, то сколько времени потребуется, чтобы пересечь границу?

 

 

3. ИСТИНА или ЛОЖЬ :

Лодка движется прямо через реку. Река течет на север со скоростью 3 м/с. Если бы течение реки было больше, то время, необходимое лодке для достижения противоположного берега, не изменилось бы.

а. Истинный

б. Ложь

 

 

4. Лодка выходит из точки А и движется прямо через реку шириной 60 м со скоростью 4 м/с (относительно воды). Речная вода течет на север со скоростью 3 м/с (относительно берега). Лодка достигает противоположного берега в точке C. Что из следующего заставит лодку достичь противоположного берега в точке ЮЖНЕЕ от C?

а. Лодка движется по реке со скоростью 5 м/с.

б. Лодка движется по реке со скоростью 3 м/с.

в. Река течет на север со скоростью 4 м/с.

д. Река течет на север со скоростью 2 м/с.

эл. Ерунда! Ничто из этого не влияет на место приземления лодки.

 

 

Перейти к следующему уроку:

Векторы, Часть 6

Векторы, Часть 6

Векторы в двух и трех измерениях

Часть 6: Прогнозы

1. Используйте апплет ниже, чтобы исследовать проекция вектора v (зеленый) на другой вектор Вт (желтый) в пространстве, которое мы вскоре свяжем со скалярным произведением < v , w >. Вы можете настроить компоненты желтого и зеленого векторов, а затем задать апплет для вычисления проекции зеленого вектора на желтый. Ползунок внизу позволяет вращать вид векторов. К помогут вам сориентироваться, проекции зеленого и желтого векторов на также показаны плоскости xy . Проекция вектора в на w является вектором в том же или противоположном направлении, что и w , поэтому должны быть определены две вещи: «одинаковые или противоположные» и длина проекции. Подумайте, как оба они могут быть связаны с точкой продукт.

Воспользуемся идеей проектирования один вектор на другой, чтобы разрешить вектор v на его компоненты параллельно и перпендикулярно вектору в . Идея иллюстрируется в следующую фигуру, которая нарисована в плоскости, определяемой соотношением и и с .

На этом рисунке показано соотношение и . в зеленом и w в синем (частично затенен u и p ). вектор p — это проекция v на w , и это также компонент v параллельно ш . Компонент v перпендикулярно w равно q , и ясно, что v = p + q . Таким образом, если мы можем найти p из v и w , то мы можем вычислить q как q = v — p .

2. Для обозначения направление w , мы сначала вычисляем единичный вектор u (т. е. u имеет длину 1) в том же направлении, что и u . Как рассчитывается u от до ? Объясните, почему p = |p| ты . Как |p| относительно длины v и косинуса угла между их?
3. Обратите внимание, что потому что может можно рассчитать, взяв скалярное произведение на с любым из векторов с или с . (Мы не можем использовать p для этой цели, потому что мы не знать, что это такое — это то, что мы пытаемся найти.) Теперь поместите все собрать вместе, чтобы получить формулу для p , найдя u , cos , |р| и, наконец, p сам.

   No related posts.