Нод чисел онлайн трех. Нод и нок двух чисел, алгоритм евклида
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми .
Определение. Натуральные числа называют взаимно простыми , если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа
(т. е. две двойки).
Остаются множители 2 * 2 * 3.
Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и Ь называют наименьшее натуральное число,
которое кратно и a, и b.
Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных
чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел.
Число, равное сумме всех его делителей (без самого числа),
они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные
числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э.
Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде
произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше,
в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались невычеркнутыми только простые числа.
Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД .
Здесь мы поговорим про нахождение наименьшего общего кратного (НОК) , и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.
Навигация по странице.
Вычисление наименьшего общего кратного (НОК) через НОД
Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b) . Рассмотрим примеры нахождения НОК по приведенной формуле.
Пример.
Найдите наименьшее общее кратное двух чисел 126 и 70 .
Решение.
В этом примере a=126
, b=70
.
Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b)
. То есть, сначала нам предстоит найти наибольший общий делитель чисел 70
и 126
, после чего мы сможем вычислить НОК этих чисел по записанной формуле.
Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .
Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)= 126·70:14=630 .
Ответ:
НОК(126, 70)=630 .
Пример.
Чему равно НОК(68, 34) ?
Решение.
Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .
Ответ:
НОК(68, 34)=68 .
Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b : если число a делится на b , то наименьшее общее кратное этих чисел равно a .
Нахождение НОК с помощью разложения чисел на простые множители
Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители .
Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел
.
Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b) . Действительно, произведение чисел a и b равно произведению всех множителей, участвующих в разложениях чисел a и b . В свою очередь НОД(a, b) равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a и b (о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).
Приведем пример. Пусть мы знаем, что 75=3·5·5
и 210=2·3·5·7
. Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7
. Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75
и в разложении числа 210
(такими множителями являются 3
и 5
), тогда произведение примет вид 2·3·5·5·7
.
Значение этого произведения равно наименьшему общему кратному чисел 75
и 210
, то есть, НОК(75, 210)= 2·3·5·5·7=1 050
.
Пример.
Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.
Решение.
Разложим числа 441 и 700 на простые множители:
Получаем 441=3·3·7·7 и 700=2·2·5·5·7 .
Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7 . Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7 ): 2·2·3·3·5·5·7·7 . Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100 .
Ответ:
НОК(441, 700)= 44 100 .
Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a
добавить недостающие множители из разложения числа b
, то значение полученного произведения будет равно наименьшему общему кратному чисел a
и b .
Для примера возьмем все те же числа 75 и 210 , их разложения на простые множители таковы: 75=3·5·5 и 210=2·3·5·7 . Ко множителям 3 , 5 и 5 из разложения числа 75 добавляем недостающие множители 2 и 7 из разложения числа 210 , получаем произведение 2·3·5·5·7 , значение которого равно НОК(75, 210) .
Пример.
Найдите наименьшее общее кратное чисел 84 и 648 .
Решение.
Получаем сначала разложения чисел 84 и 648 на простые множители. Они имеют вид 84=2·2·3·7 и 648=2·2·2·3·3·3·3 . К множителям 2 , 2 , 3 и 7 из разложения числа 84 добавляем недостающие множители 2 , 3 , 3 и 3 из разложения числа 648 , получаем произведение 2·2·2·3·3·3·3·7 , которое равно 4 536 . Таким образом, искомое наименьшее общее кратное чисел 84 и 648 равно 4 536 .
Ответ:
НОК(84, 648)=4 536 .
Нахождение НОК трех и большего количества чисел
Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел.
Теорема.
Пусть даны целые положительные числа a 1 , a 2 , …, a k , наименьшее общее кратное m k этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2) , m 3 =НОК(m 2 , a 3) , …, m k =НОК(m k−1 , a k) .
Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.
Пример.
Найдите НОК четырех чисел 140 , 9 , 54 и 250 .
Решение.
В этом примере a 1 =140 , a 2 =9 , a 3 =54 , a 4 =250 .
Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9) . Для этого по алгоритму Евклида определяем НОД(140, 9) , имеем 140=9·15+5 , 9=5·1+4 , 5=4·1+1 , 4=1·4 , следовательно, НОД(140, 9)=1 , откуда НОК(140, 9)=140·9:НОД(140, 9)= 140·9:1=1 260 . То есть, m 2 =1 260 .
Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54)
. Вычислим его через НОД(1 260, 54)
, который также определим по алгоритму Евклида: 1 260=54·23+18
, 54=18·3
.
Тогда НОД(1 260, 54)=18
, откуда НОК(1 260, 54)=
1 260·54:НОД(1 260, 54)=
1 260·54:18=3 780
. То есть, m 3 =3 780
.
Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250) . Для этого находим НОД(3 780, 250) по алгоритму Евклида: 3 780=250·15+30 , 250=30·8+10 , 30=10·3 . Следовательно, НОД(3 780, 250)=10 , откуда НОК(3 780, 250)= 3 780·250:НОД(3 780, 250)= 3 780·250:10=94 500 . То есть, m 4 =94 500 .
Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .
Ответ:
НОК(140, 9, 54, 250)=94 500 .
Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее
.
Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.
Пример.
Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение.
Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7 , 6=2·3 , 48=2·2·2·2·3 , 7 (7 – простое число , оно совпадает со своим разложением на простые множители) и 143=11·13 .
Для нахождения НОК данных чисел к множителям первого числа 84
(ими являются 2
, 2
, 3
и 7
) нужно добавить недостающие множители из разложения второго числа 6
. Разложение числа 6
не содержит недостающих множителей, так как и 2
и 3
уже присутствуют в разложении первого числа 84
. Дальше к множителям 2
, 2
, 3
и 7
добавляем недостающие множители 2
и 2
из разложения третьего числа 48
, получаем набор множителей 2
, 2
, 2
, 2
, 3
и 7
. К этому набору на следующем шаге не придется добавлять множителей, так как 7
уже содержится в нем. Наконец, к множителям 2
, 2
, 2
, 2
, 3
и 7
добавляем недостающие множители 11
и 13
из разложения числа 143
.
Получаем произведение 2·2·2·2·3·7·11·13
, которое равно 48 048
.
Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
Yandex.RTB R-A-339285-1
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.
Определение 1
Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .
Пример 1
Необходимо найти НОК чисел 126 и 70 .
Решение
Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .
Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .
Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .
Ответ: НОК (126 , 70) = 630 .
Пример 2
Найдите нок чисел 68 и 34 .
Решение
НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .
Ответ: НОК (68 , 34) = 68 .
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.
Определение 2
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.
Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
Пример 3
У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .
Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .
Пример 4
Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .
Ответ: НОК (441 , 700) = 44 100 .
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Определение 3
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.
Пример 5
Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .
Пример 6
Необходимо вычислить НОК чисел 84 и 648 .
Решение
Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК (84 , 648) = 4 536 .
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел.
На этот случай есть теорема.
Теорема 1
Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Пример 7
Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .
Решение
Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .
Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .
Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .
Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .
НОК четырех чисел из условия примера равно 94500 .
Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Определение 4
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Пример 8
Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение
Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 .
Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
Пример 9
НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .
Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .
Пример 10
Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .
Решение
Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел − 145 и − 45 равно 1 305 .
Ответ: НОК (− 145 , − 45) = 1 305 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.
- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2.
Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 — делится на 3, но не делится на 18.
24 · 2 = 48 — делится на 3, но не делится на 18.
24 · 3 = 72 — делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:
Делим произведение на их НОД:
Таким образом, НОК (12, 8) = 24.
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа — 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Делим произведение на их НОД:
Таким образом, НОК (12, 8, 9) = 72.
НОД И НОК ЧИСЕЛ презентация, доклад
НОД И НОК ЧИСЕЛ
учитель математики МОУ лицея №1
Бугаева Вера Михайловна
г.Комсомольска–на–Амуре
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
Наибольшее натуральное число на которое де-лятся без остатка числа a и b, называют наи-большим общим делителем чисел a и b.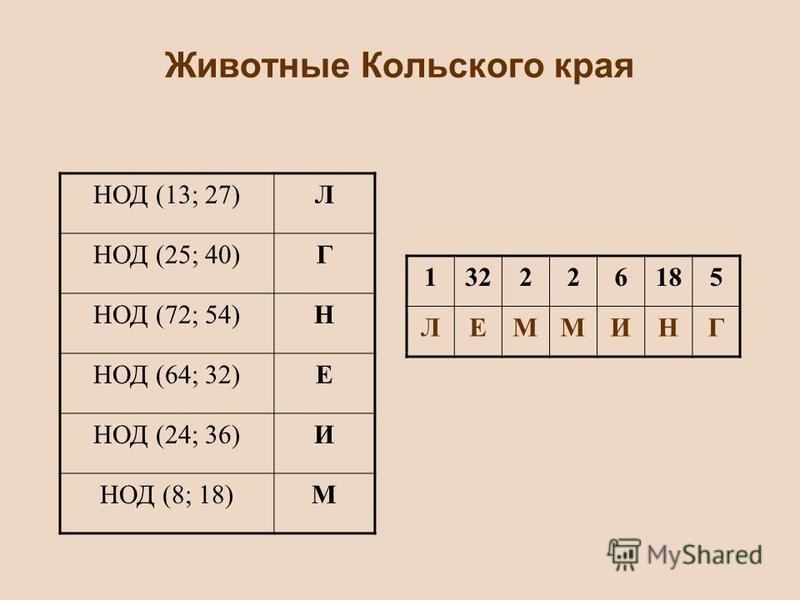
Например: НОД чисел 48 и 36 равен 12, т.е. наи-
большему из натуральных чисел, ко-
торое делит нацело и 48, и 36.
НОД(48;36)=12.
ПОМНИ!
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
разложить их на простые множители;
из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
найти произведение оставшихся множителей.
Например: НОД (96, 72)=24
96=2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3, 72=2 ∙ 2 ∙ 2 ∙ 3 ∙ 3
Остались множители: 2 ∙ 2 ∙ 2 ∙ 3=24.
ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№1. Найдите НОД чисел: а)108 и 72; б) 150 и 225 .
Решение. Разложим числа на простые множители:
108 2 72 2 150 2 225 5
54 2 36 2 75 5 45 5
27 3 18 2 15 5 9 3
9 3 9 3 3 3 3 3
3 3 3 3 1 1 1 1
1 1
Найдем одинаковые множители ( выделены одним цветом)
НОД(108; 72) = 36, т.
к. НОД(150; 225) = 75, т.к.
2 ∙ 2 ∙ 3 ∙ 3 = 36. 5 ∙ 5 ∙ 3 = 75.
Числа
правят миром.
Пифагор
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
ВЗАИМНО ПРОСТЫЕ ЧИСЛА
Найти наибольший общий делитель чисел:
а) 22 и 39; б) 56 и 31; в) 73 и 45; г) 44 и 63.
Если вы решали все примеры верно, то в ответе
всегда получалась 1.
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Наименьшим общим кратным натуральных чи-сел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Например: НОК чисел 75 и 60 равен300, т.е. наименьшему из натуральных чисел, которые
делятся без остатка на числа 75 и 60.
НОК(75 и 60) =300
ПОМНИ!
Чтобы найти наименьшее общее кратное несколь-
ких натуральных чисел , надо:
разложить их на простые множители;
выписать множители, входящие в разложение
одного из чисел;
добавить к ним недостающие множители из
разложений остальных чисел;
найти произведение получившихся множите-
лей.
∙
ДАВАЙТЕ ПОПРАКТИКУЕМСЯ
№2. Найдите НОК чисел: а) 108 и 72; б) 150 и 225.
Решение. Разложим числа на простые множители:
108 2 72 2 150 2 225 5
54 2 36 2 75 5 45 5
27 3 18 2 15 5 9 3
9 3 9 3 3 3 3 3
3 3 3 3 1 1
1 1
НОК(150; 225) = 5 ∙ 5 ∙ 3 ∙ 3 ∙ 2 = 450
НОК(108; 72) = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 2 = 216
РЕШИ САМОСТОЯТЕЛЬНО
№1.Найдите:
а) НОД (81 и 243) б) НОК(15 и 18)
в) НОД(72 и 108) г) НОК(36 и 48)
д) НОД(168 и 180) е) НОК(252 и 360)
ж) НОД(360 и 1050) з) НОК(396 и 180)
и)НОД(270;450 и 555) к) НОК(72;120 и 264)
Позволяет
решать
различные
задачи
Сокращение
дробей
Отыскание общего
знаменателя
дробей
ПРИМЕНЕНИЕ НОД И НОК ЧИСЕЛ
№2.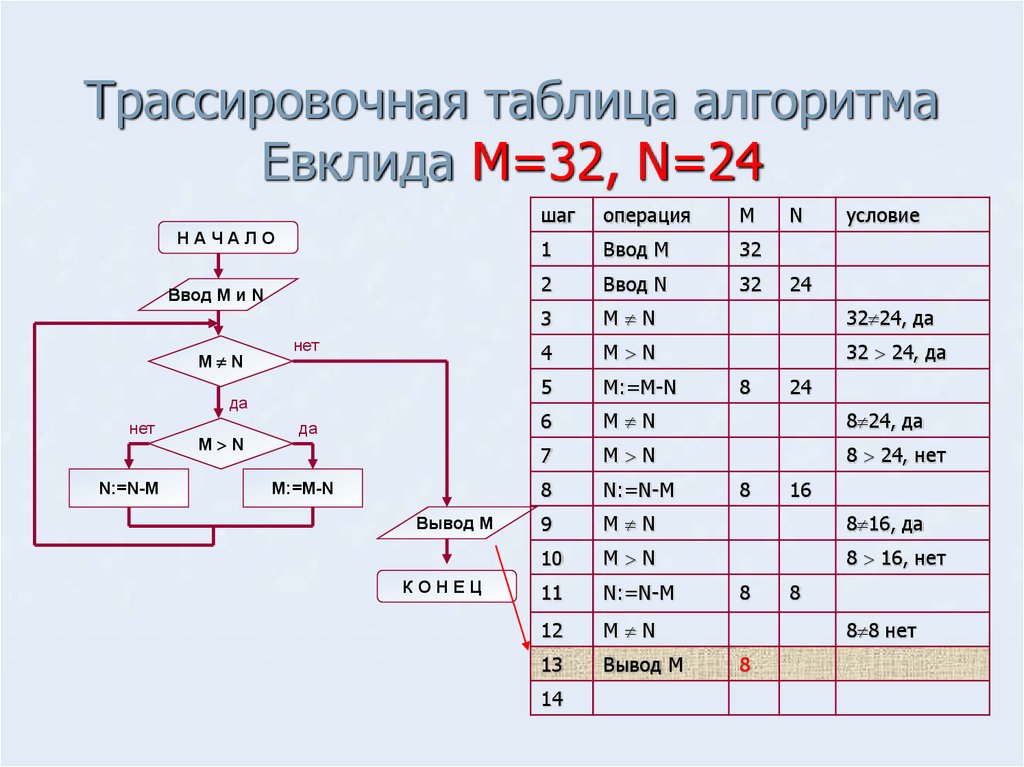
Сократите дроби:
а) ; б) ; в) ; г) .
№3. Приведите дроби к общему знаменателю:
а) и ; б) и .
ПРОВЕРЬ СЕБЯ
№1. а) 81; б) 90; в) 36 ; г) 144; д) 12; е)2520 ; ж) 30;
з) 1980; и) 15; к) 3960.
№2. а) ; б) ; в) ; г) .
№3. и ; и .
Попытайся сократить такую дробь: . Трудно? А как выполнить это
задание быстро и легко, не раскладывая числа на простые множители?
Оказывается это возможно осуществить с помощью алгоритма Евклида.
АЛГОРИТМ ЕВКЛИДА
Во многих случаях, когда числитель и знаменатель делятся на число (например на 19, на 37 и т.
д.), а признака делимости мы не знаем, НОК числителя и знаменателя находят с помо-щью, так называемого, алгоритма Евклида.
Суть его проста: делится большее число на меньшее. Затем меньшее делится на первый остаток. При этом получается второй остаток. Дальше первый остаток делится на второй и процесс продолжается. Он конечен и последний неравный нулю остаток и будет наибольший общим делителем. Прием этот занимателен, он называется –алгоритм Евклида – реко-мендуем его испробовать.
Продемонстрируем его на примере.
СОКРАТИТЬ ДРОБЬ: .
Для того, чтобы сократить данную дробь найдем с помощью алгоритма Евкли-
да НОД чисел 5959 и 13433. Делим 13433 на 5959.
13433 5959
11918 2
5959 1515
4545 3
1515 1414
1414 1
1414 101
101 14
404 =
404
0
Последний неравный нулю остаток, т.е. 101 и будет наибольшим общим дели-
телем.
Разделим на 101 числитель и знаменатель. Получим дробь: .
РЕШИ САМОСТОЯТЕЛЬНО
№1. С помощью алгоритма Евклида сократить дроби:
а) б) в) г) д)
; ; ; ; .
№2. Найдите НОД чисел:
а) 2304 и 5220; б) 8136 и 12250; в) 1348 и 1126;
г) 42628 и 33124; д) 71004 и 154452.
№3. Какой наименьшей длины должна быть доска, чтобы ее можно было раз-
резать поперек на части, равные 20см и 27см, не получив обрезков?
№4. Какое наибольшее число одинаковых комплектов можно составить из
елочных игрушек, если имеется 12 зайцев, 24 лисицы, 16 морковок и 48
яблок?
№5. Найдите НОК и НОД чисел, затем сравните произведение этих чисел с
произведением НОК и НОД:
а) 14 и21; б) 24 и 36; в) 32 и 48; г) 18 и24; д) 25 и 35.
РЕШАЕМ И ПРОВЕРЯЕМ
№1.
№2.
№3.
№4.
№5.
а) НОД (14; 21) = 7; б) НОД (24; 36) = 12;
НОК (14; 21) = 42. НОК (24; 36) = 72.
в) НОД (32; 48) = 16; г) НОД (18; 24) = 6;
НОК (32; 48) = 96. НОК (18; 24) = 72.
д) НОД (25; 35) = 5;
НОК (25; 35) =175.
ЗАМЕЧАТЕЛЬНОЕ СВОЙСТВО НОК И НОД
Заметили ли вы, что для любых натуральных чисел a и b выпол-
няется равенство:
НОД(a;b) НОК(a;b) = a b
Это свойство позволяет по заданным числам и известному НОД
находить НОК этих чисел.
a b
НОК(a;b) =
НОД(a;b)
ПРЕДЛАГАЮ РЕШИТЬ ЗАДАЧИ
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в коробке.
Какое наименьшее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну?
Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка» и 36 конфет «Белочка», если надо использовать все конфеты? Сколько конфет «Ласточка» и «Белочка» будет в каждом подар-ке?
Для поездки за город работникам завода было выделено несколько ав-тобусов, с одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477 человек — на озеро. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?
Конфеты «Сладкая математика» продаются по 12 штук в коробке, а кон-феты «Геометрия с орехами» – по 15 штук в коробке. Какое наимень-шее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну?
Коля, Серёжа и Ваня регулярно ходили в кинотеатр. Коля бывал в нём каждый 3-й день, Серёжа — каждый 7-й, Ваня — каждый 5-й.
Сегодня все ребята были в кино. Когда все трое встретятся в кинотеатре в сле-дующий раз?
ОТВЕТЫ
№1. НОД (36; 48) = 12; 36 : 12 = 3 (шт) конфет «Белочка»
48 : 12 = 4 (шт) конфет « Ласточка»
№2. НОД (424; 477) = 53; (424 + 477) : 53 = 17 (чел)
№3. 5 коробок «Сладкая математика», 4 коробки «Геометрия с ореха-
ми» . НОК(15; 12) = 60, 60 : 12 = 5, 60 : 15 = 4.
№4. На 105 день. НОК (3; 5; 7) = 105.
Спасибо за работу !
Успехов в учебе!
Презентация по математике на тему НОД и НОК чисел доклад, проект
Делители.
Наибольший общий делитель.
Наименьшее общее кратное.
Довлатбегян Виктория Александровна
учитель высшей категории
МБОУ «Лицей»
г.Протвино МО
Решите __________
84 : л = 14 84 : т = 7 84 : е = 21 84 : л = 4 84 : ь = 3 84 : д = 28 84 : е = 6 84 : и = 12
уравнения
л = т = е = л = ь = д = е = и =
6
12
4
21
28
3
14
7
л = т = е = л = ь = д = е = и =
6
12
4
21
28
3
14
7
Расположите числа в порядке возрастания
Делитель
3
4
6
7
12
14
21
28
«Числа правят миром» — Пифагор
12
Назовите все возможные варианты деления 12 яблок на равные части
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
12:
1, 2, 3, 4, 6, 12
Найдите все делители для чисел:
9:
18:
15:
20:
36:
48:
1, 3, 9
1, 2, 3, 6, 9, 18
1, 3, 5, 15
1, 2, 4, 5, 10, 20
1, 2, 3, 4, 6, 9, 12, 18, 36
1, 2, 3, 4, 6, 8, 12, 16, 42, 48
Подчеркните общие делители чисел:
9:
18:
15:
20:
36:
48:
1, 3, 9
1, 2, 3, 6, 9, 18
1, 3, 5, 15
1, 2, 4, 5, 10, 20
1, 2, 3, 4, 6, 9, 12, 18, 36
1, 2, 3, 4, 6, 8, 12, 16, 42, 48
Из общих делителей выделите наибольшее число:
Какое наибольшее число одинаковых подарков можно составить из 48 конфет «Ласточка», и 36 конфет «Чебурашка» если надо использовать все конфеты
48
36
: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
: 1, 2, 3, 4, 6, 9, 12, 18, 36
12
4
3
Наибольший Общий Делитель
НОД
На какое наибольшее количество ребят можно разделить поровну 12 яблок и 9 конфет?
12
9
12
6
3
1
2
2
3
9
3
1
3
3
НОД (9,12)=3
Нахождение наибольшего общего делителя:
Разложить числа на простые множители.
Найти одинаковые множители . У одного из чисел взять их в кружок.
Найти произведение тех множителей, которые взяли в кружок.
Наибольший общий делитель (НОД)
Пример нахождения
НОД чисел (способ 1):
Делители числа 12:
1; 2; 3; 4; 6; 12.
Делители числа 16:
1; 2; 4; 8; 16.
НОД чисел (12;16)=4
Наибольший общий делитель (НОД)
Пример нахождения НОД чисел (способ 2):
12=2·2·3
16=2·2·2·2
НОД чисел (1
НОД чисел (12;16)=4
НОД (36,48)=
?
36
18
9
3
1
2
2
3
3
48
24
12
6
3
1
2
2
2
2
3
НОД (36,48)=
2 · 2 · 3 =
12
НОД (9, 18) =
НОД (10, 7) =
НОД (15,20) =
НОД (35,14)=
НОД (24,60)=
9
1
5
7
12
№ 148
№ 152
Проверяем:
НОД (18, 60) =
НОД (72, 96, 120) =
НОД (35, 88) =
6
24
1
Самостоятельно:
НОД (7, 21) =
НОД (25, 9) =
НОД (8, 12) =
НОД (15, 40)=
НОД (7, 11)=
7
1
4
5
1
Ребята получили на новогодней ёлке одинаковые подарки.
Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на ёлке? Сколько апельсинов и сколько яблок было в каждом подарке?
123
41
1
3
41
82
41
1
2
41
НОД (123, 82) =
41
НОД (35, 40) =
НОД (77, 20) =
НОД (10, 30, 41) =
НОД (231, 280)=
5
1
1
7
Проверяем:
Находим:
НОД (18, 14, 6) =
НОД (26, 15, 9) =
НОД (12, 24, 48) =
НОД (30, 50, 70)=
2
1
12
10
Проверяем:
Числа
правят
миром.
ПИФАГОР
V век до н.э.
Взаимно простые числа
Для поездки за город было выделено несколько автобусов с одинаковым количеством мест в каждом.
В лес поехали 424 человека, а на озеро – 277 человек. Все места в автобусах были заняты, и ни одного человека в автобусе не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?
Решение
424
212
106
53
1
2
2
2
53
477
159
53
1
3
3
53
НОД (424, 477) =
53
1
2
424 : 53 =
8
3
477 : 53 =
9
4
8 + 9 =
17
— Хлопните в ладоши, если число кратно 2
«Я самый внимательный»
— Запищите, если число кратно 5
— Топайте ногами, если число кратно 10
15
67
38
560
435
226
1000
539
3255
Что больше, произведение или сумма чисел:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
0 · 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9
0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
0
45
Назовите четырёхзначное число, записанное с помощью цифр:
1, 5, 7, 8
: 1578
— кратное 2
7518
5178 …
— кратное 5
: 1785
7185
8175 …
— кратное 3
: 1578
5718
7815 …
Наименьшее Общее Кратное
НОК
От одной пристани до другой ходят два катера.
Начинают работу одновременно в 8 ч утра. Первый катер на рейс туда и обратно тратит 2 часа, а второй – 3 часа. Через какое наименьшее время оба катера окажутся на первой пристани и сколько рейсов за это время сделает каждый катер?
Задача.
Решение
— кратные 2
— кратные 3
: 2, 4, 6, 8, 10, 12, 14, 16, 18…
: 3, 6, 9, 12, 15, 18, 21…
Наименьшее кратное:
6
Через 6 часов после начала работы два катера
одновременно окажутся на первой пристани
1
2
6 : 2 = 3 (рейса)
— 1 катер
3
6 : 3 = 2 (рейса)
— 2 катер
6
9
= 2 · 3
= 3 · 3
НОК (6, 9) =
2 · 3
· 3
НОК (6, 9) =
?
= 18
Нахождение наменьшего общего кратного:
Разложить числа на простые множители.
Выписать множители, входящие в разложение одного из чисел.
Добавить к ним недостающие множители из разложений других чисел.
Найти произведение получившихся множителей.
Наименьшее общее кратное (НОК)
Пример нахождения
НОК чисел (способ 1):
Кратные числу 12:
12; 24; 36; 48…
Кратные числу 16:
16; 32; 48…
НОК чисел (12;16)=48
Наименьшее общее кратное (НОК)
Пример нахождения
НОК чисел (способ 2):
12= 2·2·3
16=2·2·2·2
2·2·3·2·2=48
НОК чисел (12;16)=48
Шаг Володи 75 см, а шаг Кати 60 см. На каком наименьшем расстоянии они сделают по целому числу шагов?
?
Решение
Задача.
НОК (60,75) =
?
60
30
15
5
1
2
2
3
5
75
25
5
1
3
5
5
НОК (60,75) =
2 · 2 · 3 · 5
= 300 (см)
· 5
300 см
300 : 75 = 4
300 : 60 = 5
НОД и НОК в задачах
Задача
Ребята получили на
новогодние елки одинаковые
подарки.
Во всех подарках
вместе было 123 апельсина и
82 яблока. Сколько ребят
присутствовало на елке?
Сколько апельсинов и
сколько яблок было в каждом
подарке?
Решение задачи
Найдем НОД чисел 123 и 82
123=3·41
82=2 ·41
НОД(123,82)=41
123:41=3 (апельсина)
82:41=2 (яблока)
Ответ: на елке присутствовал 41 ребенок, в каждом подарке было по 3 апельсина и 2 яблока.
НОК (35, 12) =
?
35
12
= 5 · 7
= 2 · 2 · 3
НОК (35, 12) =
12 · 35
= 420
НОК (45,180) =
?
45
180
= 3 · 3 · 5
= 2 · 2 · 3 · 3 · 5
НОК (45,180) =
180
НОК (72, 99) =
?
72
99
= 2 · 2 · 2 · 3 · 3
= 3 · 3 · 11
НОК (72, 99) =
99 · 2 · 2 · 2
= 792
НОК (210,350) =
?
210
350
= 2 · 3 · 5 · 7
= 2 · 5 · 5 · 7
НОК (45,180) =
= 1050
350 · 3
НОД (9, 12) =
НОК (9, 12) =
?
?
9
12
= 3 · 3
= 2 · 2 · 3
НОД (9, 12) =
3
НОК (9, 12) =
36
9 · 12
3 · 36
108
=
Реши самостоятельно:
1.
Напишите все делители числа 24 45
2. Найдите наибольший общий делитель чисел 75 и 45 12 и 24
3. Найдите наименьшее общее кратное чисел 30 и 40 20 и 70
Проверь себя:
2) НОД (75,45)=3 5=15
1)24: 1, 2, 3, 4, 6, 8, 12, 24
1)45: 1, 3, 5, 9, 15, 45
2)НОД (12,24)=2 2 3=12
3)НОК (30,40)= =2 2 2 3 5=120
3)НОК (20,70)= =2 2 5 7=140
.
.
.
.
.
.
.
.
.
.
Объяснение дерева решений (классификация)
Деревья классификации и регрессии (CART) — один из наиболее часто используемых алгоритмов в машинном обучении, как это показано в Gradient Boosting. Это означает, что самые популярные пакеты, такие как XGBoost и LightGBM, используют CART для построения деревьев.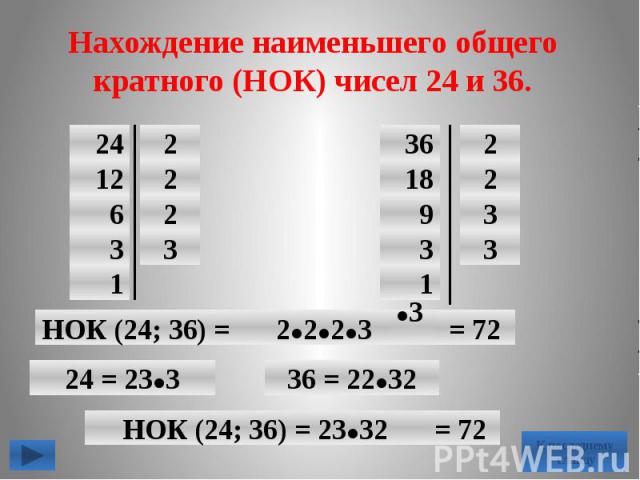
Дерево решений — это общий термин, и они могут быть реализованы разными способами — не путайте термины, мы имеем в виду одно и то же, когда говорим деревья классификации, и когда говорим деревья решений. Но дерево решений не обязательно является деревом классификации, оно также может быть деревом регрессии.
Мы будем изучать примесь Джини, которая поможет нам измерить качество разделения . Примесь Джини — это метрика классификации, которая измеряет, как мы должны создавать внутренние узлы и конечные узлы. Этот показатель отличается от индекса Джини и улучшения прироста информации/примесей, но похож на него.
- Терминология деревьев
- Примесь Джини: конечные узлы
- Загрязнение Джини: внутренние узлы
- Пример: построение дерева классификации
- Шаг 1: Поиск корневого узла
- Лихорадка
- Кашель и головная боль
- Работа с дискретными и непрерывными значениями
- Работа с: категориальными данными
- Шаг 2: Поиск внутренних узлов
- Левая сторона дерева
- Проверка последних двух листовых узлов
- Подведение итогов строительства дерева
- Шаг 1: Поиск корневого узла
- Регуляризация для тележек
- Дополнительное чтение
Терминология деревьев
Давайте сразу перейдем к определениям.
У нас есть корневые узлы, внутренние узлы и конечные узлы, каждый из которых показан на рисунке ниже:
- Корневой узел: самый первый узел в дереве.
- Внутренний узел: узлы, которые связаны с более глубокими узлами.
- Конечные узлы: узлы, которые не связаны с более глубокими узлами, но имеют связанный с ними внутренний узел.
В этой статье мы будем обозначать корневые и внутренние узлы синим цветом, а конечные узлы — мятно-зеленым.
Некоторая общая терминология для деревьев — понятие родителей и детей. Узлы выше определенного узла называются родительскими узлами, а узлы ниже называются дочерними узлами.
Примесь Джини для конечных узлов
При вычислении примеси Джини для одного конечного узла у нас может быть несколько классов $C$ – например. классы «ДА» и «НЕТ». Ниже приведены шаги:
- Вычислить вероятности всех классов, учитывая выборки в листе $k$ 92
- Перебрать каждый конечный узел от $k=1$ до $K$ конечных узлов.
- Найдите примесь Джини для текущего $k$-го листа (с помощью первого уравнения, которое только что было объяснено.
- Подсчитайте количество наблюдений в $k$-м листе.
- Разделите на общее количество наблюдения во всех листовых узлах. лист содержит какие наблюдения? 9{K \, лист \, узлы}
\left(\frac{count(L_k)}{count(L_1,…,L_k)}\right) Gini(L_k)
$$Мы снова расширили определения в верхнем уравнении и упростили термины в нижнем уравнении. Определения математически одинаковы, но сумма/количество может сбивать с толку. Все, о чем вам нужно думать при расчете, это то, сколько наблюдений мы можем в настоящее время учитывать во внутреннем узле?
Пример построения дерева классификации
В первую очередь нам нужен набор данных, чтобы хотя бы начать думать о построении дерева классификации. Давайте определим этот набор данных, как показано ниже, с 5 примерами.
Мы хотим предсказать, есть ли у человека грипп. Нам дан набор данных, где у нас есть четыре признака: есть ли у человека лихорадка, кашель, головная боль и/или грипп? Мы используем $1 = \text{YES}$ и $0 = \text{NO}$, при этом каждое наблюдение индексируется в крайнем левом столбце.
ЛИХОРАДКА КАШЕЛЬ ГОЛОВНАЯ БОЛЬ ГРИПП 0 1 0 0 1 1 0 1 1 1 2 0 1 1 0 3 0 1 0 0 4 1 1 0 1 … … … … … 267 0 1 0 1 Как видно из таблицы, у нас есть $N=268$ наблюдений и $M=4$ признаков.
Обратите внимание, что N и M — это стандартные обозначения; N означает наблюдения, а M означает особенности. Мы также предполагаем, что в этом наборе данных нет пропущенных значений.Поиск корневого узла
Чтобы построить дерево решений, мы должны начать с поиска наилучшего признака для корневого узла — признака, который лучше всего разделяет наблюдения, измеряемые примесями.
Мы итеративно просматриваем функцию за функцией, чтобы найти примесь для каждой функции. Мы буквально проверяем, какая функция лучше всего разделяет данные.
Лихорадка
Начнем с лихорадки – и мы спросим, насколько хорошо функция лихорадка разделяет наши 268 наблюдений на грипп НЕТ и грипп ДА? После разделения на лихорадку ДА/НЕТ мы смотрим, сколько наблюдений на каждом листе имеет ДА/НЕТ для гриппа.
154 наблюдения оказались в левом конечном узле, а 114 наблюдений оказались в правом конечном узле. Мы можем видеть, что лихорадка хорошо разделяет наши данные, просто взглянув на соотношение $FLU=0$ и $FLU=1$ в каждом концевом узле.Это разделение выглядит хорошо, но давайте на самом деле измерим, насколько оно хорошо, используя наши уравнения ранее. Начнем с первого уравнения.
Шаг 1: Расчет примесей Джини для каждого конечного узла.
Мы можем рассматривать корневой узел как внутренний узел при вычислении примеси. Чтобы расширить уравнение, мы знаем наши два класса ДА (1) и НЕТ (0). Большая греческая сигма $\Sigma$ работает как цикл foreach, где мы просто перебираем каждый класс от $c=1$ до $C$ классов. 92
$$Но подождите, как мы измеряем вероятности? Мы могли бы спросить, учитывая наблюдения в Листе 1, насколько вероятно, что человек болеет гриппом? Теперь, как мы на самом деле измеряем это, помещая класс в числитель и общее количество наблюдений в листе в знаменателе.
$$
p(1|L_1) = \frac{138}{154},p(0|L_1) = \frac{16}{154}
$$В этих случаях мы можем думать о $ p(c|L_k)$ как подсчет количества наблюдений с классом c, деленное на количество наблюдений в листе k $\frac{count(c)}{count(L_k)}$.
92
= 0,266
$$Теперь, когда у нас есть примесь Джини для каждого листа, мы можем вычислить примесь Джини для признака лихорадки по второму уравнению.
Шаг 2: Расчет примесей Джини для лихорадки.
Мы знаем примесь Джини $L_1$ и $L_2$, мы только что вычислили их выше на шаге 1. Второй шаг — расширение суммирования. Мы понимаем, что у нас есть только два конечных узла, поэтому нам просто нужно расширить его до двух листьев.
9{К} \ влево (\ гидроразрыва { количество (L_k) } { количество(L_1,…,L_K) } \right)Джини(L_k) \\ знак равно \ влево (\ гидроразрыва { количество (L_1) } { количество (L_1 + L_2) } \право)Джини(L_1)\,+ \ влево (\ гидроразрыва { количество (L_2) } { количество (L_1 + L_2) } \right)Джини(L_2) \\ знак равно \влево(\фрак{154}{268} \вправо)0,186 + \ влево (\ гидроразрыва {114} {268} \ вправо) 0,266 \\ знак равно 0,22 \end{выравнивание} $$Мы получаем примесь Джини $0,22$.
Далее мы рассчитаем примесь Джини для других признаков — в конце мы выбираем корень как признак с наименьшей примесью Джини, поскольку мы можем считать этот признак наиболее чистым.Кашель и головная боль
Теперь, когда я уже показал вам, как вычислить примесь Джини для первого признака, мы быстро пройдемся по примеси Джини для признаков кашля и головной боли, поскольку тип данных одинаков. 9{К} \ влево (\ гидроразрыва { количество (L_k) } { количество(L_1,…,L_K) } \right)Джини(L_k) \\ знак равно \ влево (\ гидроразрыва { количество (L_1) } { количество (L_1 + L_2) } \право)Джини(L_1)\,+ \ влево (\ гидроразрыва { количество (L_2) } { количество (L_1 + L_2) } \right)Джини(L_2) \\ знак равно \влево(\фракция{132}{268} \вправо)0,496 + \ влево (\ гидроразрыва {136} {268} \ вправо) 0,3825 \\ знак равно 0,438 \end{выравнивание} $$ 9{К}} \ влево (\ гидроразрыва { количество (L_k) } { количество(L_1,.
..,L_K)
}
\right)Джини(L_k)
\\
знак равно
\ влево (\ гидроразрыва
{
количество (L_1)
}
{
количество (L_1 + L_2)
}
\право)Джини(L_1)\,+
\ влево (\ гидроразрыва
{
количество (L_2)
}
{
количество (L_1 + L_2)
}
\right)Джини(L_2)
\\
знак равно
\влево(\фракция{148}{268} \вправо)0,491
+ \ влево (\ гидроразрыва {120} {268} \ вправо) 0,339
\\
знак равно
0,423
\end{выравнивание}
$$Окончательная примесь Джини составляет $0,423$ для функции головной боли. Поскольку примесь Джини для признака лихорадки является самой низкой, признак лихорадки теперь становится корнем.
Лихорадка становится корневым узлом с примесью Джини на уровне $0,22$.Работа с дискретными/непрерывными значениями
Что, если бы наши данные вместо этого имели дискретные значения, например, возраст человека — 10, 15 и т. д. Как бы мы рассчитали примесь Джини? Мы не можем точно найти вероятность, потому что мы сейчас не работаем с классами.
ЛИХОРАДКА КАШЕЛЬ ГОЛОВНАЯ БОЛЬ ВОЗРАСТ ГРИПП 0 1 0 0 10 1 1 0 1 1 15 1 2 0 1 1 55 0 3 0 1 0 31 0 4 1 1 0 22 1 … … … … … … 267 0 1 0 21 1 Ну, на самом деле, мы можем найти вероятность и вычислить примесь Джини — нам просто нужно установить некоторые пороги для разделения.
Позвольте мне показать вам, как это сделать.Ниже приведен способ расчета примеси Джини для функции:
- Сортировать объект по возрастанию или убыванию.
- Для максимально возможного количества точек данных найдите среднее значение двух соседних строк. Мы называем каждое из этих средних значений порогом.
- Используйте каждое среднее значение в качестве порога и рассчитайте примесь Джини.
- Используйте порог с наименьшей примесью Джини для сравнения с другими функциями.
Если у нас есть первые 5 строк признака возраста в виде массива
[10, 15, 55, 31, 22], мы можем отсортировать его так, чтобы массив стал[10, 15, 22, 31, 55]. Затем мы можем найти средние значения между соседними точками данных.Таким образом, метод состоит в том, чтобы перебирать каждую строку, а затем находить среднее значение текущей строки плюс значение следующей строки. Это легко достигается путем сохранения индекса текущей строки и поиска следующего значения в массиве путем поиска index+1.
- Первый порог: $(10+15)/2 = 12,5$
- Второй порог: $(15+22)/2 = 18,5$
- Третий порог: $(22+31)/2 = 26,5$
- Четвертый порог: $(31+55)/2 = 43$
Теперь у нас есть четыре порога
[12.5, 18.5, 26.5, 43]. Мы находим примесь Джини, задавая вопрос: какова вероятность того, что данный вес МЕНЬШЕ заданного порога?$$
p(\text{all$_\text{веса}$} < \text{threshold}| \text{threshold})
$$И наоборот, какова вероятность того, что данное вес БОЛЬШЕ заданного порога?
$$
p(\text{all$_\text{веса}$} > \text{порог} | \text{порог})
$$Отлично, это идеально вписывается в наши расчеты примесей Джини, поскольку мы просто разделили наблюдения на два конечных узла для каждого порога. Мы строим 4 потенциальных разделения в дереве решений, а затем оцениваем, насколько хорошо прошло разделение. Обратите внимание, что мы перешли от использования 5 строк данных для создания пороговых значений к использованию всего набора данных для расчета примеси Джини.
На практике вы хотели бы сделать возможными пороги для всех соседних строк, но для этого примера мы будем использовать небольшое количество порогов для ясности. 92=0,4909
$$$$
Джини(I_1) = \left(\frac{83}{268}\right)0,4738 + \left(\frac{185}{268}\right)0,4909 = 0,4856
$$Поскольку примесь Джини для порога 26,5 является самой низкой, это означает, что мы разделяем на этом пороге, так как это оптимальное разделение по сравнению с остальными.
Работа с категориальными данными
Предположим, мы добавим в таблицу еще одну характеристику, называемую цветом глаз. Эта функция содержит строку букв, описывающую цвет глаз человека (очевидно). Но важной частью является строка, поскольку мы не можем точно вычислить примесь Джини на основе строкового значения.
ЛИХОРАДКА КАШЕЛЬ ГОЛОВНАЯ БОЛЬ КРАСКА ДЛЯ ГЛАЗ ГРИПП 0 1 0 0 Синий 1 1 0 1 1 Синий 1 2 0 1 1 Коричневый 0 3 0 1 0 Коричневый 0 4 1 1 0 Зеленый 1 . ..… … … … … 267 0 1 0 Коричневый 1 Какое решение? Современные решения, такие как scikit-learn или XGBoost, строят свои деревья решений, допуская только 3 типа данных: булевы значения, числа с плавающей запятой и целые числа . Это означает, что они также отвергают дату и время и все остальное, что не относится к этим трем типам данных. Вы также можете кодировать наблюдения даты и времени, но это тема для другого дня.
Это именно тот подход, которому мы должны следовать, и мы должны отклонять любые данные, которые имеют другой тип данных, чем логические значения, числа с плавающей запятой и целые числа. Это означает, что нам нужно преобразовать нашу строку в один из трех типов данных, чтобы алгоритм ее принял — популярный выбор — горячее кодирование.
Допустим, мы обнаружили, что существует три категориальных значения признака цвета глаз: синий, зеленый и коричневый .
Основная идея заключается в том, что мы превращаем каждое категориальное значение в отдельную функцию с логическим значением.ЛИХОРАДКА КАШЕЛЬ ГОЛОВНАЯ БОЛЬ ЦВЕТ ДЛЯ ГЛАЗ_Синий ЦВЕТ ДЛЯ ГЛАЗ_Зеленый ЦВЕТ ДЛЯ ГЛАЗ_Коричневый ГРИПП 0 1 0 0 1 0 0 1 1 0 1 1 1 0 0 1 2 0 1 1 0 0 1 0 3 0 1 0 0 0 1 0 4 1 1 0 0 1 0 1 . ..… … … … … … … 267 0 1 0 0 0 1 1 Вы видите, как мы получили три новые функции: ЦВЕТ_ГЛАЗ_ГОЛУБОЙ, ЦВЕТ_ГЛАЗ_ЗЕЛЕНЫЙ и ЦВЕТ_ГЛАЗ_КОРИЧНЕВЫЙ. Мы присваиваем им логическое значение (1 или 0), и на этом этапе мы можем обращаться с ними как со всеми другими функциями и вычислять примесь Джини, как я показал вам ранее.
Построение полного дерева решений
Теперь, когда мы рассмотрели, как мы вычисляем корневой узел, мы пройдемся по вычислению дочерних узлов в дереве, пока не закончим. Напомним, что мы обнаружили, что лихорадка была лучшей характеристикой в корневом узле, и она разделяет наблюдения таким образом, что 154 наблюдения идут слева, а 114 наблюдений — справа в дереве решений.
Сначала расширяем левую сторону, затем правую. Следующим шагом является вычисление примеси Джини для оставшихся признаков: кашля и головной боли.
Мы всегда сначала исследуем левую сторону вещей, затем возвращаемся и исследуем правую сторону. Это действительно тот же процесс, что и раньше, как вы увидите через мгновение.Здание с левой стороны
Сначала мы пытаемся разделить 154 наблюдения по признаку кашля. Процедура будет выглядеть точно так же, как и раньше — главное, что вам нужно понять, это то, что мы продолжаем пытаться разделить по новой функции, чем глубже мы погружаемся в дерево. Вот как это выглядит, когда мы исследуем лучшие функции для разделения в левой части дерева. Обратите внимание, как левый зеленый лист на изображении выше становится новым элементом синего цвета.
Обратите внимание, что функцию лихорадки больше нельзя использовать для разделения наблюдений, так как мы считаем, что эта функция используется. Функция может быть повторно использована только в том случае, если родительские узлы еще не использовали эту функцию, но, поскольку лихорадка находится в корне дерева, родительских узлов нет.
92=0,3911
$$$$
Джини(I_1) = \left(\frac{124}{154}\right)0,2919 + \left(\frac{30}{154}\right)0,3911 = 0,3112
$$Итак, примесь Джини для функции кашля составляет $0,3112$.
Следующим признаком является головная боль. Разделение выглядит следующим образом при разделении наблюдений на основе того, была ли у человека головная боль.
На первый взгляд функция головной боли также не разделяет наблюдения. Если вы посмотрите на соотношение между $FLU=1$ и $FLU=0$, мы увидим, что соотношение от кашля лучше. 92=0,4909
$$$$
Джини(I_1) = \left(\frac{80}{154}\right)0,4297 + \left(\frac{74}{154}\right)0,4909 = 0,4591
$$И оказалось, что примесь Джини для признака головной боли составляет 0,4591$, что намного выше, чем примесь Джини для признака кашля, который составлял 0,3112$. Теперь разделимся по признаку головной боли.
Последние два конечных узла
Теперь нам просто нужно посмотреть, разделяет ли головная боль два конечных узла лучше, чем то, что уже есть.
Начинаем снова с левой стороны.Теперь мы сопоставляем примесь Джини листа с потенциальным новым внутренним узлом. Напомним, примесь Джини для левого листа, где $кашель = 1$, равнялась 0,2919$, а примесь Джини для правого листа, где $кашель = 0$, равнялась 0,3911$. Это баллы, которые нам нужно побить, если мы хотим разделить нашу головную боль с последней функцией.
Давайте вычислим примесь Джини для головной боли с левой стороны, учитывая, что приведенное выше изображение показывает, как головная боль разделяет наблюдения. 92=0,3402
$$$$
Джини(I_1) = \left(\frac{101}{124}\right)0,076 + \left(\frac{23}{124}\right)0,3402 = 0,125
$$Мы разделились по признаку головной боли, поскольку примесь Джини $0,125$ для признака головной боли ниже, чем предыдущая примесь Джини $0,2919$ для листа, где $кашель = 1$.
Последнее, что нам нужно сделать, это вернуться и проверить второй листовой узел. Нам нужно знать, меньше ли примесь Джини $0,3911$.
Теперь, когда мы увидели раскол, он по-прежнему выглядит многообещающе. Впрочем, посмотрим, что из себя представляет примесь Джини. 92=0,4082
$$$$
Джини(I_1) = \left(\frac{16}{30}\right)0,375 + \left(\frac{14}{30}\right)0,4082 = 0,3905
$$Поскольку $0,3905$ меньше $0,3911$, нам снова придется разделить. На этом завершается построение левой стороны дерева.
Краткий обзор построения дерева
Давайте разобьем построение дерева на этапы для справки и максимально упростим понимание.
- Рассчитайте примесь Джини для каждого признака, как кандидата на то, чтобы стать следующим узлом в дереве классификации.
- а. Для каждой функции в unused_features
- б. Для каждого класса в функции
- в. Рассчитать примесь Джини для класса
- д. Рассчитать примесь Джини для признака
- Сравните все примеси Джини для всех неиспользуемых признаков и разделите наблюдения на основе признака с наименьшим примесем Джини.
- а. Сравните примеси Джини для всех неиспользуемых функций
- б. Если одна из примесей Джини меньше, чем примесь Джини для листового узла, разделите наблюдения с помощью функции с наименьшей примесью Джини.
Обратите внимание, что стратегия для корневого узла такая же, как и для внутренних узлов при поиске наилучшего разделения, за исключением того факта, что нет предыдущих конечных узлов, что означает, что мы пропускаем часть шага 2b.
Регуляризация для CART
Регуляризация — это когда мы пытаемся контролировать сложность модели машинного обучения таким образом, чтобы не подгонять или не подгонять наш набор данных. Обычно регуляризация работает путем добавления штрафа к оценке на основе параметров модели — штраф велик, когда параметры имеют большие значения, и штраф мал, когда параметры имеют малые значения.
Каковы примеры регуляризации деревьев классификации?
- Обрезка после тренировки. Это возвращает в дерево классификации и удаляет внутренние узлы и конечные узлы на основе вычислений оценки дерева. Алгоритм называется минимальной сложности сокращения сложности .
- Максимальная глубина дерева. Это может ограничить количество разбиений, которые мы можем использовать в дереве.
- Минимальное количество образцов, необходимое для разделения. Это делает так, что листовому узлу требуется не менее n наблюдений в конечном узле, если этот конечный узел должен быть разделен по признаку.
Есть и другие параметры, которые мы можем настроить, но это основные.
Вам понравилась эта статья? Затем вам понравится следить за реализацией деревьев классификации с нуля в Python, которая будет следующей.
Дополнительная литература
Я рекомендую посмотреть StatQuest для визуального объяснения деревьев классификации. Он действительно проходит через всю концепцию и хорошо объясняет.
Книги
- Деревья классификации и регрессии Лео Брейман и др. 1984. Это оригинальная книга о ТЕЛЕГАХ, поэтому, если у вас есть относительно хорошая математическая подготовка и вы хотите более сильную интуицию, рекомендуем прочитать ее.
- Введение в статистическое обучение, автор Hastie et al. 2013. Эта книга представляет собой общую книгу по машинному обучению и статистике. В главе 8 на стр. 303–332 есть несколько замечательных разделов, посвященных деревьям решений и ансамблевым методам.
Узловое стадирование — PMC
1. Steinkamp HJ, Cornehl M, Hosten N, Pegios W, Vogl T, Felix R. Шейная лимфаденопатия: отношение диаметра по длинной оси к диаметру по короткой оси как предиктор злокачественности. Бр Дж Радиол. 1995; 68: 266–70. дои: 10.1259/0007-1285-68-807-266. PMid:7735765. [PubMed] [Google Scholar]
2. Na DG, Lim HK, Byun HS, Kim HD, Ko YH, Baek JH. Дифференциальный диагноз шейной лимфаденопатии: полезность цветной допплерографии. AJR Am J Рентгенол. 1997;168:1311–6. [PubMed] [Google Scholar]
3. Steinkamp HJ, Mueffelmann M, Böck JC, Thiel T, Kenzel P, Felix R. Дифференциальная диагностика поражений лимфатических узлов: полуколичественный подход с цветной допплерографией.
Бр Дж Радиол. 1998; 71: 828–33. [PubMed] [Google Scholar]4. Чой М.Ю., Ли Дж.В., Джанг К.Дж. Различие между доброкачественными и злокачественными причинами шейной, подмышечной и паховой лимфаденопатии: значение допплеровского спектрального анализа. AJR Am J Рентгенол. 1995;165:981–4. [PubMed] [Google Scholar]
5. Magarelli N, Guglielmi G, Savastano M, et al. Поверхностная воспалительная и первичная неопластическая лимфаденопатия: диагностическая точность энергетической допплерографии. Евр Дж Радиол. 2004; 52: 257–63. doi:10.1016/j.ejrad.2003.10.020. PMid:15544903. [PubMed] [Google Scholar]
6. Adibelli ZH, Unal G, Gül E, Uslu F, Koçak U, Abali Y. Дифференциация доброкачественных и злокачественных шейных лимфатических узлов: значение B-режима и цветная допплерография. Евр Дж Радиол. 1998;28:230–4. doi: 10.1016/S0720-048X(97)00174-5. [PubMed] [Google Scholar]
7. Schroeder RJ, Maeurer J, Gath HJ, Willam C, Hidajat N. Анализ васкуляризации реактивно увеличенных лимфатических узлов с помощью цветной дуплексной сонографии.
J Oral Maxillofac Surg. 1999;57:1090–5. doi: 10.1016/S0278-2391(99)
-4. [PubMed] [Google Scholar]8. Дорфман Р.Е., Альперн М.Б., Гросс Б.Х., Сандлер М.А. Верхние абдоминальные лимфатические узлы: критерии нормального размера, определенные с помощью КТ. Радиология. 1991; 180:319–22. [PubMed] [Академия Google]
9. Magnusson, A. Размер нормальных забрюшинных лимфатических узлов. Acta Radiol Diagn (Stockh) 1983; 24:315–8. [PubMed] [Google Scholar]
10. Эйнштейн Д.М., Сингер А.А., Чилкот В.А., Десаи Р.К. Абдоминальная лимфаденопатия: спектр результатов КТ. Рентгенография. 1991; 11: 457–72. [PubMed] [Google Scholar]
11. Винникомб С.Дж., Норман А.Р., Николсон В., Муж Дж.Е. Нормальные тазовые лимфатические узлы: оценка с помощью КТ после бипедальной лимфангиографии. Радиология. 1995; 194:349–55. [PubMed] [Академия Google]
12. Гросс Б.Х., Глейзер Г.М., Оррингер М.Б., Спизарный Д.Л., Флинт А. Метастатическая бронхогенная карцинома в лимфатические узлы нормального размера: частота и значимость.
Радиология. 1988; 166 (1 часть 1): 71–4. [PubMed] [Google Scholar]13. Kayser K, Bach S, Bülzebruck H, Vogt-Moykopf I, Probst G. Место, размер и опухолевое поражение резецированных внелегочных лимфатических узлов при раке легкого. Дж. Хирург Онкол. 1990;43:45–9. дои: 10.1002/jso.2930430112. PMid:2153261. [PubMed] [Google Scholar]
14. Staples CA, Müller NL, Miller RR, Evans KG, Nelems B. Узлы средостения при бронхогенной карциноме: сравнение КТ и медиастиноскопии. Радиология. 1988;167:367–72. [PubMed] [Google Scholar]
15. McLoud TC, Bourgouin PM, Greenberg RW, et al. Бронхогенная карцинома: анализ стадирования в средостении с помощью КТ путем корреляционного картирования лимфатических узлов и отбора проб. Радиология. 1992; 182:319–23. [PubMed] [Google Scholar]
16. Brown G, Richards CJ, Bourne MW, et al. Морфологические предикторы состояния лимфатических узлов при раке прямой кишки с использованием МРТ высокого пространственного разрешения с гистопатологическим сравнением.
Радиология. 2003; 227: 371–7. doi: 10.1148/radiol.2272011747. Среднее: 12732695. [PubMed] [Google Scholar]17. Мацукума К., Цукамото Н., Мацуяма Т., Оно М., Накано Х. Предоперационное КТ-исследование лимфатических узлов при раке шейки матки – его корреляция с гистологическими данными. Гинекол Онкол. 1989; 33: 168–71. дои: 10.1016/0090-8258(89)
-1. [PubMed] [Google Scholar]18. Yang WT, Lam WW, Yu MY, Cheung TH, Metreweli C. Сравнение динамической спиральной КТ и динамической МРТ в оценке тазовых лимфатических узлов при раке шейки матки. AJR Am J Рентгенол. 2000;175:759–66. [PubMed] [Google Scholar]
19. Scatarige JC, Fishman EK, Kuhajda FP, Taylor GA, Siegelman SS. Узловые метастазы с низкой аттенюацией при карциноме яичка. J Comput Assist Томогр. 1983; 7: 682–7. [PubMed] [Google Scholar]
20. Barentsz JO, Jager GJ, van Vierzen PB, et al. Стадирование рака мочевого пузыря после трансуретральной биопсии: ценность быстрой динамической МРТ с контрастным усилением.
Радиология. 1996; 201:185–93. [PubMed] [Google Scholar]21. Noworolski SM, Fischbein NJ, Kaplan MJ, et al. Проблемы динамической МРТ с контрастным усилением шейных лимфатических узлов для выявления метастатического заболевания. J Magn Reson Imaging. 2003; 17: 455–62. дои: 10.1002/jmri.10280. PMid:12655585. [PubMed] [Академия Google]
22. Муж Ю.Э., Кох Д.М. Рак мочевого пузыря. В: Муж Дж. Э., Резнек Р. Х., редакторы. Визуализация в онкологии. Лондон: Мартин Дуниц Лтд.; 2004. стр. 343–74. [Google Scholar]
23. Голлуб М.Дж., Кастеллино Р.А. Хиллиозные цистерны: потенциальная имитация ретрокруральной лимфаденопатии на КТ. Радиология. 1996; 199: 477–80. [PubMed] [Google Scholar]
24. Schreurs LM, Pultrum BB, Koopmans KP, et al. Лучшая оценка узловых метастазов с помощью слияния ПЭТ/КТ по сравнению с параллельной ПЭТ/КТ при раке пищевода. Противораковый Рез. 2008; 28 (3B): 1867–73. [PubMed] [Академия Google]
25. Tiguert R, Gheiler EL, Tefilli MV, et al.
Размер лимфатических узлов не коррелирует с наличием метастазов рака предстательной железы. Урология. 1999; 53: 367–71. doi: 10.1016/S0090-4295(98)00518-4. [PubMed] [Google Scholar]26. Голимбу М., Моралес П., Аль-Аскари С., Браун Дж. Расширенная тазовая лимфаденэктомия при раке предстательной железы. Дж Урол. 1979; 121: 617–20. [PubMed] [Google Scholar]
27. Sohn KM, Lee JM, Lee SY, Ahn BY, Park SM, Kim KM. Сравнение МРТ и КТ при стадировании рака желудка. AJR Am J Рентгенол. 2000; 174:1551–7. [PubMed] [Академия Google]
28. Спенсер Дж., Голдинг С. КТ-оценка состояния лимфатических узлов при раке предстательной железы. Бр Дж Радиол. 1992; 65: 199–201. дои: 10.1259/0007-1285-65-771-199. PMid:1547445. [PubMed] [Google Scholar]
29. Kim SH, Choi BI, Lee HP, et al. Рак шейки матки: сравнение данных КТ и МРТ. Радиология. 1990; 175:45–51. [PubMed] [Google Scholar]
30. Kim SH, Kim SC, Choi BI, Han MC. Рак шейки матки: оценка метастазов в тазовые лимфатические узлы с помощью МРТ.
Радиология. 1994;190:807–11. [PubMed] [Google Scholar]31. Williams AD, Cousins C, Soutter WP, et al. Обнаружение метастазов в тазовых лимфатических узлах при гинекологических злокачественных новообразованиях: сравнение КТ, МРТ и позитронно-эмиссионной томографии. AJR Am J Рентгенол. 2001; 177: 343–8. [PubMed] [Google Scholar]
32. Fukuda H, Nakagawa T, Shibuya H. Метастазы в тазовые лимфатические узлы от карциномы в полости таза: диагностика с помощью КТ тонкого среза. Клин Радиол. 1999; 54: 237–42. дои: 10.1016/S0009-9260(99)-3. [PubMed] [Google Scholar]
33. Oyen RH, Van Poppel HP, Ameye FE, Van de Voorde WA, Baert AL, Baert LV. Стадирование лимфатических узлов локализованной карциномы предстательной железы с помощью КТ и тонкоигольной аспирационной биопсии под контролем КТ: проспективное исследование 285 пациентов. Радиология. 1994; 190:315–22. [PubMed] [Google Scholar]
34. Костакоглу Л., Леонард Дж. П., Коулман М., Голдсмит С. Дж. Роль ФДГ-ПЭТ в лечении лимфомы.
Clin Adv Hematol Oncol. 2004;2:115–21. [PubMed] [Академия Google]35. Eisenhauera EA, Therasse P, Bogaerts J, et al. Новые критерии оценки ответа при солидных опухолях: пересмотренное руководство RECIST (версия 1.1) Eur J Cancer. 2009; 45: 228–47. doi:10.1016/j.ejca.2008.10.026. PM: 1
74. [PubMed] [Google Scholar]
36. Harisinghani MG, Barentsz J, Hahn PF, et al. Неинвазивное обнаружение клинически скрытых метастазов в лимфатических узлах при раке предстательной железы. N Engl J Med. 2003; 348: 2491–9. дои: 10.1056/NEJMoa022749. PMid:12815134. [PubMed] [Академия Google]
37. Thoeny HC, Triantafyllou M, Birkhaeuser FD, et al. Комбинация сверхмалых суперпарамагнитных частиц магнитно-резонансной томографии с усилением оксидом железа и диффузионно-взвешенной достоверно выявляет метастазы в тазовые лимфатические узлы в узлах нормального размера у пациентов с раком мочевого пузыря и простаты. Евр Урол. 2009; 55: 761–9. doi:10.1016/j.eururo.2008.12.034. PMid:19144456.
[PubMed] [Google Scholar]Количество лимфатических узлов и показатели выживаемости после резекции рака толстой и прямой кишки
Gastrointest Cancer Res. 2009 г.март-апрель; 3 (2 Приложение 1): S33–S35.
Информация об авторе Информация об авторских правах и лицензии Заявление об ограничении ответственности
Во время резекции толстой и прямой кишки может быть важно удалить и исследовать достаточное количество лимфатических узлов. Более обширная узловая резекция была связана с более низкой частотой рецидивов рака; позволяет более точно определить стадию рака и, таким образом, более целесообразно использовать адъювантную химиотерапию для пациентов с положительными лимфоузлами; и был связан с улучшением выживаемости после резекции рака толстой и прямой кишки. На количество исследованных лимфатических узлов влияют многие факторы, в том числе объем хирургической резекции, возраст пациента, локализация опухоли и методы патологии. Минимум 12 узлов был одобрен в качестве согласованного стандарта для проведения колэктомии в больнице при раке толстой кишки.
Однако использование количества лимфатических узлов, исследованных на уровне стационара, не может существенно повлиять на стадирование, использование адъювантной химиотерапии или выживаемость пациентов. При раке прямой кишки повышенное внимание к адекватным периферическим радиальным краям и использование предоперационной лучевой терапии для опухолей промежуточного и высокого риска может усложнить оценку взаимосвязи между количеством исследованных лимфатических узлов и результатами лечения пациентов; данные свидетельствуют о том, что количество лимфатических узлов (общее и количество положительных) в ректальном образце значительно ниже после проведения предоперационной лучевой терапии. Несмотря на то, что остается мало споров о прогностической важности увеличения числа лимфатических узлов для отдельных пациентов, неясно, является ли количество лимфатических узлов полезным индикатором качества больницы.Качество хирургической резекции играет решающую роль в исходах лечения пациентов с раком толстой и прямой кишки.
Патологическая стадия, включая гистологическую степень, лимфатическую инвазию, инвазию сосудов, молекулярные маркеры и наличие поражения лимфатических узлов, дает важную прогностическую информацию. В дополнение к описанию степени поражения лимфатических узлов может быть важно исследовать достаточное общее количество лимфатических узлов. Адекватная хирургическая резекция важна для местного контроля рака. Получение большего количества лимфатических узлов может принести пользу пациентам, поскольку позволяет более точно определить стадию рака и правильно использовать адъювантную химиотерапию для пациентов с положительными лимфатическими узлами (стадия III).В результате наблюдается высокий уровень интереса к подсчету лимфатических узлов и показателям выживаемости пациентов с раком толстой и прямой кишки. В этой статье будет рассмотрена связь между количеством лимфатических узлов и долгосрочной выживаемостью; проверить, существует ли минимальное, подходящее или оптимальное количество лимфатических узлов, которые следует удалить после резекции по поводу рака толстой или прямой кишки; и изучить значение подсчета лимфатических узлов как индикатора качества лечения рака.
За прошедшие годы несколько исследований с использованием ретроспективных когортных данных и данных административных требований продемонстрировали улучшение выживаемости среди больных раком толстой кишки, у которых после резекции было исследовано большее количество узлов. В нескольких обсервационных исследованиях была обнаружена связь между оценкой «адекватного» количества лимфатических узлов и улучшением выживаемости. 1 , 2 Во многих исследованиях преимущества наблюдались в группах стадирования узлов, отмечая улучшение выживаемости с увеличением числа удаленных лимфатических узлов среди пациентов с раком толстой кишки с поражением узлов и поражением узлов. 3 , 4 Поскольку увеличение выживаемости наблюдалось у пациентов с известным поражением лимфатических узлов, было предложено терапевтическое преимущество извлечения верхних лимфатических узлов.
В недавнем систематическом обзоре изучалось, связано ли количество лимфатических узлов, извлеченных после резекции толстой кишки, с выживаемостью.
5 Шестнадцать из 17 исследований, включающих в общей сложности 61 371 пациента, показали положительную связь между количеством исследованных лимфатических узлов и выживаемостью больных раком толстой кишки II и III стадии. Данные убедительны, и существует общее согласие относительно прогностического значения этой переменной для долгосрочной выживаемости отдельных пациентов с раком толстой кишки.Однако связь между количеством лимфатических узлов и выживаемостью при раке прямой кишки не столь однородна. Анализ 1664 пациентов из национального межгруппового исследования адъювантной терапии рака прямой кишки выявил связь между большим количеством обследованных узлов и выживаемостью только у пациентов с отрицательными узлами. 6 Хотя такие результаты могут подтверждать роль адекватного извлечения лимфоузлов для определения стадии, установить причинно-следственную связь между объемом резекции, количеством исследованных лимфоузлов и выживаемостью невозможно, поскольку эта связь не наблюдалась у пациентов с положительными лимфоузлами.
Международный союз по борьбе с раком, Американский объединенный комитет по раку и согласованная группа Национального института рака рекомендовали оценку не менее 12 узлов для обеспечения адекватного отбора проб. 7 – 9 Колледж американских патологоанатомов в течение многих лет рекомендовал патоморфологическое исследование не менее 12 лимфатических узлов, чтобы точно предсказать их отсутствие. 10 Если после тщательного макроскопического исследования обнаружено менее 12 узлов, рекомендуется использовать дополнительные методы улучшения зрения.
Тем не менее, популяционные данные показывают, что только 37% больных раком толстой кишки имеют адекватную оценку лимфатических узлов (т. е. исследуют не менее 12 узлов). 11 Фактически, озабоченность по поводу повсеместного занижения стадии больных привела к разработке рекомендаций по рассмотрению адъювантной химиотерапии у больных раком толстой кишки с небольшим количеством обследуемых узлов.
12 В недавнем систематическом обзоре подсчета лимфатических узлов сообщалось о широком диапазоне пороговых значений количества лимфоузлов, необходимого для связанного с этим улучшения выживаемости. 5 Выводы варьировались от 6 узлов 13 до 40 узлов. 14 Минимум в 12 узлов был одобрен многими группами, потому что было предположение о «убывающей отдаче» после изучения 12–17 узлов. 5 Однако неясно, улучшает ли более высокая скорость извлечения лимфатических узлов определение стадии рака толстой кишки, и причинно-следственный механизм между числом лимфатических узлов и выживаемостью остается неясным.
Многие факторы влияют на количество исследованных лимфатических узлов, включая объем хирургической резекции, возраст пациента, расположение опухоли и методы патологии. Факторы пациента также должны быть приняты во внимание; пожилой возраст и ожирение связаны с уменьшением восстановления лимфатических узлов.
11 , 15 Определенную роль может играть локализация опухоли, поскольку правосторонние опухоли обычно ассоциируются с большим количеством исследованных лимфатических узлов. 5 Количество пораженных лимфатических узлов также может отражать улучшенный иммунный ответ пациента; как таковая, взаимосвязь между количеством узлов и выживаемостью может быть искажена реакцией опухоль-хозяин, поскольку более сильный иммунологический ответ приводит к улучшению выживаемости. 16 Необходимо также учитывать факторы, зависящие от хирурга. Безусловно, объем резекции определяет хирург в операционной. Принятые онкологические принципы хирургической резекции включают резекцию пораженного сегмента толстой кишки и проксимальную перевязку питающей сосудистой ножки с лимфаденэктомией единым блоком связанных дренирующих лимфатических узлов. Если опухоль обнаружена между двумя дренирующими сосудами, важно включить распределение обоих этих сосудов.
Патологическая оценка после хирургической резекции имеет решающее значение для определения последующего лечения, поскольку адъювантная химиотерапия показана пациентам с метастазами в лимфатические узлы. Кроме того, лапароскопические резекции толстой кишки должны проводиться по тем же стандартам, что и открытые операции. 17 Резекция рака прямой кишки по анатомическим соображениям требует наличия адекватного окружного края. Выполнение тотальной мезоректальной эксцизии (ТМЭ) гарантирует, что жир, сосуды и лимфатические сосуды, содержащиеся в висцеральной тазовой фасции, удаляются единым блоком с ректальным раком. Вовлечение опухоли периферического края является наиболее важным фактором в прогнозировании местного рецидива и независимо увеличивает риск смерти от заболевания. 18 Также следует учитывать различия в объеме патологоанатомического исследования. Исследования показали, что различия в количестве исследованных лимфатических узлов могут быть связаны с тем, что ассистенты патологоанатома обрабатывают образцы 19 , или с практикой самих патологоанатомов.
20 Рак прямой кишки, особенно в контексте неоадъювантной терапии, заслуживает особого внимания при обсуждении частоты обследования лимфатических узлов. Предоперационная лучевая терапия, по-видимому, уменьшает количество исследованных лимфоузлов. 21 Неизвестно, уменьшает ли предоперационная химиолучевая терапия количество лимфатических узлов в большей степени, чем только облучение. Из-за более широкого использования предоперационной лучевой терапии у пациентов с раком прямой кишки среднего и высокого риска прогностическое значение количества лимфатических узлов при раке прямой кишки менее ясно.
Хотя стадия зависит от количества положительных узлов, большее количество проверенных узлов не обязательно предсказывает наличие большего количества задействованных узлов. Чтобы помочь скорректировать проблему низкого количества лимфатических узлов, было предложено использовать «соотношения лимфатических узлов», чтобы помочь стратифицировать риск у пациентов со стадией III.
Исследования показывают, что более низкое отношение количества положительных лимфоузлов к общему количеству исследованных лимфоузлов (рассчитанное как доля) связано как с безрецидивной выживаемостью, так и с общей выживаемостью при раке толстой кишки. 22 Недавно Национальный форум по качеству совместно с основными заинтересованными сторонами в области лечения рака, такими как Американское общество клинической онкологии (ASCO), Комиссия Американского колледжа хирургов по раку (CoC) и Национальный комплексный Раковая сеть (NCCN) одобрила минимальное количество 12 лимфатических узлов в качестве меры качества для улучшения результатов лечения пациентов с раком толстой кишки. 23 Хотя существует общепринятая связь между большим количеством извлеченных лимфатических узлов и улучшением долгосрочной выживаемости отдельных пациентов, механизм, лежащий в основе этой связи, полностью неизвестен. Индикатор качества предназначен для применения на уровне стационара, что кажется уместным, учитывая множество переменных, которые могут повлиять на результат.
Однако неясно, приведет ли этот показатель в конечном итоге к улучшению выживаемости пациентов с раком толстой кишки.Основываясь на недавнем анализе на уровне больниц, кажется, что большинство больниц не соответствуют минимальному количеству узлов в 12. 24 , 25 Количество лимфатических узлов, которые больницы исследуют в резекционных образцах рака толстой кишки, по-видимому, не оказывает существенного влияния на стадирование, использование адъювантной химиотерапии или выживаемость пациентов. 25 Вполне вероятно, что неучтенные факторы, связанные с пациентом или больницей, искажают взаимосвязь. Хотя существует консенсус в отношении того, что качество лечения рака можно улучшить, неясно, является ли обеспечение минимального количества лимфатических узлов правильной мерой качества для использования.
В то время как минимум 12 узлов обычно считается необходимым для точного стадирования, доказательства в поддержку этой меры как индикатора качества лечения рака отсутствуют на уровне стационара.
Многочисленные исследования и достаточные данные подтверждают, что удаление большего количества лимфатических узлов связано с улучшением выживаемости отдельных пациентов, но причинно-следственная связь, лежащая в основе этой взаимосвязи, неизвестна. При резекциях рака важно придерживаться строгих онкологических принципов, включая перевязку сосудов и полную резекцию брыжейки толстой кишки единым блоком, лимфаденэктомию и периферические края (при раке прямой кишки). Кроме того, патологоанатомам важно тщательно исследовать резецированные образцы.Раскрытие потенциальных конфликтов интересов
Д-р Вонг сообщил об отсутствии потенциальных конфликтов интересов.
1. Гольдштейн Н.С. Восстановление лимфатических узлов из 2427 образцов колоректальной резекции pT3 за 45 лет: рекомендации по минимальному количеству восстановленных лимфатических узлов на основе прогностических вероятностей. Ам Джей Патол. 2002;26:179–189. [PubMed] [Google Scholar]
2.
Swanson RS, Compton CC, Stewart AK, et al. Прогноз рака толстой кишки T3N0 зависит от количества исследованных лимфатических узлов. Энн Сург Онкол. 2003; 10: 65–71. [PubMed] [Академия Google]3. Чен С.Л., Бильчик А.Я. Более обширная узловая диссекция улучшает выживаемость при раке толстой кишки I-III стадий. Энн Сург. 2006; 244: 602–610. [Бесплатная статья PMC] [PubMed] [Google Scholar]
4. LeVoyer TE, Sigurdson ER, Hanlon AL, et al. Выживаемость при раке толстой кишки связана с увеличением числа анализируемых лимфатических узлов: вторичное исследование межгруппового исследования INT-0089. Дж. Клин Онкол. 2003;21:2912–2919. [PubMed] [Google Scholar]
5. Chang GJ, Rodriguez-Bigas MA, Skibber JM, et al. Оценка лимфатических узлов и выживаемость после радикальной резекции рака толстой кишки: систематический обзор. J Natl Cancer Inst. 2007;99: 433–441. [PubMed] [Google Scholar]
6. Tepper JE, O’Connell MJ, Niedzwiecki D, et al. Влияние количества извлеченных узлов на исход у пациентов с раком прямой кишки.
Дж. Клин Онкол. 2001; 19: 157–163. [PubMed] [Google Scholar]7. Собин Л.Х., Грин Ф.Л. Классификация TNM: уточнение количества региональных узлов для pN0. Рак. 2001;92:452. [PubMed] [Google Scholar]
8. Wittekind CH, Wagner G, редакторы. TNM-классификация злокачественных опухолей. Нью-Йорк, штат Нью-Йорк: Спрингер; 1997. Ободочная и прямая кишка; стр. 64–67. [Google Scholar]
9. Nelson H, Petrelli N, Carlin A, et al. Руководство 2000 г. по хирургии рака толстой и прямой кишки. J Natl Cancer Inst. 2001; 93: 583–596. [PubMed] [Google Scholar]
10. Compton CC, Fielding LP, Burgart LJ, et al. Прогностические факторы при колоректальном раке: Консенсусное заявление Коллегии американских патологоанатомов, 1999 г. Arch Pathol Lab Med. 2000; 124:979–994. [PubMed] [Google Scholar]
11. Baxter NN, Virnig DJ, Rothenberger DA, et al. Оценка лимфатических узлов у пациентов с колоректальным раком: популяционное исследование. J Natl Cancer Inst. 2005;97: 219–225.
[PubMed] [Google Scholar]12. Benson AB, Schrag D, Somerfield MR, et al. Рекомендации Американского общества клинической онкологии по адъювантной химиотерапии рака толстой кишки II стадии. Дж. Клин Онкол. 2004; 22:3408–4219. [PubMed] [Google Scholar]
13. Caplin S, Cerottini JP, Bosman FT, et al. Для пациентов с колоректальной карциномой Dukes B (стадия II по TNM) исследование шести или менее лимфатических узлов связано с плохим прогнозом. Рак. 1998; 83: 666–672. [PubMed] [Академия Google]
14. Джозеф Н.Э., Сигурдсон Э.Р., Хэнлон А.Л. и соавт. Точность определения отрицательности узлов при колоректальном раке на основе количества узлов, извлеченных при резекции. Энн Сург Онкол. 2003; 10: 213–218. [PubMed] [Google Scholar]
15. Gorog D, Nagy P, Peter A, et al. Влияние ожирения на восстановление лимфатических узлов из образцов ректальной резекции. Патол Онкол Рез. 2003;9:180–183. [PubMed] [Google Scholar]
16. Pages F, Berger A, Camus M, et al. Эффекторные Т-клетки памяти, раннее метастазирование и выживаемость при колоректальном раке.
N Engl J Med. 2005; 353: 2654–2666. [PubMed] [Академия Google]17. Флешман Дж., Сарджент Д.Дж., Грин Э. и др. Лапароскопическая колэктомия при раке не уступает открытой хирургии на основании 5-летних данных исследования COST Study Group. Энн Сург. 2007;246:655–662. [PubMed] [Google Scholar]
18. Birbeck KF, Macklin CP, Tiffin NJ, et al. Частота вовлечения окружного края варьируется у разных хирургов и позволяет предсказать результаты хирургического лечения рака прямой кишки. Энн Сург. 2002; 235:449–457. [Бесплатная статья PMC] [PubMed] [Google Scholar]
19. Остади М.А., Харниш Дж.Л., Стегиенко С. и соавт. Факторы, влияющие на количество лимфатических узлов, извлеченных в образцах колоректального рака. Surg Endosc. 2007;21:2142–2146. [PubMed] [Академия Google]
20. Lemmens VE, van Lijnschoten I, Janssen-Heijnen ML, et al. Образцы практики патологии влияют на оценку лимфатических узлов и исход рака толстой кишки: популяционное исследование. Энн Онкол. 2006; 17: 1803–1809.
$$
Мы немного расширили термины в верхнем уравнении для лучшей удобочитаемости, в то время как нижнее уравнение мы продолжим использовать.
$p(c|L_k)$ выглядит следующим образом:
Какова вероятность того, что класс $c$ верен, учитывая наблюдения в k-м листе (называемом $Leaf_k$)?
Если вас еще не устраивает мысль о вероятностях, я написал бесплатный пост, объясняющий некоторые основы теории вероятностей. Посетите пост и вернитесь позже, если вы чувствуете, что вам нужно освежить в памяти теорию вероятностей.
Теория вероятностей: теорема Байеса, правило суммы и правило произведения
В этом посте вам нужно слушать и действительно изучать основы. Все современные подходы к машинному обучению используют теорию вероятностей. АльфаСтар [https://deepmind.com/blog/alphastar-mastering-real-time-strategy-game-starcraft-ii/] — это пример, когда DeepMind создал множество различных ИИ с использованием новых…
Casper HansenMachine Learning From Scratch
Примесь Джини для внутренних узлов
Следующее, что нам нужно объяснить, это то, как вычисляется примесь Джини для внутреннего узла (и корневого узла, подробнее об этом позже).
Следующие шаги:
Обратите внимание, что N и M — это стандартные обозначения; N означает наблюдения, а M означает особенности. Мы также предполагаем, что в этом наборе данных нет пропущенных значений.
92 
Далее мы рассчитаем примесь Джини для других признаков — в конце мы выбираем корень как признак с наименьшей примесью Джини, поскольку мы можем считать этот признак наиболее чистым.
..,L_K)
}
\right)Джини(L_k)
\\
знак равно
\ влево (\ гидроразрыва
{
количество (L_1)
}
{
количество (L_1 + L_2)
}
\право)Джини(L_1)\,+
\ влево (\ гидроразрыва
{
количество (L_2)
}
{
количество (L_1 + L_2)
}
\right)Джини(L_2)
\\
знак равно
\влево(\фракция{148}{268} \вправо)0,491
+ \ влево (\ гидроразрыва {120} {268} \ вправо) 0,339
\\
знак равно
0,423
\end{выравнивание}
$$
Позвольте мне показать вам, как это сделать.
На практике вы хотели бы сделать возможными пороги для всех соседних строк, но для этого примера мы будем использовать небольшое количество порогов для ясности. 92=0,4909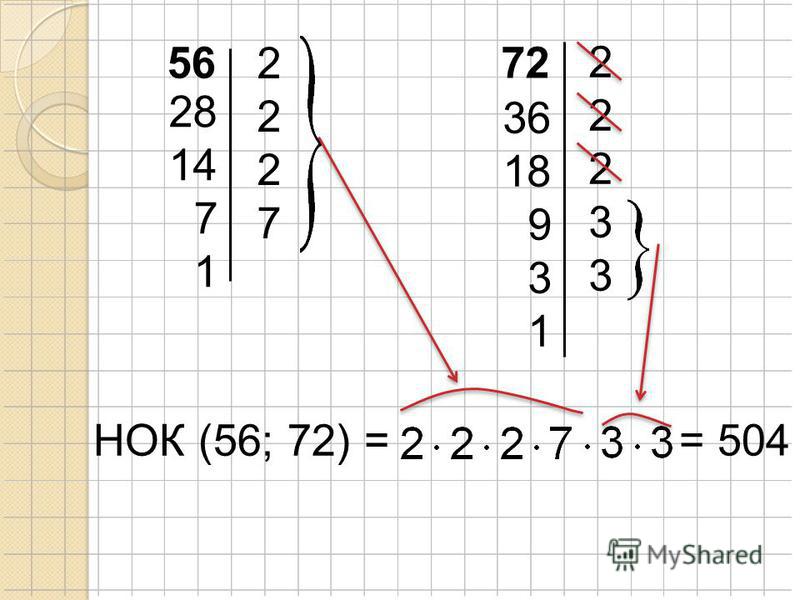 
..
Основная идея заключается в том, что мы превращаем каждое категориальное значение в отдельную функцию с логическим значением.
..
Мы всегда сначала исследуем левую сторону вещей, затем возвращаемся и исследуем правую сторону. Это действительно тот же процесс, что и раньше, как вы увидите через мгновение.
92=0,3911 
Начинаем снова с левой стороны.
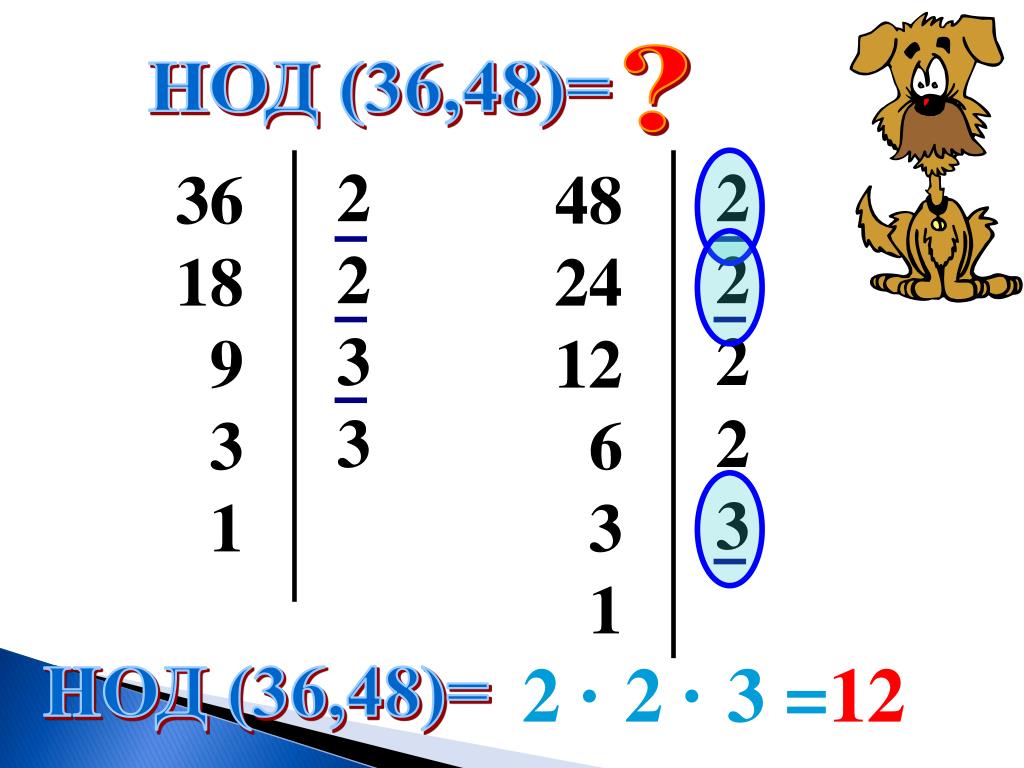
Алгоритм называется минимальной сложности сокращения сложности .
Бр Дж Радиол. 1998; 71: 828–33. [PubMed] [Google Scholar]
J Oral Maxillofac Surg. 1999;57:1090–5. doi: 10.1016/S0278-2391(99)
Радиология. 1988; 166 (1 часть 1): 71–4. [PubMed] [Google Scholar]
Радиология. 2003; 227: 371–7. doi: 10.1148/radiol.2272011747. Среднее: 12732695. [PubMed] [Google Scholar]
Радиология. 1996; 201:185–93. [PubMed] [Google Scholar]
Размер лимфатических узлов не коррелирует с наличием метастазов рака предстательной железы. Урология. 1999; 53: 367–71. doi: 10.1016/S0090-4295(98)00518-4. [PubMed] [Google Scholar]
Радиология. 1994;190:807–11. [PubMed] [Google Scholar]
Clin Adv Hematol Oncol. 2004;2:115–21. [PubMed] [Академия Google]
[PubMed] [Google Scholar]
Однако использование количества лимфатических узлов, исследованных на уровне стационара, не может существенно повлиять на стадирование, использование адъювантной химиотерапии или выживаемость пациентов. При раке прямой кишки повышенное внимание к адекватным периферическим радиальным краям и использование предоперационной лучевой терапии для опухолей промежуточного и высокого риска может усложнить оценку взаимосвязи между количеством исследованных лимфатических узлов и результатами лечения пациентов; данные свидетельствуют о том, что количество лимфатических узлов (общее и количество положительных) в ректальном образце значительно ниже после проведения предоперационной лучевой терапии. Несмотря на то, что остается мало споров о прогностической важности увеличения числа лимфатических узлов для отдельных пациентов, неясно, является ли количество лимфатических узлов полезным индикатором качества больницы.
Патологическая стадия, включая гистологическую степень, лимфатическую инвазию, инвазию сосудов, молекулярные маркеры и наличие поражения лимфатических узлов, дает важную прогностическую информацию. В дополнение к описанию степени поражения лимфатических узлов может быть важно исследовать достаточное общее количество лимфатических узлов. Адекватная хирургическая резекция важна для местного контроля рака. Получение большего количества лимфатических узлов может принести пользу пациентам, поскольку позволяет более точно определить стадию рака и правильно использовать адъювантную химиотерапию для пациентов с положительными лимфатическими узлами (стадия III).
5 Шестнадцать из 17 исследований, включающих в общей сложности 61 371 пациента, показали положительную связь между количеством исследованных лимфатических узлов и выживаемостью больных раком толстой кишки II и III стадии. Данные убедительны, и существует общее согласие относительно прогностического значения этой переменной для долгосрочной выживаемости отдельных пациентов с раком толстой кишки.
12 
11 , 15 Определенную роль может играть локализация опухоли, поскольку правосторонние опухоли обычно ассоциируются с большим количеством исследованных лимфатических узлов. 5 Количество пораженных лимфатических узлов также может отражать улучшенный иммунный ответ пациента; как таковая, взаимосвязь между количеством узлов и выживаемостью может быть искажена реакцией опухоль-хозяин, поскольку более сильный иммунологический ответ приводит к улучшению выживаемости. 16 
Патологическая оценка после хирургической резекции имеет решающее значение для определения последующего лечения, поскольку адъювантная химиотерапия показана пациентам с метастазами в лимфатические узлы. Кроме того, лапароскопические резекции толстой кишки должны проводиться по тем же стандартам, что и открытые операции. 17 
20 
Исследования показывают, что более низкое отношение количества положительных лимфоузлов к общему количеству исследованных лимфоузлов (рассчитанное как доля) связано как с безрецидивной выживаемостью, так и с общей выживаемостью при раке толстой кишки. 22 
Однако неясно, приведет ли этот показатель в конечном итоге к улучшению выживаемости пациентов с раком толстой кишки.
Многочисленные исследования и достаточные данные подтверждают, что удаление большего количества лимфатических узлов связано с улучшением выживаемости отдельных пациентов, но причинно-следственная связь, лежащая в основе этой взаимосвязи, неизвестна. При резекциях рака важно придерживаться строгих онкологических принципов, включая перевязку сосудов и полную резекцию брыжейки толстой кишки единым блоком, лимфаденэктомию и периферические края (при раке прямой кишки). Кроме того, патологоанатомам важно тщательно исследовать резецированные образцы.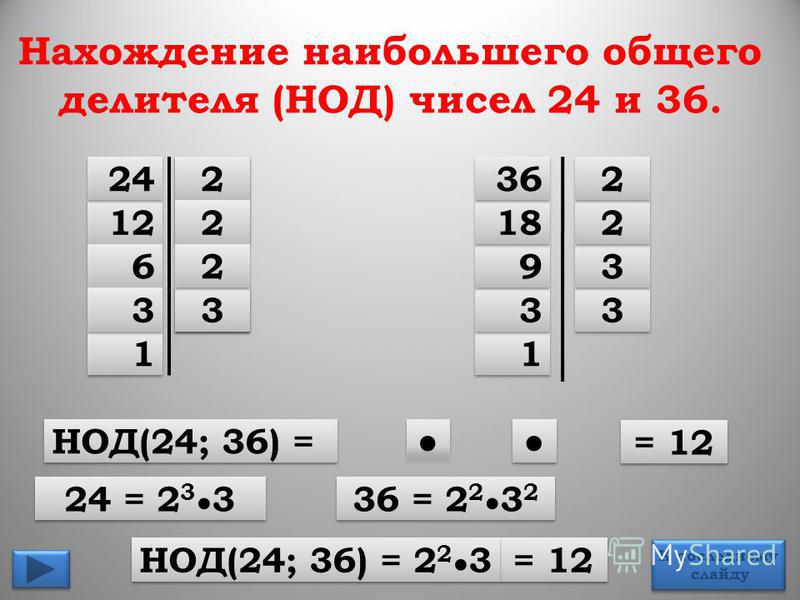
Swanson RS, Compton CC, Stewart AK, et al. Прогноз рака толстой кишки T3N0 зависит от количества исследованных лимфатических узлов. Энн Сург Онкол. 2003; 10: 65–71. [PubMed] [Академия Google]
Дж. Клин Онкол. 2001; 19: 157–163. [PubMed] [Google Scholar]
[PubMed] [Google Scholar]
N Engl J Med. 2005; 353: 2654–2666. [PubMed] [Академия Google]