Ноль в степени 0 – Почему при вычислении 0^0 на калькуляторе получается 1? Всегда думал, что ноль в степени ноль не имеет смысла, как и ноль в отрицательной степени.

Почему число в степени 0 равно 1?

☰

Существует правило, что любое число, кроме нуля, возведенное в нулевую степень, будет равно единице:
2⁰ = 1;      1.5⁰ = 1;      10000⁰ = 1

Однако почему это так?

Когда число возводится в степень с натуральным показателем, то имеется в виду, что оно умножается само на себя столько раз, каков показатель степени:

4³ = 4 × 4 × 4;      2⁶ = 2 × 2 × 2 × 2 × 2 × 2

Когда же показатель степени равен 1, то при возведении имеется всего лишь один множитель (если тут вообще можно говорить о множителях), и поэтому результат возведения равен основанию степени:

18¹ = 18;      (–3.4)¹ = –3.4

Но как в таком случае быть с нулевым показателем? Что на что умножается?

Попробуем пойти иным путем. Известно, что если у двух степеней одинаковые основания, но разные показатели, то основание можно оставить тем же самым, а показатели либо сложить друг с другом (если степени перемножаются), либо вычесть показатель делителя из показателя делимого (если степени делятся):

3² × 3¹ = 3²⁺¹ = 3³ = 3 × 3 × 3 = 27
4⁵ ÷ 4³ = 4^5–3 = 4² = 4 × 4 = 16

А теперь рассмотрим такой пример:

8² ÷ 8² = 8^2–2 = 8⁰ = ?

Что если мы не будем пользоваться свойством степеней с одинаковым основанием и произведем вычисления по порядку их следования:

8² ÷ 8² = 64 ÷ 64 = 1

Вот мы и получили заветную единицу. Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя.

И отсюда становится понятно, почему выражение 0⁰ не имеет смысла. Ведь нельзя делить на 0.

Можно рассуждать по-другому. Если имеется, например, умножение степеней 5

2 × 5⁰ = 5²⁺⁰ = 5², то отсюда следует, что 5² было умножено на 1. Следовательно, 5⁰ = 1.

scienceland.info

Задача: Сколько будет ноль в нулевой степени?

dude4fun сказал(а): ↑

через пределы:

но

ответ: неопределенность

кстати, стандарт IEEE 754 не запрещает для мат функции power() вернуть 1 для аргумента 0^0.

тем не менее,

http://www.wolframalpha.com/input/?i=0^0

тему можно закрывать, а мне поставить 0^0 лайков

Нажмите, чтобы раскрыть…

как то вы просто и быстро закрыли тему о которой математики не могут договориться уже около 300 лет. Эйлер, к примеру, еще в 18 веке считал, что ноль в нулевой степени равен 1.Раз уж Вы заговорили о пределах, то можно попробовать через пределы рассмотреть функцию x^x и что с ней происходит при стремящемся к 0 х

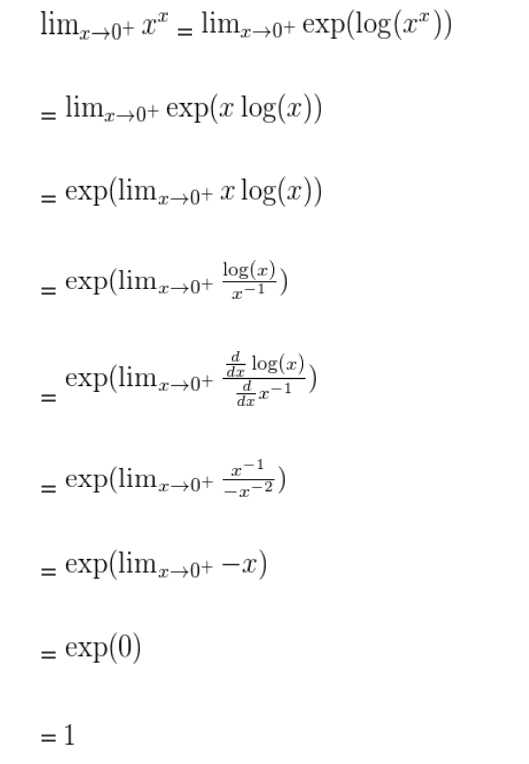
таким образом при стремящемся к нулю х , функция х^х=1, что означает 0^0=1
но не суть, ряд современных математиков разделяют мение Эйлера, что ноль в нолевой степени следует считать равным 1. Логика следующая. х^0 всегда следует считать равным 1 для того, чтобы биномиальная теорема была верна при х=0 и у=0, либо когда х=-у. Есть мнение, что биномиальная теорема слишком важна, чтобы делать из нее исключения, с другой стороны функцией 0^х можно пренебречь.

зы
что касается возврата неопределенности в вольфрамовской альфе, то у них так логический движок запрограммирован.
google возвращает 1, Ruby возвращает 1, R возвращает 1, калькуляторы майкрософт и эппл также возвращают 1

 

www.bmwclub.ru

Ответы@Mail.Ru: Ноль в степени ноль

неопределенность

Ноль в степени ноль КАК ЧИСЛО есть по определению единица. Такое определение принято, чтобы сохранить непрерывность функции ч в степени 0 для всех значений х, включая х=0). Если это ноль в степени ноль есть ФУНКЦИЯ, то это неопределённость.

Любое число, отличное от нуля, возведённое в нулевую степень, равно единице. Ноль в нулевой степени не определён.

Ноль в нулевой — единица, в дискретной математике 🙂 Ну а обычное определение — было 2 постами выше. т. е. скорее единица, чем неопределенность =)

Народ, ноль в нулевой степени не определен Лично я это со старших классов школы помню Да, виндовский калькулятор выдает 1, но это не верно Microsoft Excel — выдает ошибку при попытке вычисления 0 в нулевой степени.

Неопределенность. Смотрите Лопиталя 🙂

Если функцию (1+х) ⁿ разложить по формулеп Тейлора: (1+х) ⁿ =1+nx+n(n-1)x²/2!+..(каждый следующий член начинается с n) то при n=0 получаем 1 при любом х. Так что это вопрос определения.

предел (x)^0 при x->0 существует и равен 1, к тому же как тут (надеюсь верно) говорят, в дискретной математике у 0^0 есть значение равное 1 мое мнение: 1

Единица, поскольку 1 ноль раз умножить на 0 — получаем 0.

<a rel=»nofollow» href=»http://www.cleverstudents.ru/limits/types_of_uncertainties.html» target=»_blank»>http://www.cleverstudents.ru/limits/types_of_uncertainties.html</a>

touch.otvet.mail.ru

чему равен 0 в степени 0?

я думал, что это простой вопрос.. .0 в 0 — не существует, как врочем и log0 0 в любой степени 0.. и любое число в 0 степени равно 1… -заминка с 0 в 0… можете на калькулаторе проверить, в Экселе (=0^0) хоть где.. .нет существует… <a rel=»nofollow» href=»http://www.say2world.com» target=»_blank»>www.say2world.com</a> — интересно, занимательно, познавательно

Математику надо знать, число 0 в степени 0 не существует, просто не определено по определению.

из мат анализа 0^0 это неопределенность то ли первого, то ли второго рода (точно не помню) , при решении пределов эт все стараются как то разложить

Как раз таки ПО ОПРЕДЕЛЕНИЮ 0 в 0 степени равен 1. Это сделано из тех простых соображений, чтобы функция х в 0 степени была непрерывной для всех значений х. Но это именно формальное определение, верное для ЧИСЕЛ. Если 0 в 0 степени получается как функциональная неопределённость, то её надо раскрывать по соответствующим правилам.

ноль — он и в Африке ноль.. . степень — это количество перемножений данного числа на самого себя.. . если ноль в степени ноль, то его не умножали ни разу на ноль. . так нулем он и остался..

Любое число в степени ноль — один

touch.otvet.mail.ru