Среднее значение случайной величины – Характеристики случайной дискретной величины Среднее значение случайной величины

Характеристики случайной дискретной величины Среднее значение случайной величины

Пусть для случайной величины x возможные значения:

X1, x2, …, xk.

Измерения проводятся N раз, результат x_i наблюдается N_i раз, тогда

.

Среднее значение

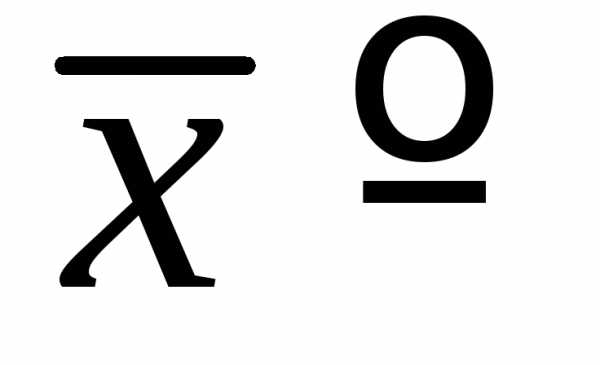(сумма результатов измерений)/(число всех измерений) = .

При с учетом (1.1)

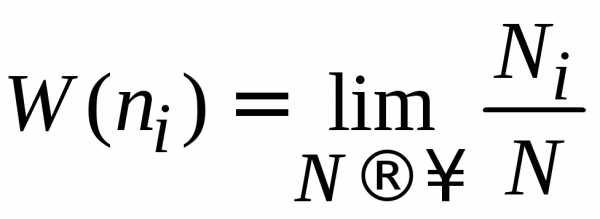
получаем

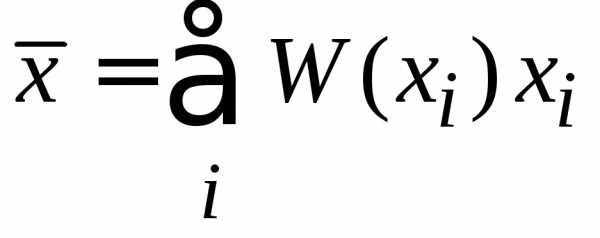. (1.5)

Для функции случайной величины

. (1.5а)

Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.

При 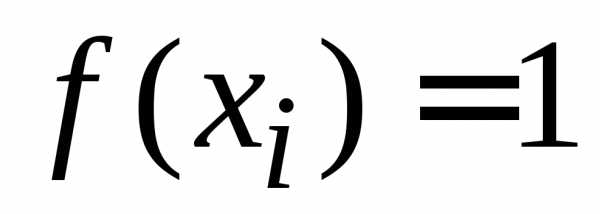получаем 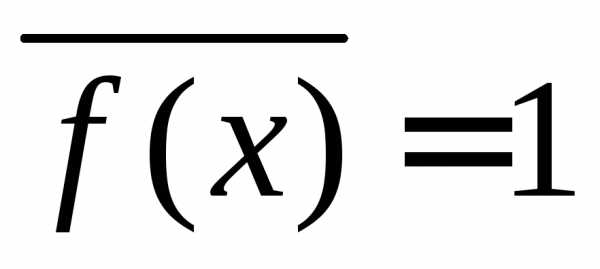и (1.5а) дает нормировку вероятностей

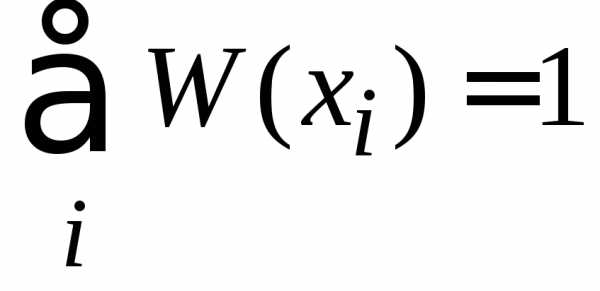. (1.6)

Свойства среднего

Для постоянной и независимых случайных величинx и y выполняется:

1)

– постоянный множитель выносится из под знака усреднения;

2)

– среднее от суммы/разности равно сумме/разности средних;

3)

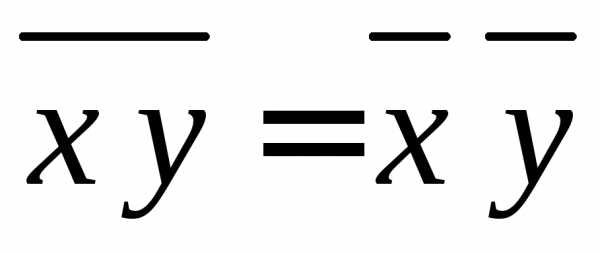
– среднее от произведения независимых величин равно произведению их средних.

Доказательство свойства 1

Из определения среднего (1.5а)

получаем

.

Доказательство свойства 2

Функция 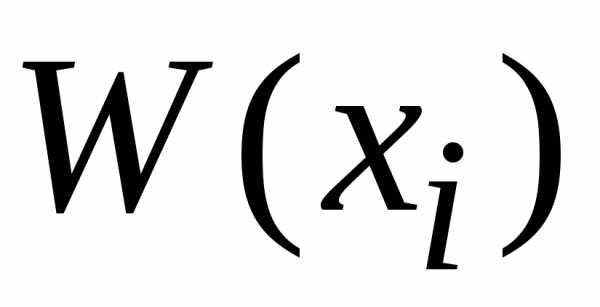, описывающая распределение вероятности дляслучайной величины x, одинакова для функци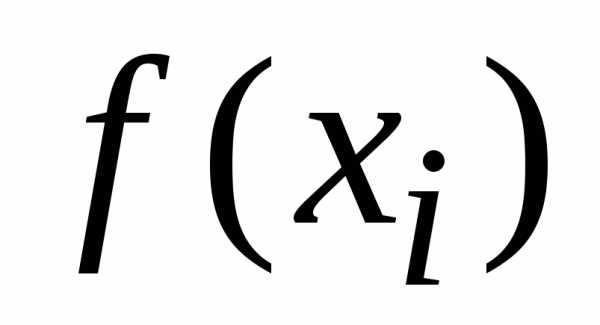й и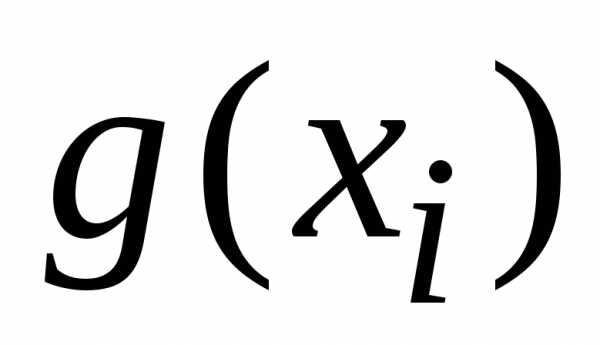, тогда из определения среднего (1.5а)

;

Доказательство свойства 3

Используем определение среднего и функцию распределения независимых случайных величин x и y. Согласно теореме о независимых событиях их вероятности перемножаются

.

Тогда получаем

.

Основные определения

Отклонение от среднего случайной величины

.

Среднее отклонение от среднего случайной величины равно нулю

.

Среднее квадратичное величины

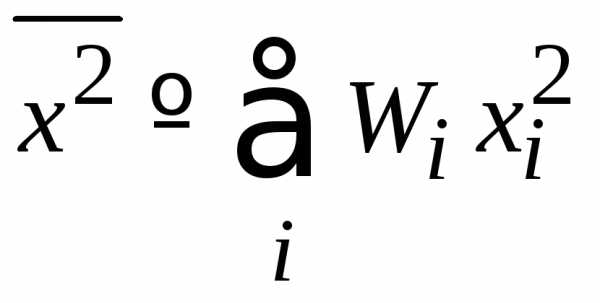. (1.7)

Для средних значений случайных величин x и y выполняется неравенство Коши–Буняковского–Шварца

. (1.7а)

Из (1.7а) при 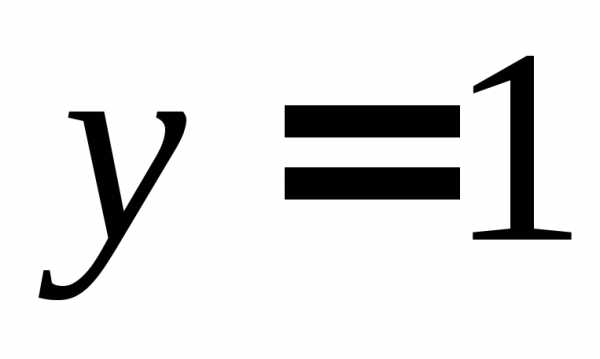находим

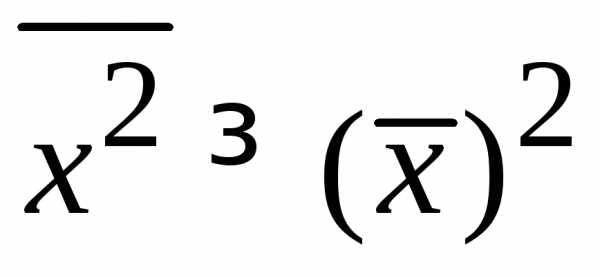. (1.7б)

Среднее квадратичное больше или равно квадрату среднего.

Дисперсия –­ среднее квадратичное отклонение от среднего

. (1.8)

Из (1.7б) получаем .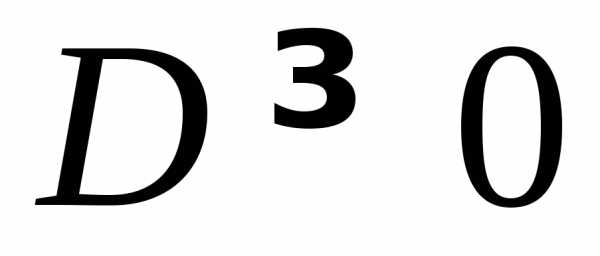

Флуктуация – корень квадратный из дисперсии

. (1.9)

Относительная флуктуация

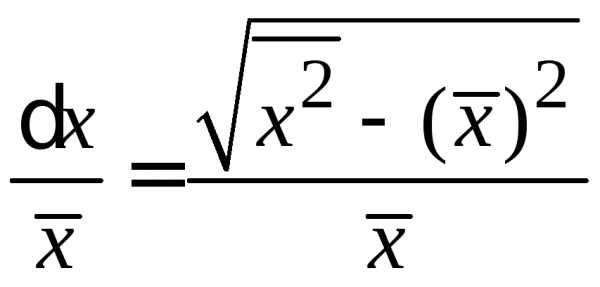. (1.10)

Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с .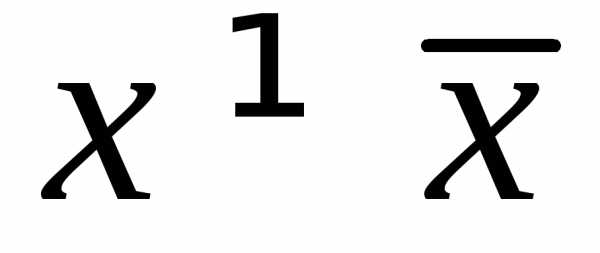

Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и для макроскопической системы она мала

. Примером аддитивной величины (от лат. additivus – «прибавляемый») является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.

Доказательство

Аддитивная величина X для системы равна сумме значений x_k для N независимых подсистем

.

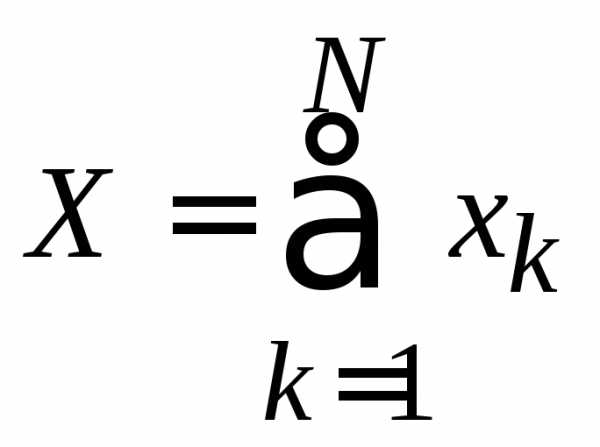По свойству 2 усреднения – среднее от суммы равно сумме средних

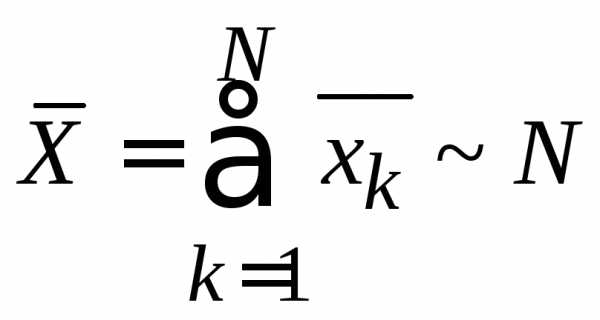
– пропорциональна числу подсистем.

Отклонение от среднего

,

дисперсия

.

При возведении в квадрат 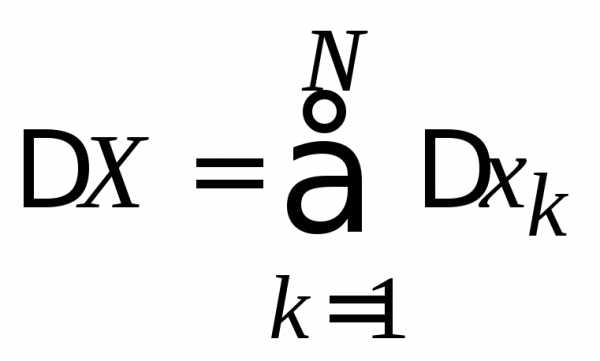и усреднении результата для перекрестных произведений учтено свойство 3 усреднения –среднее от произведения независимых величин равно произведению их средних

, ,

и использовано, что среднее отклонение от среднего равно нулю

.

Не равными нулю остаются квадраты величин. В результате флуктуация

.

Относительная флуктуация

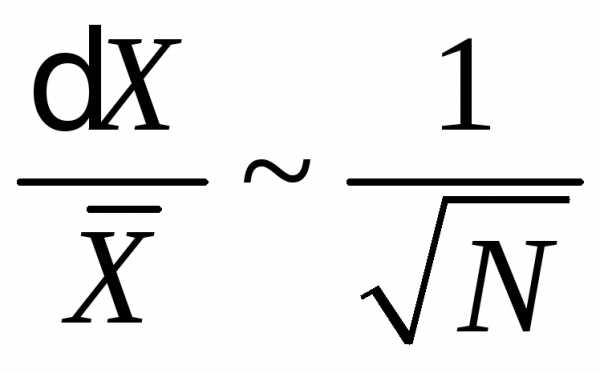(П.1.11)

уменьшается обратно пропорционально корню квадратному из числа независимых подсистем.

Производящая функция. Имеется случайная величина n, которая принимает дискретные значения в интервале . Вероятность получения результатаn равна 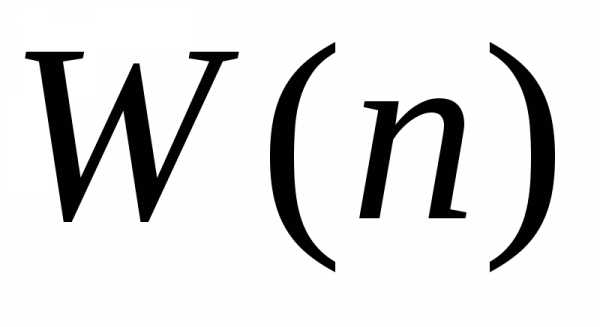. Определяем производящую функцию

. (П.1.14)

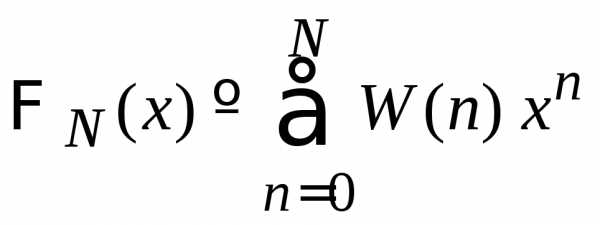
Если известна производящая функция, то распределение вероятности получаем из (П.1.14)

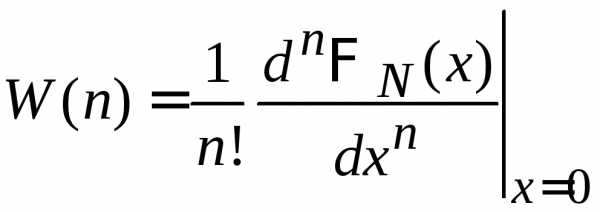, (П.1.15)

где использовано

Условие нормировки (1.6)

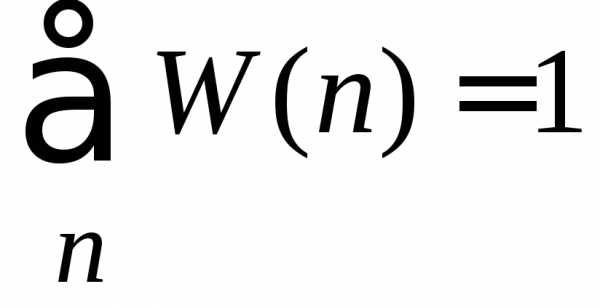
требует выполнения

. (П.1.16)

Для получения средних значений случайной величины дифференцируем (П.1.14)

,

и находим

. (П.1.17)

Двукратное дифференцирование (П.1.14)

дает

. (П.1.18)

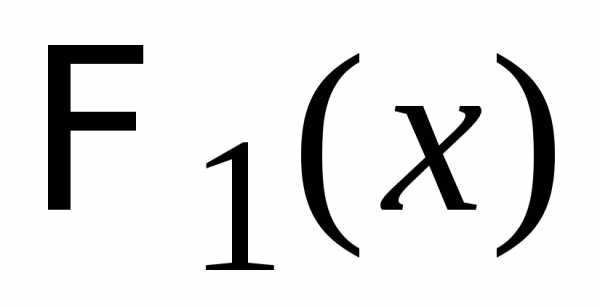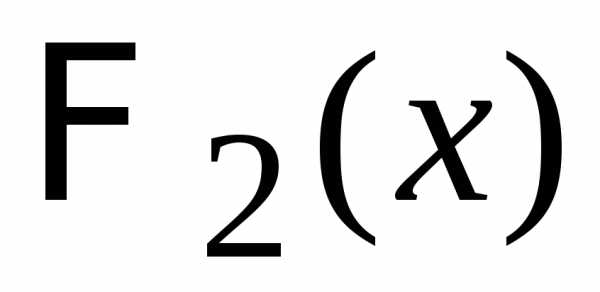Теорема о произведении производящих функций. Если происходят два независимых вида событий, которые описываются распределениями вероятностей с производящими функциями и, то распределение для суммы событий выражается произведением их производящих функций

. (П.1.19).

studfiles.net

2.Среднее значение (момента) случайных величин. Математическое ожидание, дисперсия.

Под моментом случайной величины подразумевается произведение значения этой величины на вероятность ее обнаружения.

Математическое ожидание — понятие среднего значения случайной величины в теории вероятностей. Обозначается или иногда (в русской литературе). В статистике часто используют обозначение .

Рассмотрим случайную величину с числовыми значениями. Часто оказывается полезным связать с этой функцией число – ее «среднее значение» или, как говорят, «среднюю величину», «показатель центральной тенденции». По ряду причин, некоторые из которых будут ясны из дальнейшего, в качестве «среднего значения» обычно используют математическое ожидание.

Определение. Математическим ожиданием случайной величины Х называется число

(Формула для дискретных значений)

(Формула для непрерывных значений)

т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.

[ Пример. Вычислим математическое ожидание числа, выпавшего на верхней грани игрального кубика. Непосредственно из определения МО следует, что

]

Дисперсия случайной величины — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается в русской литературе и в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.

Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда где символ обозначает математическое ожидание.

Свойства

если независимы;

[Пример

Пусть случайная величина имеет стандартное непрерывное равномерное распределение на т. е. её плотность вероятности задана равенством

Тогда

и

Тогда

]

Sources:Мат. ожидание 1, Мат. ожидание 2, Дисперсия

Дополнение: Момент случайной величины

3. Характеристическая функция случайных величин.

Характеристическая функция случайной величины

— один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости (сходимости по распределению).

Пусть есть случайная величина с распределением . Тогда характеристическая функция задаётся формулой:

.

Пользуясь формулами для вычисления математического ожидания, определение характеристической функции можно переписать в виде:

,

то есть характеристическая функция — это преобразование Фурье распределения случайной величины.

(Ф1). Характеристическая функция всегда существует:

Полезно вспомнить, что даже (Мат. ожидание) существует не всегда.

[ Доказательство. Воспользуемся свойством (Дисперсия не может быть отрицательной), равносильным неравенству :

(Ф2). По характеристической функции однозначно восстанавливается распределение (функция распределения, плотность или таблица распределения). Другими словами, если две случайные величины имеют одинаковые характеристические функции, то и распределения этих величин совпадают. ]

Формулы, с помощью которых по характеристической функции восстанавливается распределение, в анализе называют формулами «обратного преобразования Фурье». Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения и она находится по формуле

Ни одна из формул обратного преобразования Фурье нам не понадобится.

(Ф3). Характеристическая функция случайной величины связана с характеристической функцией случайной величины равенством

[ Пример.

Пусть имеет распределение Бернулли.

Случайная величина имеет распределение Бернулли, если она принимает всего два значения: и с вероятностями и соответственно. Таким образом:

,

.

Тогда:

. ]

Sources: Хар. функции 1, Хар. функции 2

Дополение: Хар.функции через привычные обозначения матожидания

studfiles.net

Математическое ожидание (среднее, среднее значение)

Математическое ожидание – это среднее значение случайной величины (теоретическое среднее). М.о. – одна из важнейших вероятностных характеристик случайной величины.

Буквенное обозначение математического ожидания случайной величины X : M(X).

Для дискретной случайной величины X математическое ожидание вычисляется как полная сумма произведений значений случайной величины на вероятности этих значений:

M(X) = x₁  P(x₁) + x₂  P(x₂) + … + x_N  P(x_N) =,

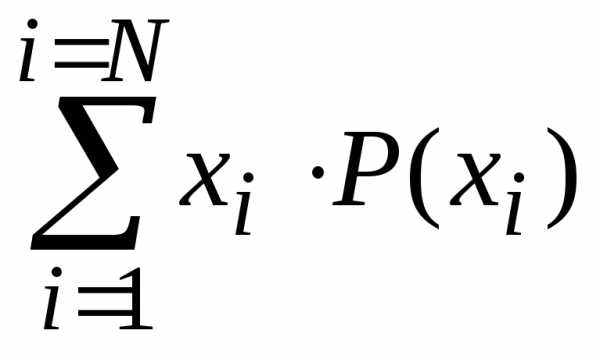где N – число возможных значений случайной величины X.

Для непрерывной случайной величины X математическое ожидание вычисляется как

M(X) =

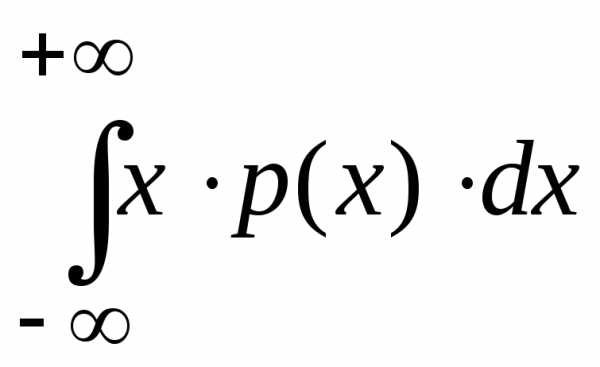
Математическое ожидание для дискретной случайной величины численно равно абсциссе центра закона распределения, для непрерывной случайной величины – абсциссе центра плотности распределения.

Термином математическое ожидание M(X) обозначается не только вероятностная характеристика, но и так называемая операция усреднения, т.е. взвешенное суммирование с весами, равными значениям закона распределения P(x_i), или интегрирование с ядром, равным плотности распределения p(x).

Запись M(…) используется для обозначения не только математического ожидания случайной величины X, но и для так называемой операции усреднения, т.е. суммирования с множителями (весами), равными значениям закона распределения P(x_i), или интегрирования с ядром, равным плотности распределения p(x).

Математическое ожидание совпадает с абсциссой центра тяжести закона распределения или плотности распределения. В ряде случаев близко к наиболее вероятному значению.

Дисперсия (рассеяние)

Дисперсия – это вероятностная характеристика степени рассеяния возможных значений случайной величины относительно её математического ожидания.

Буквенное обозначение дисперсии случайной величины X : D(X).

Дисперсия численно равна среднему квадрату отклонения случайной величины от своего среднего (математического ожидания):

D(X) = M( ( X – M(X) )² ).

Для дискретной случайной величины дисперсия вычисляется так:

D(X) = (x₁–M(X))² P(x₁) + … + (x_N–M(X))² P(x_N) =.

Для непрерывной случайной величины

D(X) = .

Единица измерения дисперсии – квадрат единицы измерения случайной величины.

Среднеквадратическое отклонение (стандартное отклонение)

Среднеквадратическое отклонение также как и дисперсия характеризует отклонение возможных значений случайной величины от математического ожидания, являясь вероятностной характеристикой закона распределения или плотности распределения.

Среднеквадратическое отклонение вычисляется как квадратный корень из дисперсии

.

В отличие от дисперсии, среднеквадратическое отклонение удобно тем, что измеряется в тех же единицах измерения, что и сама случайная величина.

Нормальное распределение (распределение Гаусса)

Нормальное распределение – особый вид плотности распределения непрерывной случайной величины

= N ( m;  ²) .

Нормальное распределение N ( m;  ²) зависит только от двух параметров, название которых соответствует их смыслу: m – математическое ожидание;  ² – дисперсия.

График нормального распределения представляет собой гладкую симметричную «колоколообразную» кривую с быстро убывающими «хвостами». Максимум нормального распределения располагается над точкой математического ожидания. Ширина вершинной части кривой определяется дисперсией. Чем дисперсия больше, тем кривая шире. И, при этом, ниже – для сохранения единичности площади под кривой.

Нормальное распределение возникает везде, где суммируется множество близких по силе случайных воздействий, причём вероятностные характеристики каждого из них не существенны. Поэтому нормально распределённые случайные величины имеют весьма широкое распространение.

studfiles.net

Характеристики случайной дискретной величины Среднее значение случайной величины

Пусть для случайной величины x возможные значения:

X1, x2, …, xk.

Измерения проводятся N раз, результат x_i наблюдается N_i раз, тогда

.

Среднее значение

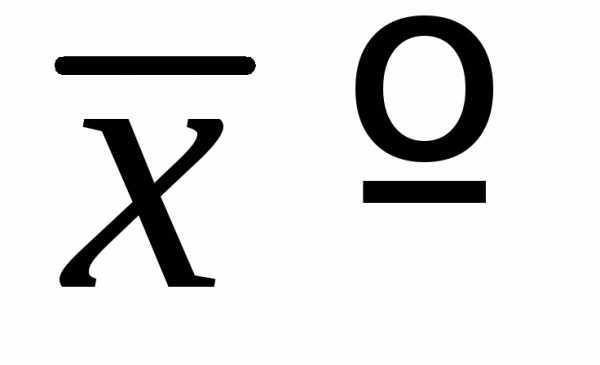(сумма результатов измерений)/(число всех измерений) = .

При с учетом (1.1)

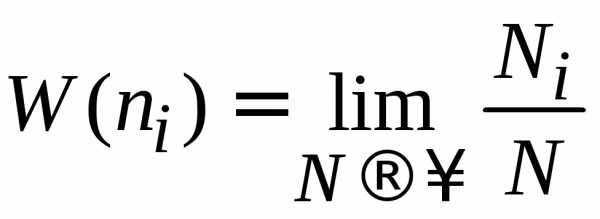
получаем

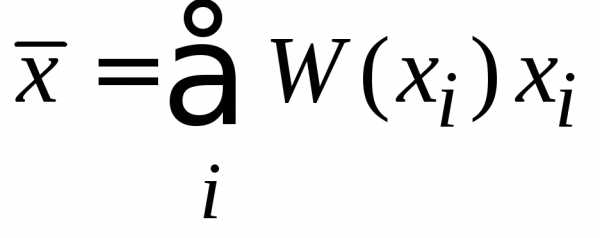. (1.5)

Для функции случайной величины

. (1.5а)

Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.

При 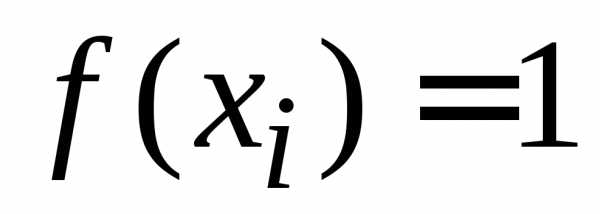получаем 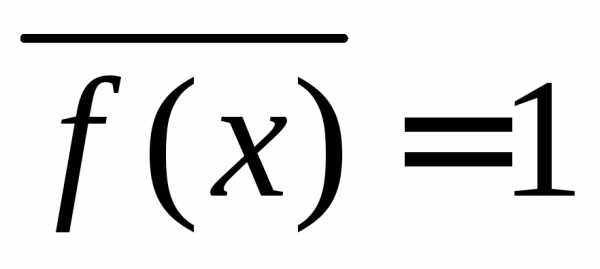и (1.5а) дает нормировку вероятностей

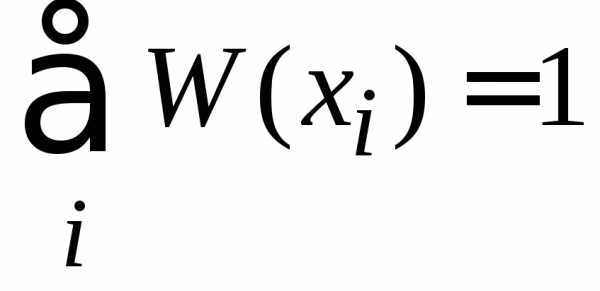. (1.6)

Свойства среднего

Для постоянной и независимых случайных величинx и y выполняется:

1)

– постоянный множитель выносится из под знака усреднения;

2)

– среднее от суммы/разности равно сумме/разности средних;

3)

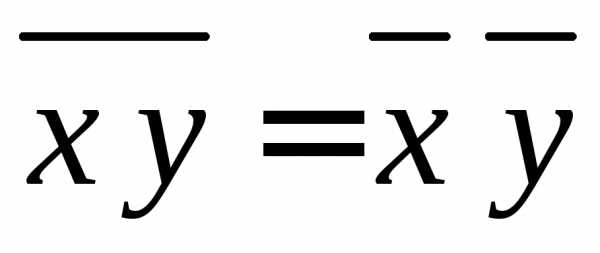
– среднее от произведения независимых величин равно произведению их средних.

Доказательство свойства 1

Из определения среднего (1.5а)

получаем

.

Доказательство свойства 2

Функция 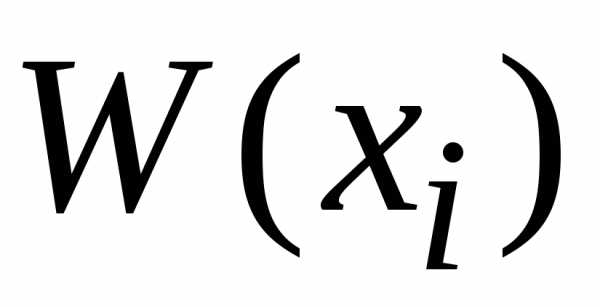, описывающая распределение вероятности дляслучайной величины x, одинакова для функци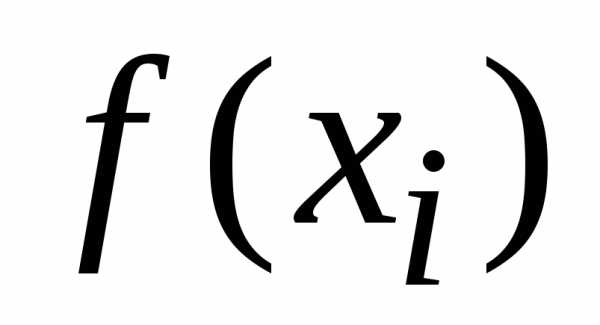й и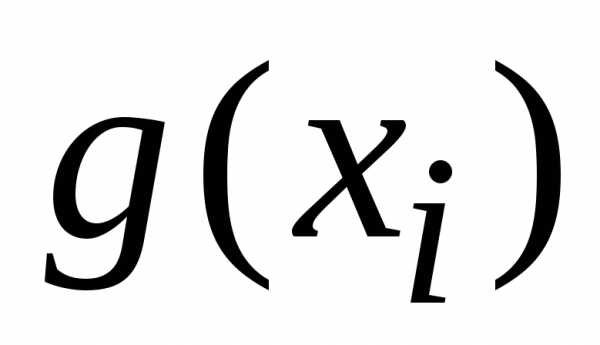, тогда из определения среднего (1.5а)

;

Доказательство свойства 3

Используем определение среднего и функцию распределения независимых случайных величин x и y. Согласно теореме о независимых событиях их вероятности перемножаются

.

Тогда получаем

.

Основные определения

Отклонение от среднего случайной величины

.

Среднее отклонение от среднего случайной величины равно нулю

.

Среднее квадратичное величины

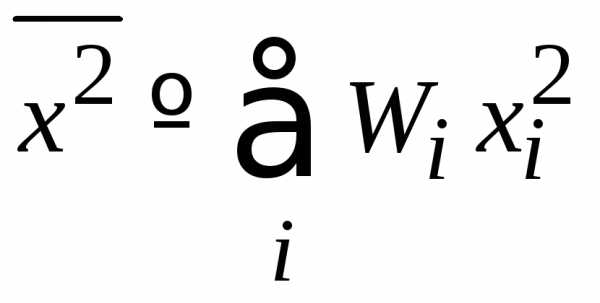. (1.7)

Для средних значений случайных величин x и y выполняется неравенство Коши–Буняковского–Шварца

. (1.7а)

Из (1.7а) при 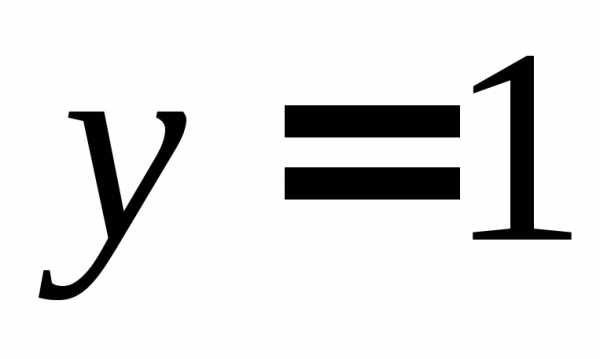находим

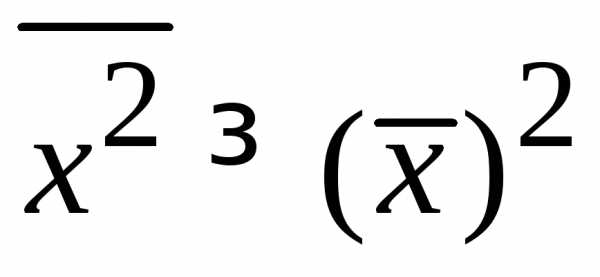. (1.7б)

Среднее квадратичное больше или равно квадрату среднего.

Дисперсия –­ среднее квадратичное отклонение от среднего

. (1.8)

Из (1.7б) получаем .

Флуктуация – корень квадратный из дисперсии

. (1.9)

Относительная флуктуация

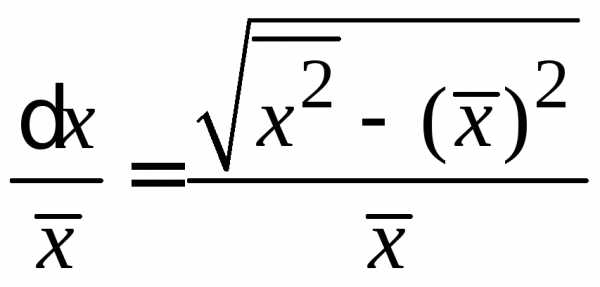. (1.10)

Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с .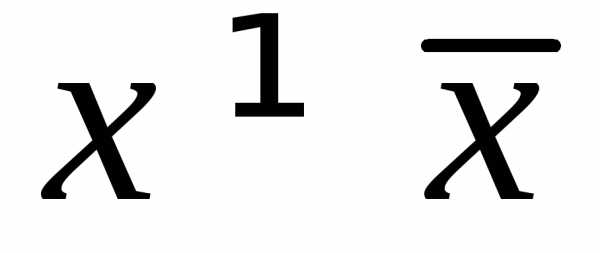

Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и для макроскопической системы она мала. Примером аддитивной величины (от лат. additivus – «прибавляемый») является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.

Доказательство

Аддитивная величина X для системы равна сумме значений x_k для N независимых подсистем

.

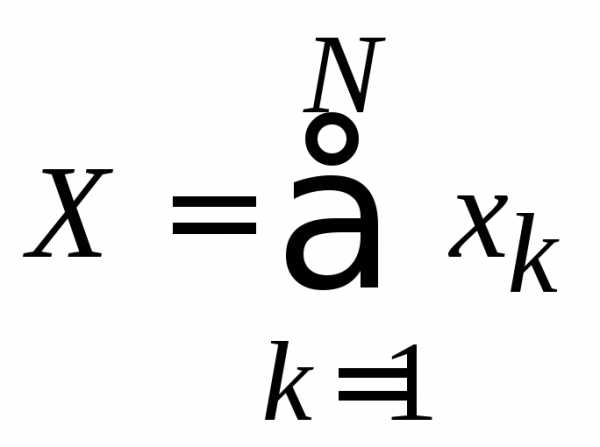По свойству 2 усреднения – среднее от суммы равно сумме средних

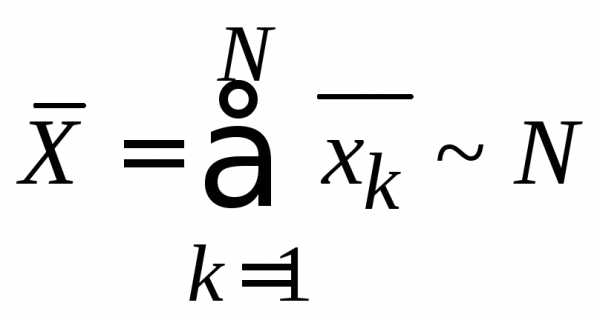
– пропорциональна числу подсистем.

Отклонение от среднего

,

дисперсия

.

При возведении в квадрат 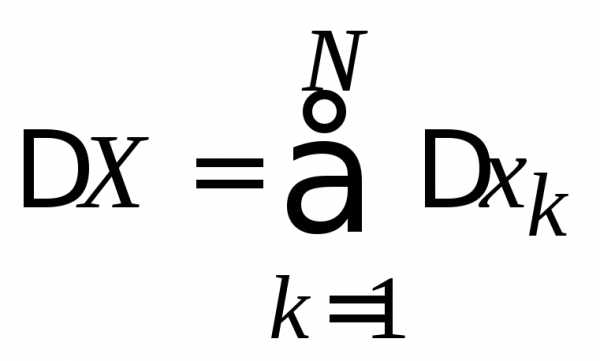и усреднении результата для перекрестных произведений учтено свойство 3 усреднения –среднее от произведения независимых величин равно произведению их средних

, ,

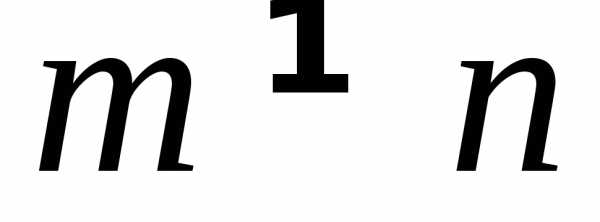и использовано, что среднее отклонение от среднего равно нулю

.

Не равными нулю остаются квадраты величин. В результате флуктуация

.

Относительная флуктуация

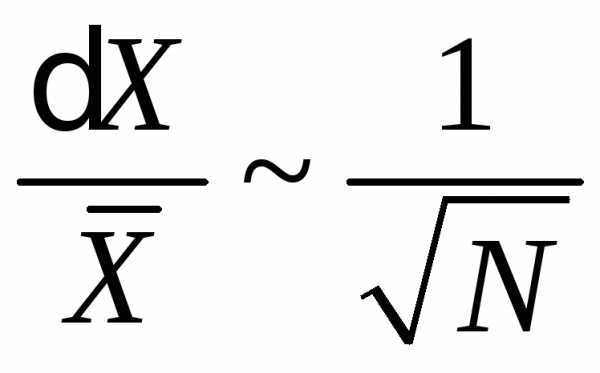(П.1.11)

уменьшается обратно пропорционально корню квадратному из числа независимых подсистем.

Производящая функция. Имеется случайная величина n, которая принимает дискретные значения в интервале . Вероятность получения результатаn равна 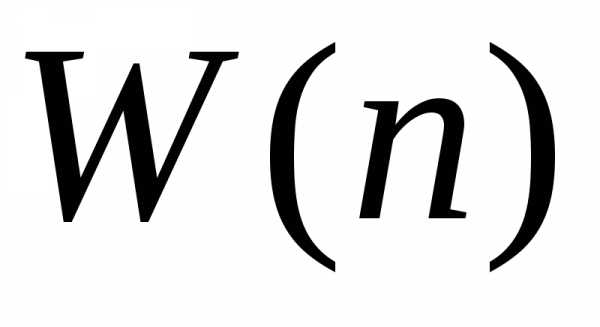. Определяем производящую функцию

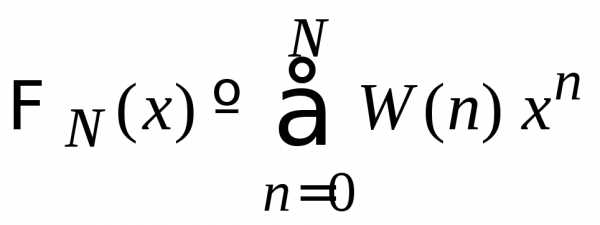. (П.1.14)

Если известна производящая функция, то распределение вероятности получаем из (П.1.14)

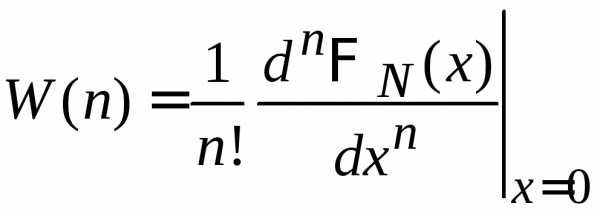, (П.1.15)

где использовано

Условие нормировки (1.6)

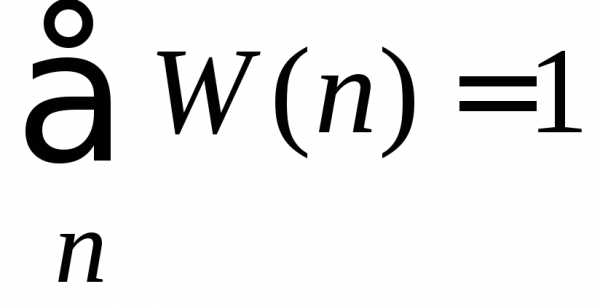
требует выполнения

. (П.1.16)

Для получения средних значений случайной величины дифференцируем (П.1.14)

,

и находим

. (П.1.17)

Двукратное дифференцирование (П.1.14)

дает

. (П.1.18)

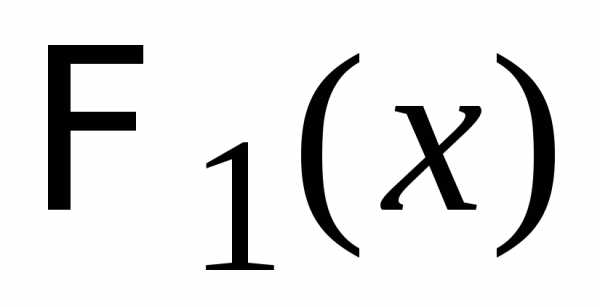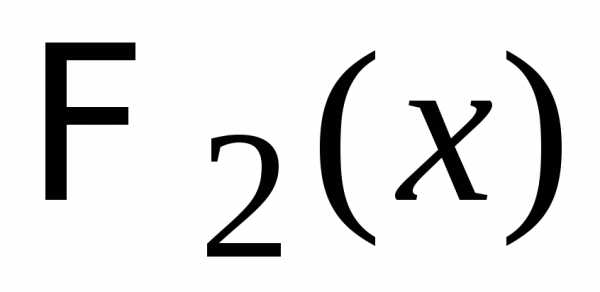Теорема о произведении производящих функций. Если происходят два независимых вида событий, которые описываются распределениями вероятностей с производящими функциями и, то распределение для суммы событий выражается произведением их производящих функций

. (П.1.19).

studfiles.net

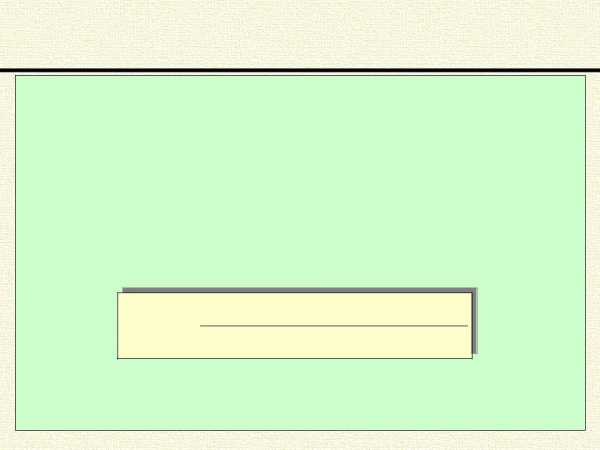
Среднее арифметическое значение случайной величины (k=1)

Средним арифметичским значением дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Если x имеет конечное число значений xi, которые встречаются fi раз то среднее значение x вычисляют

по формуле:

x x1 f1 x2 f2 … xn fn ар f1 f2 … fn

В самом простом случае, когда значения xi встречаются только

по одному разу, формула упрощается и принимает вид:

xар x1x2… xn n

Среднее арифметическое значение случайной величины (k=1)

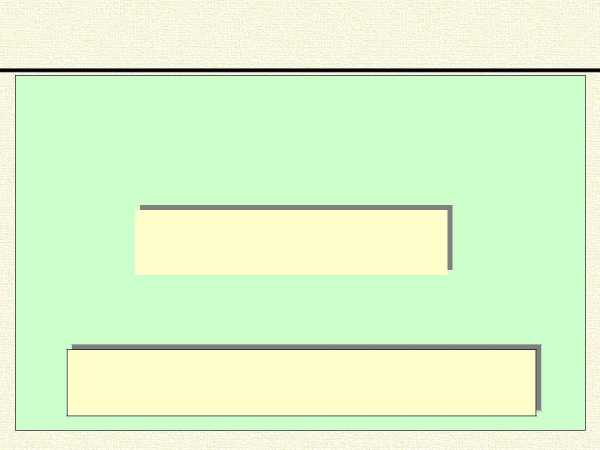
Среднее средних значений

Если большое количество данных разбито на k групп, для которых подсчитаны групповые средние значения, то чтобы подсчи- татьобщеесреднее Х нужно умножить групповые средние

xар1, xар2,…,xарk на соответствующее количество данных в группах n1, n2,…nk и сложить эти произведения, а затем разделить сумму на общее количество данных.

x xар1 n1 xар2 n2 … xарknkар.общ. n1 n2 … nk

Среднее значение суммы случайных величин

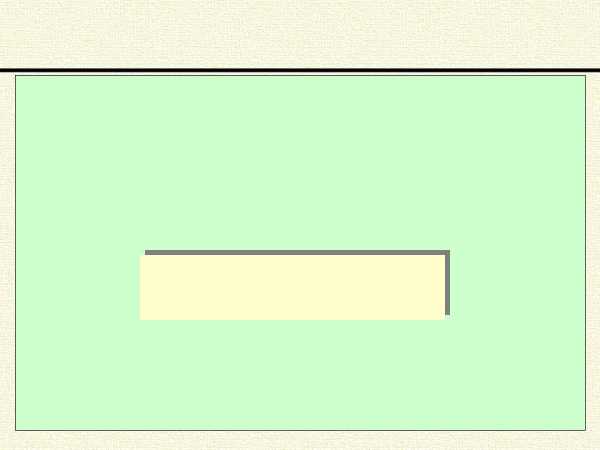
Среднее значение суммы случайных величин равно сумме средних значений случайных величин. Так, для двух наборов случайных величин Х1, Х2,…, Хk и Y1, Y2,.…, Yn, с соответству-

ющими вероятностями появления p1, p2,…, pk и q1, q2,.…, qn, расчетная формула имеет вид:

k

n

Х Y

XipiYjq j

X

Y

i 1

j 1

В случае большего количества наборов случайных величин формула имеет аналогичный вид:

k

n

m

XipiYjq jZ jrj

Х Y Z

X

Y

Z

i 1

j 1

j 1

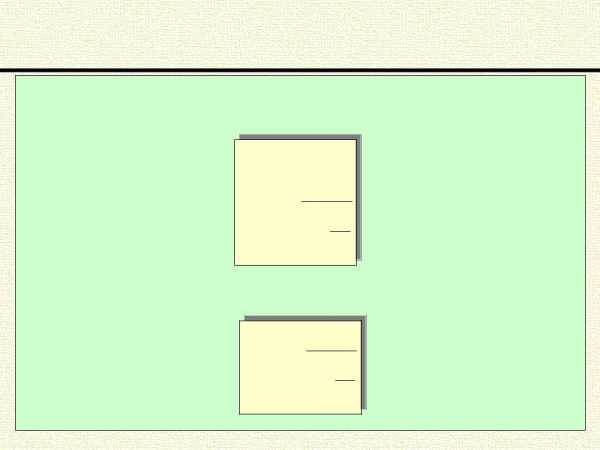
Среднее значение произведения случайных величин

Среднее значение произведения взаимно независимых случайных величин равно произведению средних значений случайных величин. Так, для двух наборов независимых случайных величин Х1, Х2,…, Хk и Y1, Y2,.…, Yn, с соответствующими вероятностя-

ми появления p1, p2,…, pk и q1, q2,.…, qn, расчетная формула имеет вид:

k

n

Х Y

XipiYjq j

X

Y

i 1

j 1

Среднее гармоническое значение случайных величин (k= -1)

Если случайная величина x имеет конечное число значенийxi, которые встречаютсяfi раз, то среднее гармоническое:

n

fi

xгармi 1 f n

i 1 xi i

В самом простом случае, когда все fi одинаковые.

xгарм nn1i 1 xi

Среднее квадратическое значение случайных величин (k=2)

Если случайная величина x имеет конечное число значенийxi, которые встречаютсяfi раз, то среднее квадратическое:

n

xi2 fi

xквi 1n

fi

i 1

В самом простом случае, когда fi =1:

n

xi2

xкв i 1n

Среднее геометрическое значение случайных величин

Если случайная величина x имеет конечное число значенийxi, которые встречаютсяfi раз, то среднее геометрическое значениеx вычисляют по формуле:

n xгеом n xifi

i 1

В самом простом случае, когда значения xi встречаются только по одному разу, формула упрощается и принимает вид:

n

xгеомn xi i1

Среднее геометрическое значение случайных величин

Пример. Перевозка грузов по автотранспортному предприятию

такова:
		Январь	Февраль	Март
	Перевезено грузов,	37,0	40,5	42,0
	тыс. т

Определить среднемесячный темп роста объёма грузовых перевозок.

Решение: Коэффициенты роста объёма грузовых перевозок:

K1		40,5	1,095		K2		42,0	1,037
	37,0					40,5

Среднемесячный коэффициент роста определяется по формуле средней геометрической:

K 2K1 K2 21,095 1,037 1,066

или 106,6% (средний темп роста).

Средняя хронологическая случайных величин

Если случайные величины y1,y2,…,yn представляют собой мо-

ментальный динамический ряд, то средний уровень такого ряда оценивается по формуле средней хронологической взвешенной:

n

yiti

yхрон.вз. i 1 n

ti

i 1

Где yхрон.вз. — средний уровень ряда;yi – уровни динамического

ряда; ti — время, в течение которого данный уровень ряда оставался неизменным.

Средняя хронологическая случайных величин

Пример №1. На 1 января 2001 года число сотрудников компании «Бест»состав—ляло 551 человек, 2 января уволился 1 сотрудник, 6 января было принято на работу 24 человека, 16 января было принято 6 человек, 25 января уволилось 10 сотрудников. Найти среднее значение числа сотрудников компании в январе 2001 года.

	Число календарных дней,
Численность сотрудников	в течение которых данная
компании «Бест», чел.	численность сотрудников	y t
(y)	оставалась без изменения
	( t)
551	2	1102
550	4	2200
574	10	5740
580	9	5220
570	6	3420
ИТОГО	31	17682
	yхрон.вз. 17682 570 чел.
	31

studfiles.net

Тема 14. Числовые характеристики случайной величины. «Меры положения»: среднее арифметическое, среднее геометрическое, мода, медиана. «Меры рассеяния»: дисперсия, эксцесс, асимметрия.

Для сравнения совокупностей значений СВ могут быть использованы различные величины. Перечислим некоторые из них:

— мода,

— медиана,

— среднее.

Эти термины объединяют одним термином – меры центральной тенденции, или, короче – центральные тенденции, подчеркивая тем самым возможность измерить, охарактеризовать совокупность значений СВ одним числом, к которому стремятся все ее значения.

«Меры положения»

1. Средняя арифметическая величина. Понятие средней арифметической

Средним арифметическим значением (часто его называют просто «среднее») называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности остается неизменным.

Исходя из определения, формула для расчета средней арифметической величины имеет вид:

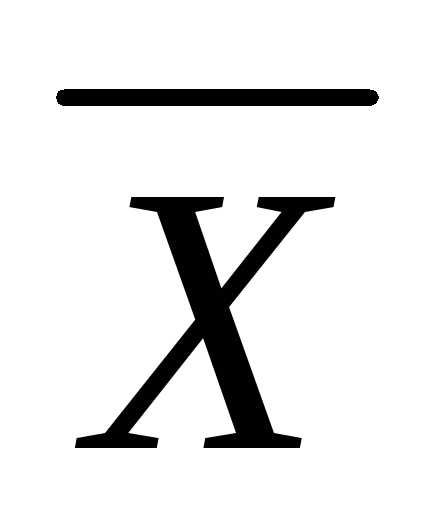= х₁ + х₂ + … + х_n = ,

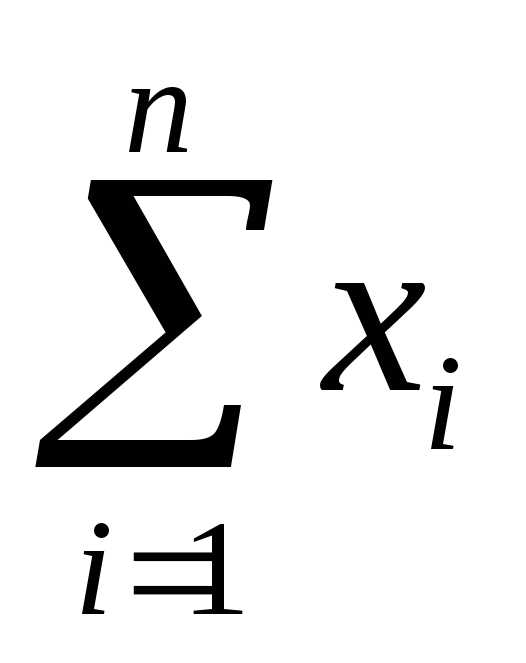где 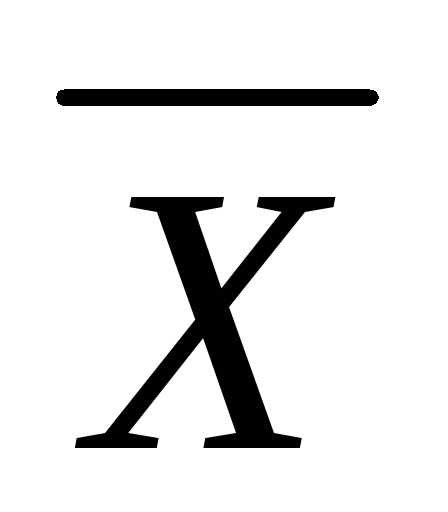– средняя величина,n – количество значений, которое принимает СВ.

Результат можно получить как сумму произведений значений признака в каждой группе х_i на число элементов в группе с таким количеством. Получим формулу

=,

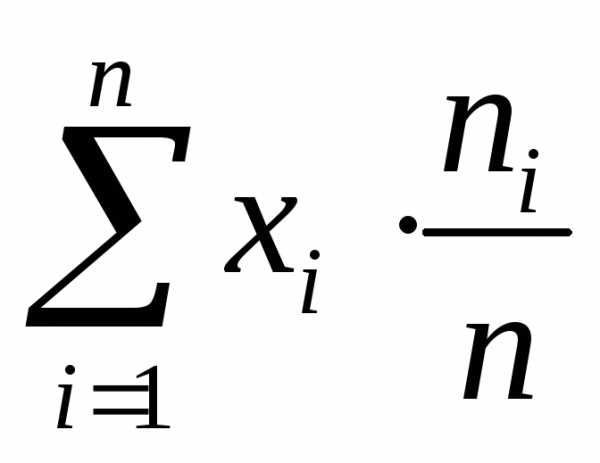где n – число групп.

Такую форму средней арифметической называют взвешенной арифметической в отличие от простой средней.

В качестве «весов» здесь выступают числа единиц совокупности в разных группах.

Свойства средней величины

Имеется несколько замечательных свойств средней величины.

1. Сумма отклонений индивидуальных значений от среднего значения признака равна нулю.

1.1. Для взвешенной средней сумма взвешенных отклонений равна нулю.

2. Если каждое индивидуальное значение признака умножить или разделить на одно и то же число, то и средняя величина увеличится или уменьшится во столько же раз.

3. Если к каждому индивидуальному значению признака добавить/вычесть постоянное число, то средняя величина возрастет / уменьшится на это же число.

4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится.

5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической величины меньше, чем от любого другого числа.

2. Мода

Модой дискретной случайной величины Х – обозначается Mo(X) называется значение случайной величины, имеющее наибольшую вероятность.

Отметим, что мода – это число, которое встречается чаще всего, а не частота встречаемости этого значения.

Если в вариационном ряду имеются два или несколько равных (и даже несколько различных, но больших чем соседние) значений признака, то вариационный ряд считается бимодальным («верблюдоподобным») либо мультимодальным. Это говорит о неоднородности совокупности значений, возможно, представляющей собой «агрегат» нескольких совокупностей с разными модами.

Графически мода — это абсцисса самой высокой точки в распределении СВ.

3. Медиана

Если упорядочить данные по величине, начиная с самой маленькой величины, и заканчивая самой большой, то медиана также будет характеристикой усреднения в упорядоченном наборе данных.

Определение. Медиана делит упорядоченный ряд значений пополам с равным числом (количеством) значений как выше, так и ниже ее.

Или: медиана определяется как величина, относительно которой по крайней мере 50% выборочных значений не меньше и по крайней мере 50% — больше.

Медиана (обозначается 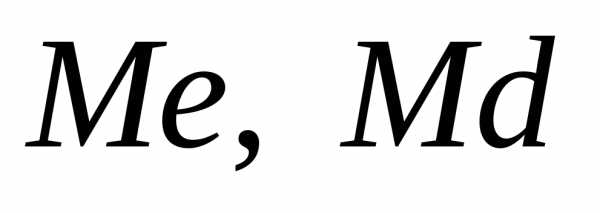) – это так называемое «серединное значение» упорядоченного ряда значений СВ.

Исходя из определения, количество значений, расположенных левее и правее медианы на числовой оси, одинаково.

studfiles.net

Характеристики случайной дискретной величины Среднее значение величины

Пусть для x возможны значения: x₁, x₂, …, x_k.

Измерения проводятся N раз, результат x_i наблюдается N_i раз, тогда

.

Среднее значение

.

При согласно (1.1) получаем

,

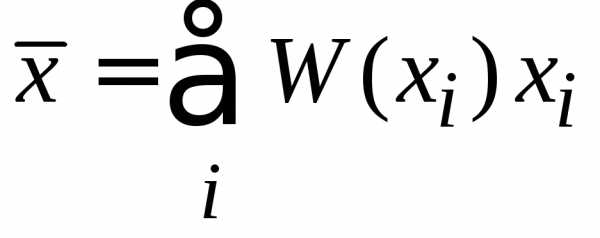. (1.5)

Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.

При 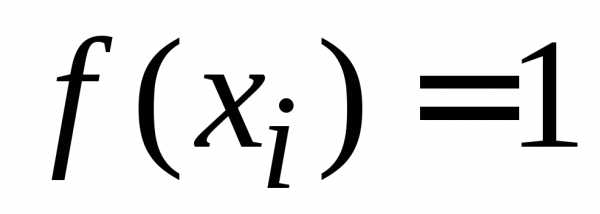получаем 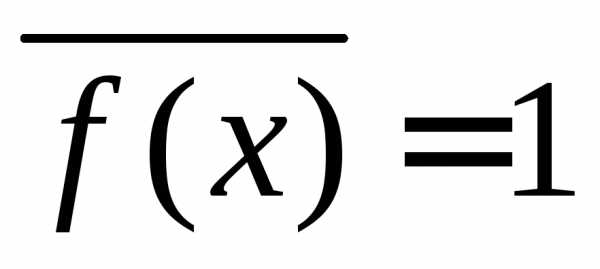и (1.5) дает нормировку вероятностей

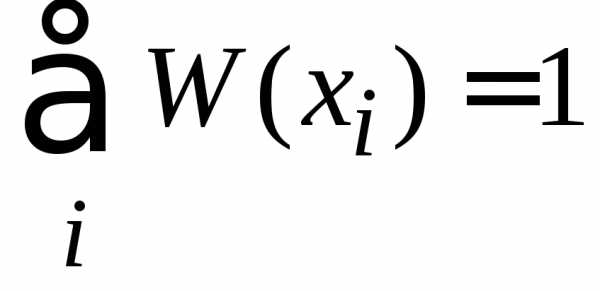. (1.6)

Свойства среднего

Для и независимых случайных величинx и y выполняются

1. ,

2. ,

3. .

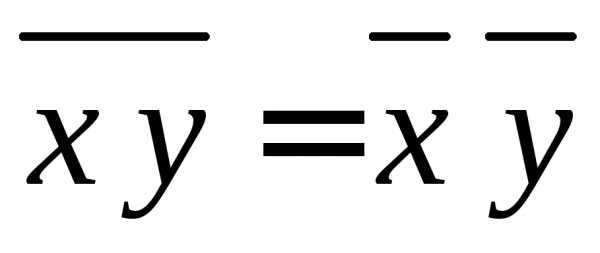Доказательство 2. Используя (1.5),получаем

;

Доказательство 3.

,

где для независимых случайных величин учтена теорема 2

.

Отклонение от среднего

.

Среднее отклонение от среднего

.

Среднее квадратичное величины

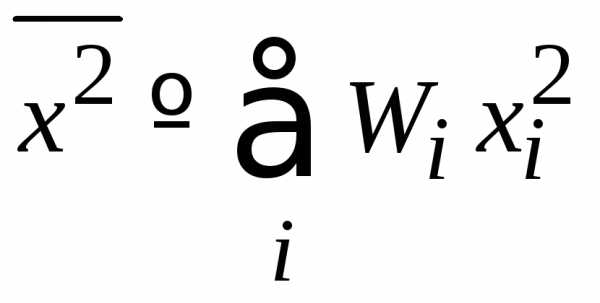. (1.7)

Среднее квадратичное отклонения от среднего – дисперсия

. (1.8)

Флуктуация

. (1.9)

Относительная флуктуация

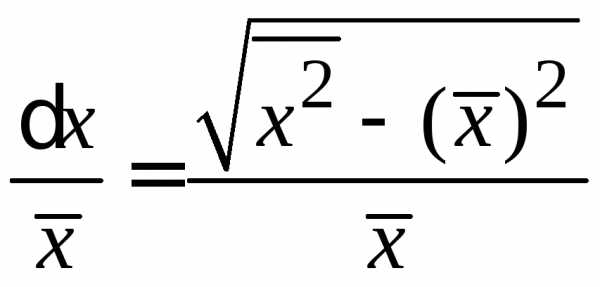. (1.10)

Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с .

Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и мала для макроскопической системы. Примером аддитивной величины (от лат. additivus – прибавляемый) является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.

Доказательство

Аддитивная величина X для системы равна сумме значений x_k для N независимых подсистем

, .

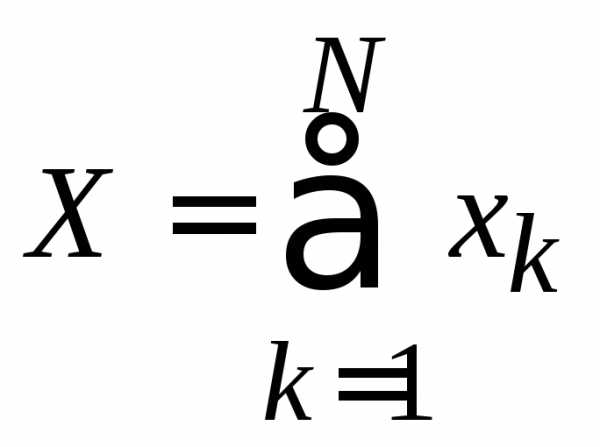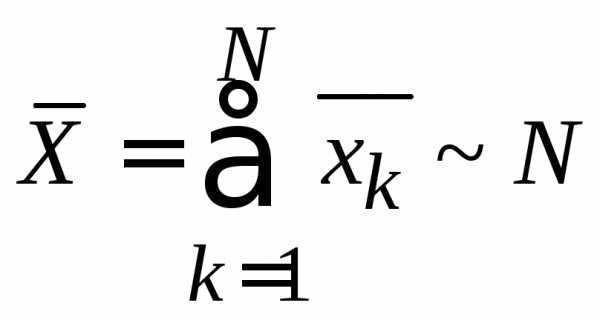Тогда

,

,

,

где

,

и усреднение произведений характеристик статистически независимых подсистем

, .

Относительная флуктуация

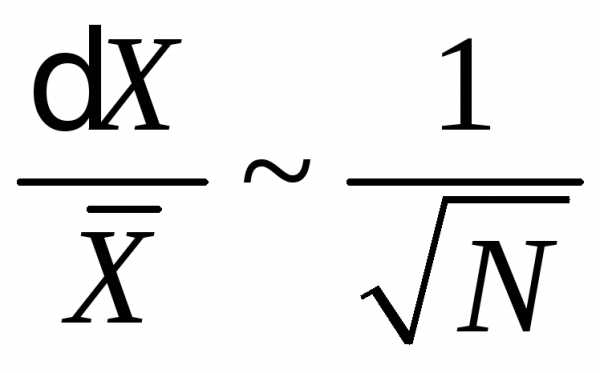. (П.1.2)

Характеристики случайНой непрерывНой величиНы

Плотность вероятности случайной величины x равна вероятности ее обнаружения в единичном интервале около значения x

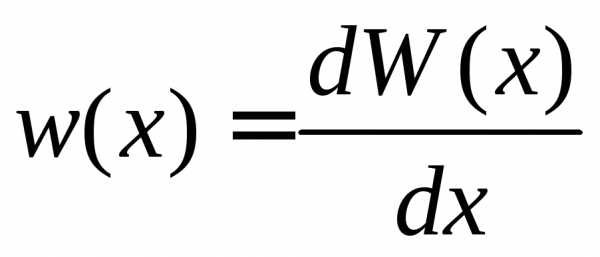. (1.11)

Вероятность нахождения в интервале

.

Пример: Пусть – скорость частицы идеального газа. Вероятность обнаружения частицы со скоростью в интервале

,

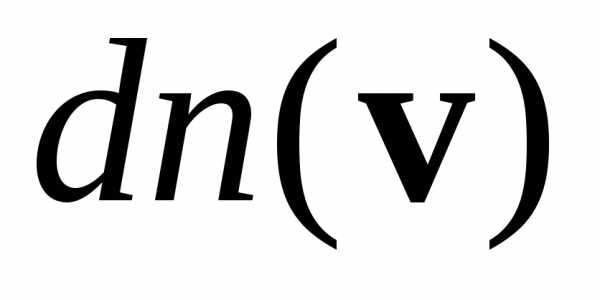–концентрация частиц со скоростями в интервале ,

n – концентрация частиц со всевозможными скоростями.

Условие нормировки

. (1.12)

Средние значения

,

. (1.13)

Биномиальное распределение

Описывает N независимых частиц или N независимых случаев.

Если p – вероятность признака у одной частицы, или вероятность одного случая, то вероятность того, что n любых частиц обладают этим признаком, или вероятность одновременного возникновения n случаев:

, (1.14)

; ;

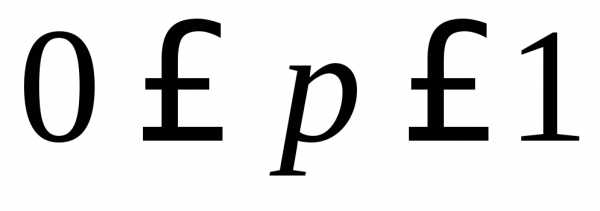–биномиальный коэффициент.

Распределение обосновал Якоб Бернулли в 1713 г.

Доказательство:

Объект – идеальный газ из N тождественных частиц в объеме V.

Получим вероятность обнаружения n любых частиц в объеме .

1. Вероятность найти определенную частицу в объеме V согласно определению вероятности (1.4а)

.

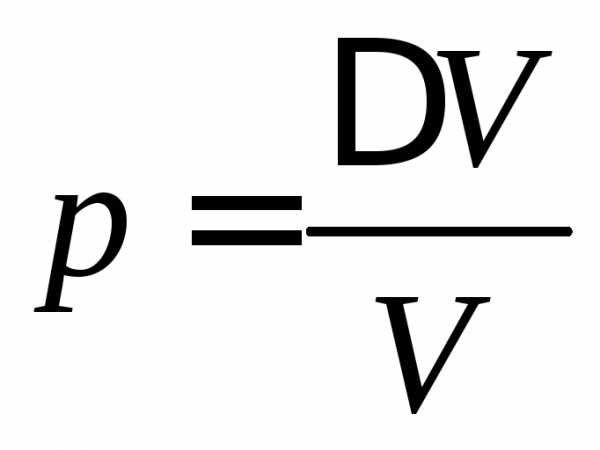Вероятность найти определенную частицу вне объема V

.

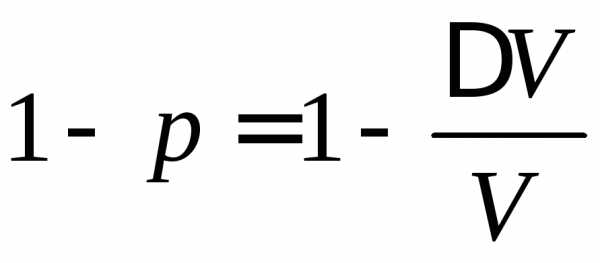Несовместимые события образуют полный набор и удовлетворяют условию нормировки.

2. Вероятность найти n определенных частиц в объеме V согласно теореме об умножении вероятностей независимых событий (1.4б)

.

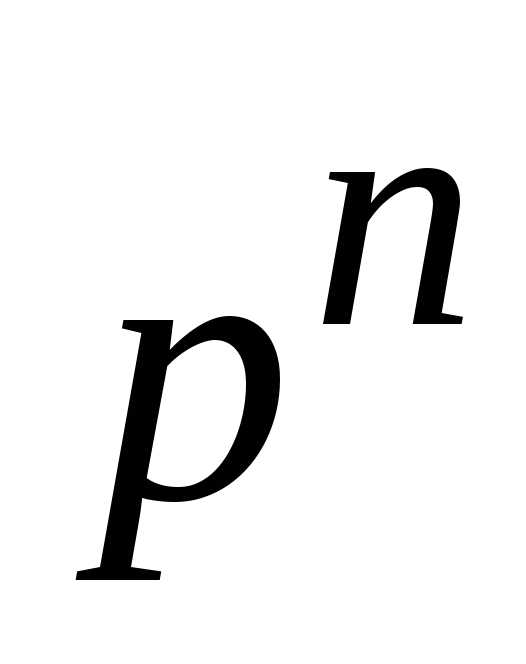Вероятность найти (N – n) определенных частиц вне объема V

.

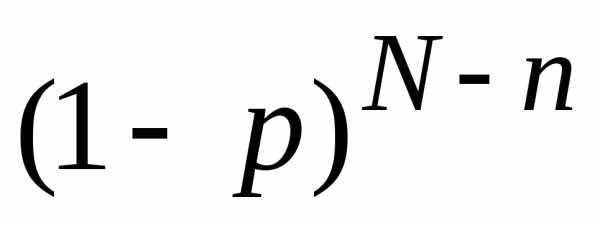3. Вероятность найти одновременно n определенных частиц в объеме V и (N – n) других частиц вне этого объема

.

4. Взаимная перестановка тождественных частиц дает состояние, не отличимое от исходного. Число таких состояний равно числу сочетаний n частиц из общего числа N, т. е. равно .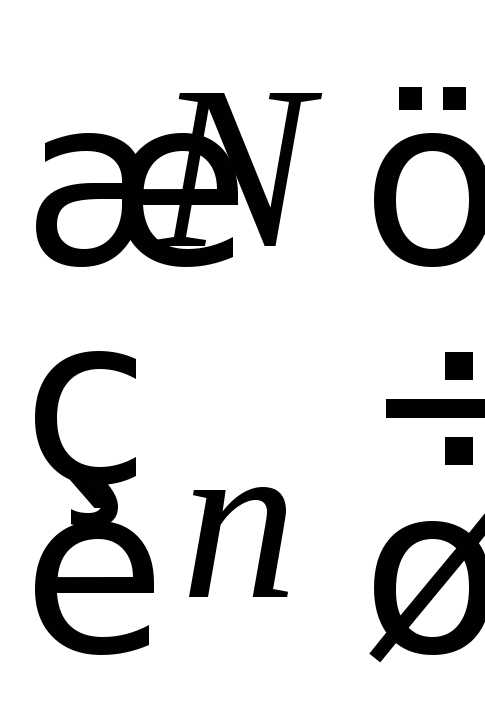

5. В результате вероятность найти n любых частиц в объеме V и (N – n) любых других частиц вне V

.

studfiles.net