| 2.10. Геометрический смысл смешанного произведения. Задачи, решаемые с помощью смешанного произведения |  Векторная алгебра > 2.10. Геометрический смысл смешанного произведения. Задачи, решаемые с помощью смешанного произведения
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
16 a
Рис. 16 b
Поскольку площадь треугольника , где — площадь параллелограмма, построенного на векторах
и , а высоты тетраэдра и параллелепипеда, построенных на
векторах совпадают, то
gif»>
Определение смешанного произведения
Смешанное произведение векторов – это произведение трёх векторов пространства:
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Определение: смешанным произведением некомпланарных векторов , взятых в данном порядке, называется объём
параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.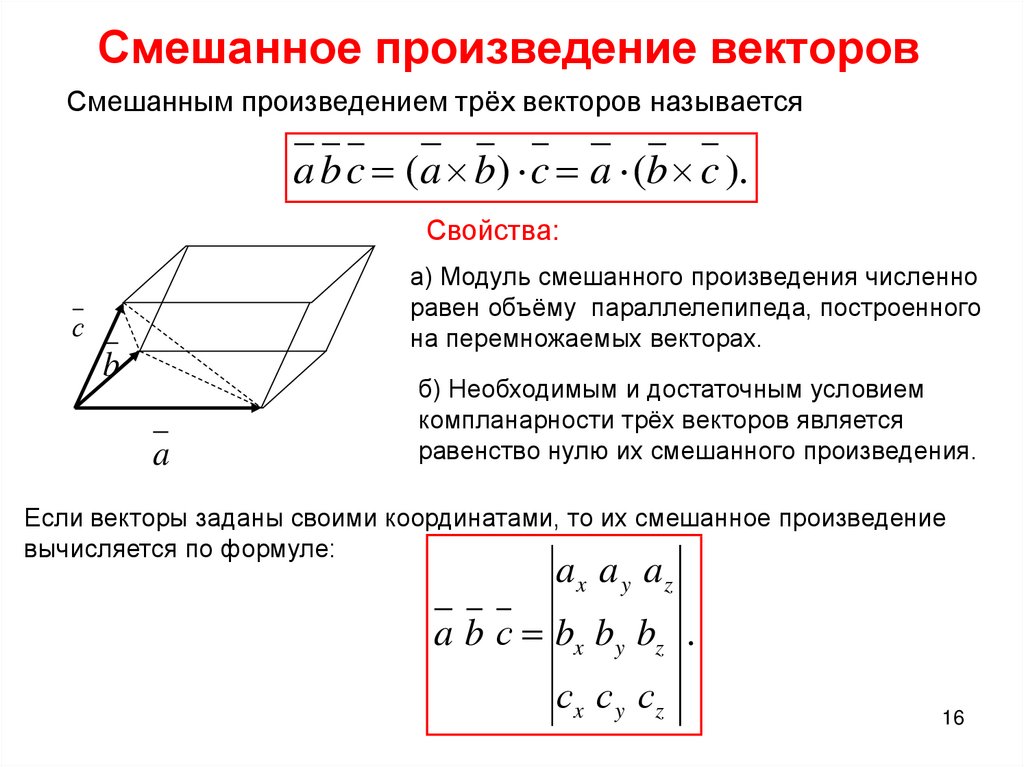
Выполним рисунок, и ниже я снова подробно разберу определение:
1) Исходные векторы , обозначенные красными стрелками, не компланарны (со случаем компланарности разберёмся отдельно)
2) Векторы взяты в определённом порядке, то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Смешанное произведение векторов является ЧИСЛОМ: . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению, смешанное произведение – это объём параллелепипеда, построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета; невидимые нам линии изображены пунктиром)
Примечание: чертёж является схематическим.
4) Не будем заново «париться» с понятием ориентации базиса и пространства. Смысл заключительной части определения состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах :
Знак модуля уничтожает возможный «минус» смешанного произведения.
И ещё одна важная формула. В курсе геометрии доказано, что объём тетраэдра (на рисунке отсечён «синей» плоскостью)
равен одной шестой объёма параллелепипеда:Тетраэдр часто называют треугольной пирамидой, поскольку все грани тетраэдра – треугольники.
Теперь случай компланарности.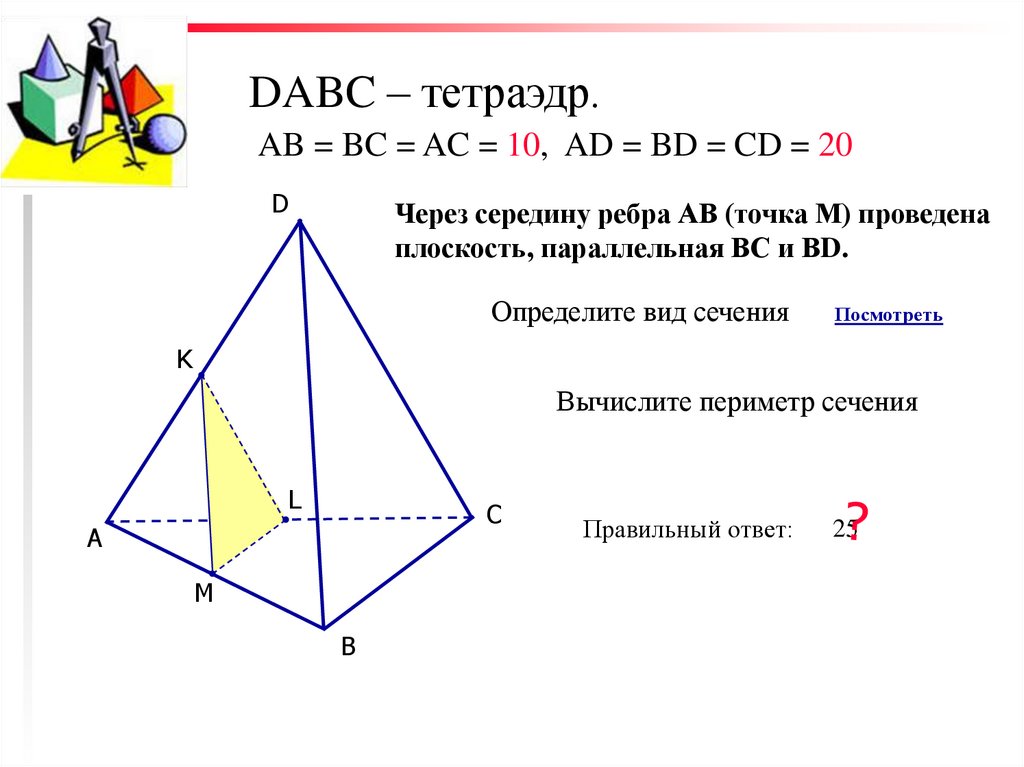
Если векторы компланарны, то их можно расположить в одной плоскости. В результате параллелепипед «складывается»
в плоскость, и объём такого вырожденного параллелепипеда равен нулю: .
1.10.2. Как вычислить смешанное произведение?
1.9.3. Векторное произведение в координатах
| Оглавление |
Автор: Aлeксaндр Eмeлин
векторов — Объем тетраэдра с использованием перекрестного и скалярного произведения
Задавать вопрос
спросил
Изменено 6 месяцев назад
Просмотрено 96 тысяч раз
$\begingroup$
Рассмотрим тетраэдр на изображении: Докажите, что объем тетраэдра равен $\frac16 |a \times b \cdot c|$.
Я знаю, что объем тетраэдра равен произведению площади основания на высоту, а здесь высота равна $h$, а площадь основания я считаю площадью треугольника $BCD$.
Итак, что у меня есть:
$$\begin{align} \text{базовая площадь} &= \frac12 \lvert a \times b \rvert \\ \text{высота $h$} &= \lvert c\rvert \cos \theta \end{выравнивание}$$
Таким образом, объем равен $$V=\frac12 \lvert a \times b\rvert \cdot \lvert c\rvert \cos \theta $$
Но я не знаю, как из этого получить $\frac16 | a \times b \cdot c|$.
Пожалуйста, сообщите.
- векторы
- объем
- перекрестное произведение
$\endgroup$
3
$\begingroup$
Вот один из способов думать об этом. Тетраэдр — это $\dfrac{1}{6}$ объема параллелепипеда, образованного $\vec{a},\vec{b},\vec{c}$.
Объем параллелепипеда равен скалярному тройному произведению $|(a \times b) \cdot c|$. Таким образом, объем тетраэдра $\dfrac{1}{6} |(a \times b) \cdot c|$
Чтобы решить вопрос так, как вы пытаетесь, обратите внимание, что $V = \dfrac{1}{3}Bh = \dfrac{1}{6}||a \times b|| \cdot ч$. Тогда $h = ||c|| \cdot |\cos(\theta)|$. Таким образом, имеем $V = \dfrac{1}{6}||a \times b|| \cdot ||с|| \cdot |\cos(\theta)|$. Теперь видим, что $|c \cdot (a \times b)| = ||с|| \cdot ||(a \times b)|| \cdot |\cos(\theta)|$ и, таким образом, $V = \dfrac{1}{6}|(a \times b) \cdot c|$.
Я также хотел бы сказать, что используемые вами обозначения немного странные. Во избежание путаницы $|x|$ обозначает абсолютное значение, а $||x||$ обозначает величину.
$\endgroup$
2
$\begingroup$
Подсказка: $\mathbf{a}\times\mathbf{b}$ «указывает прямо вверх».
Следовательно, она параллельна показанной вами линии $h$. Следовательно, он имеет с $c$ тот же угол, что и угол $h$.
$\endgroup$
$\begingroup$
Объем будет (площадь основания) x 1/3 высоты —————-(1) теперь в этом случае, если мы возьмем за основание треугольник BCD, его площадь будет равна
= 1/2 |a||b||sin(m)| = 1/2 |а х б| ———————(2)
где m — угол между a и b, следовательно, b sin(m) — длина проекции b перпендикулярно а , т. е. высоте треугольника BCD, если мы возьмем а за его основание.
теперь высота тетраэдра будет проекцией c перпендикулярно основанию единичный вектор, перпендикулярный основанию BCD, равен = (a x b)/|a x b| = n
, следовательно, высота тетраэдра (h), которая может быть выражена как проекция c на n
h = |c||n||cos(θ)| = c.n = c.(a x b)/|a x b| ————-(3)
из уравнений 1,2 и 3 получаем
объем = 1/2|a x b| 1/3[c.
(a x b)]/|a x b|
= 1/6[c.(a x b)]
= 1/6[(a x b).c]
PS- Я все еще учусь в старшей школе, и это мой первый пост здесь, поэтому извините, если я напортачил.
$\endgroup$
1
аналитическая геометрия — Найдите объем тетраэдра
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 5к раз
$\begingroup$
Пусть
$A(2,1,3), B(3,2,5), C(3,3,6), D(4,4,2)$
Найдите объем $V$ тетраэдра $ABCD$.
Мое решение:
$\vec{AB} = (1, 1, 2), \vec{AC} = (1, 2, 3), \vec{AD} = (2, 3, -1) $
$$V=\begin{vmatrix}1&1&2\\1&2&3\\2&3&-1 \end{vmatrix}=-6$$
Мой вопрос: правильно ли мое решение и может ли объем быть отрицательным числом?
- аналитическая геометрия
$\endgroup$
$\begingroup$
Обратите внимание, что объем тетраэдра = объем пирамиды с треугольным основанием =
$$= 1/3\,\text{ * }\,\text{основание}\,\text{область}\,\text{ * }\,\text{высота}$$
Тогда, если $\vec a,\,\vec b,\,\vec c$ являются векторами, соответствующими трем совпадающим сторонам, вышеизложенное получается как
$$
V = 1/3\влево| {\ left( {1/2 \, \ vec b \ times \, \ vec a} \right) \ cdot \ vec c} \ right | = 1/6\влево| {\;\ влево| {\начать{массив}{*{20}с}
{c_x} и {c_y} и {c_z} \\
{b_x} & {b_y} & {b_z} \\
{a_x} & {a_y} & {a_z} \\
\end{массив} } \right|\;} \right|
$$
Вы должны взять абсолютное значение, потому что $\vec b \times \,\vec a$
— вектор, ориентация которого относительно $\vec c$ будет определять положительный или отрицательный
скалярный результат двойного произведения.
$\endgroup$
$\begingroup$
Объем трехмерного параллелепипеда со сторонами AB, AC и AD равен
$$\left|\det(AB, AC, AD)\right|.$$
Параллелепипед всегда в $6$ раз больше объемен как соответствующий тетраэдр $ABCD$, поэтому объем тетраэдра $ABCD$ равен
$$\frac{1}{6}\left|\det(AB, AC, AD)\right|.$ $
В данном случае это означает, что тетраэдр имеет объем ровно $1$.
$\endgroup$
$\begingroup$
Если вы сделали это, используя $B$ в качестве исходной точки (используя $BA, BC, BD$ в указанном порядке)
ты бы нашел
$$
V=\frac16 \влево| \pmatrix{-1&-1&-2\\0&1&1\\1&2&-3} \right| = \frac16 \cdot 6
$$
Определитель равен объему только с точностью до множителя $\pm 1$; вы можете видеть это, потому что, если вы измените порядок любых двух сторон, определитель изменит знак.