ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ • Большая российская энциклопедия
ОБРА́ТНЫЕ ТРИГОНОМЕТРИ́ЧЕСКИЕ ФУ́НКЦИИ (аркфункции, круговые функции), функции, обратные тригонометрическим функциям. Значения О. т. ф. являются решением следующей задачи: найти число по заданному значению его тригонометрич. функции. Шести осн. тригонометрич. функциям соответствуют шесть О. т. ф.: арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс (названия происходят от лат. arc – дуга), они обозначаются соответственно $\textrm{Arcsin}\,x, \textrm{Arccos}\,x, \textrm{Arctan}\,x, \textrm{Arccot}\,x, \textrm{Arcsec}\,x, \textrm{Arccosec}\,x $(две последние функции мало употребительны и далее не рассматриваются). Согласно этому определению, напр., величина $y=\textrm{Arcsin}\,x$ есть решение уравнения $\sin y=x$, т. е. $y$ есть длина дуги, синус которой равен $x$, т. о., $\sin(\textrm{Arcsin}\,x)=x$.
{–1}x.$
| Таблица 1. Свойства обратных тригонометрических функций | |||
| Функция | Область определения | Множество значений | Монотонность |
| $\arcsin x$ | $-1⩽x⩽1$ | $\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]$ | возрастает |
| $\arccos x$ | $-1⩽x⩽1$ | $[0, \pi]$ | убывает |
| $\arctan x$ | $-\infty \lt x +\infty$ | $\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]$ | возрастает |
| $\textrm {arccot}\,x$ | $-\infty \lt x \lt +\infty$ | $[0, \pi]$ | убывает |
| Таблица 2. Значения обратных тригонометрических функций арксинус и арккосинус | ||
| Аргумент | Функция | |
| $$\arcsin x$$ | $$\arccos x$$ | |
| $$-1$$ | $$-\frac{\pi}{2}$$ | $$\pi$$ |
| $$-\frac{\sqrt3}{2}$$ | $$-\frac{\pi}{3}$$ | $$\frac{5\pi}{6}$$ |
| $$-\frac{\sqrt 2}{2}$$ | $$-\frac{\pi}{4}$$ | $$\frac{3\pi}{4}$$ |
| $$-\frac{1}{2}$$ | $$-\frac{\pi}{6}$$ | $$\frac{2\pi}{3}$$ |
| $$0$$ | $$0$$ | $$\frac{\pi}{2}$$ |
| $$\frac{1}{2}$$ | $$\frac{\pi}{6}$$ | $$\frac{\pi}{3}$$ |
| $$\frac{\sqrt 2}{2}$$ | $$\frac{\pi}{4}$$ | $$\frac{\pi}{4}$$ |
| $$\frac{\sqrt 3}{2}$$ | $$\frac{\pi}{3}$$ | $$\frac{\pi}{6}$$ |
| $$1$$ | $$-\frac{\pi}{2}$$ | $$0$$ |
Таблица 3.  Значения обратных тригонометрических функций арктангенс и арккотангенс | ||
Аргумент | Функция | |
| $$\arctan x$$ | $$\textrm{arccot}\,x $$ | |
| $$-\infty$$ | $$-\frac{\pi}{2}$$ | $$\pi$$ |
| $$-\sqrt3$$ | $$-\frac{\pi}{3}$$ | $$\frac{5\pi}{6}$$ |
| $$-1$$ | $$-\frac{\pi}{4}$$ | $$\frac{3\pi}{4}$$ |
| $$-\frac{\sqrt3}{3}$$ | $$-\frac{\pi}{6}$$ | $$\frac{2\pi}{3}$$ |
| $$0$$ | $$0$$ | $$\frac{\pi}{2}$$ |
| $$\frac{\sqrt3}{3}$$ | $$\frac{\pi}{6}$$ | $$\frac{\pi}{3}$$ |
| $$1$$ | $$\frac{\pi}{4}$$ | $$\frac{\pi}{4}$$ |
| $$\sqrt 3$$ | $$\frac{\pi}{3}$$ | $$\frac{\pi}{6}$$ |
| $$+\infty$$ | $$\frac{\pi}{2}$$ | $$0$$ |
Впервые спец.
символы для О. т. ф. использовал Д. Бернулли (1729, 1736), совр. обозначения для О. т. ф. ввели в 1772 австр. математик К. Шерфер и Ж. Лагранж.
Обратные тригонометрические функции действительного переменного $arcsinx, arccosx, arctgx, arcctgx$ определяются как обратные к функциям $\sin x, \cos x, \tan x, \cot x$, заданным соответственно на промежутках $[-π/2, π/2], [0, π], (-π/2, π/2), (0, π)$. Т. о., равенство$$y=\arcsin x$$означает, что $\sin y=x$ и $-π/2 \leqslant y \leqslant π/2:$$$\{ y=\arcsin x \} ⇔ \{ \sin y=x, -π/2 \leqslant y \leqslant π/2 \}.$$
Аналогично,$$\{ y= \arccos x \} ⇔ \{ \cos y=x, 0 \leqslant y \leqslant π \}, \\ \{ y= \arctan x \} ⇔ \{ \tan y=x, -\pi/2 \lt y \lt \pi/2 \}, \\ \{y = \arctan x \} ⇔ \{\cot y=x, 0 \lt y \lt \pi \}.$$ Эти О. т. ф. однозначны, непрерывны и их свойства вытекают из свойств тригонометрич. функций (табл. 1). Значения О. т. ф. для некоторых значений аргумента приведены в таблицах 2 и 3.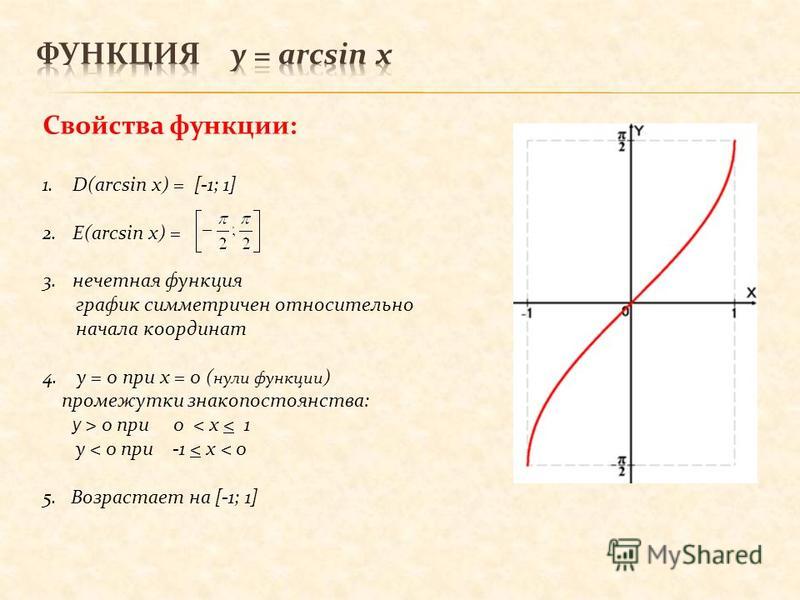
2-1,}\\ \textrm{Arctan}\,z=\frac{i}{2}\textrm{Ln}\frac{1-iz}{1+iz},\\ \textrm{Arccot}\,z=\frac{i}{2}\textrm{Ln}\frac{z-i}{z+i}.$$
3.9: Производные обратных тригонометрических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 80080
- OpenStax
- OpenStax
Определение производных обратных тригонометрических функций
Теперь найдем производные обратных тригонометрических функций, \(y = \arcsin x,\) \(y = \arccos x,\) \(y = \arctan x, \) \( y = \text{arccot}\, x,\) \(y = \text{arcsec}\, x,\) и \(y = \text{arccsc}\, x.\)
Один из способов сделать это, который особенно полезен для понимания того, как получаются эти производные, — использовать комбинацию неявного дифференцирования и прямоугольных треугольников.
Пример \(\PageIndex{1}\): найти производную от \(y = \arcsin x\)
Найти производную от \(y = \arcsin x\).
Решение:
Чтобы найти производную \(y = \arcsin x\), мы сначала перепишем это уравнение в терминах его обратной формы. То есть \[ \sin y = x \label{inverseEqSine}\]
Теперь это уравнение показывает, что \(y\) можно считать острым углом в прямоугольном треугольнике с отношением синусов \(\dfrac{x {1}\). Поскольку отношение синуса дает нам длину противоположной стороны по длине гипотенузы, это означает, что противоположная сторона имеет длину \(х\), а гипотенуза имеет длину \(1\). См. рисунок \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\)
Теперь давайте неявно продифференцируем уравнение \ref{inverseEqSine} относительно \(x\).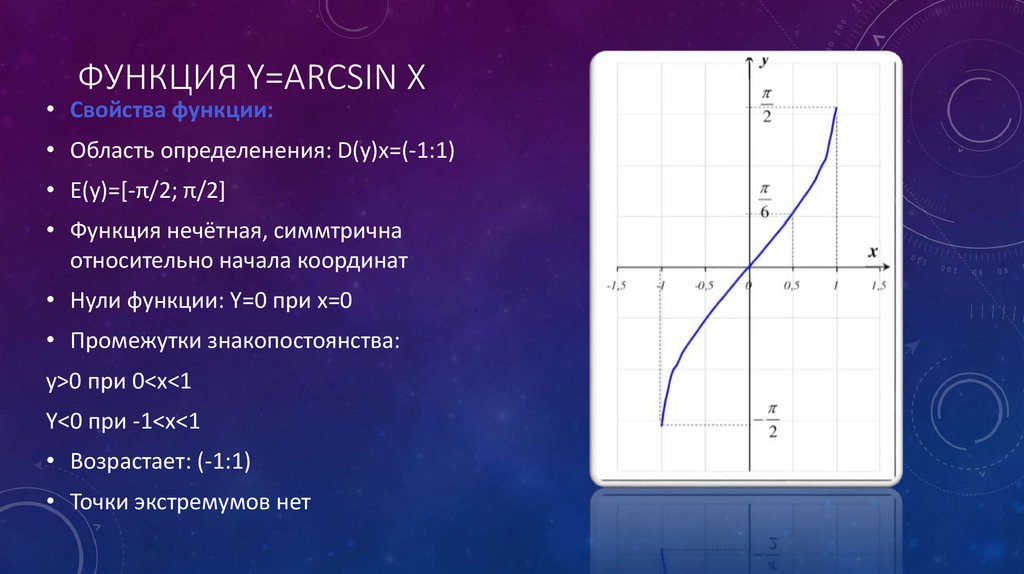
\[\cos y \cdot \frac{dy}{dx} = 1\]
Затем мы решаем это для \(\dfrac{dy}{dx}\).
\[\frac{dy}{dx} =\frac{1}{\cos y}\]
Глядя на рисунок \(\PageIndex{1}\), мы видим, что \(\cos y = a \). Теперь воспользуемся теоремой Пифагора, чтобы найти выражение для \(а\) через \(х\), используя известные нам другие стороны прямоугольного треугольника. 92} \end{выравнивание*} \]
Пример \(\PageIndex{2}\): найти производную от \(y = \text{arcsec}\, x\)
Найти производную от \(y = \text{arcsec}\, x\ ).
Решение:
Чтобы найти производную от \(y = \text{arcsec}\, x\), мы сначала перепишем это уравнение в терминах его обратной формы. То есть \[ \sec y = x \label{inverseEqSec}\]
Как и прежде, пусть \(y\) считается острым углом в прямоугольном треугольнике с отношением секущих \(\dfrac{x}{ 1}\). Поскольку отношение секущей является обратным отношением косинуса, оно дает нам длину гипотенузы по длине прилежащей стороны, так что это означает, что гипотенуза имеет длину \(x\), а прилежащая сторона имеет длину из \(1\).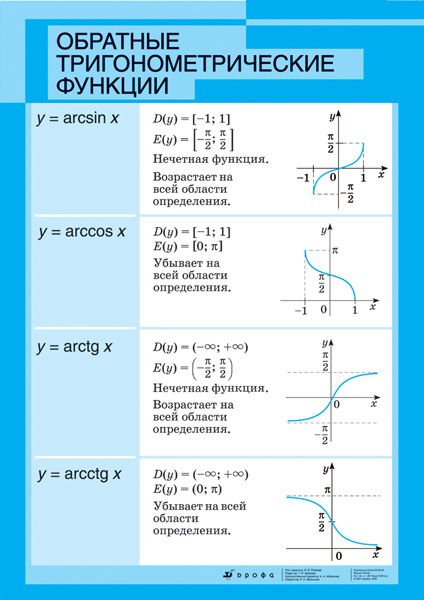
Рисунок \(\PageIndex{3}\)
Дифференцирующее уравнение \ref{inverseEqSec} неявно относительно \(x\), дает нам:
\[\sec y\tan y \ cdot \frac{dy}{dx} = 1\]
Решая это для \(\dfrac{dy}{dx}\), мы получаем:
\[\frac{dy}{dx} =\frac{ 1}{\sec y\tan y}\]
Чтобы найти \(\tan y\) через \(x\), нам нужно найти длину противоположной стороны, \(a\) , в терминах \(x\). По теореме Пифагора имеем: 92 — 1}}.\]
Но это не совсем правильно, по крайней мере, не для отрицательных значений \(x\). Рассматривая график \(y = \text{arcsec}\, x\) на рисунке \(\PageIndex{5}\), мы видим, что его наклон всегда положителен. Но при отрицательных значениях \(х\) указанный выше вид производной был бы отрицательным (и явно неверным).
Рисунок \(\PageIndex{5}\)
Как мы докажем ниже, фактическая формула производной для этой функции: 92 — 1}}\]
Рассмотрим домен и диапазон исходной функции, \(y = \text{arcsec}\, x:\)
\[\text{Домен: } (-\infty, — 1] \cup [1, \infty) \quad \text{or} \quad |x| \geq 1\]
\[\text{Диапазон: } \big[0, \frac{\pi}{2}\big) \cup \big(\frac{\pi}{2}, \pi\big ] \quad \text{or} \quad 0 \leq y \leq \pi, y \ne \frac{\pi}{2}\]
Обратите внимание, что область определения производной является подмножеством области определения исходная функция, исключая конечные точки, \(x = -1\) и \(x = 1.
Мы видим, что эта функция позволяет \(y\) принимать все значения между \(0\) и \(\pi\), кроме \(y = \frac{ \pi}{2}\), где исходное выражение \(\dfrac{1}{\sec y\tan y}\) не определено. Это подмножество диапазона исходной функции \(y = \text{arcsec}\, x.\). Обратите внимание, что в производной \(y\) не может принимать значения конечных точек этого интервала, а они были частью диапазона \(y = \text{arcsec}\, x.\)
Теперь рассмотрим, что для всех значений \(y\) в этом диапазоне между \(0\) и \(\pi \), выражение для \(\dfrac{dy}{dx}\) положительно, так как оба 92} = |x|.\]
Это означает, что на самом деле здесь мы получаем нечто более интересное: \[ \frac{d}{dx}\big(\arcsin(\cos x) \big) = \frac{ -\sin x}{|\sin x|}\]
Эта функция чередует значения \(-1\) и \(1\), когда \(\sin x\) положительное и отрицательное значение соответственно.
См. график функции \( y = \arcsin(\cos x)\) ниже на рисунке \(\PageIndex{6}\).
Рисунок \(\PageIndex{6}\): График \(y = \arcsin(\cos x)\).
2}} \\ 92-1}} \end{align*} \]
Авторы
- Пол Сибургер (Общественный колледж Монро)
Эта страница под названием 3.9: Производные обратных тригонометрических функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- да
- Включено
- да
- Теги
- источник@https://openstax.
org/details/books/calculus-volume-1 - источник[1]-math-48769
- источник@https://openstax.
org/details/books/calculus-volume-1Справка по предварительному исчислению
Студенты, нуждающиеся в помощи Precalculus, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Precalculus. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы получите много помощи Precalculus в кратчайшие сроки. Получите помощь сегодня с нашей обширной коллекцией необходимой информации Precalculus.
Большинство учащихся изучают отдельные математические предметы средней школы – алгебру, геометрию и тригонометрию – как отдельные курсы. Однако, если вы планируете в конечном итоге изучать высшую математику, вы можете оказаться на продвинутом курсе, где рассматривается несколько предметов, чтобы лучше подготовить вас к поступлению в колледж.
Содержание курсов Precalculus может варьироваться в зависимости от школы. Тем не менее, независимо от того, на чем сосредоточен ваш класс, вы можете найти помощь в изучении Precalculus, используя бесплатные средства обучения Varsity Tutors «Learn by Concept». Всеобъемлющий контент организован как интерактивная учебная программа, включающая как основные категории, так и множество более мелких разделов и тем.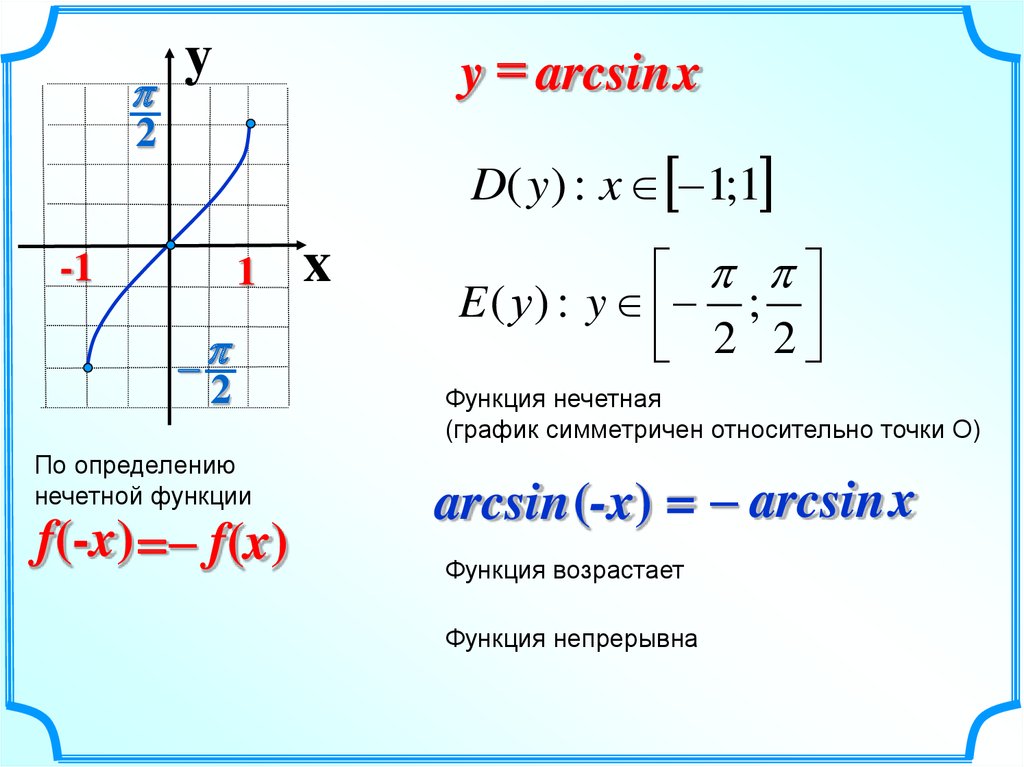
Полезность Learn by Concept заключается не только в вопросах и ответах. Каждый правильный ответ сопровождается подробным объяснением процесса, использованного для получения этого ответа. Таким образом, вы можете шаг за шагом решать сложные многоступенчатые задачи, чтобы увидеть, какие формулы и концепции используются. Если вы ответили правильно, вы можете проверить свою работу, чтобы увидеть, поняли ли вы процесс. Если вы ответили неправильно, вы можете легко определить, допустили ли вы простую ошибку или есть концепция, которую вам следует подробнее рассмотреть на следующих учебных занятиях.
В течение учебного года вы можете использовать инструмент «Учись по понятиям» в качестве учебного пособия по предварительному исчислению. Некоторые курсы Precalculus посвящены конкретным концепциям исчисления, таким как конические сечения или евклидовы векторы, в то время как другие уделяют больше внимания матрицам и степенным функциям; инструмент Learn by Concept содержит весь этот материал и многое другое, включая полиномиальные функции, последовательности и тригонометрические функции. Каждая из категорий также раскрывается в конкретных концепциях. С тысячами примеров вопросов и вопросов почти по всем отдельным темам у вас есть доступ к большому количеству обзоров Precalculus для всего, с чем вам нужна помощь.
Инструмент Learn by Concept лучше всего использовать вместе с другими бесплатными инструментами обучения.