Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости.  § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры.  § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. 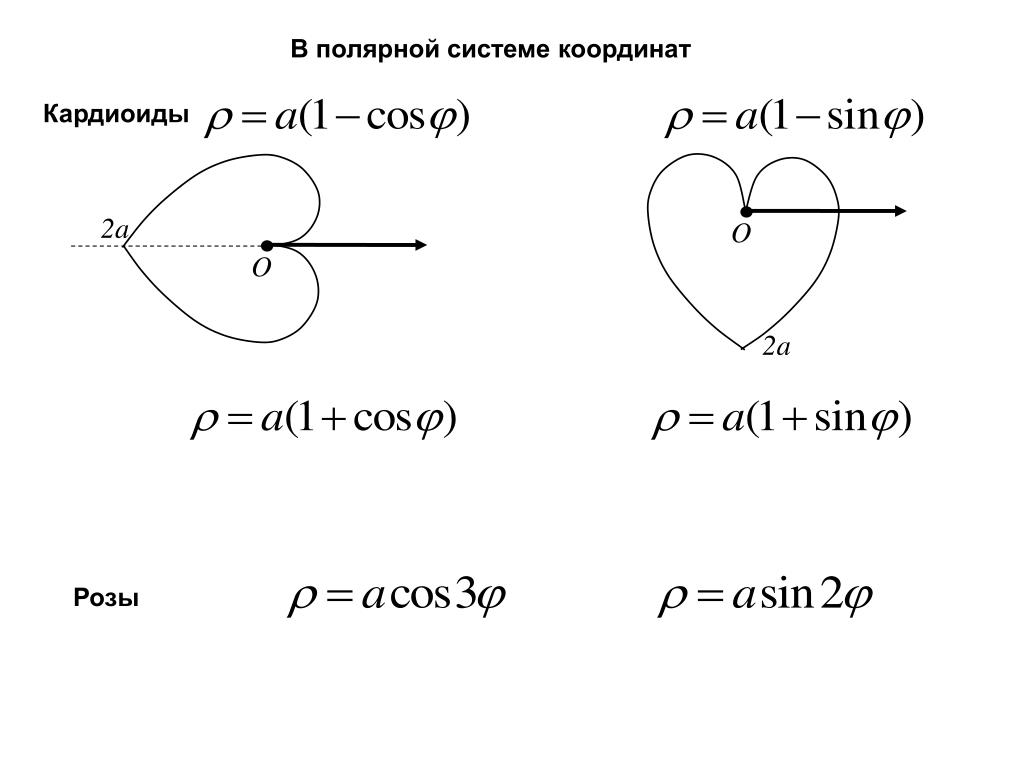 Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III.  ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка.  Конструкции В. Г. Шухова.Упражнения Ответы |
Как нарисовать звезду (и не только) в полярных координатах / Хабр
Вопрос о формуле для многоугольника в полярных координатах регулярно возникает на тематических ресурсах — и так же регулярно остаётся без внятного ответа. В лучшем случае попадается решение через функцию остатка от деления — что не является «чистым» с математической точки зрения, поскольку не позволяет производить над функцией аналитические преобразования. Видимо, настоящие математики слишком заняты решением проблем тысячелетия и поисками простого доказательства теоремы Ферма, чтобы обращать внимание на подобные банальные задачи. К счастью, в этом вопросе воображение важнее знания, и для решения этой задачи не нужно быть профессором топологических наук — достаточно знания школьного уровня.
Формула для равностороннего многоугольника в полярных координатах выглядит очень просто
и имеет следующие параметры:
— угол;
— количество выпуклых вершин;
— определяет, через какое количество вершин стороны будут лежать на одной прямой.
— жёсткость — при мы получим окружность вне зависимости от прочих параметров, при — многоугольник с прямыми линиями, при промежуточных значениях от до — промежуточные фигуры между окружностью и многоугольником.
С этой формулой можно нарисовать звезду двумя путями:
1)
2) . В этом случае требуется сделать два оборота вместо одного:
Параметр влияет на многоугольник следующим образом (здесь он изменяется от -1 до 5):
Параметр в анимации:
Комплексная форма и модификации
Можно переписать исходную формулу в комплексном виде, и, несмотря на наличие в ней мнимых единиц, значение радиуса по-прежнему будет оставаться действительным:
На первый взгляд это может показаться бессмысленным, поскольку формула стала чуть более громоздкой — но не стоит спешить с выводами.
Как вы наверняка заметили, вращение вектора перестало быть равномерным — и именно из-за появления мнимой составляющей в радиусе.
Квадрокруги и прочее
или
(выбирайте, какая больше нравится).
В чуть более развёрнутом случае можно определить промежуточные фигуры между кругом и квадратом через точку на плоскости
Можно также добавить вариативности этим фигурам с сохранением условия прохождения их через точку — модулируя непосредственно сам параметр в зависимости от угла таким образом, чтобы при прохождении через диагонали его множитель был равен единице. Например, подставив вместо функцию , мы получим дополнительный параметр , которым можно регулировать дополнительные изгибы. В частности, для получится следующее:
В ещё более развёрнутом случае можно определить не просто квадрат — а прямоугольник, и по прежнему в полярных координатах:
И даже посчитать его площадь (через эллиптические интегралы):
Примечание
Для крайних значений ( и ) эта функция имеет особые точки, которые можно посчитать через предел и они ожидаемо будут равны и .
Это позволит делать профили с переходом из окружности в прямоугольник с контролируемой площадью сечения. Здесь площадь константна:
А здесь площадь расширяется по экспоненциальному закону:
Переход к декартовым координатам
Любую формулу в полярных координатах можно выразить через уравнение в декартовых координатах, причём как минимум двумя способами — в зависимости от чего будет изменяться вид градиента на границе фигуры. Для этого достаточно посчитать угол через арктангенс от координат и привести формулу к константе через радиус-вектор вычитанием
или делением
Второй вариант предпочтительнее, поскольку даёт прямые градиенты вдоль сторон многоугольника.
Примечание
Здесь также нужно помнить, что в точке (0,0) возникает неопределенность из-за деления на ноль — которая, впрочем, легко разрешается через предел (который будет равным в первом случае и нулю во втором).
Выражение также можно упростить до , коэффициенты числителя которого при разложении образуют знакочередующий вариант последовательности A034839.
Значение формулы из правой части уравнения (во 2-м случае) будет меняться от до если точка попадает внутрь фигуры, и от до бесконечности — если нет. Выбирая различные функции для преобразования её в яркость, можно получать различные варианты растеризации. Для экспоненты ( для первого и для второго варианта) получим
или, если с насыщением
Можно использовать классический фильтр нижних частот , в котором — порядок фильтра, определяющий степень затухания.
Для первого варианта:
И для второго:
Можно использовать и кусочно-непрерывную функцию, явно задавая границы интерполяции.
Помимо растеризации как таковой, можно задавать и деформации — например, сжать шахматную доску в круг:
Или даже натянуть её на сферу:
Формула
Классический стиль повествования в математических текстах состоит из чередования лемм/теорем и их доказательств — как если бы доказуемые утверждения появлялись у авторов в голове откровением свыше.
И хотя в этом и бывает доля истины, чаще появлению формул предшествует некоторая исследовательская работа, описание которой может дать большее понимание их смысла, чем формальное доказательство; а верность утверждений, в свою очередь, можно проследить через верность шагов, к ним приведших.
Так и здесь — если бы статья началась с формулы в комплексной форме, то её появление было бы неочевидным и контр-интуитивным, а заявленные свойства требовали бы дополнительных доказательств. Но в тригонометрической форме записи историю её появления вполне возможно проследить.
1) начинаем с самого простого случая — задаче начертить прямую в полярных координатах. Для этого нужно решить уравнение , решение которого очевидно .
2) далее аргумент секанса нужно «зациклить», чтобы обеспечить изломы в прямой. Именно на этом этапе другие решения используют «грязный хак» в виде остатка от деления. Здесь же используется последовательное взятие прямой и обратной функции синуса —
Такой подход позволяет производить стандартные математические операции над получившейся формулой,
например
можно её продифференцировать и получить функцию для прямоугольной волны:
Благодаря этой же записи можно упростить функцию квадрата в полярных координатах до более эстетического вида, используя представление тригонометрический функций в комплексном виде.
2))] /. \[Phi] -> ArcTan[x, y]
// TrigToExp // Simplify
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} &
// TrigToExp // Simplify // FullSimplify
↓
Заключение
Как видите, даже в такой простой и банальной вещи как многоугольник, можно найти и придумать что-то новое. И на этом история не заканчивается — осталась неизвестной формула площади для общего случая, осталась неизвестной формула для произвольного, а не только правильного многоугольника, остались без рассмотрения разложения в степенные и тригонометрические ряды. Также, вероятно, подобного рода формула существует и для 3-мерного случая.
Поэтому если вам говорят, что в математике уже всё придумано и остались лишь задачи недоступные пониманию обычного человека — не верьте. Есть много сугубо практических задач, о существовании которых настоящие математики не подозревают, или их решение им не интересно из-за отсутствия достаточного хайпа вокруг них, или потому что у них уже есть примерное представление путей достижения для их решения.
Не бойтесь браться за задачи, решение которых отсутствует в википедии, не бойтесь публиковать их решения и не бойтесь читать комментарии под статьями о бесполезности всего сущего.
P.S. скачать оригинальный документ для Mathematica можно здесь.
Площадь в полярных координатах
Площадь в полярных координатахПриведу эвристическое обоснование формулы площади область, ограниченная полярной кривой.
Как видно из рисунка, полярная область «заметается» как если вращающимся лучом прожектора.
Посмотрите на небольшой клиновидный кусочек региона. Это подразумевает угол и радиус r.
Если маленький, клин составляет примерно круговой клин. Площадь кругового клина радиуса r и угла , так что это хорошее приближение к области клиновидной части выше.
Как обычно, я получаю общую площадь путем интегрирования, чтобы сложить площади из маленьких кусочков:
Во многих из этих задач на полярные области вы найдете формулы двойного угла полезными при выполнении интегралы:
Пример.
Найти площадь области внутри
кардиоида.
Вся кардиоида трассируется один раз от 0 до . Площадь
Пример. Найти площадь области внутри .
Четырехлепестковая роза вычерчивается один раз от 0 до .
Вы также можете использовать симметрию. Обратите внимание, что для . Следовательно правый лист прослеживается как идет от до , так что вы можете найти площадь этого листа и умножить на 4.
Пример. Найти площадь области внутри круг, но вне кардиоиды .
Рассматриваемая область представляет собой площадь внутри круга от 0 до минус площадь внутри кардиоиды от 0 к .
Я упрощу подынтегральную функцию, прежде чем делать первообразную:
(Я использовал идентификатор .)
Интеграл становится
Пример.
Найти площадь региона снаружи
но внутри.
Кривые пересекаются, когда . Это дает . Площадь является
Пример. Вот график .
Отметьте приблизительные точки на графике, которые соответствуют , , , и . Нарисуйте стрелки, которые показывают, как график прослеживается как возрастание. Затем найти площадь области внутри внешнего цикла, но вне внутренняя петля.
Обратите внимание, что внутренний цикл в третьем квадранте прослеживается как идет от 0 до . Почему баллы падают в третий квадрант , когда углы между 0 и ? Потому что для этих значений радиуса r отрицательно!
Вы можете найти площадь внутри внешнего цикла и за пределами внутреннего цикла путем вычитания площади внутреннего цикла из площади внешнего цикла.
По симметрии площадь всей внутренней петли в два раза больше площади
нижняя часть. Как мы только что заметили, нижняя часть прослеживается
от 0 до .
Итак
площадь внутренней петли
Продолжите вычисление площади внутреннего цикла:
Как видно на картинке, верхняя внешняя петля прочерчена. от до . По симметрии площадь внутри всей внешней петли вдвое превышает площадь верхней внешней петли.
Прежде чем приступить к вычислениям, давайте проясним распространенную путаницу. Люди часто думают, что при переходе от к верхнему внешнему циклу материал внутреннего цикла как-то «автомагически» вычитается.
Ну, это не так. Подумайте, как формула площади для полярной полученный. Область разбита на тонкие клинья, вершины которых в происхождении. Площадь типичного клина находится по формуле площади.
Посмотрите на несколько клиньев для верхней внешней петли. Вы можете видеть, что они простираться от начала координат через внутренний цикл .
Таким образом, когда формула площади применяется к внешнему циклу, она находит
область от начала координат до внешнего контура.
Это
неважно, что внутренний цикл мешает.
После этого я вычислю площадь внешнего цикла. Это
(Подробности не расписываю, так как по сути они одинаковые как и для области внутреннего цикла.)
Площадь внутри внешнего цикла и снаружи внутреннего цикла равна
Пример. Найдите площадь области, которая внутри обоих и одновременно.
(То есть найти площадь пересечения ул. внутренности кривых.)
Найдите место пересечения кривых:
Это дает .
Область имеет форму дольки апельсина и может быть разбита на Два куска. Кусок А — это площадь внутри (круг, который поднимается вверх по ось Y) от до . Кусок B — это площадь внутри (круг, который идет вдоль оси x) от до . Площадь в этот пример представляет собой сумму площадей A и B, поэтому
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2020 Брюс Икенага
Полярные координаты · Алгебра и тригонометрия
Полярные координаты · Алгебра и тригонометрияВ этом разделе вы будете:
- Наносить точки с использованием полярных координат.
- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Найдите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
В более чем 12 км от порта парусник попадает в непогоду и сбивается с курса ветром со скоростью 16 узлов (см. [ссылка]). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Нанесение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах (x,y)
в декартовой плоскости координат. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы вводим полярных координат , которые являются точками, помеченными (r,θ)
и нанесены на полярную сетку.
Полярная сетка представлена серией концентрических кругов, исходящих из полюс или начало координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью x-, которая теперь рассматривается как полярная ось , а начало координат — как полюс. Первая координата r
— радиус или длина направленного отрезка прямой от полюса. Угол θ,
, измеренное в радианах, указывает направление r.
Двигаемся против часовой стрелки от полярной оси на угол θ,
и измерьте направленный отрезок длиной r
в направлении θ.
Несмотря на то, что мы измеряем θ
Сначала, а затем r,
полярная точка записывается с координатой r первой. Например, чтобы построить точку (2,π4),
мы бы переместили π4
единиц против часовой стрелки, а затем длину 2 от полюса. Эта точка нанесена на сетку в [ссылка].
Нанесение точки на полярную сетку
Нанесите точку (3,π2)
на полярную сетку.
Угол π2
находится путем пролистывания в направлении против часовой стрелки на 90° от полярной оси. Точка расположена на расстоянии 3 единиц от полюса в направлении π2
, как показано на [ссылка].
Постройте точку (2, π3)
в полярной сетке .
0003
Нанесение точки в полярной системе координат с отрицательной составляющей
Нанесение точки (−2, π6)
на полярную сетку.
Мы знаем, что π6
находится в первом квадранте. Однако r=−2.
Мы можем построить точку с отрицательным значением r
двумя способами:
- Построить точку
(2,π6)
, переместив
π6против часовой стрелки и продолжение направленного отрезка на 2 единицы в первый квадрант.
Затем проследите направленный отрезок обратно через полюс и продолжайте движение на 2 единицы в третий квадрант; - Переместить
π6
в направлении против часовой стрелки и проведите отрезок, направленный от полюса на 2 единицы в отрицательном направлении, в третий квадрант.
Затем проследите направленный отрезок обратно через полюс и продолжайте движение на 2 единицы в третий квадрант;См. [ссылка](а). Сравните это с графиком полярной координаты (2,π6)
, показанным в [ссылка](b).
Нанесите точки (3,−π6)
и (2,9π4)
на одну и ту же полярную сетку.
Преобразование полярных координат в прямоугольные координаты
Когда задан набор из полярных координат , нам может понадобиться преобразовать их в прямоугольные координаты . Для этого мы можем вспомнить отношения, существующие между переменными x, y, r,
и θ.
cos θ=xr→x=rcos θsin θ=yr→y=rsin θ
При опускании перпендикуляра из точки плоскости на ось x- образуется прямоугольный треугольник, как показано на [ссылка]. Простой способ запомнить приведенные выше уравнения — подумать о cos θ
как прилежащая сторона по гипотенузе и sin θ
как противолежащая сторона гипотенузы.
Преобразование полярных координат в прямоугольные
Для преобразования полярных координат (r, θ)
в прямоугольные координаты (x, y),
let
cos θ=900→x=rcos000 →y=rsin θ
При заданных полярных координатах преобразовать в прямоугольные координаты.
- Учитывая полярную координату
(г, θ),
напишите
х=rcos θи
у=rsin θ. - Оценить
cos θ
и
грех θ. - Умножить
cos θ
на
r, чтобы найти координату x- прямоугольной формы.
- Умножить
sin θ
на
r, чтобы найти координату y- прямоугольной формы.
Запись полярных координат как прямоугольных координат
Запишите полярные координаты (3,π2)
в виде прямоугольных координат.
Использовать эквивалентные отношения.
x=rcos θx=3cos π2=0y=rsin θy=3sin π2=3
Прямоугольные координаты (0,3).
См. [ссылка].
Запись полярных координат в виде прямоугольных координат
Запись полярных координат (−2,0)
в виде прямоугольных координат.
См. [ссылка]. Записав полярные координаты прямоугольными, мы имеем
x=rcos θx=−2cos(0)=−2y=rsin θy=−2sin(0)=0
Прямоугольные координаты также (−2,0).
Запишите полярные координаты (−1,2π3)
в виде прямоугольных координат.
(х, у)=(12,−32)
Преобразование прямоугольных координат в полярные координаты
Чтобы преобразовать прямоугольных координат в полярных координат , мы будем использовать два других знакомых соотношения.
Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки.
Преобразование прямоугольных координат в полярные координаты
Преобразование прямоугольных координат в полярные требует использования одного или нескольких соотношений, показанных в [ссылка].
cos θ=xr или x=rcos θsin θ=yr или y=rsin θ r2=x23+y2tan θ=yx 9000
Запись прямоугольных координат в виде полярных координат
Преобразование прямоугольных координат (3,3)
в полярные координаты.
Мы видим, что исходная точка (3,3)
находится в первом квадранте. Чтобы найти θ,
, используйте формулу tan θ=yx.
Это дает
TAN θ = 33 TAN θ = 1 TAN — 1 (1) = π4
, чтобы найти R,
Мы заменяем значения для X
и Y
в формулу R = X2+Y2 .
Мы знаем, что r
должно быть положительным, так как π4
находится в первом квадранте. Таким образом,
r=32+32r=9+9r=18=32
Итак, r=32
и θ=π4,
дает нам полярную точку (32,π4).
См. [ссылка].
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки (−32, 5π4)
и (32,−7π4)
будут совпадать с исходным решением (32, π4).
Точка (−32, 5π4)
указывает на дальнейшее движение против часовой стрелки на π,
, что прямо противоположно π4.
Радиус выражается как −32.
Однако угол 5π4
расположен в третьем квадранте, а так как r
отрицательно, то продлеваем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и (32, π4).
Точка (32, −7π4)
— это ход дальше по часовой стрелке на −7π4,
от π4.
Радиус, 32,
тот же.
Преобразование уравнений между полярными и прямоугольными формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами.
Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
Имея уравнение в полярной форме, постройте его график с помощью графического калькулятора.
- Измените MODE на POL , представляя полярную форму.
- Нажмите кнопку Y= , чтобы открыть экран, позволяющий ввести шесть уравнений: r1, r2, . . . , r6.
- Введите полярное уравнение, установите равным р.
- Нажмите ГРАФИК .
Запись декартова уравнения в полярной форме
Запишите декартово уравнение x2+y2=9
в полярной форме.
Цель состоит в том, чтобы исключить из уравнения x
и y
и ввести r
и θ.
В идеале мы запишем уравнение r
как функцию θ.
Чтобы получить полярную форму, мы будем использовать соотношения между (x,y)
и (r,θ).
Поскольку x=rcos θ
и y=rsin θ,
, мы можем подставить и решить для r.
(rcos θ)2+(rsin θ)2=9 r2cos2θ+r2sin2θ=9 r2(cos2θ+sin2θ)=9 r=±3Используйте свойство квадратного корня.
Таким образом, x2+y2=9,r=3,
и r=−3
должны генерировать один и тот же граф. См. [ссылка].
Чтобы нарисовать круг в прямоугольной форме, мы должны сначала решить для y.
x2+y2=9 y2=9−x2 y=±9−x2
Обратите внимание, что это две отдельные функции, так как круг не проходит тест вертикальной линии. Поэтому нам нужно ввести в калькулятор положительный и отрицательный квадратный корень отдельно, как два уравнения вида Y1=9−x2
и Y2=−9−x2.
Нажмите ГРАФИК.
Переписать декартово уравнение как полярное уравнение
Переписать декартово уравнение x2+y2=6y
как полярное уравнение.
Это уравнение похоже на предыдущий пример, но требует других шагов для преобразования уравнения.
Мы все еще можем следовать тем же процедурам, которые мы уже изучили, и сделать следующие замены:
R2 = 6 лет x2+y2 = r2. r2=6rsin θЗамените y=rsin θ. r2−6rsin θ=0 Установить равным 0. r(r−6sin θ)=0 Умножить и решить. r=0Мы отвергаем r=0, так как он представляет только одну точку (0,0). или r=6sin θ
Следовательно, уравнения x2+y2=6y
и r=6sin θ
должны дать нам один и тот же график. См. [ссылка].
Декартово или прямоугольное уравнение наносится на прямоугольную сетку, а полярное уравнение наносится на полярную сетку. Ясно, что графики идентичны.
Переписать декартово уравнение в полярной форме
Переписать декартово уравнение y=3x+2
как полярное уравнение.
Мы будем использовать соотношения x=rcos θ
и y=rsin θ.
y=3x+2 rsin θ=3rcos θ+2 rsin θ−3rcos θ=2r(sin θ−3cos θ)=2Isolater. r=2sin θ−3cos θРешите для r.
Перепишите декартово уравнение y2=3−x2
в полярной форме.
г=3
Определение и построение полярных уравнений путем преобразования в уравнения прямоугольной формы
Мы научились преобразовывать прямоугольные координаты в полярные и увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Графическое изображение полярного уравнения путем преобразования в прямоугольное уравнение
Преобразуйте полярное уравнение r=2sec θ
в прямоугольное уравнение и нарисуйте соответствующий график.
Преобразование составляет
r = 2sec θ r = 2cos θ rcos θ = 2 x = 2
Обратите внимание, что уравнение r = 2sec θ
, нарисованное на полярной сетке, явно такое же, как и вертикальная линия x = 2
нарисован на прямоугольной сетке (см. [ссылка]). Точно так же, как x=c
— стандартная форма для вертикальной линии в прямоугольной форме, r=csec θ
— стандартная форма для вертикальной линии в полярной форме.
Аналогичное обсуждение показало бы, что график функции r=2csc θ
будет горизонтальной линией y=2.
Фактически, r=ccsc θ
является стандартной формой горизонтальной линии в полярной форме, соответствующей прямоугольной форме y=c.
Переписывание полярного уравнения в декартовой форме
Перепишите полярное уравнение r=31−2cos θ
как декартово уравнение.
Цель состоит в том, чтобы исключить θ
и r,
и ввести x
и y.
Очищаем дробь, а затем используем подстановку. Чтобы заменить r
на x
и y,
, мы должны использовать выражение x2+y2=r2.
r=31−2cos θr(1−2cos θ)=3 r(1−2(xr))=3Используйте cos θ=xr, чтобы исключить θ. r−2x=3 r=3+2xИзолировать r. r2=(3+2x)2В квадрате с обеих сторон. x2+y2=(3+2x)2Используйте x2+y2=r2.
Уравнение Декарта: x2+y2=(3+2x)2.
Однако, чтобы изобразить это на графике, особенно с помощью графического калькулятора или компьютерной программы, мы хотим изолировать y.
x2+y2=(3+2x)2 y2=(3+2x)2−x2 y=±(3+2x)2−x2
Когда все наше уравнение было изменено с r
и θ
3
3
до x
и y,
мы можем остановиться, если только нас не попросят найти для y
или упростить. См. [ссылка].
Форма графика в виде песочных часов называется гипербола . Гиперболы имеют много интересных геометрических свойств и приложений, которые мы будем исследовать далее в разделе «Аналитическая геометрия».
Анализ
В этом примере правая часть уравнения может быть расширена, а уравнение еще больше упрощено, как показано выше. Однако уравнение нельзя записать в виде одной функции в декартовой форме. Мы можем захотеть записать прямоугольное уравнение в стандартной форме гиперболы. Для этого мы можем начать с исходного уравнения.
x2+y2=(3+2x)2 x2+y2-(3+2x)2=0x2+y2-(9+12x+4×2)=0 x2-y2-9-12x-4x 2 = 0 12x+y2=9Умножить на −1. 3×2+12x−y2=−9 3(x2+4x+ )−y2=−9 Организуйте термины, чтобы заполнить квадрат для x. 3(x2+4x+4)−y2=−9+12 3(x+2)2−y2=3 (x+2)2−y23=1
Перепишите полярное уравнение r=2sin θ
в декартовой форме.
x2+y2=2y
или, в стандартной форме для окружности, x2+(y−1)2=1
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение r=sin(2θ)
в декартовой форме.
r=sin(2θ)Используйте для синуса тождество двойного угла. r=2sin θcos θИспользуйте cos θ=xr и sin θ=yr. r=2(xr)(yr) Упростить. r=2xyr2 Умножьте обе части на r2. r3=2xy(x2+y2)3=2xyAs x2+y2=r2,r=x2+y2.
Это уравнение также можно записать в виде
(x2+y2)32=2xy или x2+y2=(2xy)23
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными координатами.
- Введение в полярные координаты
- Сравнение полярных и прямоугольных координат
Ключевые уравнения
| Формулы преобразования | cos θ=xr→x=rcos θsin θ=yr→y=rsin θ r2=x2+y2tan θ=yx |
Ключевые понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или источника.
- Для построения точки в форме
(r,θ), θ>0,
двигаться против часовой стрелки от полярной оси на угол
θ,, а затем продолжить направленный отрезок от полюса на длину
гв направлении
θ.Если
θотрицательно, двигайтесь по часовой стрелке и продолжайте направленный отрезок на длину
гв направлении
θ.См. [ссылка].
- Если
r
отрицательное, продлите направленный отрезок в направлении, противоположном
θ.См. [ссылка].
- Чтобы преобразовать полярные координаты в прямоугольные, используйте формулы
х=rcos θ
и
у=rsin θ.См. [ссылка] и [ссылка].
- Чтобы преобразовать прямоугольные координаты в полярные, используйте одну или несколько формул:
cos θ=xr,sin θ=yr,tan θ=yx,
и
г=х2+у2.См. [ссылка].
- Преобразование уравнений между полярной и прямоугольной формой означает выполнение соответствующих замен на основе доступных формул вместе с алгебраическими манипуляциями. См. [ссылка], [ссылка] и [ссылка].
- Использование соответствующих замен позволяет переписать полярное уравнение в виде уравнения прямоугольной формы, а затем изобразить его на прямоугольной плоскости. См. [ссылка], [ссылка] и [ссылка].
Секционные упражнения
Устный
Чем полярные координаты отличаются от прямоугольных координат?
Для полярных координат точка на плоскости зависит от угла от положительной оси x- и расстояния от начала координат, в то время как в декартовых координатах точка представляет горизонтальное и вертикальное расстояния от начала координат. Для каждой точки координатной плоскости существует одно представление, но для каждой точки полярной плоскости существует бесконечное количество представлений.
Чем полярные оси отличаются от х — и у -оси декартовой плоскости?
Объясните, как изображаются полярные координаты.
Определите θ
для точки, затем переместите r
единиц от полюса, чтобы нанести точку. Если r
отрицательно, переместите r
единиц от полюса в противоположном направлении, но под тем же углом. Точка находится на расстоянии r
от начала координат под углом θ
от полярной оси.
Как расположены точки (3,π2)
и (−3,π2)
связаны?
Объясните, почему точки (−3,π2)
и (3,−π2)
совпадают.
Точка (−3,π2)
имеет положительный угол, но отрицательный радиус и нанесена на график путем перемещения на угол π2
и последующего перемещения на 3 единицы в отрицательном направлении. Это помещает точку на 3 единицы ниже отрицательной оси y . Точка (3,−π2)
имеет отрицательный угол и положительный радиус и наносится на график, сначала перемещаясь на угол −π2
, а затем переместиться на 3 единицы вниз, что является положительным направлением для отрицательного угла. Точка также находится на 3 единицы ниже отрицательной оси и .
Алгебраический
Для следующих упражнений преобразуйте заданные полярные координаты в декартовы координаты с r>0
и 0≤θ≤2π.
Не забывайте учитывать квадрант, в котором находится данная точка при определении θ
за точку.
(7,7π6)
(5,π)
(−5,0)
(6,−π4)
(−3,π6)
(−332,−32)
(4,7π4)
Для следующих упражнений преобразуйте заданные декартовы координаты в полярные координаты с r>0, 0≤θ<2π.
Не забудьте учесть квадрант, в котором находится данная точка.
(4,2)
(25, 0,464)
(−4,6)
(3,−5)
(34,5,253)
(-10,-13)
(8,8)
(82,π4)
Для следующих упражнений преобразуйте данное декартово уравнение в полярное уравнение.
y=4
r=4cscθ
y=2×4
r=sinθ2cos4θ3
х2+у2=4у
x2+y2=3x
r=3cosθ
х2-у2=х
x2−y2=3y
r=3sinθcos(2θ)
х2+у2=9
x2=9y
r=9sinθcos2θ
9xy=1
r=19cosθsinθ
Для следующих упражнений преобразуйте данное полярное уравнение в декартово уравнение. Если возможно, напишите в стандартной форме коники и определите представленное коническое сечение.
г=3sin θ
r=4cos θ
x2+y2=4x
или (x−2)24+y24=1;
круг
г=4sin θ+7cos θ
r=6cos θ+3sin θ
3y+x=6;
строка
r=2сек θ
r=3csc θ
y=3;
строка
r=rcos θ+2
r2=4сек θ csc θ
xy=4;
гипербола
r2=4
x2+y2=4;
круг
r=14cos θ−3sin θ
r=3cos θ−5sin θ
x−5y=3;
строка
Графический
Для следующих упражнений найдите полярные координаты точки.
(3,3π4)
(5,π)
Для следующих упражнений нанесите точки.
(−2,π3)
(-1,-π2)
(3.5,7π4)
(−4,π3)
(5,π2)
(4,−5π4)
(3,5π6)
(−1,5,7π6)
(−2,π4)
(1,3π2)
Для следующих упражнений преобразуйте уравнение из прямоугольной в полярную форму и постройте график на полярной оси.
5x−y=6
r=65cosθ−sinθ
2х+7у=-3
x2+(y−1)2=1
r=2sinθ
(х+2)2+(у+3)2=13
х=2
r=2cosθ
х2+у2=5у
x2+y2=3x
r=3cosθ
Для следующих упражнений преобразуйте уравнение из полярной формы в прямоугольную и постройте график на прямоугольной плоскости.
r=−4
x2+y2=16
θ=−2π3
θ=π4
у=х
r=сек θ
r=−10sin θ
x2+(y+5)2=25
r=3cos θ
Технология
Используйте графический калькулятор, чтобы найти прямоугольные координаты (2,−π5).
Округлить до тысячных.
(1,618,−1,176)
Используйте графический калькулятор, чтобы найти прямоугольные координаты (−3,3π7).
Округлить до тысячных.
Используйте графический калькулятор, чтобы найти полярные координаты (−7,8)
в градусах. Округлить до тысячных.
(10.630,131.186°)
Используйте графический калькулятор, чтобы найти полярные координаты (3,−4)
в градусах. Округлить до сотых.
Используйте графический калькулятор, чтобы найти полярные координаты (−2,0)
в радианах. Округлить до сотых.
(2,3.14) или (2,π)
Расширения
Опишите график r=asec θ;a>0.
Опишите график r=asec θ;a<0.
Вертикальная линия с a
единиц слева от оси и .
Опишите график r=acsc θ;a>0.
Опишите график r=acsc θ;a<0.
Горизонтальная линия с a
единиц ниже оси x .
Какие полярные уравнения дадут косую линию?
Для следующего упражнения постройте график полярного неравенства.
r<4
0≤θ≤π4
θ=π4, r ≥ 2
θ=π4, r ≥−3
0≤θ≤π3, r < 2
−π6<θ≤π3,−3 , где указывает угол поворота от полярной оси и представляет собой радиус или расстояние точки от полюса в направлении Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected] Атрибуция: Глоссарий
Эта работа находится под лицензией Creative Commons Attribution 4. 0 International License.