8 класс область определения функции
Вы искали 8 класс область определения функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и d y как найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «8 класс область определения функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 8 класс область определения функции,d y как найти,e y функции,высшая математика функции область определения функции,график функции область определения функции,естественная область определения функции это,как найти d f функции,как найти область определения функции алгебра 8 класс,как найти область определения функции и значения,как найти область определения функции и область значений,как найти область определения функции и область значения,как обозначается область определения,как обозначается область определения функции и область значения,найдите область значений и область определения функции,нахождение области значения и области определения функции,область значений и область определения функции,область значения и область определения функции как найти,область значения это х или у,область определения как обозначается,область определения функции и область изменения функции,функция область определения и область,чем отличается область значения от области определения функции,чем отличается область определения функции от области значения,что называется областью определения функции,что такое естественная область определения функции.
Решить задачу 8 класс область определения функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Ответы на все модули (для контрольного теста) по предмету математический анализ.
Автор admin На чтение 11 мин. Просмотров 1.1k. Опубликовано
Ответы на все модули (для контрольного теста) по предмету математический анализ.
Полностью взято тут.
Укажите область определения функции
Какая поверхность называется графиком функции n переменных?
n-мерная гиперповерхность в пространстве , точки которой имеют вид
Найдите область определения функции
Какая функция у = f(x) называется возрастающей на промежутке X?
если большему значению аргумента из этого промежутка соответствует большее значение функции
Какая функция называется явной?
если функция задана формулой y = f(x), в которой правая часть не содержит зависимой переменной
Найдите область определения функции
Укажите область определения функции
Укажите область определения функции
Укажите область определения функции
Укажите область определения функции
Укажите область определения функции
Какова область определения функции ?
f(x) ≠ 0
Укажите область определения функции
Какая функция называется четной?
если для любых значений х из области определения
Укажите область определения функции
На каком из рисунков изображена область определения функции ?
Укажите область определения функции
Какая из перечисленных функций не относится к трансцендентным функциям?
дробно-рациональная функция
Укажите область определения функции
Какая из перечисленных функций не относится к алгебраическим функциям?
логарифмическая функция
На каком из рисунков изображена область определения функции ?
В каком из перечисленных случаев величина называется параметром?
если она сохраняет постоянное значение лишь в условиях данного процесса
Укажите область определения функции
Относительно чего симметричен график нечетной функции?
относительно начала координат
График какой функции симметричен относительно оси ординат?
четной функции
Найдите интервал сходимости ряда , не исследуя концов интервала
Разложите в степенной ряд f(x) = sin 2x
Исследуйте сходимость ряда
расходится
Найдите радиус сходимости ряда
R = 2
Найдите интервал сходимости ряда
Найдите интервал сходимости ряда, не исследуя концов интервала
Разложите в степенной ряд f(x) = arctg 3x
Исследуйте сходимость ряда
сходится
Исследуйте сходимость ряда
расходится
Исследуйте сходимость ряда
сходится
Исследуйте сходимость ряда
расходится
Исследуйте сходимость ряда
сходится
Какой ряд называется знакопеременным рядом?
числовой ряд, члены которого имеют различные знаки
Исследуйте ряд на сходимость
расходится
Укажите необходимый признак сходимости ряда
eсли ряд сходится, то его n-й член стремится к нулю при
Исследуйте сходимость ряда
расходится
Исследуйте сходимость ряда
расходится
Исследуйте ряд на сходимость
сходится
Исследуйте сходимость ряда
сходится
Исследуйте сходимость ряда
сходится
Найдите радиус сходимости ряда
R = 1
Исследуйте сходимость ряда
сходится
Исследуйте сходимость ряда
расходится
Найдите интервал сходимости ряда
Найдите радиус сходимости ряда
R = 1
Найдите предел
0,1
Найдите предел
Найдите предел
Найдите предел
∞
Найдите предел
e-1
Найдите предел
5
Найдите предел
Найдите
4
Найдите предел
1
Найдите предел
5
Найдите предел
32
Найдите предел
18
Найдите предел
Найдите предел
Найдите предел
∞
Найдите предел
Найдите предел
0
Найдите предел
Найдите предел
Найдите предел
1,5
Найдите предел
Найдите предел
∞
Найдите предел
Найдите предел
Найдите предел функции при
0
Найдите частные производные функции двух переменных
Найдите полный дифференциал функции
Найдите частные производные второго порядка функции z = xy + xsin y
Дана функция .
Решите уравнение
Найдите производную функции
Дана функция . Найдите y′(36)
Найдите частные производные функции трех переменных
Вычислите предел по правилу Лопиталя
Найдите производную функции f(t) = ln(2cos t)
Чему, согласно правилу Лопиталя, равен предел отношения двух бесконечно малых или бесконечно больших функций, если последний существует?
пределу отношения производных двух бесконечно малых или бесконечно больших функций
Вычислите предел по правилу Лопиталя
0
Найдите производную функции
Найдите частные производные функции двух переменных z = xsin y + ysin x
Найдите полный дифференциал функции
dz = (y cosxy + 2xy2) dx + (x cosxy + 2yx2) dy
Найдите производную функции
Вычислите предел по правилу Лопиталя
Найдите производную функции
Найдите производную функции
Вычислите предел по правилу Лопиталя
1
Найдите производную функции
Чему равна производная постоянной функции?
0
Найдите частные производные второго порядка функции
Укажите формулу для производной произведения функций u и v, если они дифференцируемы в некоторой точке, и их произведение также дифференцируемо в этой точке
Найдите среднюю скорость движения тела, совершаемого по закону , для промежутка времени от
12
Вычислите предел по правилу Лопиталя
4
Найдите промежутки возрастания или убывания функции
возрастает при и убывает при
В каких точках выпукла или вогнута кривая
выпукла во всех точках
В каких точках выпукла или вогнута кривая
вогнута во всех точках
Каково необходимое условие возрастания функции?
если функция y = f(x) дифференцируема и возрастает на интервале (a; b), то для всех x из этого интервала
Найдите вертикальные асимптоты к графику функции
х = 0 и х = 1
Найдите точки максимума (минимума) функции
(2; 4) — точка максимума
Что называется асимптотой кривой?
прямая l, если расстояние от переменной точки М кривой до этой прямой стремится к нулю при удалении точки М в бесконечность
Какая кривая y = f(x) называется выпуклой на интервале (a, b)?
если все точки кривой лежат ниже любой ее касательной на этом интервале
Найдите точку перегиба кривой
Найдите точку перегиба кривой
(0; 0)
Определите поведение функции
возрастает
Найдите промежутки возрастания или убывания функции
убывает при , возрастает при
Найдите наименьшее значение функции на отрезке [0; 3]
Что называется критическими точками второго рода?
точки области определения, в которых вторая производная функции y = f(x) обращается в нуль или не существует
Исследуйте функцию на экстремумы
максимум в точке ; минимум в точке 0
Найдите промежутки возрастания или убывания функции
убывает при x > 2, возрастает x < 2
Найдите наибольшее и наименьшее значения функции на промежутке
Исследуйте функцию на монотонность и экстремум
— промежуток возрастания, — промежуток убывания, x = 0 — точка максимума
Найдите точки максимума (минимума) функции
— точка максимума
Вертикальные асимптоты к графику функции имеют вид
x = 4, x = 0
Укажите необходимое условие экстремума
в точке экстремума функции ее производная либо равна нулю (f'(x) = 0), либо не существует
Определите поведение функции
убывает
Определите поведение функции при x = 0
возрастает
Число называется наибольшим значением функции на отрезке [a; b], если
для всех x из этого отрезка выполняется неравенство
Найдите точки максимума (минимума) функции
— точка минимума, (1; 0,5) — точка максимума
Найдите интеграл
Найдите
Чему равен неопределенный интеграл от алгебраической суммы функций?
алгебраической сумме интегралов от этих функций
Найдите
Найдите первообразную для функции
Найдите интеграл
Найдите
Найдите
Найдите
Найдите
Найдите интеграл
Найдите
Найдите
Найдите
Укажите формулу интегрирования по частям
Найдите
Найдите интеграл
Найдите первообразную функции
Сколько первообразных может иметь каждая функция?
бесконечно много первообразных
Найдите первообразную для функции
Найдите
Найдите
Найдите
Найдите
Найдите
Вычислите определенный интеграл
2
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
8
Вычислите определенный интеграл
0,24
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Укажите какая из сумм является интегральной
Вычислите определенный интеграл
Вычислите определенный интеграл
0,25
Вычислите определенный интеграл
Вычислите определенный интеграл
0,5
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
0,4
Вычислите определенный интеграл
2
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
Вычислите определенный интеграл
45
Найдите площадь фигуры, ограниченной прямыми y = 5x, x = 2 и осью Ox
10
Найдите площадь фигуры, ограниченной параболами:
9
Вычислите площадь плоской фигуры, ограниченной линиями: и y = 0
Сила в 6 кГ растягивает пружину на 8 см.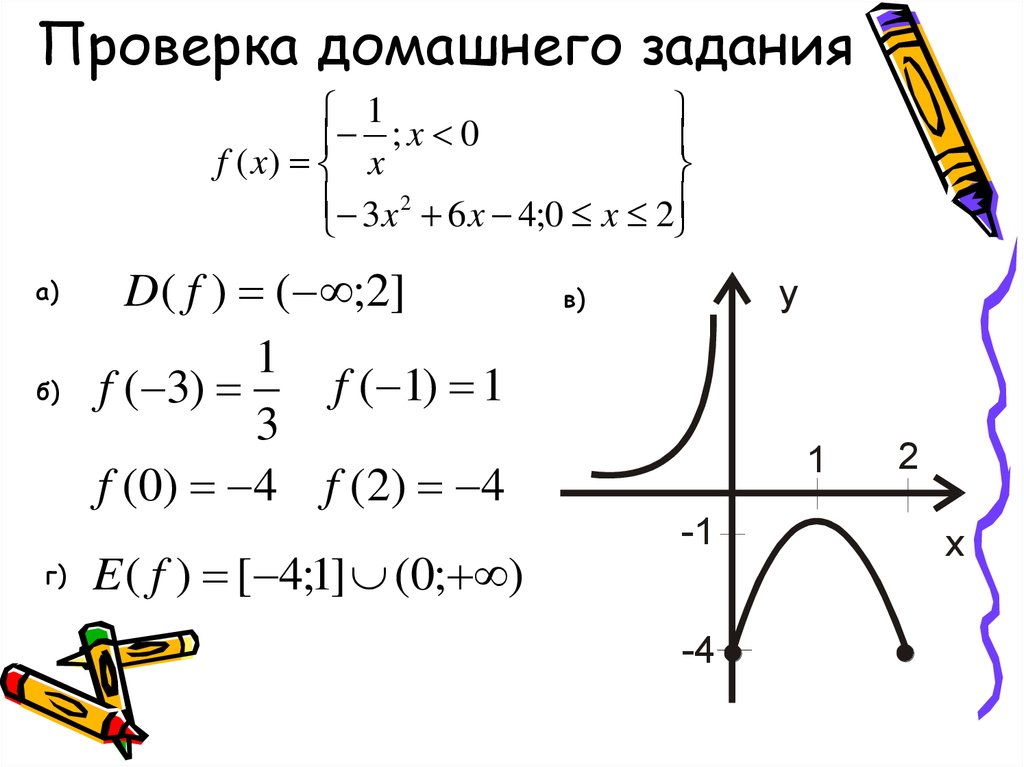
Какую работу она производит?
0,24 кГм
Найдите площадь области, ограниченной прямыми и осью Ox
10
Найдите площадь фигуры, ограниченной линиями , y = 0
Найдите площадь фигуры, ограниченной линиями , y = 0, x = 0, x = 2
14/3
Найдите площадь фигуры, заключенной между кривой , прямыми , x = 2 и осью Ox
Тело движется прямолинейно со скоростью м/с. Найдите путь, пройденный точкой за первые 5 с от начала движения
140 м
Какую работу совершает сила в 8 H при растяжении пружины на 6 см?
0,24 Дж
Найдите площадь фигуры, ограниченной линиями
Вычислите силу давления воды на стенку шлюза, длина которого 20 м и высота 5 м, считая шлюз доверху заполненным водой
2,45 МН
Найдите площадь фигуры, заключенной между прямыми y = 4x — 5, x = -3, x=-2 и осью Ox
15
Найдите площадь фигуры, ограниченной отрезком оси Ox, графиком функции y = cosx, отрезками прямых и x = π
Найдите площадь фигуры, ограниченной линиями , y = 0
8
Найдите площадь фигуры, ограниченной линиями
Найдите площадь фигуры, ограниченной прямыми y = 4x, x = 4 и осью Ox
32
Вычислите площадь плоской фигуры, ограниченной линиями: , y = 0, ,
1
Найдите площадь фигуры, ограниченной линиями , y = 0
36
Скорость падающего в пустоте тела определяется по формуле v = 9,8t м/сек.
Какой путь пройдет тело за первые 10 секунд падения?
490 м
Найдите площадь фигуры, ограниченной линиями , y = 0
Скорость точки, движущейся прямолинейно, задана уравнением . Вычислите путь, пройденный точкой за 3 с от начала движения
48 м
Найдите площадь области, ограниченной кривой , прямыми , x = 2 и осью Ox
17
Найдите площадь плоской фигуры, ограниченной линиями , x = 2 и отрезком оси Ox
6
Вычислите силу давления воды на одну из стенок аквариума имеющего длину 30 см и высоту 20 см
58,8 Н (6 кГ)
Найдите общее решение уравнения (x + y)dx + xdy = 0
Среди перечисленных уравнений укажите однородные уравнения:
1. ;
2. ;
3. ;
4. ;
5. ;
6.
1, 4, 5
Что называется порядком дифференциального уравнения?
наивысший порядок производной, входящей в дифференциальное уравнение
Найдите частное решение уравнения 2(z + 3)dt = (t + 2)dz, если при
z = — (t + 2)2— 3
Среди перечисленных дифференциальных уравнений укажите уравнение с разделяющимися переменными
Даны дифференциальные уравнения:
1.
2.
3.
4.
5.
6.
Укажите среди них однородные уравнения
1, 3, 5
Найдите общее решение уравнения
Найдите частное решение уравнения 2sdt = tds, если при t = 1 s = 2
Найдите общее решение уравнения y′′ = cos x
Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?
частным решением
Найдите частное решение уравнения , если при t = 0 s = 0
Найдите общее решение уравнения
Найдите частное решение уравнения xdx = dy, если при x = 1 y = 0
Найдите общее решение уравнения (3x + 2)dy + (y + 2)dx = 0
–
Укажите общее решение дифференциального уравнения
Найдите общее решение уравнения
Найдите общее решение уравнения y′ = sin x + 2
y = — cosx + 2x + C1
Найдите общее решение уравнения
Среди перечисленных дифференциальных уравнений укажите уравнения с разделяющимися переменными:
1.
;
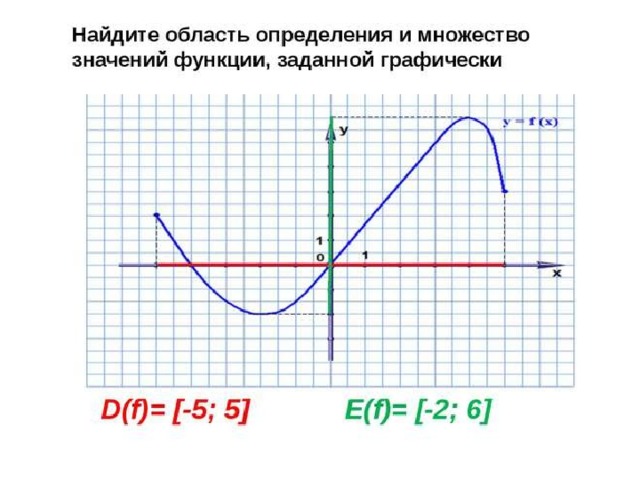2. ;
3.
4.
5. ;
6.
2, 3, 5
Среди перечисленных дифференциальных уравнений укажите однородное уравнение
Найдите общее решение уравнения
Найдите общее решение уравнения
Найдите общее решение уравнения
Среди перечисленных дифференциальных уравнений укажите уравнение с разделяющимися переменными
y′ + ycos x = 0
Какое уравнение называется дифференциальным уравнением?
уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков
Какую подстановку используют при решении уравнений Бернулли?
y = u ∙ v
Среди перечисленных дифференциальных уравнений укажите линейное уравнение
Среди перечисленных дифференциальных уравнений указать уравнение Бернулли:
1. ;
2. ;
3.
;
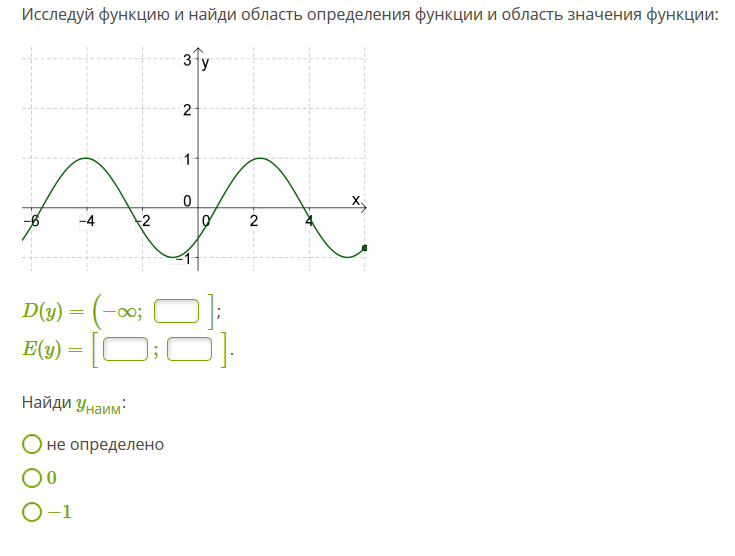4.
3
Найдите общее решение уравнения
Найдите общее решение уравнения
Найдите общее решение уравнения
Найдите общее решение уравнения
Среди перечисленных уравнений укажите линейные уравнения первого порядка:
1. ;
2. ;
3. ;
4.
2, 4
Найдите общее решение уравнения
Найдите общее решение уравнения
Решите уравнение
Укажите частное решение дифференциального уравнения y′ + 2y = 4 удовлетворяющее начальному условию y(0) = 5
Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли
Найдите общее решение уравнения
Даны дифференциальные уравнения:
1.
2.
3.
4.
Укажите среди них линейные уравнения
1, 3
Найдите общее решение уравнения
Найдите общее решение уравнения
Найдите общее решение уравнения
y = C1e-x + C2ex
Найдите общее решение уравнения
Решите уравнение y″ — 6y′ + 9y = 0
Найдите частное решение дифференциального уравнения y′ + 4y = 2, удовлетворяющее начальному условию y(0) = 6
При решении каких уравнений используют подстановку ?
при решении однородных уравнений
Укажите общее решение уравнения
y = x (tg x + C)
Решите уравнение
Укажите общее решение уравнения
Домен | bartleby
Что такое домен?
Простыми математическими терминами домен определяется как пространство, в котором будут лежать все возможные входные данные для функции.
Его также можно выразить как набор отклонений для требуемой функции.
Как работает домен?
Обычно для домена рассматриваются два разных набора. Данные отображаются из одного набора в другой набор с помощью функций.
Следует отметить, что рассматриваемая функция может быть определена на самом домене. Другими словами, каждая точка области удовлетворяет требуемой функции. Так выбирается домен. В результате область определения функции и область определения функции совпадают. Однако для частичных функций такого совпадения не происходит. Это связано с тем, что при рассмотрении частичной функции ее область определения содержит по крайней мере все элементы, присутствующие в области определения. Другими словами, домен действует как надмножество для домена определения частичной функции.
Формула
Если есть два набора A и B, такие, что данные отображаются из A в B, то это записывается как:
f: A → B
Здесь f — функция, элементы из набора A в набор B.
Как определяется домен?
Когда рассматривается функция, можно сказать, что она состоит из домена, если функция может быть определена в каждой точке внешнего набора данных. Кроме того, домен, кодовый домен и граф являются частью функции, если функция записана в форме (X, Y, G), где X — домен, Y — кодовый домен, а G — график функции.
Если функцию можно просто определить в графической форме, то домен может или не может быть частью функции.
Например, если мы рассмотрим косинусоидальную кривую, то набор действительных чисел R можно назвать областью определения функции. Точно так же, если мы рассмотрим функцию квадратного корня, то ее область определения будет равна множеству всех чисел, которые равны или больше нуля, учитывая, что комплексные числа были исключены в обоих случаях.
Обычно домены также могут быть представлены на осях. Если декартова система координат используется для представления функции, которая имеет область определения подмножества действительных чисел, то ось x может использоваться для представления области.
Что такое природный домен?
Естественная область определения функции состоит из всех значений, на которых функция может быть правильно определена. Обычно такие домены можно принимать за действительные числа во всех случаях. В определенных ситуациях также могут быть взяты комплексные числа и целые числа. Если снова рассмотреть функцию квадратного корня, ее естественная область определения будет состоять из неотрицательных действительных чисел. Это когда функция действительного числа была рассмотрена.
Какой диапазон?
Если рассматриваются естественные домены, то каких бы значений ни достигала функция, набор всех таких значений определяется как диапазон.
Что такое теория категорий?
В доменах данные отображаются с помощью функций и представлены стрелками. Эти стрелки также известны как морфизмы. Когда морфизмы рассматриваются не как функции, тогда на место вступает теория категорий. Формулировка идей относительно областей относительно теории категорий строится гораздо более абстрактно.
Объект, от которого начинается стрелка в морфизме, называется областью определения морфизма.
Где находится домен?
Как указывалось ранее, домен представляет собой набор всех возможных значений, которые служат входными данными для требуемой функции. Независимые переменные также возможны из-за того, что все значения лежат в домене.
Обычно домен можно найти в двух основных местах. Если рассматриваемая функция является дробью, то область определения обычно находят со знаменателем, делая его не равным нулю. Домен также можно найти в квадратном корне с положительной цифрой, лежащей под ним.
Как найти домен функции?
Область определения функции можно определить многими способами. Но прежде чем перейти к этому, важно отметить, что значения, принимаемые независимыми переменными, могут использоваться в соответствии с требованиями. Наиболее распространенные случаи включают отсутствие отрицательного числа под квадратным корнем и отсутствие нулевого знаменателя дроби.
В обычных случаях множество действительных чисел R является универсальным доменом для всех функций, за исключением тех случаев, когда функции имеют определенные типы ограничений. Они следующие:
- Если функция является нормальным линейным уравнением или квадратным уравнением, то множество действительных чисел R является областью определения таких функций.
- Если функция имеет дробную форму, то числа, у которых знаменатель равен нулю, исключаются из множества действительных чисел R, и это новое множество является областью определения.
- Если функции поставляются с заранее заданными интервалами, верхняя и нижняя границы самого интервала могут быть взяты в качестве входных данных, которые являются не чем иным, как доменом.
- Если есть значения, для которых указанная функция не может быть определена, то эти конкретные значения также ограничены областью определения набора действительных чисел R.
Каковы различные приложения домена?
Домен имеет различные приложения в области математики.
Помимо исчисления, домены одинаково полезны и в других отраслях. Например, домен определен в топологии. В топологии связное открытое множество является доменом. Он также присутствует в реальном анализе и комплексном анализе. В обоих случаях открытое связное подмножество, лежащее в векторном пространстве, вещественное или комплексное, является его областью. Если изучаются УЧП или уравнения в частных производных, то открытое связное подмножество, лежащее в евклидовом пространстве, или R n можно назвать доменом. Именно в этом месте могут быть определены или поставлены неизвестные функции задач.
Практическая задача
Найдите область определения функции-
x2x−1
⇒ Поскольку данная функция является дробью, знаменатель приравнивается к ненулевому.
Следовательно,
x−1≠0=>x≠1
Следовательно, множество всех действительных чисел R, кроме 1, является областью определения данной функции.
Контекст и приложения
Домены являются неотъемлемой частью программы исчисления по математике.
Это важная тема для школьных экзаменов, экзаменов на доску, вступительных экзаменов в колледж, CSIR, NEET, IITJEE, ISI, CMI и так далее.
Эта тема важна для профессиональных экзаменов как для студентов, так и для выпускников, особенно для
- Бакалавр наук по математике
- Магистр наук по математике
Домен и диапазон | Калькулятор Медик
Блок 1
День 1
День 2
День 3
День 4
День 5
День 6
День 7
День 8
День 9
День 10
День 11
День 12
День 13
День 14
День 15
Все модули
Цели обучения
Соедините домен функции с ее возможными входами, а диапазон функции с ее возможными выходами
Определение области определения и диапазона функции графически, аналитически и численно
Краткий план урока
Первый опыт
Хотя учащиеся уже много лет используют слова домен и диапазон, этот урок посвящен определению домена и диапазона в нескольких представлениях.
Учащихся просят соединить графические представления с числовыми представлениями и алгебраическими представлениями, замечая, где данное значение x не имеет связанной с ним упорядоченной пары на графике, выдает ОШИБКУ при оценке функции на калькуляторе или вызывает неопределенность функции. .
При наблюдении за группами задавайте вопросы, чтобы учащиеся объяснили, почему область применения данной функции ограничена определенными значениями. Студенты должны быть в состоянии сообщить о вертикальных асимптотах в случае рациональных функций и о том, как квадратный корень из отрицательного числа дает мнимые значения, которые не видны на графике.
Формализация позже
Этот урок посвящен функциям квадратного корня (особенно тем, которые представляют полуокружности) и рациональным функциям. Студентам часто бывает трудно найти область аналитически, потому что они склонны полагаться на запоминание и приемы вместо того, чтобы связывать функции со своими графиками.
2-492). Пусть учащиеся увидят разницу, глядя на графики, а также решая алгебраически. Это можно построить следующим образом:
Могу ли я подключить 6? Почему или почему нет? Можно ли подключить 7? Почему или почему нет? Могу ли я подключить 8? А 7.1?
Почему одни значения работают, а другие нет?
Где переломный момент? (т.е. когда мы начинаем получать «ошибки»?)
Что вы знаете о квадратных корнях? Что это говорит нам о выражении под квадратным корнем? 92-49 положительный? При каких значениях x это произойдет?
Предложите учащимся проверить конкретные значения, прежде чем замечать закономерности и делать обобщения. Есть два распространенных заблуждения о домене. Во-первых, это ложная идея о том, что квадратный корень из 0 не определен. Спросите учащихся, могут ли они придумать число, которое при умножении само на себя дает 0. Они должны сделать вывод, что 0 удовлетворяет этому условию!
Второе заблуждение чаще встречается в отношении рациональных функций, а именно: если числа, меньшие или равные 7, не допускаются, то допускаются числа, большие или равные 8.